Updates to and Performance of the cBathy Algorithm for Estimating Nearshore Bathymetry from Remote Sensing Imagery
Abstract
:1. Introduction
2. cBathy Versions—Version 1.0
2.1. Version 1.1 Update
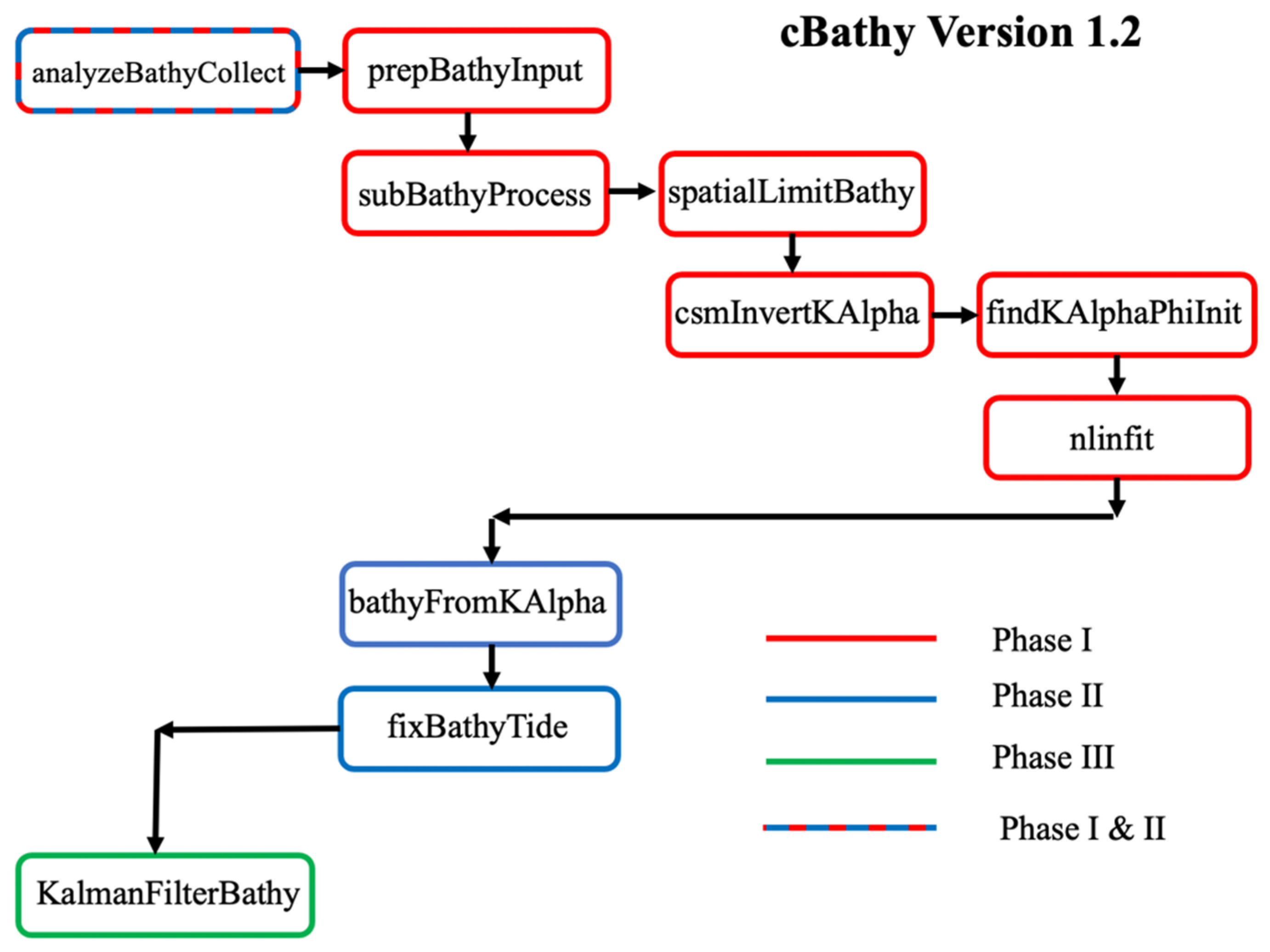
2.2. Version 1.2 Update
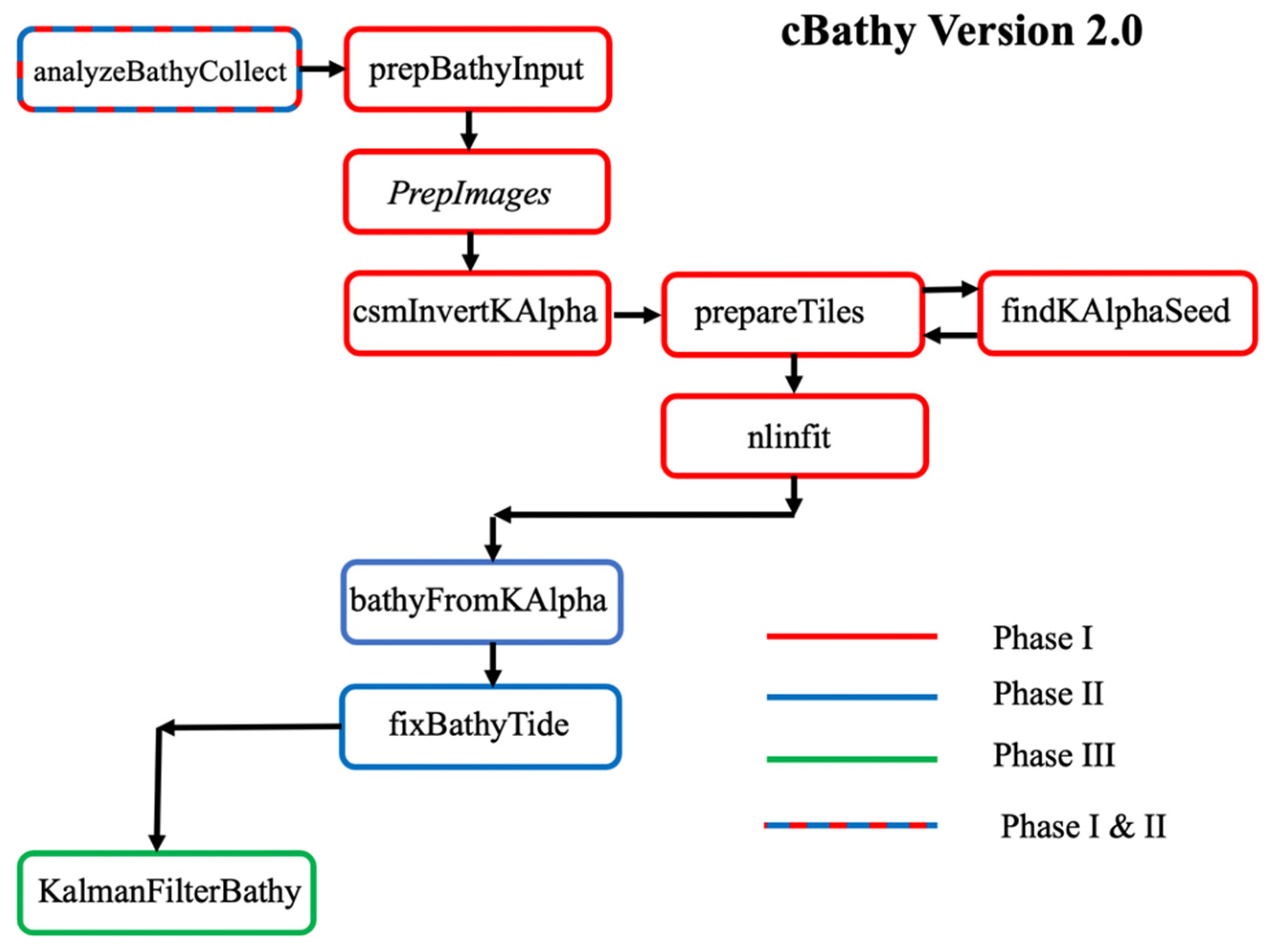
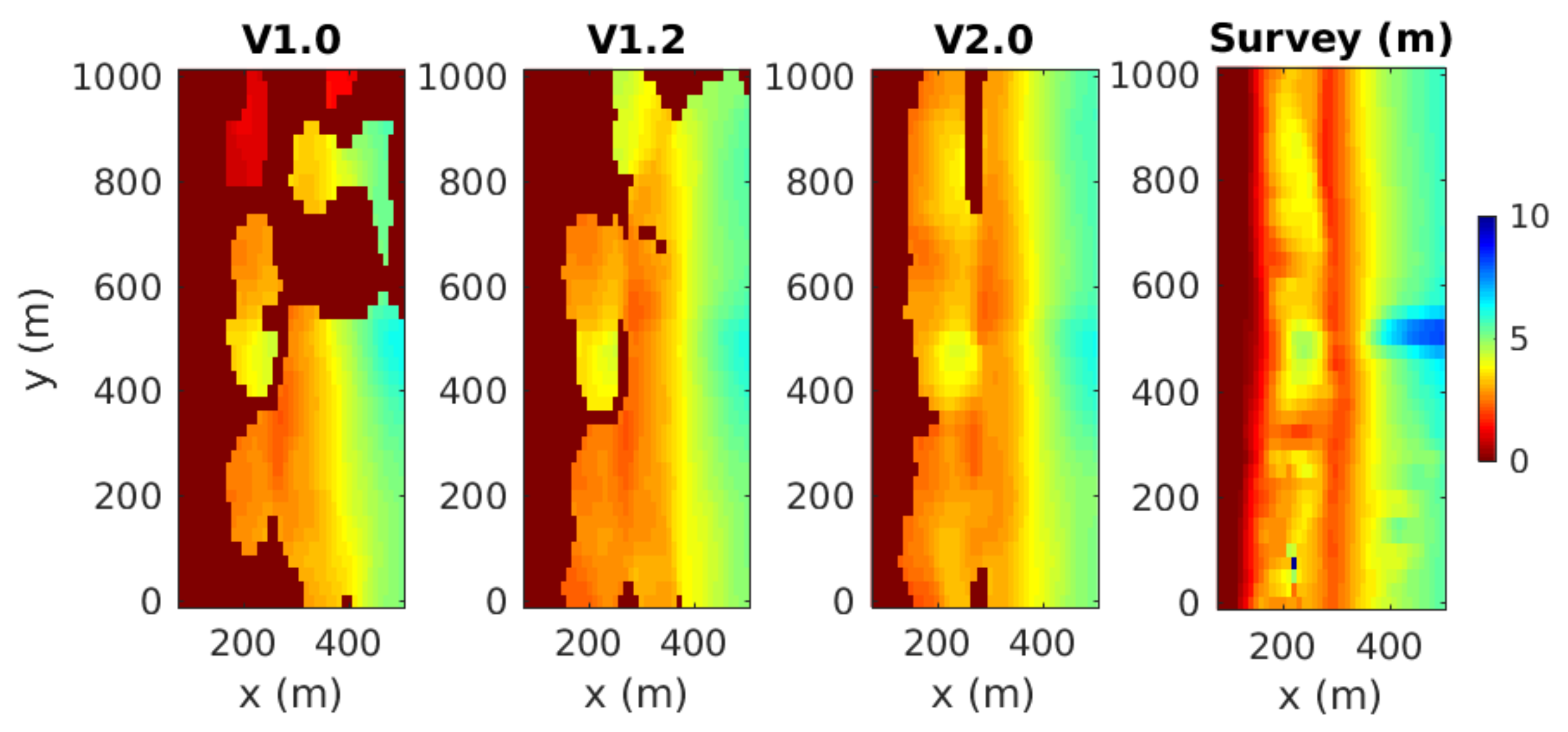
2.3. Version 2.0
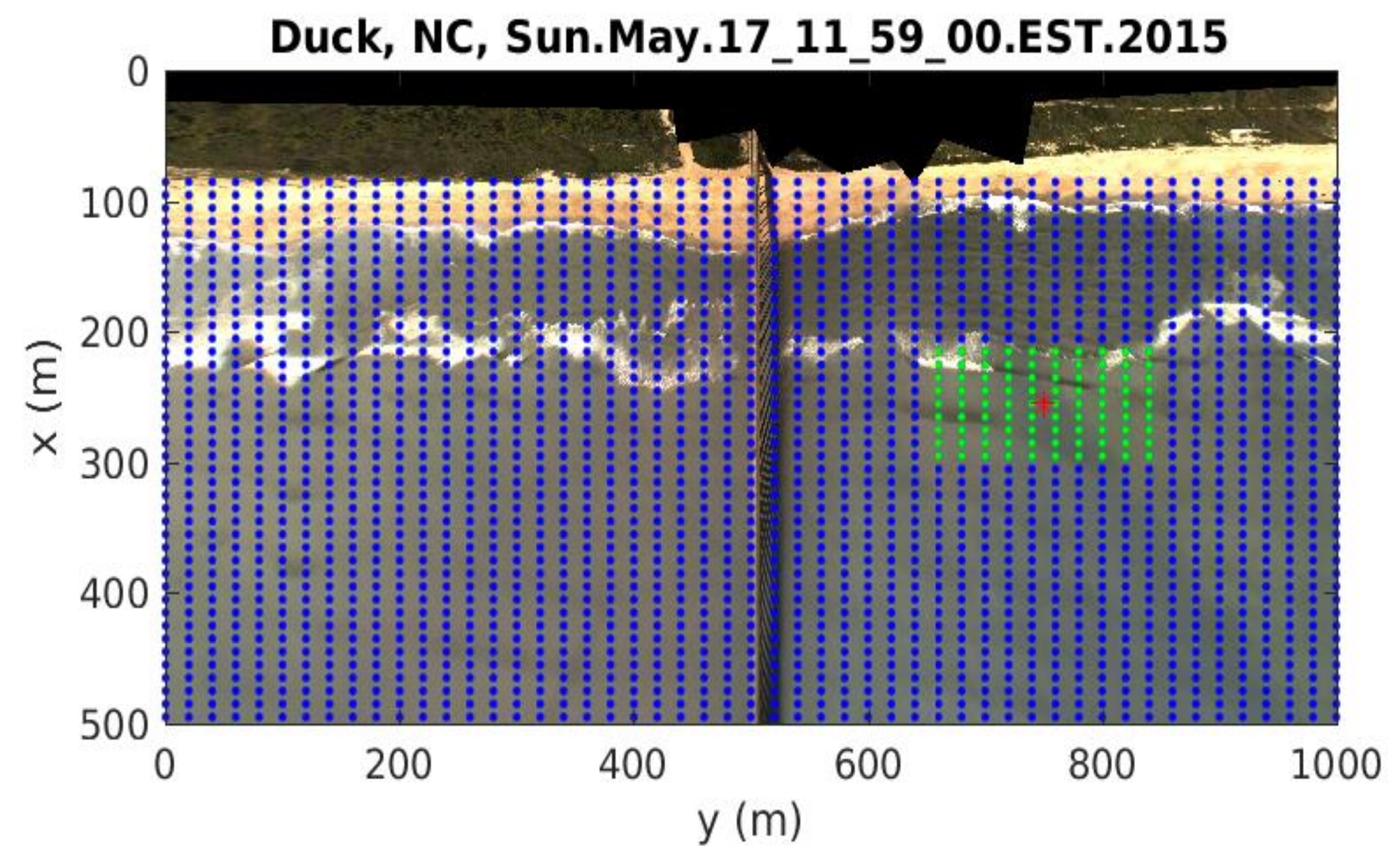
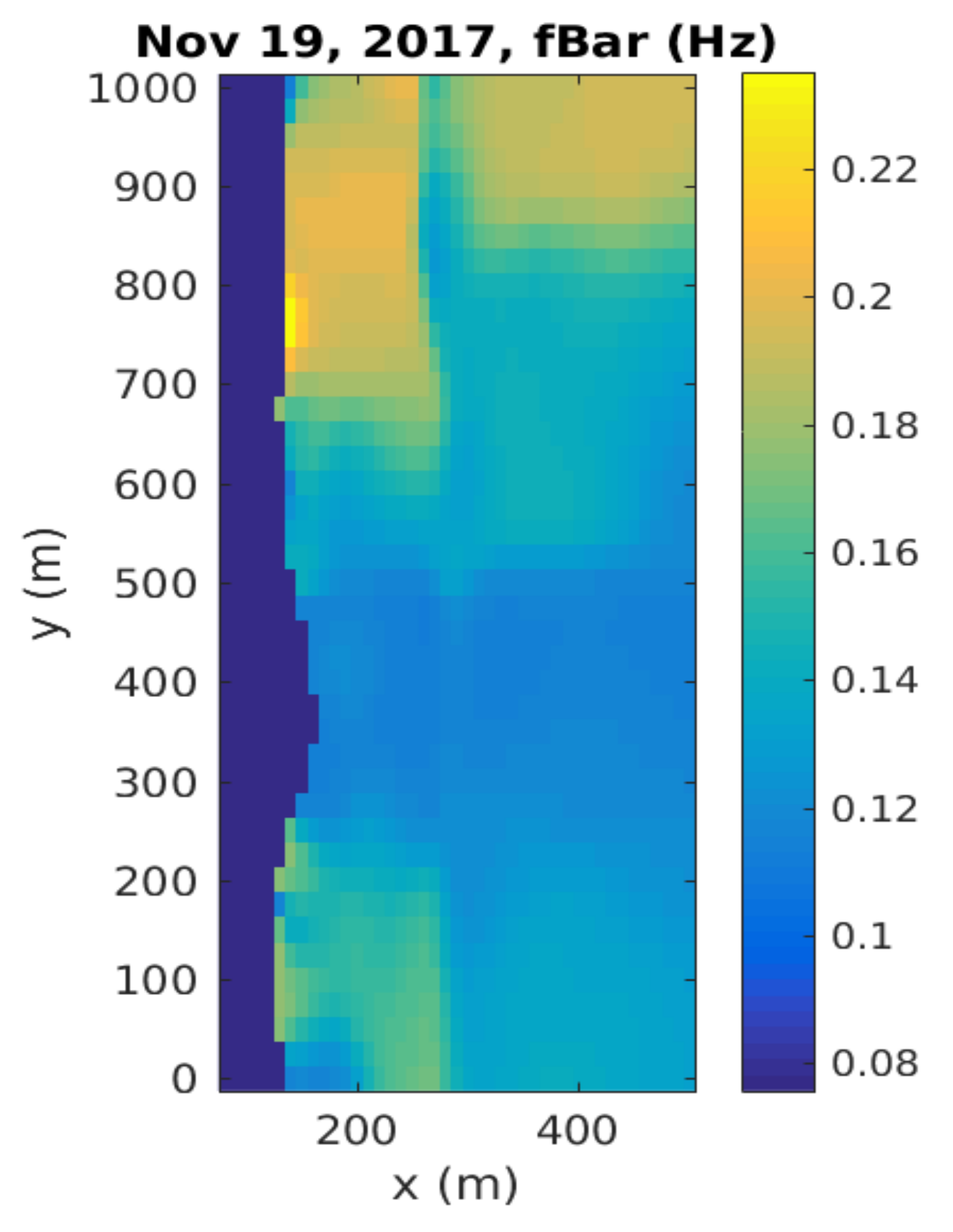
2.3.1. Automatic Tile Sizes
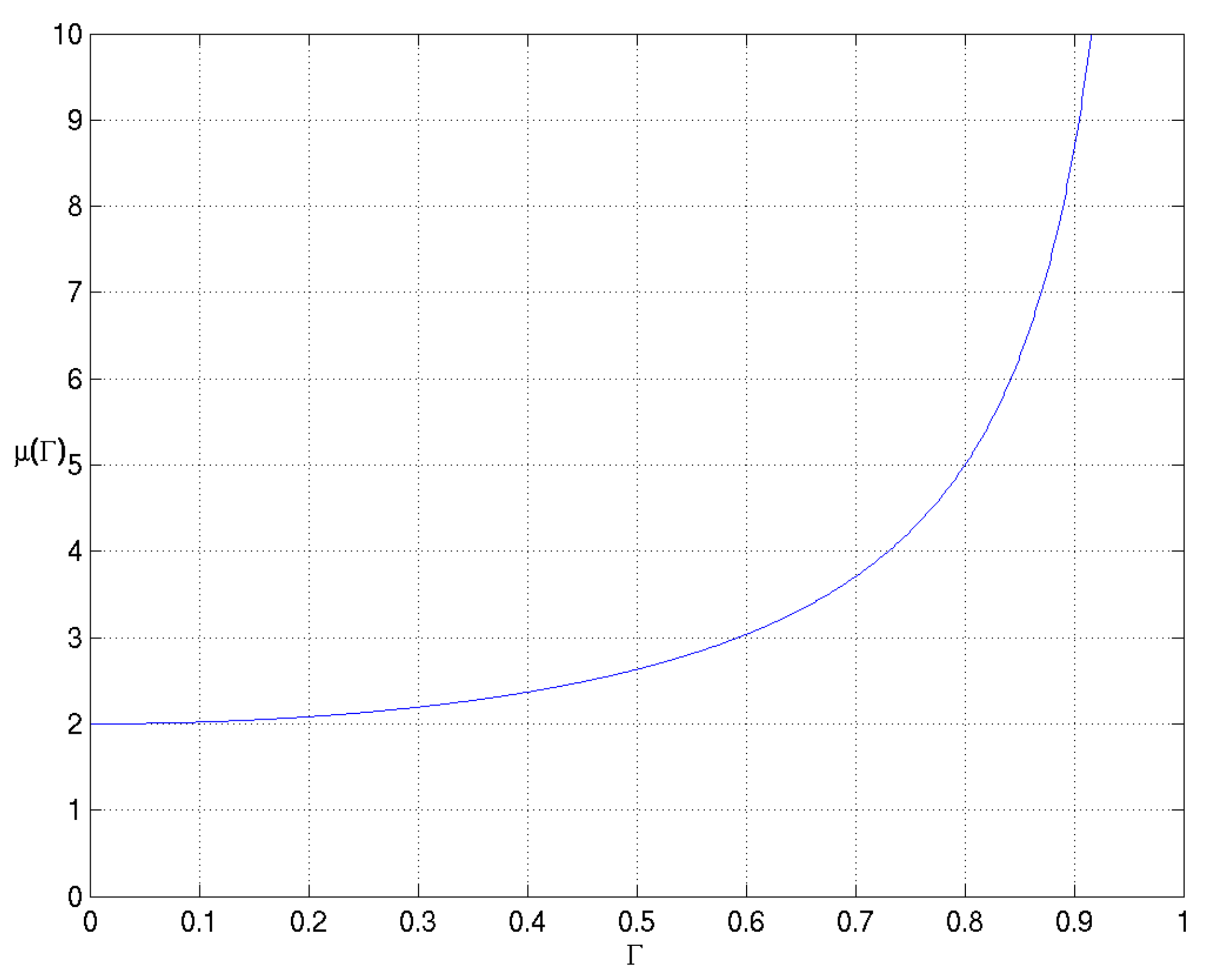
2.3.2. Reduction in the Number of Search Variables
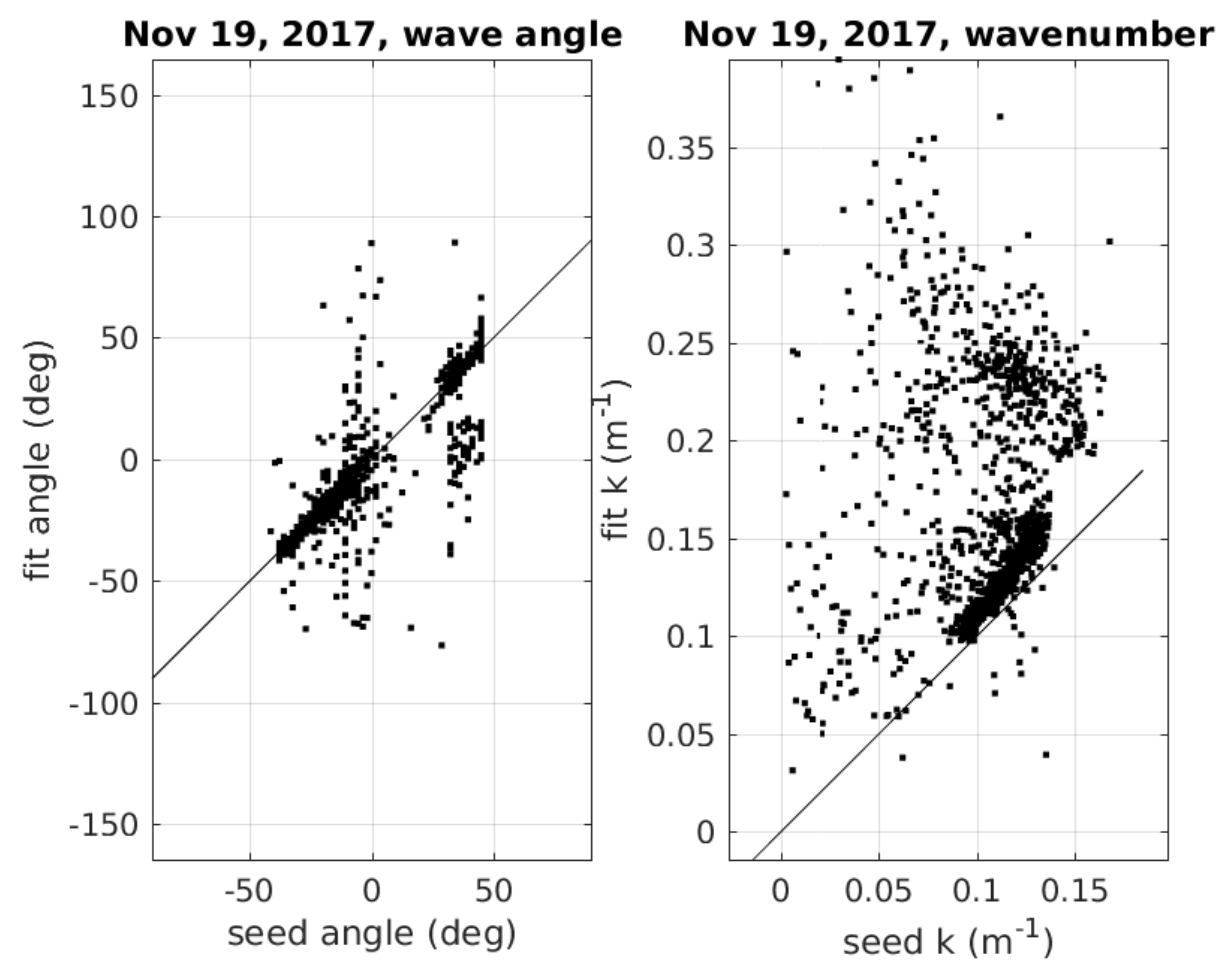
2.3.3. Improved Seed Algorithm
2.4. Algorithm Organization Changes
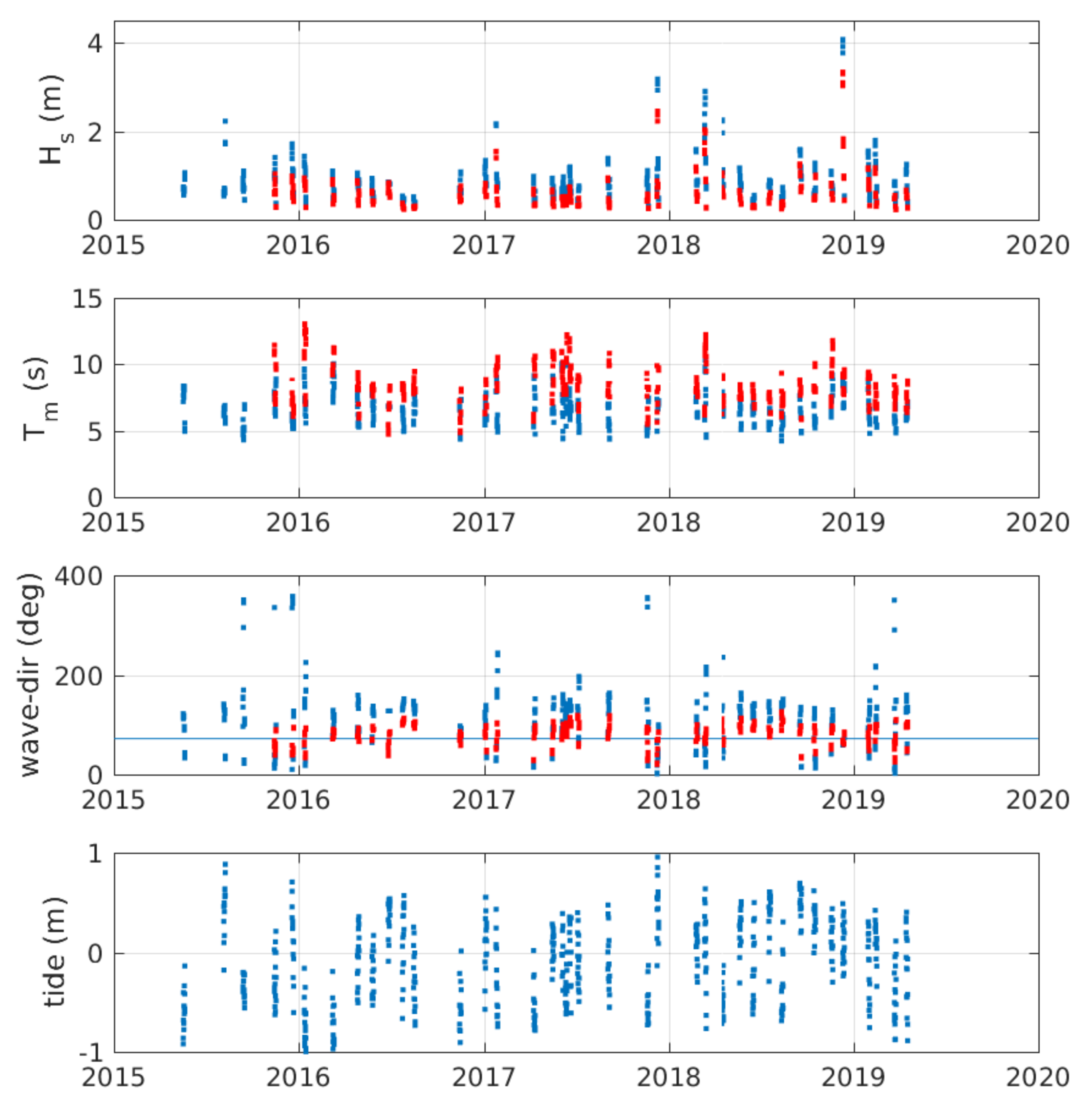
3. Bathymetry Test Bed Datasets
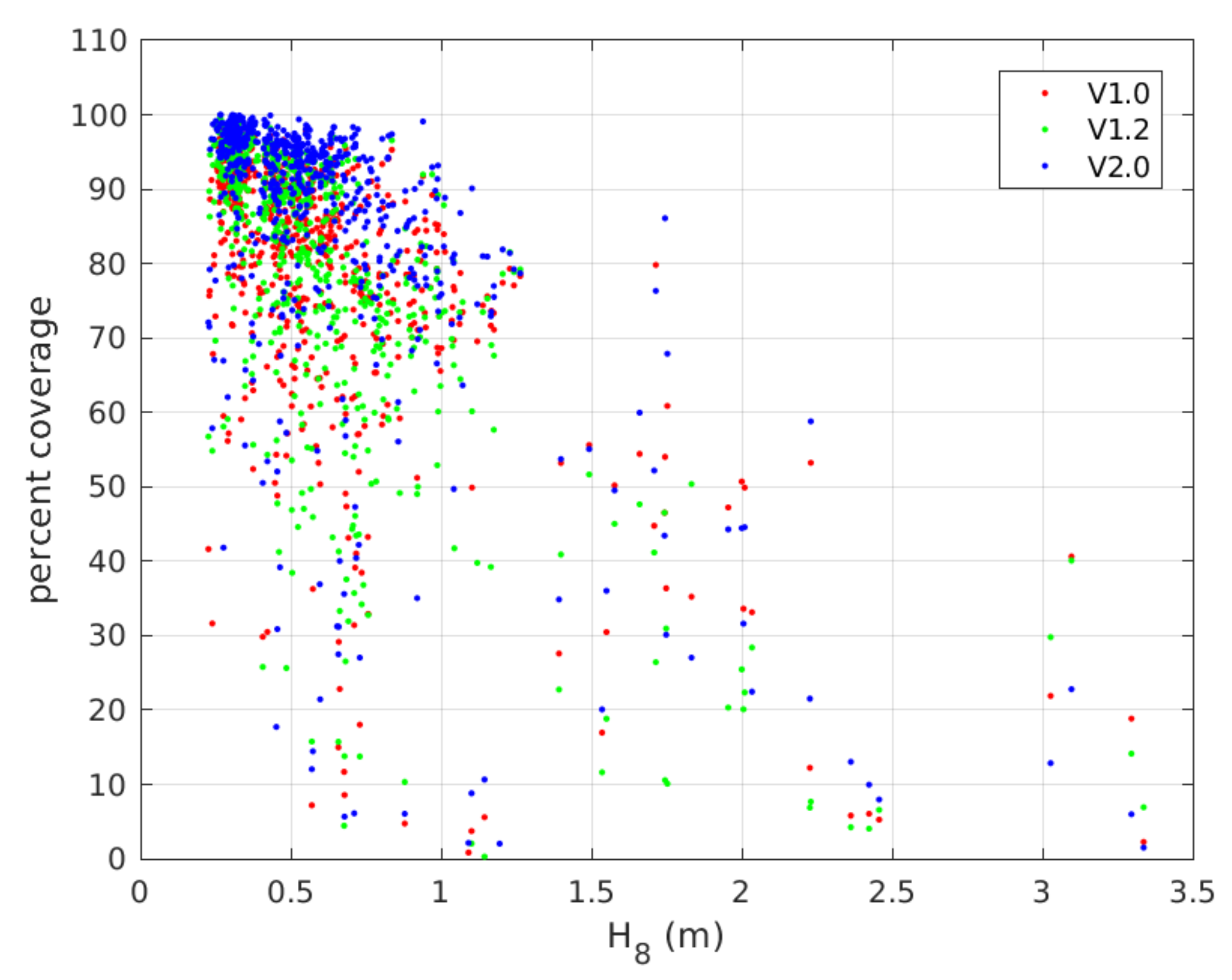
4. cBathy Phase 2 Version Performance Statistics
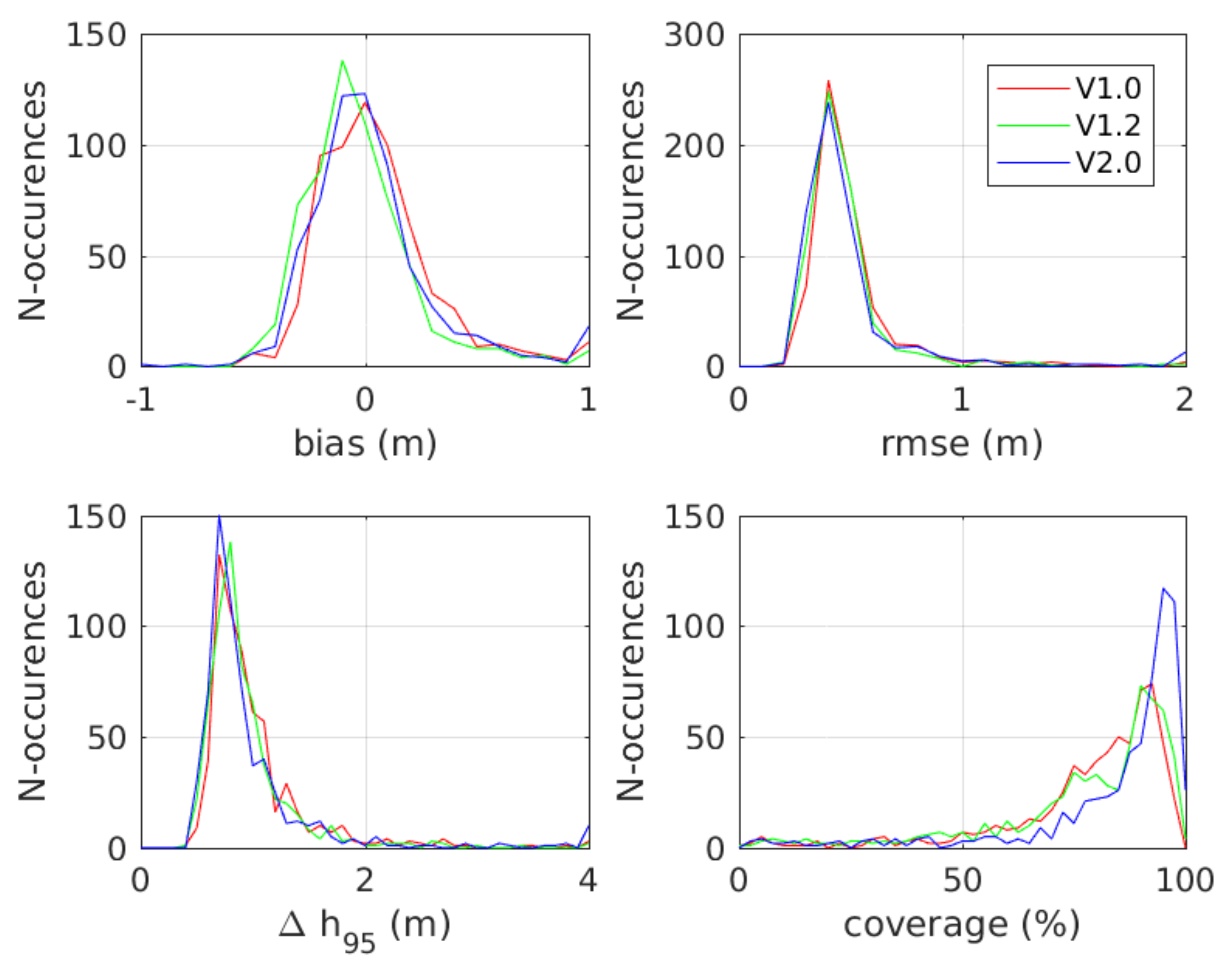
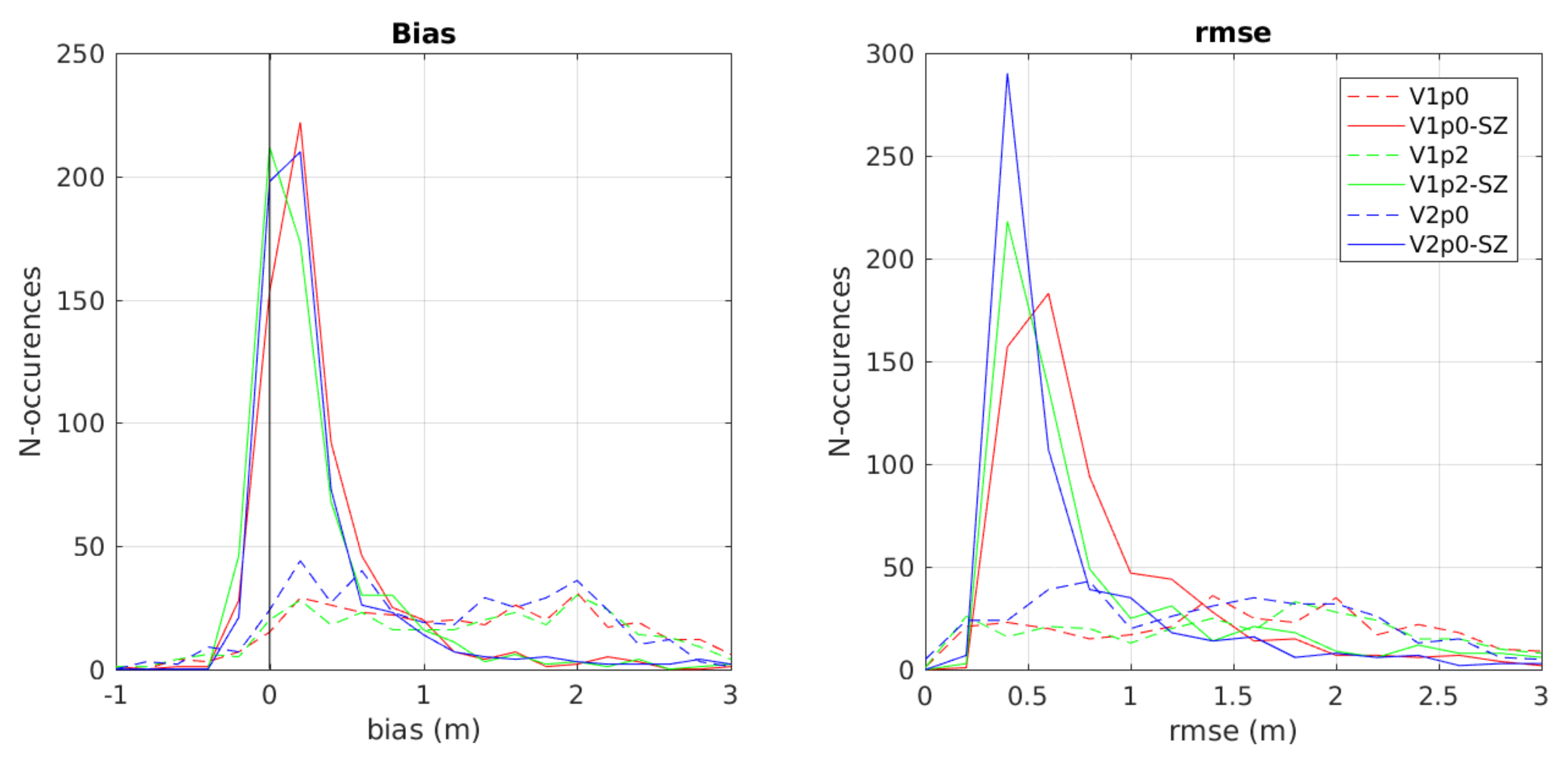
4.1. Bulk Analysis of cBathy Version Statistics
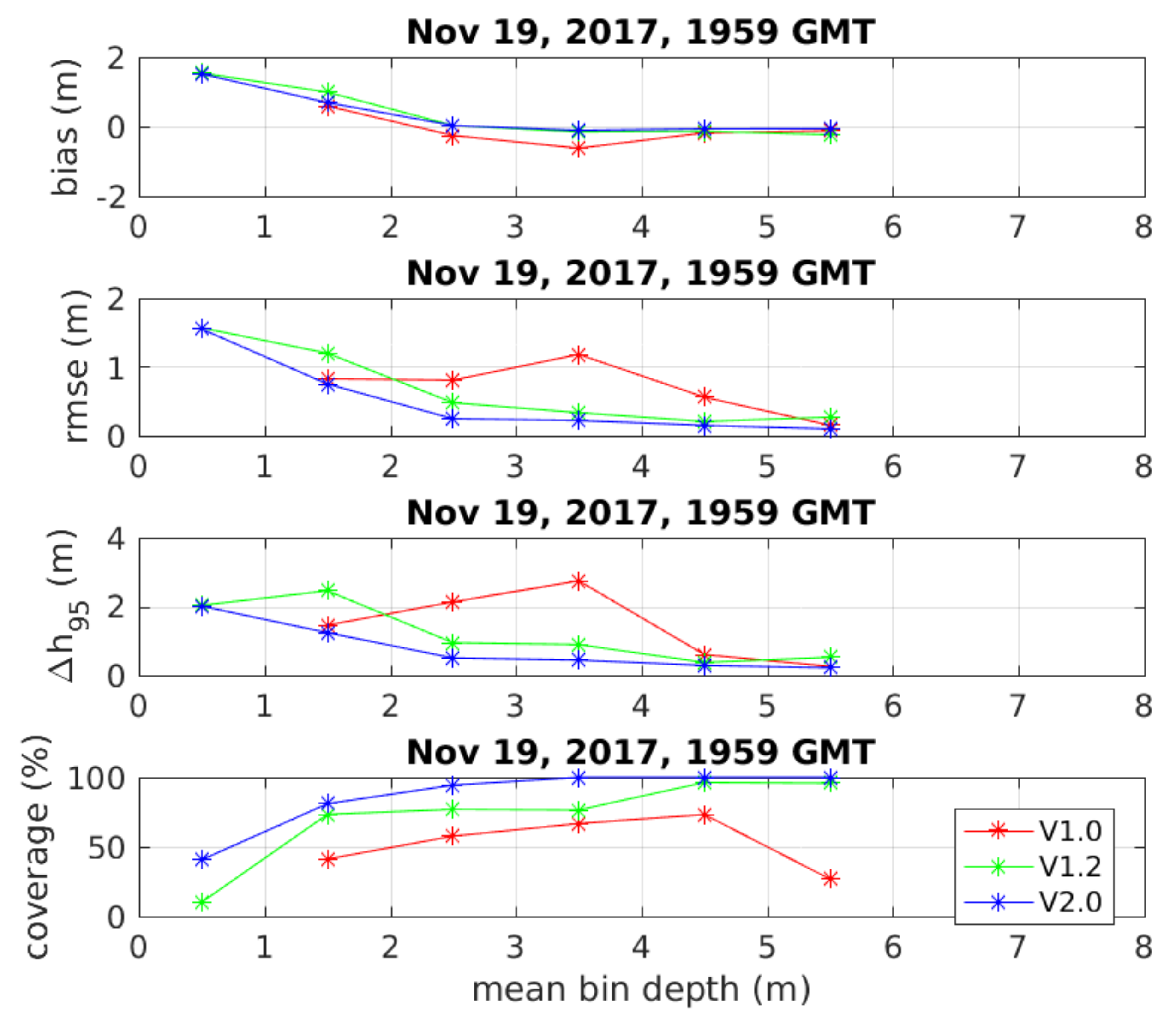
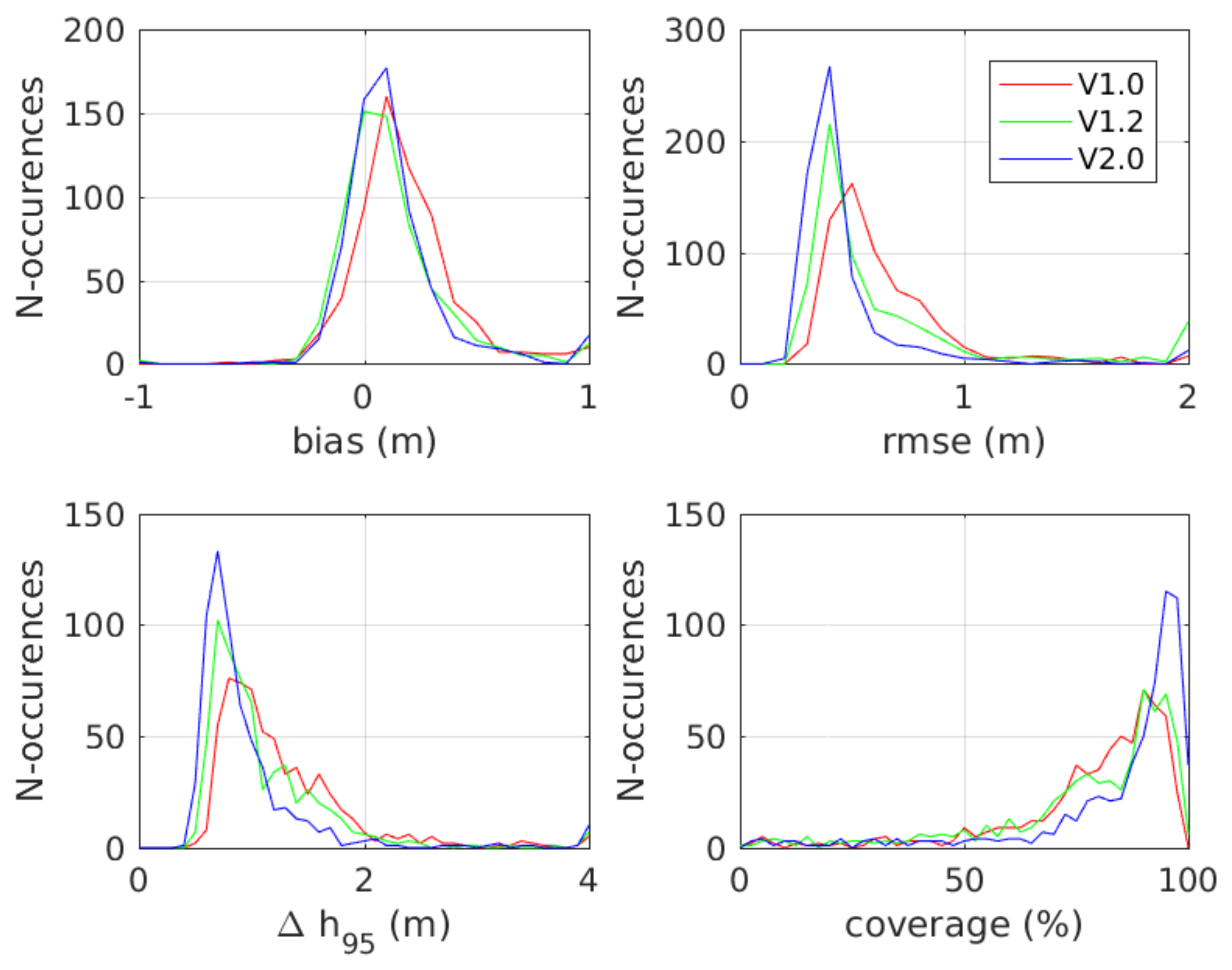
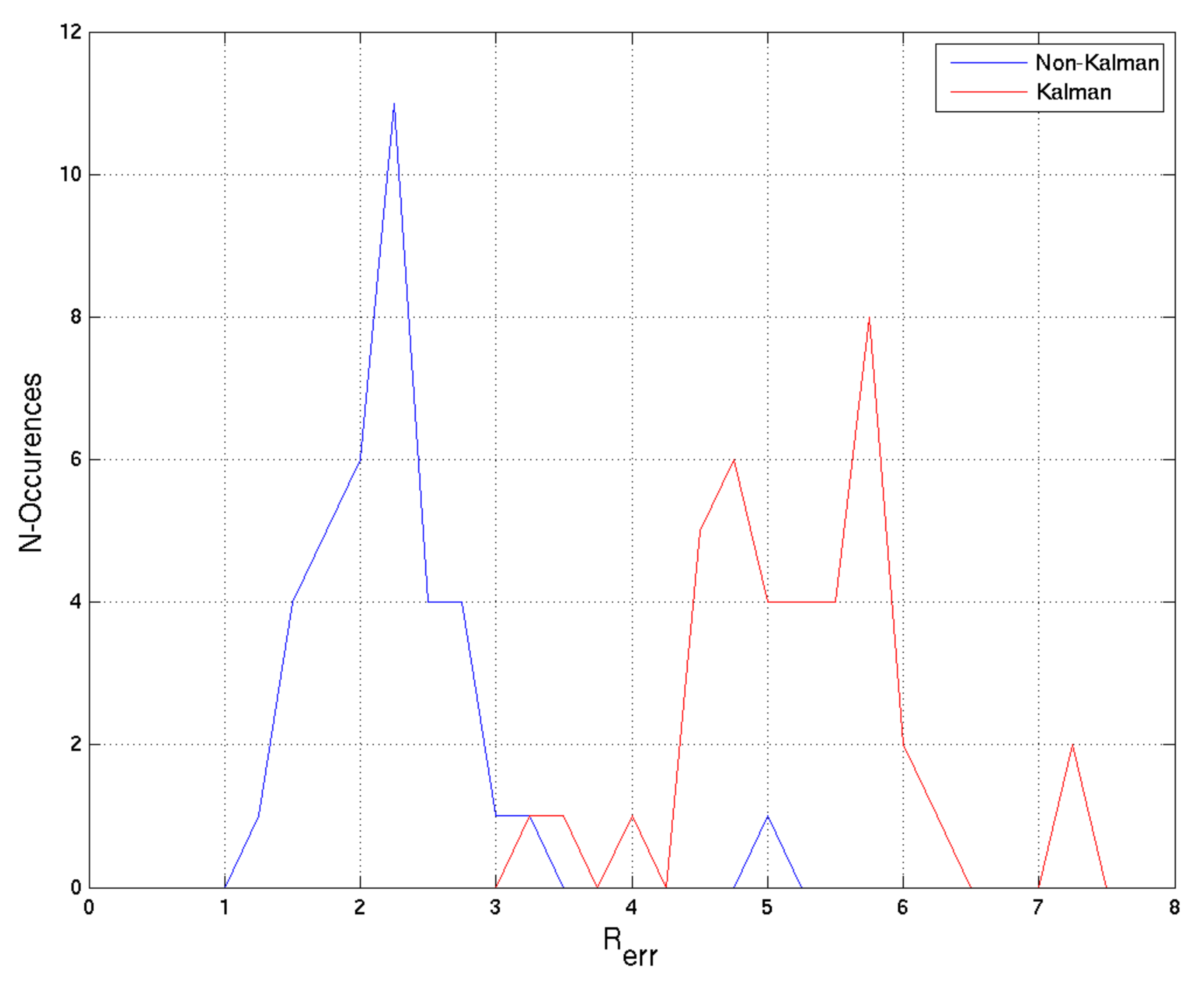
4.2. Kalman-Filtered Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Holman, R.A.; Plant, N.G.; Holland, K.T. cBathy: A robust algorithm for estimating nearshore bathymetry. J. Geophys. Res. 2013, 118, 1–15. [Google Scholar] [CrossRef]
- Davidson, M.A.; Van Koningsveld, M.; de Kruif, A.; Rawson, J.; Holman, R.; Lamberti, A.; Medina, R.; Kroon, A.; Aarninkhof, S.G.J. The CoastView project: Developing video-derived Coastal State Indicators in support of coastal zone management. Coast. Eng. 2007, 54, 463–475. [Google Scholar] [CrossRef]
- Kroon, A.; Davidson, M.A.; Aarninkhof, S.G.J.; Archetti, R.; Armaroli, C.; Gonzales, M.; Medri, S.; Osorio, A.; Aagaard, T.; Holman, R.; et al. Application of remote sensing video systems to coastline management problems. Coast. Eng. 2007, 54, 493–505. [Google Scholar] [CrossRef]
- Radermacher, M.A.; De Schipper, M.A.; Reniers, A. Sensitivity of rip current forecasts to errors in remotely-sensed bathymetry. Coast. Eng. 2018, 135, 66–76. [Google Scholar] [CrossRef] [Green Version]
- Sembiring, L.; van Dongeren, A.; WInter, G.; Ormondt, V.; Briere, C.; Roelvink, D. Nearshore bathymetry from video the application to rip current predictions for the Dutch Coast. J. Coast. Res. 2014, 70, 354–359. [Google Scholar] [CrossRef]
- Benveniste, J.; Cazenave, A.; Vignudelli, S.; Fenoglio-Marc, L.; Shah, R.; Almar, R.; Andersen, O.; Birol, F.; Bonnefond, P.; Bouffard, J.; et al. Requirements of a coastal hazard observing system. Front. Mar. Sci. 2019, 6, 348. [Google Scholar] [CrossRef] [Green Version]
- Melet, A.; Teatini, P.; Le Cozannet, G.; Jamet, C. Earth observations for monitoring marine coastal hazards and their drivers. Surv. Geophys. 2020, 41, 1489–1534. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. On the use of Sentinel-2 satellites and lidar surveys for the change detection of shallow bathymetry: The case study of North Carolina inlets. Coast. Eng. 2021, 169, 103936. [Google Scholar] [CrossRef]
- Johnson, S.Y.; Cochrane, G.R.; Golden, N.A.; Dartnell, P.; Hartwell, S.; Chochran, S. The California Seafloor and Coastal Mapping Program—Providing science and geospatial data for California’s State Waters. Ocean Coast. Manag. 2017, 140, 88–104. [Google Scholar] [CrossRef] [Green Version]
- Lyzenga, D.R. Passive remote-sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Poupardin, A.; Heinrich, P.; Hebert, H.; Schindele, F.; Jamelot, A.; Reymond, D.; Sugioka, H. On the role of frequency dispersion on the transw-Pacific tsunamis: Study of the 2010 and 2015 Chilean tsunamis. In Proceedings of the Oceans 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016. [Google Scholar]
- Poursanidis, D.; Traganos, D.; Chrysoulakis, N.; Reinartz, P. Cubesats allow high spatiotemporal estimates of satellite-derived bathymetry. Remote Sens. 2019, 11, 1299. [Google Scholar] [CrossRef] [Green Version]
- Caballero, I.; Stumpf, R.P.; Meredith, A. Preliminary Assessment of Turbidity and Chlorophyll Impact on Bathymetry Derived from Sentinel-2A and Sentinel-3A Satellites in South Florida. Remote Sens. 2019, 11, 645. [Google Scholar] [CrossRef] [Green Version]
- Pike, S.; Traganos, D.; Poursanidis, D.; Williams, J.; Medcalf, K.; Reinartz, P.; Chrysoulakis, N. Leveraging Commercial High-Resolution Multispectral Satellite and Multibeam Sonar Data to Estimate Bathymetry: The Case Study of the Caribbean Sea. Remote Sens. 2019, 11, 1830. [Google Scholar] [CrossRef] [Green Version]
- Bergsma, E.W.; Almar, R.; Maisongrande, P. Radon-Augmented Sentinel-2 Satellite Imagery to Derive Wave-Patterns and Regional Bathymetry. Remote Sens. 2019, 11, 1918. [Google Scholar] [CrossRef] [Green Version]
- Bergsma, E.W.; Almar, R.; Rolland, A.; Binet, R.; Brodie, K.L.; Bak, A.S. Coastal morpholgy from space: A showcase of monitoring the topography-bathymetry continuum. Remote Sens. Environ. 2021, 261, 112469. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Almar, R.; Bergsma, E.W. Satellite optical imagery in Coastal Engineering. Coast. Eng. 2021, 167, 103919. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Almar, R. Coastal coverage of ESA’ Sentinel 2 mission. Adv. Space Res. 2020, 65, 2636–2644. [Google Scholar] [CrossRef]
- Brodie, K.L.; Palmsten, M.L.; Hesser, T.J.; Dickhudt, P.J.; Raubenheimer, B.; Ladner, H.; Elgar, S. Evaluation of video-based linear depth inversion performance and applications using altimeters and hydrographic surveys in a wide range of environmental conditions. Coast. Eng. 2018, 136, 147–160. [Google Scholar] [CrossRef] [Green Version]
- Gawehn, M.; van Dongeren, A.; de Vries, S.; Swinkels, C.; Hoekstra, R.; Aarninkhof, S.G.J.; Friedman, J.I. The application of a radar-based depth inversion method to monitor near-shore nourishments on an open sandy coast and an ebb-tidal delta. Coast. Eng. 2020, 159, 103716. [Google Scholar] [CrossRef]
- Bouvier, C.; Balouin, Y.; Castelle, B. Video monitoring of sandbar-shoreline response to an offshore submerged structure at a microtidal beach. Geomorphology 2017, 295, 297–305. [Google Scholar] [CrossRef]
- Lippmann, T.C.; Holman, R.A. Quantification of sand bar morphology: A video technique based on wave dissipation. J. Geophys. Res. 1989, 94, 995–1011. [Google Scholar] [CrossRef]
- van Enckevort, I.M.J.; Ruessink, B.G. Video observations of nearshore bar behaviour. Part 1: Alongshore uniform variability. Cont. Shelf Res. 2003, 23, 501–512. [Google Scholar] [CrossRef]
- Van Enckevort, I.M.J.; Ruessink, B.G. Video observations of nearshore bar behaviour. Part 2: Alongshore uniform variability. Cont. Shelf Res. 2003, 23, 513–532. [Google Scholar] [CrossRef]
- Plant, N.G.; Holman, R.A. Intertidal beach profile estimation using video images. Mar. Geol. 1997, 140, 1–24. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A. Estimation of wave phase speed and nearshore bathymetry from video imagery. J. Geophys. Res. 2000, 105, 22015–22033. [Google Scholar] [CrossRef]
- Piotrowski, C.C.; Dugan, J.P. Accuracy of bathymetry and current retrievals from airborne optical time-series imaging of shoaling waves. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2602–2612. [Google Scholar] [CrossRef]
- Dugan, J.P.; Piotrowski, C.C.; Williams, J.Z. Water depth and surface current retrievals from airborne optical measurements of surface gravity wave dispersion. J. Geophys. Res. 2001, 106, 16903–16915. [Google Scholar] [CrossRef] [Green Version]
- Trizna, D.B. Errors in bathymetric retrievals using linear dispersion in 3-D FFT analysis of marine radar ocean wave imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2465–2469. [Google Scholar] [CrossRef]
- Holman, R.A.; Brodie, K.L.; Spore, N.J. Surf zone characterization using a small quadcopter: Technical issues and procedures. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2017–2027. [Google Scholar] [CrossRef]
- Brodie, K.L.; Bruder, B.L.; Slocum, R.K.; Spore, N.J. Simultaneous Mapping of Coastal Topography and Bathymetry From a Lightweight Multicamera UAS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6844–6864. [Google Scholar] [CrossRef]
- Hashimoto, K.; Shimozono, T.; Matsuba, Y.; Okabe, T. Unmanned Aerial Vehicle depth inversion to monitor river-mouth bar dynamics. Remote Sens. 2021, 13, 412. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Plant, N.; Cohen, A.; Roelvink, D.; Haller, M.; Catalan, P. Beach Wizard: Nearshore bathymetry estimation through assimilation of model computations and remote observations. Coast. Eng. 2008, 55, 1016–1027. [Google Scholar] [CrossRef]
- Aarninkhof, S.G.J.; Turner, I.L.; Dronkers, T.D.T.; Caljouw, M.; Nipius, L. A video technique for mapping intertidal beach bathymetry. Coast. Eng. 2003, 49, 275–289. [Google Scholar] [CrossRef]
- Soto, F.; Catalan, P. Bathymetry inversion in the surf zone via assimilation of remotely-sensed wave breaking energy dissipation. Coast. Eng. Proc. 2020, 26. [Google Scholar] [CrossRef]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave celerity from video imaging. In Proceedings of the 31st Conference on Coastal Engineering, Hamburg, Germany, 31 August–5 September 2008; pp. 661–673. [Google Scholar]
- Plant, N.G.; Holland, K.T.; Haller, M. Ocean wavenumber estimation from wave-resolving time series imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2644–2658. [Google Scholar] [CrossRef]
- Simarro, G.; Calvete, D.; Luque, P.; Orfila, A.; Ribas, F. UBathy: A new approach for bathymetry inversion from video imagery. Remote Sens. 2019, 11, 2722. [Google Scholar] [CrossRef] [Green Version]
- Bergsma, E.W.; Almar, R. Video-based depth inversion techniques, a method comparison with synthetic cases. Coast. Eng. 2018, 138, 199–209. [Google Scholar] [CrossRef]
- Rutten, J.; de Jong, D.; Ruessink, B.G. Accuracy of nearshore bathymetry inverted from X-band radar and optical video data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1106–1116. [Google Scholar] [CrossRef]
- Honegger, D.; Haller, M.; Holman, R. High-resolution bathymetry estimates via X-band marine radar: 1. beaches. Coast. Eng. 2019, 149, 39–48. [Google Scholar] [CrossRef]
- Bak, A.S.; Brodie, K.L.; Hesser, T.J.; Smith, J.M. Applying dynamically updated nearshore bathymetry estimates to operational nearshore wave modeling. Coast. Eng. 2019, 145, 53–64. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. cBathy Bathymetry Estimation in the Mixed Wave-Current Domain of a Tidal Estuary. J. Coast. Res. 2013, 65, 1391–1396. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A.; Lippmann, T.C.; Stanley, J.; Plant, N. Practical use of video imagery in nearshore oceanographic field studies. IEEE J. Ocean Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Holman, R.A.; Stanley, J. The history and technical capabilities of Argus. Coast. Eng. 2007, 54, 477–491. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Conley, D.C.; Davidson, M.; O’Hare, T.J. Video-based nearshore bathymetry estimation in macro-tidal environments. Mar. Geol. 2016, 374, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Walker, R.E. Marine Light Field Statistics; John Wiley and Sons, Inc.: New York, NY, USA, 1994; p. 675. [Google Scholar]



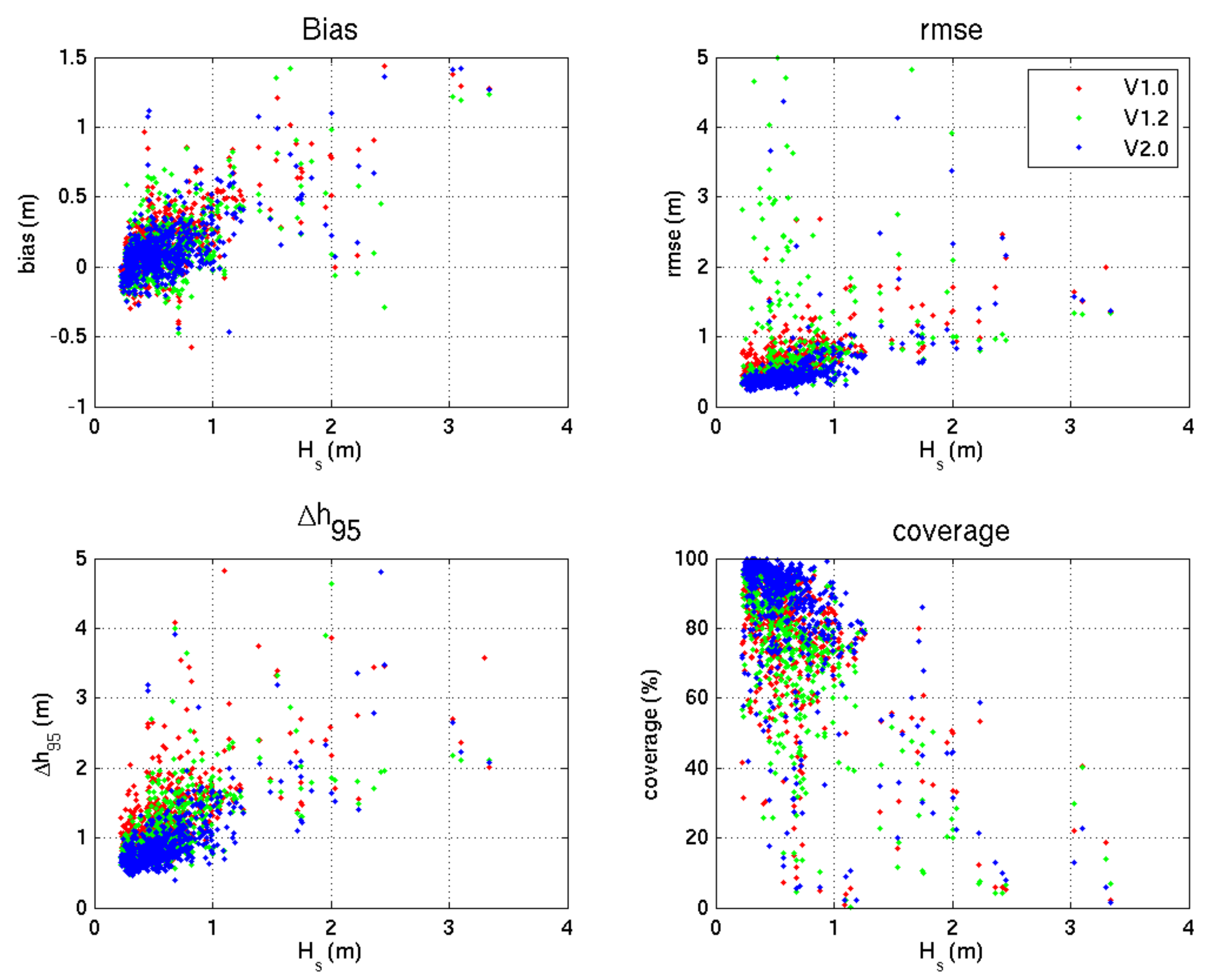
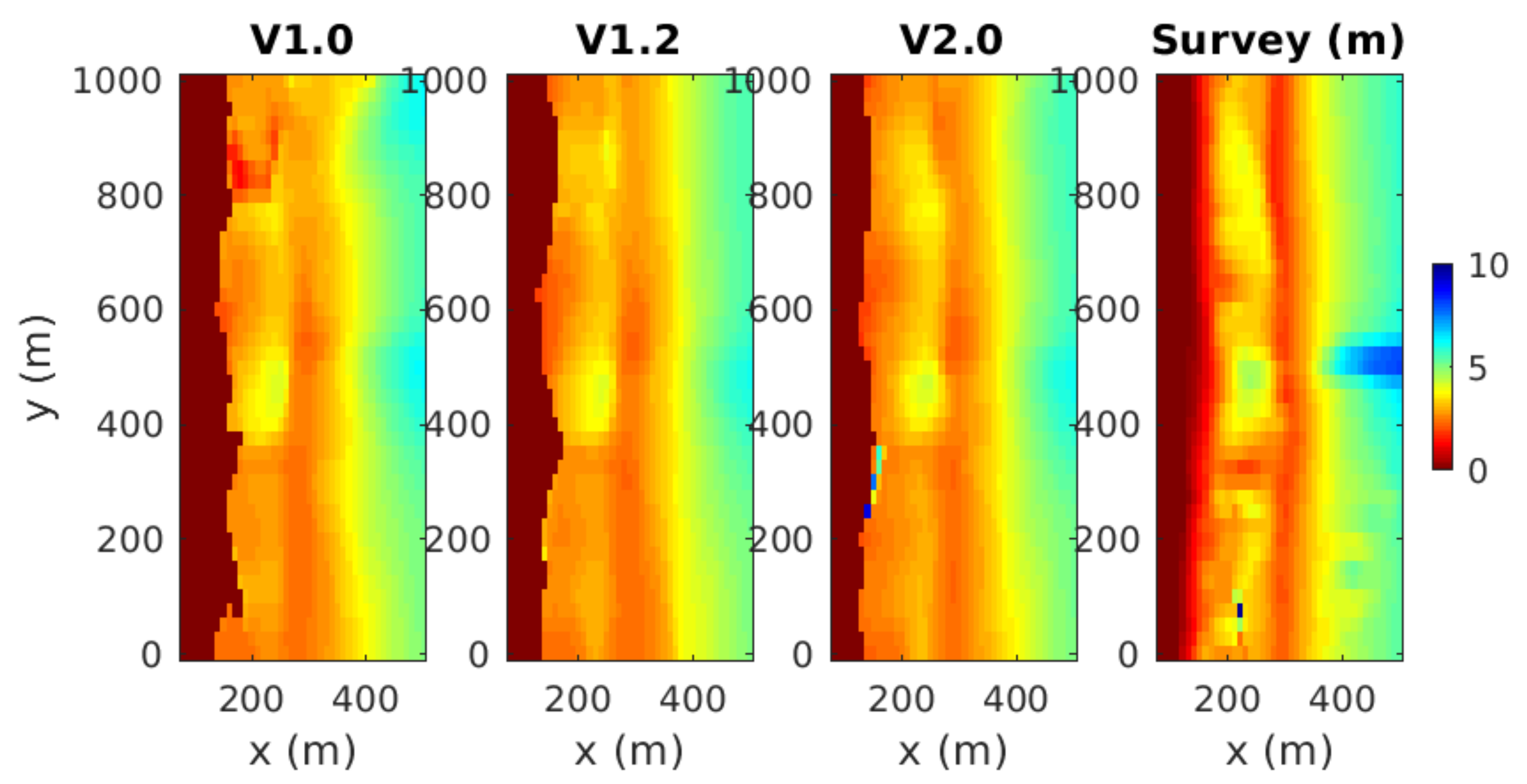
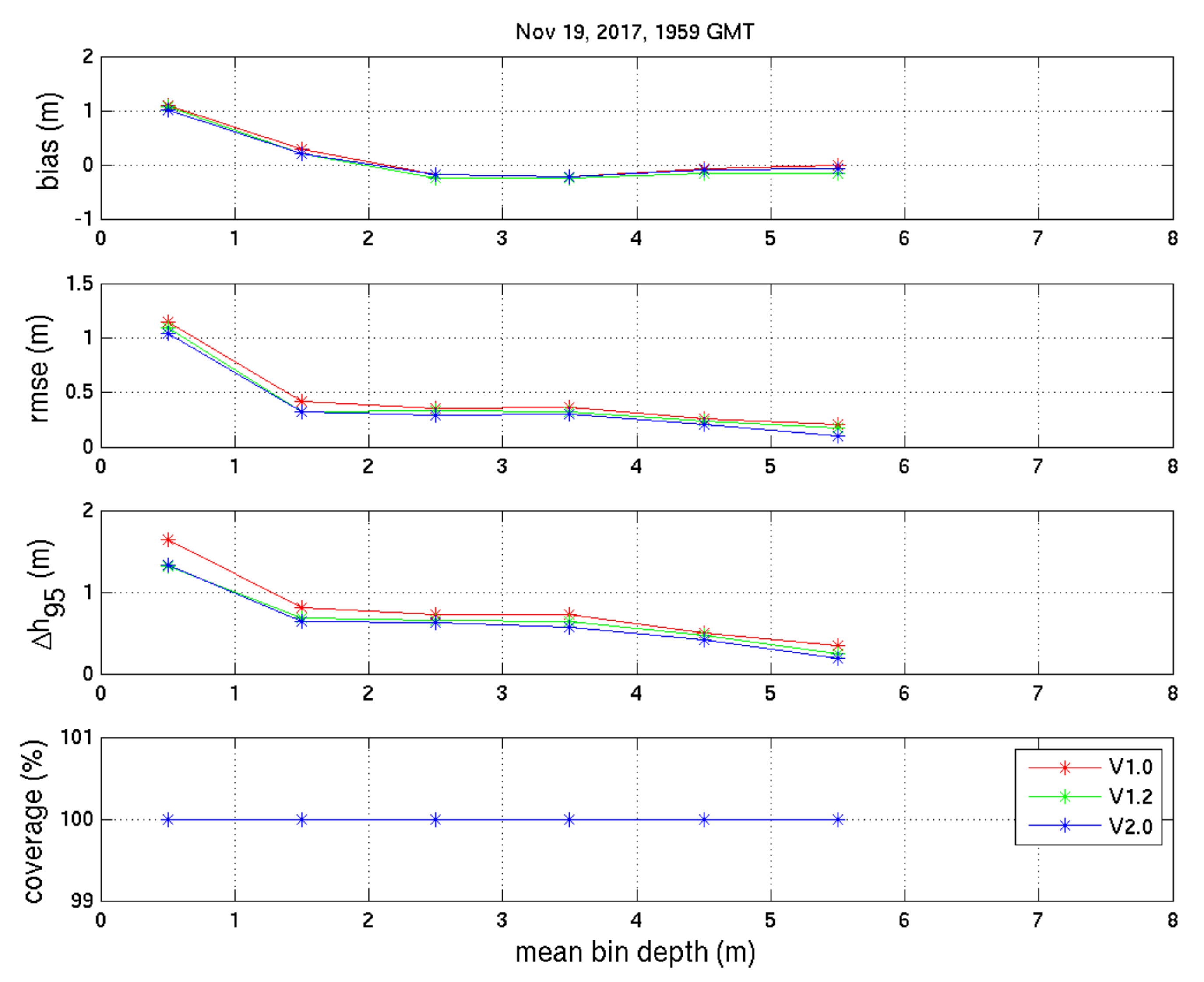
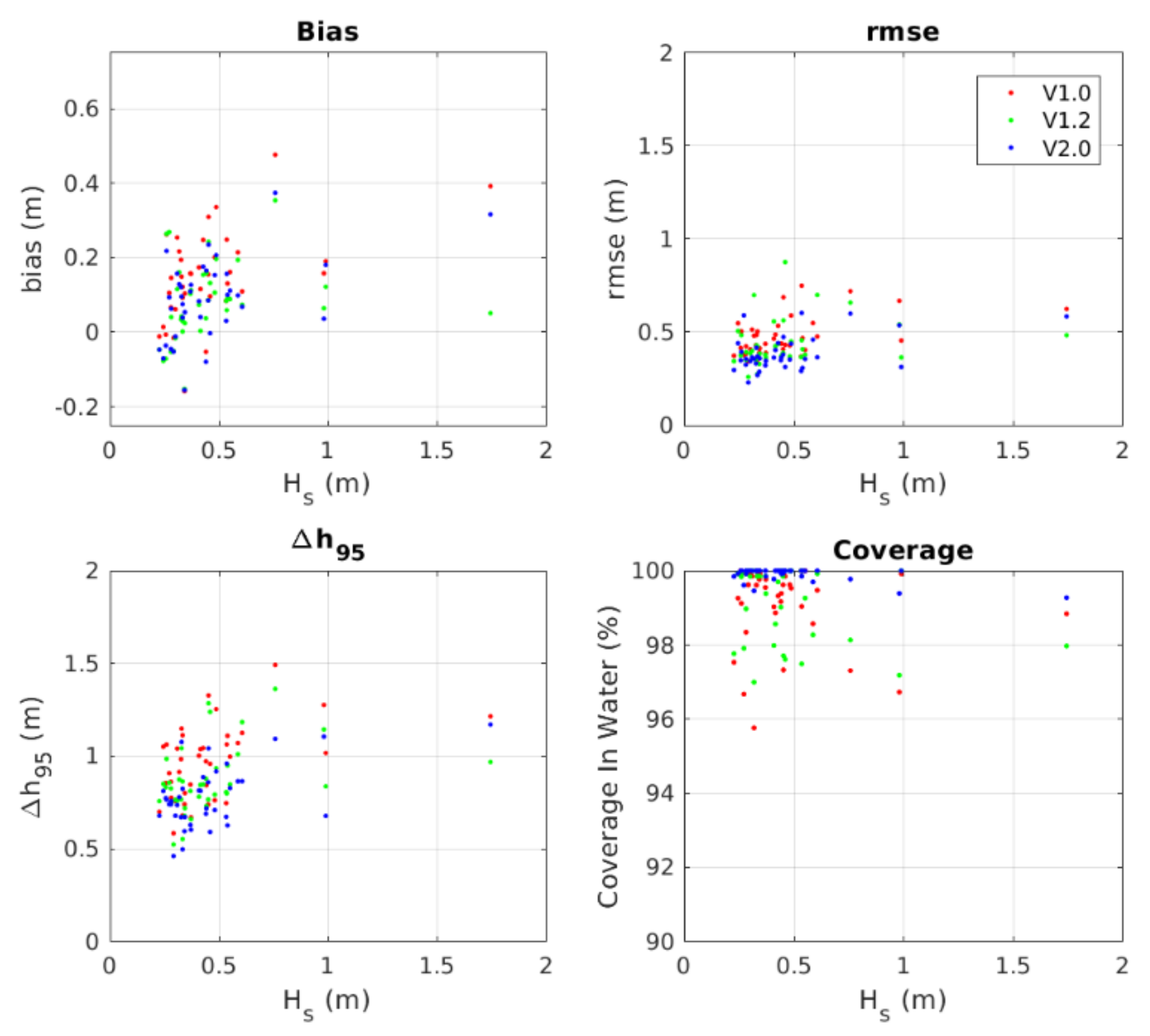
| Full Dataset | |||
| Statistic | V1.0 | V1.2 | V2.0 |
| Bias (m) | 0.19 | 0.14 | 0.16 |
| rmse (m) | 0.64 | 0.82 | 0.56 |
| Δh95 (m) | 1.27 | 1.25 | 1.19 |
| Coverage (%) | 78.7 | 78.0 | 84.7 |
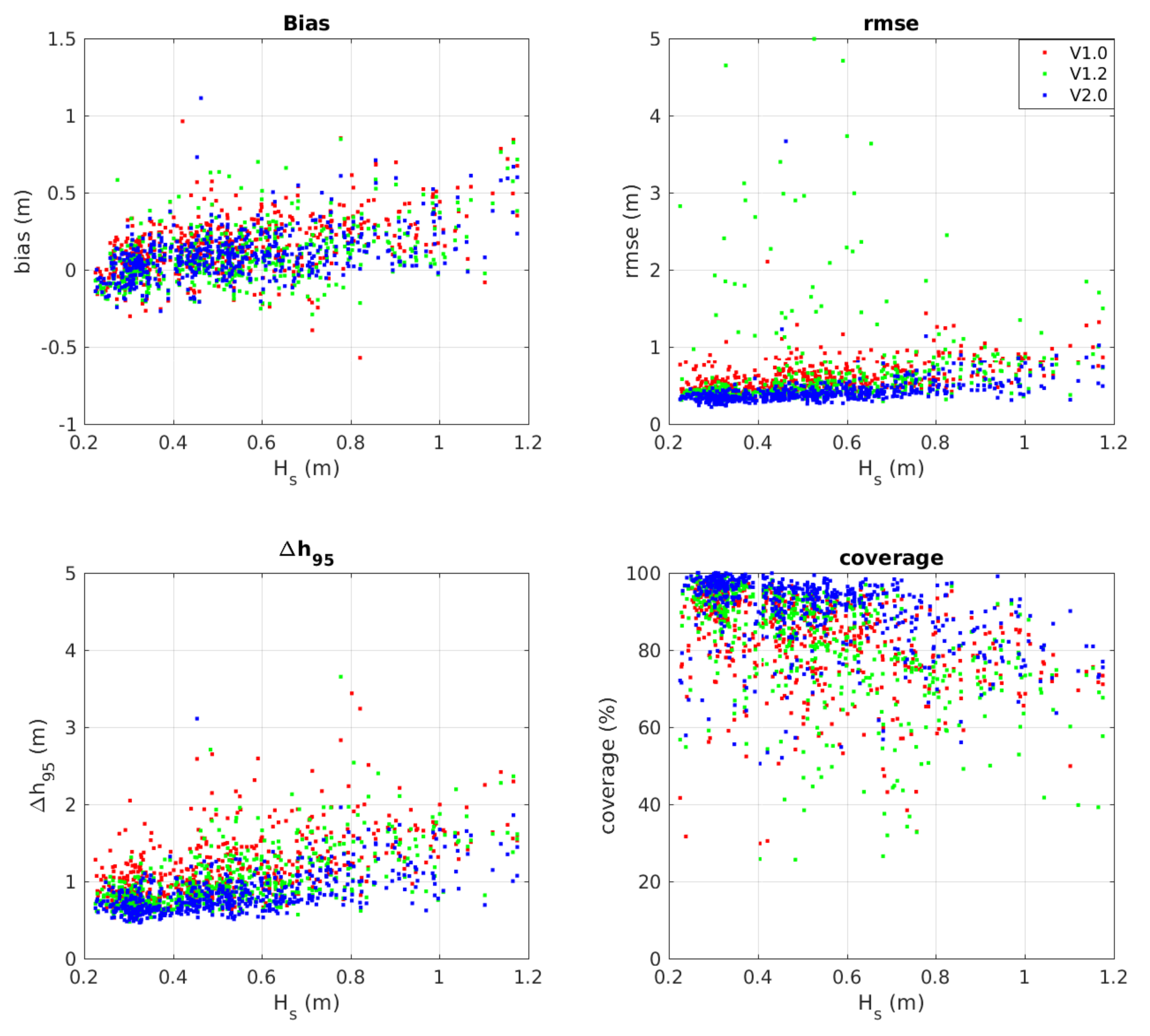
| Reduced Dataset | |||
| Bias (m) | 0.15 | 0.09 | 0.09 |
| rmse (m) | 0.58 | 0.66 | 0.41 |
| Δh95 (m) | 1.16 | 1.01 | 0.85 |
| Coverage (%) | 82.8 | 82.3 | 90.0 |
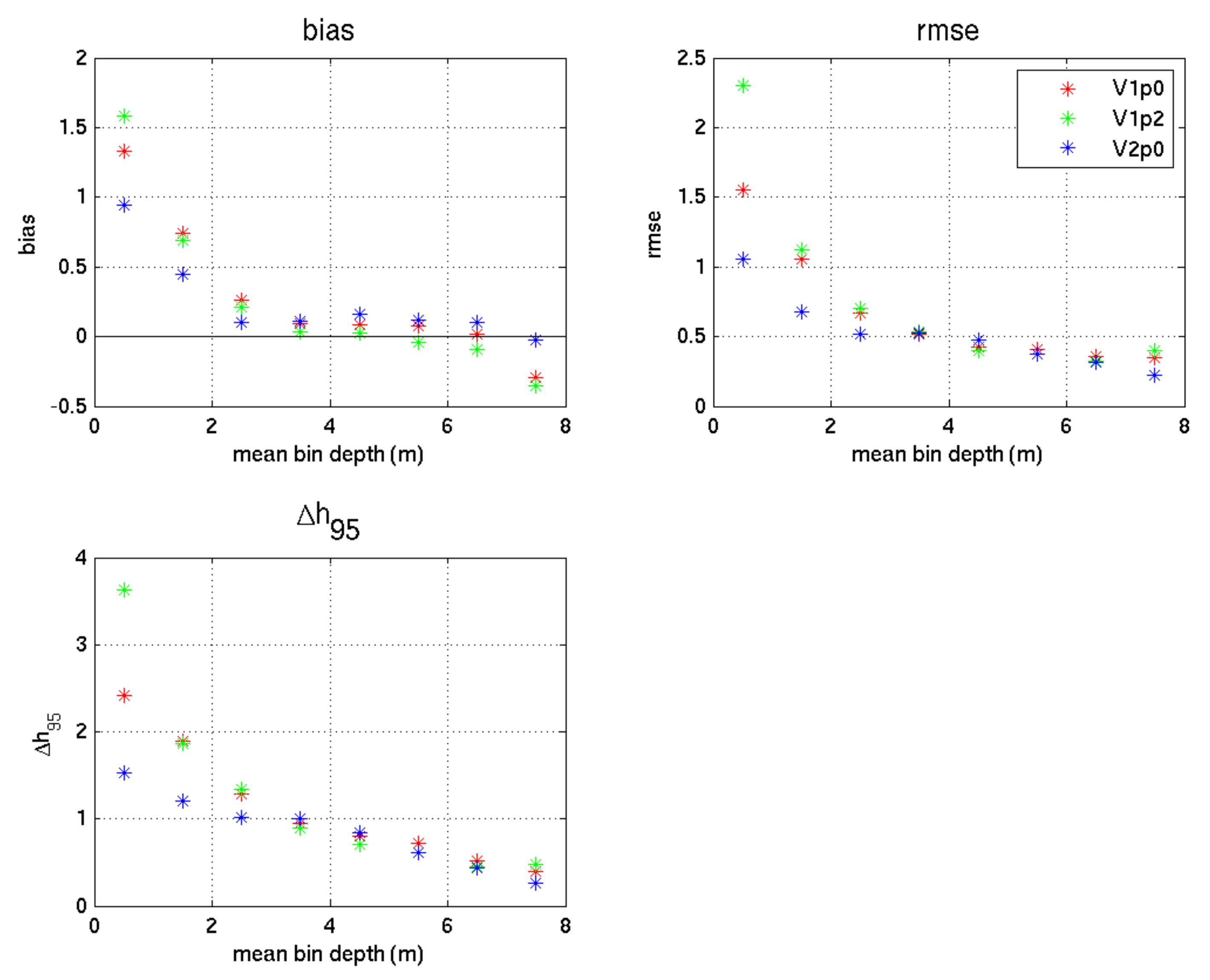
| Full Dataset | |||
|---|---|---|---|
| Statistic | V1.0 | V1.2 | V2.0 |
| Bias (m) | 0.15 | 0.08 | 0.08 |
| rmse (m) | 0.47 | 0.66 | 0.38 |
| Δh95 (m) | 0.96 | 0.86 | 0.78 |
| Coverage (%) | 99.1 | 99.2 | 99.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holman, R.; Bergsma, E.W.J. Updates to and Performance of the cBathy Algorithm for Estimating Nearshore Bathymetry from Remote Sensing Imagery. Remote Sens. 2021, 13, 3996. https://doi.org/10.3390/rs13193996
Holman R, Bergsma EWJ. Updates to and Performance of the cBathy Algorithm for Estimating Nearshore Bathymetry from Remote Sensing Imagery. Remote Sensing. 2021; 13(19):3996. https://doi.org/10.3390/rs13193996
Chicago/Turabian StyleHolman, Rob, and Erwin W. J. Bergsma. 2021. "Updates to and Performance of the cBathy Algorithm for Estimating Nearshore Bathymetry from Remote Sensing Imagery" Remote Sensing 13, no. 19: 3996. https://doi.org/10.3390/rs13193996
APA StyleHolman, R., & Bergsma, E. W. J. (2021). Updates to and Performance of the cBathy Algorithm for Estimating Nearshore Bathymetry from Remote Sensing Imagery. Remote Sensing, 13(19), 3996. https://doi.org/10.3390/rs13193996







