Inversion for Inhomogeneous Surface Duct without a Base Layer Based on Ocean-Scattered Low-Elevation BDS Signals
Abstract
:1. Introduction
2. Propagation of Ocean-Scattered Low-Elevation BDS Signals in Tropospheric Ducts
2.1. BDS Signal Characteristics
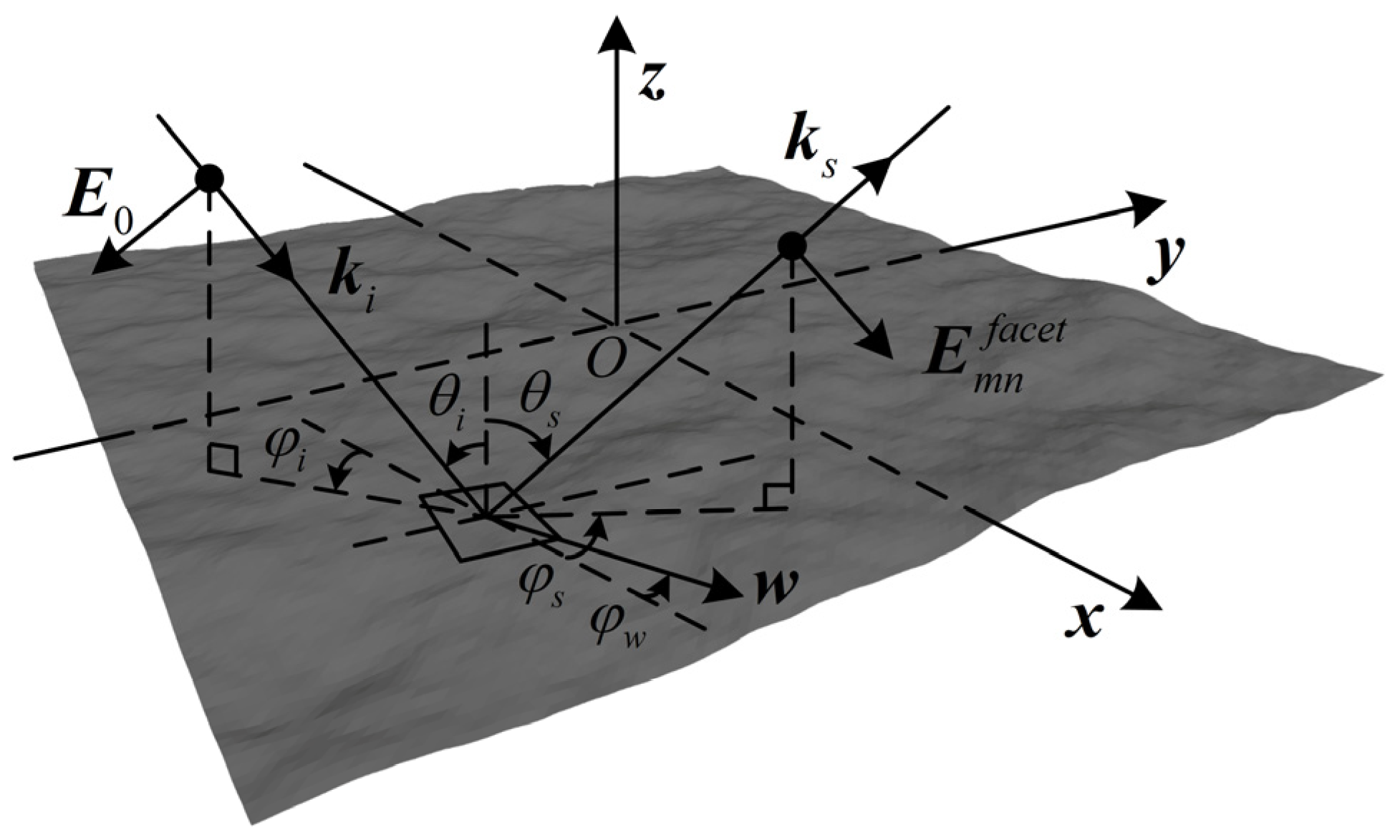
2.2. Bistatic Scattering from Ocean Surface
2.3. Received Power of Ocean-Scattered Signals in Tropospheric Ducts
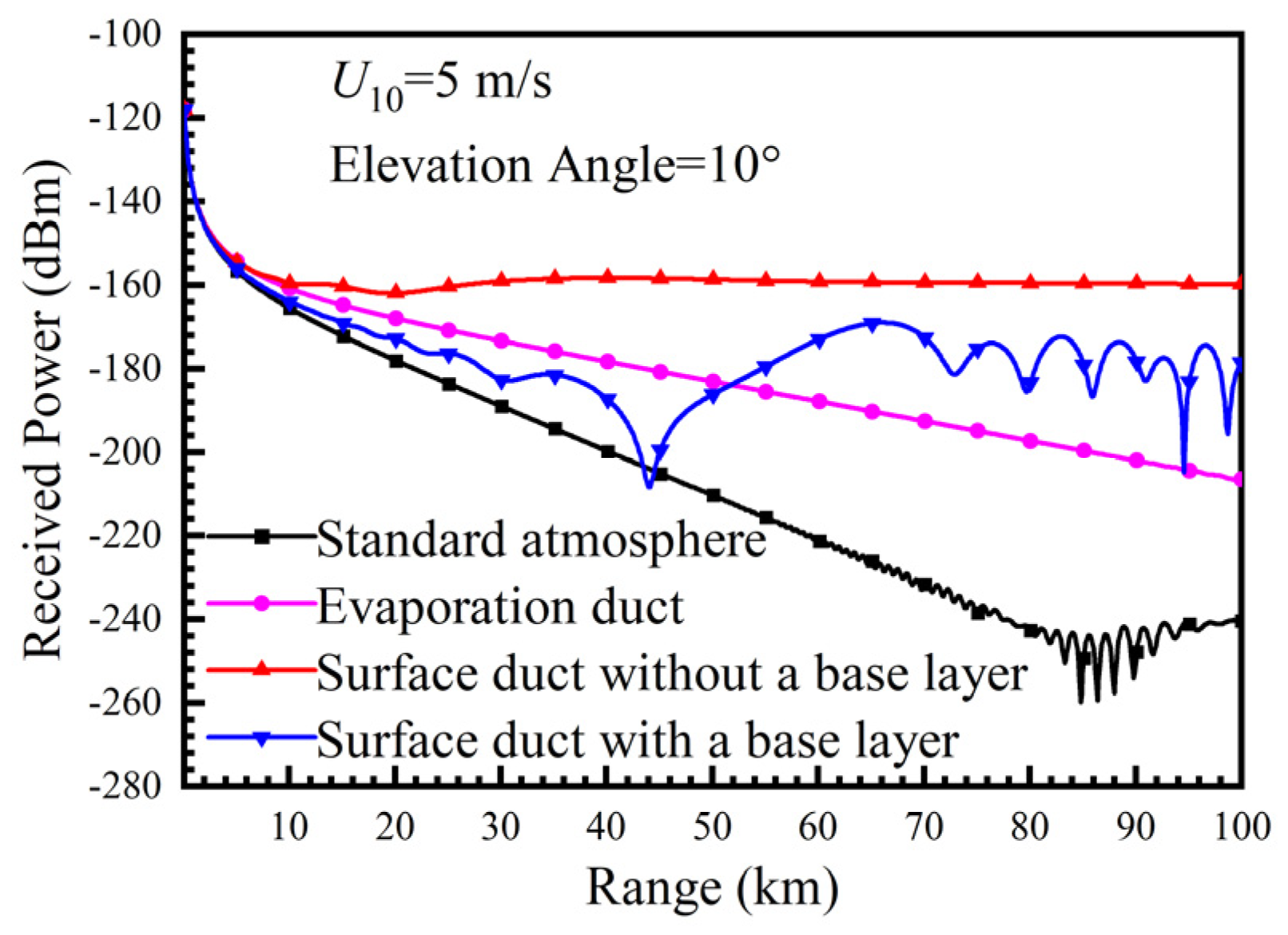
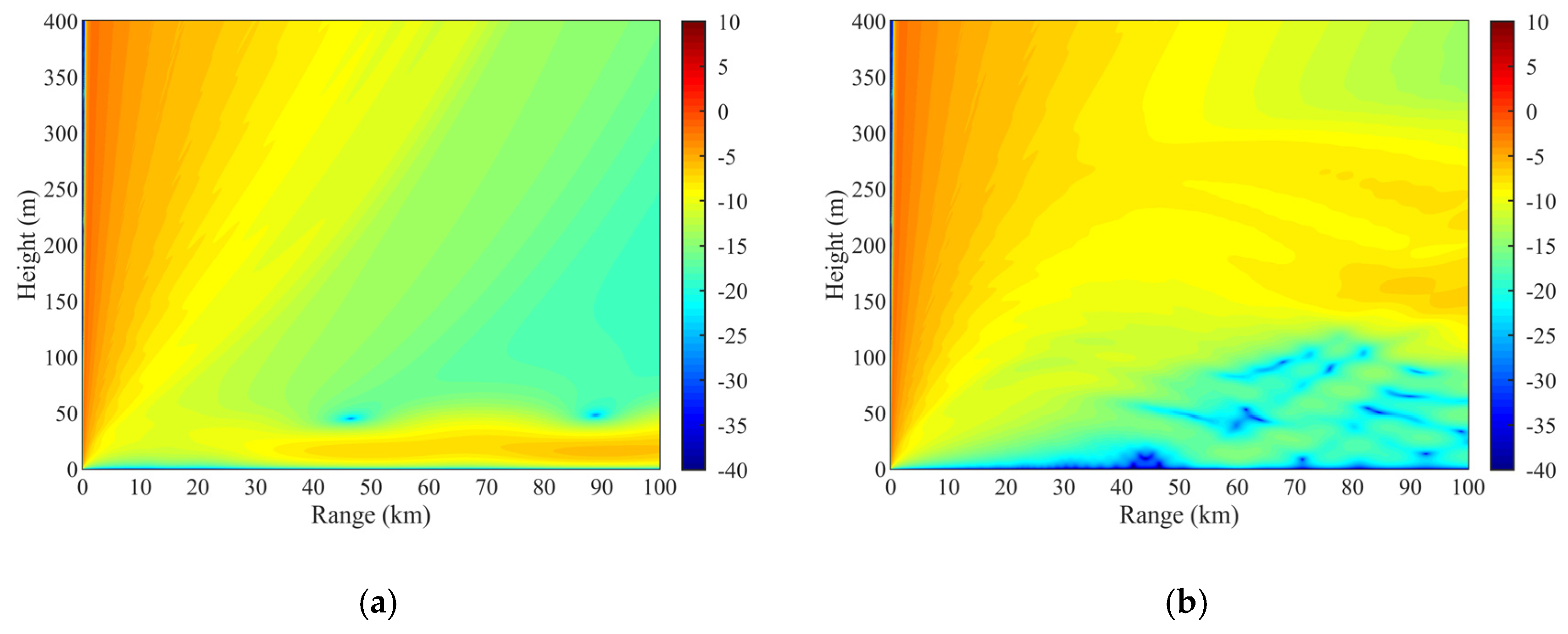
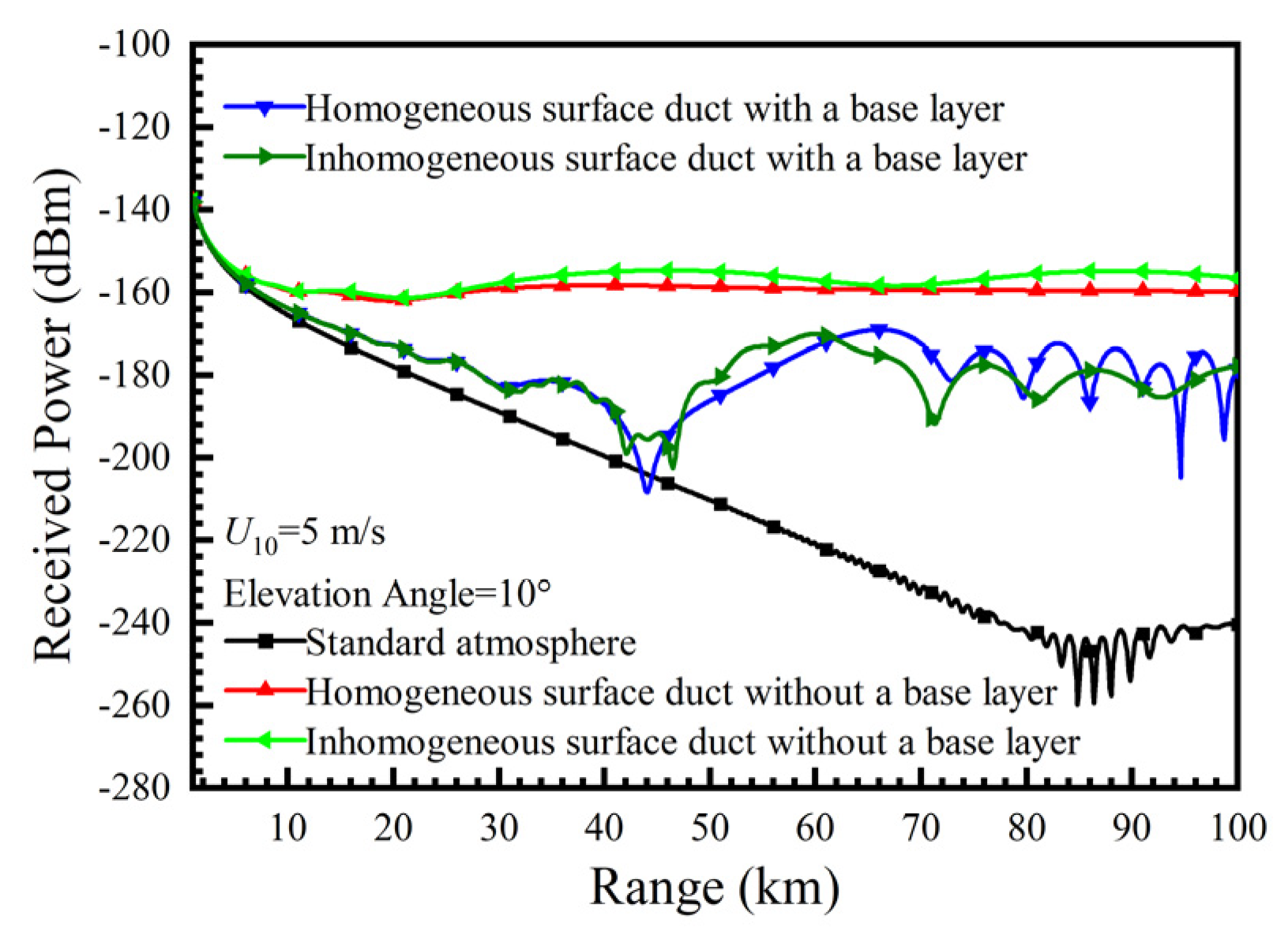
2.4. Effects of Tropospheric Ducts on the Propagation of Ocean-Scattered Low-Elevation Signals
3. Estimation of the Regional Distribution of Tropospheric Ducts
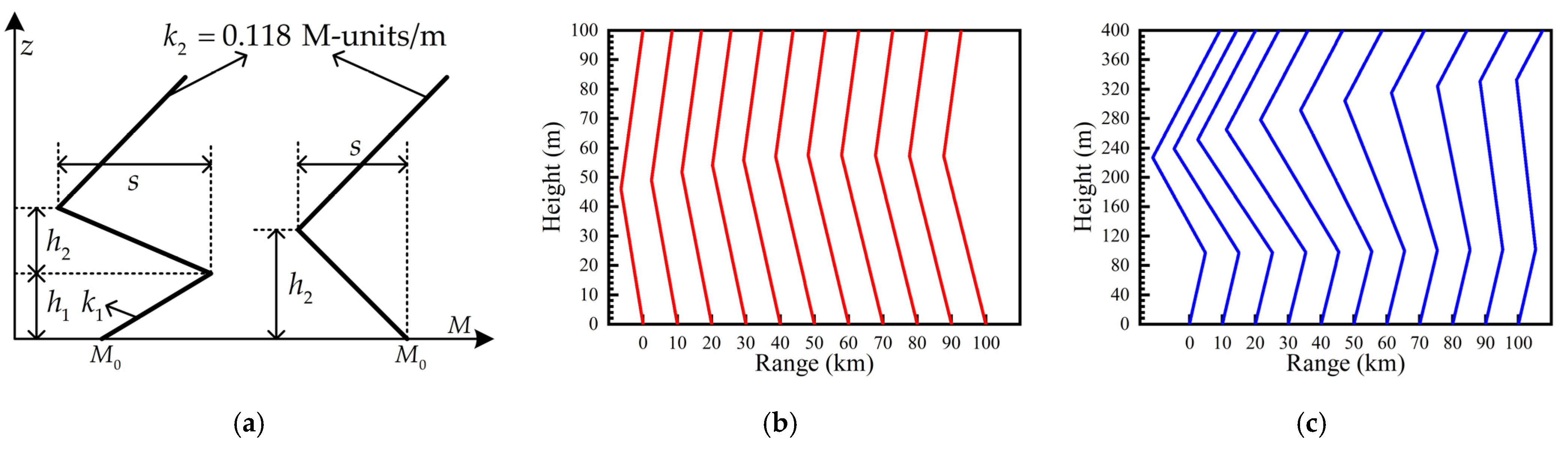
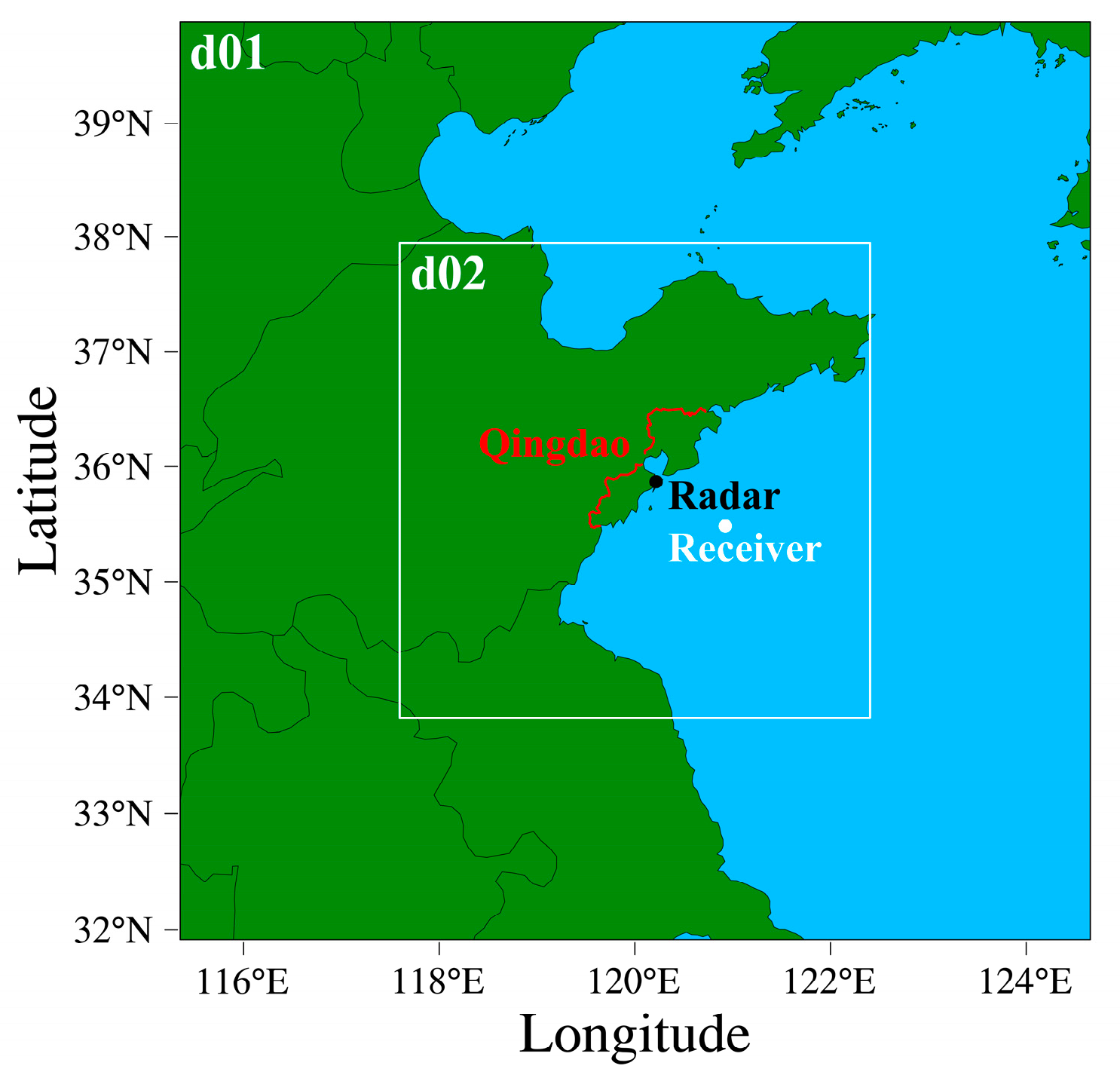
3.1. Estimation of Tropospheric Ducts Using the WRF Model
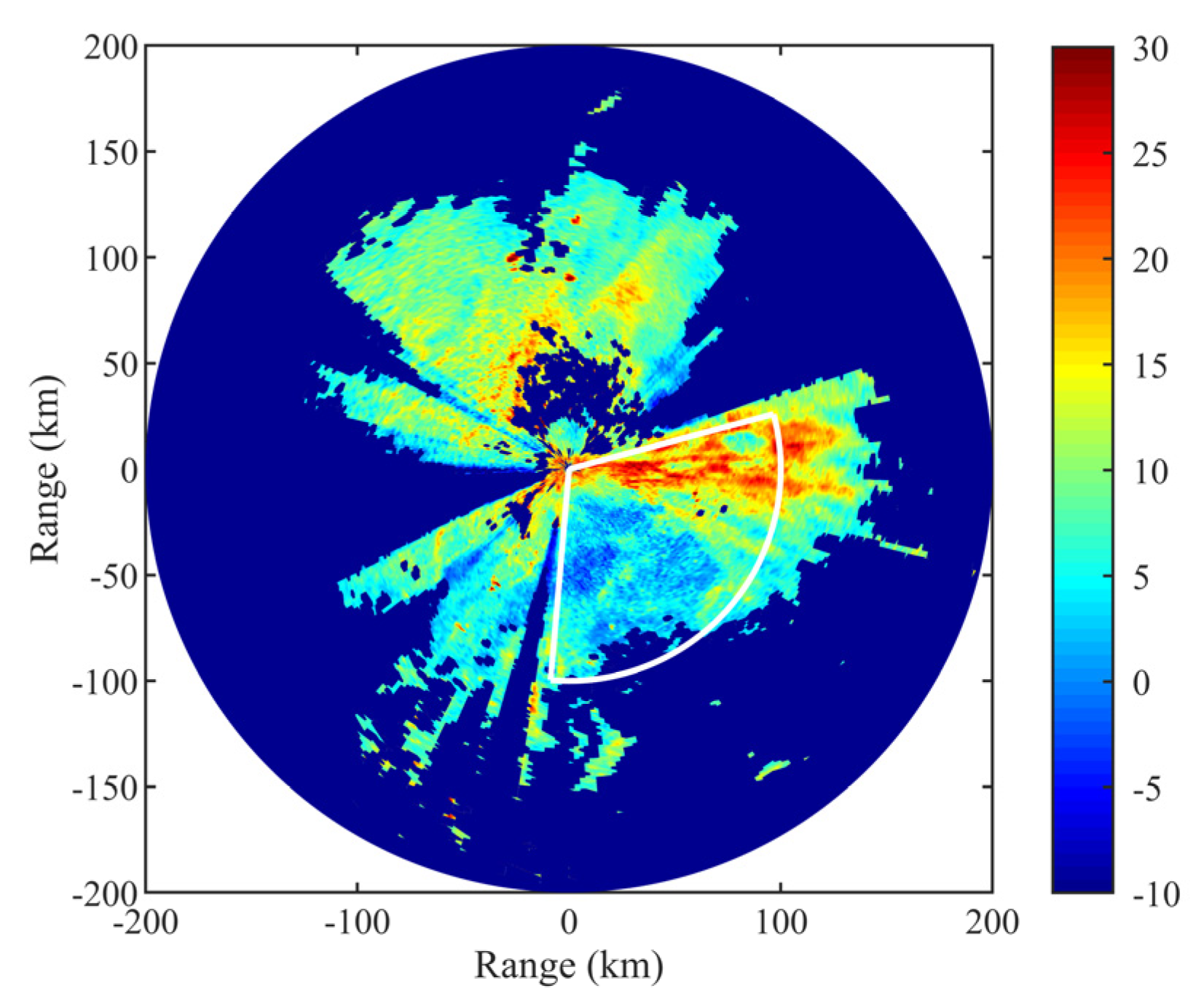
3.2. Estimation of Tropospheric Ducts Using the RFC Method
4. Inversion Method of Inhomogeneous Surface Duct without a Base Layer Based on Ocean-Scattered Low-Elevation BDS Signals
4.1. Estimation of the Satellite Azimuth and Elevation Angles
4.2. Inversion Process
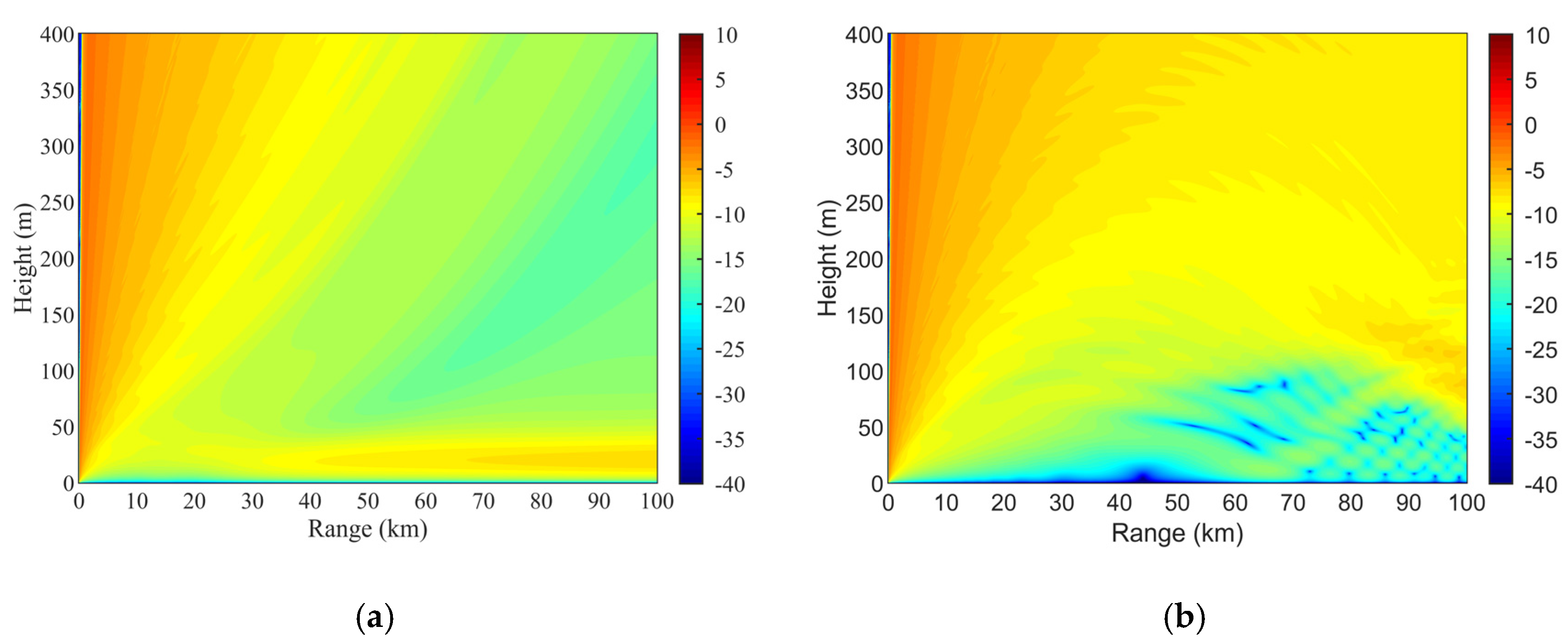
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prtenjak, M.T.; Horvat, I.; Tomažić, I.; Kvakić, M.; Viher, M.; Grisogono, B. Impact of mesoscale meteorological processes on anomalous radar propagation conditions over the northern Adriatic area. J. Geophys. Res. Atmos. 2015, 120, 8759–8782. [Google Scholar] [CrossRef]
- Magaldi, A.V.; Mateu, M.; Bech, J.; Lorente, J. A long term (1999–2008) study of radar anomalous propagation conditions in the western Mediterranean. Atmos. Res. 2016, 169, 73–85. [Google Scholar] [CrossRef]
- Bech, J.; Magaldi, A.; Codina, B.; Lorente, J. Effects of anomalous propagation conditions on weather radar observations. In Doppler Radar Observations-Weather Radar, Wind Profiler, Ionospheric Radar, and Other Advanced Applications; Bech, J., Chau, J.L., Eds.; InTech: Rijeka, Croatia, 2012; Volume 2, pp. 307–332. [Google Scholar]
- Alappattu, D.P.; Wang, Q.; Kalogiros, J. Anomalous propagation conditions over eastern Pacific Ocean derived from MAGIC data. Radio Sci. 2016, 51, 1142–1156. [Google Scholar] [CrossRef] [Green Version]
- Sirkova, I. Duct occurrence and characteristics for Bulgarian Black sea shore derived from ECMWF data. J. Atmos. Sol.-Terr. Phy. 2015, 135, 107–117. [Google Scholar] [CrossRef]
- Torres, S.M.; Warde, D.A. Ground clutter mitigation for weather radars using the autocorrelation spectral density. J. Atmos. Ocean. Technol. 2014, 31, 2049–2066. [Google Scholar] [CrossRef]
- Sirkova, I. Anomalous tropospheric propagation: Usage possibilities and limitations in radar and wireless communications systems. In AIP Conference Proceedings; AIP Publishing LLC.: Melville, NY, USA, 2019; Volume 2075, p. 120017. [Google Scholar]
- Wang, H.; Su, S.P.; Tang, H.C.; Jiao, L.; Li, Y.B. Atmospheric duct detection using wind profiler radar and RASS. J. Atmos. Ocean. Technol. 2019, 36, 557–565. [Google Scholar] [CrossRef]
- Burk, S.D.; Thompson, W.T. Mesoscale modeling of summertime refractive conditions in the Southern California Bight. J. Appl. Meteorol. 1997, 36, 22–31. [Google Scholar] [CrossRef]
- Haack, T.; Wang, C.G.; Garrett, S.; Glazer, A.; Mailhot, J.; Marshall, R. Mesoscale modeling of boundary layer refractivity and atmospheric ducting. J. Appl. Meteorol. Climatol. 2010, 49, 2437–2457. [Google Scholar] [CrossRef]
- Liang, Z.C.; Ding, J.L.; Fei, J.F.; Cheng, X.P.; Huang, X.G. Maintenance and sudden change of a strong elevated ducting event associated with high pressure and marine low-level jet. J. Meteorol. Res. 2020, 34, 1287–1298. [Google Scholar] [CrossRef]
- Yang, S.B.; Li, X.F.; Wu, C.; He, X.; Zhong, Y. Application of the PJ and NPS evaporation duct models over the South China Sea (SCS) in winter. PLoS ONE 2017, 12, e0172284. [Google Scholar] [CrossRef]
- Zhang, J.P.; Wu, Z.S.; Zhu, Q.L.; Wang, B. A four-parameter M-profile model for the evaporation duct estimation from radar clutter. Prog. Electromagn. Res. 2011, 114, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Karimian, A.; Yardim, C.; Gerstoft, P.; Hodgkiss, W.S.; Barrios, A.E. Refractivity estimation from sea clutter: An invited review. Radio Sci. 2011, 46, RS6013. [Google Scholar] [CrossRef] [Green Version]
- Gerstoft, P.; Rogers, L.T.; Krolik, J.L.; Hodgkiss, W.S. Inversion for refractivity parameters from radar sea clutter. Radio Sci. 2003, 38, 8053. [Google Scholar] [CrossRef]
- Yang, C.; Guo, L. Inferring the atmospheric duct from radar sea clutter using the improved artificial bee colony algorithm. Int. J. Microw. Wirel. Technol. 2018, 10, 437–445. [Google Scholar] [CrossRef]
- Tepecik, C.; Navruz, I. A novel hybrid model for inversion problem of atmospheric refractivity estimation. AEU-Int. J. Electron. Commun. 2018, 84, 258–264. [Google Scholar] [CrossRef]
- Guo, X.W.; Wu, J.J.; Zhang, J.P.; Han, J. Deep learning for solving inversion problem of atmospheric refractivity estimation. Sustain. Cities Soc. 2018, 43, 524–531. [Google Scholar] [CrossRef]
- Pozderac, J.; Johnson, J.; Yardim, C.; Merrill, C.; de Paolo, T.; Terrill, E.; Ryan, F.; Frederickson, P. X-band beacon-receiver array evaporation duct height estimation. IEEE Trans. Antennas Propag. 2018, 66, 2545–2556. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, K.D. Study on evaporation duct estimation from point-to-point propagation measurements. IET Sci. Meas. Technol. 2018, 12, 456–460. [Google Scholar] [CrossRef]
- Wickert, J.; Dick, G.; Schmidt, T.; Asgarimehr, M.; Antonoglou, N.; Arras, C.; Brack, A.; Ge, M.; Kepkar, A.; Männel, B.; et al. GNSS remote sensing at GFZ: Overview and recent results. ZfV Z. Geodäsie Geoinf. Landmanag. 2020, 145, 266–278. [Google Scholar]
- Wickert, J.; Cardellach, E.; Martin-Neira, M.; Bandeiras, J.; Bertino, L.; Andersen, O.B.; Camps, A.; Catarino, N.; Chapron, B.; Fabra, F.; et al. GEROS-ISS: GNSS REflectometry, Radio Occultation, and Scatterometry onboard the International Space Station. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4552–4581. [Google Scholar] [CrossRef] [Green Version]
- Development of the BeiDou Navigation Satellite System (Version 4.0). Available online: http://www.beidou.gov.cn/xt/gfxz/201912/P020191227430565455478.pdf (accessed on 7 September 2021).
- Marchan-Hernandez, J.F.; Valencia, E.; Rodriguez-Alvarez, N.; Ramos-Perez, I.; Bosch-Lluis, X.; Camps, A.; Eugenio, F.; Marcello, J. Sea-state determination using GNSS-R data. IEEE Geosci. Remote Sens. Lett. 2010, 7, 621–625. [Google Scholar] [CrossRef]
- Jin, S.G.; Qian, X.D.; Wu, X. Sea level change from BeiDou Navigation Satellite System-Reflectometry (BDS-R): First results and evaluation. Glob. Planet. Chang. 2017, 149, 20–25. [Google Scholar] [CrossRef]
- Ansari, K.; Bae, T.S.; Inyurt, S. Global positioning system interferometric reflectometry for accurate tide gauge measurement: Insights from South Beach, Oregon, United States. Acta Astronaut. 2020, 173, 356–362. [Google Scholar] [CrossRef]
- Simone, A.D.; Park, H.; Riccio, D.; Camps, A. Sea target detection using spaceborne GNSS-R delay-Doppler maps: Theory and experimental proof of concept using TDS-1 data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4237–4255. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Zavorotny, V.U. Bistatic radar equation for signals of opportunity revisited. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1959–1968. [Google Scholar] [CrossRef]
- Semmling, A.M.; Beckheinrich, J.; Wickert, J.; Beyerle, G.; Schön, S.; Fabra, F.; Pflug, H.; He, K.; Schwabe, J.; Scheinert, M. Sea surface topography retrieved from GNSS reflectometry phase data of the GEOHALO flight mission. Geophys. Res. Lett. 2014, 41, 954–960. [Google Scholar] [CrossRef] [Green Version]
- Cardellach, E.; Li, W.Q.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First precise spaceborne sea surface altimetry with GNSS reflected signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2000, 13, 102–112. [Google Scholar] [CrossRef]
- Li, W.Q.; Cardellach, E.; Fabra, F.; Ribo, S.; Rius, A. Lake level and surface topography measured with spaceborne GNSS-Reflectometry from CYGNSS mission: Example for the Lake Qinghai. Geophys. Res. Lett. 2018, 45, 13332–13341. [Google Scholar] [CrossRef]
- Dong, Z.N.; Jin, S.G. 3-D water vapor tomography in Wuhan from GPS, BDS and GLONASS observations. Remote Sens. 2018, 10, 62. [Google Scholar] [CrossRef] [Green Version]
- Li, X.X.; Zus, F.; Lu, C.X.; Dick, G.; Ning, T.; Ge, M.R.; Wickert, J.; Schuh, H. Retrieving of atmospheric parameters from multi-GNSS in real time: Validation with water vapor radiometer and numerical weather model. J. Geophys. Res. Atmos. 2015, 120, 7189–7204. [Google Scholar] [CrossRef] [Green Version]
- Shoji, Y.; Sato, K.; Yabuki, M.; Tsuda, T. Comparison of shipborne GNSS-derived precipitable water vapor with radiosonde in the western North Pacific and in the seas adjacent to Japan. Earth Planets Space 2017, 69, 153. [Google Scholar] [CrossRef]
- Astudillo, J.M.; Lau, L.; Tang, Y.T.; Moore, T. A novel approach for the determination of the height of the tropopause from ground-based GNSS obsevartions. Remote Sens. 2020, 12, 293. [Google Scholar] [CrossRef] [Green Version]
- Bai, W.H.; Liu, C.L.; Meng, X.G.; Sun, Y.Q.; Kirchengast, G.; Du, Q.F.; Wang, X.Y.; Yang, G.L.; Liao, M.; Yang, Z.D.; et al. Evaluation of atmospheric profiles derived from single-and zero-difference excess phase processing of BeiDou radio occultation data from the FY-3C GNOS mission. Atmos. Meas. Tech. 2018, 11, 819–833. [Google Scholar] [CrossRef] [Green Version]
- Gorbunov, M.E.; Kirchengast, G. Wave-optics uncertainty propagation and regression-based bias model in GNSS radio occultation bending angle retrievals. Atmos. Meas. Tech. 2018, 11, 111–125. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.N.; Ao, C.O.; Juárez, M.T. GNSS-RO refractivity bias correction under ducting layer using surface-reflection signal. Remote Sens. 2020, 12, 359. [Google Scholar] [CrossRef] [Green Version]
- Sokolovskiy, S.; Schreiner, W.; Zeng, Z.; Hunt, D.; Lin, Y.C.; Kuo, Y.H. Observation, analysis, and modeling of deep radio occultation signals: Effects of tropospheric ducts and interfering signals. Radio Sci. 2014, 49, 954–970. [Google Scholar] [CrossRef]
- Wang, H.G.; Wu, Z.S.; Kang, S.F.; Zhao, Z.W. Monitoring the marine atmospheric refractivity profiles by ground-based GPS occultation. IEEE Geosci. Remote Sens. Lett. 2012, 10, 962–965. [Google Scholar] [CrossRef]
- Liao, Q.X.; Sheng, Z.; Shi, H.Q.; Xiang, J.; Yu, H. Estimation of surface duct using ground-based GPS phase delay and propagation loss. Remote Sens. 2018, 10, 724. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.P.; Wu, Z.S.; Zhao, Z.W.; Zhang, Y.S.; Wang, B. Propagation modeling of ocean-scattered low-elevation GPS signals for maritime tropospheric duct inversion. Chin. Phys. B 2012, 21, 109202. [Google Scholar] [CrossRef]
- Liu, X.Z.; Wang, H.G.; Wu, Z.S. Influence of maritime tropospheric duct on ocean-scattered low-elevation GPS signal propagation. In Proceedings of the 2019 International Symposium on Antennas and Propagation (ISAP2019), Xi’an, China, 27–30 October 2019. [Google Scholar]
- BeiDou Navigation Satellite System Signal in Space Interface Control Document: Open Service Signal B1I (Version 3.0). Available online: http://www.beidou.gov.cn/xt/gfxz/201902/P020190227593621142475.pdf (accessed on 7 September 2021).
- Alessi, S.; Acutis, F.D.; Picardi, G.; Seu, R. Surface bistatic scattering coefficient by means the facet model radar altimetry application. In Proceedings of the 26th European Microwave Conference, Prague, Czech Republic, 9–12 September 1996; Volume 1, pp. 337–340. [Google Scholar]
- Franceschetti, G.; Iodice, A.; Riccio, D.; Ruello, G.; Siviero, R. SAR raw signal simulation of oil slicks in ocean environments. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1935–1949. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, H.; Yin, H.C. Facet-based investigation on EM scattering from electrically large sea surface with two-scale profiles: Theoretical model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1967–1975. [Google Scholar] [CrossRef]
- Linghu, L.X.; Wu, J.J.; Wu, Z.S.; Wang, X.B. Parallel computation of EM backscattering from large three-dimensional sea surface with CUDA. Sensors 2018, 18, 3656. [Google Scholar] [CrossRef] [Green Version]
- Tessendorf, J. Simulating Ocean Water. SIGGRAPH 2001, 1, 5. [Google Scholar]
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Cartwright, D.E.; Smith, N.D. Observations of the directional spectrum of sea waves using motions of a floating buoy. In Ocean Wave Spectra; Prentice Hall: Englewood Cliffs, NJ, USA, 1963; pp. 111–136. [Google Scholar]
- Meissner, T.; Wentz, F.J. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1836–1849. [Google Scholar] [CrossRef] [Green Version]
- Levy, M. Parabolic Equation Methods for Electromagnetic Wave Propagation; The Institution of Engineering and Technology: London, UK, 2000. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Mesoscale and Microscale Meteorology Division, National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Liu, X.Z.; Wu, Z.S.; Wang, H.G. Inversion method of regional range-dependent surface ducts with a base layer by Doppler weather radar echoes based on WRF model. Atmosphere 2020, 11, 754. [Google Scholar] [CrossRef]
- Stark, H.; Woods, J.W. Probability and Random Processes with Applications to Signal Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001; pp. 518–524. [Google Scholar]
- Blum, C.; Li, X.D. Swarm intelligence in optimization. In Swarm Intelligence; Blum, C., Merkle, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 43–85. [Google Scholar]



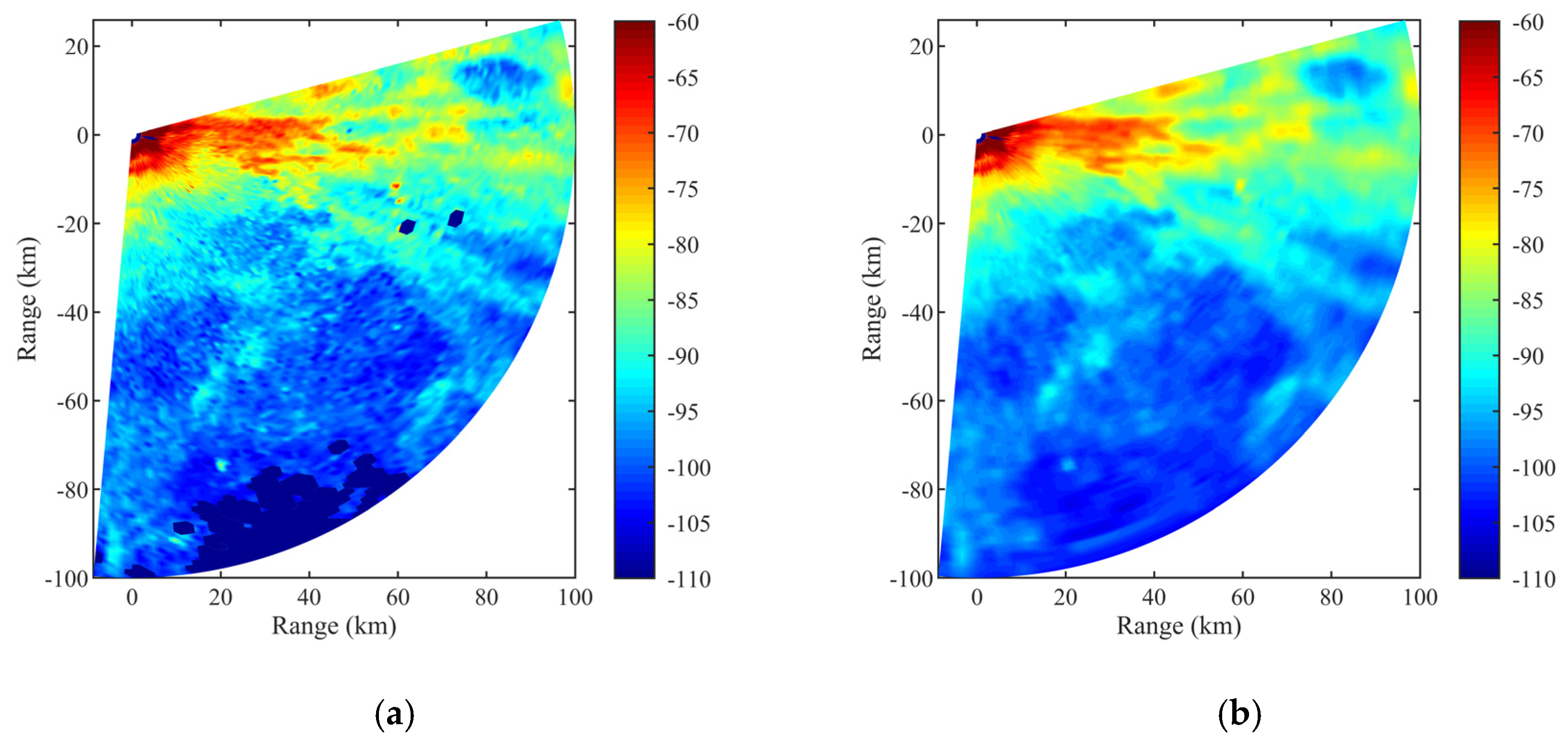




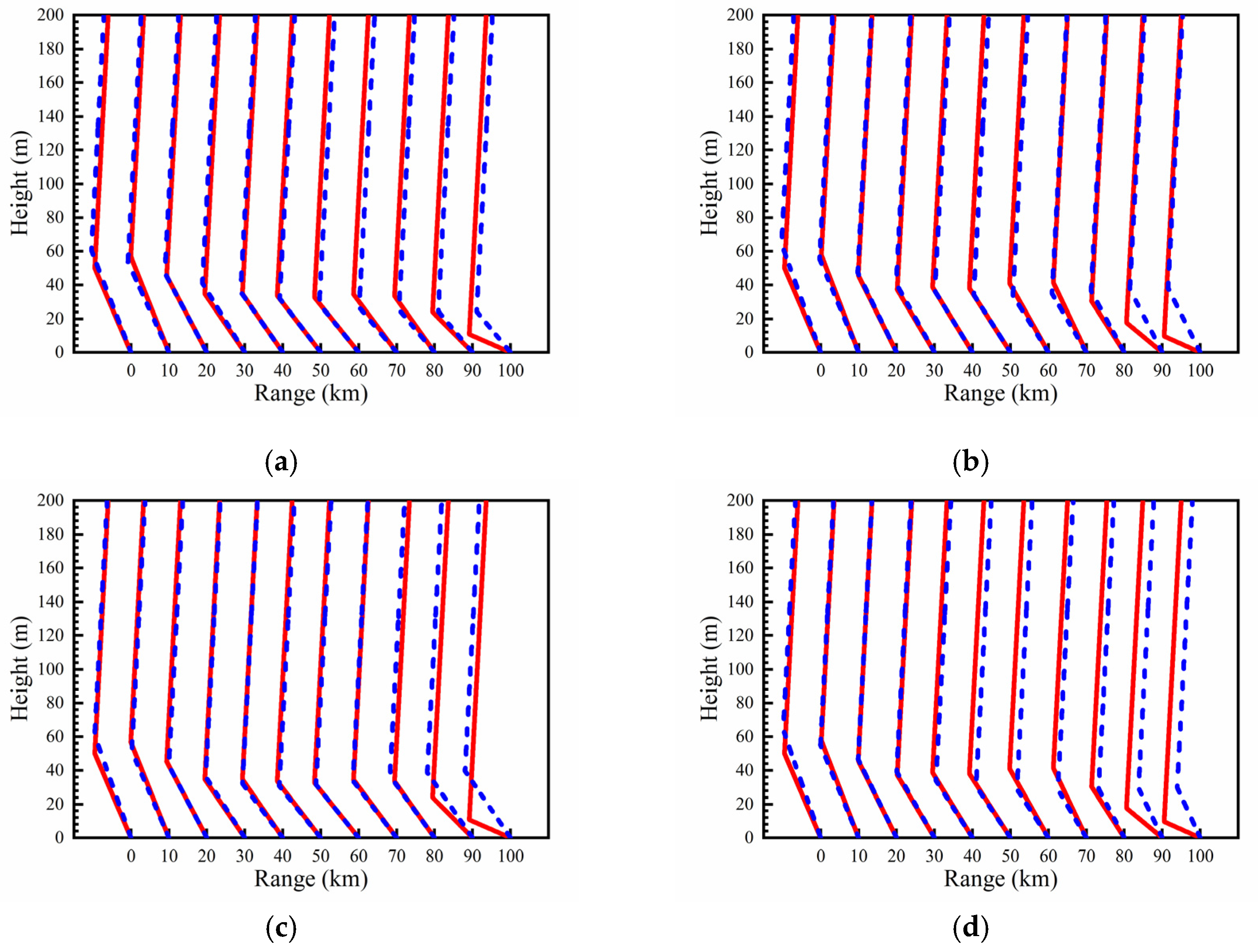
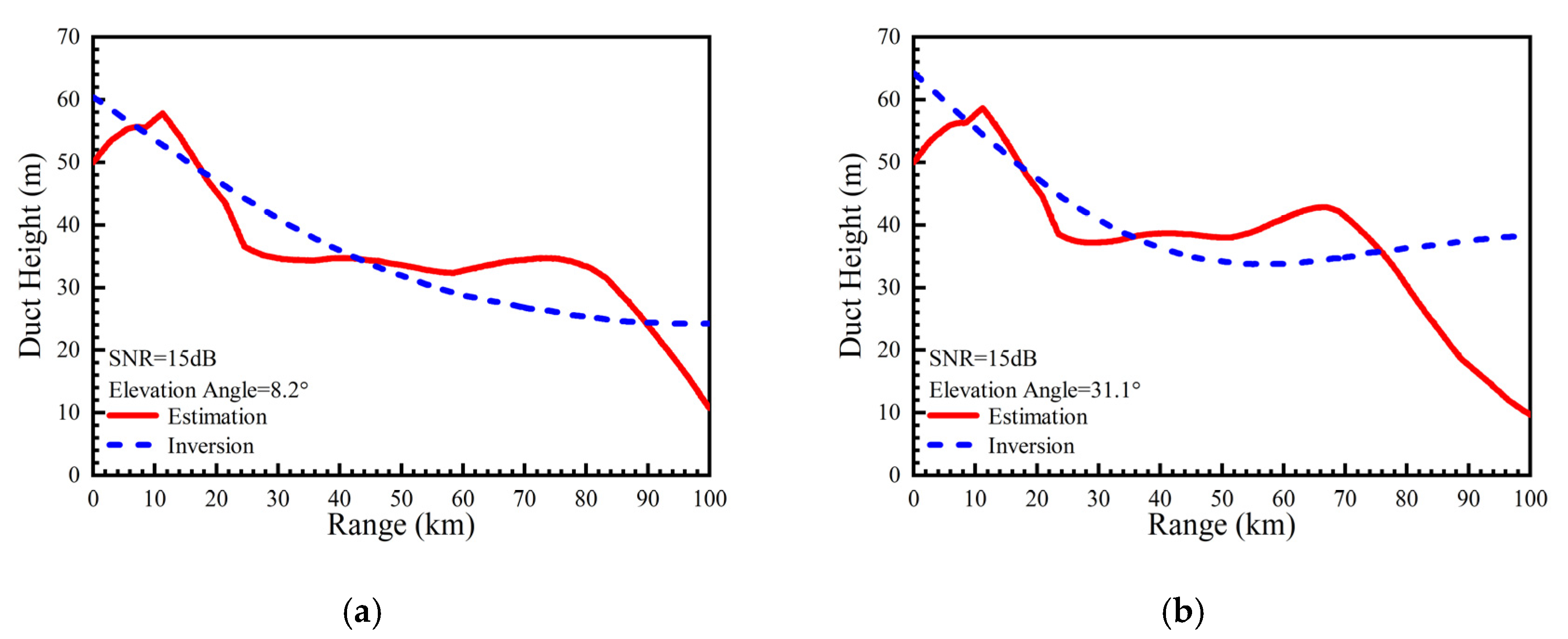
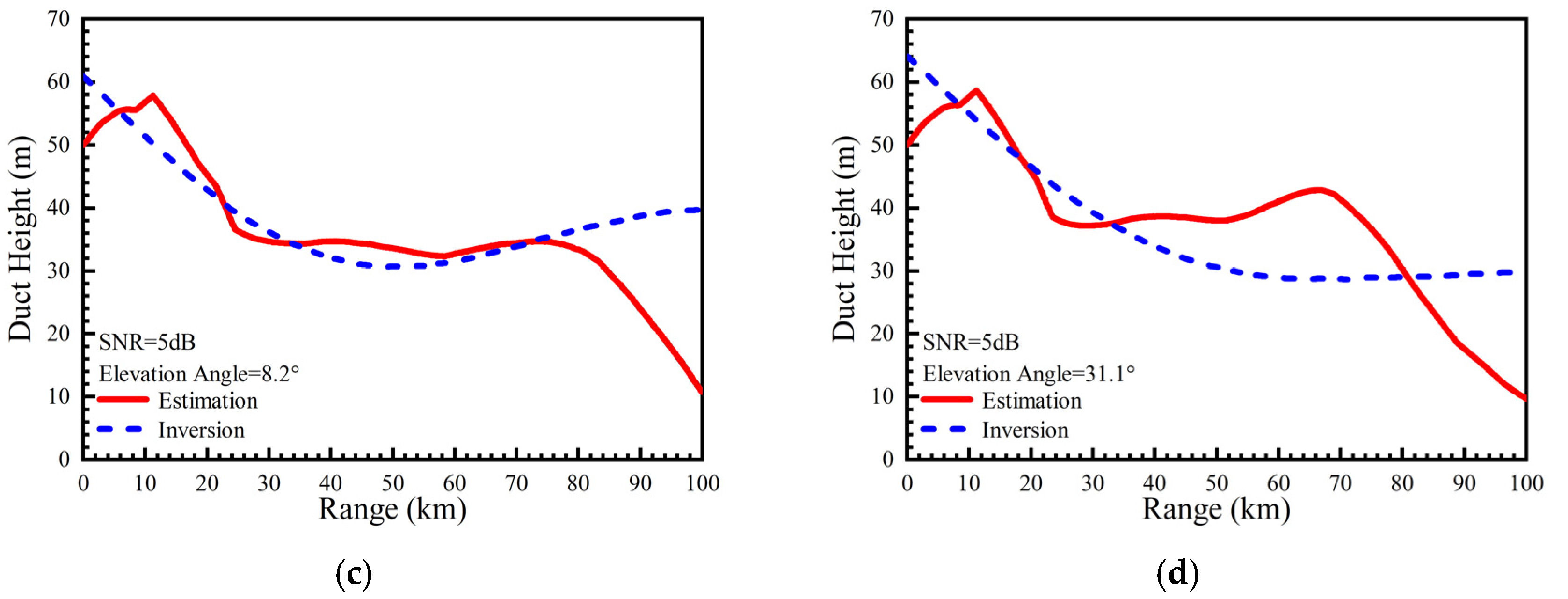


| Parameter | Value |
|---|---|
| Carrier Frequency | 1561.098 MHz |
| Signal Bandwidth | 4.092 MHz |
| Minimum Received Power | −163 dBW |
| Polarization Mode | RHCP |
| Modulation Mode | BPSK |
| Signal Multiplexing Mode | CDMA |
| Parameters | SNR (dB) | Azimuth (deg.) | MAE | RSME |
|---|---|---|---|---|
| Duct height (m) | 15.0 | 8.5 | 4.48 | 5.36 |
| 31.1 | 7.16 | 10.02 | ||
| All | 8.71 | 14.65 | ||
| 5.0 | 8.5 | 4.97 | 8.09 | |
| 31.1 | 7.22 | 8.79 | ||
| All | 9.07 | 16.70 | ||
| Duct strength (M-units) | 15.0 | 8.5 | 4.79 | 5.38 |
| 31.1 | 2.88 | 3.55 | ||
| All | 4.72 | 6.02 | ||
| 5.0 | 8.5 | 2.64 | 3.56 | |
| 31.1 | 6.67 | 8.56 | ||
| All | 4.38 | 5.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Cao, Y.; Wu, Z.; Wang, H. Inversion for Inhomogeneous Surface Duct without a Base Layer Based on Ocean-Scattered Low-Elevation BDS Signals. Remote Sens. 2021, 13, 3914. https://doi.org/10.3390/rs13193914
Liu X, Cao Y, Wu Z, Wang H. Inversion for Inhomogeneous Surface Duct without a Base Layer Based on Ocean-Scattered Low-Elevation BDS Signals. Remote Sensing. 2021; 13(19):3914. https://doi.org/10.3390/rs13193914
Chicago/Turabian StyleLiu, Xiaozhou, Yunhua Cao, Zhensen Wu, and Hongguang Wang. 2021. "Inversion for Inhomogeneous Surface Duct without a Base Layer Based on Ocean-Scattered Low-Elevation BDS Signals" Remote Sensing 13, no. 19: 3914. https://doi.org/10.3390/rs13193914
APA StyleLiu, X., Cao, Y., Wu, Z., & Wang, H. (2021). Inversion for Inhomogeneous Surface Duct without a Base Layer Based on Ocean-Scattered Low-Elevation BDS Signals. Remote Sensing, 13(19), 3914. https://doi.org/10.3390/rs13193914








