GNSS Signal Availability Analysis in SSV for Geostationary Satellites Utilizing multi-GNSS with First Side Lobe Signal over the Korean Region
Abstract
:1. Introduction
2. Figure of Performance for Analysis
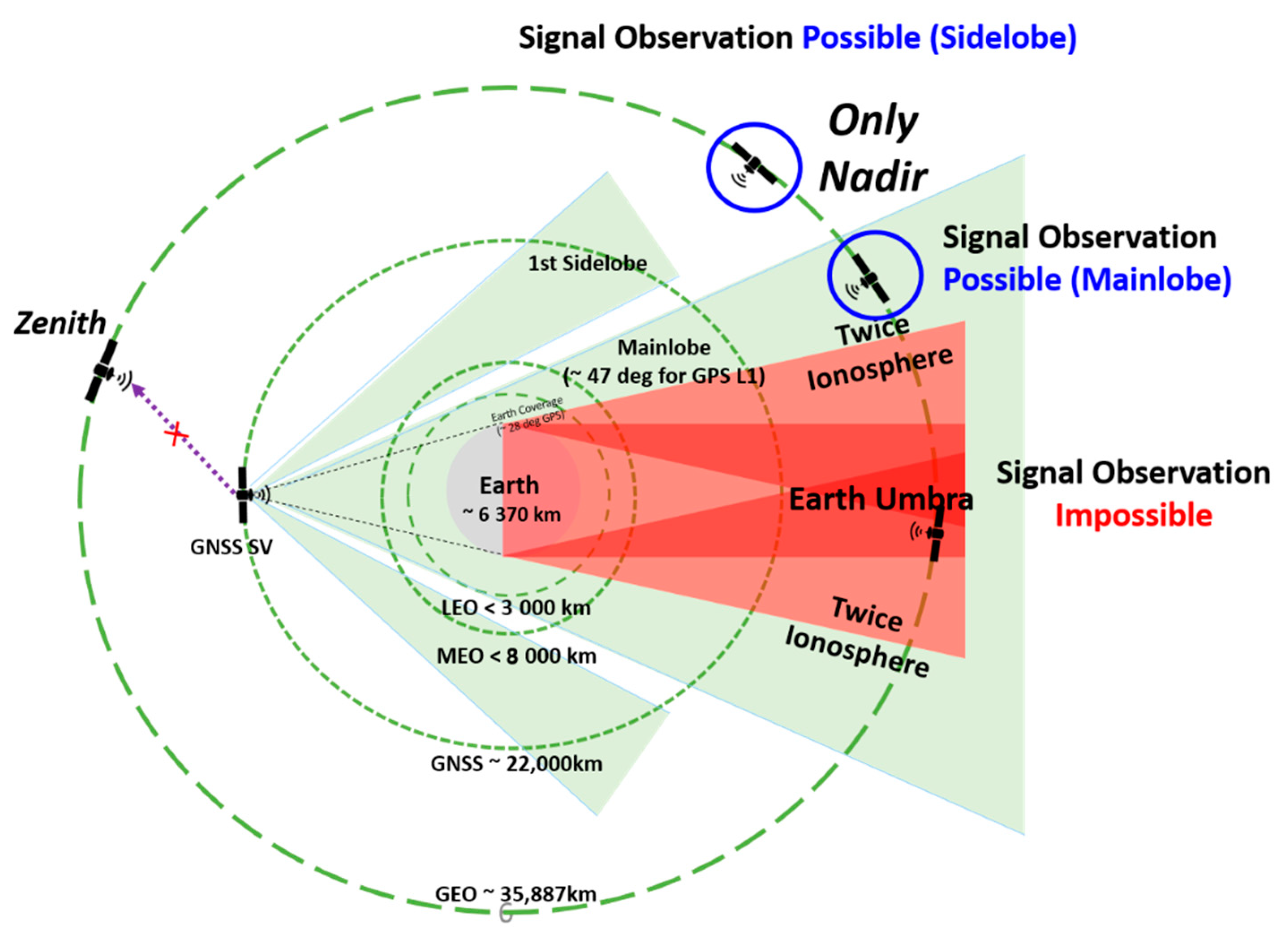
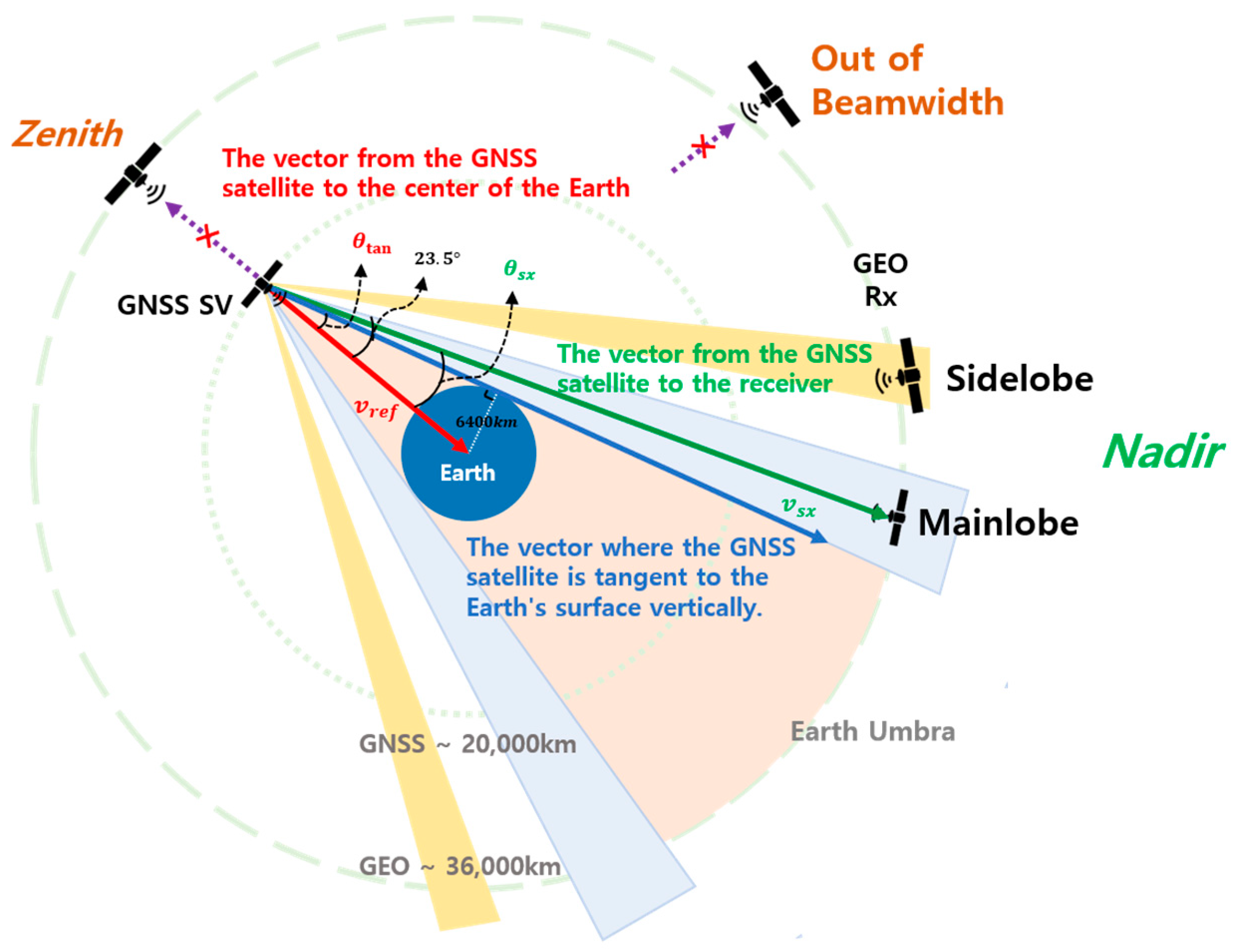
2.1. Visible Satellite Determination by Reflecting Geometric Structure
2.2. GDOP
2.3. Link-Budget
2.4. UERE
2.5. Navigation Error
3. Simulation Results and Discussion
3.1. Simulation Configuration
3.2. Performance Analysis
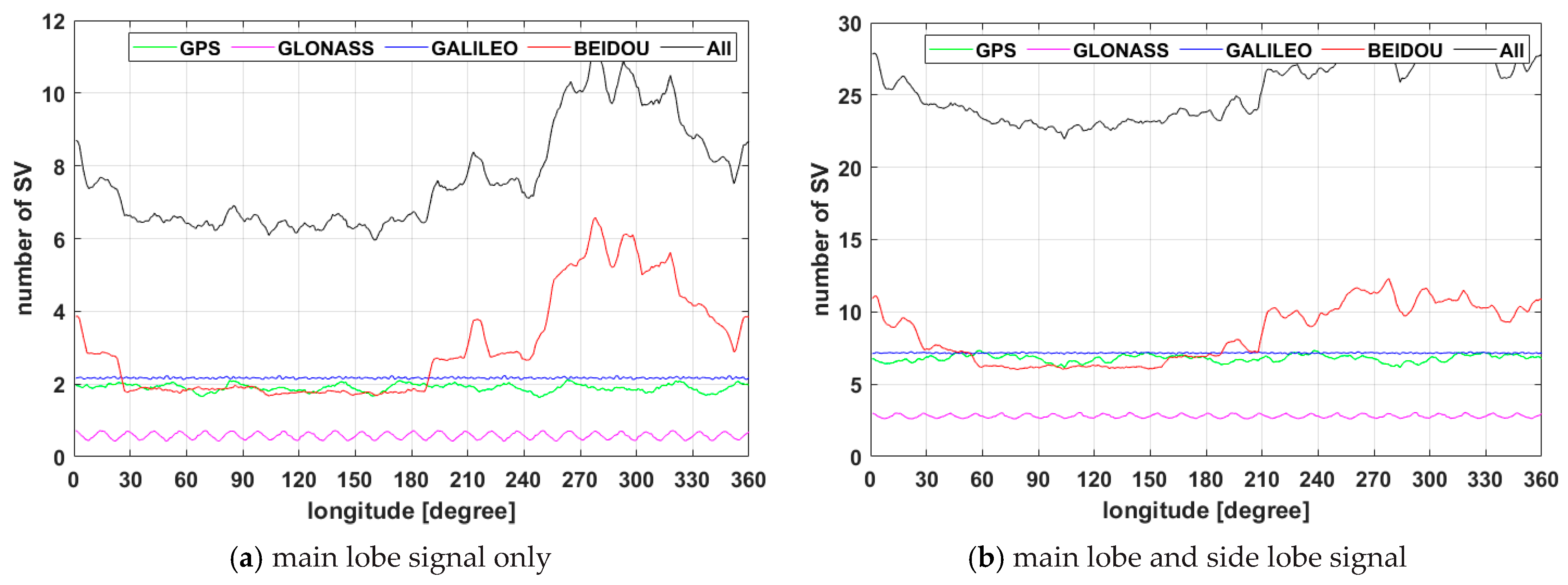
3.2.1. Visibility Test of GNSS Satellites
3.2.2. GDOP Test
3.2.3. Link-Budget Test
3.2.4. UERE Test
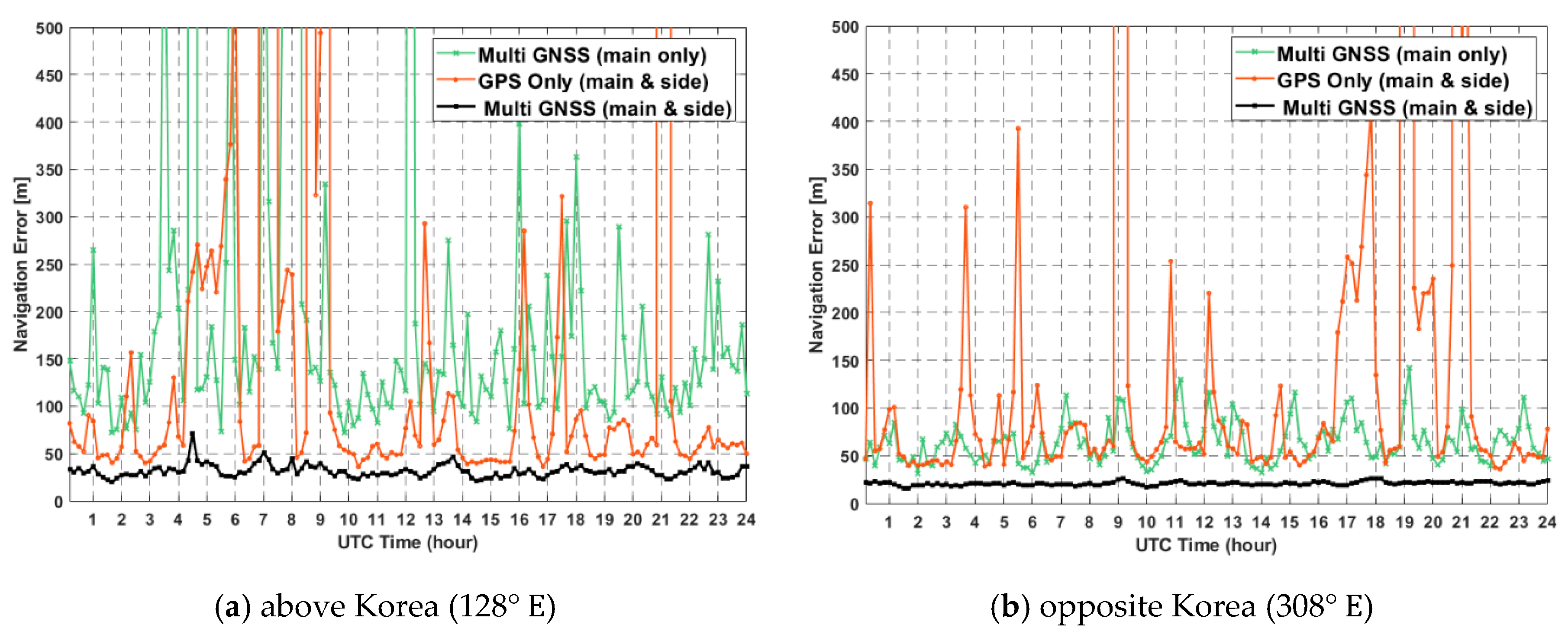
3.2.5. Navigation Solution Error
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Link-Budget Analysis
| Off-Nadir Angle (Deg) | 14.04° | 17.01° | 19.00° | 21.06° | 23.50° |
|---|---|---|---|---|---|
| Power at the satellite antenna input (dBW) | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 |
| Range (km) | 67,709 | 67,112 | 66,652 | 66,127 | 65,440 |
| Path loss (dB) | 167.61 | 167.54 | 167.48 | 167.41 | 167.32 |
| Satellite antenna gain (dB) | 14.98 | 12.56 | 10.80 | 7.35 | –1.34 |
| Atmospheric loss (dB) | 0 | 0 | 0 | 0 | 0 |
| Effective area of omnidirectional receive antenna (dB) | –25.4 | –25.4 | –25.4 | –25.4 | –25.4 |
| Received signal power (dB) | –163.74 | –166.07 | –167.77 | –171.16 | –179.76 |
| Preamplifier noise floor (dB) | –4 | –4 | –4 | –4 | –4 |
| Cable/filter losses (dB) | –1 | –1 | –1 | –1 | –1 |
| Correlation loss (dB) | –1 | –1 | –1 | –1 | –1 |
| Receiver antenna gain (dB) | 5 | 5 | 5 | 5 | 5 |
| Noise power (dBW/Hz) | 204 | 204 | 204 | 204 | 204 |
| C/No (dBHz) | 39.26 | 36.93 | 35.23 | 31.84 | 23.24 |
References
- Bauer, F.H.; Moreau, M.C.; Dahle-Melsaether, M.E.; Petrofski, W.P.; Stanton, B.J.; Thomason, S.; Harris, G.A.; Sena, R.P.; Parker, T., III. The GPS space service volume. In Proceedings of the ION GNSS 2006, Fort Worth, TX, USA, 26–29 September 2006; pp. 2503–2514. [Google Scholar]
- Force, D.A.; Miller, J.J. Combined global navigation satellite systems in the space service volume. In Proceedings of the 2013 International Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2013; pp. 803–807. [Google Scholar]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 1–12. [Google Scholar] [CrossRef]
- GPS World Staff. Korea Will Launch Its Own Satellite Positioning System; GPS World: Cleveland, OH, USA, 2018; Available online: https://www.gpsworld.com/korea-will-launch-its-own-satellite-positioning-system/ (accessed on 17 August 2021).
- Choi, B.-K.; Roh, K.-M.; Ge, H.; Ge, M.; Joo, J.-M.; Heo, M.B. Performance analysis of the Korean Positioning System using observation simulation. Remote Sens. 2020, 12, 3365. [Google Scholar] [CrossRef]
- NASA, NASA Artemis Programme. Available online: https://www.nasa.gov/specials/artemis/ (accessed on 17 August 2021).
- ESA, European Service Module. Available online: https://www.esa.int/Science_Exploration/Human_and_Robotic_Exploration/Orion/European_Service_Module (accessed on 17 August 2021).
- ESA, European Large Logistic Lander (EL3). Available online: http://www.esa.int/Science_Exploration/Human_and_Robotic_Exploration/Exploration/European_Large_Logistics_Lander (accessed on 17 August 2021).
- ESA, Who’s Ready to Serve the Lunar Missions. Available online: https://www.esa.int/Applications/Telecommunications_Integrated_Applications/Who_s_ready_to_serve_the_lunar_missions (accessed on 17 August 2021).
- SSTL, SSTL Lunar Pathfinder Mission. Available online: https://www.sstl.co.uk/what-we-do/lunar-mission-services (accessed on 17 August 2021).
- Rathinam, A.; Dempster, A.G. Effective utilization of space service volume through combined GNSS. In Proceedings of the ION GNSS+ 2016, Portland, OR, USA, 12–16 September 2016; pp. 223–227. [Google Scholar] [CrossRef]
- United Nations. Office for Outer Space Affairs, The Interoperable GNSS Space Service Volume; United Nations Office: Vienna, Austria, 2019. [Google Scholar] [CrossRef]
- Jing, S.; Zhan, X.; Lu, J.; Feng, S.; Ochieng, W. Characterisation of GNSS space service volume. J. Navig. 2015, 68, 107–125. [Google Scholar] [CrossRef]
- Park, Y.; Won, J.-H. GNSS signal use in space service volume. In Proceedings of the Korean GNSS Society Conference, Jeju, Korea, 2–4 November 2016. [Google Scholar]
- Park, Y.; Kwon, K.-H.; Won, J.-H. Performance analysis of multi-constellation and multi-frequency GNSS receivers in deep space. In Proceedings of the ION GNSS+ 2017, Portland, OR, USA, 25–29 September 2017; pp. 1127–1132. [Google Scholar] [CrossRef]
- Shyshkov, F.; Pogurelskiy, O.; Konin, V. Differences in measurements with separate use of frequencies L1 and L2 for the application of satellite navigation in near-earth space. In Proceedings of the 2017 IEEE Microwaves, Radar and Remote Sensing Symposium, Kiev, Ukraine, 29–31 August 2017; pp. 67–70. [Google Scholar] [CrossRef]
- Jing, S.; Zhan, X.; Liu, B.; Chen, M. Weak and dynamic GNSS signal tracking strategies for flight missions in the space service volume. Sensors 2016, 16, 1412. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M.; Zhan, X.; Liu, B.; Yuan, W. SSV visibility evaluation based on different GPS transmitting antenna characteristics. In Proceedings of the CPGPS, Harbin, China, 19–21 May 2017; pp. 152–156. [Google Scholar] [CrossRef]
- Shehaj, E.; Capuano, V.; Botteron, C.; Blunt, P.; Farine, P.-A. GPS based navigation performance analysis within and beyond the space service volume for different transmitters, Antenna Patterns. Aerospace 2017, 4, 44. [Google Scholar] [CrossRef] [Green Version]
- Capuano, V.; Shehaj, E.; Blunt, P.; Botteron, C.; Farine, P.A. High accuracy GNSS based navigation in GEO. Acta Astronaut. 2017, 136, 332–341. [Google Scholar] [CrossRef]
- Shin, H.; Kwon, K.-H.; Won, J.-H. The impact of non-MEO GNSS Satellite for the longitude of geostationary orbit. In Proceedings of the Korean GNSS Society Conference, Jeju, Korea, 7–9 November 2018; pp. 578–581. [Google Scholar]
- Ji, G.-H.; Shin, H.; Won, J.-H. Analysis of multi-constellation GNSS receiver performance utilizing 1-st side-lobe signal on the use of SSV for KPS satellites. IET Radar Sonar Navig. 2021, 15, 485–499. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006; ISBN 9780970954411. [Google Scholar]
- Moreau, M.C.; David, E.P.; Carpenter, J.R.; Kelbel, D.; Davis, G.W.; Axelrad, P. Results from the GPS flight experiment on the high earth orbit AMSAT OSCAR-40 spacecraft. In Proceedings of the ION GPS 2002, Portland, OR, USA, 25–29 September 2002; pp. 122–133. [Google Scholar]
- Teunissen, P.; Montenbruck, O. (Eds.) Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-42926-7. [Google Scholar]
- Chibout, B.; Macabiau, C.; Escher, A.-C.; Ries, L.; Issler, J.-L. Investigation of new processing techniques for geostationary satellite positioning. In Proceedings of the 2006 National Technical Meeting of the Institute of Navigation, Monterey, CA, USA, 18–20 January 2006; pp. 250–259. [Google Scholar]
- Su, X.; Geng, T.; Li, W.; Zhao, Q.; Xie, X. Chang’E-5T orbit determination using onboard GPS observations. Sensors 2017, 17, 1260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, J.; Tang, G.; Hu, S.; Zhang, Y.; Liu, L. Orbit determination for CE5T based upon GPS data. J. Syst. Eng. Electron. 2016, 38, 1121–1125. [Google Scholar]

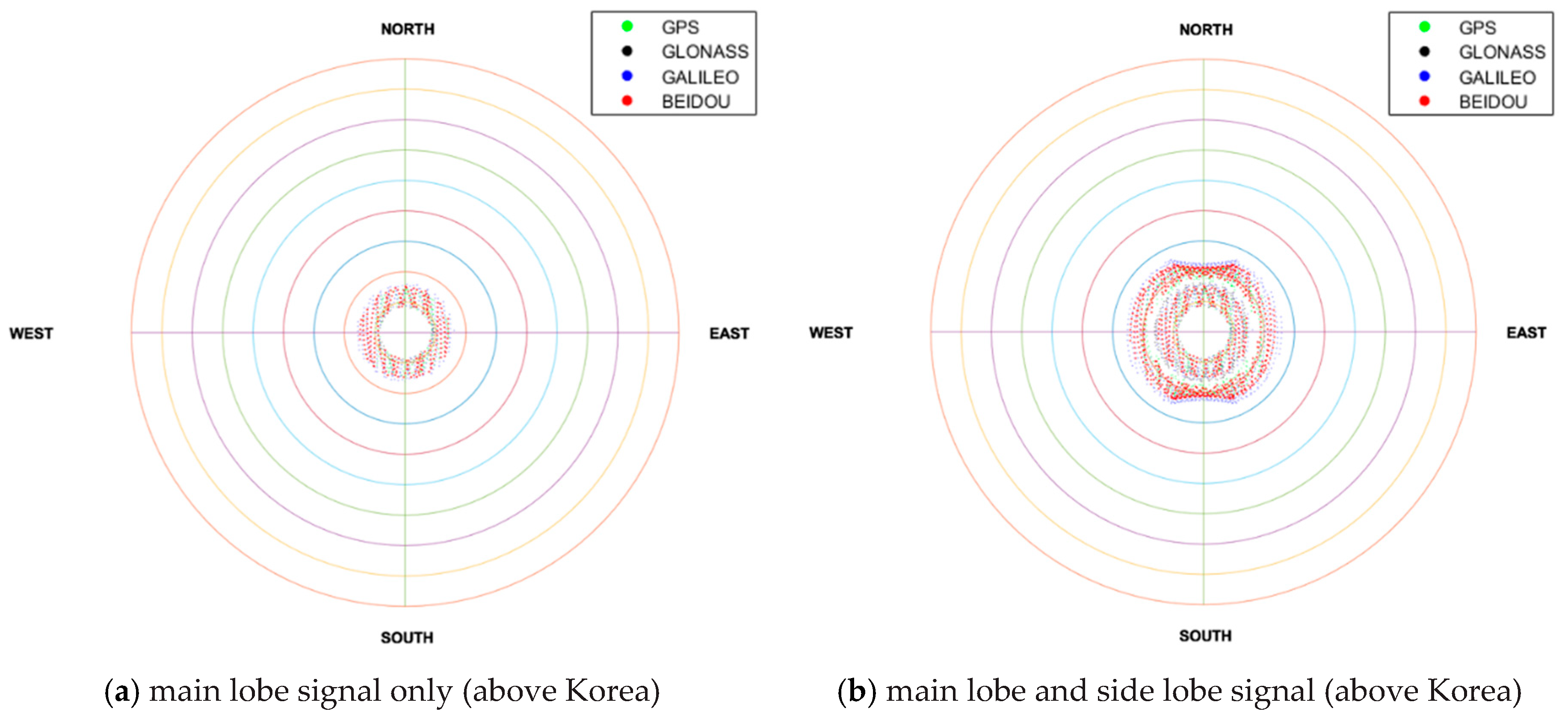
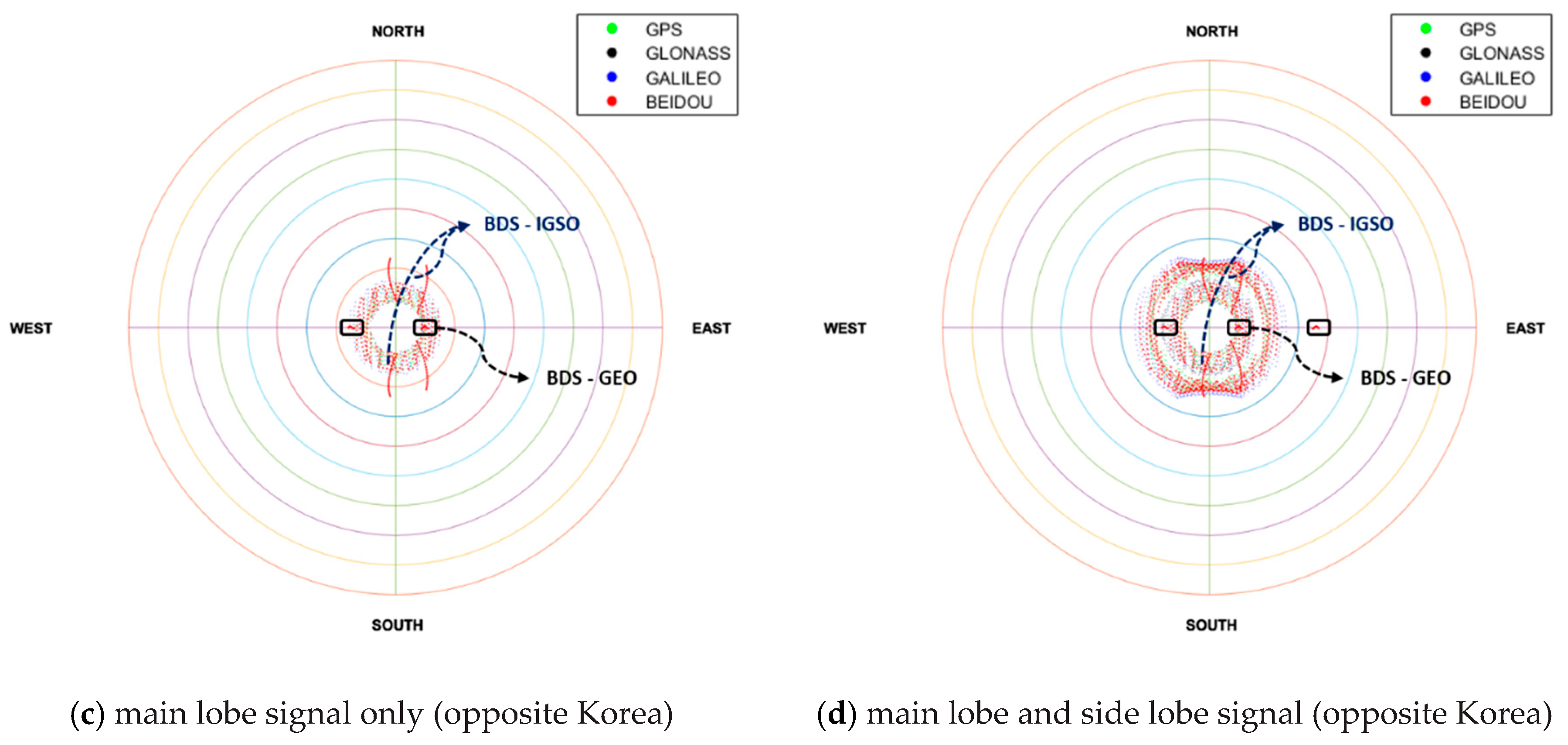


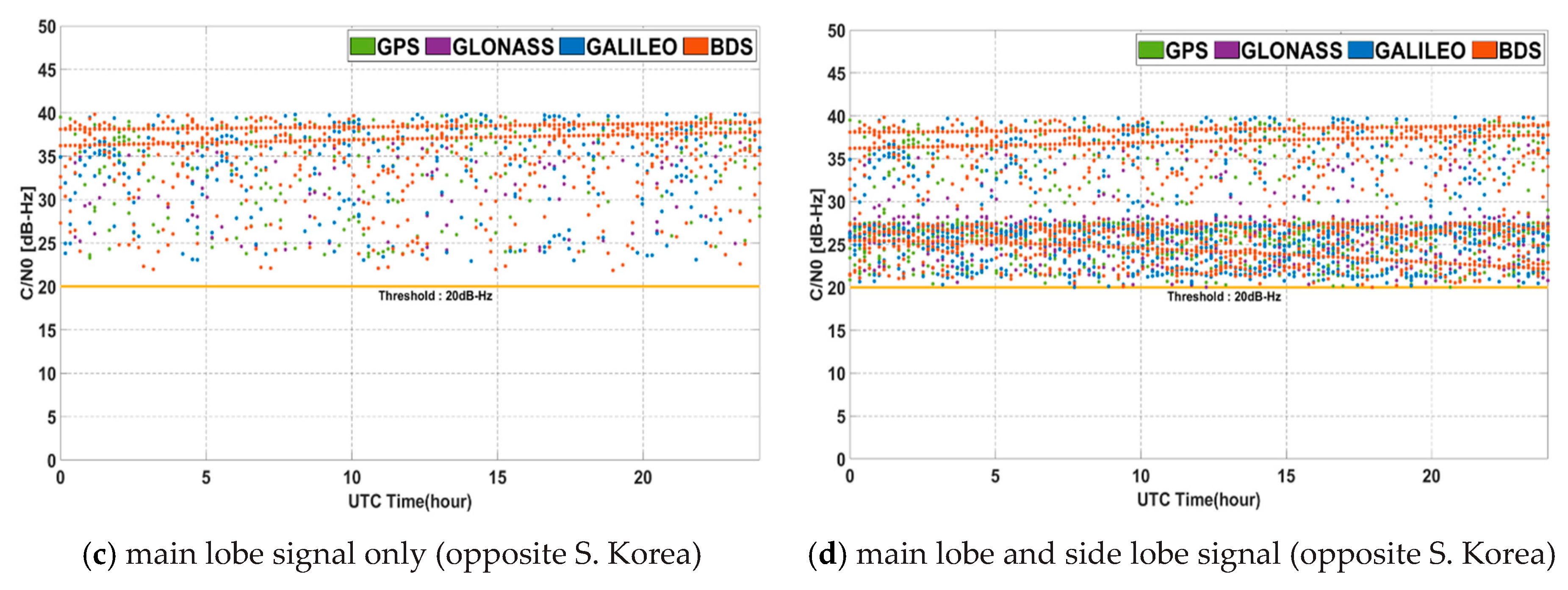
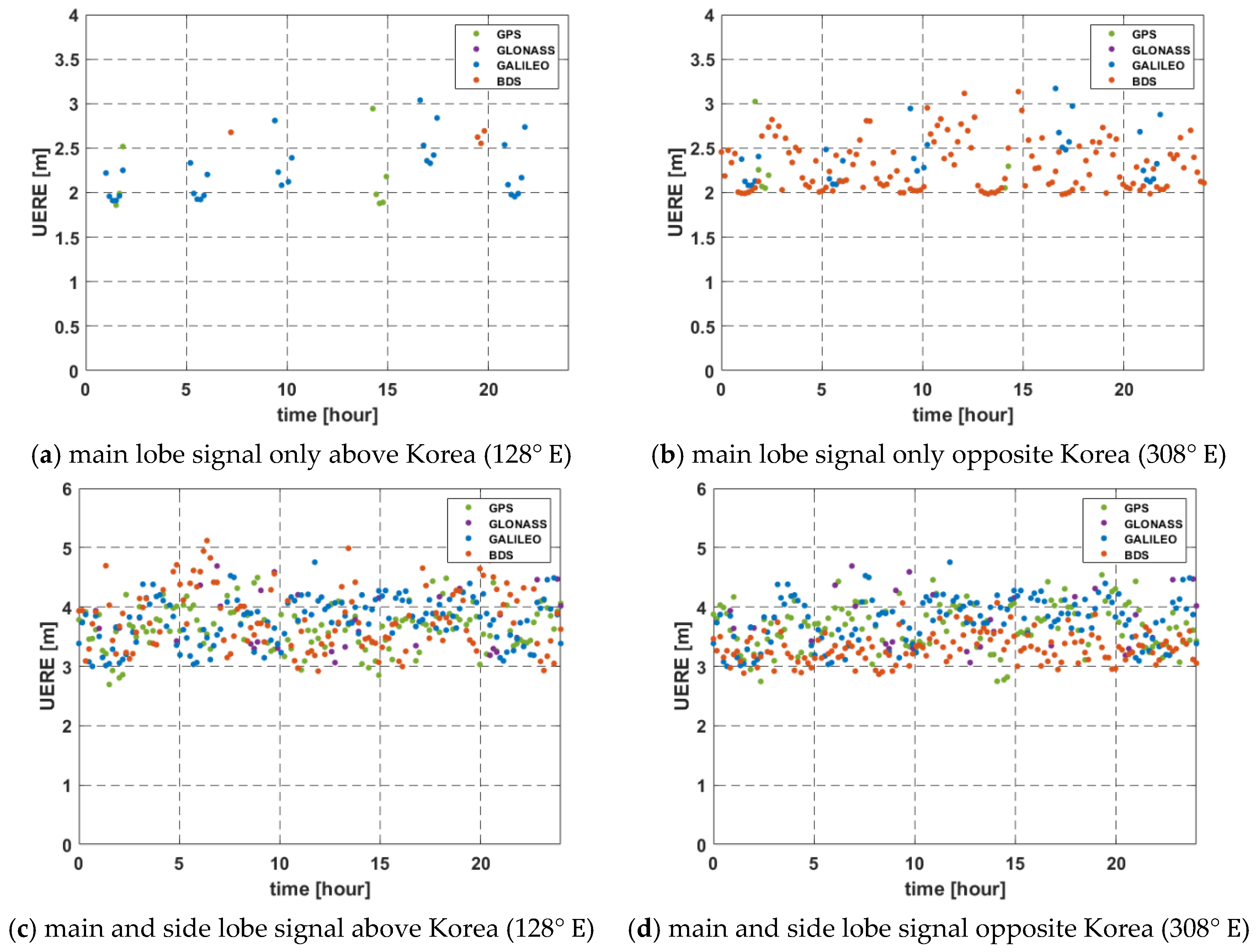
| Parameter | Configuration |
|---|---|
| Simulation time | 0–86,400 sec (0–24 h), epoch interval: 600 s (10 min) |
| Orbit | GEO (Korean Peninsula (128°E), the opposite side of Korea (308° E)) |
| Multi-GNSS (number of satellites) | GPS (32), GLONASS (24), GALILEO (30), BDS (35) |
| Beam-width | Main lobe (23.5°), first side lobe (27°–39°) |
| Receiver setting | C/N0 threshold: 20 dB-Hz DLL bandwidth: 1 Hz Correlator spacing: 0.1 chip |
| Performance | Satellite visibility, GDOP, C/N0, UERE, Navigation Error |
| Type | Main Lobe Signal Only | (Main + Side) Lobe Signal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure | GPS | GLO | GAL | BDS | Multi | GPS | GLO | GAL | BDS | Multi | |
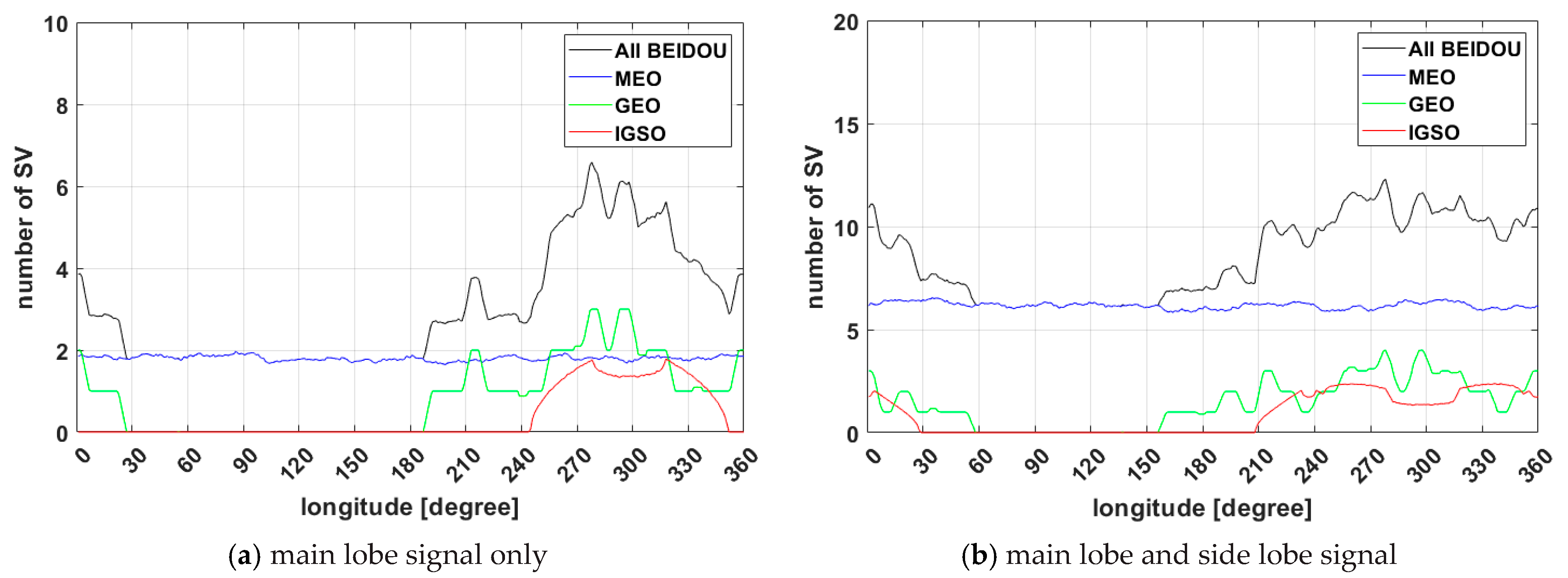
| All Orbit (GEO) | At least 4 (%) | 0 | 0 | 0 | 23.33 | 100 | 100 | 0 | 100 | 100 | 100 |
| Min (#) | 1.63 | 0.42 | 2.13 | 1.67 | 5.96 | 6.15 | 2.60 | 7.06 | 6.02 | 21.95 | |
| Avg (#) | 1.90 | 0.58 | 2.17 | 3.01 | 7.66 | 6.80 | 2.80 | 7.16 | 8.47 | 25.22 | |
| Max (#) | 2.11 | 0.72 | 2.23 | 6.58 | 11.35 | 7.35 | 3.04 | 7.25 | 12.31 | 28.79 | |
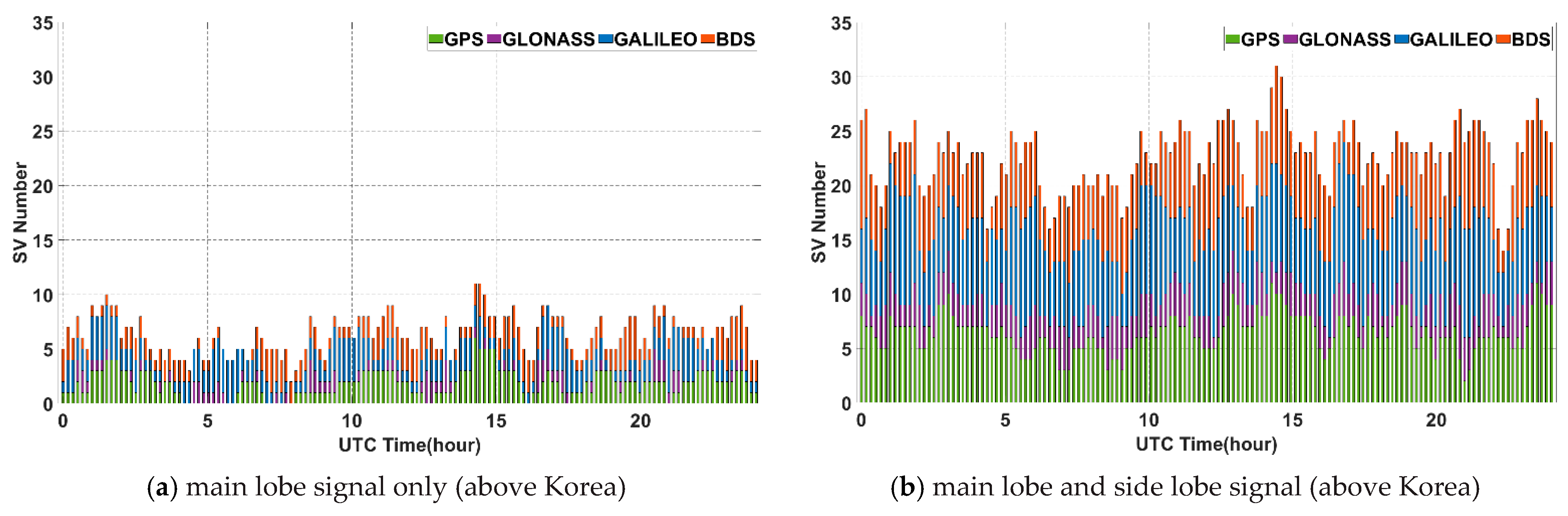
| Above Korea (128°E) | At least 1 (%) | 84.72 | 45.83 | 96.53 | 90.28 | 100 | 100 | 99.30 | 100 | 100 | 100 |
| At least 4 (%) | 5.56 | 0 | 21.53 | 5.56 | 97.92 | 95.14 | 29.86 | 99.30 | 91.67 | 100 | |
| Min (#) | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 3 | 2 | 14 | |
| Avg (#) | 1.79 | 0.63 | 2.16 | 1.76 | 6.35 | 6.49 | 2.90 | 7.17 | 6.08 | 22.63 | |
| Max (#) | 6 | 3 | 4 | 4 | 11 | 11 | 5 | 11 | 10 | 31 | |
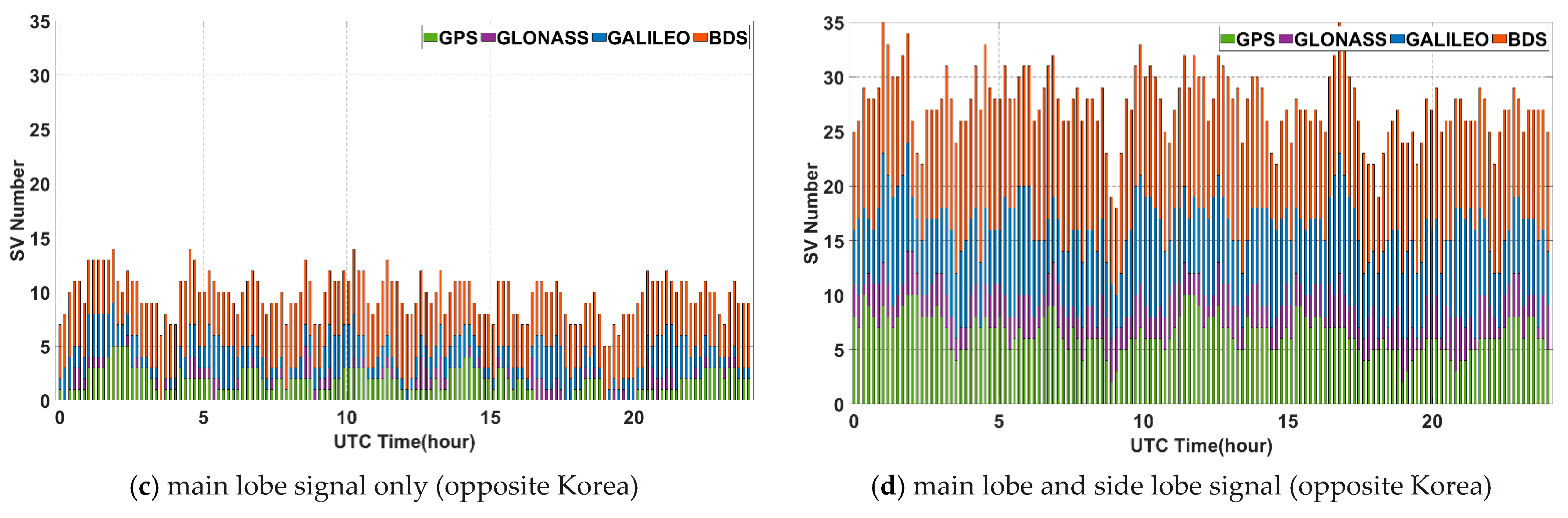
| Opposite Korea (308°E) | At least 1 (%) | 85.42 | 45.83 | 96.53 | 100 | 100 | 100 | 99.30 | 100 | 100 | 100 |
| At least 4 (%) | 4.86 | 0 | 21.53 | 97.22 | 100 | 96.53 | 29.86 | 99.31 | 100 | 100 | |
| Min (#) | 0 | 0 | 0 | 3 | 5 | 2 | 0 | 3 | 6 | 18 | |
| Avg (#) | 1.76 | 0.63 | 2.17 | 5.23 | 9.79 | 6.53 | 2.90 | 7.17 | 10.83 | 27.42 | |
| Max (#) | 5 | 3 | 4 | 8 | 14 | 10 | 5 | 11 | 15 | 35 | |
| Type | Main Lobe Signal Only | (Main + Side) Lobe Signal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure | GPS | GLO | GAL | BDS | Multi | GPS | GLO | GAL | BDS | Multi | |
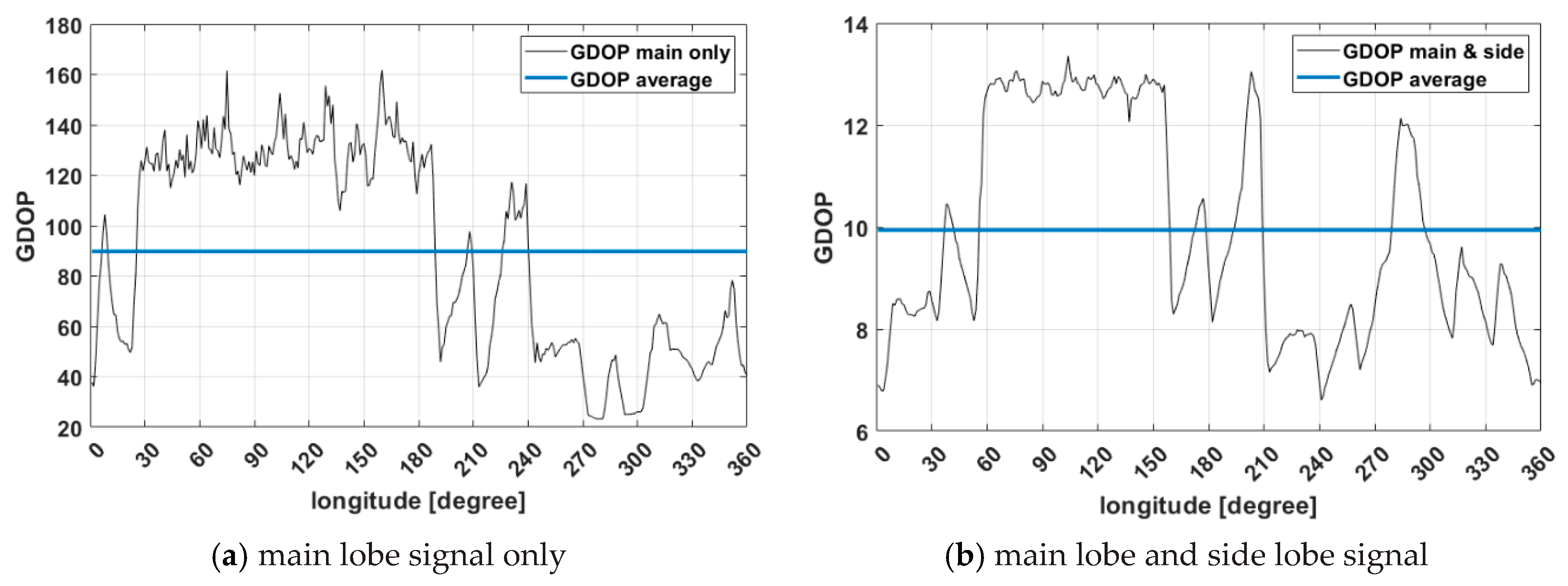
| All Orbit (GEO) | Avg | 305.9 | - | 215.4 | 185.1 | 89.77 | 47.10 | 299.0 | 32.16 | 23.68 | 9.94 |
| Above Korea (128°E) | less than 100 (%) | 4.17 | 0 | 20.83 | 2.78 | 97.22 | 95.14 | 26.39 | 99.31 | 91.67 | 100 |
| Avg | 233.14 | - | 237.41 | 331.34 | 134.04 | 42.41 | 292.53 | 31.24 | 45.31 | 12.84 | |
| Opposite Korea (308°E) | less than 100 (%) | 4.17 | 0 | 20.83 | 96.5. | 100 | 96.53 | 26.39 | 99.31 | 100 | 100 |
| Avg | 277.81 | - | 237.32 | 112.31 | 51.07 | 42.73 | 292.53 | 31.24 | 11.97 | 8.27 | |
| Type | Main Lobe Signal Only | (Main + Side) Lobe Signal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure | GPS | GLO | GAL | BDS | Multi | GPS | GLO | GAL | BDS | Multi | |
| Above Korea (128°E) | Min | 0 | 0 | 0 | 0 | 0 | 20.03 | 0 | 20.01 | 20.15 | 0 |
| Avg | 33.50 | 30.98 | 34.21 | 33.09 | 33.34 | 27.58 | 26.32 | 27.43 | 27.07 | 27.33 | |
| Max | 39.58 | 36.58 | 39.83 | 39.72 | 39.83 | 39.58 | 36.57 | 39.83 | 39.72 | 39.83 | |
| Opposite Korea (308°E) | Min | 0 | 0 | 0 | 21.85 | 0 | 20.02 | 0 | 20.01 | 20.00 | 0 |
| Avg | 33.60 | 30.98 | 34.22 | 35.35 | 34.43 | 27.53 | 26.32 | 27.43 | 29.92 | 28.36 | |
| Max | 39.63 | 36.58 | 39.83 | 39.84 | 39.84 | 39.63 | 36.58 | 39.83 | 39.84 | 39.84 | |
| Type | Main Lobe Signal Only | (Main + Side) Lobe Signal | |||
|---|---|---|---|---|---|
| Figure | GPS | Multi | GPS | Multi | |
| Above Korea (128°E) | Mean (m) | 2.67 | 2.63 | 3.15 | 3.21 |
| Std (m) | 0.47 | 0.45 | 0.46 | 0.26 | |
| Opposite Korea (308°E) | Mean (m) | 2.35 | 2.34 | 3.35 | 3.29 |
| Std (m) | 0.46 | 0.30 | 0.47 | 0.25 | |
| Type | Main Lobe Signal Only | (Main + Side) Lobe Signal | |||
|---|---|---|---|---|---|
| Figure | GPS | Multi | GPS | Multi | |
| Above Korea (128°E) | Mean (m) | 1391.02 | 279.80 | 112.79 | 35.88 |
| Std (m) | 382.44 | 439.51 | 76.22 | 7.04 | |
| Opposite Korea (308°E) | Mean (m) | 1046.14 | 93.23 | 112.96 | 23.58 |
| Std (m) | 366.13 | 36.02 | 76.54 | 1.77 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, G.-H.; Kwon, K.-H.; Won, J.-H. GNSS Signal Availability Analysis in SSV for Geostationary Satellites Utilizing multi-GNSS with First Side Lobe Signal over the Korean Region. Remote Sens. 2021, 13, 3852. https://doi.org/10.3390/rs13193852
Ji G-H, Kwon K-H, Won J-H. GNSS Signal Availability Analysis in SSV for Geostationary Satellites Utilizing multi-GNSS with First Side Lobe Signal over the Korean Region. Remote Sensing. 2021; 13(19):3852. https://doi.org/10.3390/rs13193852
Chicago/Turabian StyleJi, Gun-Hoon, Ki-Ho Kwon, and Jong-Hoon Won. 2021. "GNSS Signal Availability Analysis in SSV for Geostationary Satellites Utilizing multi-GNSS with First Side Lobe Signal over the Korean Region" Remote Sensing 13, no. 19: 3852. https://doi.org/10.3390/rs13193852
APA StyleJi, G.-H., Kwon, K.-H., & Won, J.-H. (2021). GNSS Signal Availability Analysis in SSV for Geostationary Satellites Utilizing multi-GNSS with First Side Lobe Signal over the Korean Region. Remote Sensing, 13(19), 3852. https://doi.org/10.3390/rs13193852