Forecasting Ionospheric foF2 Based on Deep Learning Method
Abstract
1. Introduction
2. Models and Data
2.1. Neural Network Models
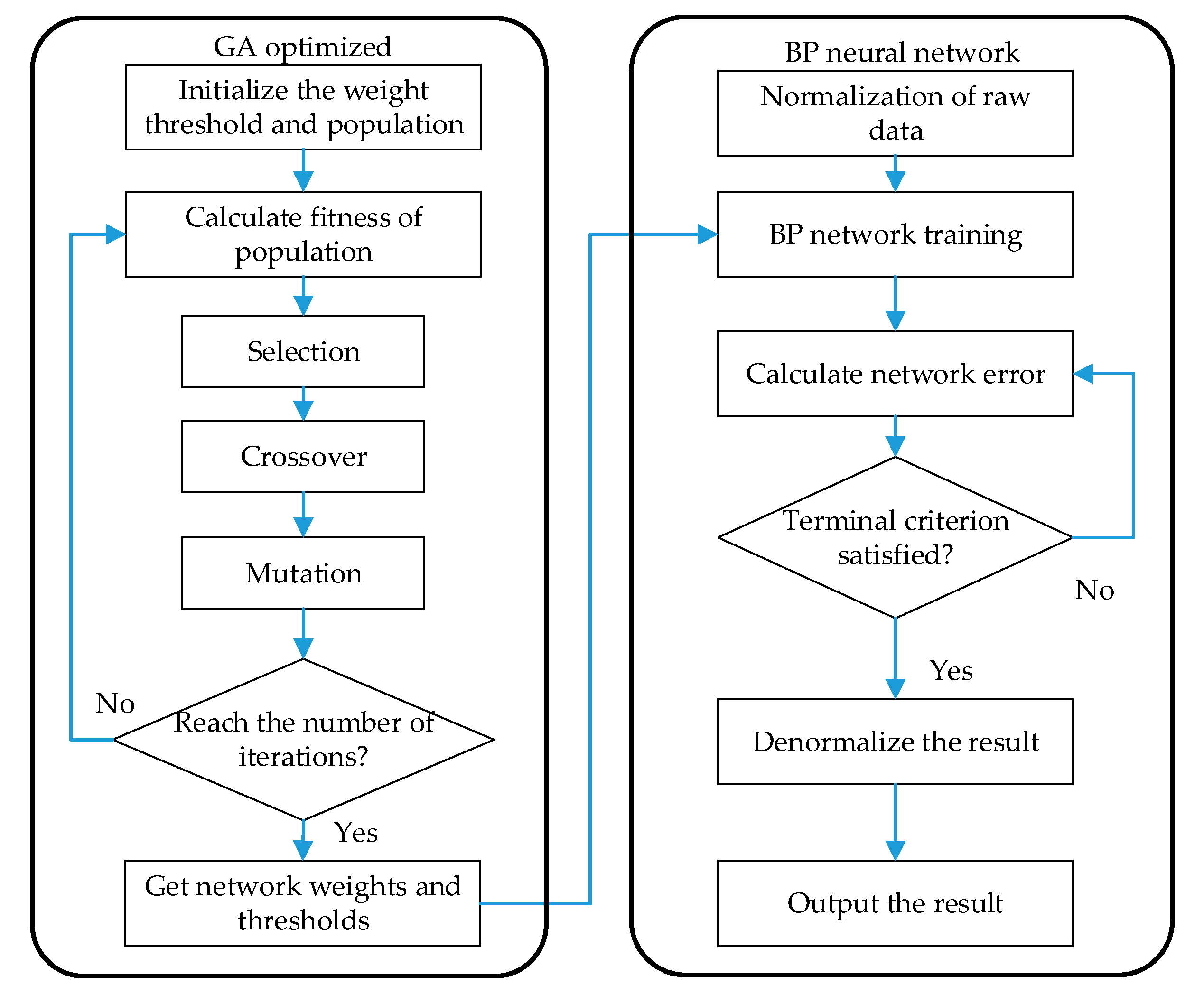
2.1.1. Methodology Description
2.1.2. Input and Output Parameters
2.1.3. Configuration and Training
2.2. Deep Learning LSTM Model
2.2.1. Methodology Description
2.2.2. Input and Output Parameters
2.2.3. Configuration and Training
2.3. Data and Processing
2.3.1. Data Sets
2.3.2. Data Preprocess
2.4. Error Analysis
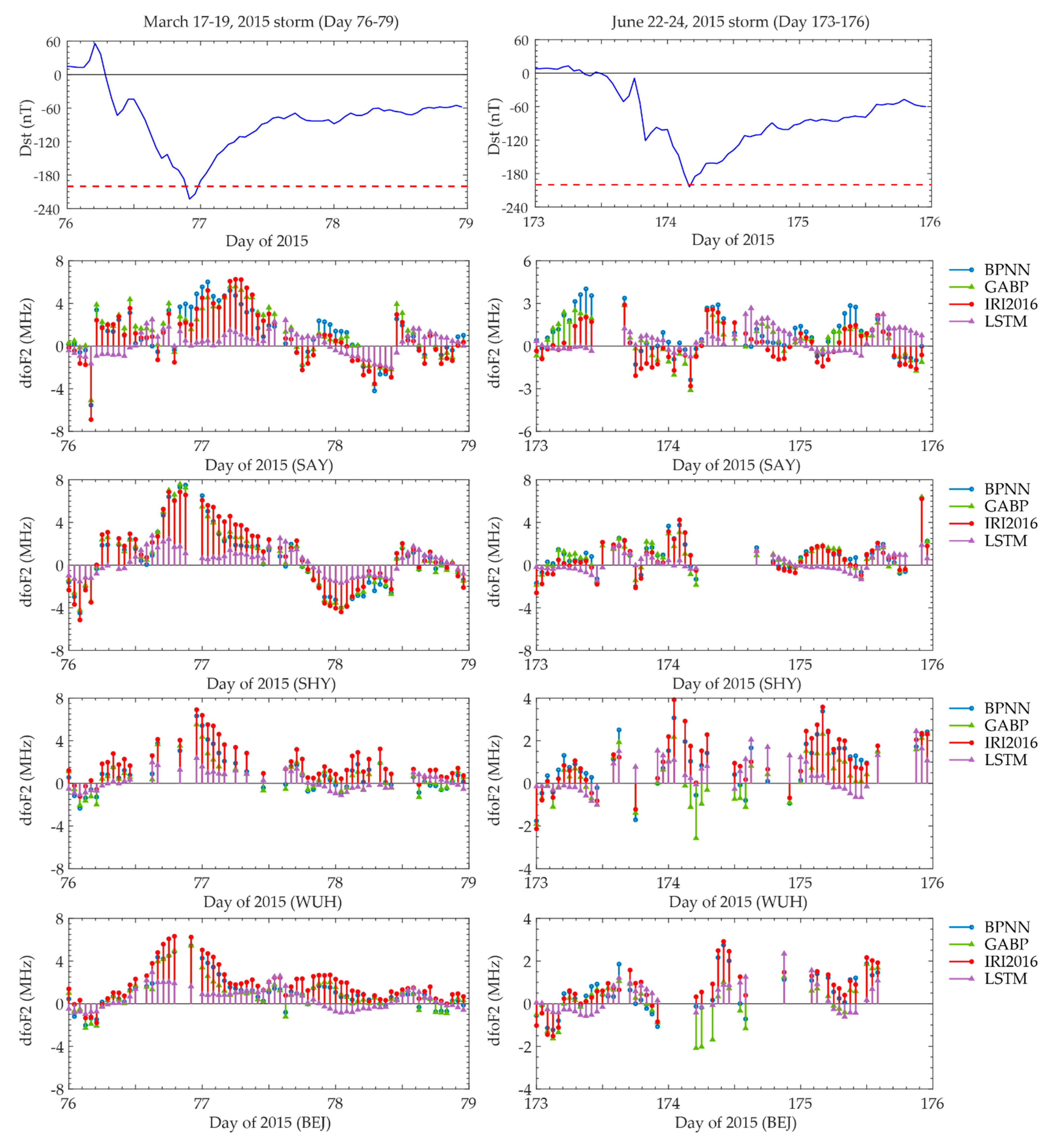
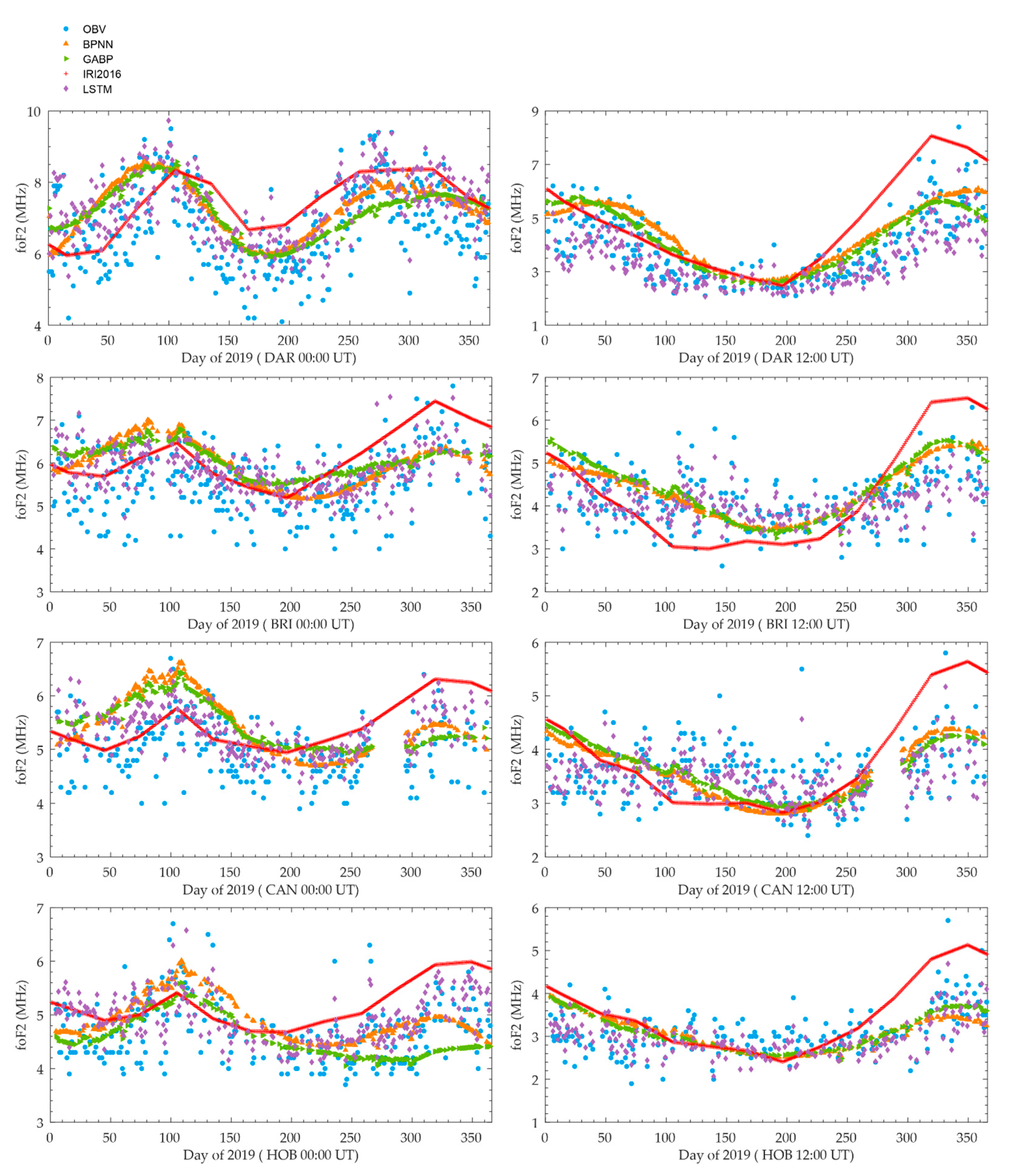
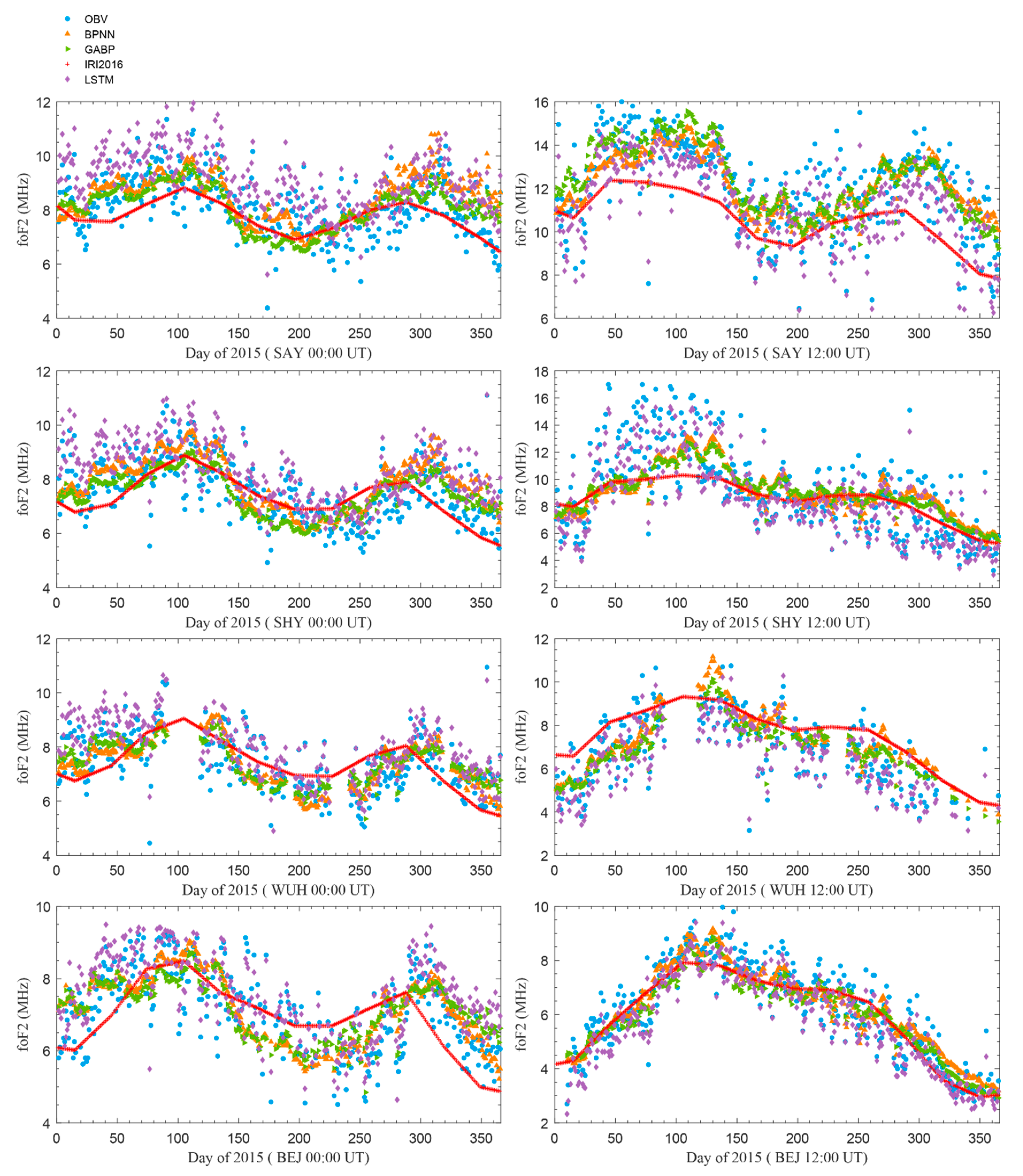
3. Results and Discussion
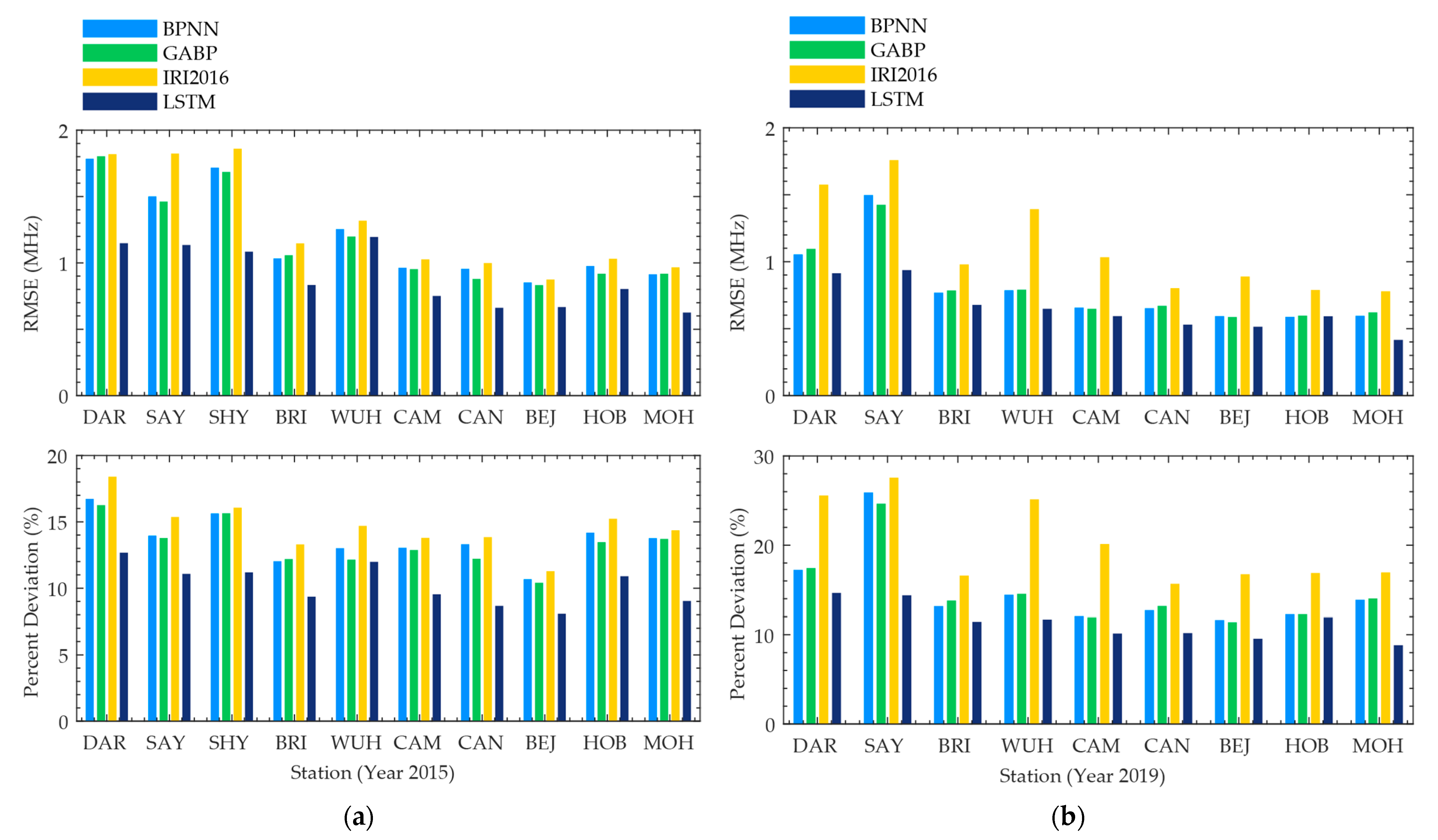
3.1. The Forecasting Performance
3.2. Diurnal Variations of Forecasting Models
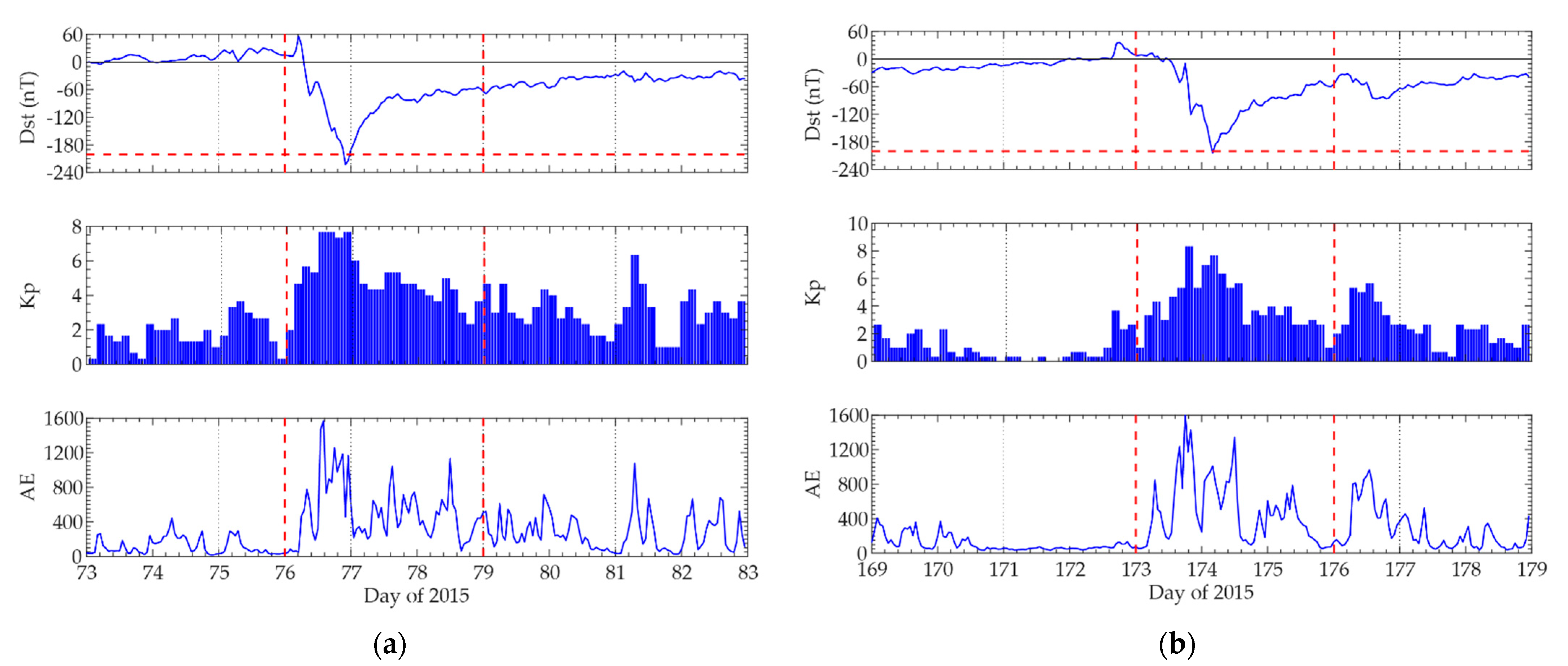
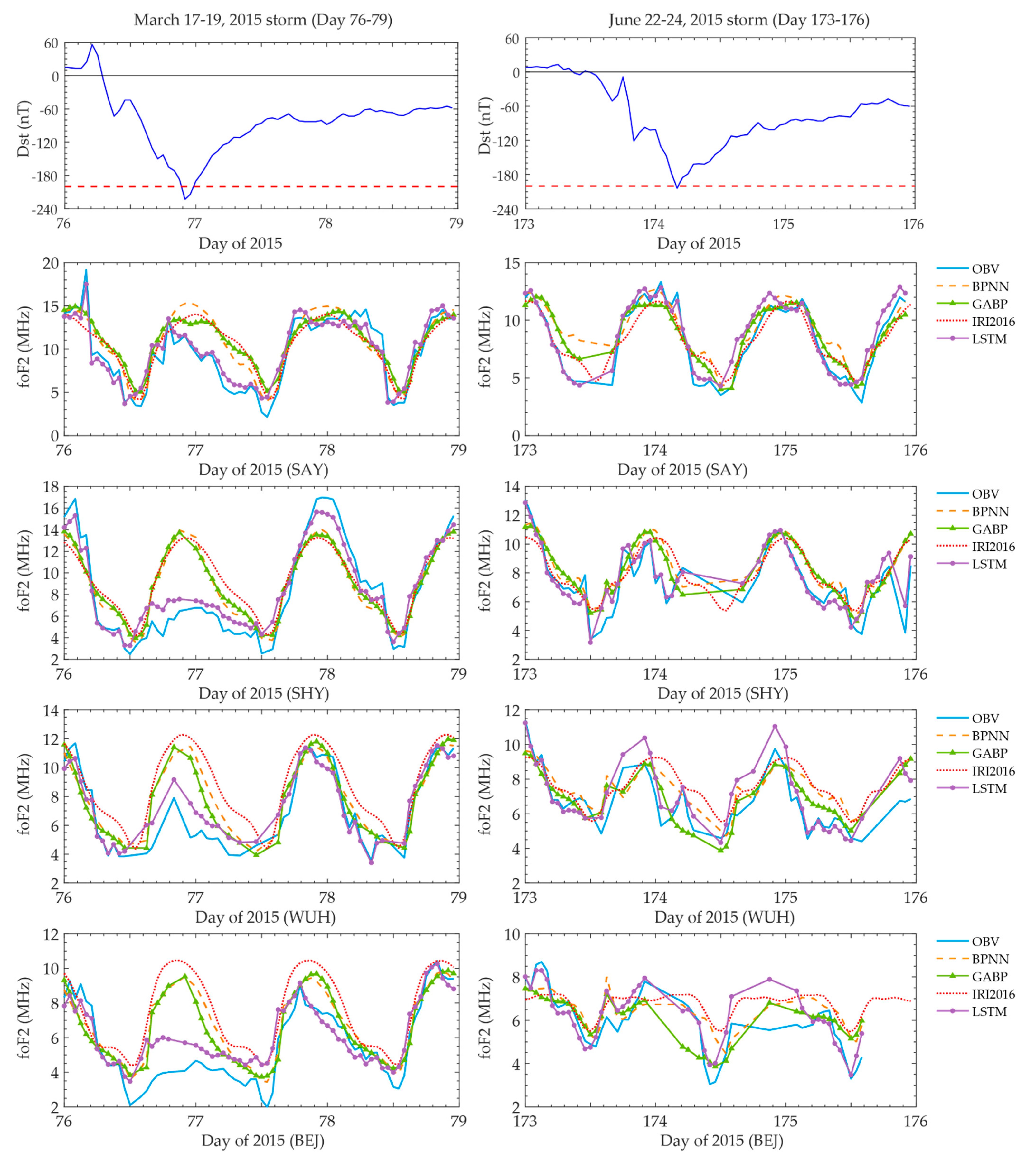
3.3. Seasonal Variations of Forecasting Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LSTM | Long-Short-Term Memory |
| foF2 | the critical frequency of the ionosphere F2 layer |
| LT | Local Time |
| SSN | the Sunspot Number |
| BPNN | a Back-Propagation Neural Network |
| GABP | a Genetic Algorithm optimized Backpropagation neural network |
| IRI | the International Reference Ionosphere model |
| HF | High Frequency |
| RNN | a Recurrent Neural Network |
| GRU | Gated Recurrent Unit |
| GA | Genetic Algorithm |
| TEC | Total Electron Content |
| URSI | Union of Radio Science International |
| COSPAR | the Committee on Space Research |
| RMSE | Root Mean Square Error |
| PD | Percentage Deviation |
| hmF2 | peak heights of the F2 layer |
| M3000F2 | M factor of F2 layer |
| NOAA | the National Oceanic and Atmospheric Administration |
| WDC | the World Data System |
References
- Blaunstein, N.; Plohotniuc, E. Ionosphere and Applied Aspects of Radio Communication and Radar; CRC Press, Taylor & Francis Group: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Goodman, J.M. Operational communication systems and relationships to the ionosphere and space weather. Adv. Space Res. 2005, 36, 2241–2252. [Google Scholar] [CrossRef]
- Hill, G.E. HF communication during ionospheric storms. J. Res. NBS 1963, 67, 23–30. [Google Scholar] [CrossRef]
- Kouris, S.S.; Xenos, T.D.; Polimeris, K.V.; Stergiou, D. TEC and foF2 variations: Preliminary results. Ann. Geophys. 2004, 47, 1325–1332. [Google Scholar] [CrossRef]
- Sezen, U.; Sahin, O.; Arikan, F.; Arikan, O. Estimation of hmF2 and foF2 Communication Parameters of Ionosphere F2-Layer Using GPS Data and IRI-Plas Model. IEEE Trans. Antennas Propag. 2013, 61, 5264–5273. [Google Scholar] [CrossRef]
- Oyeyemi, E.O.; Poole, A.W.V. Towards the development of a new global foF2 empirical model using neural networks. Adv. Space Res. 2004, 34, 1966–1972. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather. 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Laštovička, J.; Mikhailov, A.V.; Ulich, T.; Bremer, J.; Elias, A.G.; de Adler, N.O.; Jara, V.; del Rio, R.A.; Foppiano, A.J.; Ovalle, E.; et al. Long-term trends in foF2: A comparison of various methods. J. Atmos. Sol.-Terr. Phys. 2006, 68, 1854–1870. [Google Scholar] [CrossRef]
- Muhtarov, P.; Kutiev, I. Autocorrelation method for temporal interpolation and short-term prediction of ionospheric data. Radio Sci. 2016, 34, 459–464. [Google Scholar] [CrossRef]
- Sojka, J.J.; Thompson, S.R.; Schunk, R.W. Assimilation ionospheric model: Development and testing with combined ionospheric campaign Caribbean measurements. J. Radio Sci. 2001, 247–259. [Google Scholar] [CrossRef]
- Scherliess, L.; Thompson, D.C.; Schunk, R.W. Ionospheric dynamics and drivers obtained from a physics-based data assimilation model. Radio Sci. 2009, 44. [Google Scholar] [CrossRef]
- Cander, L.R.; Milosavljevic, M.M.; Stankovic, S.S.; Tomasevic, S. Ionospheric forecasting technique by artificial neural network. Electron. Lett. 1998, 34, 1573–1574. [Google Scholar] [CrossRef]
- Oyeyemi, E.O.; Poole, A.W.V.; McKinnell, L.A. On the global model for foF2 using neural networks. Radio Sci. 2005, 40, 1–15. [Google Scholar] [CrossRef]
- Oyeyemi, E.O.; Poole, A.W.V.; McKinnell, L.A. On the global short-term forecasting of the ionospheric critical frequency foF2 up to 5 h in advance using neural networks. Radio Sci. 2005, 40, 1–12. [Google Scholar] [CrossRef]
- Oyeyemi, E.O.; McKinnell, L.A.; Poole, A.W.V. Near-real time foF2 predictions using neural networks. J. Atmos. Terr. Phys. 2006, 68, 1807–1818. [Google Scholar] [CrossRef]
- Poole, A.W.V.; McKinnell, L.A. On the predictability of foF2 using neural networks. Radio Sci. 2016, 35, 225–234. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, C.; Deng, Z.; Ni, B.; Zhao, Z. Predicting foF2 in the China Region Using the Neural Networks Improved by the Genetic Algorithm. J. Atmos. Sol. Terr. Phys. 2013, 92, 7–17. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, C.; Zhao, J.; Liu, Y.; Liu, M.; Zhao, Z. The ionospheric foF2 prediction based on neural network optimization algorithm. Chin. J. Radio Sci. 2018, 33, 708–716. [Google Scholar] [CrossRef]
- Ding, S.; Su, C.; Yu, J. An optimizing BP neural network algorithm based on genetic algorithm. Artif. Intell. Rev. 2011, 36, 153–162. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.J.; Liu, Y.; Wang, X.; Zhou, C. Ionospheric foF2 disturbance forecast using neural network improved by a genetic algorithm. Adv. Space Res. 2019, 63, 4003–4014. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, R.; Lou, W.; Liu, J.; Ni, B.; Deng, Z.; Zhao, Z. Preliminary investigation of real-time mapping of foF2 in northern China based on oblique ionosonde data. J. Geophys. Res. Space Phys. 2013, 118, 2536–2544. [Google Scholar] [CrossRef]
- Zhao, X.; Ning, B.; Liu, L.; Song, G. A prediction model of short-term ionospheric foF2 based on AdaBoost. Adv. Space Res. 2013, 53, 387–394. [Google Scholar] [CrossRef]
- Habarulema, J.B.; McKinnell, L.A.; Opperman, B.D.L. A recurrent neural network approach to quantitatively studying solar wind effects on TEC derived from GPS; preliminary results. Ann. Geophys. 2009, 27, 2111–2125. [Google Scholar] [CrossRef]
- Lv, Z.; Yu, C.; Liu, A. Forecasting the Ionospheric f0F2 Parameter One Hour in Advance Using Recurrent Neural Network. In Proceedings of the 2019 International Conference on Computer, Network, Communication and Information Systems (CNCI 2019), Qingdao, China, 27–29, March 2019; pp. 249–258. [Google Scholar]
- Sun, W.; Xu, L.; Huang, X.; Zhang, W.; Yuan, T.; Chen, Z.; Yan, Y. Forecasting of ionospheric vertical total electron content (TEC) using LSTM networks. In Proceedings of the 2017 International Conference on Machine Learning and Cybernetics (ICMLC), Ningbo, China, 9–12 July 2017; Volume 2, pp. 340–344. [Google Scholar]
- Ruwali, A.; Kumar, A.S.; Prakash, K.B.; Sivavaraprasad, G.; Ratnam, D.V. Implementation of hybrid deep learning model (LSTM-CNN) for ionospheric TEC forecasting using GPS data. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1004–1008. [Google Scholar] [CrossRef]
- Cherrier, N.; Castaings, T.; Boulch, A. Forecasting ionospheric Total Electron Content maps with deep neural networks. In Proceedings of the Big Data Space (BIDS); ESA Workshop: Paris, France, 2017. [Google Scholar]
- Oliveira, T.P.; Barbar, J.S.; Soares, A.S. Computer network traffic prediction: A comparison between traditional and deep learning neural networks. Int. J. Big Data Intell. 2016, 3, 28–37. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks: Architectures, Algorithms, and Applications; Prentice-Hall: Hoboken, NJ, USA, 1994; ISBN 0133341860. [Google Scholar]
- White, H. Learning in artificial neural networks: A statistical perspective. Neural Comput. 1989, 1, 425–464. [Google Scholar] [CrossRef]
- Murata, N.; Yoshizawa, S.; Amari, S.I. Network information criterion-determining the number of hidden units for an artificial neural network model. IEEE Trans. Neural Netw. 1994, 5, 865–872. [Google Scholar] [CrossRef] [PubMed]
- Sarma, A.D.; Madhu, T. Modelling of foF2 using neural networks at an equatorial anomaly station. Curr. Sci. 2005, 89, 1245–1247. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, C.C. Analysis of Local Minimization for BP Algorithm and Its Avoidance Methods. Comput. Eng. 2002, 28, 35–36. [Google Scholar] [CrossRef]
- Wintoft, P.; Cander, L.R. Ionospheric foF2 storm forecasting using neural networks. Phys. Chem. Earth Part C Sol. Terr. Planet. Sci. 2000, 25, 267–273. [Google Scholar] [CrossRef]
- Williscroft, L.A.; Poole, A.W. Neural networks, foF2, sunspot number and magnetic activity. Geophys. Res. Lett. 1996, 23, 3659–3662. [Google Scholar] [CrossRef]
- Kumluca, A.; Tulunay, E.; Topalli, I.; Tulunay, Y. Temporal and spatial forecasting of ionospheric critical frequency using neural networks. Radio Sci. 1999, 34, 1497–1506. [Google Scholar] [CrossRef]
- Cander, L.R. Spatial correlation of foF2 and vTEC under quiet and disturbed ionospheric conditions: A case study. Acta Geophys. 2007, 55, 410–423. [Google Scholar] [CrossRef]
- Wrenn, G. Time-Weighted Accumulations ap(τ) and Kp(τ). J. Geophys. Res. 1987, 92, 10125–10129. [Google Scholar] [CrossRef]
- Secan, J.A.; Wilkinson, P.J. Statistical studies of an effective sunspot number. Radio Sci. 1997, 32, 1717–1724. [Google Scholar] [CrossRef]
- Apostolov, E.M.; Altadill, D.; Todorova, M. The 22-year cycle in the geomagnetic 27-day recurrences reflecting on the F2-layer ionization. Ann. Geophys. 2004, 22, 1171–1176. [Google Scholar] [CrossRef][Green Version]
- Liang, M.C.; Li, K.F.; Shia, R.L.; Yung, Y.L. Short-period solar cycle signals in the ionosphere observed by FORMOSAT-3/COSMIC. Geophys. Res. Lett. 2008, 35, 1–4. [Google Scholar] [CrossRef]
- Xu, J.S.; Li, X.J.; Liu, Y.W.; Jing, M. Effects of declination and thermospheric wind on TEC longitude variations in the mid-latitude ionosphere. Chin. J. Geophys. 2013, 56, 1425–1434. [Google Scholar] [CrossRef]
- Kaselimi, M.; Voulodimos, A.; Doulamis, N.; Doulamis, A.; Delikaraoglou, D.A. Causal Long Short-Term Memory Sequence to Sequence Model for TEC Prediction Using GNSS Observations. Remote Sens. 2020, 12, 1354. [Google Scholar] [CrossRef]
- Srivani, I.; Prasad, G.S.V.; Ratnam, D.V. A deep learning-based approach to forecast ionospheric delays for GPS signals. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1180–1184. [Google Scholar] [CrossRef]
- Moon, S.; Kim, Y.H.; Kim, J.H.; Kwak, Y.S.; Yoon, J.Y. Forecasting the ionospheric F2 Parameters over Jeju Station (33.43° N, 126.30° E) by Using Long Short-Term Memory. J. Korean Phys. Soc. 2020, 77, 1265–1273. [Google Scholar] [CrossRef]
- Chen, D.J.; Wu, J.; Wang, X.Y. A technology study of foF2 forecasting during the ionospheric disturbance. Chin. J. Geophys. 2007, 50, 22–27. [Google Scholar] [CrossRef]
- Bilitza, D.; Reinisch, B.W. International reference ionosphere 2007: Improvements and new parameters. Adv. Space Res. 2008, 42, 599–609. [Google Scholar] [CrossRef]
- Atulkar, R.; Bhardwaj, S.; Khatarkar, P.; Bhawre, P.; Purohit, P.K. Geomagnetic disturbances and its impact on ionospheric critical frequency (foF2) at high, mid and low latitude region. Am. J. Astron. Astrophys. 2014, 2, 61–65. [Google Scholar] [CrossRef]




| No. | URSI | Station/Abbreviation | Country | Time Zone | Lat | Lon |
|---|---|---|---|---|---|---|
| 01 | DW41K | Darwin (DAR) | Australia | UTC + 10 | −12.45 | 130.95 |
| 02 | SA418 | Sanya (SAY) | China | UTC + 8 | 18.34 | 109.62 |
| 03 | SH427 | Shaoyang (SHY) | China | UTC + 8 | 26.9 | 111.5 |
| 04 | BR52P | Brisbane (BRI) | Australia | UTC + 10 | −27.06 | 153.06 |
| 05 | WU430 | Wuhan (WUH) | China | UTC + 8 | 30.54 | 114.34 |
| 06 | CN53L | Camden (CAM) | Australia | UTC + 10 | −34.05 | 150.67 |
| 07 | CB53N | Canberra (CAN) | Australia | UTC + 10 | −35.32 | 149 |
| 08 | BP440 | Beijing (BEJ) | China | UTC + 8 | 39.98 | 116.37 |
| 09 | HO54K | Hobart (HOB) | Australia | UTC + 10 | −42.92 | 147.32 |
| 10 | MH453 | Mohe (MOH) | China | UTC + 8 | 53.49 | 122.34 |
| Year | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
| BEJ | 3973/8760 (45.35%) | 8637/8760 (98.60%) | 8327/8784 (94.80%) | 7215/8760 (82.36%) | 6567/8760 (74.97%) | 6935/8760 (79.17%) | 8012/8784 (91.21%) |
| MOH | / | / | / | / | 2643/8760 (30.17%) | 8110/8760 (92.58%) | 8012/8784 (91.21%) |
| WUH | / | / | / | / | 2845/8760 (32.48%) | 5873/8760 (67.04%) | 8523/8784 (97.03%) |
| SAY | / | 1507/8760 (17.20%) | 7374/8784 (83.95%) | 6587/8760 (75.19%) | 7958/8760 (90.84%) | 8194/8760 (93.54%) | 6261/8784 (71.28%) |
| SHY | / | / | / | / | / | / | 5641/8784 (64.22%) |
| Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
| BEJ | 8626/8760 (98.47%) | 8521/8760 (97.27%) | 8672/8760 (99.00%) | 8733/8784 (99.42%) | 7735/8760 (88.30%) | 8423/8760 (96.15%) | 6538/8760 (74.63%) |
| MOH | 8332/8760 (95.11%) | 8628/8760 (98.49%) | 8132/8760 (92.83%) | 8649/8784 (98.46%) | 8635/8760 (98.57%) | 8585/8760 (98.00%) | 8422/8760 (96.14%) |
| WUH | 8372/8760 (95.57%) | 8666/8760 (98.93%) | 7323/8760 (83.60%) | 8617/8784 (98.10%) | 8542/8760 (97.51%) | 8665/8760 (98.92%) | 8542/8760 (97.51%) |
| SAY | 8273/8760 (94.44%) | 8461/8760 (96.59%) | 8593/8760 (98.09%) | 8590/8784 (97.79%) | 8595/8760 (98.12%) | 7168/8760 (81.83%) | 8669/8760 (98.96%) |
| SHY | 8420/8760 (96.12%) | 8542/8760 (97.51%) | 8556/8760 (97.67%) | 8446/8784 (96.15%) | 8689/8760 (99.19%) | 7991/8760 (91.22%) | / |
| DAR | / | 8574/8760 (97.88%) | 6959/8760 (79.44%) | 8367/8784 (95.25%) | 8492/8760 (96.94%) | 7520/8760 (85.84%) | 8439/8760 (96.34%) |
| BRI | / | 8739/8760 (99.76%) | 7982/8760 (91.12%) | 8643/8784 (98.39%) | 8332/8760 (95.11%) | 8073/8760 (92.16%) | 8559/8760 (97.71%) |
| CAM | / | 7962/8760 (90.89%) | 7557/8760 (86.27%) | 7245/8784 (82.48%) | 8407/8760 (95.97%) | 3509/8760 (40.06%) | 2816/8760 (32.15%) |
| CAN | / | 8620/8760 (98.40%) | 7752/8760 (88.49%) | 7908/8784 (90.03%) | 8509/8760 (97.13%) | 6552/8760 (74.79%) | 7593/8760 (86.68%) |
| HOB | / | 8014/8760 (91.48%) | 6934/8760 (79.16%) | 7261/8784 (82.66%) | 8177/8760 (93.34%) | 7757/8760 (88.55%) | 7945/8760 (90.70%) |
| Station | Year | BPNN | GABP | IRI2016 | LSTM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE (MHz) | ρ | PD (%) | RMSE (MHz) | ρ | PD (%) | RMSE (MHz) | ρ | PD (%) | RMSE (MHz) | ρ | PD (%) | ||
| DAR | 2015 | 1.784 | 0.842 | 16.72 | 1.803 | 0.846 | 16.25 | 1.819 | 0.837 | 18.39 | 1.148 | 0.937 | 12.67 |
| 2019 | 1.054 | 0.873 | 17.24 | 1.095 | 0.869 | 17.44 | 1.575 | 0.860 | 25.56 | 0.913 | 0.898 | 14.65 | |
| SAY | 2015 | 1.5 | 0.908 | 13.95 | 1.462 | 0.913 | 13.78 | 1.823 | 0.894 | 15.36 | 1.134 | 0.948 | 11.07 |
| 2019 | 1.497 | 0.882 | 25.90 | 1.425 | 0.893 | 24.65 | 1.758 | 0.887 | 27.56 | 0.937 | 0.945 | 14.39 | |
| SHY | 2015 | 1.717 | 0.876 | 15.63 | 1.685 | 0.882 | 15.64 | 1.859 | 0.867 | 16.06 | 1.084 | 0.953 | 11.18 |
| BRI | 2015 | 1.033 | 0.849 | 12.02 | 1.058 | 0.841 | 12.18 | 1.147 | 0.831 | 13.29 | 0.833 | 0.907 | 9.35 |
| 2019 | 0.768 | 0.728 | 13.18 | 0.785 | 0.722 | 13.80 | 0.980 | 0.757 | 16.59 | 0.676 | 0.757 | 11.44 | |
| WUH | 2015 | 1.254 | 0.843 | 13 | 1.198 | 0.858 | 12.15 | 1.317 | 0.843 | 14.69 | 1.194 | 0.862 | 11.98 |
| 2019 | 0.786 | 0.878 | 14.44 | 0.791 | 0.885 | 14.55 | 1.392 | 0.859 | 25.13 | 0.648 | 0.919 | 11.68 | |
| CAM | 2015 | 0.963 | 0.867 | 13.04 | 0.953 | 0.869 | 12.87 | 1.026 | 0.853 | 13.79 | 0.751 | 0.921 | 9.53 |
| 2019 | 0.656 | 0.746 | 12.06 | 0.648 | 0.749 | 11.92 | 1.033 | 0.760 | 20.13 | 0.593 | 0.790 | 10.12 | |
| CAN | 2015 | 0.955 | 0.86 | 13.31 | 0.879 | 0.881 | 12.21 | 0.998 | 0.847 | 13.84 | 0.661 | 0.935 | 8.66 |
| 2019 | 0.652 | 0.772 | 12.72 | 0.670 | 0.768 | 13.19 | 0.802 | 0.776 | 15.68 | 0.529 | 0.827 | 10.19 | |
| BEJ | 2015 | 0.852 | 0.914 | 10.67 | 0.832 | 0.919 | 10.41 | 0.875 | 0.91 | 11.28 | 0.666 | 0.949 | 8.07 |
| 2019 | 0.593 | 0.860 | 11.64 | 0.587 | 0.865 | 11.38 | 0.888 | 0.847 | 16.74 | 0.514 | 0.887 | 9.55 | |
| HOB | 2015 | 0.976 | 0.85 | 14.17 | 0.918 | 0.869 | 13.47 | 1.031 | 0.826 | 15.23 | 0.803 | 0.903 | 10.89 |
| 2019 | 0.587 | 0.800 | 12.28 | 0.597 | 0.797 | 12.27 | 0.788 | 0.811 | 16.88 | 0.592 | 0.795 | 11.92 | |
| MOH | 2015 | 0.913 | 0.892 | 13.76 | 0.918 | 0.893 | 13.7 | 0.966 | 0.879 | 14.35 | 0.625 | 0.952 | 9.03 |
| 2019 | 0.595 | 0.808 | 13.87 | 0.621 | 0.815 | 14.02 | 0.779 | 0.805 | 16.94 | 0.415 | 0.897 | 8.81 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, C.; Tang, Q.; Zhao, J.; Zhang, F.; Xia, G.; Liu, Y. Forecasting Ionospheric foF2 Based on Deep Learning Method. Remote Sens. 2021, 13, 3849. https://doi.org/10.3390/rs13193849
Li X, Zhou C, Tang Q, Zhao J, Zhang F, Xia G, Liu Y. Forecasting Ionospheric foF2 Based on Deep Learning Method. Remote Sensing. 2021; 13(19):3849. https://doi.org/10.3390/rs13193849
Chicago/Turabian StyleLi, Xiaojun, Chen Zhou, Qiong Tang, Jun Zhao, Fubin Zhang, Guozhen Xia, and Yi Liu. 2021. "Forecasting Ionospheric foF2 Based on Deep Learning Method" Remote Sensing 13, no. 19: 3849. https://doi.org/10.3390/rs13193849
APA StyleLi, X., Zhou, C., Tang, Q., Zhao, J., Zhang, F., Xia, G., & Liu, Y. (2021). Forecasting Ionospheric foF2 Based on Deep Learning Method. Remote Sensing, 13(19), 3849. https://doi.org/10.3390/rs13193849










