The Operational Inflight Radiometric Uniform Calibration of a Directional Polarimetric Camera

Abstract

The directional polarimetric camera (DPC) on-board the GF-5A satellite is designed for atmospheric or water color detection, which requires high radiometric accuracy. Therefore, in-flight calibration is a prerequisite for its inversion application. For large field optical sensors, it is very challenging to ensure the consistency of radiation detection in the whole field of view in the space environment. Our work proposes a vicarious in-flight calibration method based on sea non-equipment sites (visible bands) and land non-equipment sites (all bands). Combined with environmental parameters and radiation transmission calculations, we evaluated the radiation detection accuracy of the 0° to 60° view zenith angle of the DPC in each band. Our calibration method is based on the single-day normalized radiance data measured by the DPC. Through data selection, enough calibration samples can be obtained in a single day (the number of desert samples is more than 5000, and the number of calibration samples of the ocean is more than $2.8\times {10}^6$). The measurements are compared with the simulation of 6SV VRT code or look-up tables. The massive amount of data averages the uncertainty of a single-point calculation. Although the uncertainty of a single sample is significant, the final fitting of the curve of the variation in the radiometric calibration coefficient with the observation angle can still keep the root mean squared error at approximately 2–3% or even lower, and for visible bands, the calibration results for both ocean sites and desert sites are in good agreement regarding the non-uniformity of the sensor.

1. Introduction

Polarization remote sensing is becoming an international research hotspot. The directional polarimetric camera (DPC) of atmospheric aerosols on-board the Gaofen (GF)-5A satellite developed by the Optical Remote Sensing Center of the Anhui Institute of Optics and Fine Mechanics of the Chinese Academy of Sciences is based on the global operational atmosphere aerosol monitoring load. The working principle and scientific target of the DPC are the same as those of POLDER (Polarization and Directionality of the Earth’s Reflectance), which has eight observation bands in the visible and near-infrared (NIR) regions and has polarization detection capabilities in the 490, 670 and 865 bands; the spatial resolution is 3.3 km. Due to its ±50° wide-angle observation range and the continuous working method of the rotating filter, it can measure the polarization radiation of the target reflectance from nine directions during a single pass (Figure 1).

Table 1. The parameters of the DPC on GF-5A.

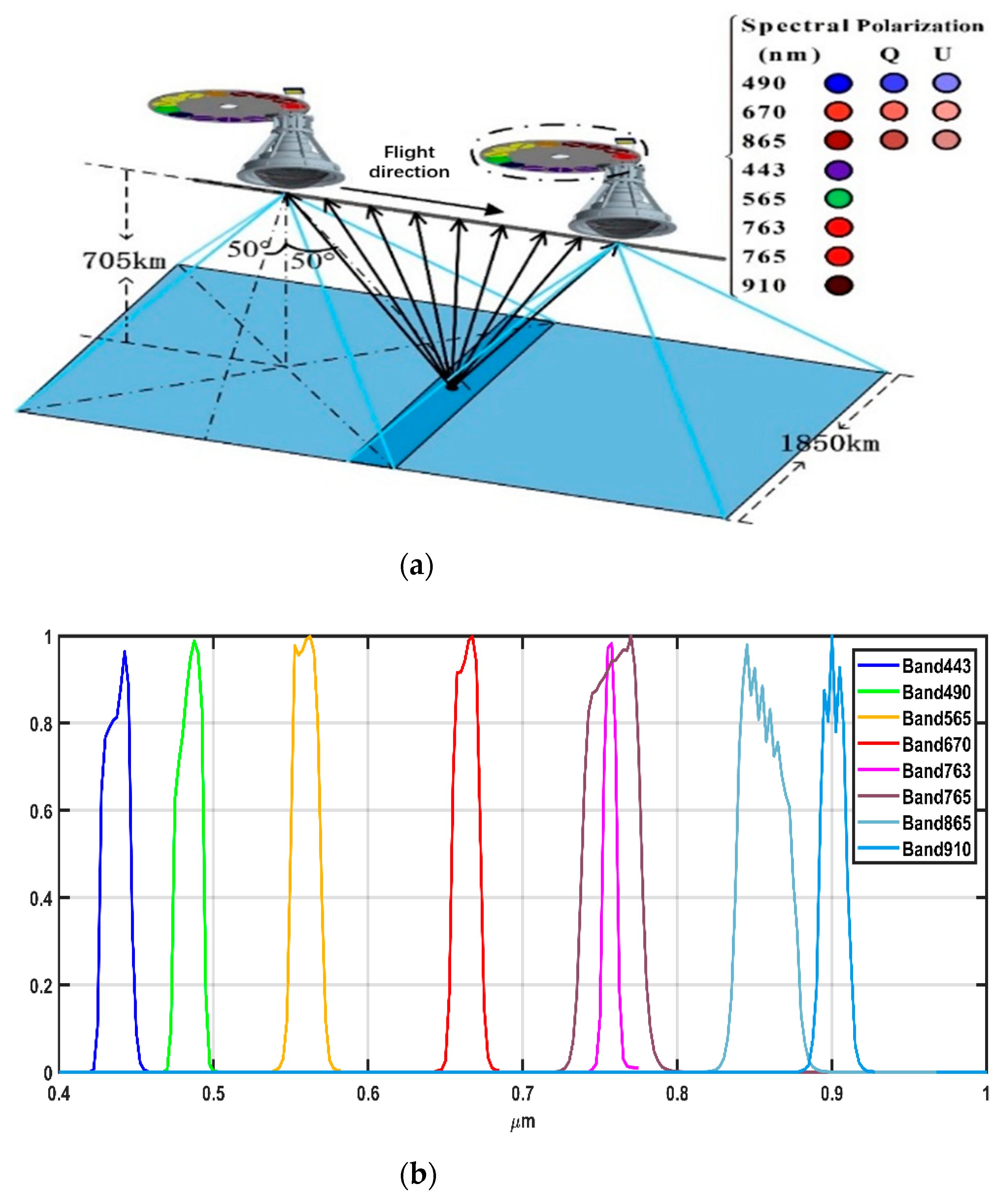
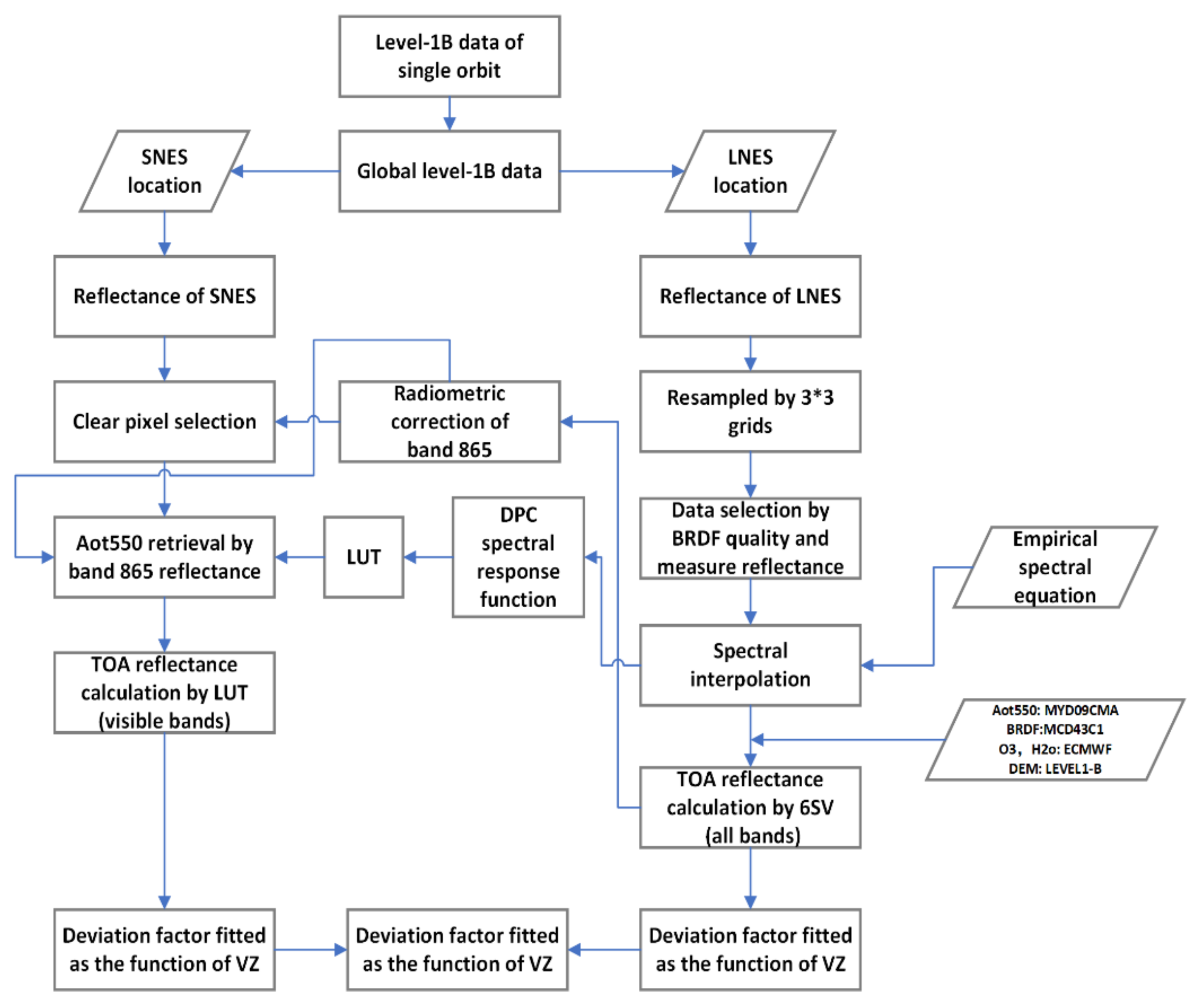
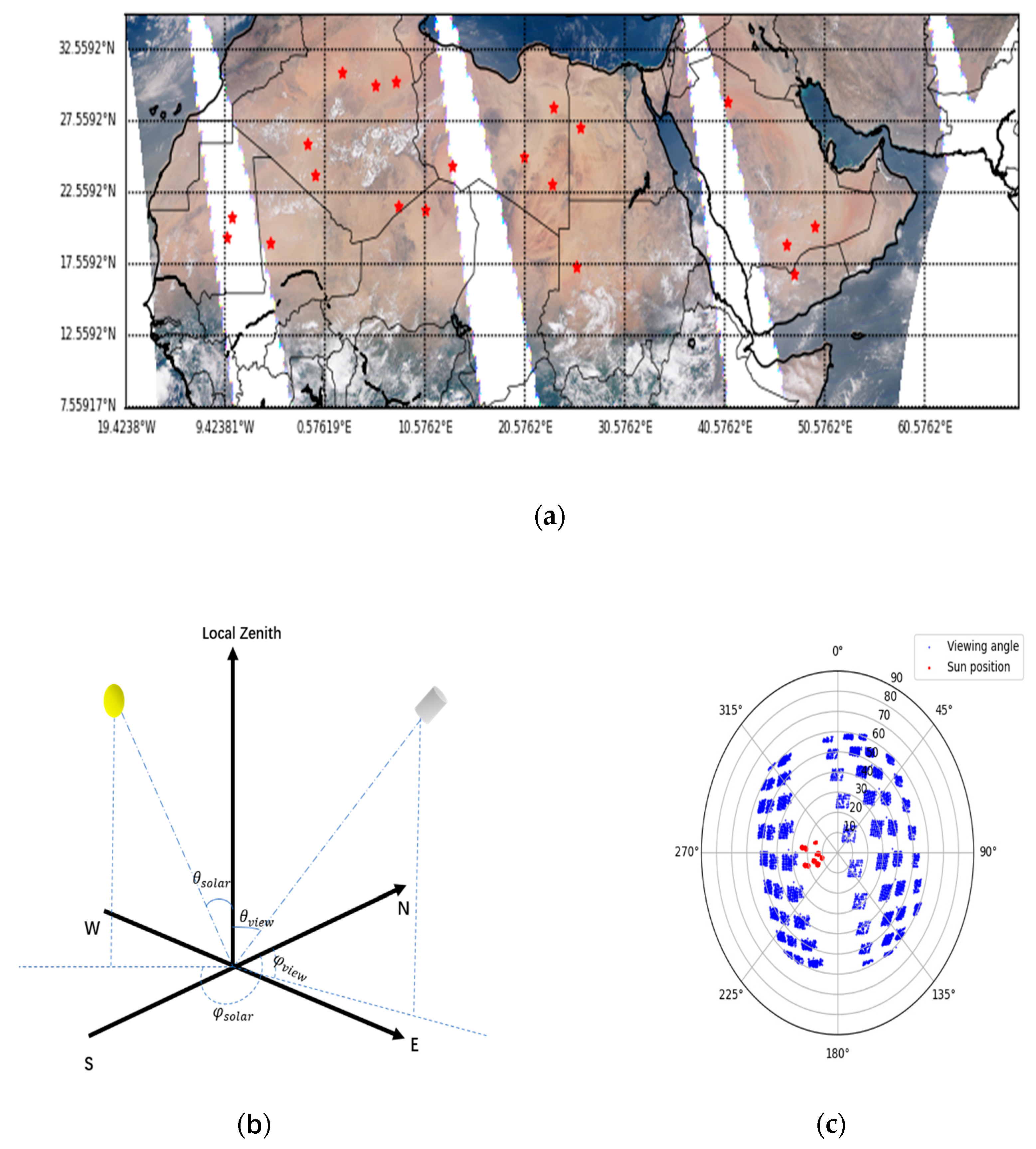
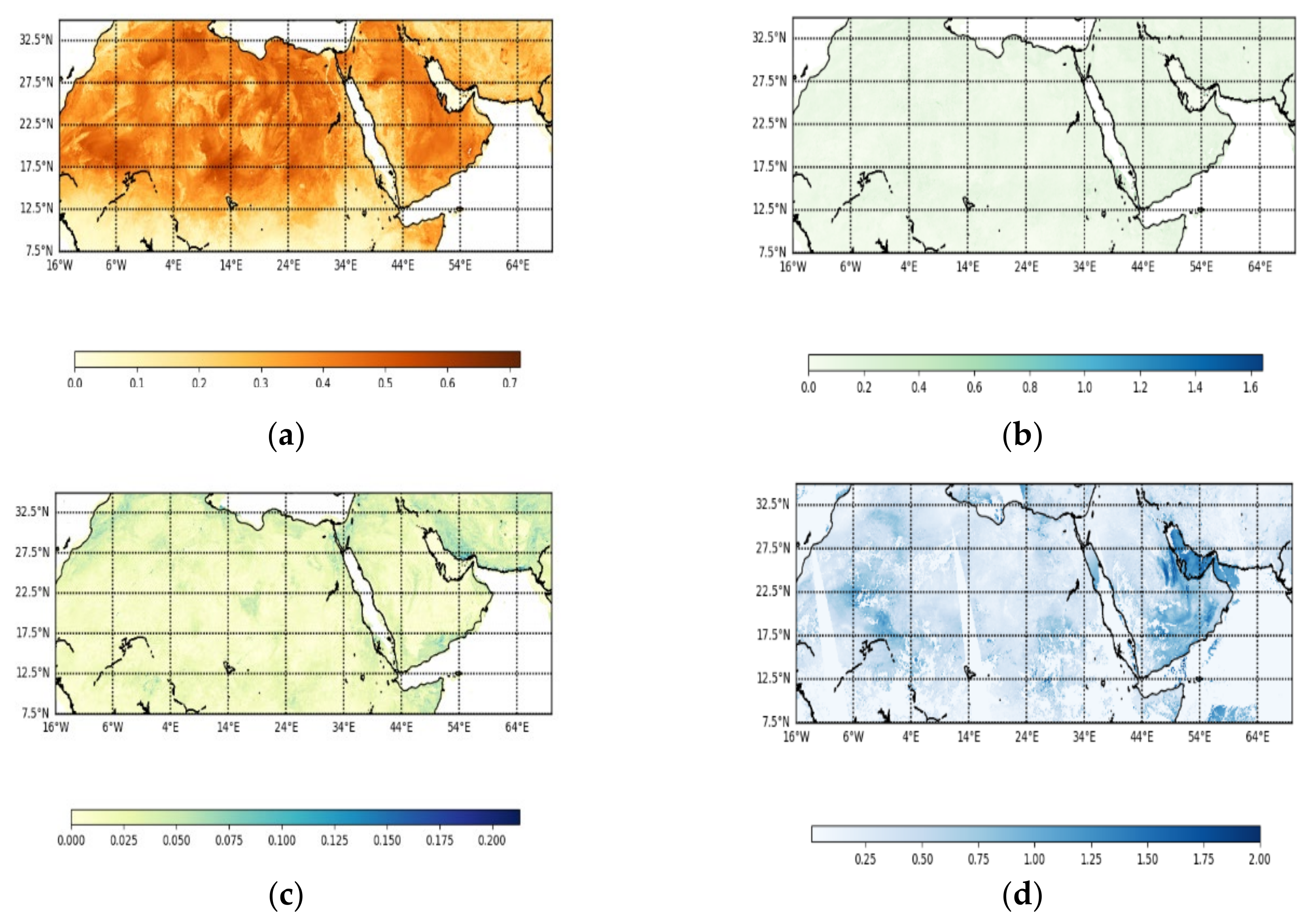
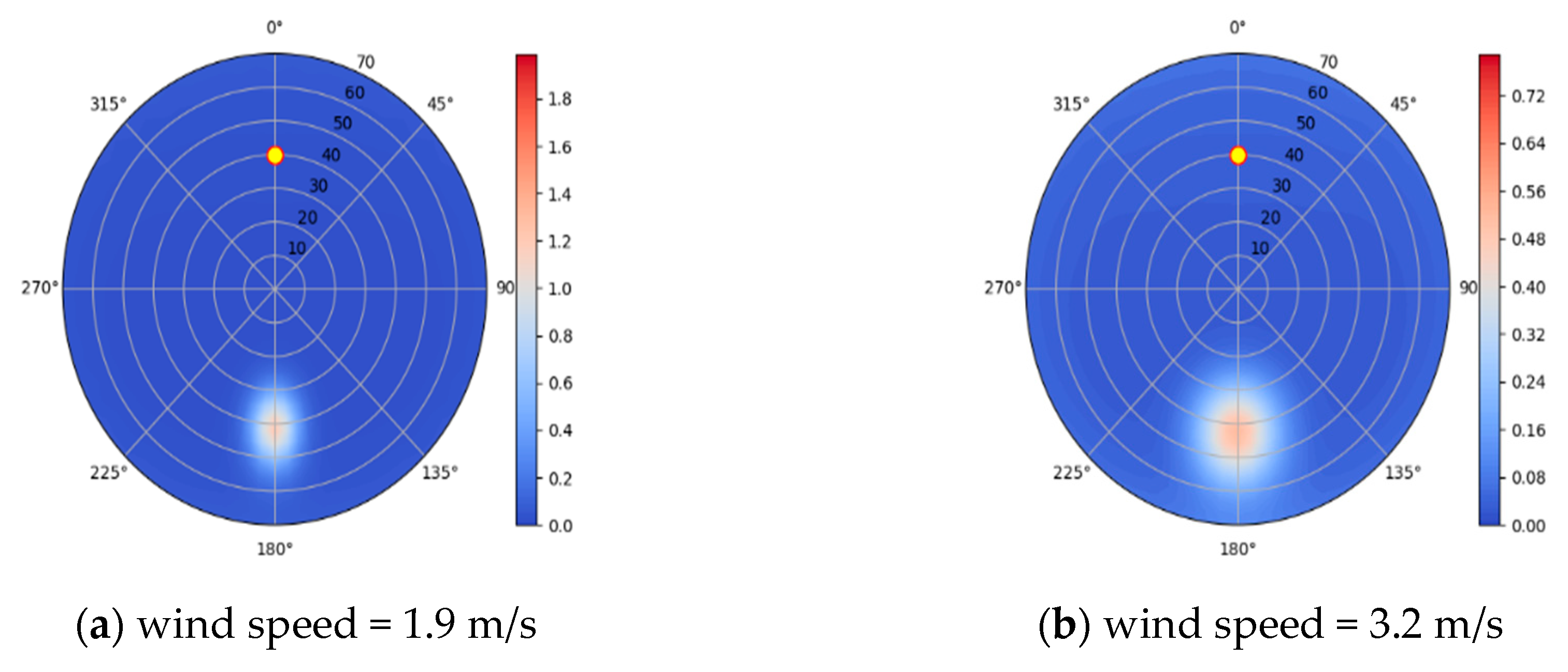
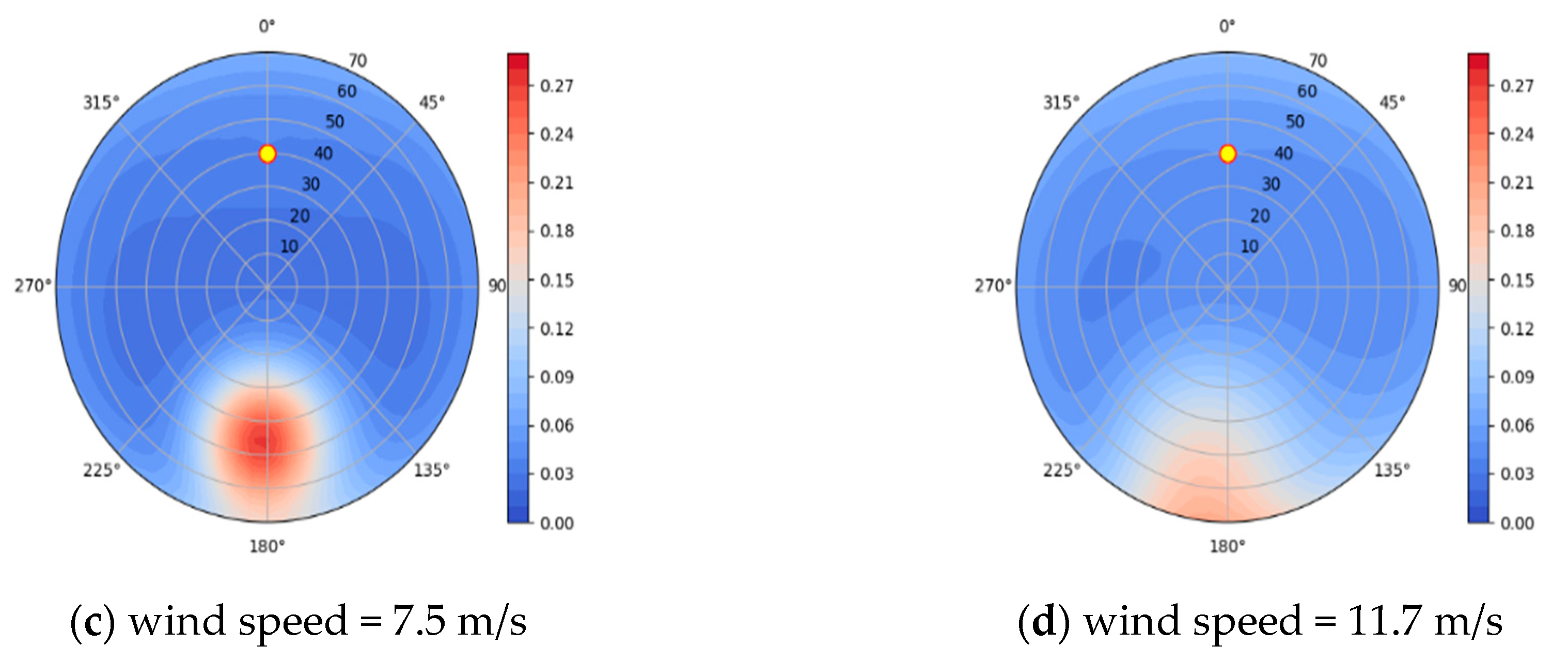
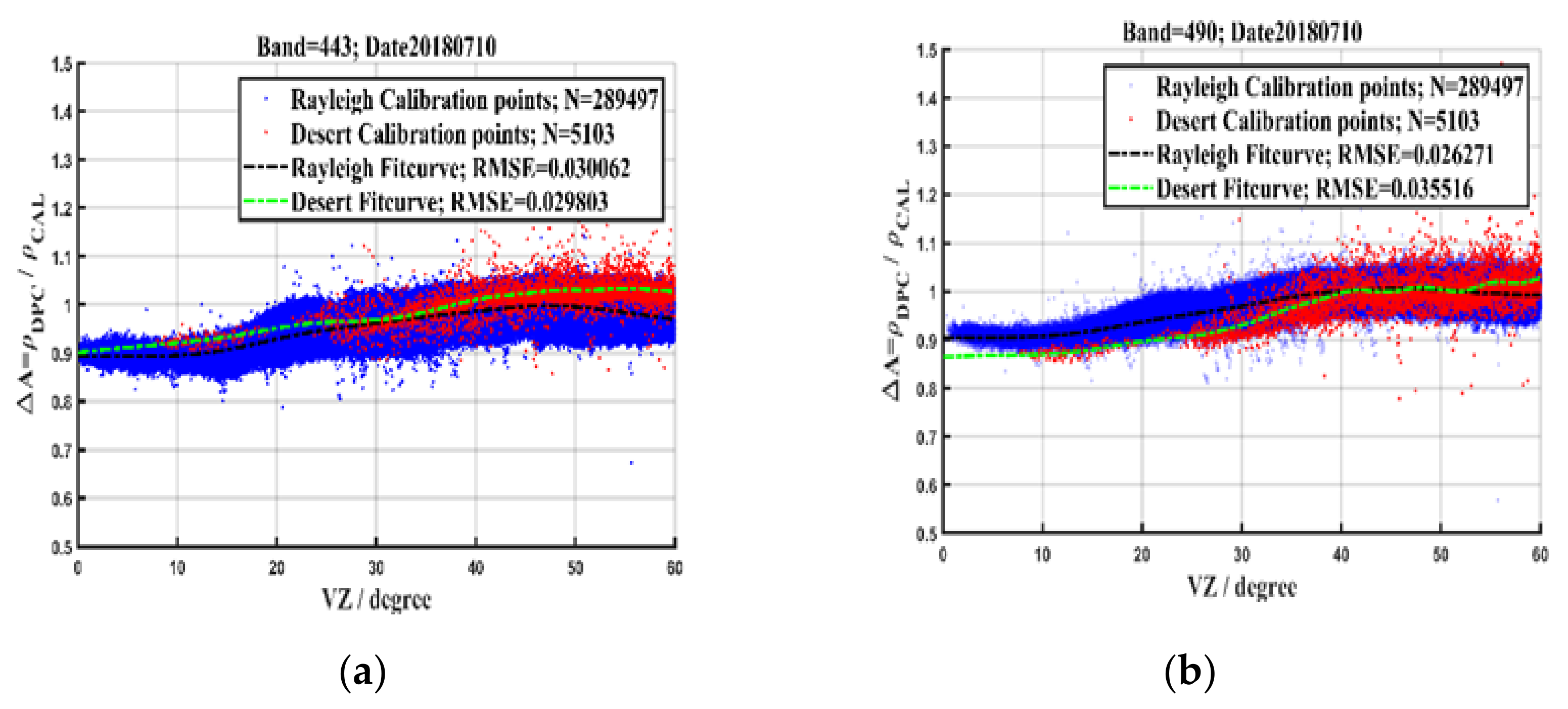
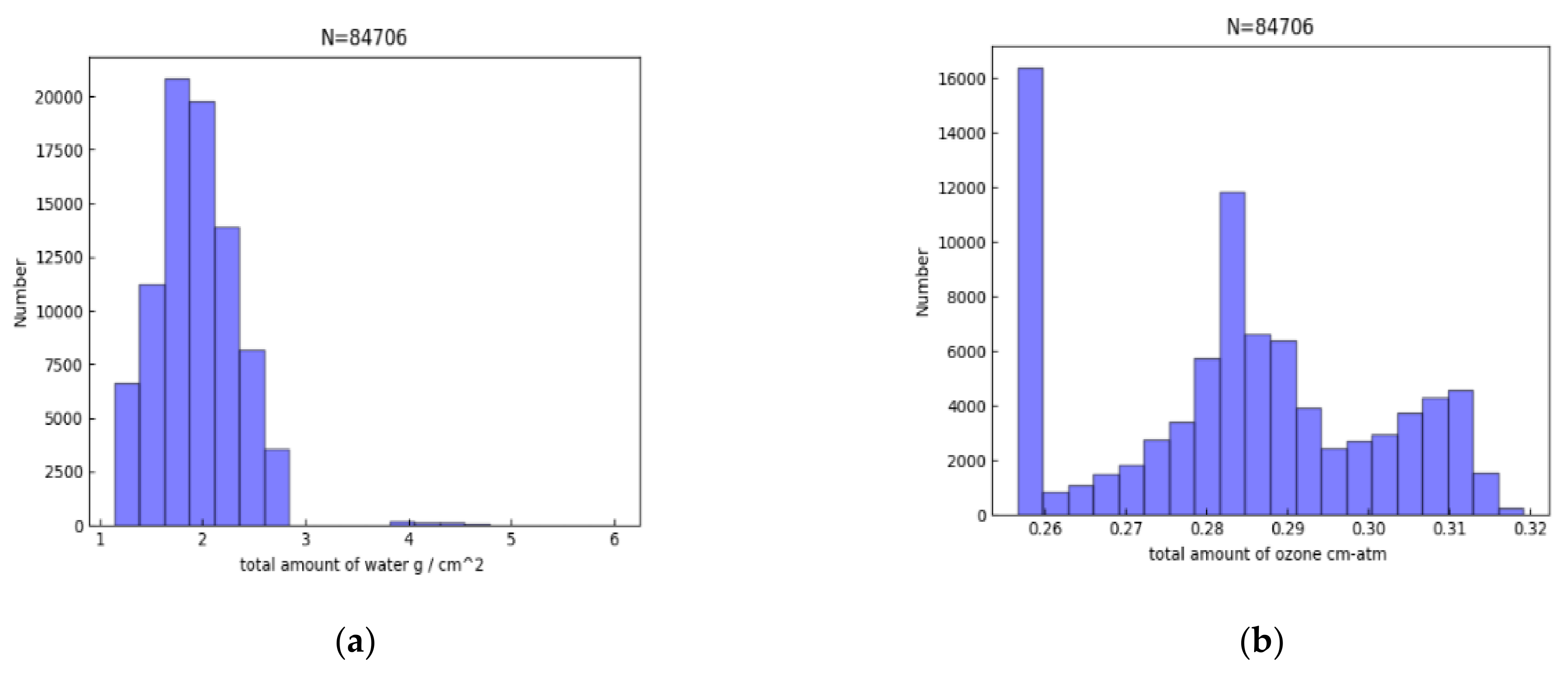
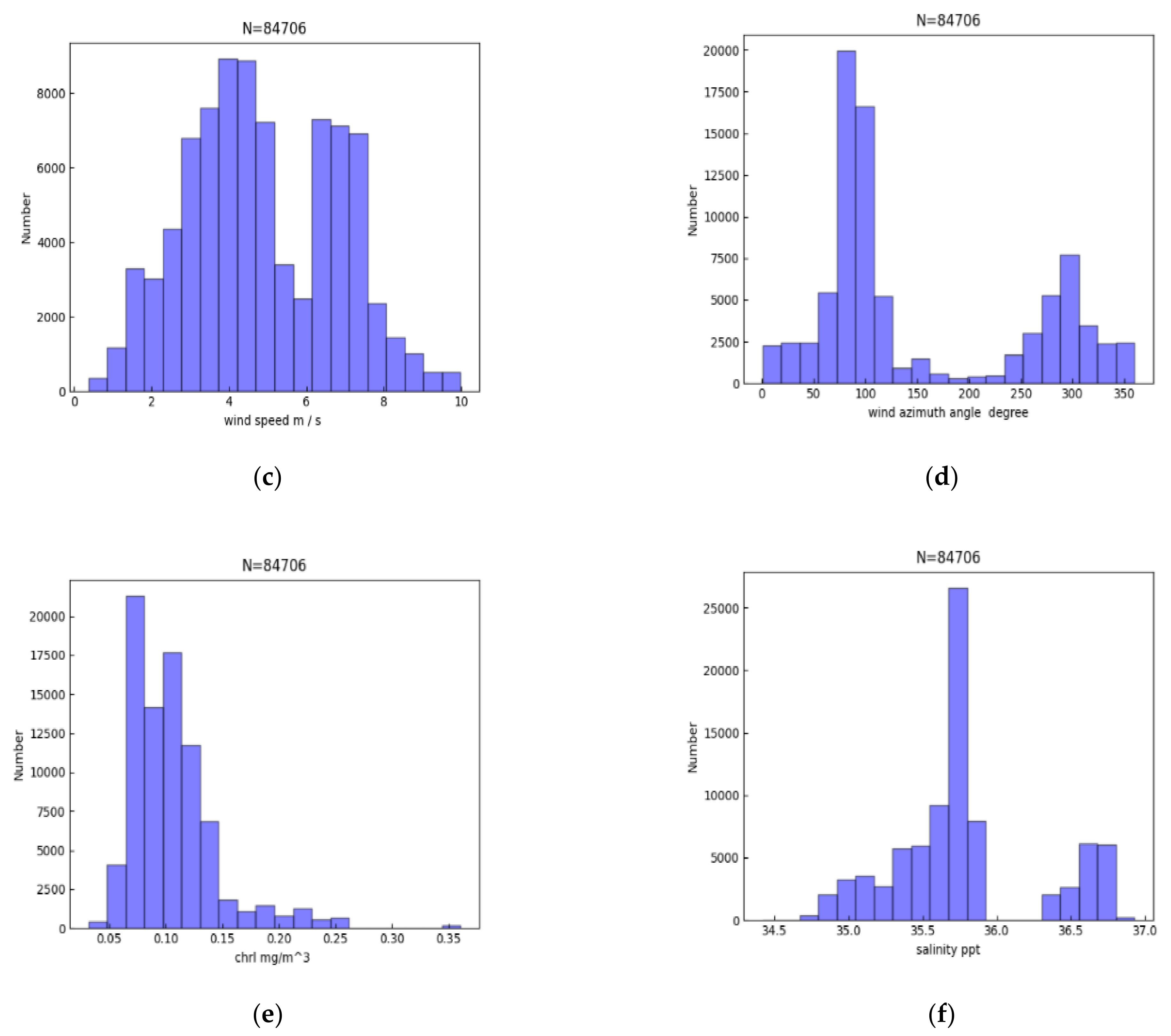
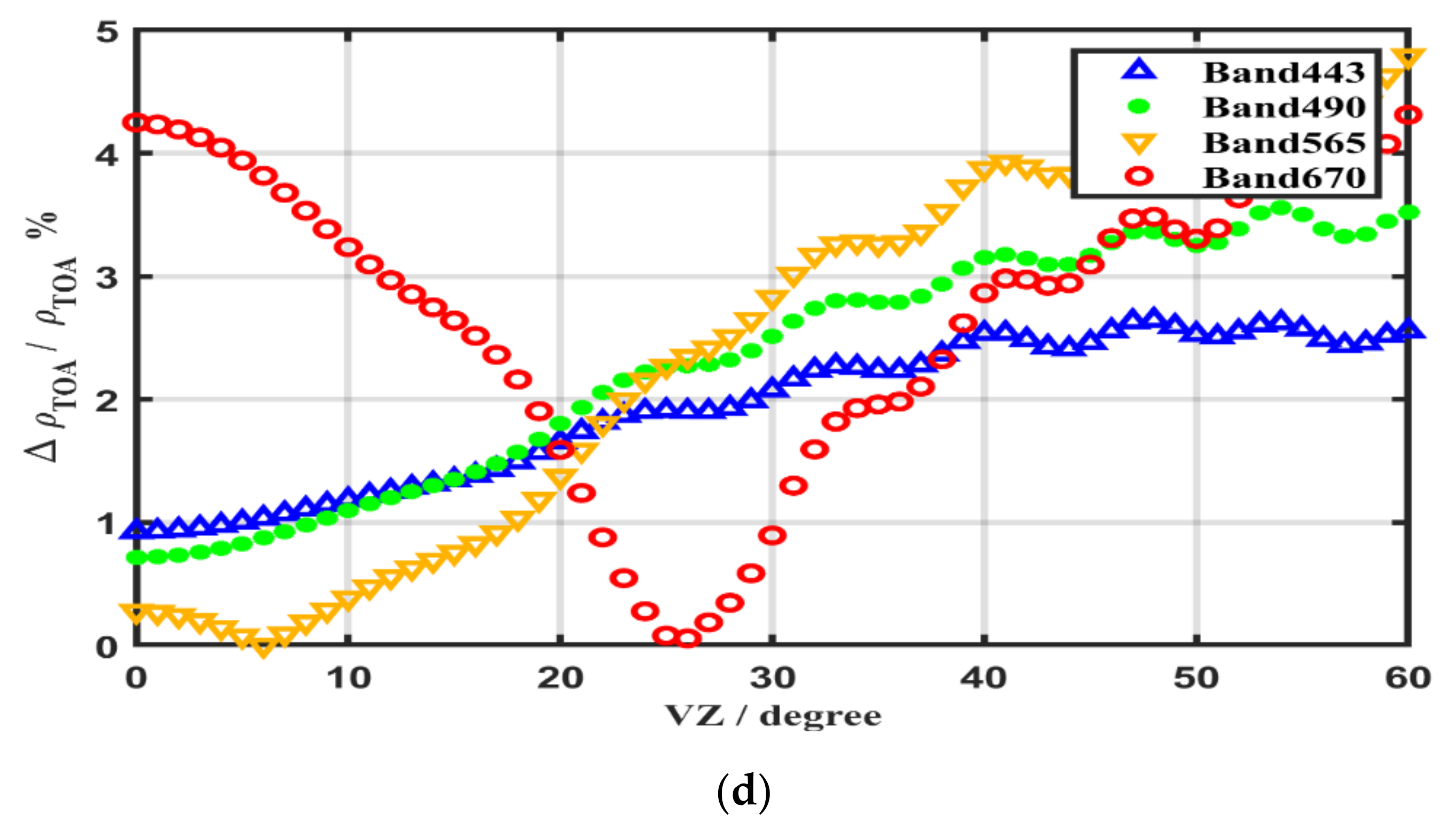
Band (nm)	443	490	565	670	763	765	865	910
Polarization	No	Yes	No	Yes	No	No	Yes	No
Central wavelength (nm)	443.3	488.9	564.7	668.8	761.4	763.1	861.8	907.1
Band width (nm)	20	20	20	20	10	40	40	10
Saturation reflectance	1.2	1.2	1.2	1.15	0.7	1.0	1.2	0.8

lists the technical parameters and scientific research descriptions of each waveband of the load. For more detailed technical characteristics of the sensor, please refer to the DPC laboratory calibration and review materials [1,2,3,4].

The remote sensing of aerosols, ocean water color and clouds requires a high radiation accuracy of 2% or better. Therefore, in addition to radiation calibration in the laboratory (the accuracy is about 5%), sensors also need to adjust the radiation calibration coefficient and validate the data quality in-flight because of the uncertain factors after launch. DPC is a frame imaging remote sensor, and the optical path of the instrument is fixed. Therefore, the design of the on-board calibrator needs to consider the complex rotating mechanical structure design (such as robotic arms, etc.), which will significantly increase the cost and risk and occupy more space on the satellite platform. As a DPC does not have an on-board calibrator, it is an inevitable choice to use natural features for vicarious calibration [5,6,7]. For optical remote sensors with a large field of view, the use of equipment sites by in situ measurement has the disadvantage of insufficient calibration samples and difficulty in comprehensively evaluating the quality of DPC data of the whole viewing angle. Therefore, the use of large-scale uniform ground objects for calibration calculation statistics is a necessary supplement, and the Working Group of Calibration and Validation (WGCV) of the International Organization for Satellite Observations (CEOS) recommends sea non-equipment sites (SNESs) and land non-equipment sites (LNESs) for the calibration of low-spatial-resolution atmospheric detection sensors (http://wgcv.ceos.org/).

LNES calibration sites are located mainly in North Africa, particularly in Arabia, Libya, and Algerie et al., considered radiometrically stable and bright. These sites have been used for POLDER in-flight multi-angle calibration by the cross-calibration method [8,9,10]. Other sensors also use this technique to perform radiometric validation [11] or to monitor sensor degradation [12]. Recently, Zhou et al. [13] analyzed the moderate-resolution imaging spectroradiometer (MODIS) bidirectional reflectance distribution function (BRDF) product in desert sites and forests and established BRDF look-up tables (LUTs) for cross-calibration. The feasibility and accuracy of the radiometric calibration of an LNES site using the BRDF products of MODIS have been verified.

For SNESs, the signals in the visible light spectrum of the sensor are mainly from atmospheric molecular scattering (Rayleigh scattering), except for the specular reflection direction. In 1992, E. Vermote et al. used two methods to calibrate the on-orbit radiation of the SPOT satellite in the visible light band [14] to avoid the extra error caused by the intensity of incident solar radiation. These two methods, i.e., calculating the apparent reflectance and comparing it with the measured reflectance are used to measure the change in the on-orbit calibration coefficient, which is called the "reflectance basis method". The same calibration principle is also used in the visible light band of POLDER/PARASOL. After that, based on ocean scenes, the load radiation calibration work carried out using Rayleigh scattering as the calibration model became more extensive and detailed [15,16,17].

After comprehensively considering the two scenarios and calibration methods, and because the uniformity of the radiation detection in the wide field of view of the instrument has not been tested on actual DPC data, this paper’s objective was to establish an accurate in-flight radiometric calibration and validation method. With this, we can evaluate the radiometric deviation of all DPC bands in a wide field of view using single-day level-1B data and achieve long-term in-flight monitoring. The preprocessing of the transformation of raw data (level 0) to level-1B data (normalized radiance) includes smearing effect removal, stray light correction, radiometric calculation by preflight calibration coefficients, and finally, pixel geolocation to a sinusoidal equal-area projection that has a grid number of 12,168 × 6084. The capacity of single-orbit data is approximately 2.5 GB when in the h5 format, and there are 15–16 pieces of orbit data in one day. Therefore, the amount of data in a single day is approximately 40–50 GB. Thus, the in-flight calibration of a DPC must be considered to process these vast data efficiently and automatically. In response to this situation, we have established a complete set of level-1 data processing systems to select calibration samples based on single-day detection data. Then, we developed a joint calibration method using North African deserts and ocean calibration sites. The radiometric deviations calculated by these two methods are both fitted as a function of the view zenith angle. The results show that the variation increases as the view zenith angle increases. The fitting error of the two methods is between 2 and 4% and can be better than 2% in the NIR band. In the visible band, the absolute deviation of the two methods is no more than 6%.

2. Materials and Methods

The laboratory instrument radiometric model of the DPC can be expressed as follows:

$$D{N}_{i,j}^{k,a}=G·t·A^k·T^{k,a}·P_{i,j}^k·\left(H{1}_{i,j}^k{I}_{i,j}^k+H{2}_{i,j}^k{Q}_{i,j}^k+H{3}_{i,j}^k{U}_{i,j}^k\right)+C$$

(1)

where DN is the digital number with no unit; k denotes the sequence of the band; i, j denote the pixel number of the sensor; G is the gain of the CCD; t is the integral time; $A^k$ is the absolute calibration coefficient; $T^{k, a}$ is the relative transmittance of the polarizer; $P_{i,j}^k$ is the relative transmittance of the optical system; $H{1}_{i,j}^k$, $H{2}_{i,j}^k$ and $H{3}_{i,j}^k$ are polarization effect parameters which correspond to the polarization rate of the optics ε; $I_{i,j}^k$, $Q_{i,j}^k$ and $U_{i,j}^k$ are Stokes parameters of the reflected polarized radiation and C is the dark current with no unit. It should be noted that this equation is the model used in laboratory calibration. The coefficients are both obtained using different sources and methods and are used as the program’s input to produce level-1B data by process level-0 of the DPC at CRESDA (China Centre for Resources Satellite Data and Application). However, Equation (1) is unsuitable for in-flight calibration because “perfect” calibration sites cannot be found among the natural targets. The vicarious radiometric calibration method based on normalized radiance data is related to Equation (2), as suggested by the WGCV:

$$L_{i,j}^k=A^k·B_{i,j}^k·G·\left(D{N}_{ij}^k-C\right)$$

(2)

where $L_{i,j}^k$ is the measured radiance with the unit of $W·c{m}^{-2}·s{r}^{-1}·n{m}^{-1}$; $A^k$ is the calibration coefficient of each channel (band) with the number k and $B_{i,j}^k$ is the equalization factor relative to a specific detector, which can be considered a factor describing the relative changes in calibration coefficients with various row numbers i and column numbers j of the detectors. After launch, both $A^k$ and $B_{i,j}^k$ need to be monitored during the lifetime in space of the sensors. Based on this equation, our calibration method is designed as follows and the flow chart is shown in Figure 2.

First, the level-1B data of the DPC (approximately 15–16 orbits per day) are combined into one global dataset; this step assumes that the calibration coefficient will not vary during a single day. The level-1B data include the normalized equivalent radiance measured by 8 bands of the DPC and geolocated by a sinusoidal equal-area projection, which can be expressed as follows:

$$NI=\frac{\pi L_{eq}}{E\left(\lambda \right)}$$

(3)

where $E\left(\lambda \right)$ is the extraterrestrial solar radiance and $L_{eq}$ is the normalized equivalent radiance, which can be expressed as follows:

$$L_{eq}=\frac{{{\displaystyle \int }}_0^{\infty }L\left(\lambda \right) S\left(\lambda \right)d\lambda }{S\left(\lambda \right)d\lambda }$$

(4)

where $L\left(\lambda \right)$ is the spectral radiance and $S\left(\lambda \right)$ is the spectral response function of the DPC, which is shown in Figure 1b. From Equation (3), one can calculate the directional reflectance by simply dividing the cosine of the solar zenith angle.

After the first step, we divide the data of the calibration area according to the locations of the SNES and LNES, filter each LNES with a 3 × 3 window for mean value filtering and automatically match the surface and atmospheric parameters. Surface spectral interpolation is performed according to the spectral empirical formula of the desert area [18] to obtain the surface spectral resampled reflectance values of each channel of the DPC. We obtain the meteorological data from MODIS Aqua (aerosol optical thickness at 550 nm, BRDF) [19] and ECMWF (O₂, H₂O). We simulate the atmospheric radiation by the 6SV code at each DPC band and compare it with the measured values of the DPC to obtain the radiometric deviation ratio $\Delta A$. Finally, we carry out a fitting by the smoothing spline method against the view zenith angle to obtain $\Delta A_{{\theta }_v}$, and $\Delta B_{{\mathsf{\theta }}_{\mathrm{v}}}=\Delta A_{{\mathsf{\theta }}_{\mathrm{v}}}/\Delta A_0$. After obtaining the calculation result over the LNES, we adjust the measured reflectance of the NIR band by the correction factors and use it to select clean locations over the SNES. The pre-calculated LUTs to estimate the aerosol optical thickness (aot550) under the maritime aerosol profile, combined with the wind speed data from ECMWF, are then used to calculate the calibration deviation value of the shortwave band, and finally, the same fitting method is used to fit the relative change curve, which is compared with the desert result to ensure the radiometric uniformity of the visible bands of the DPC.

3. Results

3.1. Desert Calibration Results

Over the bright desert targets in Figure 3, one can accurately simulate the radiative transfer code by the input of the surface BRDF parameters and synchronized atmospheric parameters; thus, the code can be used for absolute radiation calibration or cross-calibration [19,20,21,22,23,24,25,26]. In our work, we used the BRDF product of MODIS because it can be easily obtained from NASA and input into the Py6S module [24]. The BRDF product of MODIS supplies the weighting parameters associated with the Ross–Li model [25]. The semi-empirical model is formulated as a linear combination of kernels:

$$R=f_{iso}+f_{geo}{k}_{geo}+f_{vol}{k}_{vol}$$

(5)

where $f_{iso}, f_{geo}$ and $f_{vol}$ are coefficients of the kernels; $k_{geo}$ is the Ross-Thick kernel and $k_{vol}$ is the Li-Sparse kernel, which are functions of the geometry; and $R$ is the directional reflectance.

The area of a single desert site is 100 × 100 km² (approximately 30 × 30 pixels). After filtered by a 3 × 3 grid window, 10 × 10 pixels were selected for each area, for a total of 20 sites and nine viewing angles, and a total of 18,000 samples could be selected. Due to the lack of cloud masks in level-1B DPC data, we used thresholds of $\rho$_443 < 0.25, $\rho$_670 < 0.57 and $\rho$_865 < 0.65 to avoid cloud pixels, where $\rho$ represents the measured reflectance of the DPC. The homogenous index is defined as the standard deviation of the nine neighborhood pixels at the original resolution, and pixels with an index greater than 3% were eliminated. After data selection, we obtained more than 5000 calibration samples on 10 July 2018, distributed in more than 600 pixels. The BRDF parameters were selected by the latitude and longitude of the DPC geolocation data and are shown in Figure 4.

To study the spectral ground reflectance, the arctan-base function can be used to reproduce the spectral reflectance from 400 to 1100 nm over desert sites [20].

$$\rho \left(\lambda \right)=\mathsf{{\rm K}}\frac{2}{\pi }\arctan \left[\alpha \left(\lambda -\beta \right)\right]+\gamma$$

(6)

where $\lambda$ is the wavelength in nm$;\mathsf{{\rm K}}$, $\gamma$, $\alpha$ and $\beta$ are used to adjust the model for the behavior of the spectral reflectance of the given desert site. Here, we used the isotropic component ($f_{iso}$) at 469, 555, 645 and 858.5 nm of the MCD43 product to reproduce the spectral reflectance of the DPC at the bottom of the atmosphere and then simulate the top-of-atmosphere (TOA) reflectance at all DPC bands using the Py6S interface. The ratio $\Delta A$ is defined as the measured reflectance divided by the calculated reflectance, which expresses the deviation between in-flight and preflight radiometric calibration:

$$\Delta A=\frac{{\rho }_{DPC}\left({\theta }_v\right)}{{\rho }_{Cal}\left({\theta }_v\right)}$$

(7)

where ${\rho }_{DPC}\left({\theta }_v\right)$ and ${\rho }_{Cal}\left({\theta }_v\right)$ represent the directional reflectance as an unknown function of the view zenith angle measured by the DPC in flight and calculated by Py6S, respectively. After considering that the calculation error of the 6SV will increase for a larger view zenith angle, we selected the data of the view zenith angle threshold of 60°, and we neglected the sample for which the BRDF quality factor is not equal to zero (which means very good quality). The aerosol depth (aot550) from the MYD09CMA products is plotted in Figure 4d. The total amounts of ozone and water of the atmosphere come from the ECMWF (https://cds.climate.copernicus.eu/). The deviation versus view zenith angle at the NIR (763–910) bands are plotted in Figure 5a–d. The curves plotted in green are the fit results obtained using the smoothing spline method in MATLAB 2018, and the factor $\Delta B\left({\theta }_v\right)=\frac{\Delta A_f\left({\theta }_v\right)}{\Delta A_f\left({\theta }_v=0\right)}$ can be used to evaluate the radiometric uniformity of the sensor, where $\Delta A_f\left({\theta }_v\right)$ is the deviation factor calculated by the fitted function at the specific view zenith angle ${\theta }_v$.

From the above results, we found that with the change in the observation zenith angle, the calibration factor of radiation detection has a relative deviation of approximately 1 to 5% in the NIR bands (the ratio of the center to the edge), and the fitting error is less than 2.3%; thus, we used the fit curves to determine the deviation ratio at the view zenith angle of 0°, 30° and 60° for every band listed in

Table 2. The deviation factor of the DPC calibrated by the LNES at different view zenith angles for several NIR bands.

Band	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=0°\right)$$/ \mathbf{\Delta }\mathit{B} \left(\mathbf{Predict}\right)$	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=30°\right)$$/\mathbf{\Delta }\mathit{B}$	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=60°\right)$$/\mathbf{\Delta }\mathit{B}$
Band 763	0.94/1.00	0.95/1.01	0.97/1.03
Band 765	0.94/1.00	0.97/1.03	0.99/1.05
Band 865	0.92/1.00	0.95/1.03	0.95/1.03
Band 910	0.92/1.00	0.94/1.02	0.93/1.01

. In the visible band, we found larger non-uniformity through this calibration method. To confirm this conclusion, we used broader calibration sites over the ocean for statistical calibration. The results are shown in Section 3.2.

3.2. SNES Calibration Results

Sea non-equipped sites are mainly distributed in the deep ocean, far away from the coast. The field and range we selected are listed in

Table 3. The locations of the SNESs selected in our calibration.

Site Name	$\mathit{L}\mathit{a}\mathit{t}$	$\mathit{L}\mathit{o}\mathit{n}$
AltS	−19.9°–−9.9°	−32.3°–−11.0°
PacSE	−44.9°–−20.7°	−130.2°–−89°
PacNW	10.0°–22.7°	139.5°–165.6°
AltN	17.0°–27.0°	−62.5°–−44.2°
IndS	−29.9°–−21.2°	89.5°–100.1°
PacN	15.0°–23.5°	−179.0°–−160.0°

below.

According to the area shown in the superscript, each scene has hundreds of thousands of pixels to be selected from observation data from nine angles. Therefore, we used a more stringent screening method that includes the following:

1. We calculated the Rayleigh scattering reflectance through the LUT and the geometry data. After subtracting the Rayleigh scattering reflectance from the measured reflectance of band 865, we eliminated all values greater than 0.0035 so that the obtained optical thickness is basically within 0.2 and cloud pixels can be excluded. The calibration result from the LNES was used to correct the measured value of band 865.

2. Assuming that the wind speed is 11.7 m/s, the sunglint reflectance component was calculated according to the LUT and the observation angle, and the observation points with sunglint reflectance greater than 0.0005 were excluded.

After traversing all calibration locations and calibration angles, we obtained more than 280,000 calibration samples (distributed over 80,000 pixels) for a single day, depicting the Rayleigh scattering calibration results. The radiative transfer principle above clean ocean sites can be expressed as follows [19]:

$${\rho }_t\left(\lambda \right)={\rho }_{atm}\left(\lambda \right)+T\left(\lambda \right){\rho }_g\left(\lambda \right)+t\left(\lambda \right){\rho }_w\left(\lambda \right)+t\left(\lambda \right){\rho }_{foam}\left(\lambda \right)$$

(8)

where ${\rho }_{atm}\left(\lambda \right)$ is the atmospheric reflectance contribution, which includes aerosol scattering, molecular multiple scattering (Rayleigh scattering) and Rayleigh–aerosol interactions; ${\rho }_g\left(\lambda \right)$, ${\rho }_w\left(\lambda \right)$ and ${\rho }_{foam}\left(\lambda \right)$ are the specular reflection (sunglint), the water-leaving reflectance and the reflectance of whitecaps of the ocean surface; and T(λ) and t(λ) are the atmospheric direct and diffuse transmittances, respectively. Based on Equation (8), the LUTs for the TOA reflectance of several DPC bands (443, 490, 565, 670, 765 and 865 nm) were generated under different conditions. We plotted the apparent reflectance at the 670 nm band as an example (Figure 6).

Figure 6 shows the BRDF distribution at the TOA over the clean ocean. The simulation values were set as follows: aot550 = 0.1, pigment concentration = 0.07 mg/m³, solar view zenith = 40° and salinity = 37 ppt; the aerosol type was set to maritime; the wind direction was set to 90°. Through the BRDF under different wind speeds, it was clearly revealed that when the wind speed is low, the scope of the specular reflection area is smaller, and the energy is higher. When the wind speed is high, the energy of the mirror reflection area is weakened, and the scope is enlarged. This characteristic is related to the probability distribution characteristic of the specular reflection on rough surfaces, which is explained in more detail in other research [6]. In our work, we set other parameters as follows: ozone = 0.25 cm-atm; water content = 2.5 $\mathrm{g}/{\mathrm{cm}}^2$; aot = 0, 0.01, 0.05, 0.1, 0.15 and 0.2; wind speed = 1, 1.9, 3.2, 4.2, 6.7, 7.5 and 11.7 m/s; and maritime aerosol type. Therefore, there were 42 LUTs in total. The angle of each LUT was set as follows: solar zenith angle, 0–70°, with an interval of 5°; observation zenith angle, 0–70°, with an interval of 3.5°; relative azimuth angle, 0–180°, with an interval of 5°. Thus, each LUT had three dimensional arrays of six bands, and each array had 13 × 21 × 37 elements. We first used wind speed values from the ECMWF to choose the LUTs at the closed wind speed condition, then retrieved the aot550 by the measured reflectance of the 865 nm band and used the aot550 to calculate the apparent reflectance of visible bands. The calculation results are shown in Figure 7a–d, where the results are compared with the desert calibration results.

Figure 7 shows that the radiometric deviation calculated by using desert and ocean sites shows significant non-uniformity varying with the view zenith angle. We used two fit curves for each visible band over the LNES and SENS to determine the deviation ratio at view zenith angles of 0°, 15°, 30°, 45° and 60°, and the results are listed in

Table 4. The deviation factor of the DPC calibrated by the SNES and LNES at different view zenith angles.

Band	Site	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=0°\right)/\mathbf{\Delta }\mathit{B}$	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=15°\right)/\mathbf{\Delta }\mathit{B}$	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=30°\right)/\mathbf{\Delta }\mathit{B}$	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=45°\right)/\mathbf{\Delta }\mathit{B}$	$\mathbf{\Delta }\mathit{A}\left(\mathit{V}\mathit{Z}=60°\right)/\mathbf{\Delta }\mathit{B}$
443	SNES	0.89/1.00	0.91/1.02	0.96/1.08	1.00/1.12	0.97/1.09
	LNES	0.88/1.00(Predict)	0.92/1.05	0.95/1.08	1.02/1.16	1.02/1.16
490	SNES	0.90/1.00	0.92/1.02	0.97/1.08	1.00/1.11	1.00/1.11
	LNES	0.87/1.00(Predict)	0.88/1.01	0.93/1.07	1.00/1.15	1.02/1.17
565	SNES	0.87/1.00	0.92/1.06	0.95/1.09	0.97/1.11	0.98/1.13
	LNES	0.88/1.00(Predict)	0.92/1.05	0.97// 1.10	1.02/1.16	1.02/1.16
670	SNES	0.90/1.00	0.94/1.04	0.95/1.06	0.97/1.08	0.97/1.08
	LNES	0.90/1.00(Predict)	0.94/1.04	0.94/1.05	0.98/1.09	1.00/1.11

. For band 670, ∆A = 0.9 for the central field (VZ = 0°), and ∆A = 0.97 for the edge (VZ = 60°), which indicates a nearly 8% relative radiometric deviation on the sensor. For bands 443, 490 and 565, the differences in ∆A from the central field to the edge are larger: about 9–16% for band 443, 11 to 17% for band 490 and 13–16% for band 565. The calibration results based on ocean and desert sites show similar distribution characteristics for ∆A and $\Delta B$ versus the view zenith angle. However, there are some deviations between the fit curves of these two calibration results, especially at view zenith angles larger than 45° for the blue band to the yellow band (443, 490, 565), which may be introduced in the spectral interpolation of the desert data as the spectra increase quickly with the wavelength in the region of 400–600 nm, which can be found in the other articles [11,12,13]. We finally recommend following the calibration results over an SNES in visible bands.

4. Calibration Errors and Discussion

In the desert calibration process, we used the MODIS surface reflectance and BRDF products. Based on the experience of many previous researchers, the surface BRDF has good calibration accuracy in long-wave bands. The atmospheric model comes from the ECMWF, the uncertainty of water content in the atmosphere does not exceed 10% and the error of ozone content does not exceed 15%. The uncertainty of the MODIS aerosol optical thickness is 0.05 ± 0.15τ. We set up a typical simulation program to simulate the error of each band. In the simulation, we took the lowest altitude value of 0.1 km as the input. We simulated the gas transmittance error as ∆T(water = 2.4 ± 0.24) and ∆T(ozone = 0.305 ± 0.045) because of the water content error and ozone content error. The aot550 uncertainty was set as $\Delta \tau =0.4\pm 0.1$.

Figure 8a shows the influence of the fluctuation in the TOA measurement reflectivity of several main bands of the DPC when the ozone content fluctuates within 0.305 ± 0.045 cm-atm. Except for 1~1.4% in band 565, the influence on other bands is relatively small. The simulation results of Figure 8b,c show that when the water content fluctuates within 2.4 ± 0.24 $\mathrm{g}/{\mathrm{cm}}^2$ and the aerosol optical thickness fluctuates within 0.4 ± 0.10, the impact on the DPC is mainly as follows: the uncertainty of the e water content causes 0.07% of the influence on band 910, while the result on the other bands is negligible. Aerosols cause an uncertainty of 2.5–4.5% in bands 490–670, which falls below 1.5% in other bands. In addition, according to research, in the blue, green and yellow bands, the spectral characteristics of different surface states are significantly different, which mainly depends on the composition of the gravel and the sand particle size [10]. These analyses explain the difference in the fit curve between the calibration over LNESs and SNESs for bands 443–565.

The calibration results over these two kinds of sites for band 670 are in good agreement at view zenith angles smaller than 60°. In addition, the calibration sample number of the land is much smaller than that of the ocean scene. The coverage of the data within the view zenith angle of 30° of the day is small. To evaluate the calibration error over ocean sites (SNES), we used the ECMWF data and the GIOVANNI monthly average data to statistically evaluate the calibration field environment. The deviation of its statistical value from our simulated value was taken as the calibration source deviation and then transmitted through radiation. The software calculates the error of the calibration radiation calculation. A statistical histogram of the environmental parameters is shown in Figure 9.

According to the statistical results in Figure 9, the simulation was set to fluctuate around 0.25–0.3 cm-atm of ozone content, 2–3 g/cm³ of water content (due to the existence of a large amount of data, outliers are meaningless), 34.5–37.0 ppt of salinity, and 0.07–0.25 of chlorophyll content, and the error of the aerosol model considers mainly the continental and maritime types. Based on the changes in these parameters, we simulated the relative error of the TOA reflectivity, as shown in Figure 10.

According to the analysis in Figure 10, the calculation error caused by the change in water vapor content is less than 0.6%. The calculation error caused by the change in ozone content will generate a maximum deviation of 1.5 to 2.5% in bands 565 and 670, higher than 0.5%. The change in chlorophyll content will cause a maximum deviation of 4.4% of band 443, 2.6% in band 565 and 1.5%, 1% in bands 490 and 670, respectively. In addition, the type of aerosol is the most significant uncertainty factor. We considered only a single aerosol profile, i.e., maritime, and analyzed the deviation in the continental style; the aot550 was set as 0.15 in this simulation. We found a maximum deviation of 4% in bands 565 and 670. The phenomenon caused by the variation is that there are more discrete points in the calibration process shown in Figure 10d.

5. Conclusions

In this research, an operational calibration method for all bands of a DPC has been developed, which is convenient for operating on actual measurement data. The calculation of reference reflectance based on statistical methods, public data sets obtained from the Internet for radiation transmission calculations, the establishment of LUTs, and even the analysis of calibration errors can be realized. The absolute radiation calibration factor and the relative radiation calibration factor are obtained through the data fitting method. Interactive verification of the two methods was realized in the visible light band. The statistical average of the large data volume weakens the uncertainty of the single-point calculation; thus, the overall error is within 3%. We determined that this result can be used as the basis for adjusting the DPC in-flight radiation calibration coefficient and has the potential for long-term monitoring and adjustment of the calibration coefficient. Our method also has some limitations. First, the calibration flowchart starts from level-1 data, which means the relative transmittance of the polarizer T and the polarization rate of the optics ε cannot be tested by this method. After launch, the variation in these two parameters was tested and considered stable by Tu et al. from level-0 data [27]. Second, our calibration method only considered one aerosol profile. The uncertainty of a single calibration sample is significant to ±10% or even more significant. We will thus develop a more accurate method considering different aerosol types and surface conditions in the future. We hope to use this method for in-flight calibration of the DPC before inverting applications such as aerosol and cloud detection and ocean color retrieval, etc. [28,29,30].