Abstract
Global Navigation Satellite System (GNSS) water vapor tomography provides a four-dimensional (4-D) distribution of water vapor in the atmosphere for weather monitoring. It has developed into a widely used technique in numerical weather prediction (NWP). Vertical stratification is essential in discretizing the tomographic region. Traditional discretization methods divide the tomographic area into regular voxels with an equal height interval, which ignores the dynamic exponential distribution of water vapor. In recent years, non-uniform stratification methods have been widely validated by tomographic experiments. However, such experiments have not proposed a specific calculation method for stratification thickness. Therefore, in this paper, we introduced an adaptive non-uniform stratification method that follows the exponential distribution of water vapor in the tomographic region and presented the process of iterative calculation to acquire the optimal stratification interval. The proposed approach was applied based on the exponential decreasing trend in water vapor with increasing altitude. Moreover, it could adaptively calculate the interval of stratification height according to water vapor content. The tomographic experiments were performed using Global Positioning System (GPS) data from 19 ground-based stations in the Hong Kong Satellite Positioning Reference Station Network (SatRef) from 1 to 31 August 2019. The results indicated that, compared to the traditional stratification method, the root mean square error derived from the proposed approach was reduced by 0.26 g/m3. Additionally, severe weather can negatively affect the accuracy of the tomographic results. The results also showed that the accuracy of the tomographic results was reduced with increasing altitude. Moreover, the performance of the tomographic water vapor fields below 3000 m was improved by the proposed approach.
1. Introduction
Water vapor is one of the most important components in the troposphere. It plays an important role in the transport of atmospheric energy and the evolution of convective weather. The real-time and high precision monitoring of the spatiotemporal variation of atmospheric water vapor is of great significance to improve the forecasting of mesoscale severe weather. The concept of global positioning system (GPS) meteorology was first developed by Bevis et al. [1] and has since been utilized by a large number of experiments. These experiments successfully retrieved the integrated water vapor (IWV) with accuracy up to 1–2 mm, which is comparable to water vapor radiometer (WVR) and radiosonde (RS), showing that GPS is a cost-effective, convenient and reliable tool for continuous monitoring of water vapor [2,3,4,5,6,7]. Unfortunately, IWV only represents the total amount of water vapor above a certain station, and it cannot provide the vertical distribution of water vapor [8]. Due to the influence of the troposphere, the satellite signals are refracted along the travel path from the GPS satellite to the GPS ground station [9]. Consequently, the four-dimensional (4-D) distribution of water vapor can be reconstructed from the slant wet delays (SWD) using the water vapor tomography technique [10]. Global Navigation Satellite System (GNSS) tropospheric water vapor tomography therefore has become an essential method for monitoring water vapor.
In the last two decades, many of the experiments have successfully confirmed the feasibility of GNSS tomography in reconstructing high spatiotemporal resolution water vapor fields. Flores et al. [10] carried out the first GNSS water vapor tomographic experiment. They discretized the tomographic region into 4×4×40 voxels and used the Kalman filter to perform the reconstruction of the 4-D water vapor refractive fields. They successfully described the 4-D structure of water vapor in the atmosphere and investigated the effect of vertical stratification on the accuracy of tomographic results by comparing the tomographic retrieval with the European Centre for Medium-Range Weather Forecasts (ECMWF). Since then, numerous researchers have proposed different methods of vertical stratification modeling. Hirahara [11] proposed the division method of horizontal and vertical grids and solved the tomography equations using the damped least-squares method, revealing the spatial and temporal variation of refractivity corresponding to the passage of a cold front. In the same year, the uniform stratification model with a vertical resolution of 1 km was used by Seko et al. [12] to determine the three-dimensional distribution of water vapor in the Baiu front. Tomographic approaches with non-uniform vertical resolution have been pursued by Troller et al. [13] to develop the software package Atmospheric WAter vapor TOmography Software (AWATOS). Bender et al. [14] designed a tomographic system with a uniform vertical resolution of 500 m or better to investigate the convergence and numerical parameters of different iterative algebraic reconstruction techniques (ARTs). A stratification method that can identify the appropriate vertical resolution has been developed by Chen et al. [15] based on the water vapor profiles derived from radiosonde data. Following the principle that the value of water vapor density decreases exponentially with altitude, a vertical stratification scheme with non-uniform thicknesses was developed by Yao et al. [16]. The stratification scheme increased the number of voxels crossed by satellite signals and improved the utilization of existing GNSS observation data.
Presently, it is common to divide the vertical stratification methods utilized in most studies into two categories: uniform stratification with constant vertical resolution [14,17,18,19] and non-uniform stratification with different vertical resolutions [15,16,20,21,22,23]. As an equal height interval is adopted in the vertical direction, uniform stratification can conveniently discretize the tomographic area into regular voxels. Unfortunately, a certain error will be introduced due to the incongruence between the same stratification interval and dynamic water vapor distribution. In contrast to uniform stratification, non-uniform stratification generates uneven height intervals, which can reduce the mentioned errors. Although non-uniform stratification has been widely used in water vapor tomographic experiments and studies, determination of the height interval is based on prior knowledge or experience, and there is no specific calculation method. The applicability of vertical stratification is reduced when the tomographic region is changed. Hence, the adaptive vertical stratification for the tomographic region is still unable to be realized.
In this paper, we introduce an adaptive non-uniform stratification approach that can adaptively discretize the tomographic region in an exponential trend based on the actual characteristics of atmospheric water vapor density, which compensates for the limited applicability of traditional vertical stratification. This paper is organized as follows. Section 2 presents the fundamental principle of the tomographic algorithm. The method for determining the vertical distribution characteristics of atmospheric water vapor over the tomographic region, as well as the process of establishing an adaptive non-uniform stratification model, are described in Section 3. In Section 4, tomographic experiments using data from the Satellite Positioning Reference Station Network (SatRef) and the analysis of the new approach are performed. By comparing the new approach with other developments, Section 5 discusses the advantages of the proposed approach and the specifics to be further investigated in the future. The conclusions are presented in the last section.
2. Principle of GNSS Tomography
GNSS water vapor tomography is a method to obtain the 4-D distribution of atmospheric water vapor by constructing functioning relationships among water vapor density, satellite signal propagation distance, and slant wet delays. The delay of satellite signals when they pass through the earth’s atmosphere includes the ionospheric delay, which can be corrected by using dual-frequency linear combinations and the neutral atmospheric delay, which can be used for observations of GNSS tomography. In this paper, we use the slant water vapor (SWV) as the input observation data for the tomographic model to retrieve water vapor density, which can be calculated from SWD; its formula is as follows [1]:
where k3 and k’2 are the atmospheric refractive index constants with the value of 3.776 × 105 K2/hPa and 16.52 K/hPa, respectively; Rv is the specific gas constant of water vapor with a value of 461.495 J/K/kg; Tm is the weighted mean tropospheric temperature, calculated from the numerical integration using the meteorological measurements [24]; SWD refers to the slant wet delay (SWD), which can be expressed with the following Equation [10]:
where fw is the wet mapping function, and the global mapping function (GMF) is as proposed by Böhm et al. [25]; e and ϕ are the satellite elevation angle and the azimuth angle, respectively; and refer to the wet delay gradients in the east-west and north-south directions, respectively; R refers to the residual unmodeled delay between the satellite and the receiver; and ZWD represents the zenith wet delay (ZWD), which is the portion of the zenith tropospheric delay (ZTD) except the zenith hydrostatic delay (ZHD), as follows:
The ZHD in Equation (3) can be accurately calculated using the surface station pressure according to the empirical model proposed by Saastamoinen [26], with the following formula:
where PS refers to the surface station pressure in hPa; φS is the station latitude; and hS is the station geodetic height in km.
The SWV calculated by Equations (1)–(4) is inputted as the observation of the tomographic observation equation for the retrieval of water vapor density, and the formula is as follows [10]:
where ρ(S) refers to the water vapor density in g/m3; and s represents the distance of satellite signal traveled in the troposphere in m. As atmospheric water vapor is continuously distributed in the atmosphere, it is necessary to discretize the research area in most cases. Under the assumption that the water vapor density in each discrete voxel is a constant during a tomographic period, the small influence of geometric delay in signal propagation is neglected. In discrete form, Equation (5) becomes:
where n is the number of discrete voxels in the research area; SWVi refers to the slant water vapor of the i th satellite signal in the research area; lij represents the distance traveled by the i th satellite signal in the j th voxel, which can be calculated based on two adjacent intersections between the signal and grid faces; and ρj represents the water vapor density of the j th voxel.
The matrix form of the tomographic observation equation according to the SWV observation of multiple satellite signals can be written as follows:
where Am×n and bm×1 represent the coefficient matrix consisting of distance values and the column vector made up of SWV observations, respectively; xn×1 represents the column vector of unknown water vapor density values; and m and n are the number of SWV observations and number of discrete voxels subdividing the research area, respectively.
Unfortunately, owing to the geometric distribution of existing satellites and ground-based receivers, some voxels may not be crossed by any satellite signal. Consequently, this will result in an inverse problem that turns out to be ill-posed, i.e., the solutions of unknown water vapor density values are in general not unique and not stable. The constraint conditions or prior information would therefore be introduced to solve the severe rank deficiency issue of the tomographic equations [23,27,28,29]. In this study, we introduced the common horizontal constraints and vertical constraints. The horizontal constraint is based on the hypothetical relation that the water vapor density in each voxel is a weighted mean of water vapor densities in other voxels in the same layer. The vertical constraint is based on an exponential relation that can be used to represent the average water vapor profile:
where ρj and ρk represent the water vapor density of the j th layer and the k th layer, respectively; hj and hk are the height of the j th layer and the k th layer, respectively; and H refers to the water vapor scale height, which can be calculated by the following formula:
where W represents the total vertical water vapor content in g/m2 that can be obtained from PWV; and ρS represents the surface station humidity in g/m3.
After combining all of the SWV observation equations and constraint equations, the established solution model of GNSS tomography in the matrix form is given as follow:
where Hn×n and Vv×n are the coefficient matrices of horizontal constraints and vertical constraints, respectively; and v refers to the number of vertical constraints.
To reconstruct the water vapor density field based on the matrix shown in Equation (10), the algebraic reconstruction technique (ART) is utilized in this study. ART has the advantage of avoiding the inversion of the coefficient matrix and strong noise resistance. Moreover, it has high numerical stability even under adverse conditions of fewer observation equations, uneven signal distribution, or noise. The common ART for computing the approximation of the tomographic solution is as follows:
where xk is the k th iterative solution; n is the total number of voxels; λ is the relaxation factor, which gives the weight of the correction term computed for each voxel with respect to the initial value; ai,j represents the element in i th row and j th column of the coefficient matrix of the tomographic equation; and bi refers to the i th row element in the column vector of the observed value.
3. Adaptive Non-Uniform Exponential Stratification Method
The process of the adaptive non-uniform exponential stratification (ANES) method in this paper include two main steps: (1) modeling the vertical distribution of atmospheric water vapor in the tomographic region and obtaining the function that can represent the average water vapor profile based on prior water vapor profile information; (2) calculating the height interval of each layer in an iterative way to realize the adaptive stratification of a predetermined number of stratifications according to the obtained vertical characteristic function of atmospheric water vapor. These two steps are introduced and described in detail in Section 3.1 and Section 3.2.
3.1. Modeling of Vertical Distribution Characteristics of Atmospheric Water Vapor
Before carrying out the adaptive non-uniform exponential stratification, the specific functional relationship between water vapor density and height in the tomographic region should be determined, which can be modeled based on the relation that water vapor density decreases exponentially with increasing altitude, in general. The water vapor density at height h can therefore be expressed as follows:
where ρh refers to the water vapor density at height h in g/m3; ρ0 refers to the water vapor density parameter at the surface; Dv represents the parameter of vertical distribution characteristic of water vapor; and H stands for the water vapor scale height in m.
Equation (12) raises the problem of solving the unknown parameters of the exponential function, including the water vapor density parameter at the surface and the vertical distribution characteristic parameter of water vapor. The mentioned unknown parameters can be obtained by fitting the prior water vapor density in the study area. The prior water vapor density can be calculated based on radiosonde data as follow:
where Rv is the specific gas constant of water vapor with a value of 461.495 J/K/kg; T refers to the temperature in K; and Pw represents the vapor pressure in hPa, which can be calculated according to the Goff–Gratch formula, as follows [30]:
where Td refers to the dew-point temperature in K; and T1 is a constant with a value of 273.16 K.
Figure 1 reveals the fitting schematic diagram of the average radiosonde water vapor profile in the study area, in which the blue scatter points represent the calculated water vapor density, and the red curve represents the fitting function where the formula can be expressed as follows:
where x represents the height in m; y represents the water vapor density in g/m3; a and b are the concrete values of ρ0 and Dv after fitting, respectively; and H represents the water vapor scale height in m.
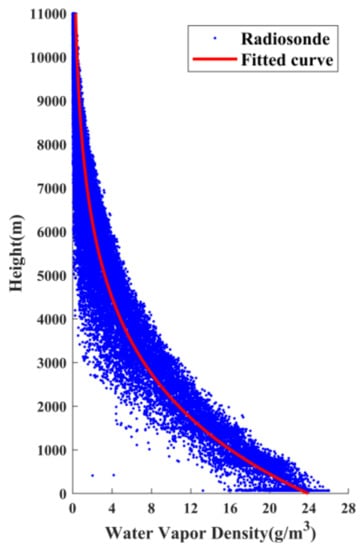
Figure 1.
Fitting schematic diagram of the average radiosonde water vapor profile in the study area.
Equation (15) represents the general distribution characteristics of atmospheric water vapor in the vertical direction in the study region and provides a specific functional relationship between the height and water vapor density for subsequent adaptive stratification.
3.2. Adaptive Non-Uniform Exponential Stratification Method
After determining the average vertical distribution characteristics of atmospheric water vapor in the tomographic region, an iterative algorithm is adopted to calculate the height interval of two adjacent stratifications: Three parameters are introduced, where L refers to the number of the stratification; D refers to the minimum height interval between adjacent stratifications in m; ρb refers to the water vapor density at the top boundary of the tomographic region in g/m3, and it can usually be determined according to the prior information or radiosonde data. Therefore, the height interval of the first stratification is [0, D] under this model, and the numerical interval of water vapor density in the first stratification can be represented as [a, a∙eb∙(-D/H)]. After dividing the first stratification, the remaining stratifications are equally divided according to the water vapor density, and the numerical interval of the water vapor density of each remaining stratification can hence be expressed as:
where a, b and H represent the same meanings as Equation (15); and n represents the number of each stratification (2 ≤ n ≤ L).
After obtaining the expected interval of water vapor density at each stratification as shown in Equation (16), the height of the height interval of the second stratification can be inferred through the water vapor density in combination with Equation (15), as follows:
where a, b, H, D, L and ρb represent the same meanings as in Equation (16).
If the height interval of the second stratification as shown in Equation (17) is greater than D m, the expected height interval calculated by the expected water vapor density in combination with Equation (15) is taken as the stratification result to complete the non-uniform exponential stratification; otherwise, the height interval of the second stratification is set to the minimum height interval D m to continue iterating.
In each iteration, the remaining stratifications are evenly divided according to the water vapor density. After dividing the bottom stratifications m times with D m as the minimum height interval, the water vapor density interval of the remaining stratifications can be expressed as the following:
where a, b, H, D, L and ρb represent the same meanings as in Equation (17); and m refers to the number of iterations that divide the bottom stratifications with D m as the minimum height interval.
In the m th iteration, after obtaining the expected water vapor density interval of remaining stratifications as shown in Equation (18), the height interval can be inferred in combination with Equation (15), and the bottom height interval can be calculated as:
where a, b, H, D, L, ρb and m represent the same meanings as in Equation (18); and Hi refers to the height interval of the lowest stratification in the remaining (L-m) stratifications in m. If Hi is greater than D m, terminate the iteration and the non-uniform exponential stratification is completed; otherwise, the lowest stratification in the remaining (L-m) stratifications will be divided unceasingly with D m as the height interval and continue to iterate.
4. Results and Validations
4.1. Processing Strategy
The GPS observation data of 19 ground-based receivers obtained from the SatRef in Hong Kong were selected during the tomographic period of the entire August of 2019. The top boundary of the tomographic region was calculated based on radiosonde water vapor profile data in August of each year from 2010 to 2018. The investigated tomographic area was therefore from 22.204° N to 22.564° N in latitude and from 113.844° E to 114.384° E in longitude, with a height range from 0 m to 10,560 m. The number of spatial voxels used for tomography was 6×4×13 with a horizontal resolution in the latitude and longitude directions of 0.090°, and the vertical resolution was set according to different stratification schemes. Figure 2 shows the geographical distribution of the GNSS receivers and the radiosonde in the tomographic area, in which the red points represent the locations of 19 GNSS receivers and the green point represents the location of the radiosonde.
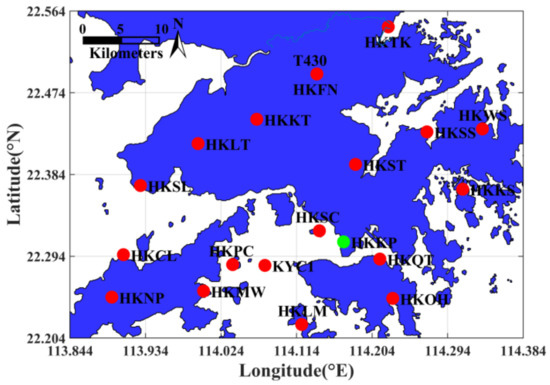
Figure 2.
Geographical distribution of Global Navigation Satellite System (GNSS) receivers and radiosonde station in the tomographic area.
The time interval in which the water vapor density of each voxel is assumed to be a constant was 30 min. The GPS-observed data was processed using GAMIT/GLOBK (v10.7) based on the double-differenced combined observation, and the processing strategies are shown in Table 1. As mentioned in Section 2, ART was used to retrieve the water vapor density. The accuracy of the initial iteration value has an important influence on the accuracy of the tomographic results. In this paper, the average vertical water vapor profile calculated from the radiosonde data of Hong Kong from 2010 to 2018 was used as the initial iteration value.

Table 1.
Processing strategies of GAMIT/GLOBK (v10.7).
4.2. Vertical Stratification Strategy
The minimum height interval is an important parameter that directly affects the height of each voxel. If the value of the minimum height interval is adjusted by a long step length, the optimal value will be missed. Therefore, the vertical stratification strategy based on the ANES was divided into five different schemes with a step length of 25 m. Introducing the traditional uniform stratification scheme for comparison, six vertical stratification schemes were used for water vapor tomographic experiments to verify the feasibility of the adaptive non-uniform exponential stratification method. Among the six vertical stratification schemes mentioned above, scheme (a) equally divides the tomographic region into 13 stratifications in the vertical direction based on the traditional uniform stratification; in schemes (b) to (f), ANES with minimum height intervals of 350, 375, 400, 425 and 450 m, respectively, were adopted to divide the tomographic region into 13 stratifications unevenly. Figure 3 displays the vertical resolution of the six stratification schemes.
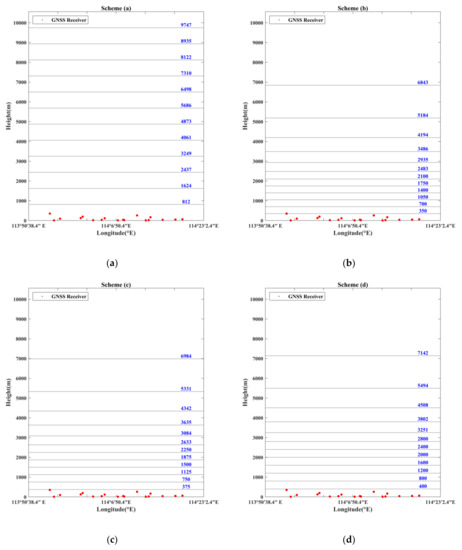
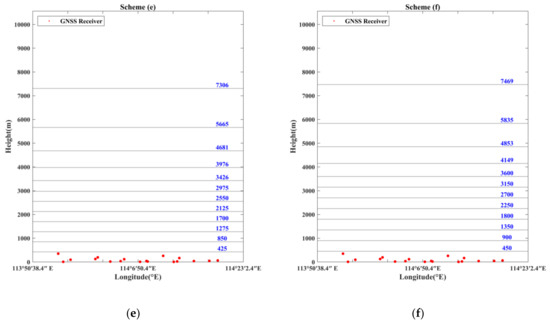
Figure 3.
Vertical resolution according to six stratification schemes: (a) uniform stratification with height interval of 812 m; (b) ANES with minimum height interval of 350 m; (c) ANES with minimum height interval of 375 m; (d) ANES with minimum height interval of 400 m; (e) ANES with minimum height interval of 425 m; (f) ANES with minimum height interval of 450 m.
After completing the determination of the vertical resolution of the six stratification strategies, we calculated the mean water vapor density of each stratification under different schemes in the period of the tomographic experiment based on the radiosonde data of HKKP. Figure 4 reveals the mean radiosonde-measured water vapor density of each stratification derived from the six schemes, in which the red columns represent the difference value of the mean water vapor density between two adjacent stratifications.
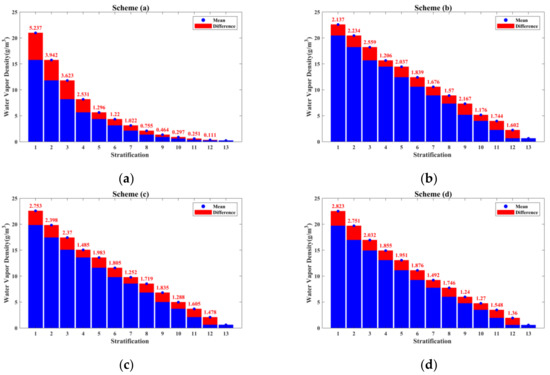
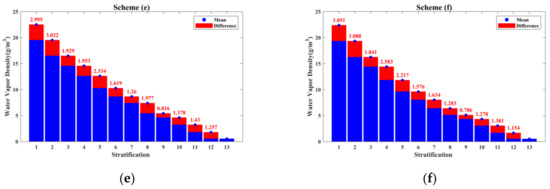
Figure 4.
Mean water vapor density of each stratification and difference value between two adjacent stratifications derived from six stratification schemes, where (a) derived from uniform stratification; (b–f) derived from ANES with minimum height intervals of 350, 375, 400, 425 and 450 m, respectively.
As shown in Figure 4, scheme (a) adopts the uniform stratification strategy, resulting in the phenomenon that the mean water vapor density of each stratification decreases exponentially with increasing stratification number. Meanwhile, the difference value of the mean water vapor density between two adjacent stratifications decreases with increasing stratification number. The maximum value of the differences was 5.237 g/m3 (between stratification 1 and stratification 2), and the minimum value of the differences was 0.111 g/m3 (between stratification 12 and stratification 13); the difference between the maximum and the minimum was 5.126 g/m3. In schemes (b) to (f), in which the vertical resolution was divided based on the ANES, the mean water vapor density of each stratification decreased linearly with increasing stratification, and the differences between the maximum and the minimum difference value derived from the six schemes were 1.383 g/m3, 1.501 g/m3, 1.583 g/m3, 2.206 g/m3, 2.302 g/m3, respectively. The above computations obtained from radiosonde data indicate that the traditional uniform stratification leads to a large difference in the difference value of the mean water vapor density between two adjacent stratifications, which is represented by a large difference in the difference value between bottom stratifications compared with a small difference between top stratifications, while the ANES can effectively avoid this problem.
The box-plot as shown in Figure 5 also illustrates the advantages of the ANES, in which both standard deviation (STD) and interquartile range (IQR) are statistics used to characterize the dispersion degree of a combination of data. As shown in the figure, comparing the traditional uniform stratification and the ANES, the length of the box-plot of scheme (a) is larger than that of the other schemes, and the STD and the IQR values of scheme (a) are also much larger than those of the other five schemes, indicating that the ANES can significantly reduce the difference of the difference value between two adjacent stratifications. Furthermore, it can also be found in Figure 5 that scheme (f) has a relatively higher STD and IQR among the schemes based on the ANES approach. The reason for this phenomenon is that the minimum height interval of scheme (f) is larger than those of the rest of the ANES schemes, which leads to the more drastic change in the difference of the mean water vapor density between two adjacent stratifications. The same conclusion can be deduced from Figure 4. As shown in the figure, in schemes (b) through (e), only three values of the difference are greater than 2 g/m3, while in scheme (f), four values are greater than 2 g/m3, and two of them are greater than 3 g/m3.
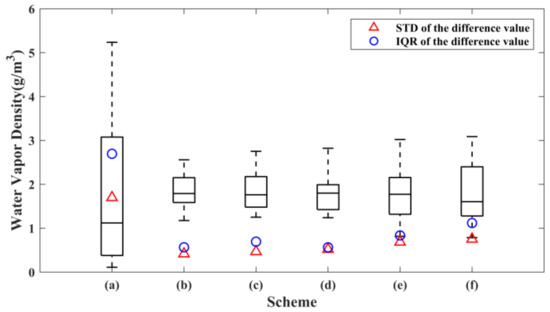
Figure 5.
Box plots of the difference value of mean water vapor density between two adjacent stratifications derived from the six stratification schemes, where (a) derived from uniform stratification; (b–f) derived from ANES with minimum height intervals of 350, 375, 400, 425 and 450 m, respectively.
The above experiments and analyses based on the radiosonde water vapor profile information of HKKP in August 2019 preliminarily proved the advantages of the ANES over the traditional uniform stratification. This paper compared and analyzed the results of the tomographic experiments derived from the six schemes to further verify the feasibility and superiority of the ANES in Section 4.3.
4.3. Tomographic Experiments and Evaluation of the ANES Approach
To further validate the performance of the proposed method, the tomographic results of scheme (b) to scheme (f) are compared with the tomographic results of scheme (a) in this section while radiosonde data are regarded as the references. Radiosonde data were often used as a reference to evaluate the quality of the water vapor density retrieved by other tomographic approaches [15,16,21]. The reliability of using radiosonde data as a reference has been verified, though the limitation of its low spatial resolution may cause errors in terms of water vapor [31,32,33]. Radiosonde data have the advantage of high vertical resolution, which can provide accurate vertical water vapor information at various altitudes, so the water vapor density derived from radiosonde data was used to validate the proposed approach in this paper.
The first part of this section is a comparison of the statistical results of the tomographic reconstructions derived from the six schemes in the experimental period of 31 days. The water vapor density value reconstructed by tomography was assessed using those derived from radiosonde data; the root mean square error (RMSE), the bias, and the mean absolute error (MAE) of the overall dataset are shown in Table 2. These statistical results of solutions had their respective characteristics. In terms of RMSE, the results of scheme (d) had the lowest RMSE value. In the bias comparison, both scheme (b) and scheme (f) had the closest bias value from 0 g/m3, while in the comparison of the MAE, scheme (f) had the advantage because of the lowest MAE value. Overall, in the comparison of the schemes based on the ANES approach, the statistical results of scheme (d) exhibited a higher accuracy than the other schemes. Further, it should be noted that the minimum height intervals of scheme (b), (c), and (d) were 350 m, 375 m, and 400 m, respectively. However, scheme (d) displayed a smaller RMSE than those of scheme (b) and (c). This phenomenon indicates that smaller height intervals do not correspond to higher accuracy. A reason for this may be that a smaller height interval reduces the height of voxels at the bottom boundary, which decreases the number of voxels passed by GNSS signals under the condition that the geometrical distribution of satellite rays is constant.

Table 2.
Statistical results of the six schemes, with results derived from differences in water vapor density between radiosonde data and tomography.
In terms of the contrast between the schemes using the ANES and that using the traditional uniform stratification, the statistical results of the ANES were superior in numerical comparisons of the RMSE, bias, and MAE. The maximum RMSE of the ANES appeared in scheme (b) with a value of 1.104 g/m3, indicating that its accuracy was the lowest in the ANES schemes, which was still lower than the RMSE of scheme (a) with a value of 1.321 g/m3. Scheme (a) had a value of 0.167 g/m3 in the bias, while the worst bias value of the ANES was −0.104 g/m3 appearing in scheme (b). The MAE value of the uniform stratification was 0.022 g/m3 greater than that of scheme (b), which was the maximum MAE value in the schemes using the ANES. Figure 6 further validates the advantages of the ANES approach by showing the correlation between the tomographic reconstructions of the six schemes and the radiosonde data in the form of scatter plots. Among the six schemes, the scatter plot of scheme (a) had both the largest RMSE and the lowest R2, revealing that the correlation between the tomographic reconstructions of the traditional stratification approach and the radiosonde data is lower than that of ANES. Moreover, by observing the scatter plots, it can be seen that scheme (a) showed distinct gaps in the water vapor density data retrieved by tomography, which demonstrates the inadequacy of the traditional stratification approach mentioned in Section 4.2.
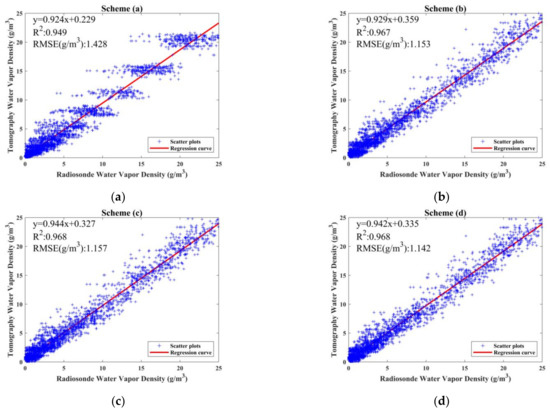
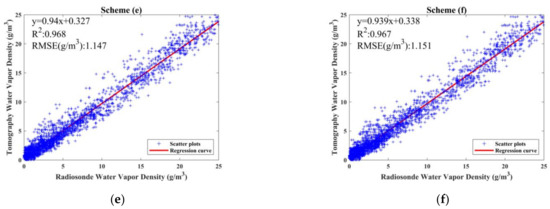
Figure 6.
Scatter plots of water vapor density between radiosonde and tomography derived from the six stratification schemes, where (a) derived from uniform stratification; (b–f) derived from ANES with minimum height intervals of 350, 375, 400, 425 and 450 m, respectively.
The comparison of statistical results and scatter plots between the traditional approach and the ANES approach generally verified the feasibility of the new stratification approach. Five schemes derived from the ANES approach were also compared with one another, with different minimum height intervals adopted for non-uniform stratification. Among the five schemes, scheme (d) with 400 m as the minimum height interval had the smallest RMSE value in both statistical results and scatter plots, revealing that a smaller height interval does not correspond to better tomographic results. This is probably because the smaller thickness leads to more voxels that cannot be crossed by satellite paths, thus worsening the ill-posedness of the tomographic equations mentioned in Section 2.
The next part of this section presents the time series of the statistical results derived from the six schemes on the time scale of 31 days. Because only radiosonde data at UTC 00:00 and UTC 12:00 could be obtained daily, two experiments were conducted per day for a total of 61 experiments in each scheme. Figure 7 displays the RMSE time series derived from the six stratification schemes. According to the time series of the RMSE, the maximum RMSEs of schemes (a) to (f) were 2.692, 2.121, 1.969, 1.930, 2.035 and 2.039 g/m3, respectively, while the minimum RMSEs were 0.943, 0.680, 0.687, 0.558, 0.662 and 0.561 g/m3, respectively. Evidently, the corresponding RMSE of the proposed method in this paper was smaller than the traditional method when the radiosonde data were taken as a reference. In addition, by observing the RMSE time series, it can be seen that higher RMSE values were generally present at UTC 12:00 of DOY 213 and UTC 12:00 of DOY 237. This was related to the strong winds and torrential rains caused by typhoons in Hong Kong from DOY 213 to DOY 214 and DOY 237 to DOY 238.
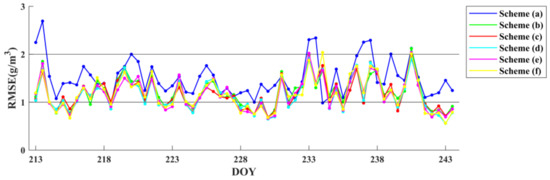
Figure 7.
Time series of the RMSE of the tomographic reconstructions derived from the six schemes using radiosonde data as a reference for 31 days (DOY 213 to DOY 243).
As the precision of the tomographic reconstructions is highly influenced by the vertical structure of the humidity field, total statistical results cannot provide a comprehensive analysis of the accuracy of tomographic reconstructions. Therefore, the following part of this section analyzed the results of tomographic retrieval on a vertical space scale. As the same tomographic error value in different layers has different qualities, in addition to using RMSE for analysis, this paper also used the concept of relative error to reflect the quality of tomographic reconstructions in each stratification. Following is the formula for calculating the relative error:
where RE refers to the relative error; DT represents the retrieval of water vapor density by water vapor tomography in g/m3; and DRS represents the water vapor density calculated from radiosonde data in g/m3.
Figure 8 presents the RMSE and relative error derived from different schemes in each stratification. By observing the variation tendency between RMSE and relative error, opposite tendencies emerged in these two statistics. Despite the RMSE of all schemes decreasing with increasing height, the relative error tended to increase. It was due to the characteristic that water vapor density decreases with increasing altitude, making it difficult for tomography to accurately retrieve humidity at high altitudes. A comparison of the six schemes in terms of RMSE and relative error shows that the tomographic reconstructions derived from the ANES had relatively small values for these two parameters in the tomographic region below 6000 m, while the values were comparable above 6000 m. In the region below 3000 m, the RMSE values of the five schemes derived from the ANES were stable within the range of 1.5 to 2 g/m3, while that of scheme (a) was consistently greater than 2 g/m3. In the region from 3000 to 6000 m, the RMSE and the relative error of the tomographic reconstructions were significantly decreased by the new approach. Therefore, the above comparison further demonstrates the marked superiority of the proposed method in the lower boundary layer.
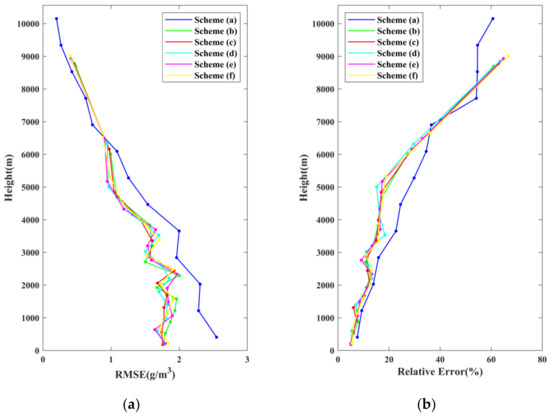
Figure 8.
Comparison of the RMSE and relative error derived from six schemes in each stratification using radiosonde data as a reference (DOY 213 to DOY 243): (a) comparison of the RMSE in each stratification; (b) comparison of the relative error in each stratification.
Furthermore, the water vapor profiles reconstructed by the ANES approach were also compared. This paper shows the comparison of the water vapor profiles during dry weather (Figure 9) and rainy days (Figure 10). It can be clearly observed from Figure 9 and Figure 10 that all of the water vapor profiles reconstructed by the tomography showed satisfactory consistency with the radiosonde data. However, the water vapor profiles derived from scheme (d) had relatively higher consistency with radiosonde data than those of the other schemes in the case of rain or not. Moreover, by comparing the differences in water vapor density between the radiosonde data and the tomographic results under different weather conditions, it was found that the differences were slightly larger in rainstorm weather, especially in the region below 3000 m. However, from the comparison of the six schemes in Figure 10, it can be seen that the water vapor profiles reconstructed by the ANES approach exhibited fluctuating water vapor variations below 3000 m and higher conformity with the radiosonde data than scheme (a) derived from the traditional approach. The above comparisons highlight that due to the consistency of the non-uniform division with the actual vertical distribution of water vapor, its performance to describe fluctuations in water vapor density was improved. Additionally, its superiority in extreme weather was also demonstrated.
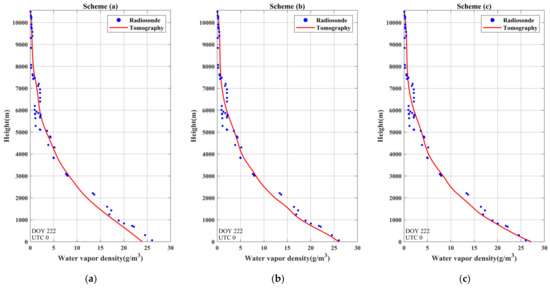
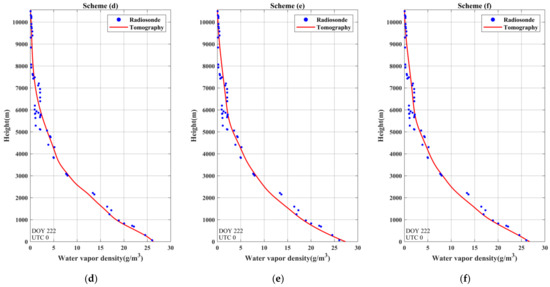
Figure 9.
Comparison of water vapor density profiles derived from six schemes on DOY 222 at UTC 00:00. (a) Derived from uniform stratification; (b–f) derived from ANES with minimum height intervals of 350, 375, 400, 425 and 450 m, respectively.
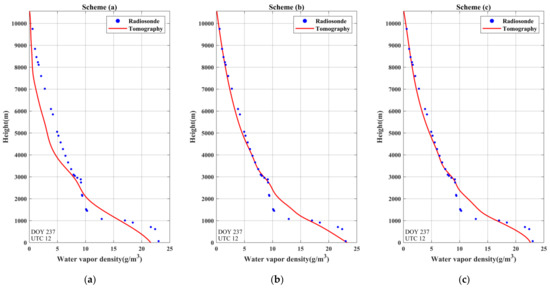
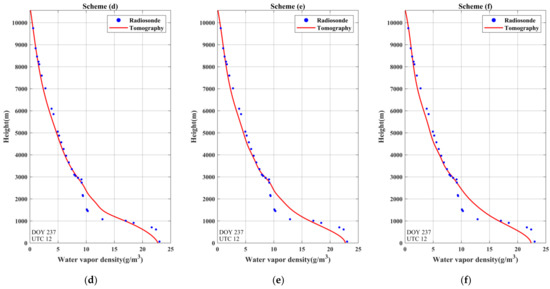
Figure 10.
Comparison of water vapor density profiles derived from six schemes on DOY 237 at UTC 12:00. (a) Derived from uniform stratification; (b–f) derived from ANES with minimum height intervals of 350, 375, 400, 425 and 450 m, respectively.
5. Discussion
As mentioned above, the results verified the feasibility and performance of the ANES method. Meanwhile, the problem that the height intervals of the uniform stratification did not conform to the dynamic exponential distribution of water vapor was solved by the proposed approach. The ANES approach implements the adaptive non-uniform stratification of the tomographic region in the vertical direction. The height intervals of the voxels discretized by the proposed approach follow the actual dynamic exponential distribution of atmospheric water vapor. Thus, in the bottom boundary area where the water vapor varies sharply, the discretization will be more detailed, and the number of retrieved parameters will increase. In contrast, the ANES approach no longer allocates excess voxels to the top boundary area where the water vapor varies gently. Moreover, the ANES approach is portable and adaptable. The specific calculation method for vertical resolution is described in Section 3 and provides a standard for non-uniform stratification. Meanwhile, taking radiosonde for example, this paper detailed the steps to obtain the function that can represent average water vapor density. At present, the radiosonde is the most accurate instrument to measure water vapor density with high vertical resolution. However, radiosonde data have the limitation of sparse spatial distribution. In the case where radiosonde data are not available, the vertical distribution of water vapor can also be obtained by other means such as ECMWF ERA-Interim data. The advantage of ECMWF is that it has a higher horizontal resolution than radiosonde. ECMWF grid points can provide three-dimensional distribution information for water vapor in the tomographic region.
The results of the research also indicate that the ANES approach improves the accuracy of tomographic reconstructions compared to the conventional approach. In addition to the approach proposed in this paper, many other influential developments have also improved the accuracy of tomographic reconstruction compared to the conventional approach [15,34,35,36,37]. Table 3 presents the tomographic strategies of the developments mentioned above and the optimal strategy in this paper. As shown in the table, the vertical resolutions of the uniform stratification model proposed by Haji-Aghajany et al. [34,35] were 0.5 km (below 5 km) and 1 km (above 5 km), respectively. This stratification strategy considered the high spatiotemporal variations in water vapor at lower altitudes but did not take into account the dynamic exponential distribution of water vapor. In contrast to the research using the uniform stratification model, Chen et al. [15] and Zhang et al. [36,37] adopted the non-uniform stratification model. A variety of strategies with different vertical resolutions were used for comparative experiments in Chen et al. [15]. These experiments investigated the non-uniform stratification model in detail, but did not propose a specific calculation method for adaptive stratification. Zhang et al. [36] applied two comparative schemes between the voxel tomography model and the node tomography model. These two schemes adopted the same vertical resolutions as in Zhang et al. [37], which took into account the non-linear decline characteristics of water vapor in the vertical direction, but did not propose a detailed solution to the problem of adaptation. The standard of the adaptive non-uniform stratification adopted by the voxel tomography model was introduced and demonstrated in detail in this paper, and the integration of the node tomography model and ANES will be important topics of further investigation.

Table 3.
Comparison of tomographic strategies used by developed approaches and their improvements to the accuracy of tomographic reconstructions.
6. Conclusions
An adaptive non-uniform exponential stratification (ANES) approach was proposed for tomography in this paper, and its feasibility and superiority were validated using 31 days of GNSS data in Hong Kong. The proposed approach firstly calculates the estimated height interval of each stratification in terms of the vertical distribution characteristic function. Then, the height interval of the lowest stratification obtained in each iteration is compared with the parameter of minimum height interval to gradually correct the estimated height interval starting from the bottom of the tomographic region. Therefore, the ANES approach can adaptively divide vertical stratifications for the tomographic region without the need to determine the height interval of vertical stratification according to fixed experience. Furthermore, the non-uniform stratification was adopted to satisfy the distribution characteristic that water vapor in the vertical direction decreases exponentially with increasing altitude, and to reduce the difference in water vapor density between two adjacent stratifications in the lower boundary layer.
By comparing the mean water vapor density calculated from the radiosonde data, we found that the mean water vapor density of each stratification derived from the uniform stratification decreases exponentially with increasing stratification. In this case, it creates a phenomenon whereby the difference in water vapor density between adjacent stratifications is relatively large in the lower boundary layer, which is not conducive to reconstruction of the water vapor density field. Tomographic experiments using GPS data for Hong Kong in the period of DOY 213 to 243, 2019 were conducted to validate the proposed ANES approach. We applied five schemes derived from the ANES with minimum height intervals of 350, 375, 400, 425, and 450 m and compared them with the traditional approach. In terms of overall statistical results, the ANES approach showed superiority over the traditional approach, where the minimum height interval of 400 m had the smallest root mean square error of 1.07 g/m3. The statistical results were analyzed, and the results show that severe weather, such as typhoons, will affect the accuracy of the tomographic results to some extent. Moreover, by comparing the vertical water vapor profile reconstructed by tomography with the radiosonde data, it was found that although all the schemes could accurately reflect the vertical distribution of atmospheric water vapor, it is difficult to use the water vapor density field reconstructed by tomography to compare with the radiosonde data with a high vertical resolution, especially under severe weather conditions. Statistical results for each stratification were studied, and the results showed that the tendencies between the RMSE and the corresponding RE were opposite with increasing altitude, which indicated that it became gradually difficult to realize the retrieval of water vapor density using tomography, as the moisture content decreased exponentially with the increasing altitude.
In future investigations, our primary focus will be on the integrated approach of the node tomography model and the ANES approach. Moreover, determining the optimal minimum height interval by analyzing the geometrical distribution of satellite rays will be another research objective. Furthermore, the algebraic reconstruction techniques (ARTs) will need to be further optimized, such as by applying the corresponding weight to the observation equations with different levels of precision to enhance the reliability and accuracy of water vapor tomography.
Author Contributions
Conceptualization, H.W. and W.Z.; Methodology, H.W.; Software, H.W.; Validation, H.W., W.Z. and N.D.; Formal analysis, H.W., W.Z. and N.D.; Investigation, H.W.; Resources, H.W.; Data curation, H.W., W.Z. and N.D.; Writing—original draft preparation, H.W.; Writing—review and editing, H.W. and W.Z.; Visualization, H.W. and W.Z.; Supervision, N.D. and W.Z.; Project administration, N.D. and W.Z.; Funding acquisition, N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This study is funded by the National Natural Science Foundation of China (41904013), the National Natural Science Foundation of China (41774026), the National Natural Science Foundation of China (41730109), the National Science Foundation of Jiangsu Normal University (19XSRS010) and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX20_2363).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the Survey and Mapping Office (SMO) of Lands Department, Hong Kong for the provision of GNSS data from the Hong Kong Satellite Positioning Reference Station Network (SatRef). GNSS data in the RINEX format used for this study can be downloaded from the website (http://www.geodetic.gov.hk/smo/gsi/programs/en/GSS/satref/ satref.htm). We also thank King’s Park Observatory for the provision of radiosonde data and the Department of Earth Atmospheric and Planetary Sciences, MIT for the GAMIT/GLOBK software. Radiosonde data from King’s Park Meteorological Station can be downloaded from the website (http://weather.uwyo.edu/upperair/sounding.html).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Baker, H.C.; Dodson, A.H.; Penna, N.T.; Higgins, M.; Offiler, D. Ground-based GPS water vapour estimation: Potential for meteorological forecasting. J. Atmos. Solar-Terr. Phys. 2001, 63, 1305–1314. [Google Scholar] [CrossRef]
- Elósegui, P.; Ruis, A.; Davis, J.L.; Ruffini, G.; Kruse, L.P. An experiment for estimation of the spatial and temporal variations of water vapor using GPS data. Phys. Chem. Earth 1998, 23, 125–130. [Google Scholar] [CrossRef]
- Rocken, C.; Hove, T.V.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Businger, S. GPS/STORM-GPS sensing of atmospheric water vapor for meteorology. J. Atmos. Ocean. Technol. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; Van, H.T.; Ware, R. GPS Meteorology: Direct estimation of the absolute value of precipitable water. J. Appl. Meteorol. 1996, 35, 830–838. [Google Scholar] [CrossRef] [Green Version]
- Baelen, J.V.; Aubagnac, J.P.; Dabas, A. Comparison of near-real time estimates of integrated water vapor derived with GPS, radiosondes, and microwave radiometer. J. Atmos. Ocean. Technol. 2005, 22, 201–210. [Google Scholar] [CrossRef]
- Emardson, T.R.; Elgered, G.; Johansson, J.M. Three months of continuous monitoring of atmospheric water vapor with a network of Global Positioning System receivers. J. Geophys. Res. Atmos. 1998, 103, 1807–1820. [Google Scholar] [CrossRef]
- Jin, S.; Luo, O.F. Variability and climatology of PWV from global 13-year GPS observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1918–1924. [Google Scholar] [CrossRef]
- Kursinski, R.; Hajj, G.A.; Leroy, S.S.; Herman, B. The GPS radio occultation technique. Terr. Atmos. Ocean. Sci. 2001, 11, 53. [Google Scholar] [CrossRef] [Green Version]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Hirahara, K. Local GPS tropospheric tomography. Earth Planets Space 2000, 52, 935–939. [Google Scholar] [CrossRef] [Green Version]
- Seko, H.; Shimada, S.; Nakamura, H.; Kato, T. Three-dimensional distribution of water vapor estimated from tropospheric delay of GPS data in a mesoscale precipitation system of the Baiu front. Earth Planets Space 2000, 52, 927–933. [Google Scholar] [CrossRef] [Green Version]
- Troller, M.; Geiger, A.; Brockmann, E.; Bettems, J.M.; Kahle, H.G. Tomographic determination of the spatial distribution of water vapor using GPS observations. Adv. Space Res. 2006, 37, 2211–2217. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Ge, M.; Deng, Z.; Wickert, J.; Kahle, H.G.; Raabe, A.; Tetzlaff, G. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques. Adv. Space Res. 2011, 47, 1704–1720. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Liu, Z. Voxel-optimized regional water vapor tomography and comparison with radiosonde and numerical weather model. J. Geodesy 2014, 88, 691–703. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Q. Maximally using GPS observation for water vapor tomography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7185–7196. [Google Scholar] [CrossRef]
- Bao, Z.; Fan, Q.; Yao, Y.; Xu, C.; Li, X. An improved tomography approach based on adaptive smoothing and ground meteorological observations. Remote Sens. 2017, 9, 886. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Fei, Y.; Shi, J.; Xu, C. An optimal weighting method of global positioning system (GPS) troposphere tomography. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 9, 5880–5887. [Google Scholar] [CrossRef]
- Xia, P.; Cai, C.; Liu, Z. GNSS troposphere tomography based on two-step reconstructions using GPS observations and COSMIC profiles. Ann. Geophys. 2013, 31, 1805–1815. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y.; Yao, W. Troposphere water vapour tomography: A horizontal parameterised approach. Remote Sens. 2018, 10, 1241. [Google Scholar] [CrossRef] [Green Version]
- Ding, N.; Zhang, S.; Zhang, Q. New parameterized model for GPS water vapor tomography. Ann. Geophys. 2017, 35, 311–323. [Google Scholar] [CrossRef] [Green Version]
- Jiang, P.; Ye, S.R.; Liu, Y.Y.; Zhang, J.J.; Xia, P.F. Near real-time water vapor tomography using ground-based GPS and meteorological data: Long-term experiment in Hong Kong. Ann. Geophys. 2014, 32, 911–923. [Google Scholar] [CrossRef] [Green Version]
- Perler, D.; Geiger, A.; Hurter, F. 4D GPS water vapor tomography: New parameterized approaches. J. Geod. 2011, 85, 539–550. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Chen, Y.; Liu, J. Determination of weighed mean tropospheric temperature using ground meteorological measurements. Geo-Spat. Inf. Sci. 2001, 4, 14–18. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J.H. Atmospheric correction for the troposphere and the stratosphere in radio ranging satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar] [CrossRef]
- Skone, S.; Hoyle, V. Troposphere modeling in a regional GPS network. J. Glob. Position. Syst. 2005, 4, 230–2391. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, T.; Gradinarsky, L. Water vapor tomography using GPS phase observations: Simulation results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2927–2941. [Google Scholar] [CrossRef]
- Bender, M.; Raabe, A. Preconditions to ground based GPS water vapour tomography. Ann. Geophys. 2007, 25, 1727–1734. [Google Scholar] [CrossRef]
- Wexler, A. Vapor pressure formulation for water in range 0 to 100°. A Revision. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1976, 80A, 775–785. [Google Scholar] [CrossRef]
- Adeyemi, B.; Joerg, S. Analysis of water vapor over Nigeria using radiosonde and satellite data. Appl. Meteorol. Clim. 2012, 51, 1855–1866. [Google Scholar] [CrossRef]
- Liu, Z.; Wong, M.S.; Nichol, J.; Chan, P.W. A multi-sensor study of water vapour from radiosonde, MODIS and AERONET: A case study of Hong Kong. Int. J. Climatol. 2013, 33, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Ha, J.; Park, K.D.; Kim, K.; Kim, Y.H. Comparison of atmospheric water vapor profiles obtained by GPS, MWR, and radiosonde. Asia-Pac. J. Atmos. Sci. 2010, 46, 233–241. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y. Hybrid regularized GPS tropospheric sensing using 3-D ray tracing technique. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1475–1479. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S. B-spline function-based approach for GPS tropospheric tomography. GPS Solut. 2020, 24, 193–205. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Zheng, N.; Ding, N.; Liu, X. A new integrated method of GNSS and MODIS measurements for tropospheric water vapor tomography. GPS Solut. 2021, 25, 88. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Ding, N.; Zhao, Q. A tropospheric tomography method with a novel height factor model including two parts: Isotropic and anisotropic height factors. Remote Sens. 2020, 12, 1848. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).