Fast and High-Quality 3-D Terahertz Super-Resolution Imaging Using Lightweight SR-CNN
Abstract
:1. Introduction
- (1)
- A fast and high-quality 3-D SR imaging method is proposed. Compared with the method based on sparsity regularization, the imaging time is reduced by two orders of magnitude and imaging quality is improved obviously.
- (2)
- A lightweight CNN is designed, which reduces the model parameters and computation significantly. The training model can achieve satisfactory convergence under small datasets and the accuracy can reasonably improve.
- (3)
- The input and output of SR-CNN both are complex data. The phenomenon that the performance of dividing complex data into real part and imaginary part is better than that of amplitude and phase is found.
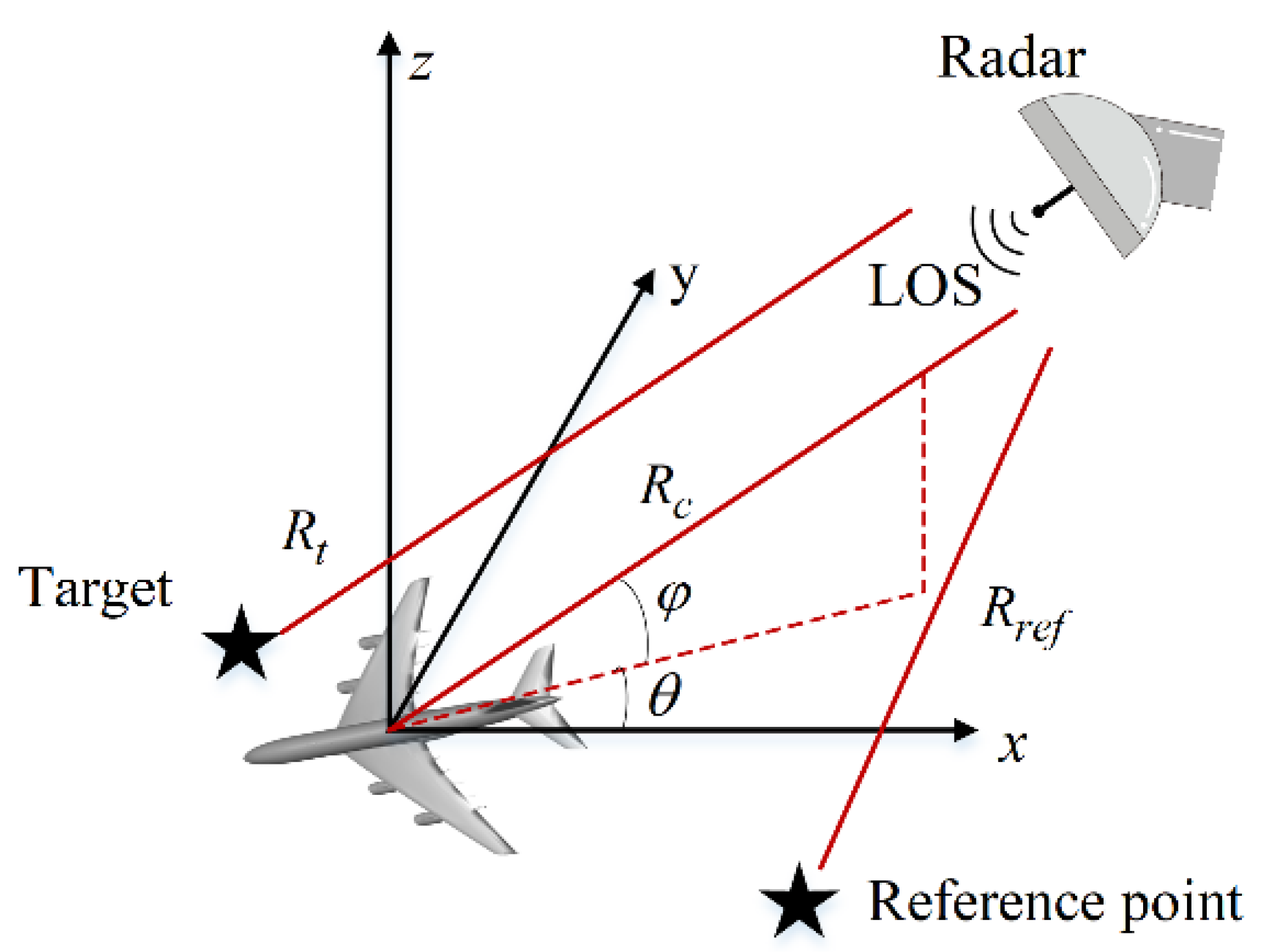
2. Methodology
2.1. Input and Output Data Generation of SR-CNN
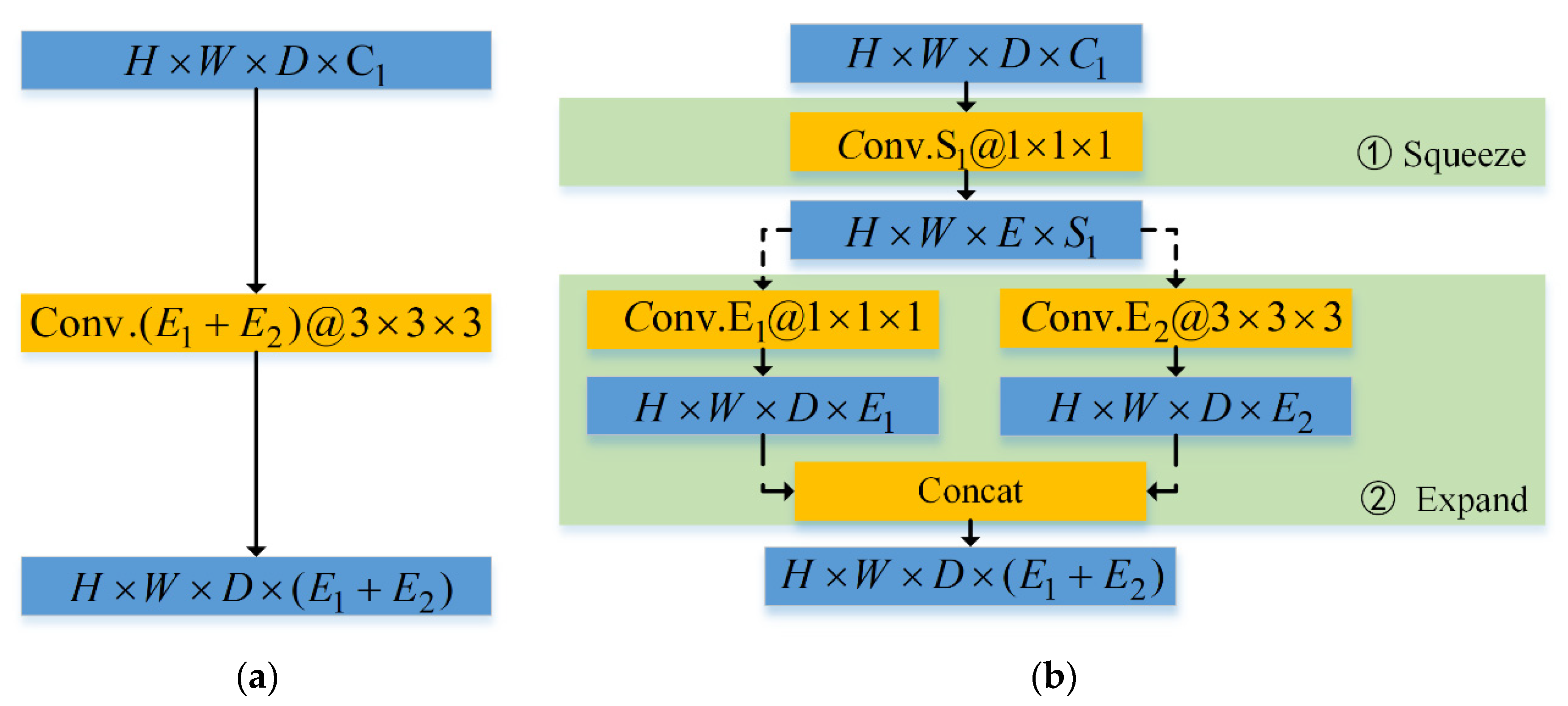
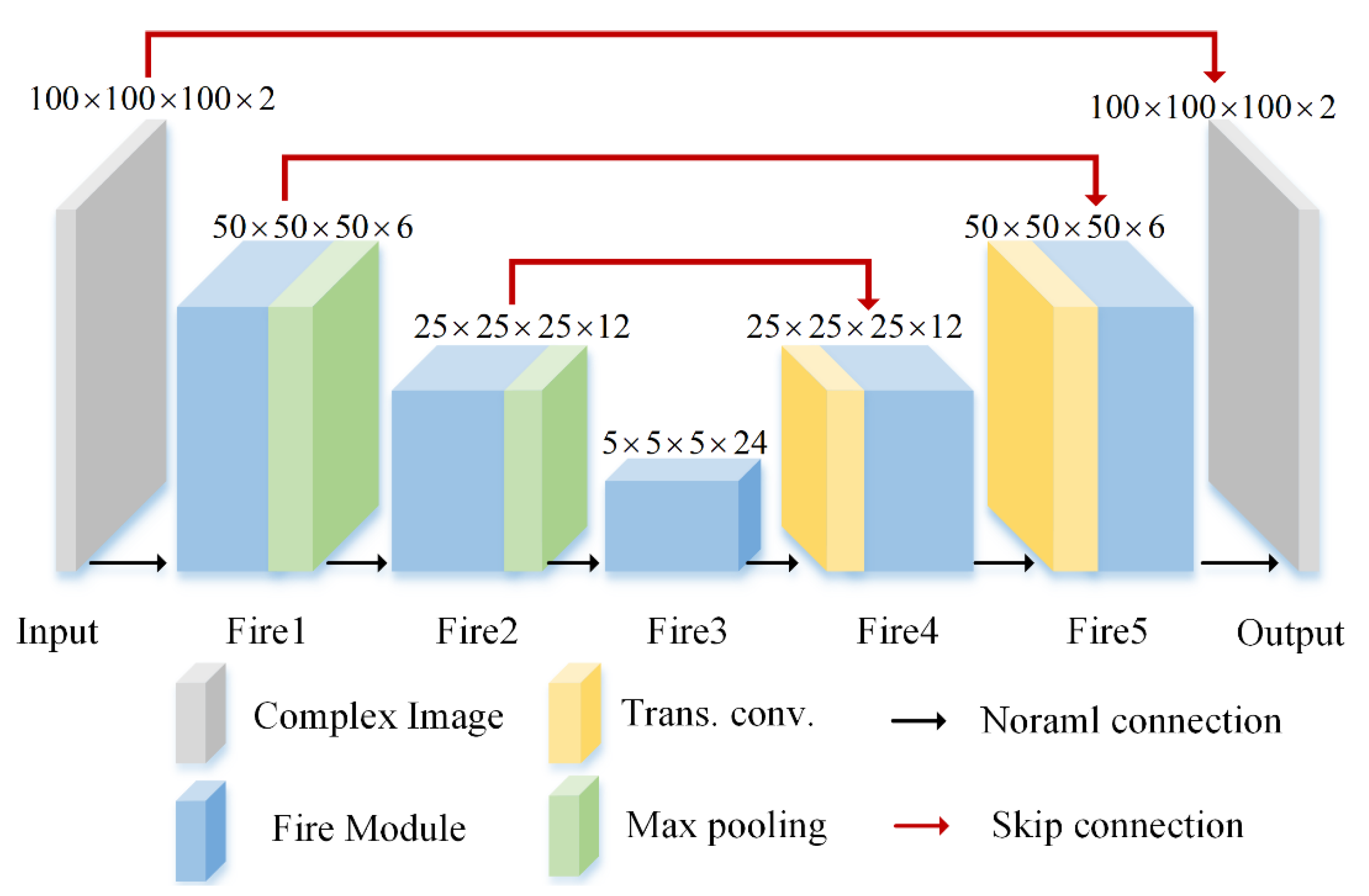
2.2. Network Structure of SR-CNN
2.3. Simution and Training Details
3. Results
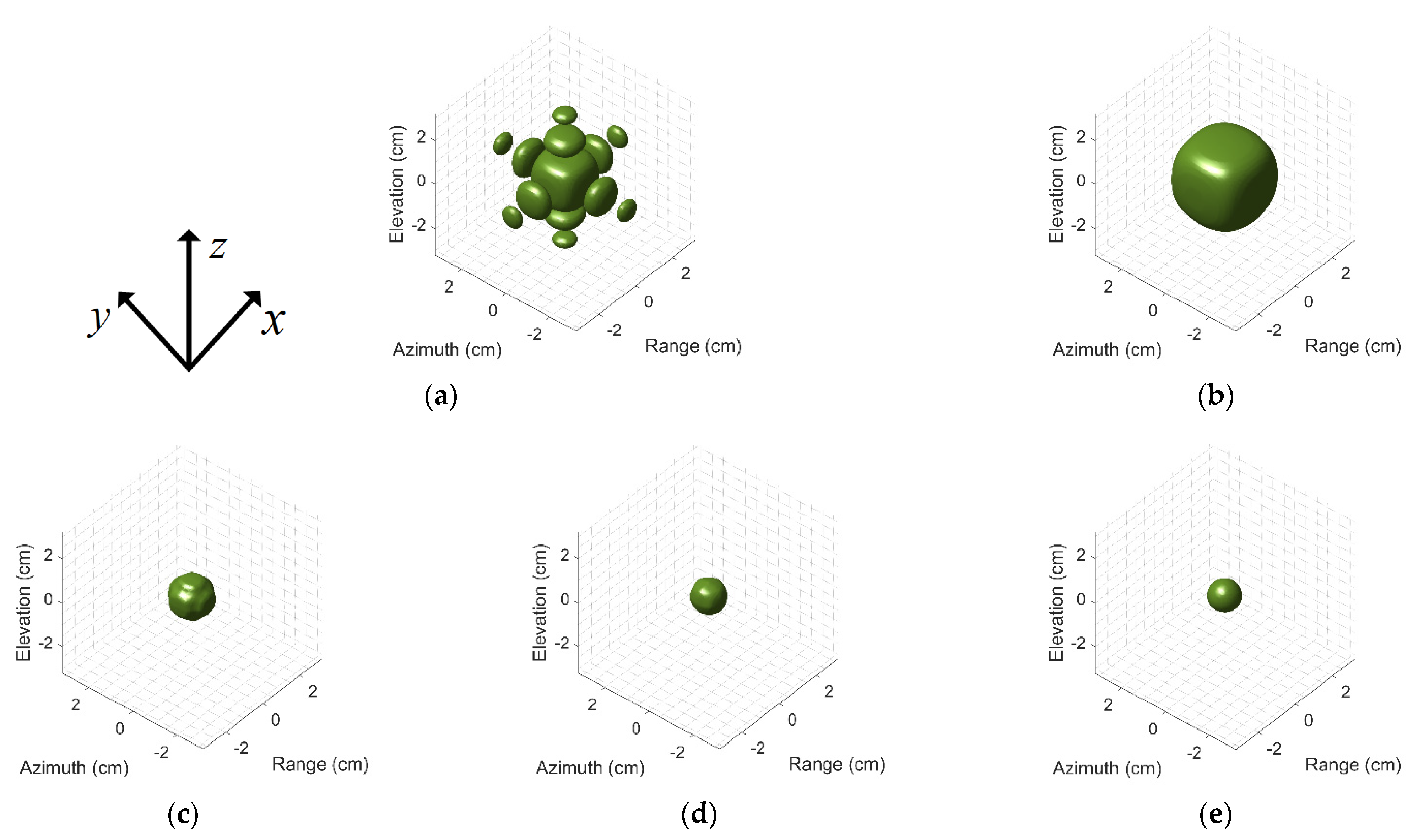
3.1. EXP1: Resolution Analysis of Different Methods
3.2. EXP2: Electromagnetic Computation Simulation of Aircraft A380
3.3. Performance Analysis for Anti-Noise Ability and Imaging Time
3.4. Ablation Experiments of Lightweight Network Structure
3.5. Comparison with Methods Based on Neural Network
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reigber, A.; Moreira, A. First Demonstration of Airborne SAR Tomography Using Multibaseline L-Band Data. IEEE Trans. Geosci. Remote Sens. 2000, 5, 2142–2152. [Google Scholar] [CrossRef]
- Misezhnikov, G.S.; Shteinshleiger, V.B. SAR looks at planet Earth: On the project of a spacebased three-frequency band synthetic aperture radar (SAR) for exploring natural resources of the Earth and solving ecological problems. IEEE Aerosp. Electr. Syst. Manag. 1992, 7, 3–4. [Google Scholar] [CrossRef]
- Pei, J.; Huang, Y.; Huo, W. SAR Automatic Target Recognition Based on Multiview Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2196–2210. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q.; Deng, B.; Qin, Y.; Wang, H. Estimation of Translational Motion Parameters in Terahertz Interferometric Inverse Synthetic Aperture Radar (InISAR) Imaging Based on a Strong Scattering Centers Fusion Technique. Remote Sens. 2019, 11, 1221. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Yeo, T.S.; Tan, C.S.; Li, J.; Shang, Y. Three-Dimensional Imaging Using Colocated MIMO Radar and ISAR Technique. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3189–3201. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Very High Resolution Spaceborne SAR Tomography in Urban Environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, Q.; Deng, B.; Qin, Y.; Wang, H. Experimental Research on Interferometric Inverse Synthetic Aperture Radar Imaging with Multi-Channel Terahertz Radar System. Sensors 2019, 19, 2330. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Li, Y.; Zhang, F.; Chen, L.; Bu, X. Automatic Regularization of TomoSAR Point Clouds for Buildings Using Neural Networks. Sensors 2019, 19, 3748. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Dong, G.; Kuang, G. Superresolution Downward-Looking Linear Array Three-Dimensional SAR Imaging Based on Two-Dimensional Compressive Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2184–2196. [Google Scholar] [CrossRef]
- Maleki, A.; Oskouei, H.D.; Mohammadi Shirkolaei, M. Miniaturized microstrip patch antenna with high inter-port isolation for full duplex communication system. Int. J. RF Microw. Comput.-Aided Eng. 2021, 31, e22760. [Google Scholar] [CrossRef]
- Mohamadzade, B.; Lalbakhsh, A.; Simorangkir, R.B.V.B.; Rezaee, A.; Hashmi, R.M. Mutual Coupling Reduction in Microstrip Array Antenna by Employing Cut Side Patches and EBG Structures. Prog. Electromagn. Res. 2020, 89, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi Shirkolaei, M. Wideband linear microstrip array antenna with high efficiency and low side lobe level. Int. J. RF Microw. Comput.-Aided Eng. 2020, 30. [Google Scholar] [CrossRef]
- Afzal, M.U.; Lalbakhsh, A.; Esselle, K.P. Electromagnetic-wave beam-scanning antenna using near-field rotatable graded-dielectric plates. J. Appl. Phys. 2018, 124, 234901. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; Limiti, E. Wideband planar array antenna based on SCRLH-TL for airborne synthetic aperture radar application. J. Electromagn. Wave 2018, 32, 1586–1599. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L.; Zeb, B.A. Single-Dielectric Wideband Partially Reflecting Surface With Variable Reflection Components for Realization of a Compact High-Gain Resonant Cavity Antenna. IEEE Trans. Antennas Propag. 2019, 67, 1916–1921. [Google Scholar] [CrossRef]
- Lalbakhsh, A.; Afzal, M.U.; Esselle, K.P.; Smith, S.L. A high-gain wideband ebg resonator antenna for 60 GHz unlicenced frequency band. In Proceedings of the 12th European Conference on Antennas and Propagation (EuCAP 2018), London, UK, 9–13 April 2018; pp. 1–3. [Google Scholar]
- Alibakhshi-Kenari, M.; Naser-Moghadasi, M.; Ali Sadeghzadeh, R.; Singh Virdee, B. Metamaterial-based antennas for integration in UWB transceivers and portable microwave handsets. Int. J. RF Microw. Comput.-Aided Eng. 2016, 26, 88–96. [Google Scholar] [CrossRef]
- Mohammadi, M.; Kashani, F.H.; Ghalibafan, J. A partially ferrite-filled rectangular waveguide with CRLH response and its application to a magnetically scannable antenna. J. Magn. Magn. Mater. 2019, 491, 165551. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, B.; Wang, H.; Qin, Y. A Doppler aliasing free micro-motion parameter estimation method in the terahertz band. J. Wirel. Com. Netw. 2017, 2017, 61. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Li, C.; Wu, S.; Zheng, S.; Fang, G. Adaptive 3D Imaging for Moving Targets Based on a SIMO InISAR Imaging System in 0.2 THz Band. Remote Sens. 2021, 13, 782. [Google Scholar] [CrossRef]
- Yang, Q.; Deng, B.; Zhang, Y.; Qin, Y.; Wang, H. Parameter estimation and imaging of rough surface rotating targets in the terahertz band. J. Appl. Remote Sens. 2017, 11, 045001. [Google Scholar] [CrossRef]
- Liu, L.; Weng, C.; Li, S. Passive Remote Sensing of Ice Cloud Properties at Terahertz Wavelengths Based on Genetic Algorithm. Remote Sens. 2021, 13, 735. [Google Scholar] [CrossRef]
- Li, Y.; Hu, W.; Chen, S. Spatial Resolution Matching of Microwave Radiometer Data with Convolutional Neural Network. Remote Sens. 2019, 11, 2432. [Google Scholar] [CrossRef] [Green Version]
- Fan, L.; Yang, Q.; Zeng, Y.; Deng, B.; Wang, H. Multi-View HRRP Recognition Based on Denoising Features Enhancement. In Proceedings of the Global Symposium on Millimeter-Waves and Terahertz, Nanjing, China, 23–26 May 2021. [Google Scholar] [CrossRef]
- Gao, J.; Cui, Z.; Cheng, B. Fast Three-Dimensional Image Reconstruction of a Standoff Screening System in the Terahertz Regime. IEEE Trans. THz Sci. Technol. 2018, 8, 38–51. [Google Scholar] [CrossRef]
- Cetin, M.; Stojanovic, I.; Onhon, O. Sparsity-Driven Synthetic Aperture Radar Imaging: Reconstruction, autofocusing, moving targets, and compressed sensing. IEEE Signal Process. Manag. 2014, 31, 27–40. [Google Scholar] [CrossRef]
- Austin, C.D.; Ertin, E.; Moses, R.L. Sparse Signal Methods for 3-D Radar Imaging. IEEE J. Sel. Top. Signal Process. 2011, 5, 408–423. [Google Scholar] [CrossRef]
- Lu, W.; Vaswani, N. Regularized Modified BPDN for Noisy Sparse Reconstruction With Partial Erroneous Support and Signal Value Knowledge. IEEE Trans. Signal Process. 2011, 60, 182–196. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Wei, S.; Shi, J. CSR-Net: A Novel Complex-Valued Network for Fast and Precise 3-D Microwave Sparse Reconstruction. IEEE J. Sel. Top. Appl. Earth Obser. Remote Sens. 2020, 13, 4476–4492. [Google Scholar] [CrossRef]
- Yang, D.; Ni, W.; Du, L.; Liu, H.; Wang, J. Efficient Attributed Scatter Center Extraction Based on Image-Domain Sparse Representation. IEEE Trans. Signal Process. 2020, 68, 4368–4381. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, M.; Wang, X.; Cai, Z.; Nie, D. Three-dimensional super resolution ISAR imaging based on 2D unitary ESPRIT scattering centre extraction technique. IET Radar Sonar Navig. 2017, 11, 98–106. [Google Scholar] [CrossRef]
- Wang, L.; Li, L.; Ding, J.; Cui, T.J. A Fast Patches-Based Imaging Algorithm for 3-D Multistatic Imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 941–945. [Google Scholar] [CrossRef]
- Yao, L.; Qin, C.; Chen, Q.; Wu, H. Automatic Road Marking Extraction and Vectorization from Vehicle-Borne Laser Scanning Data. Remote Sens. 2021, 13, 2612. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, G.; Zhou, S.; Yin, J. A Lightweight Fully Convolutional Neural Network for SAR Automatic Target Recognition. Remote Sens. 2021, 13, 3029. [Google Scholar] [CrossRef]
- Hu, C.; Wang, L.; Li, Z.; Zhu, D. Inverse Synthetic Aperture Radar Imaging Using a Fully Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1203–1207. [Google Scholar] [CrossRef]
- Qian, J.; Huang, S.; Wang, L.; Bi, G.; Yang, X. Super-Resolution ISAR Imaging for Maneuvering Target Based on Deep-Learning-Assisted Time-Frequency Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Gao, J.; Deng, B.; Qin, Y.; Wang, H.; Li, X. Enhanced Radar Imaging Using a Complex-Valued Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 35–39. [Google Scholar] [CrossRef] [Green Version]
- Qin, D.; Gao, X. Enhancing ISAR Resolution by a Generative Adversarial Network. IEEE Geosci. Remote Sens. Lett. 2021, 18, 127–131. [Google Scholar] [CrossRef]
- Zhao, D.; Jin, T.; Dai, Y.; Song, Y.; Su, X. A Three-Dimensional Enhanced Imaging Method on Human Body for Ultra-Wideband Multiple-Input Multiple-Output Radar. Electronics 2018, 7, 101. [Google Scholar] [CrossRef] [Green Version]
- Qiu, W.; Zhou, J.; Fu, Q. Tensor Representation for Three-Dimensional Radar Target Imaging With Sparsely Sampled Data. IEEE Trans. Comput. Imaging 2020, 6, 263–275. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, H.; Wang, P.; Ling, X. ATT Squeeze U-Net: A Lightweight Network for Forest Fire Detection and Recognition. IEEE Access 2021, 9, 10858–10870. [Google Scholar] [CrossRef]

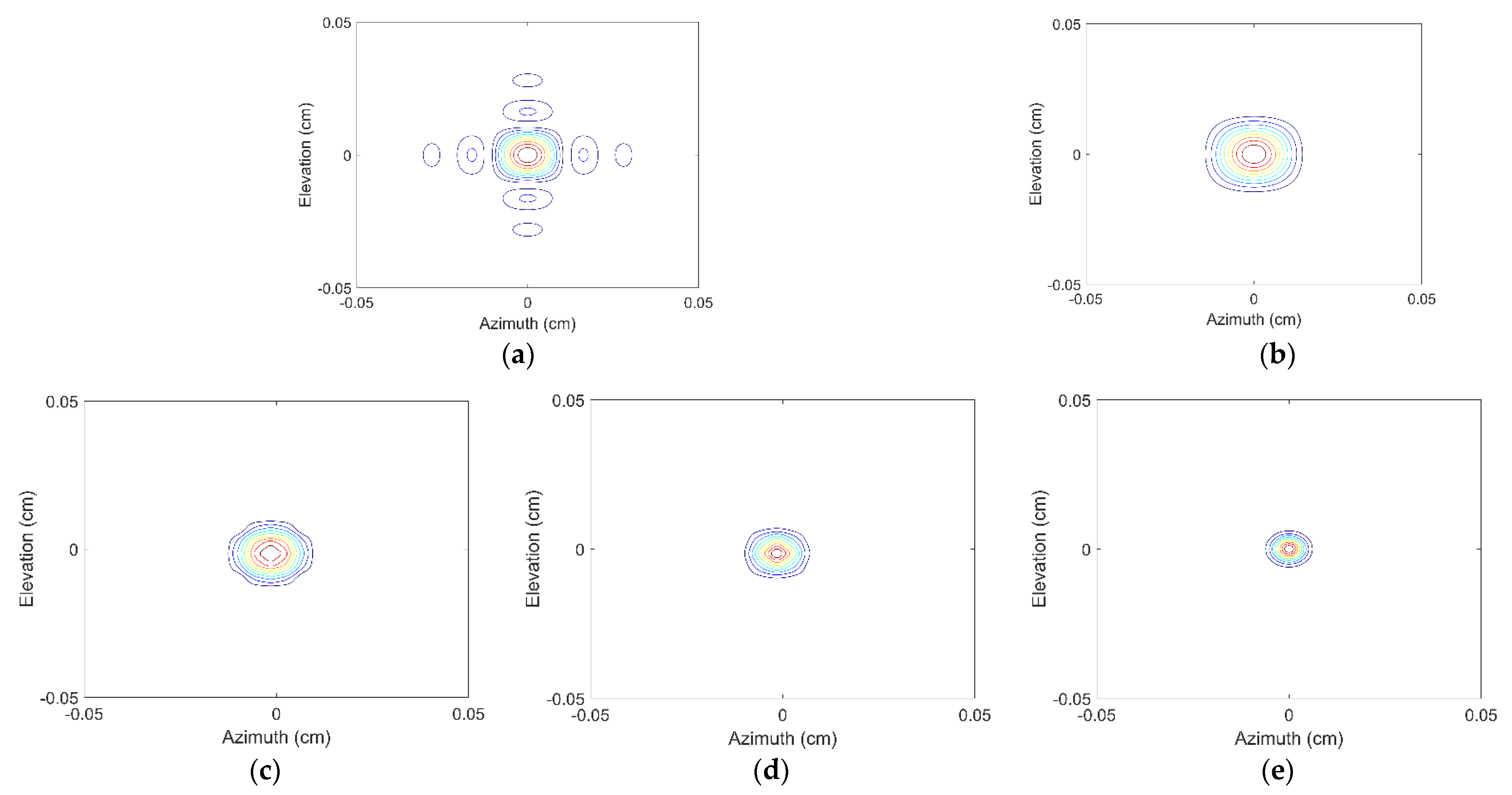
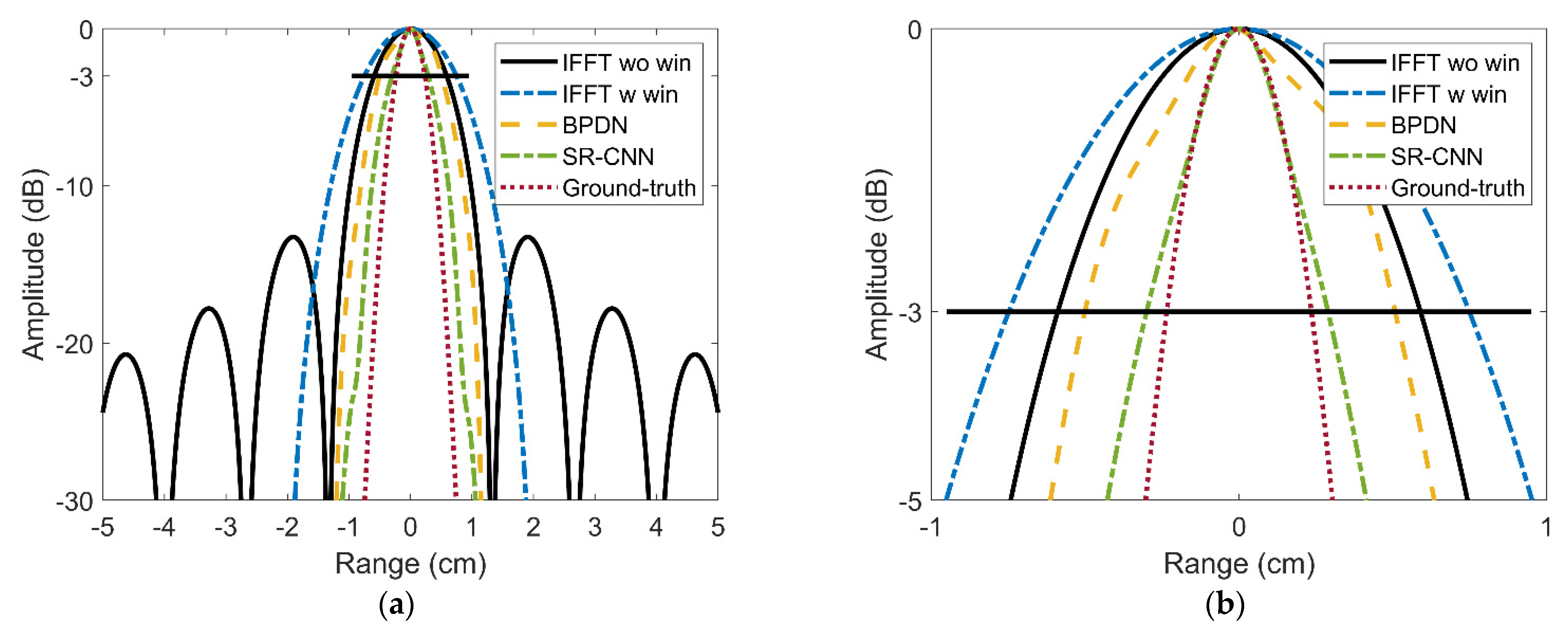




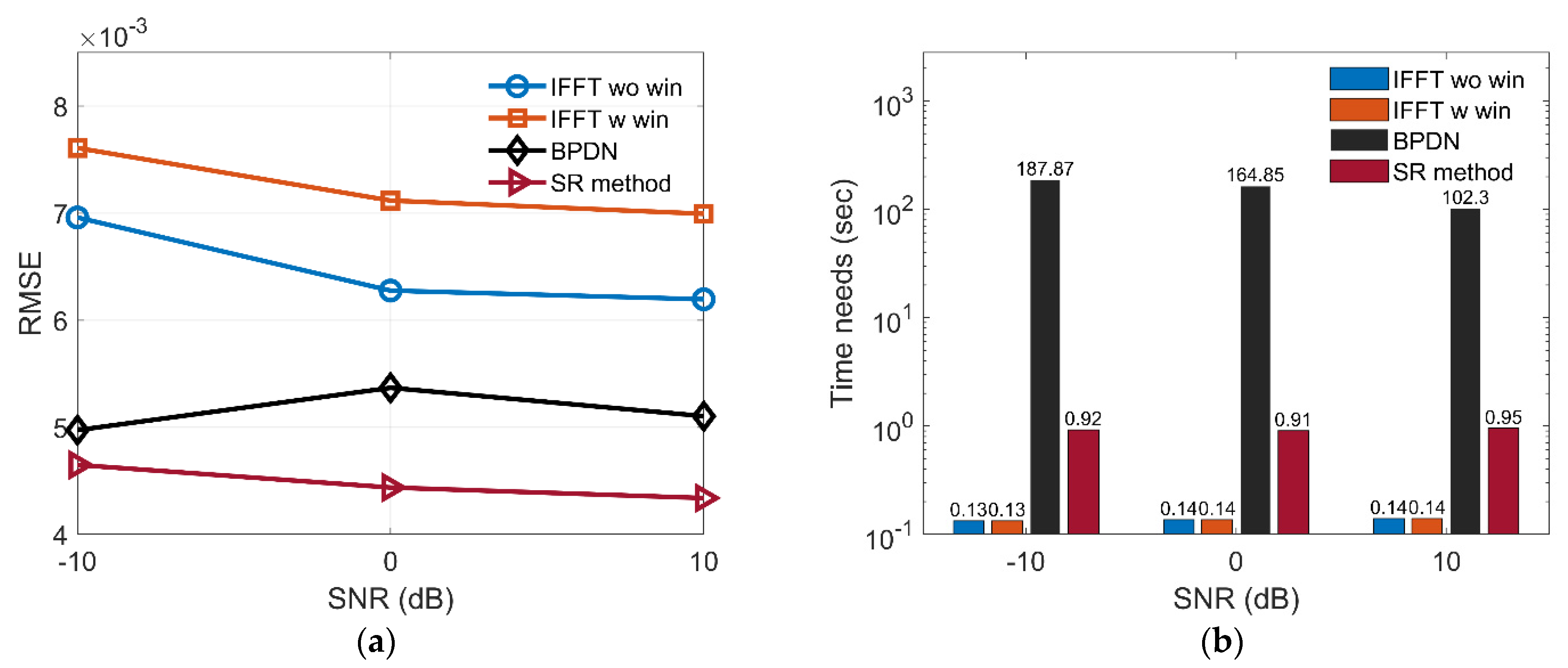

| Method | Time Needs (s) | |
|---|---|---|
| EXP 1 | EXP 2 | |
| IFFT wo win | 0.064 | 0.084 |
| IFFT w win | 0.064 | 0.084 |
| BPDN | 130.144 | 227.142 |
| SR-CNN | 0.906 | 0.965 |
| Network | Connection | Dataset Size | ||
|---|---|---|---|---|
| Direct Connection | Fire Module | 500 | 2000 | |
| Direct-500 | √ | √ | ||
| Fire-500 | √ | √ | ||
| Direct-2000 | √ | √ | ||
| Fire-2000 | √ | √ | ||
| Method | RMSE × 1000 (SNR = −10 dB) | RMSE × 1000 (SNR = 0 dB) | RMSE × 1000 (SNR = 10 dB) |
|---|---|---|---|
| The method in [37] | 5.46 | 4.81 | 4.48 |
| SR-CNN | 4.63 | 4.46 | 4.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Zeng, Y.; Yang, Q.; Wang, H.; Deng, B. Fast and High-Quality 3-D Terahertz Super-Resolution Imaging Using Lightweight SR-CNN. Remote Sens. 2021, 13, 3800. https://doi.org/10.3390/rs13193800
Fan L, Zeng Y, Yang Q, Wang H, Deng B. Fast and High-Quality 3-D Terahertz Super-Resolution Imaging Using Lightweight SR-CNN. Remote Sensing. 2021; 13(19):3800. https://doi.org/10.3390/rs13193800
Chicago/Turabian StyleFan, Lei, Yang Zeng, Qi Yang, Hongqiang Wang, and Bin Deng. 2021. "Fast and High-Quality 3-D Terahertz Super-Resolution Imaging Using Lightweight SR-CNN" Remote Sensing 13, no. 19: 3800. https://doi.org/10.3390/rs13193800
APA StyleFan, L., Zeng, Y., Yang, Q., Wang, H., & Deng, B. (2021). Fast and High-Quality 3-D Terahertz Super-Resolution Imaging Using Lightweight SR-CNN. Remote Sensing, 13(19), 3800. https://doi.org/10.3390/rs13193800






