Abstract
Frequency diverse array (FDA) radar has attracted much attention due to the angle and range dependence of the beam pattern. Multiple-input-multiple-output (MIMO) radar has high degrees of freedom (DOF) and spatial resolution. The FDA-MIMO radar, a hybrid of FDA and MIMO radar, can be used for target parameter estimation. This paper investigates a tensor-based reduced-dimension multiple signal classification (MUSIC) method, which is used for target parameter estimation in the FDA-MIMO radar. The existing subspace methods deteriorate quickly in performance with small samples and a low signal-to-noise ratio (SNR). To deal with the deterioration difficulty, the sparse estimation method is then proposed. However, the sparse algorithm has high computation complexity and poor stability, making it difficult to apply in practice. Therefore, we use tensor to capture the multi-dimensional structure of the received signal, which can optimize the effectiveness and stability of parameter estimation, reduce computation complexity and overcome performance degradation in small samples or low SNR simultaneously. In our work, we first obtain the tensor-based subspace by the high-order-singular value decomposition (HOSVD) and establish a two-dimensional spectrum function. Then the Lagrange multiplier method is applied to realize a one-dimensional spectrum function, estimate the direction of arrival (DOA) and reduce computation complexity. The transmitting steering vector is obtained by the partial derivative of the Lagrange function, and automatic pairing of target parameters is then realized. Finally, the range can be obtained by using the least square method to process the phase of transmitting steering vector. Method analysis and simulation results prove the superiority and reliability of the proposed method.
1. Introduction
MIMO radar has received widespread attention in the field of target parameter estimation, which has great development potential [1,2,3,4,5]. With constantly developing and progressing in the field of wireless communication, MIMO radar has also gained popularity in the fields of national defense, navigation, remote sensing, and unmanned driving [6,7,8,9]. It has been confirmed in practical applications that MIMO radar transmits orthogonal waveforms to form virtual array elements to enlarge the array aperture, which has a higher degree of freedom and spatial resolution [10,11,12]. Based on such advantages, MIMO radar has a high application value in overcoming the fading effect and optimizing the performance of the target location [13,14,15]. Among the wide applications of MIMO radar, target location plays an important role in both industry and research fields. For example [12], multiple unmanned aerial vehicles are used to achieve cooperative localization of maritime targets. The paper [16] proposed a DOA and polarization estimation in MIMO radar.
With the harsh electromagnetic environment, only the angle information cannot satisfy the increasing demands for target localization. Some scholars consider the range estimation as another important parameter to describe the target location more accurately. However, the beam pointing is independent of range, which makes it difficult to obtain range information with traditional MIMO radar [3]. In response to the disadvantage, FDA radar has been proposed in [17,18]. The FDA radar sets the frequency increment on the transmitting array elements so that the beam pointing changes with the target range [19]. This can be applied for the joint DOA and range estimation, which has great potential in practical applications [1,20,21].
However, for FDA-MIMO radar, the angle information and range information of the target are coupled and the phase period is ambiguous. It is possible that one target corresponds to more than one angle [22]. So as to deal with these problems, a double-pulse target location method has proposed in [23]. Firstly, the frequency increment can be preset to zero, i.e., the traditional phased array radar can be employed to estimate the angle of the target. Then the range information of targets is obtained. Moreover, the method eliminates the phase ambiguity by adjusting the frequency increment and obtains the correct target parameter. In [24,25], the subarray-based FDA has been proposed, where the transmitting array is composed of two sub-arrays, with different frequency increments of each sub-array. The angle and range coupling problem is solved by applying the nonlinear frequency offset method. In fact, FDA-MIMO radar is the most practical method for decoupling the angle and range of the target, which combines the advantages of FDA radar and MIMO radar.
Based on the idea, the [26] has proposed the FDA-MIMO radar. It has adopted the characteristics of the freedom of transmission waveform and beam range pointing, which improves the speed resolution and target observation time of the radar system [27,28]. These characteristics are very suitable for suppressing clutter interference. Currently, there are some target location methods based on FDA-MIMO radar [29,30]. A joint angle and range of target minimum variance distortion-free response method is proposed in [31], but this method cannot fully use the high DOF. In [32], the author has proposed the estimation of signal parameters via the rotational invariance technique (ESPRIT) method. To optimize the computational efficiency, the unitary ESPRIT method has been proposed in [33]. A target location method via real-valued subspace decomposition has been proposed in [34], which implements the unitary ESPRIT method in sub-array FDA-MIMO. However, these methods rely on the rotation invariant structure of the received signal and are only suitable when the frequency of the transmitting antenna increases linearly. Moreover, the subspace method relies on the accuracy of the signal subspace, while the effectiveness declines rapidly in the case of small samples or low SNR. As the singular value decomposition loses the array aperture, the performance is lower than the MUSIC method [35]. In [8], it has proposed a two-dimensional MUSIC method in FDA-MIMO radar. The method is difficult to be employed in practical applications due to the high computation complexity, which is brought by two-dimensional spectrum peak search. In addition, sparse DOA and range estimation methods attract the attention of scholars. The block sparse representation with mutual coupling has been proposed in [36]. In [37], an off-grid method based on Bayesian learning has been proposed, which implements the estimation of DOA and range. Unfortunately, high computation complexity is also a disadvantage of the sparse method, and it is hard to bear the cost of actual applications.
However, these methods introduced above have two main shortages: (1) the received signals are stacked in matrix form and the target parameters are estimated by matrix decomposition, which ignores the inherent multi-dimensional structure of the received signal [38,39]. (2) the peak search methods (MUSIC) have huge computation complexity and are not suitable to apply in practical scenarios if the work needs to deal with multi-dimensional peak search, e.g., joint DOA and range estimation. Therefore, it is necessary to study a target parameter estimation method that can effectively utilize multi-dimensional structure and overcome the performance degradation of low SNR and snapshot number. Besides, the new method also needs to reduce the dimensionality of the conventional two-dimensional MUSIC method.
In this paper, a tensor-based dimension reduction MUSIC method in FDA-MIMO radar is proposed. We use tensor storage to receive signals to capture multi-dimensional structures. Then HOSVD is used to process the signal model based on tensor and reduce the dimensionality of the MUSIC method [40]. Thus, DOA information can be estimated by a one-dimensional spectrum peak search. After that, according to the characteristic of the transmit-receive steering vector in FDA-MIMO radar, the Lagrange multiplier method is applied to estimate the transmitting steering vector. Finally, the phase of the transmitting steering vector is extracted to obtain the range of the target. As each DOA corresponds to a unique range parameter, the automatic matching work is also realized. We list the main contributions of the proposed method as follows:
(1) In the tensor domain, the proposed method realizes joint angle and range estimation of FDA-MIMO radar. The inherent multi-dimensional structure of the signal model is stored in the tensor, which improves the accuracy of target parameter estimation. This is the unique advantage of the tensor-based method.
(2) With the Lagrange multiplier method, the DOA and range parameters are decoupled, which further reduces the dimension of peak search. Then we use the one-dimensional spectrum function to estimate the DOA of the target and improve the accuracy.
(3) As the range of the target is not limited to a small interval, it’s too difficult to find the range information in a defined search area. Instead of peak search, our work uses constraint conditions to derive the transmitting steering vector. Then the phase is extracted and the least square method can be applied to estimate the range information that also reduces computation complexity. Moreover, the proposed method achieves automatic matching of the angle and range.
The definition notations are shown in Table 1 to facilitate the derivation of subsequent formulas.

Table 1.
Related notation.
2. Basic Knowledge of Tensor and Signal Model Based on Tensor
2.1. Basic Knowledge of Tensor
This section mainly defines the basic operations of tensor to facilitate the derivation and display of the proposed method. Please refer to [41,42,43] for more details.
Definition 1.
(Tensor unfolding of n-mode): Defineas an N-order tensor, whose dimension is . The n-mode tensor unfolding of can be expressed as . The -th element of is equal to -th element of that , and .
Definition 2.
(Tensor-matrix product of n-mode): It can be expressed asfor the n-mode product, which is the tensor and the matrix . Further we derive the element correspondence between and as . In addition, the dimension of is .
Definition 3.
(HOSVD of Tensor) The high-order singular value decomposition (HOSVD) is an important part of tensor decomposition [44]. It is written as
where the core tensor of is defined as , whose dimension is the same as to . Then select the left singular vector of to form .
2.2. Signal Model Based on Tensor
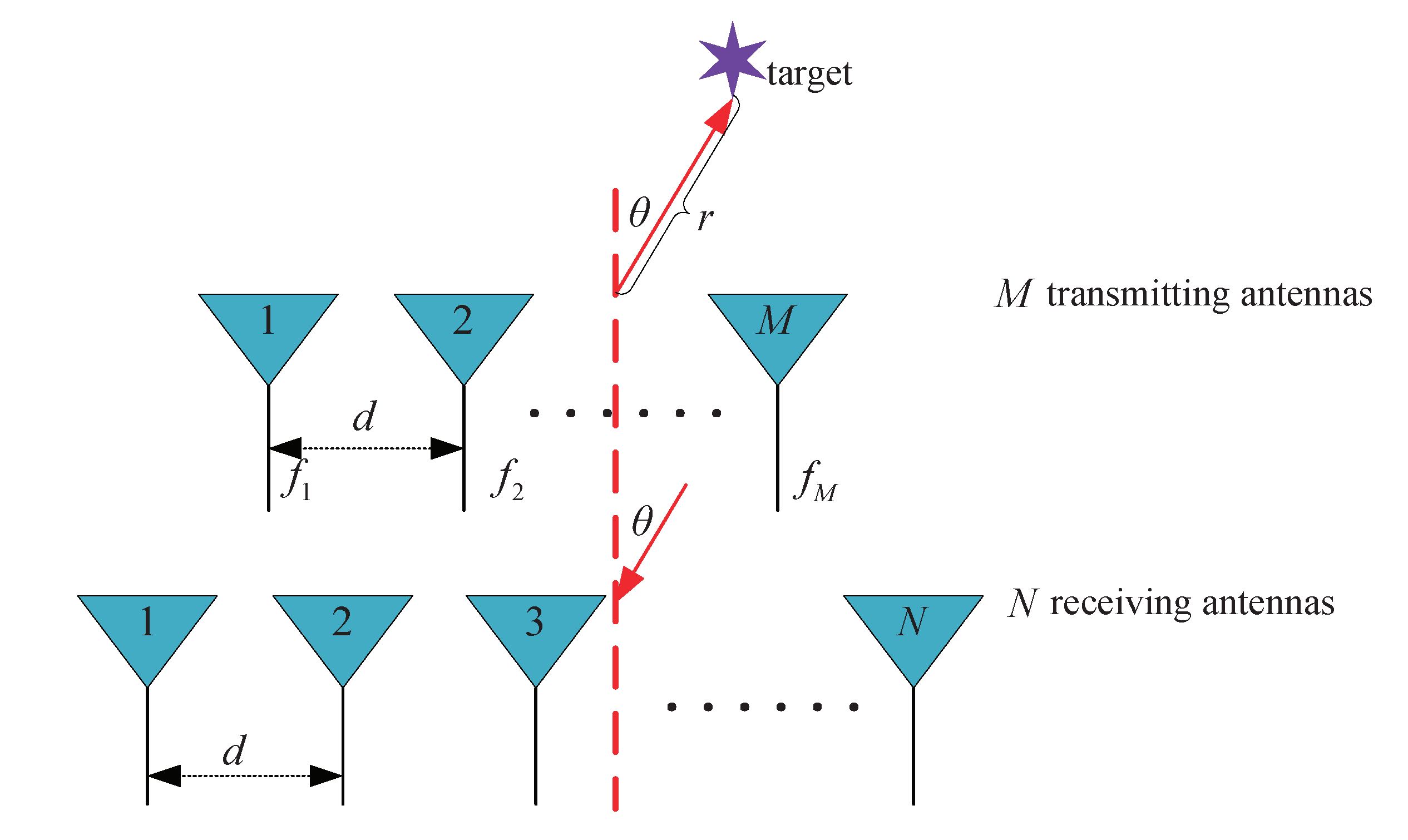
We present a monostatic FDA-MIMO radar system, as shown in Figure 1, which is wide beam and narrow-band. The uniform linear arrays(ULA) is applied to the transmitting array and the receiving array, and d represents the spacing between adjacent antennas of the array. Generally, we define the reference frequency as , which is the transmitting frequency of the first element in the transmitting array. In addition, the radar system has M transmitting elements and N receiving elements. Then denotes the transmitting frequency of m-th transmitting element, which can be defined as
where stands for the frequency increment. It should be noted that should be much smaller than .
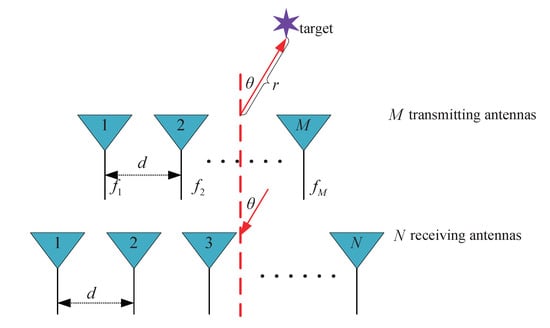
Figure 1.
Schematic diagram of monostatic FDA-MIMO radar.
The transmitted signal of the m-th transmitting element is written as
where and T denote baseband signal of the m-th transmitting antenna and the radar pulse duration, respectively. The transmitted signal is wide beam and narrow-band complex. On the premise that the waveforms are orthogonal to each other, and the time shift is set to that is derived as
Suppose there are P targets, which are unrelated to each other and in the far-field. For the p-th target, the DOA and range parameters are denoted by and , respectively. The represents the transmitting steering vector that is written as
The represents the receiving steering vector that is written as
The expression of received signal is as follows:
where the speed of light is denoted by c, and m/s.
Then arrange the received signal into the form of matrix multiplication, which is written as
where the transmitting signal is denoted by , whose elements are the product of the reflection coefficient of P targets and the doppler frequency shift, and the element can be written as . In addition, we can get where and represents the direction matrix of receiving and transmitting, respectively; represents the received additional white Gaussian noise matrix.
The received signal matrix is formed after receiving L snapshots that is denoted by
where the specific composition of the received signal is , and . After receiving L snapshots, the received noise matrix can be denoted by , which is uniform Gaussian white noise.
Then to store the received signal, we employ a third-order tensor , whose dimension is . According to the Definition 1, Equation (9) is divided into blocks along the snapshot direction. Let , then stack the blocks of following the third-dimension of , which is written as
In this way, we get the signal model based on tensor for FDA-MIMO radar. Using tensor algebra for target location can optimize the performance of target parameters estimation.
3. Doa and Range Estimation VIA Tensor for FDA-Mimo Radar
3.1. Signal Subspace Estimation VIA HOSVD
The tensor-based target location method requires HOSVD of the received signal, which is different from the traditional matrix decomposition-based method [43]. According to Definition 2 and Definition 3, the HOSVD of tensor-based received signal model is written as
where the core tensor can be denoted by , which is obtained by HOSVD. are formed of the left singular, which is obtained by the n-mode tensor unfolding of according to Definition 1, namely . Moreover, because we have assumed P targets, the rank of is P. The subspace based on the tensor is obtained by truncated HOSVD, which is written as
where denotes the truncated core tensor. Perform eigenvalue decomposition on and extract the eigenvectors corresponding to the P largest values of to form . Then substituting into Equation (12), after simplification, the result is written as
Therefore, the subspace based on tensor that is expressed as
where . Similarly, is obvious. Substituting into Equation (14), simplifying the formula is written as [38]
So far, the signal subspace based on tensor has been estimated.
3.2. DOA Estimation VIA Tensor-Based Reduced-Dimension Music
The signal subspace and the noise subspace are orthogonal to each other, which is the basis of the MUSIC method [45]. The signal subspace is transformed into a unit orthogonal column matrix by orthogonalization. After orthogonal projection, we can get the noise subspace, which can be expressed as
The tensor-based spectrum function is constructed as
where represents the orthogonal basis of , and define . However, Equation (17) involves peak searching for two-dimensional spectral peaks, which requires a lot of computation and is inefficient in practical application. Inspired by the Ref. [40], a dimensional strategy is investigated to reduce the computation complexity based on the characteristic of transmit-receive steering vector of FDA-MIMO radar, and the detail is showed as follows.
In order to facilitate the derivation of the subsequent formula, according to the properties of the Kronecker product [43]. Set , , and , we can get
Because of and , we can get the simplified , which is expressed as
So we define and simplify as follows
For the convenience of expression, we define . Inspired by the Ref. [40], the quadratic optimization of Equation (21) when constraint condition is and , so as to eliminate the solution of . Because Equation (21) is essentially an issue of conditional extreme value. We introduce the Lagrange multiplier method to address this issue, which can be constructed as follows
where is a constant.
According to the nature of Lagrangian extreme value, the partial derivative of the Equation (22), which can be expressed as
According to the constraint condition, we can get
So is derived as
It is clearly concluded from Equation (27) that the spectrum function has actually been independent of the range, thus achieving dimension reduction. DOAs of the P targets should correspond to the P largest peaks of , which is obtained by .
3.3. Range Estimation
Since the DOA and range are coupled in , if the conventional MUSIC method is used, the computation complexity is too high due to the excessive range. We use reduced-dimension to estimate the range of the target.
Defining the estimation of DOA as , and then substituting DOA into Equation (26) to estimate the corresponding transmitting steering vector . Normalize to eliminate scale ambiguity. Extract the phase of and combine it with Equation (5), which can be written as
obtain the range information of the target, we introduce the least square method. The least-square is constructed as follows
where represents the estimation parameter vector. can be expressed as
Define as the estimation of , which can be expressed as
Define the second element of as , which is the estimated value of . Substituting the DOA into Equation (31) to obtain the range information of target that can be written as
So far, using the proposed method, we have estimated the DOA and range parameters of the target.
4. Performance Analysis of the Proposed Method
4.1. Computation Complexity
We introduce the computation complexity to reflect the efficiency of the proposed method, which can be expressed as follows:
- (1) The HOSVD computation complexity of is in Equation (11);
- (2) The signal subspace estimation needs in Equation (15);
- (3) In Equation (21), the dimensionality reduction of the two-dimensional search requires ;
- (4) The spectrum peak search of DOA estimation in Equation (27) is , where represents the search times within the search DOA, and stands for factorial;
- (5) Computing the range requires ;
The total computation complexity is .
We choose ESPRIT [32], MUSIC, [8] and Tensor-ESPRIT [30] as comparison methods. According to Refs. [32,46] and combined with calculations, we can get the computation complexity of the ESPRIT, MUSIC, and Tensor-ESPRIT. Table 2 shows the computation complexity of the proposed method, ESPRIT, MUSIC, and Tensor-ESPRIT.

Table 2.
Computation complexity comparison.
It should be noted that in Table 2, represents the search times of range-dimension. The conventional target range is kilometer level, so is very large. It causes the computation complexity of MUSIC to be not at the same level as that of other methods. Subsequent simulations confirmed this view.
4.2. Cramr-Rao Bound
The received signal can be converted into
Define . Let represent the signal power, and the noise power is denoted by .
The corresponding Fisher information matrix (FIM) is expressed as
where represents the noise covariance matrix, , and .
The partial derivative can be expressed as
with
where .
The can be expressed as
where represents the mean of the array.
5. Numerical Simulations
In this section, we perform numerical simulations to analyze the effectiveness and reliability of the proposed method under different situations. The FDA-MIMO radar related parameter setting are as follows: ; ; . The independent targets are supposed at km), km), km), respectively. The radar and target parameters remain unchanged unless otherwise stated. The total of Monte Carlo trials can be denoted by T, and .
5.1. Spectrum Peak Search for DOA Estimation
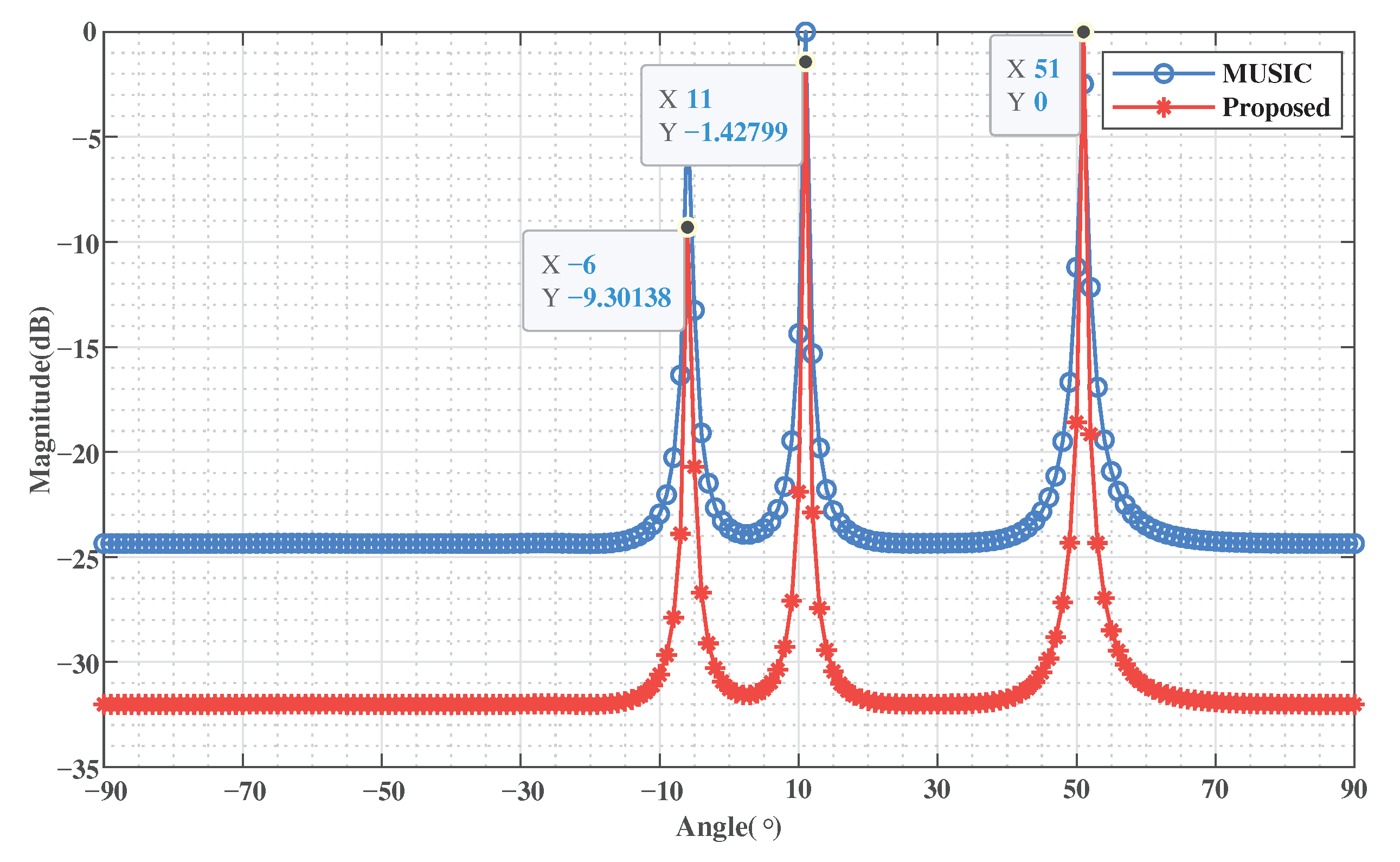
The parameters of this simulation are as follows: the number of snapshots to , and = 20 dB. Select the matrix decomposition-based classical MUSIC method as the comparison method. Comparing the performance of DOA estimation of the two methods. The spatial spectrum is shown in Figure 2.
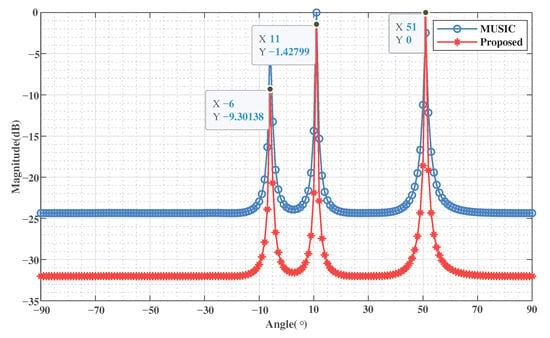
Figure 2.
The spatial spectrum of angle dimension.
In the actual simulation of the proposed method, we firstly set the search range and step size to and , respectively, to get the angle information . Then marrow down the two search parameters appropriately, namely and . In this way, the computation complexity is reduced.
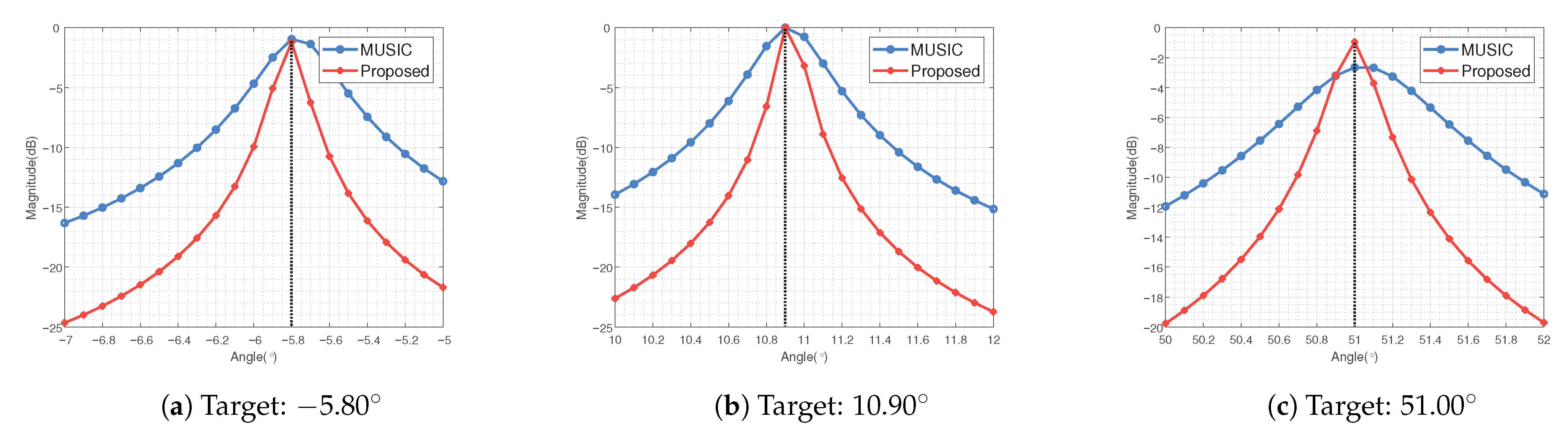
It can be found from Figure 2 that the accuracy of the signal subspace is improved, making the spatial spectrum more sharp and accurate. The reason is that the proposed method utilizes the multi-dimensional structure of the tensor-based received data to improve the estimation accuracy of the signal subspace. In order to show the difference of the spatial spectrum more clearly, the more high-precision spatial spectrum is shown in Figure 3. Figure 3 shows the part of the spatial spectrum at three target angles with the accuracy of . It can be seen from Figure 3 that the proposed method has more significant peaks and narrower bandwidth, which also proves that the proposed method has a higher resolution.

Figure 3.
Partial view of the spatial spectrum of angle dimension.
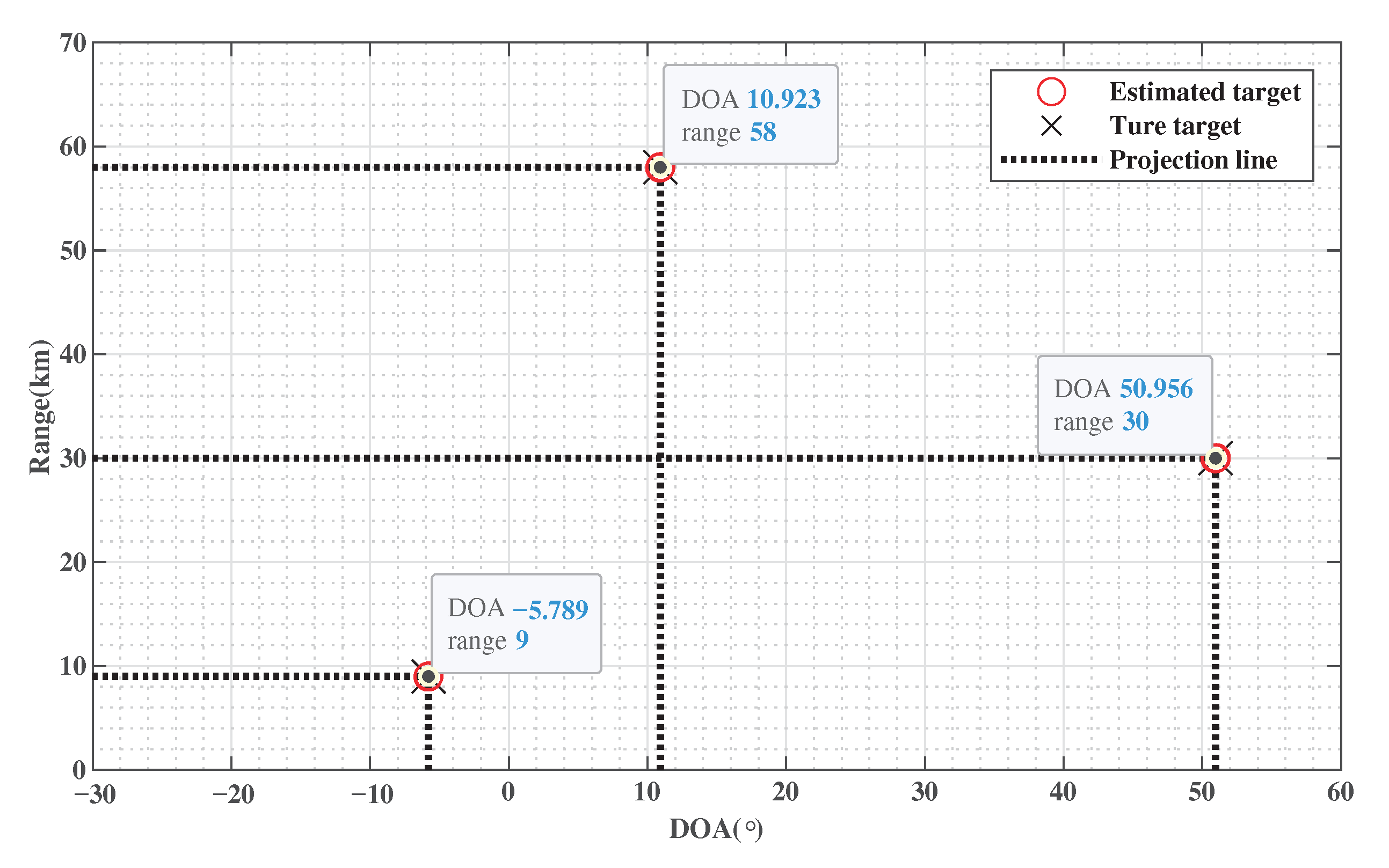
5.2. 2D Point Cloud of the Target Landing Point
In this simulation, the estimation of results are shown in Figure 4. The signal parameters are set to and = 20 dB. The DOA and range of target are displayed as X-axis and Y-axis, respectively. We can get from the Figure 4 that the landing point of the estimated target coincides with the real target position. The automatic matching of DOA and range can be realized. This can intuitively reflect the superiority of the stability and accuracy of the proposed method.
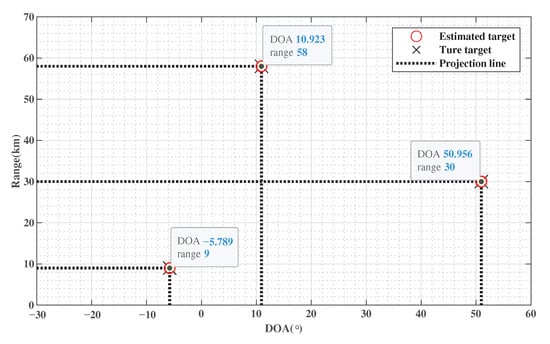
Figure 4.
2D point cloud of estimated targets.
5.3. RMSE Performance
It is important for the root mean square error (RMSE) to measure the comprehensive performance of the proposed method. The important index can be expressed as
where the estimation of DOA and range are denoted as and , which are the t-th monte carlo tarils estimation results of the p-th target, respectively. The ESPRIT, MUSIC, Tensor-ESPRIT, and CRB are used to measure the comprehensive performance of the proposed method.
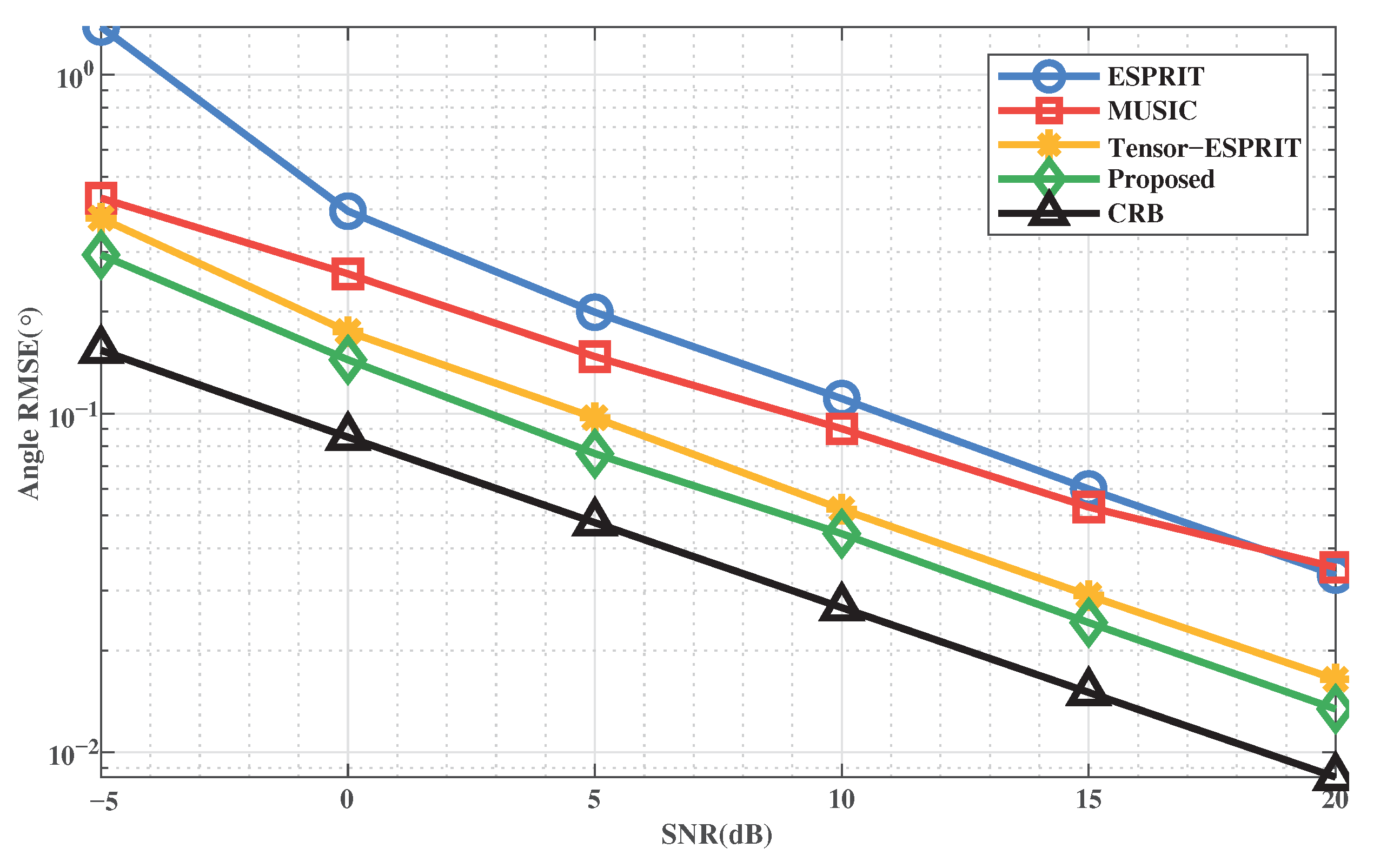
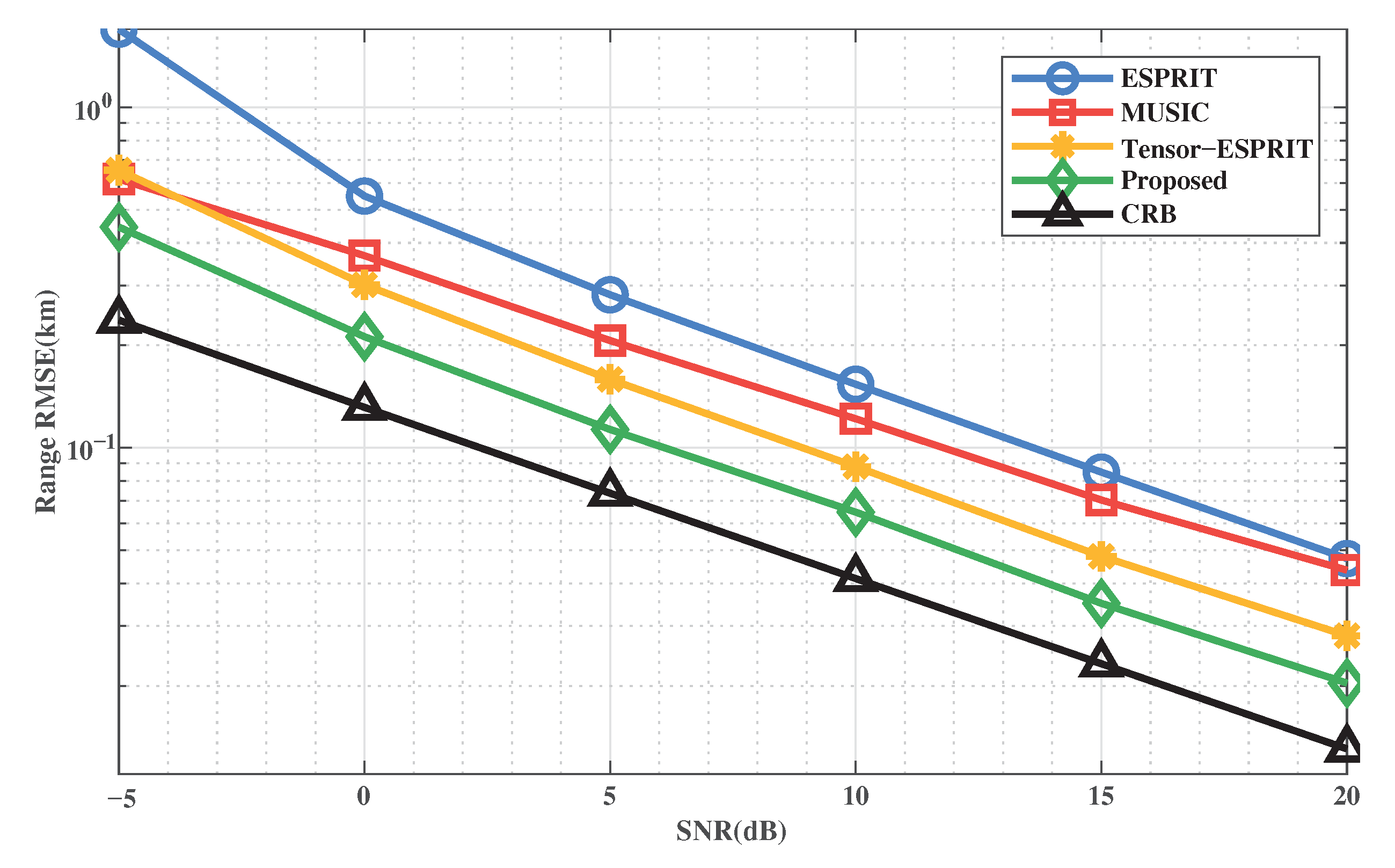
We show the performance of the methods with SNR when . The RMSE of DOA and range are shown in Figure 5 and Figure 6, respectively. We can obtain that the proposed method outperforms all other methods in accuracy and stability. This is because the proposed method uses a multi-dimensional structure through tensor, which improves the accuracy of the target location. It’s worth noting that the ESPRIT-based method loses the array aperture when decomposing and estimating the signal subspace, so the performance is lower than that of the MUSIC-based method.
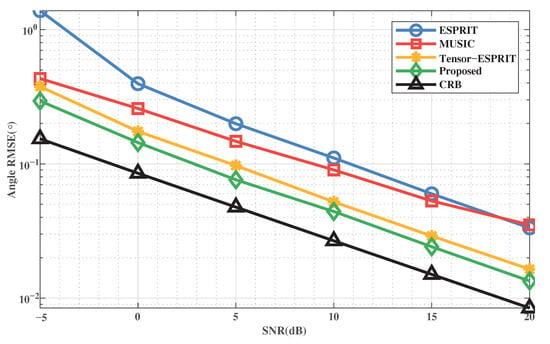
Figure 5.
RMSE of DOA estimation versus SNR.
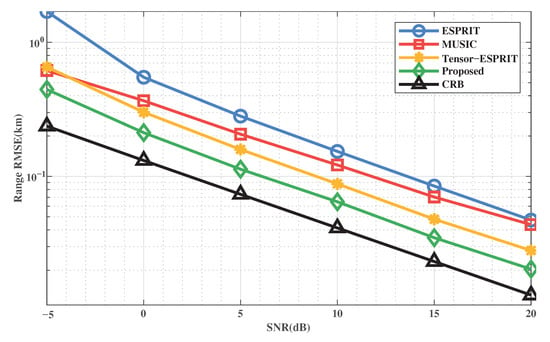
Figure 6.
RMSE of range estimation versus SNR.
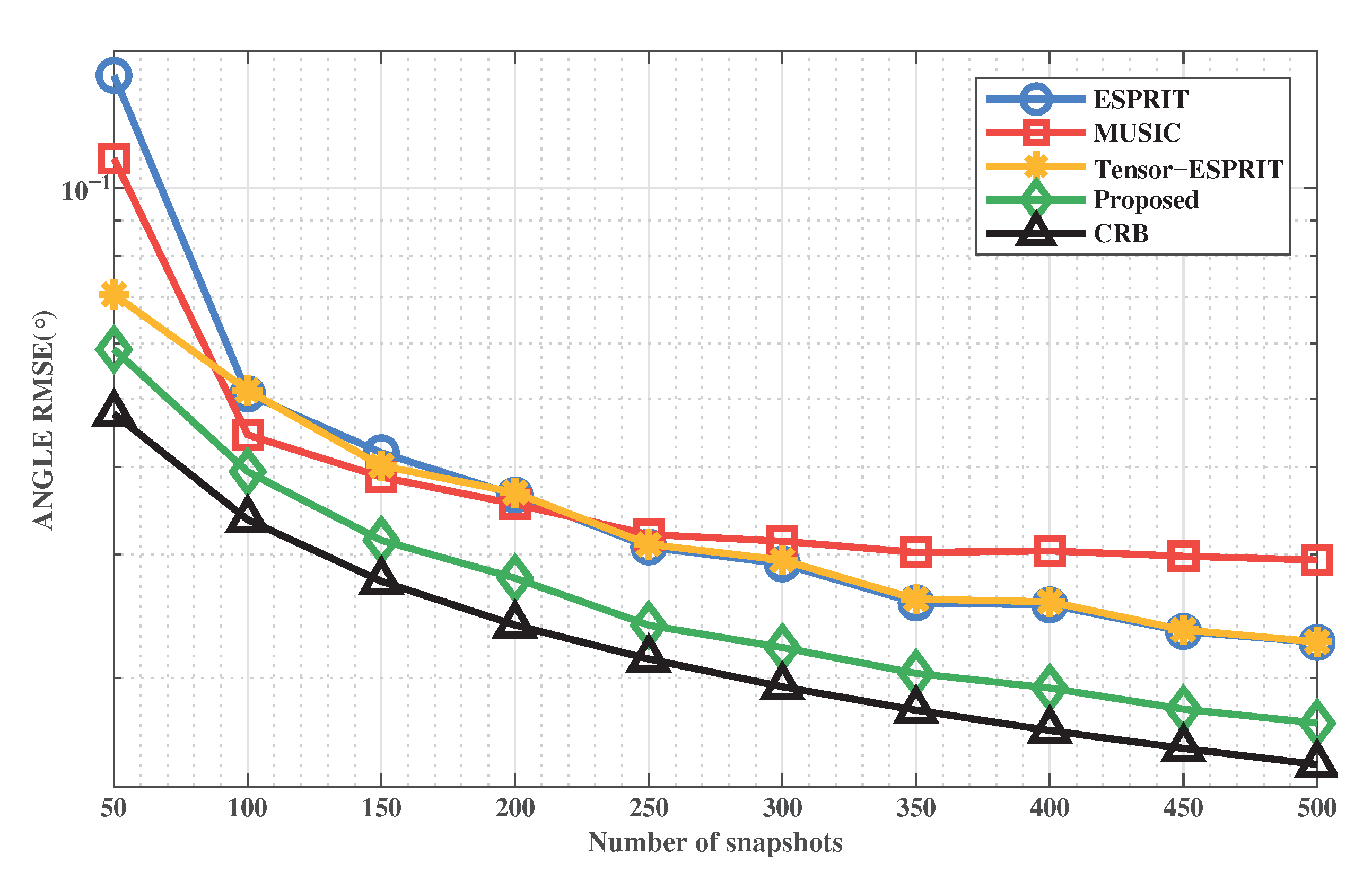
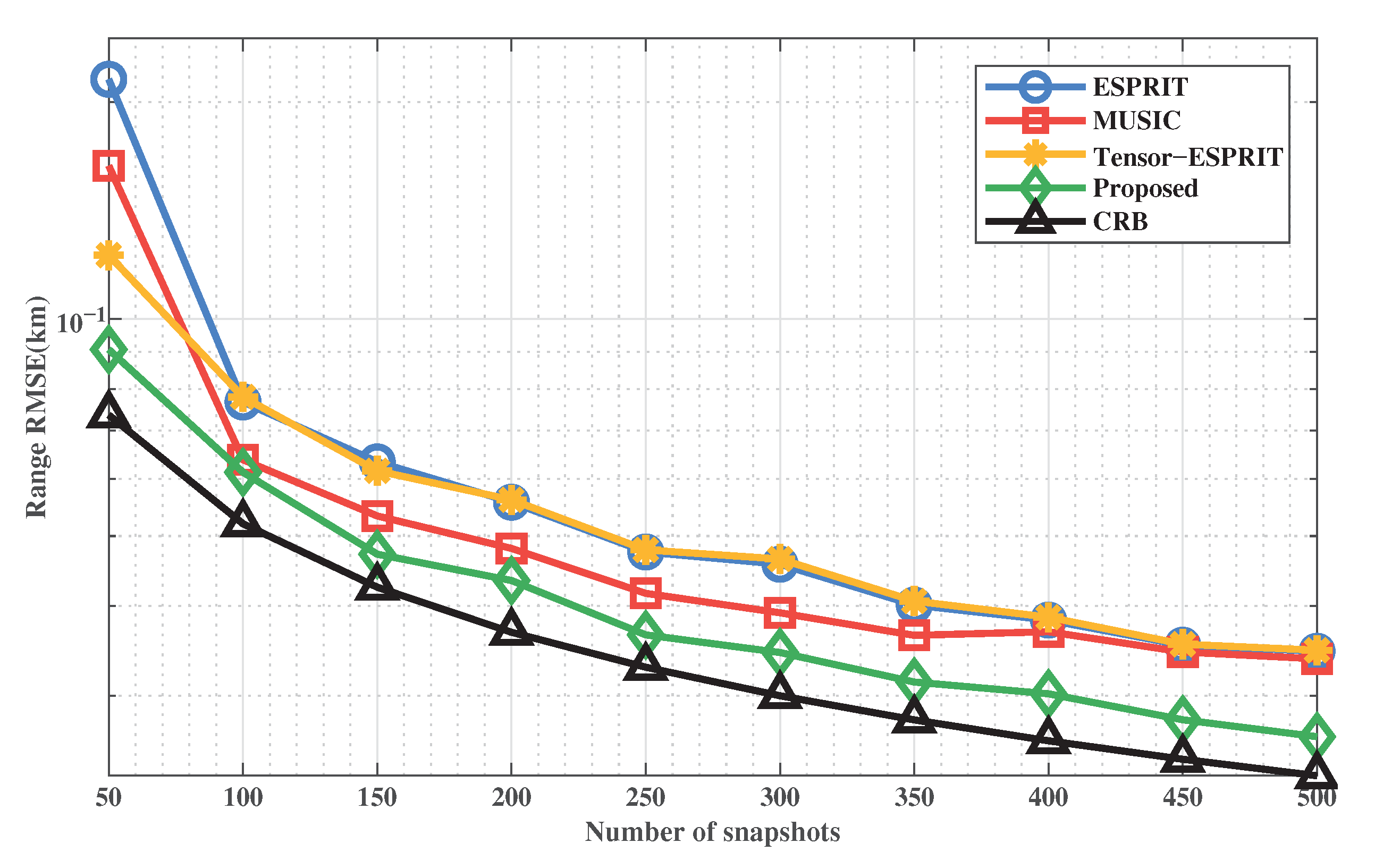
Figure 7 and Figure 8 show the RMSE of DOA and range estimation of these methods with L when = 5 dB. It corresponds to the DOA RMSE and range RMSE, respectively. Similarly, we introduce the comparison methods. We can get that the RMSE curve of the proposed method is smoother and closer to CRB. This shows that the performance of the proposed method is the best. The performance of the ESPRIT-MUSIC method will surpass that of MUSIC when the total of snapshots is high. It is because the increase in the number of snapshots compensates for the loss of the array aperture during signal decomposition. However, the proposed method uses tensor to ensure performance. In addition, the proposed method can also achieve excellent target positioning at low snapshots.
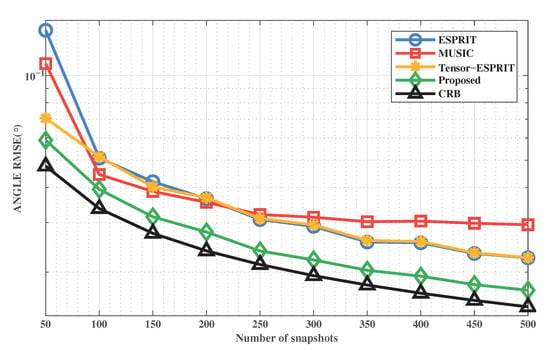
Figure 7.
RMSE of DOA estimation versus L.
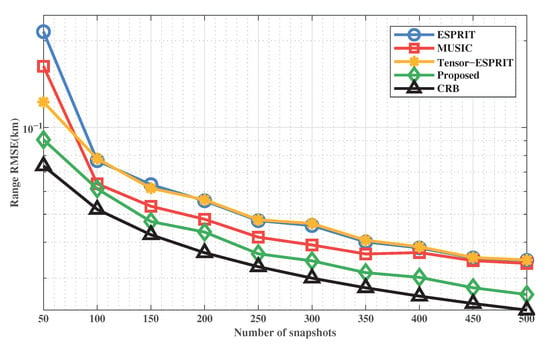
Figure 8.
RMSE of range estimation versus L.
5.4. Probability of Successful Detection
The probability of successful detection (PSD) is another important index, which can measure the stability and robustness of the method.
Define the total of successful detections as V. PSD is denoted by
If the difference between the estimated and the true of DOA and range are within and ± 0.1 km, respectively, then it can be regarded as a victory target detection. It can be regarded as a successful detection, when the difference between the estimated value and the true value of DOA and range is within and km, respectively.
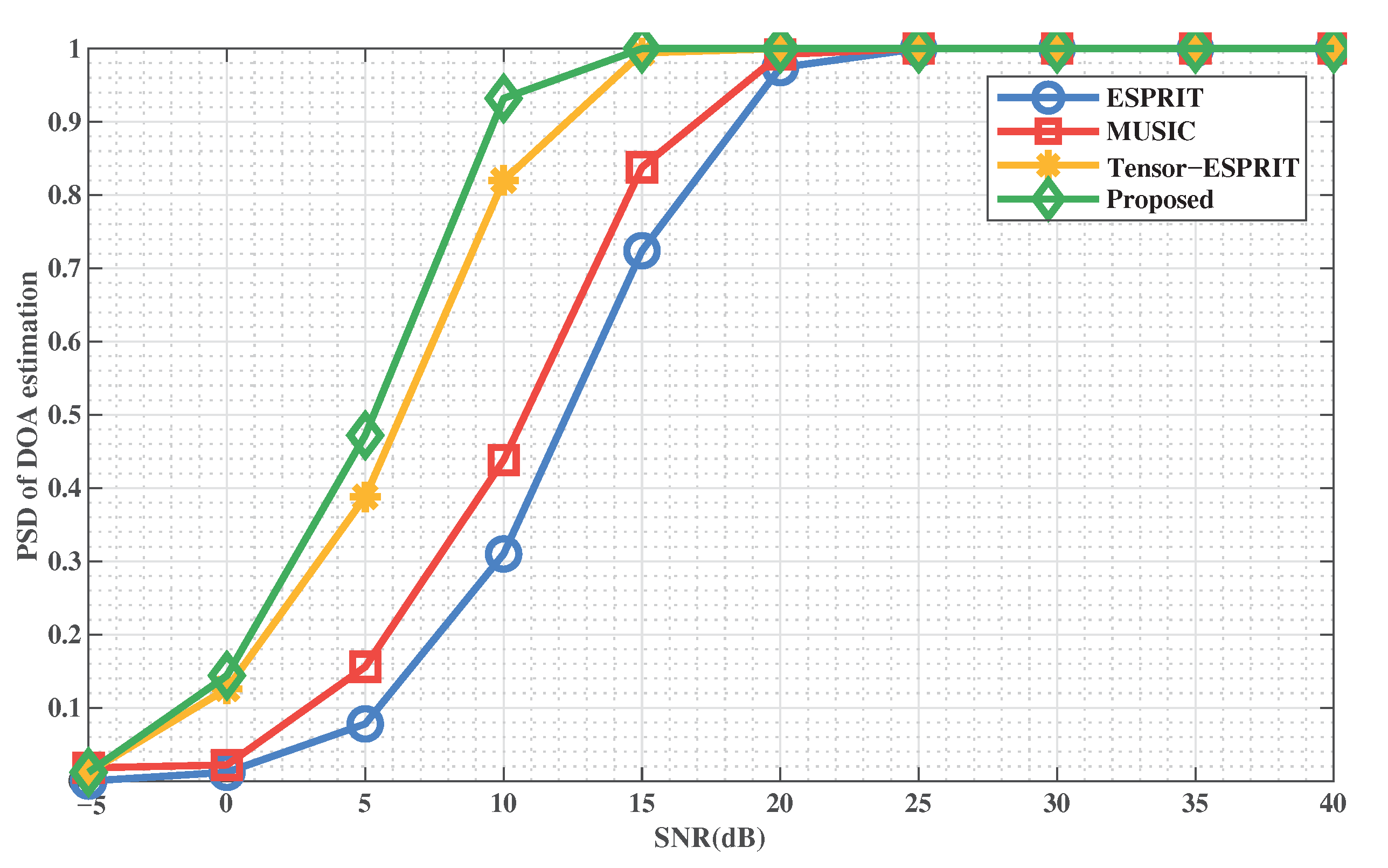
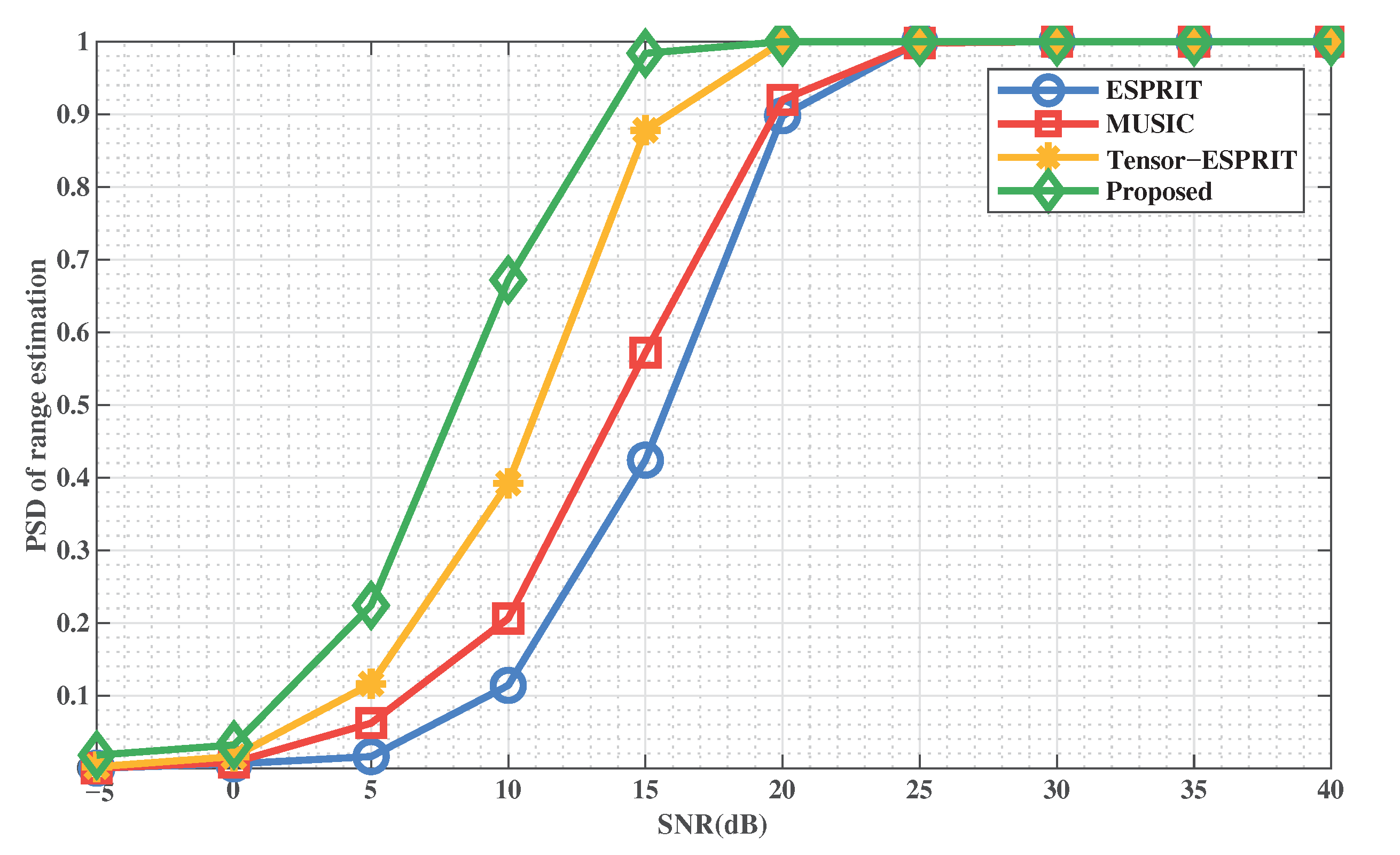
Figure 9 and Figure 10 show the PSD of DOA and range estimation with SNR when the number of snapshots is , respectively. We can conclude that the method is the best compared to the comparison methods. This indicates that the stability and effectiveness of the proposed method is excellent. In addition, the proposed method can achieve a 100% successful detection rate with a lower SNR, which indicates that our method overcomes the defect of performance degradation when SNR is low.
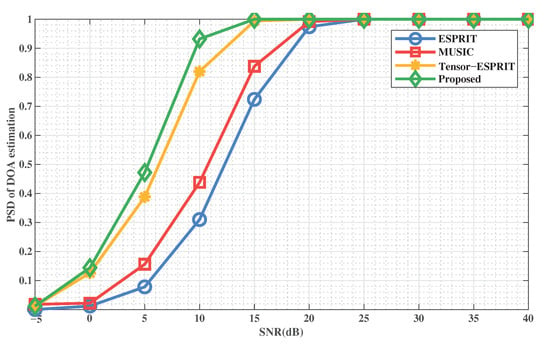
Figure 9.
PSD of DOA estimation versus SNR.
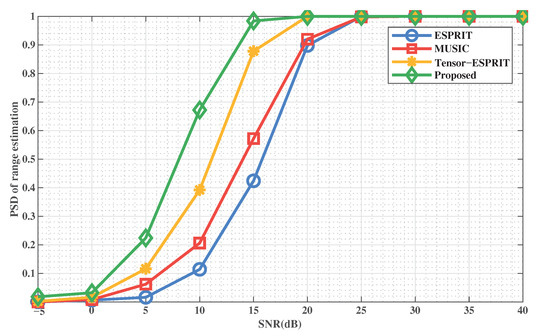
Figure 10.
PSD of range estimation versus SNR.
5.5. The Simulation Time Versus Trial Number
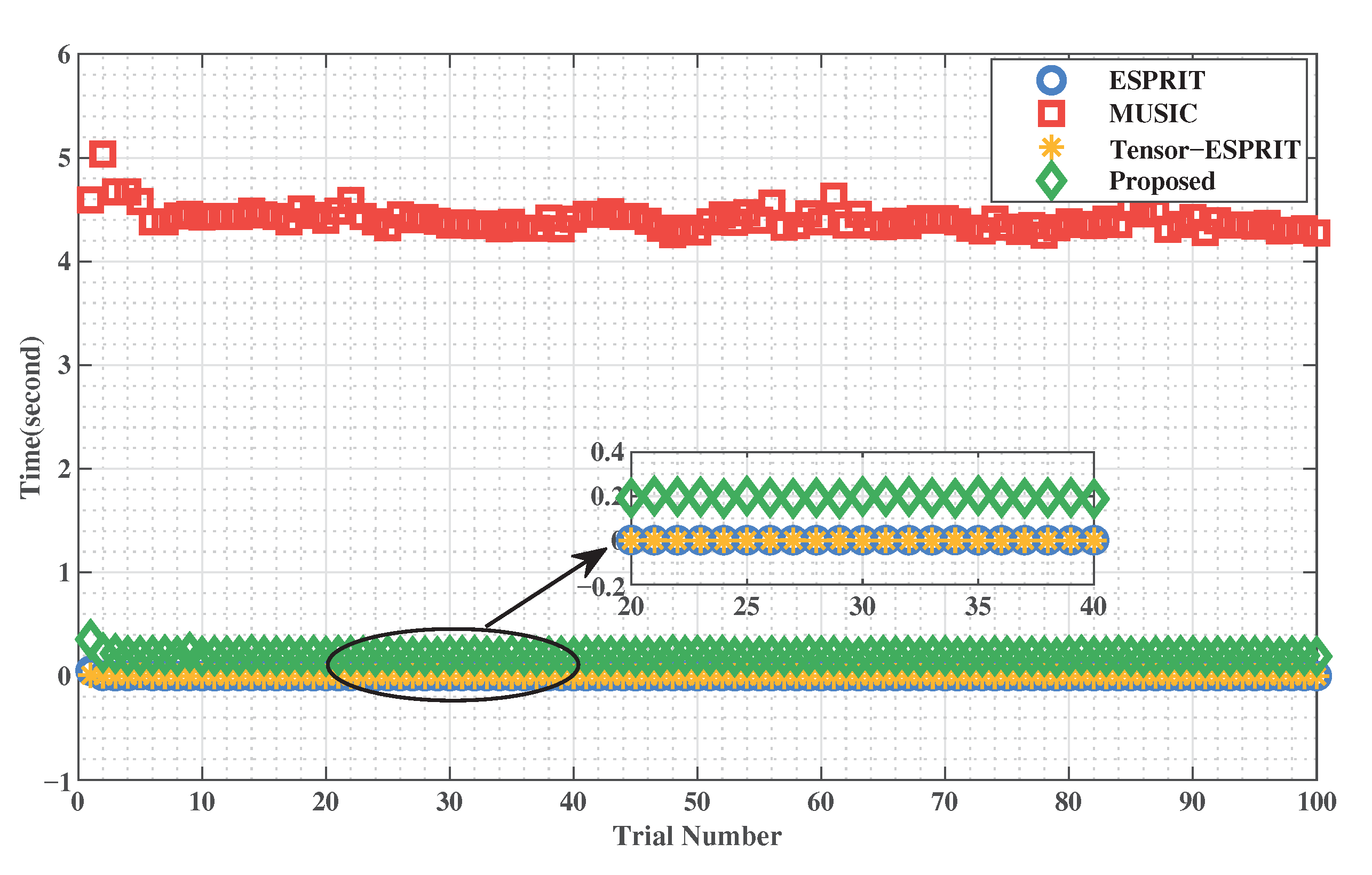
In this simulation, we compare the simulation running time of the methods, and the results are shown in Figure 11. The signal parameters are set to = 20 dB and . In particular, the total of Monte Carlo trials is . The X-axis and Y-axis represent the trial number and simulation running time, respectively.
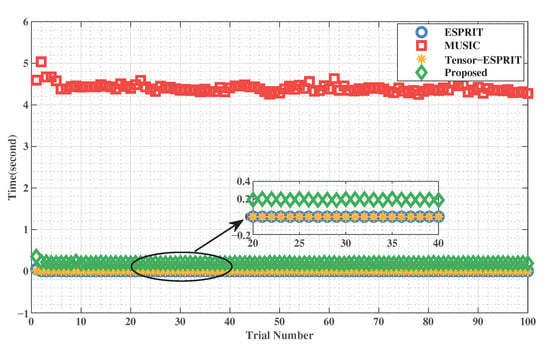
Figure 11.
The simulation running time comparison.
Figure 11 shows the simulation running time comparison of ESPRIT, MUSIC, Tensor-ESPRIT, and Proposed method. From the previous calculation of computation complexity, it can be seen that the computation complexity of MUSIC is much higher than that of the other methods, which is caused by the range-dimensional spectral peaks. The proposed method eliminates the high computational cost of range-dimension spectral peaks through reduced-dimension. It can be seen from the partial enlargement that the simulation running time of the proposed time is close to that of ESPRIT and Tensor-ESPRIT methods. This shows that the computation complexity of the proposed method is the same order of magnitude as that of ESPRIT and Tensor-ESPRIT methods. The performance of the proposed method is more excellent under the same computation complexity.
6. Conclusions
We propose a reduced-dimensionality MUSIC method based on tensor in this paper, which realizes joint DOA and range estimation in FDA-MIMO radar. A tensor-based signal model can be established to store inherent multi-dimensional structures that can optimize the performance and stability of target parameter estimation. Then use the HOSVD to obtain the signal subspace based on tensor, which can be used to construct the two-dimensional spectrum function. The Lagrange multiplier method is utilized to reduce the dimensionality of the spectrum function. The estimation of DOA is realized by a one-dimensional spectrum peak search. The constraint condition is constructed to eliminate the limit situation when the transmitting steering vector is zero matrix. We can derive the transmitting steering vector from the partial derivative of the Lagrange function. Finally, extract the phase of the transmitting steering vector. Range information is estimated by the least square method. Moreover, the high computation complexity of two-dimensional MUSIC is overcomes in the proposed method, and uses tensor-based signal model to optimize the performance of the proposed method, which can remain stable in low SNR and low snapshot. The superiority of the proposed method can be verified by numerical analysis and simulation. In the future, we will optimize the proposed method to make target location more accurate and suitable for more application.
Author Contributions
Conceptualization, X.W. and L.S.; methodology, T.X. and X.W.; writing—original draft preparation, T.X.; writing—review and editing, X.W. and X.L.; supervision, X.W.; funding acquisition, X.W. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 61861015 and 61961013), The Important Science and Technology Project of Hainan Province (ZDKJ2020010), National Key Research and Development Program of China(No. 2019CXTD400), Young Elite Scientists Sponsorship Program by CAST (No. 2018QNRC001), and the Scientific Research Setup Fund of Hainan University (No. KYQD(ZR) 1731).
Institutional Review Board Statement
No applicable.
Informed Consent Statement
No applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Cimini, R.; Chizhik, D.; Valenzuela, R. Performance of MIMO radar systems: Advantages of angular diversity. In Proceedings of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2004; Volume 1, pp. 305–309. [Google Scholar]
- Amadori, P.V.; Masouros, C. Low RF-complexity millimeter-wave beamspace-MIMO systems by beam selection. IEEE Trans. Commun. 2015, 63, 2212–2223. [Google Scholar] [CrossRef]
- Wang, H.; Wan, L.; Dong, M.; Ota, K.; Wang, X. Assistant vehicle localization based on three collaborative base stations via SBL-based robust DOA estimation. IEEE Internet Things J. 2019, 6, 5766–5777. [Google Scholar] [CrossRef]
- Wang, X.; Huang, M.; Wan, L. Joint 2D-DOD and 2D-DOA estimation for coprime EMVS–MIMO radar. Circ. Syst. Signal Process. 2021, 40, 1–17. [Google Scholar] [CrossRef]
- Wang, W.; So, H.C.; Farina, A. An overview on time/frequency modulated array processing. IEEE J. Sel. Top. Signal Process. 2016, 11, 228–246. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, C.; Liang, X.; Chen, L.; Zhang, F. Sparse Bayesian learning based three-dimensional imaging algorithm for off-grid air targets in MIMO radar array. Remote Sens. 2018, 10, 369. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Wang, W.; Gao, K. FDA-MIMO radar range–angle estimation: CRLB, MSE, and resolution analysis. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 284–294. [Google Scholar] [CrossRef]
- Zhang, L.; Wen, F. A Novel MIMO Radar Orthogonal Waveform Design Algorithm Based on Intelligent Ions Motion. Remote Sens. 2021, 13, 1968. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE Radar Conference (IEEE Cat. No. 04CH37509), Philadelphia, PA, USA, 29–29 April 2004; pp. 71–78. [Google Scholar]
- Wan, L.; Sun, L.; Liu, K.; Wang, X.; Lin, Q.; Zhu, T. Autonomous vehicle source enumeration exploiting non-cooperative UAV in software defined internet of vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3603–3615. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.T.; Meng, D.; Dong, M.; Ota, K.; Wang, H. Multi-UAV cooperative localization for marine targets based on weighted subspace fitting in SAGIN environment. IEEE Internet Things J. 2021, in press. [Google Scholar]
- Fishler, E.; Haimovich, A.; Blum, R.S.; Cimini, L.J.; Chizhik, D.; Valenzuela, R.A. Spatial diversity in radars—Models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Xu, L.; Roberts, W. On parameter identifiability of MIMO radar. IEEE Signal Process. Lett. 2007, 14, 968–971. [Google Scholar]
- Hu, Z.; Wang, W.; Dong, F. MIMO Radar Accurate Imaging and Motion Estimation for 3-D Maneuvering Ship Target. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar]
- Wan, L.; Liu, K.; Liang, Y.C.; Zhu, T. DOA and polarization estimation for non-circular signals in 3-D millimeter wave polarized massive MIMO systems. IEEE Trans. Wirel. Commun. 2021, 20, 3152–3167. [Google Scholar] [CrossRef]
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Frequency diverse array radars. In Proceedings of the 2006 IEEE Conference on Radar, Verona, NY, USA, 24–27 April 2006; p. 3. [Google Scholar]
- Wang, W.Q. Frequency diverse array antenna: New opportunities. IEEE Antennas Propag. Mag. 2015, 57, 145–152. [Google Scholar] [CrossRef]
- Antonik, P.; Wicks, M.C.; Griffiths, H.D.; Baker, C.J. Range-dependent beamforming using element level waveform diversity. In Proceedings of the 2006 International Waveform Diversity & Design Conference, Lihue, HI, USA, 22–27 January 2006; pp. 1–6. [Google Scholar]
- Smith, C.M.; Feder, H.J.S.; Leonard, J.J. Multiple target tracking with navigation uncertainty. In Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No. 98CH36171), Tampa, FL, USA, 18 December 1998; Volume 1, pp. 760–761. [Google Scholar]
- Wan, L.; Sun, Y.; Sun, L.; Ning, Z.; Rodrigues, J.J. Deep learning based autonomous vehicle super resolution DOA estimation for safety driving. IEEE Trans. Intell. Transp. Syst. 2020, 22, 4301–4315. [Google Scholar] [CrossRef]
- Secmen, M.; Demir, S.; Hizal, A.; Eker, T. Frequency diverse array antenna with periodic time modulated pattern in range and angle. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; pp. 427–430. [Google Scholar]
- Wang, W.; Shao, H. Range-angle localization of targets by a double-pulse frequency diverse array radar. IEEE J. Sel. Top. Signal Process. 2013, 8, 106–114. [Google Scholar] [CrossRef]
- Wang, W. Subarray-based frequency diverse array radar for target range-angle estimation. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 3057–3067. [Google Scholar] [CrossRef]
- Cui, C.; Xu, J.; Gui, R.; Wang, W.Q.; Wu, W. Search-free DOD, DOA and range estimation for bistatic FDA-MIMO radar. IEEE Access 2018, 6, 15431–15445. [Google Scholar] [CrossRef]
- Zhang, J.J.; Papandreou-Suppappola, A. MIMO radar with frequency diversity. In Proceedings of the 2009 International Waveform Diversity and Design Conference, Kissimmee, FL, USA, 8–13 February 2009; pp. 208–212. [Google Scholar]
- Gao, K.; Shao, H.; Chen, H.; Cai, J.; Wang, W.Q. Impact of frequency increment errors on frequency diverse array MIMO in adaptive beamforming and target localization. Digit. Signal Process. 2015, 44, 58–67. [Google Scholar] [CrossRef]
- Xu, T.; Yang, Y.; Huang, M.; Wang, H.; Wu, D.; Qu, Y. Tensor-Based Angle and Range Estimation Method in Monostatic FDA-MIMO Radar. Math. Probl. Eng. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Wang, W.Q.; So, H.C. Transmit subaperturing for range and angle estimation in frequency diverse array radar. IEEE Trans. Signal Process. 2014, 62, 2000–2011. [Google Scholar] [CrossRef]
- Xu, T.; Wang, X.; Su, T.; Wan, L.; Sun, L. Vehicle Location in Edge Computing Enabling IoTs Based on Bistatic FDA-MIMO Radar. IEEE Access 2021, 9, 46398–46408. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhu, S.; Huang, L.; So, H.C. Joint range and angle estimation using MIMO radar with frequency diverse array. IEEE Trans. Signal Process. 2015, 63, 3396–3410. [Google Scholar] [CrossRef]
- Li, B.; Bai, W.; Zheng, G. Successive ESPRIT algorithm for joint DOA-range-polarization estimation with polarization sensitive FDA-MIMO radar. IEEE Access 2018, 6, 36376–36382. [Google Scholar] [CrossRef]
- Liu, F.; Wang, X.; Huang, M.; Wan, L.; Wang, H.; Zhang, B. A Novel Unitary ESPRIT Algorithm for Monostatic FDA-MIMO Radar. Sensors 2020, 20, 827. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Wang, X.; Huang, M.; Wan, L. Joint angle and range estimation for bistatic FDA-MIMO radar via real-valued subspace decomposition. Signal Process. 2021, 185, 108065. [Google Scholar] [CrossRef]
- van Belzen, F.; Weiland, S.; de Graaf, J. Singular value decompositions and low rank approximations of multi-linear functionals. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3751–3756. [Google Scholar]
- Wang, Q.; Wang, H.; Dou, T.; Hou, C. Block Sparse Representation based DOA Estimation for FDA with Unknown Mutual Coupling. In Proceedings of the 2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland, New Zealand, 5–8 August 2018; pp. 536–538. [Google Scholar]
- Liu, Q.; Wang, X.; Huang, M.; Lan, X.; Sun, L. DOA and Range Estimation for FDA-MIMO Radar with Sparse Bayesian Learning. Remote Sens. 2021, 13, 2553. [Google Scholar] [CrossRef]
- Nion, D.; Sidiropoulos, N.D. Tensor algebra and multidimensional harmonic retrieval in signal processing for MIMO radar. IEEE Trans. Signal Process. 2010, 58, 5693–5705. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; De Lathauwer, L.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Itskov, M. Tensor Algebra and Tensor Analysis for Engineers; Springer: New York, NY, USA, 2007. [Google Scholar]
- Zhang, X. Matrix Analysis and Applications; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, W.; Liu, J.; Liu, Q.; Wang, B. Tensor-based real-valued subspace approach for angle estimation in bistatic MIMO radar with unknown mutual coupling. Signal Process. 2015, 116, 152–158. [Google Scholar] [CrossRef]
- Liu, X.; Liao, G. Direction finding and mutual coupling estimation for bistatic MIMO radar. Signal Process. 2012, 92, 517–522. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).