Development and Validation of Machine-Learning Clear-Sky Detection Method Using 1-Min Irradiance Data and Sky Imagers at a Polluted Suburban Site, Xianghe
Abstract
:1. Introduction
2. Site, Data and Methods
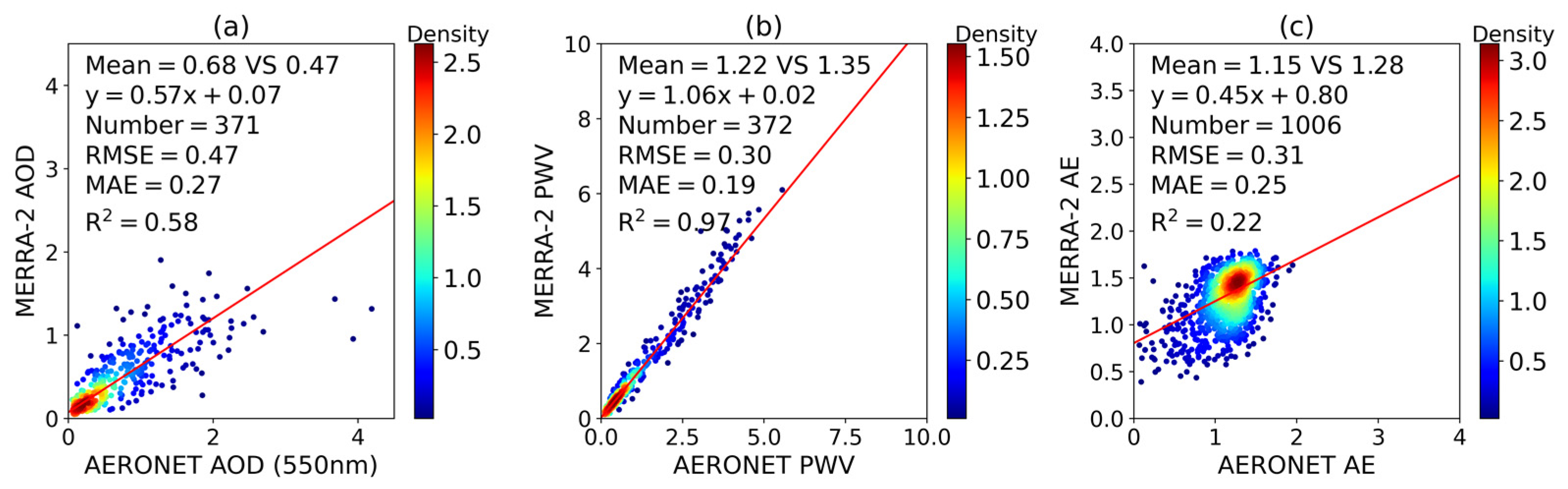
2.1. Site and Data
2.2. Conventional CSD Methods
2.3. Machine-Learning Methods
3. Model Construction and Sensitivity Analysis
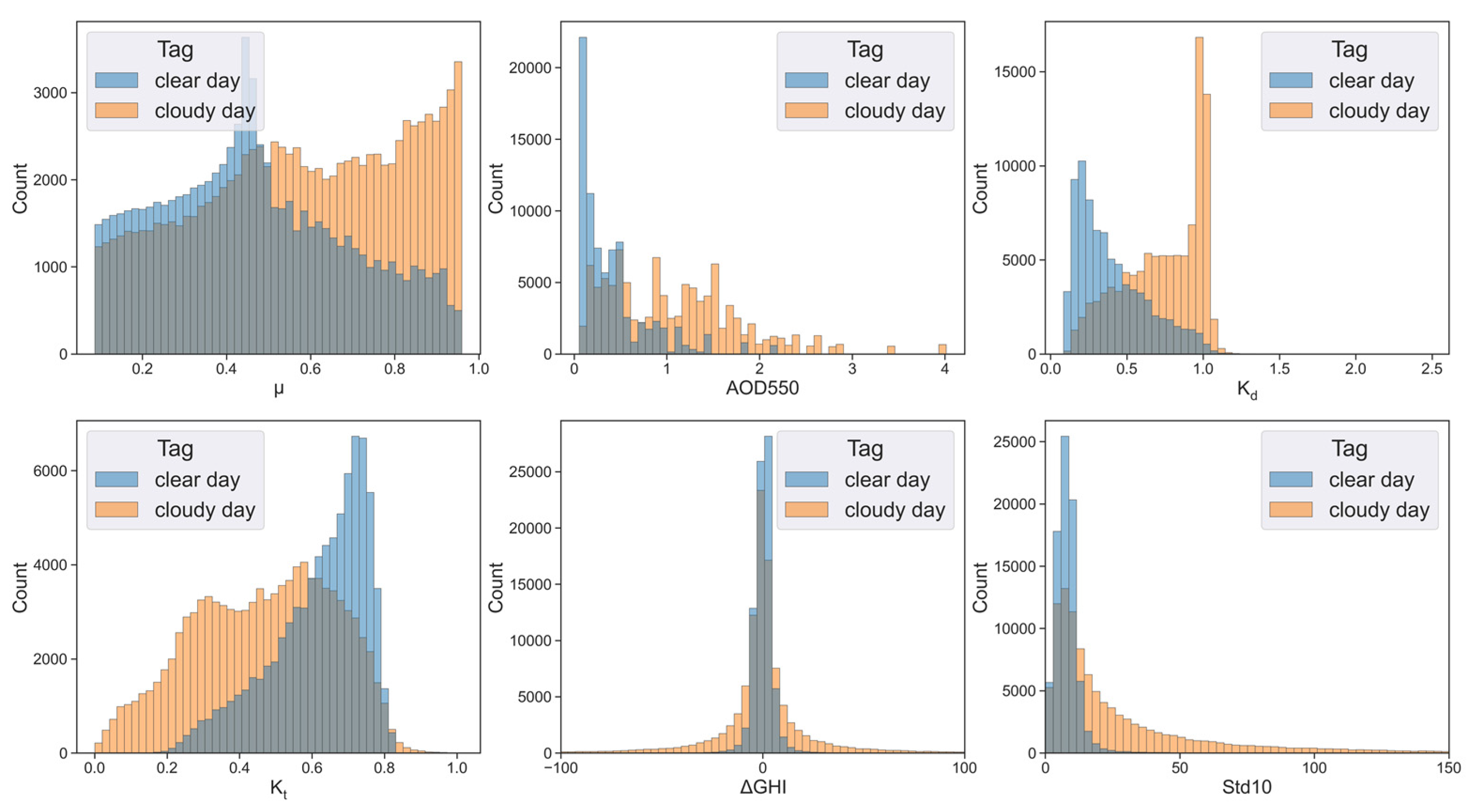
3.1. Choice of Input Features
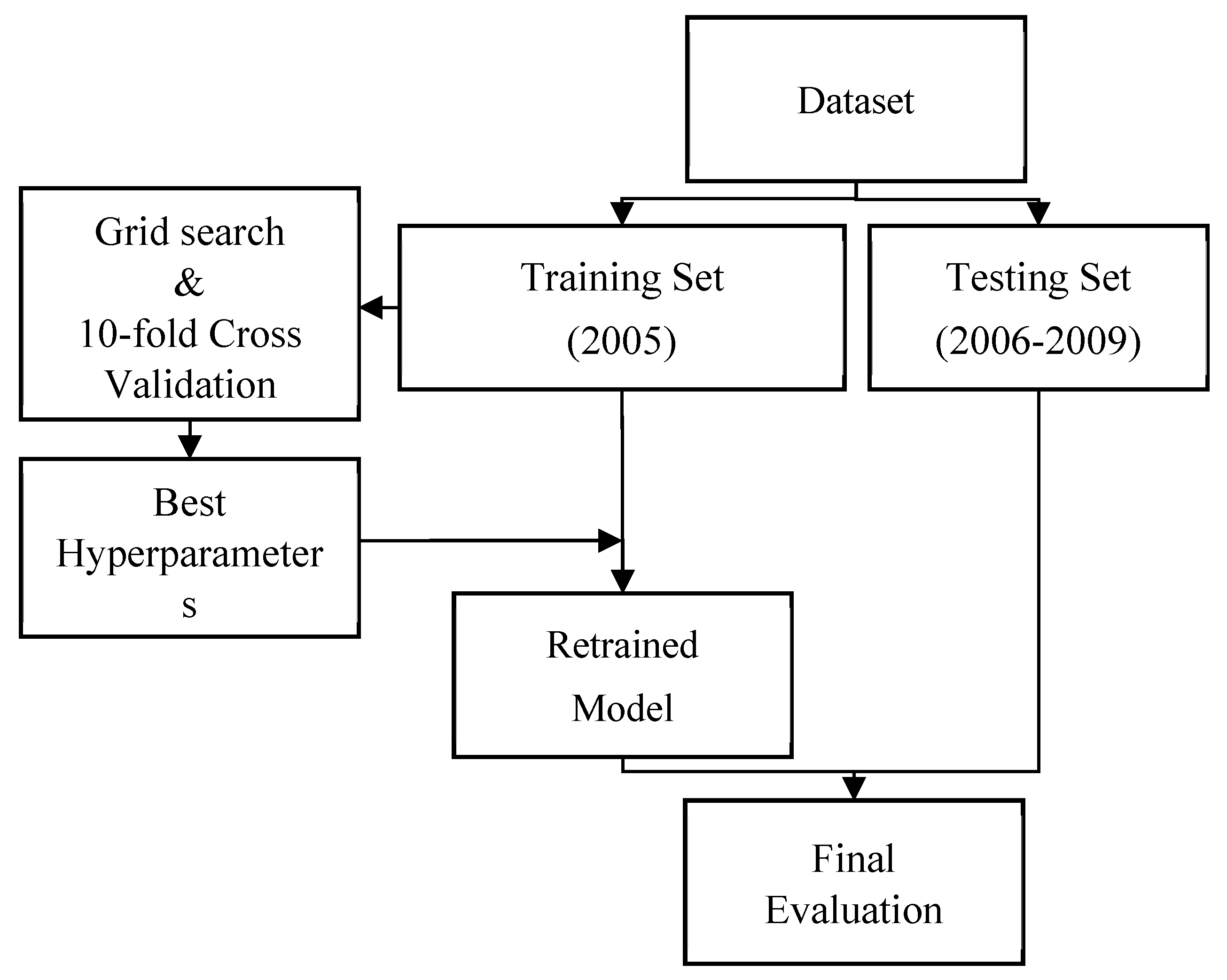
3.2. Model Construction
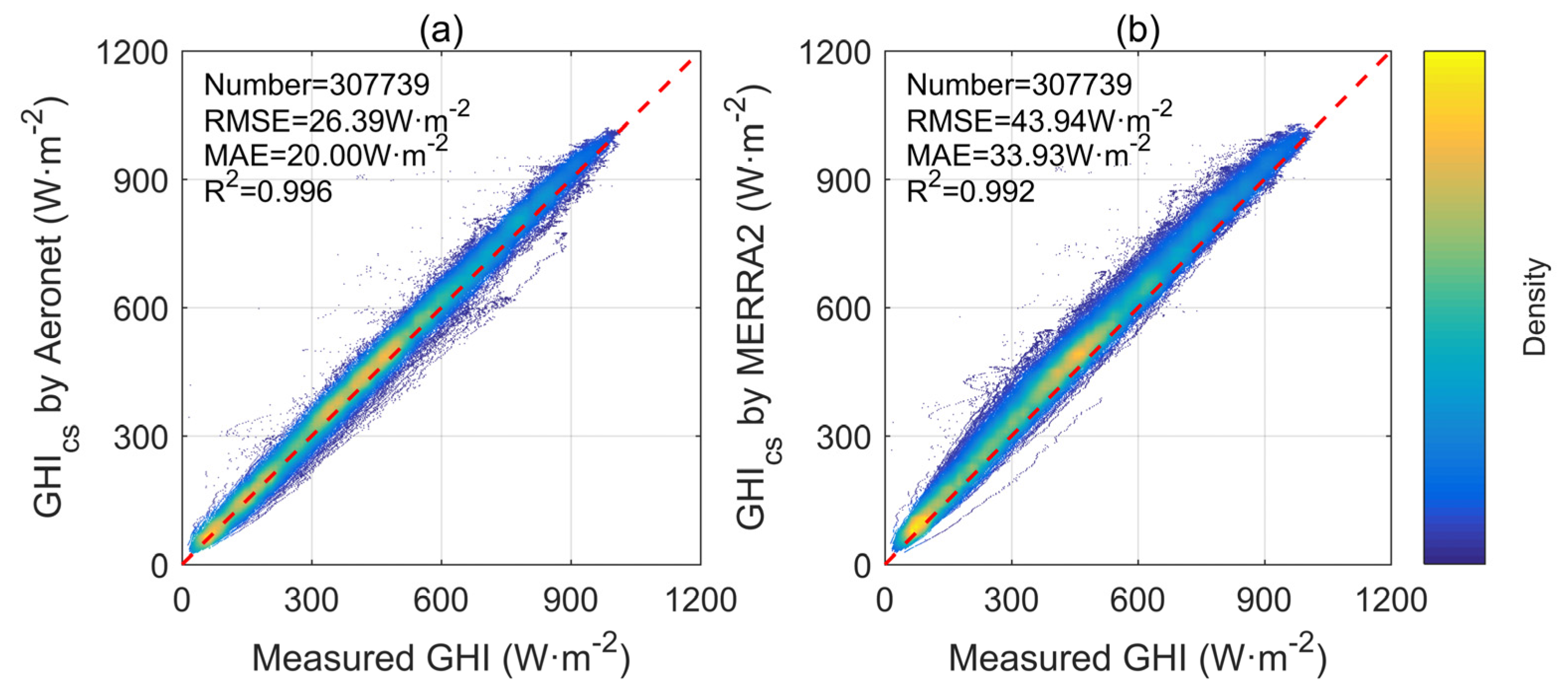
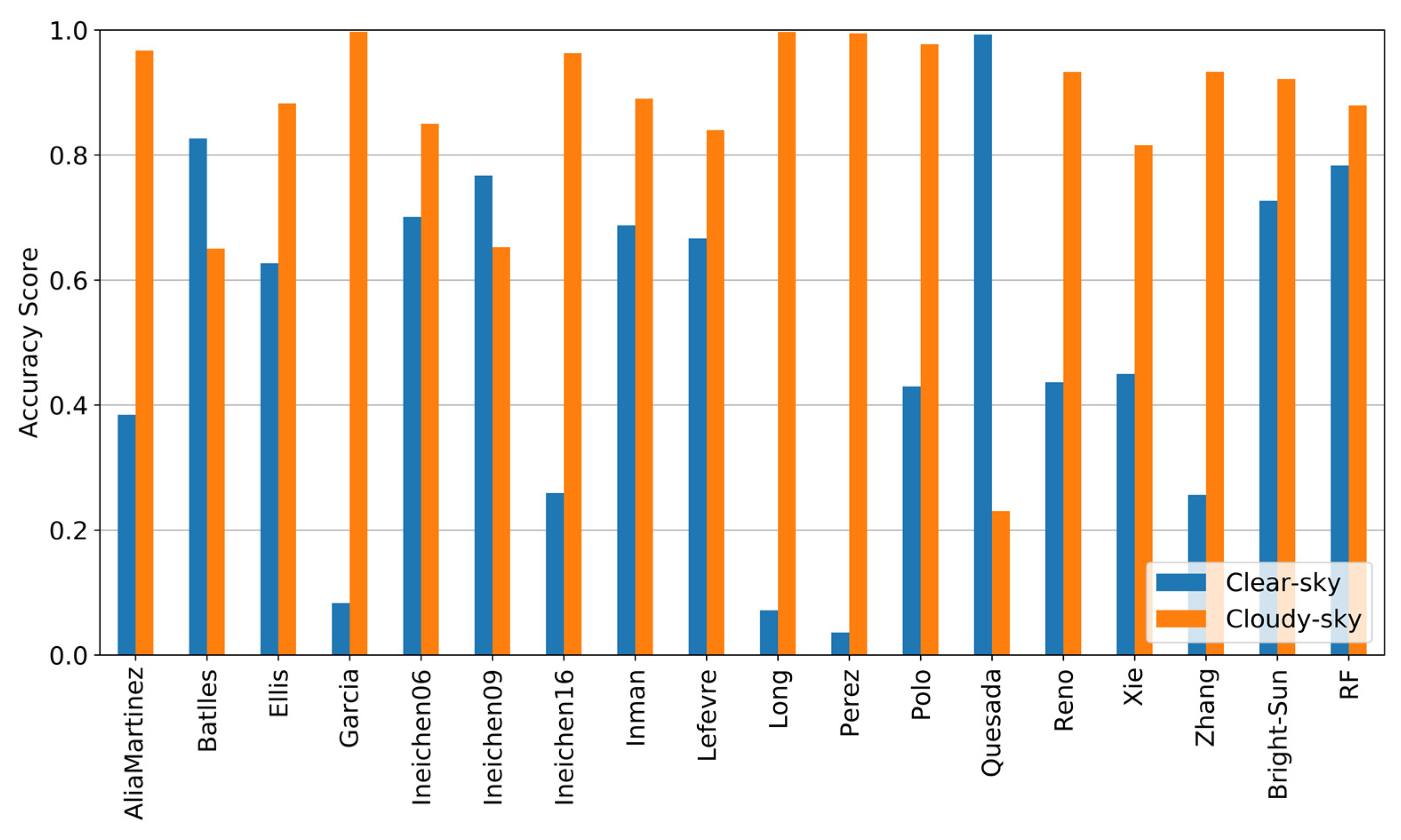
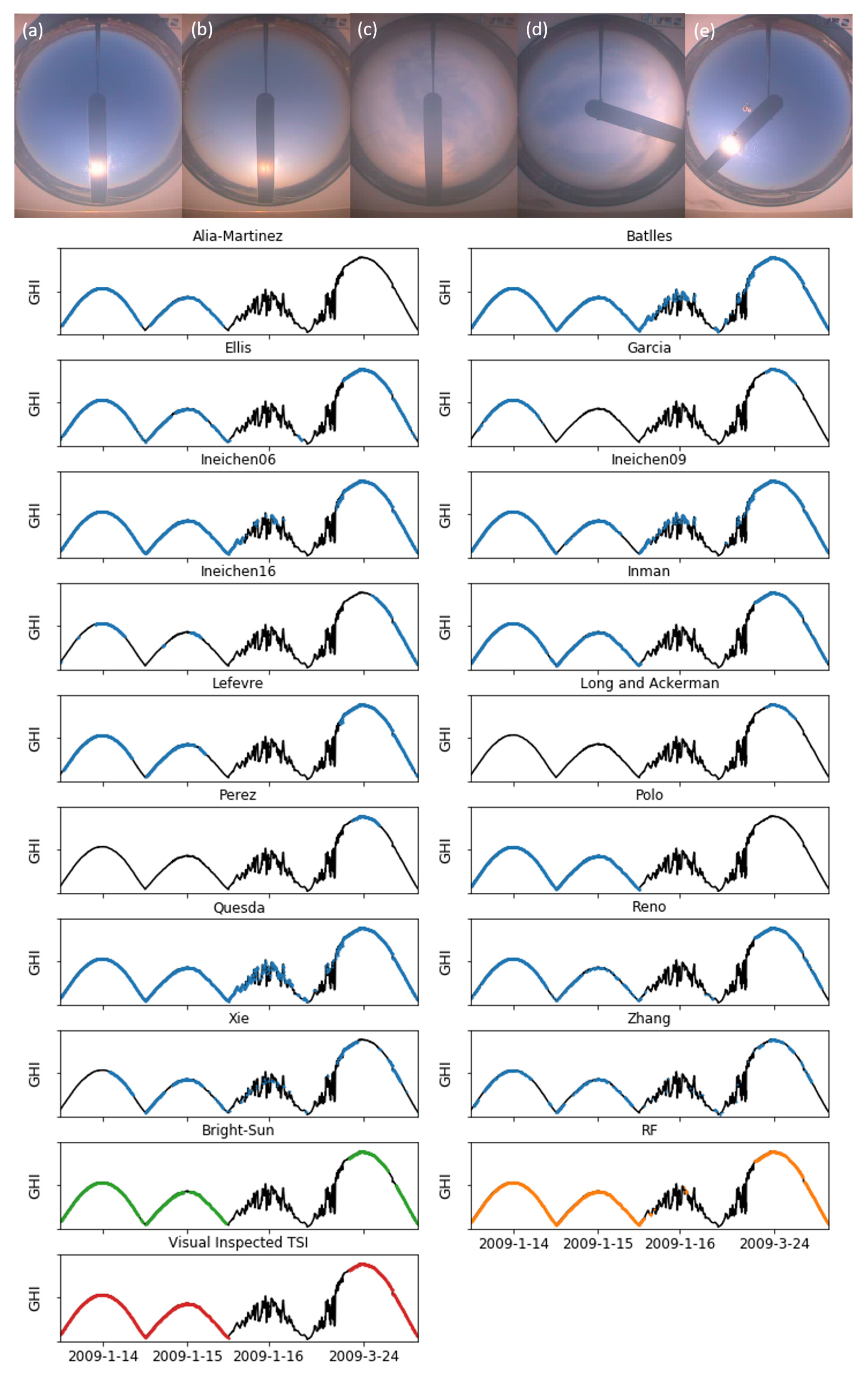
4. Results
5. Discussion
5.1. Inuput Features
5.2. Training Set Size
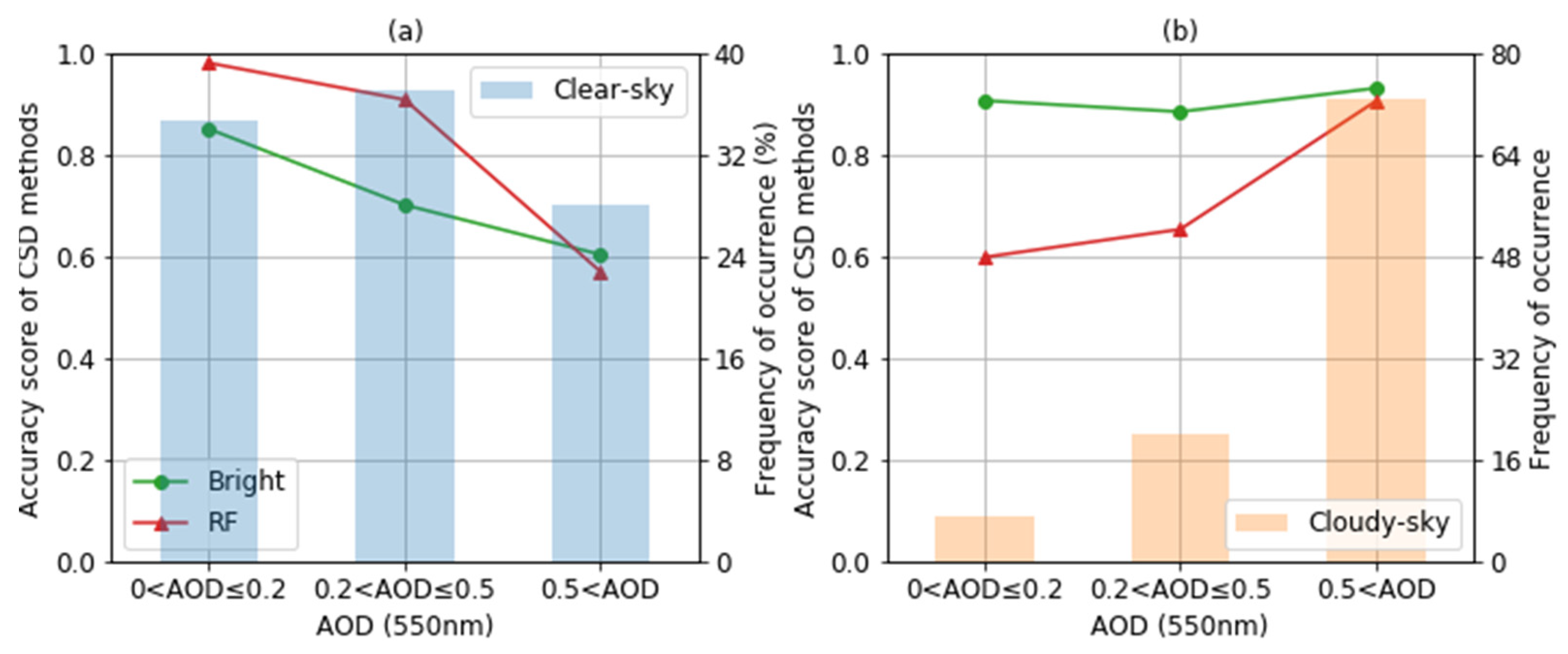
5.3. Validation over SURFRAD Network
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Huang, G.; Li, Z.; Li, X.; Liang, S.; Yang, K.; Wang, D.; Zhang, Y. Estimating surface solar irradiance from satellites: Past, present, and future perspectives. Remote Sens. Environ. 2019, 233, 111371. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Bright, J.M.; Lingfors, D.; Habte, A.; Sengupta, M. A posteriori clear-sky identification methods in solar irradiance time series: Review and preliminary validation using sky imagers. Renew. Sustain. Energy Rev. 2019, 109, 412–427. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef] [Green Version]
- Ineichen, P.; Barroso, C.S.; Geiger, B.; Hollmann, R.; Marsouin, A.; Mueller, R. Satellite Application Facilities irradiance products: Hourly time step comparison and validation over Europe. Int. J. Remote Sens. 2009, 30, 5549–5571. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Arias, J.A.; Gueymard, C.A.; Cebecauer, T. Direct normal irradiance modeling: Evaluating the impact on accuracy of worldwide gridded aerosol databases. AIP Conf. Proc. 2019, 2126. [Google Scholar] [CrossRef]
- Bright, J.M.; Sun, X.; Gueymard, C.A.; Acord, B.; Wang, P.; Engerer, N.A. BRIGHT-SUN: A globally applicable 1-min irradiance clear-sky detection model. Renew. Sustain. Energy Rev. 2020, 121. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Y.; Wang, D.; Liu, X.; Wang, Y. A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 2021, 235, 113960. [Google Scholar] [CrossRef]
- Lary, D.J.; Zewdie, G.K.; Liu, X.; Wu, D.; Levetin, E.; Allee, R.J.; Malakar, N.; Walker, A.; Mussa, H.; Mannino, A.; et al. Machine Learning Applications for Earth Observation BT—Earth Observation Open Science and Innovation; Mathieu, P.-P., Aubrecht, C., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 165–218. ISBN 978-3-319-65633-5. [Google Scholar]
- Xia, M.; Lu, W.; Yang, J.; Ma, Y.; Yao, W.; Zheng, Z. A hybrid method based on extreme learning machine and k-nearest neighbor for cloud classification of ground-based visible cloud image. Neurocomputing 2015, 160, 238–249. [Google Scholar] [CrossRef]
- Ghasemian, N.; Akhoondzadeh, M. Introducing two Random Forest based methods for cloud detection in remote sensing images. Adv. Sp. Res. 2018, 62, 288–303. [Google Scholar] [CrossRef]
- Gorooh, V.A.; Kalia, S.; Nguyen, P.; Hsu, K.L.; Sorooshian, S.; Ganguly, S.; Nemani, R.R. Deep Neural Network Cloud-Type Classification (DeepCTC) model and its application in evaluating PERSIANN-CCS. Remote Sens. 2020, 12, 316. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Tejera, S.; Silva-Pérez, M.A.; Ramírez-Santigosa, L.; Lillo-Bravo, I. Classification of days according to DNI profiles using clustering techniques. Sol. Energy 2017, 146, 319–333. [Google Scholar] [CrossRef]
- Kang, B.O.; Tam, K.S. A new characterization and classification method for daily sky conditions based on ground-based solar irradiance measurement data. Sol. Energy 2013, 94, 102–118. [Google Scholar] [CrossRef]
- Lee, Y.; Wahba, G.; Ackerman, S.A. Cloud classification of satellite radiance data by multicategory support vector machines. J. Atmos. Ocean. Technol. 2004, 21, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.; Che, H.; Zhu, J.; Chen, H.; Cong, Z.; Deng, X.; Fan, X.; Fu, Y.; Goloub, P.; Jiang, H.; et al. Ground-based remote sensing of aerosol climatology in China: Aerosol optical properties, direct radiative effect and its parameterization. Atmos. Environ. 2016, 124, 243–251. [Google Scholar] [CrossRef]
- Coimbra, C.F.M.; Kleissl, J.; Marquez, R. Overview of Solar-Forecasting Methods and a Metric for Accuracy Evaluation; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 9780123971777. [Google Scholar]
- Liu, M.; Zhang, J.; Xia, X. Evaluation of multiple surface irradiance-based clear sky detection methods at Xianghe—A heavy polluted site on the North China Plain. Atmos. Ocean. Sci. Lett. 2021, 14, 100016. [Google Scholar] [CrossRef]
- Gueymard, C.A. REST2: High-performance solar radiation model for cloudless-sky irradiance, illuminance, and photosynthetically active radiation - Validation with a benchmark dataset. Sol. Energy 2008, 82, 272–285. [Google Scholar] [CrossRef]
- Sun, X.; Bright, J.M.; Gueymard, C.A.; Acord, B.; Wang, P.; Engerer, N.A. Worldwide performance assessment of 75 global clear-sky irradiance models using Principal Component Analysis. Renew. Sustain. Energy Rev. 2019, 111, 550–570. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Song, Z.; Fu, D.; Zhang, X.; Wu, Y.; Xia, X.; He, J.; Han, X.; Zhang, R.; Che, H. Diurnal and seasonal variability of PM2.5 and AOD in North China plain: Comparison of MERRA-2 products and ground measurements. Atmos. Environ. 2018, 191, 70–78. [Google Scholar] [CrossRef]
- Polo, J.; Zarzalejo, L.F.; Martín, L.; Navarro, A.A.; Marchante, R. Estimation of daily Linke turbidity factor by using global irradiance measurements at solar noon. Sol. Energy 2009, 83, 1177–1185. [Google Scholar] [CrossRef]
- Alia-Martinez, M.; Antonanzas, J.; Urraca, R.; Martinez-De-Pison, F.J.; Antonanzas-Torres, F. Benchmark of algorithms for solar clear-sky detection. J. Renew. Sustain. Energy 2016, 8. [Google Scholar] [CrossRef]
- Quesada-Ruiz, S.; Linares-Rodríguez, A.; Ruiz-Arias, J.A.; Pozo-Vázquez, D.; Tovar-Pescador, J. An advanced ANN-based method to estimate hourly solar radiation from multi-spectral MSG imagery. Sol. Energy 2015, 115, 494–504. [Google Scholar] [CrossRef]
- Batlles, F.J.; Olmo, F.J.; Tovar, J.; Alados-Arboledas, L. Comparison of cloudless sky parameterizations of solar irradiance at various Spanish midlatitude locations. Theor. Appl. Climatol. 2000, 66, 81–93. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Zelenka, A. Making full use of the clearness index for parameterizing hourly insolation conditions. Sol. Energy 1990, 45, 111–114. [Google Scholar] [CrossRef] [Green Version]
- Reno, M.J.; Hansen, C.W. Identification of periods of clear sky irradiance in time series of GHI measurements. Renew. Energy 2016, 90, 520–531. [Google Scholar] [CrossRef] [Green Version]
- Ellis, B.H.; Deceglie, M.; Jain, A. Automatic Detection of Clear-sky Periods Using Ground and Satellite Based Solar Resource Data. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa, HI, USA, 10–15 June 2018; pp. 2293–2298. [Google Scholar] [CrossRef]
- Ineichen, P. Comparison of eight clear sky broadband models against 16 independent data banks. Sol. Energy 2006, 80, 468–478. [Google Scholar] [CrossRef] [Green Version]
- Inman, R.H.; Edson, J.G.; Coimbra, C.F.M. Impact of local broadband turbidity estimation on forecasting of clear sky direct normal irradiance. Sol. Energy 2015, 117, 125–138. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Liu, Y. A new approach for simultaneously retrieving cloud albedo and cloud fraction from surface-based shortwave radiation measurements. Environ. Res. Lett. 2013, 8. [Google Scholar] [CrossRef] [Green Version]
- Long, C.N.; Ackerman, T.P. Identification of clear skies from broadband pyranometer measurements and calculation of downwelling shortwave cloud effects. J. Geophys. Res. Atmos. 2000, 105, 15609–15626. [Google Scholar] [CrossRef]
- García, R.D.; García, O.E.; Cuevas, E.; Cachorro, V.E.; Romero-Campos, P.M.; Ramos, R.; De Frutos, A.M. Solar radiation measurements compared to simulations at the BSRN Izaña station. Mineral dust radiative forcing and efficiency study. J. Geophys. Res. 2014, 119, 179–194. [Google Scholar] [CrossRef]
- Zhang, W.; Kleiber, W.; Florita, A.R.; Hodge, B.M.; Mather, B. A stochastic downscaling approach for generating high-frequency solar irradiance scenarios. Sol. Energy 2018, 176, 370–379. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Pedregosa, F.; Grisel, O.; Weiss, R.; Passos, A.; Brucher, M.; Varoquax, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
| Hyperparameter | Threshold | Interval | Optimum |
|---|---|---|---|
| max_depth | 10–110 | 20 | 10 |
| max_features | ‘log2’, ‘sqrt’ | - | ‘sqrt’ |
| min_samples_split | 2–20 | 2 | 12 |
| n_estimators | 10–210 | 20 | 150 |
| Features | Importance |
|---|---|
| μ | 0.09 |
| Kd | 0.38 |
| Kt | 0.14 |
| ΔGHI | 0.06 |
| Std10 | 0.32 |
| Max_Depth | Max_Features | Min_Samples_Split | n_Estimators | Mean Accuracy Score on Testing Set | |
|---|---|---|---|---|---|
| Inputs without kd | 10 | ‘log2’ | 12 | 190 | 0.81 |
| max_depth | max_features | min_samples_split | n_estimators | Mean Accuracy Score on Testing Set | |
|---|---|---|---|---|---|
| 1 Month | 30 | ‘log2’ | 20 | 10 | 0.79 |
| 3 Months | 10 | ‘sqrt’ | 16 | 10 | 0.83 |
| 6 Months | 10 | ‘sqrt’ | 8 | 190 | 0.83 |
| 9 Months | 10 | ‘sqrt’ | 16 | 10 | 0.83 |
| TP | TN | FP | FN | Mean Accuracy Score | |
|---|---|---|---|---|---|
| GWN | 662 | 11,831 | 776 | 755 | 0.89 |
| PSU | 715 | 64,684 | 1271 | 2000 | 0.97 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Xia, X.; Fu, D.; Zhang, J. Development and Validation of Machine-Learning Clear-Sky Detection Method Using 1-Min Irradiance Data and Sky Imagers at a Polluted Suburban Site, Xianghe. Remote Sens. 2021, 13, 3763. https://doi.org/10.3390/rs13183763
Liu M, Xia X, Fu D, Zhang J. Development and Validation of Machine-Learning Clear-Sky Detection Method Using 1-Min Irradiance Data and Sky Imagers at a Polluted Suburban Site, Xianghe. Remote Sensing. 2021; 13(18):3763. https://doi.org/10.3390/rs13183763
Chicago/Turabian StyleLiu, Mengqi, Xiangao Xia, Disong Fu, and Jinqiang Zhang. 2021. "Development and Validation of Machine-Learning Clear-Sky Detection Method Using 1-Min Irradiance Data and Sky Imagers at a Polluted Suburban Site, Xianghe" Remote Sensing 13, no. 18: 3763. https://doi.org/10.3390/rs13183763
APA StyleLiu, M., Xia, X., Fu, D., & Zhang, J. (2021). Development and Validation of Machine-Learning Clear-Sky Detection Method Using 1-Min Irradiance Data and Sky Imagers at a Polluted Suburban Site, Xianghe. Remote Sensing, 13(18), 3763. https://doi.org/10.3390/rs13183763










