Reduced-Dynamic Precise Orbit Determination of Haiyang-2B Altimetry Satellite Using a Refined Empirical Acceleration Model
Abstract
:1. Introduction
2. Spectral Analysis of HY-2B Empirical Accelerations
2.1. POD Processing and Models
2.2. Frequency Characteristics
2.3. Refined PEA Model of HY-2B
3. Improvements in HY-2B POD
3.1. Performance Analysis of the Refined PEA Model
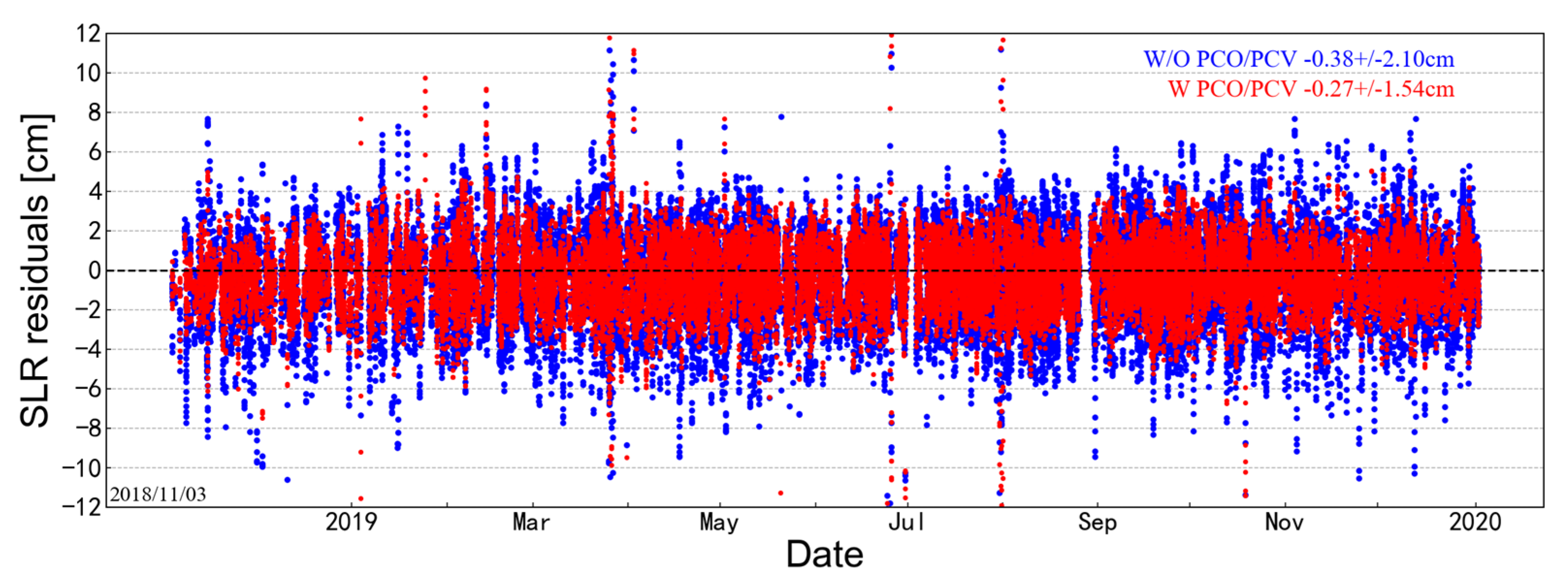
3.2. GPS Antenna Offset Calibration
3.3. Single-Receiver Ambiguity Resolution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NSOAS. HY-2: A Marine Remote Sensing Satellite Series Planned by China. 2021. Available online: http://www.nsoas.org.cn/index.html (accessed on 1 August 2021).
- Rudenko, S.; Neumayer, K.H.; Dettmering, D.; Esselborn, S.; Schone, T.; Raimondo, J.C. Improvements in Precise Orbits of Altimetry Satellites and Their Impact on Mean Sea Level Monitoring. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3382–3395. [Google Scholar] [CrossRef] [Green Version]
- Hackel, S.; Gisinger, C.; Balss, U.; Wermuth, M.; Montenbruck, O. Long-Term Validation of TerraSAR-X and TanDEM-X Orbit Solutions with Laser and Radar Measurements. Remote Sens. 2018, 10, 762. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Guo, X.; Qu, L.Z.; Zhao, Q.L. Precise Orbit Determination of FY-3C with Calibration of Orbit Biases in BeiDou GEO Satellites. Remote Sens. 2018, 10, 382. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Ries, J.C.; Davis, G.W.; Eanes, R.J.; Schutz, B.E.; Shum, C.K.; Watkins, M.M.; Marshall, J.A.; Nerem, R.S.; Putney, B.H.; et al. Precision Orbit Determination for Topex/Poseidon. J. Geophys. Res.-Oceans 1994, 99, 24383–24404. [Google Scholar] [CrossRef]
- Flohrer, C.; Otten, M.; Springer, T.; Dow, J. Generating precise and homogeneous orbits for Jason-1 and Jason-2. Adv. Space Res. 2011, 48, 152–172. [Google Scholar] [CrossRef]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: Orbit and network validation. J. Geod. 2018, 93, 2315–2334. [Google Scholar] [CrossRef] [Green Version]
- Strugarek, D.; Sosnica, K.; Arnold, D.; Jäggi, A.; Zajdel, R.; Bury, G.; Drozdzewski, M. Determination of Global Geodetic Parameters Using Satellite Laser Ranging Measurements to Sentinel-3 Satellites. Remote Sens. 2019, 11, 2282. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.C.; Guo, J.Y.; Zhou, M.S.; Jin, X.; Zhao, C.M.; Chang, X.T. Geometric solution method of SLR station coordinate based on multi-LEO satellites. Chin. J. Geophys. 2020, 63, 4333–4344. [Google Scholar] [CrossRef]
- Wu, S.C.; Yunck, T.P.; Thornton, C.L. Reduced-dynamic technique for precise orbit determination of low earth satellites. J. Guid. Control Dyn. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Li, M.; Li, W.W.; Shi, C.; Jiang, K.C.; Guo, X.; Dai, X.L.; Meng, X.G.; Yang, Z.D.; Yang, G.L.; Liao, M. Precise orbit determination of the Fengyun-3C satellite using onboard GPS and BDS observations. J. Geod. 2017, 91, 1313–1327. [Google Scholar] [CrossRef] [Green Version]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Mao, X.; Arnold, D.; Girardin, V.; Villiger, A.; Jäggi, A. Dynamic GPS-based LEO orbit determination with 1 cm precision using the Bernese GNSS Software. Adv. Space Res. 2021, 67, 788–805. [Google Scholar] [CrossRef]
- Montenbruck, O.; van Helleputte, T.; Kroes, R.; Gill, E. Reduced dynamic orbit determination using GPS code and carrier measurements. Aerosp. Sci. Technol. 2005, 9, 261–271. [Google Scholar] [CrossRef]
- Jiang, K.C.; Li, M.; Wang, M.; Zhao, Q.L.; Li, W.W. TJS-2 geostationary satellite orbit determination using onboard GPS measurements. GPS Solut. 2018, 22, 87. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations. J. Geod. 2018, 92, 711–726. [Google Scholar] [CrossRef] [Green Version]
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geod. 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Bock, H.; Jäggi, A.; Beutler, G.; Meyer, U. GOCE: Precise orbit determination for the entire mission. J. Geod. 2014, 88, 1047–1060. [Google Scholar] [CrossRef]
- Van den Ijssel, J.; Encarnação, J.; Doornbos, E.; Visser, P. Precise science orbits for the Swarm satellite constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; van den Ijssel, J.; Arnold, D. Reduced dynamic and kinematic precise orbit determination for the Swarm mission from 4 years of GPS tracking. GPS Solut. 2018, 22, 79. [Google Scholar] [CrossRef]
- Švehla, D.; Rothacher, M. Kinematic and reduced-dynamic precise orbit determination of low earth orbiters. Adv. Geosci. 2003, 1, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-Stochastic Orbit Modeling Techniques for Low-Earth Orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Hackel, S.; Montenbruck, O.; Steigenberger, P.; Balss, U.; Gisinger, C.; Eineder, M. Model improvements and validation of TerraSAR-X precise orbit determination. J. Geod. 2016, 91, 547–562. [Google Scholar] [CrossRef]
- Hackel, S. Refinement of Reduced-Dynamic Orbit Determination for Low Earth Satellites; Technische Universität München: Munich, Germany, 2019. [Google Scholar]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.X.; Zhang, Q.; Zhang, K.K.; Zhu, Y.T.; Zhang, W. Improving LEO precise orbit determination with BDS PCV calibration. GPS Solut. 2019, 23, 109. [Google Scholar] [CrossRef]
- Visser, P.N.A.M.; van den Ijssel, J.A.A. Calibration and validation of individual GOCE accelerometers by precise orbit determination. J. Geod. 2015, 90, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Peter, H.; Jäggi, A.; Fernández, J.; Escobar, D.; Ayuga, F.; Arnold, D.; Wermuth, M.; Hackel, S.; Otten, M.; Simons, W.; et al. Sentinel-1A—First precise orbit determination results. Adv. Space Res. 2017, 60, 879–892. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Schaer, S.; Villiger, A.; Arnold, D.; Dach, R.; Prange, L.; Jäggi, A. The CODE ambiguity-fixed clock and phase bias analysis products: Generation, properties, and performance. J. Geod. 2021, 95, 81. [Google Scholar] [CrossRef]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.-C. Zero-difference GPS ambiguity resolution at CNES–CLS IGS Analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Rebischung, P.; Schmid, R. IGS14/igs14.atx: A new framework for the IGS products. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Shako, R.; Förste, C.; Abrikosov, O.; Bruinsma, S.; Marty, J.-C.; Lemoine, J.-M.; Flechtner, F.; Neumayer, H.; Dahle, C. EIGEN-6C: A High-Resolution Global Gravity Combination Model Including GOCE Data. In Observation of the System Earth from Space—Champ, Grace, Goce and Future Missions; Flechtner, F., Sneeuw, N., Schuh, W.-D., Eds.; Advanced Technologies in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 155–161. [Google Scholar]
- Petit, G.; Luzum, B. IERS Conventions; Bureau International des Poids et Mesures: Sevres, France, 2010. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Standish, E.M. JPL Planetary and Lunar Ephemerides, DE405/LE405. Interoffice Memorandum: JPL IOM 312.F-98-048, 1998, August 26. Available online: ftp://ssd.jpl.nasa.gov/pub/eph/planets/ioms/de405.iom.pdf (accessed on 1 August 2021).
- McCarthy, D.D.; Petit, G. IERS Conventions (2003). IERS Tech. Note 2004, 32, 1. [Google Scholar]
- Vielberg, K.; Kusche, J. Extended forward and inverse modeling of radiation pressure accelerations for LEO satellites. J. Geod. 2020, 94, 43. [Google Scholar] [CrossRef] [Green Version]
- Bruinsma, S. The DTM-2013 thermosphere model. J. Space Weather Space Clim. 2015, 5, A1. [Google Scholar] [CrossRef] [Green Version]
- ILRS. SLRF2014 Station Coordinates. 2020. Available online: ftp://gdc.cddis.eosdis.nasa.gov/pub/slr/products/resource/SLRF2014_POS+VEL_2030.0_200325.snx (accessed on 1 August 2021).
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Hugentobler, U.; Montenbruck, O. Satellite Orbits and Attitude. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 59–90. [Google Scholar]
- Dewitte, S.; Clerbaux, N. Measurement of the Earth Radiation Budget at the Top of the Atmosphere—A Review. Remote Sens. 2017, 9, 1143. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Gill, E.; Lutze, F.H. Satellite Orbits: Models, Methods, and Applications. Appl. Mech. Rev. 2002, 55, B27. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Strugarek, D.; Sosnica, K.; Jäggi, A. Characteristics of GOCE orbits based on Satellite Laser Ranging. Adv. Space Res. 2019, 63, 417–431. [Google Scholar] [CrossRef]
- Strugarek, D.; Sośnica, K.; Zajdel, R.; Bury, G. Detector-specific issues in Satellite Laser Ranging to Swarm-A/B/C satellites. Measurement 2021, 182, 109786. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zelensky, N.P.; Rowlands, D.D.; Lemoine, F.G.; Williams, T.A. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue: Jason-1 Calibration/Validation. Mar. Geod. 2010, 26, 399–421. [Google Scholar] [CrossRef]
- Haines, B.; Bar-Sever, Y.; Bertiger, W.; Desai, S.; Willis, P. One-Centimeter Orbit Determination for Jason-1: New GPS-Based Strategies. Mar. Geod. 2004, 27, 299–318. [Google Scholar] [CrossRef]
- Zajdel, R.; Sosnica, K.; Bury, G. A New Online Service for the Validation of Multi-GNSS Orbits Using SLR. Remote Sens. 2017, 9, 1049. [Google Scholar] [CrossRef] [Green Version]
- Pearlman, M.; Arnold, D.; Davis, M.; Barlier, F.; Biancale, R.; Vasiliev, V.; Ciufolini, I.; Paolozzi, A.; Pavlis, E.C.; Sośnica, K.; et al. Laser geodetic satellites: A high-accuracy scientific tool. J. Geod. 2019, 93, 2181–2194. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, H.; Fan, W.; Zhou, X.; Chen, Q.; Jiang, W. Assessment of single-difference and track-to-track ambiguity resolution in LEO precise orbit determination. GPS Solut. 2021, 25, 62. [Google Scholar] [CrossRef]





| Model | Description |
|---|---|
| Observation model | |
| Observation | Undifferenced ionosphere-free code and carrier phase combinations |
| Interval and arc length | 30 s and 30 h |
| GPS orbit and clocks | CNES-CLS ‘GRG’ products; 30 s sampling |
| GPS satellite biases | CNES-CLS wide-lane satellite biases |
| GPS satellite PCO and PCV | IGS ATX models [33] |
| HY-2B attitude | Nominal |
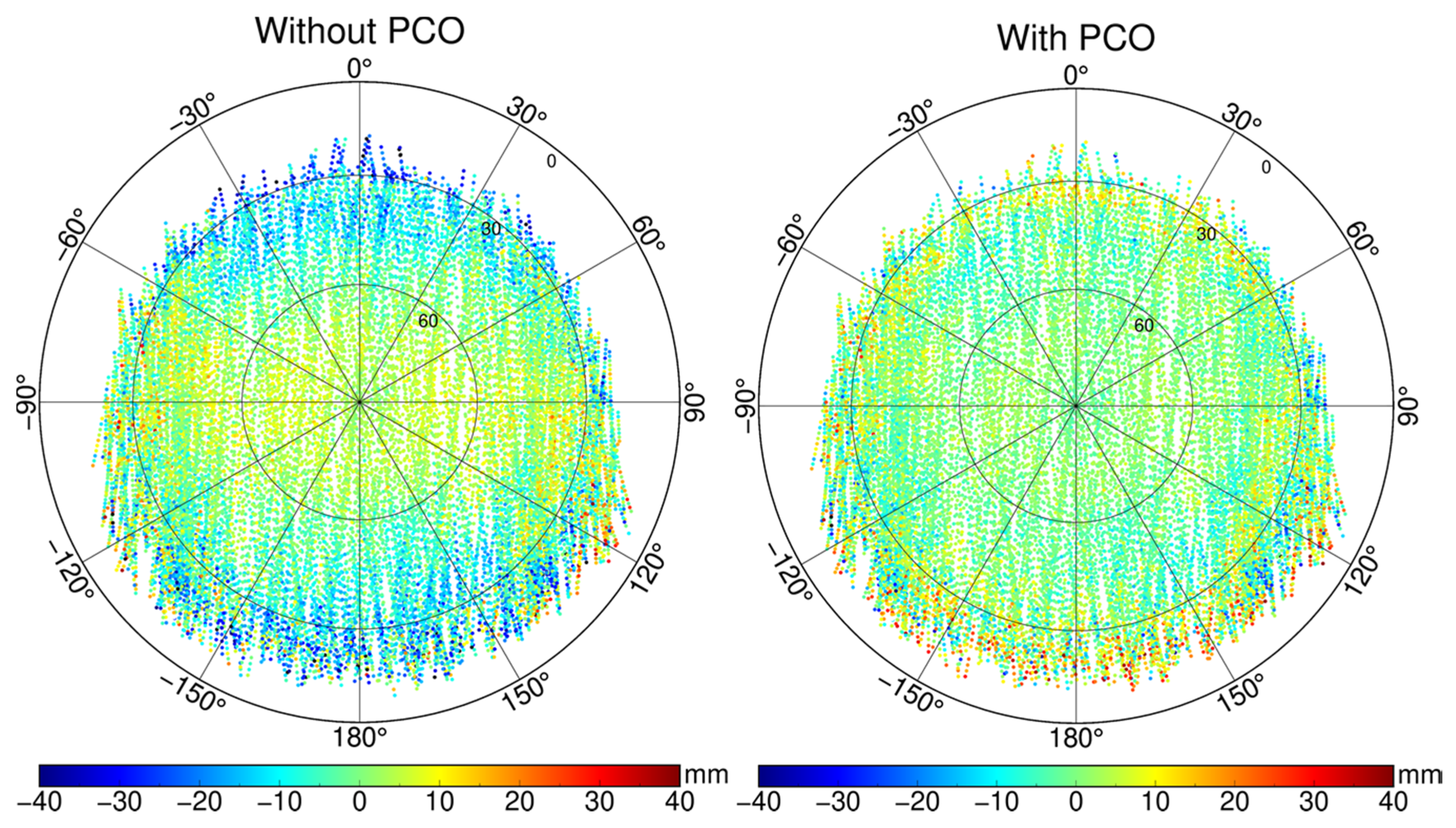
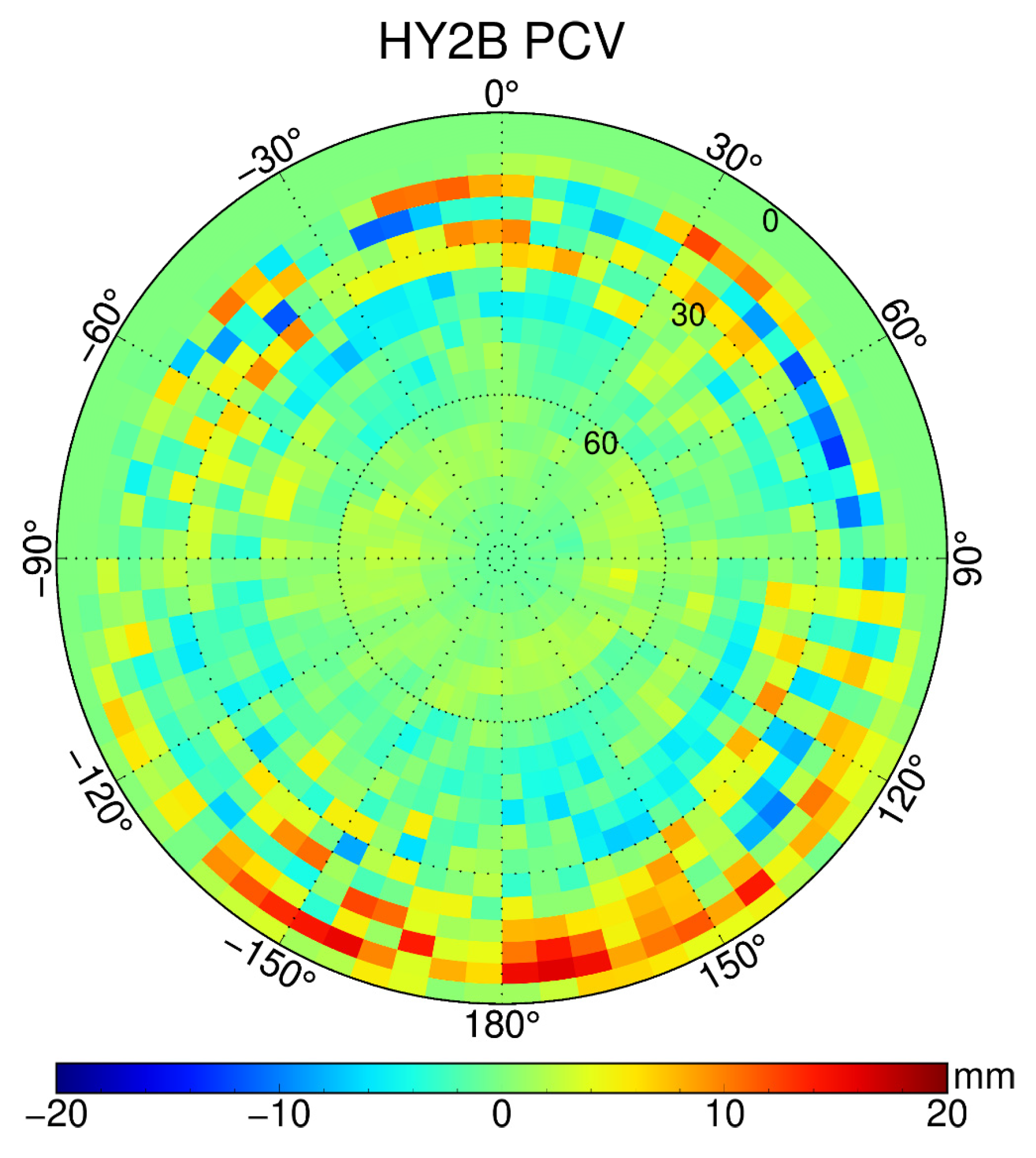
| HY-2B PCO and PCV | Corrected using calibrated values |
| Dynamic model | |
| Earth gravity | EIGEN6C (120 × 120) [34] |
| Solid Earth and pole tides | IERS 2010 conventions [35] |
| Ocean tides | FES 2004 (30 × 30) [36] |
| N-body disturbance | JPL DE405 [37] |
| Relativity | IERS 2003 [38] |
| Solar radiation | 13-plate macro-model, radiation pressure coefficients (VIS and IR) [39] |
| Atmospheric drag | 13-plate macro-model, atmospheric density model adopting DTM-2013 [40] |
| Empirical acceleration | Piecewise periodic acceleration |
| Estimated parameters | |
| Initial state | Position and velocity at the initial epoch |
| Receiver clock offset | Each epoch as white noise |
| Phase ambiguities | Each continuous tracking arc as a float |
| Solar radiation coefficients | One per 30 h arc |
| Drag coefficients | One per 180 min |
| Empirical coefficients | One per 180 min, amplitudes of periodic accelerations acting on the along- and cross-track directions |
| SLR validation | |
| Station coordinates | SLRF2014 [41] |
| Ocean tide loading | FES 2004 [36] |
| Tropospheric delay | Mendes and Pavlis [42] |
| Relativity | Space-time curvature correction |
| Solution Type | Along-Track | Cross-Track | Radial | |||
|---|---|---|---|---|---|---|
| Periodic Acc. | Constant Acc. | Periodic Acc. | Constant Acc. | Periodic Acc. | Constant Acc. | |
| 110 | 1 CPR | No | 1 CPR | No | No | No |
| 410 | 4 CPR | No | 1 CPR | No | No | No |
| 460 + C | 4 CPR | No | 5.5 CPR | Yes | No | No |
| 111 | 1 CPR | No | 1 CPR | No | 1 CPR | No |
| 412 | 4 CPR | No | 1 CPR | No | 2 CPR | No |
| 462 + C | 4 CPR | No | 5.5 CPR | Yes | 2 CPR | No |
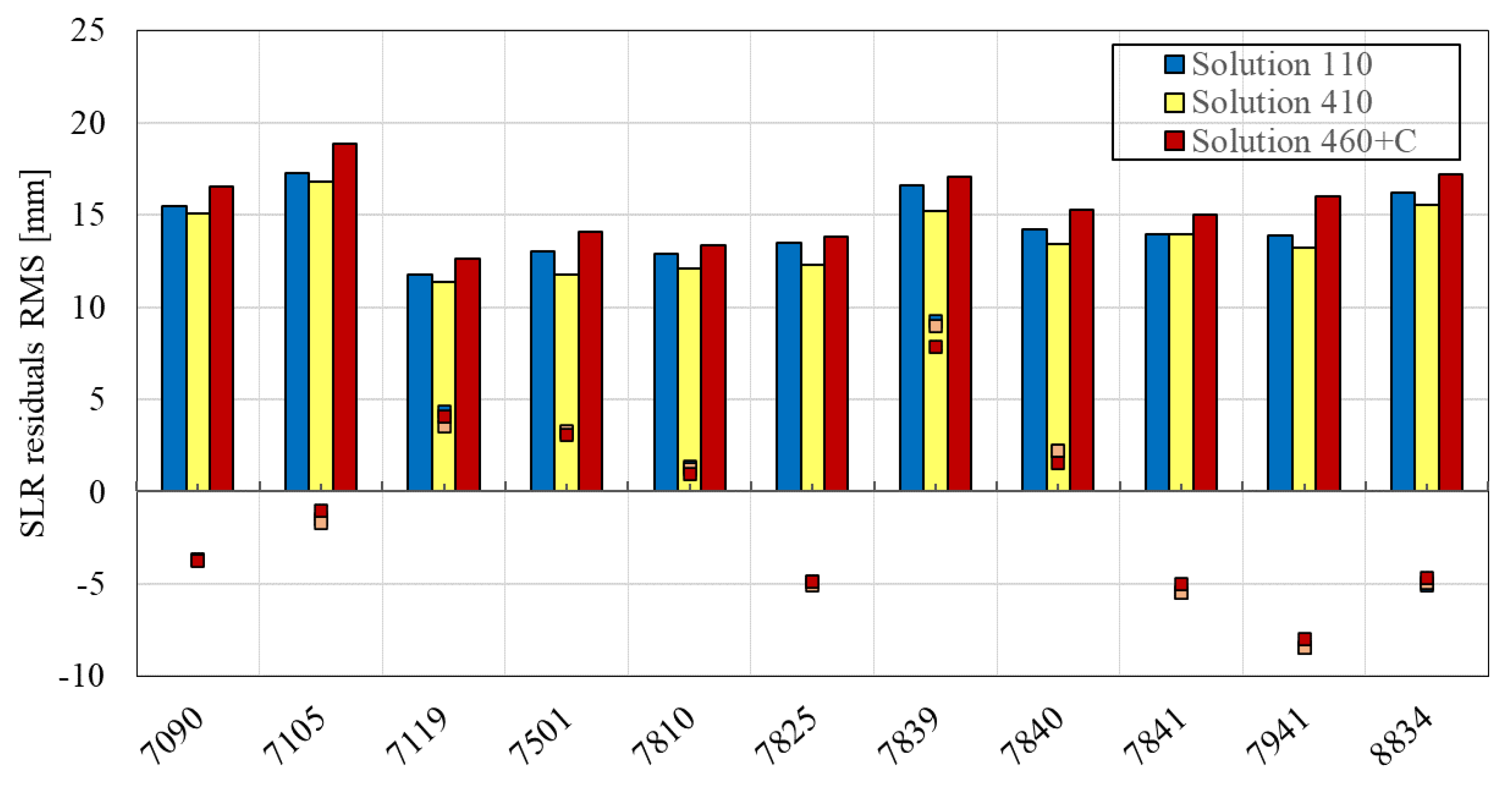
| PEA Solution | Mean (mm) | RMS (mm) | Note |
|---|---|---|---|
| 110 | 2.6 | 16.6 | r |
| 410 | −1.5 | 15.7 | r |
| 460 + C | −2.0 | 16.5 | r |
| 111 | −4.4 | 18.1 | |
| 412 | −5.4 | 18.5 | |
| 462 + C | −2.1 | 17.5 |
| Item | Reference (x, y, z) (mm) | Notes |
|---|---|---|
| CoM location | (+1332.000, −8.600, +3.400) | Nov. 2018 |
| GPS antenna location | (+347.290, −175.140, −1372.680) | Main antenna (GPS a) |
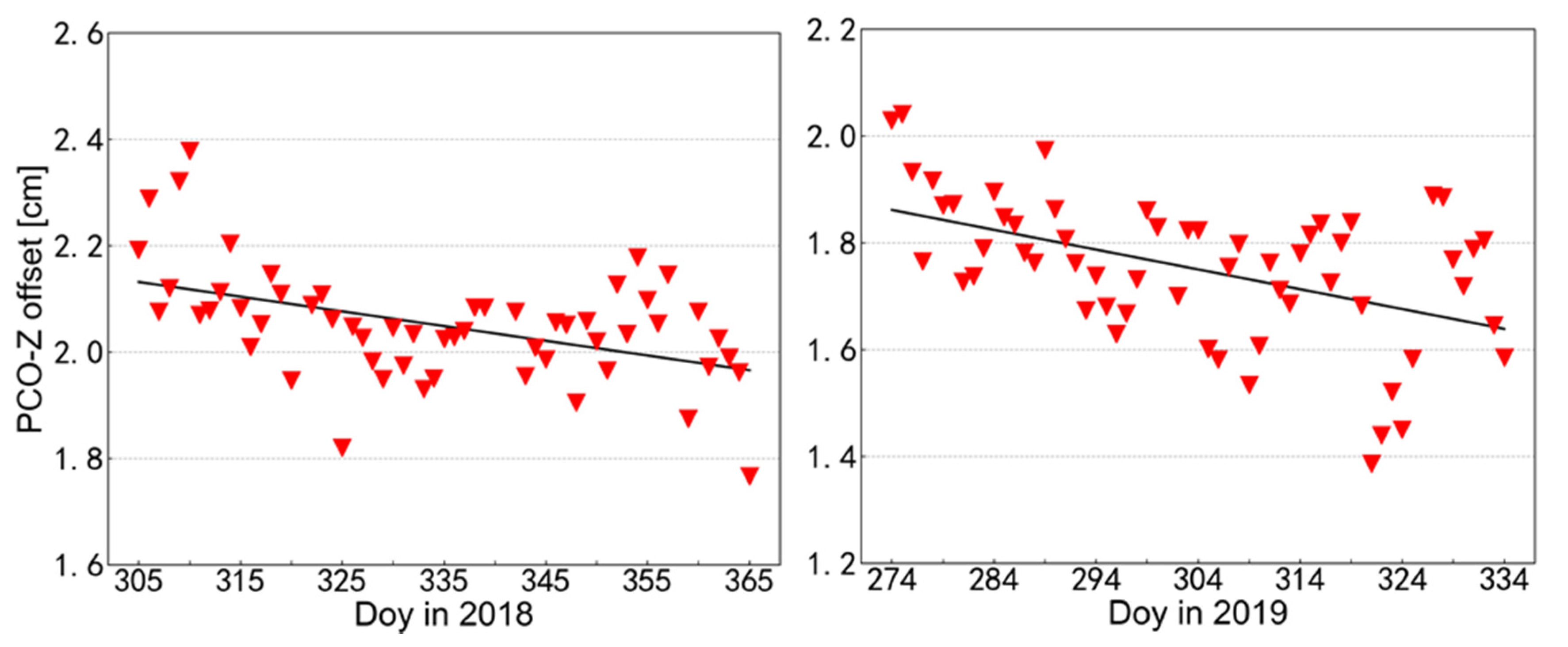
| GPS antenna PCO | (+0.0, +0.0, +20.0) | Estimated PCO-offset valid for ionosphere-free L1/L2 |
| Station (ID) | Nnp | Float Amb. | Amb. Fixed | ||
|---|---|---|---|---|---|
| Mean (mm) | STD (mm) | Mean (mm) | STD (mm) | ||
| Yarragadee (7090) | 10,496 | −3.3 | 16.0 | −3.3 | 13.7 |
| Greenbelt (7105) | 3102 | −4.2 | 17.3 | −4.0 | 14.8 |
| Haleakala (7119) | 1010 | 3.2 | 11.8 | 3.3 | 10.2 |
| Hartebeest (7501) | 2265 | 3.4 | 15.6 | 1.9 | 11.3 |
| Zimmerwald (7810) | 3990 | −0.4 | 12.4 | −1.1 | 10.2 |
| Mt. Stromlo (7825) | 5447 | −5.1 | 13.3 | −5.5 | 9.9 |
| Graz (7839) | 2224 | 7.2 | 16.2 | 6.2 | 13.7 |
| Herstmonceux (7840) | 2726 | −0.2 | 13.8 | −1.4 | 12.2 |
| Potsdam (7841) | 1212 | −8.8 | 13.6 | −9.3 | 11.7 |
| Matera (7941) | 2024 | −9.8 | 13.8 | −9.7 | 11.4 |
| Wettzel (8834) | 1730 | −8.2 | 17.5 | −8.8 | 13.7 |
| Total | 36,226 | −2.3 | 15.7 | −2.7 | 13.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, M.; Jiang, K.; Li, W.; Qin, G.; Zhao, Q.; Peng, H.; Lin, M. Reduced-Dynamic Precise Orbit Determination of Haiyang-2B Altimetry Satellite Using a Refined Empirical Acceleration Model. Remote Sens. 2021, 13, 3702. https://doi.org/10.3390/rs13183702
Wang Y, Li M, Jiang K, Li W, Qin G, Zhao Q, Peng H, Lin M. Reduced-Dynamic Precise Orbit Determination of Haiyang-2B Altimetry Satellite Using a Refined Empirical Acceleration Model. Remote Sensing. 2021; 13(18):3702. https://doi.org/10.3390/rs13183702
Chicago/Turabian StyleWang, Youcun, Min Li, Kecai Jiang, Wenwen Li, Geer Qin, Qile Zhao, Hailong Peng, and Mingsen Lin. 2021. "Reduced-Dynamic Precise Orbit Determination of Haiyang-2B Altimetry Satellite Using a Refined Empirical Acceleration Model" Remote Sensing 13, no. 18: 3702. https://doi.org/10.3390/rs13183702
APA StyleWang, Y., Li, M., Jiang, K., Li, W., Qin, G., Zhao, Q., Peng, H., & Lin, M. (2021). Reduced-Dynamic Precise Orbit Determination of Haiyang-2B Altimetry Satellite Using a Refined Empirical Acceleration Model. Remote Sensing, 13(18), 3702. https://doi.org/10.3390/rs13183702









