Simulating the Leaf Area Index of Rice from Multispectral Images
Abstract
:1. Introduction
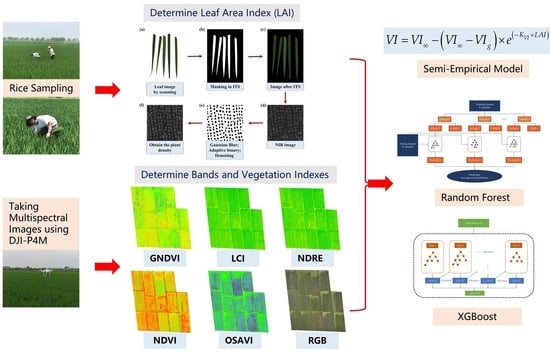
2. Materials and Methods
2.1. Study Site
2.2. Data Collection
2.2.1. Multispectral Images
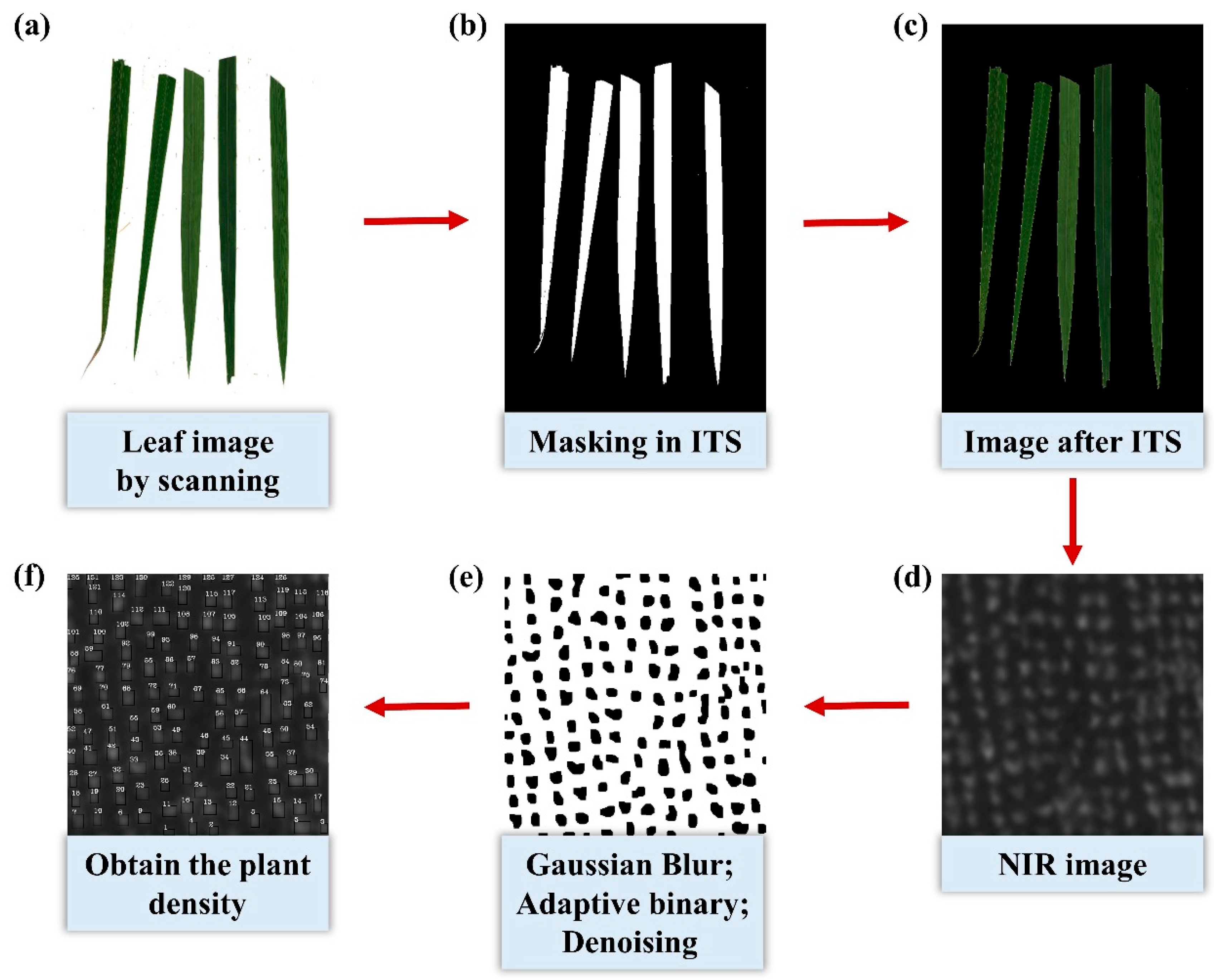
2.2.2. Plant Sampling and Leaf Area Index
2.3. Semi-Empirical Model (SEM)
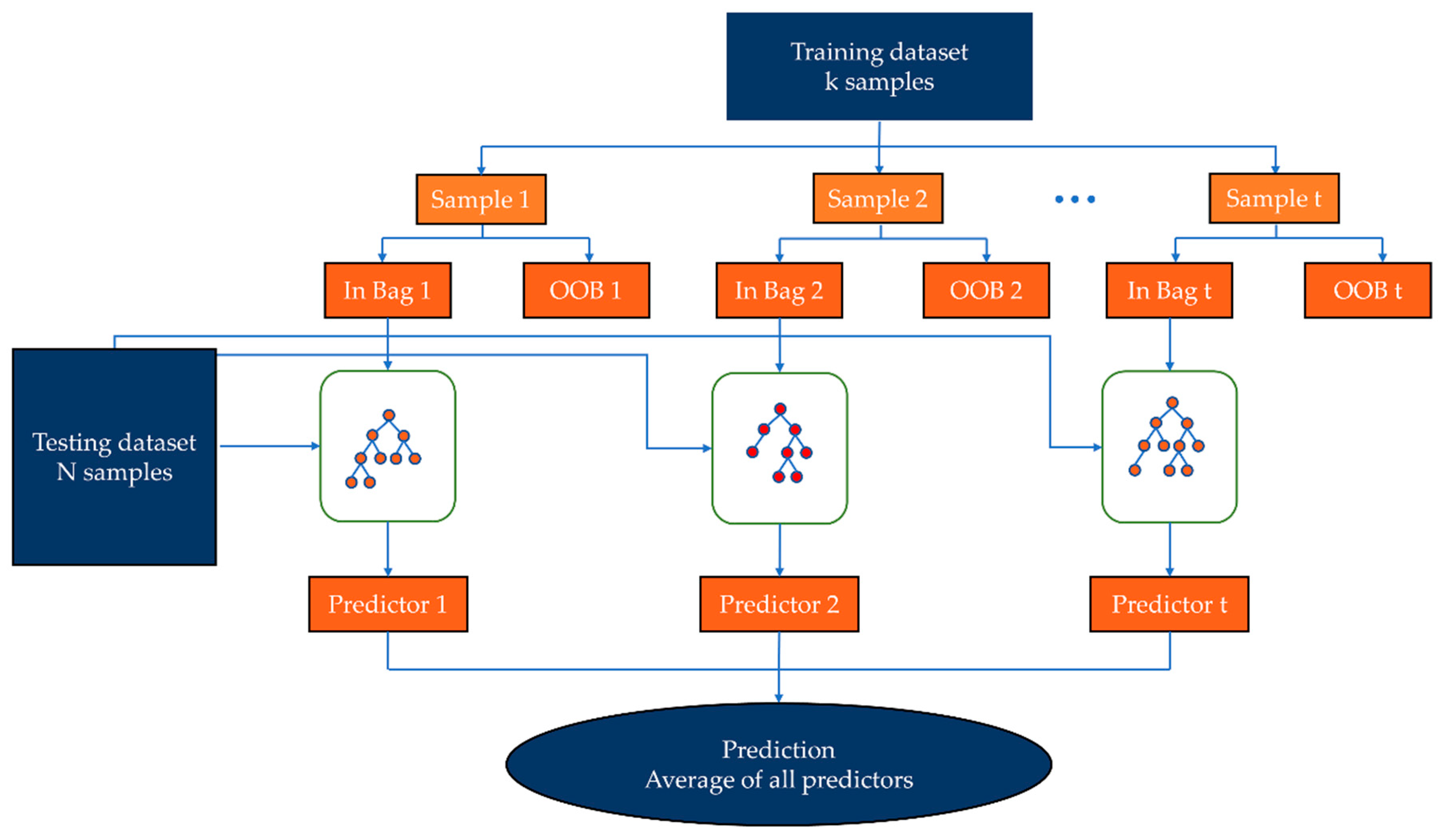
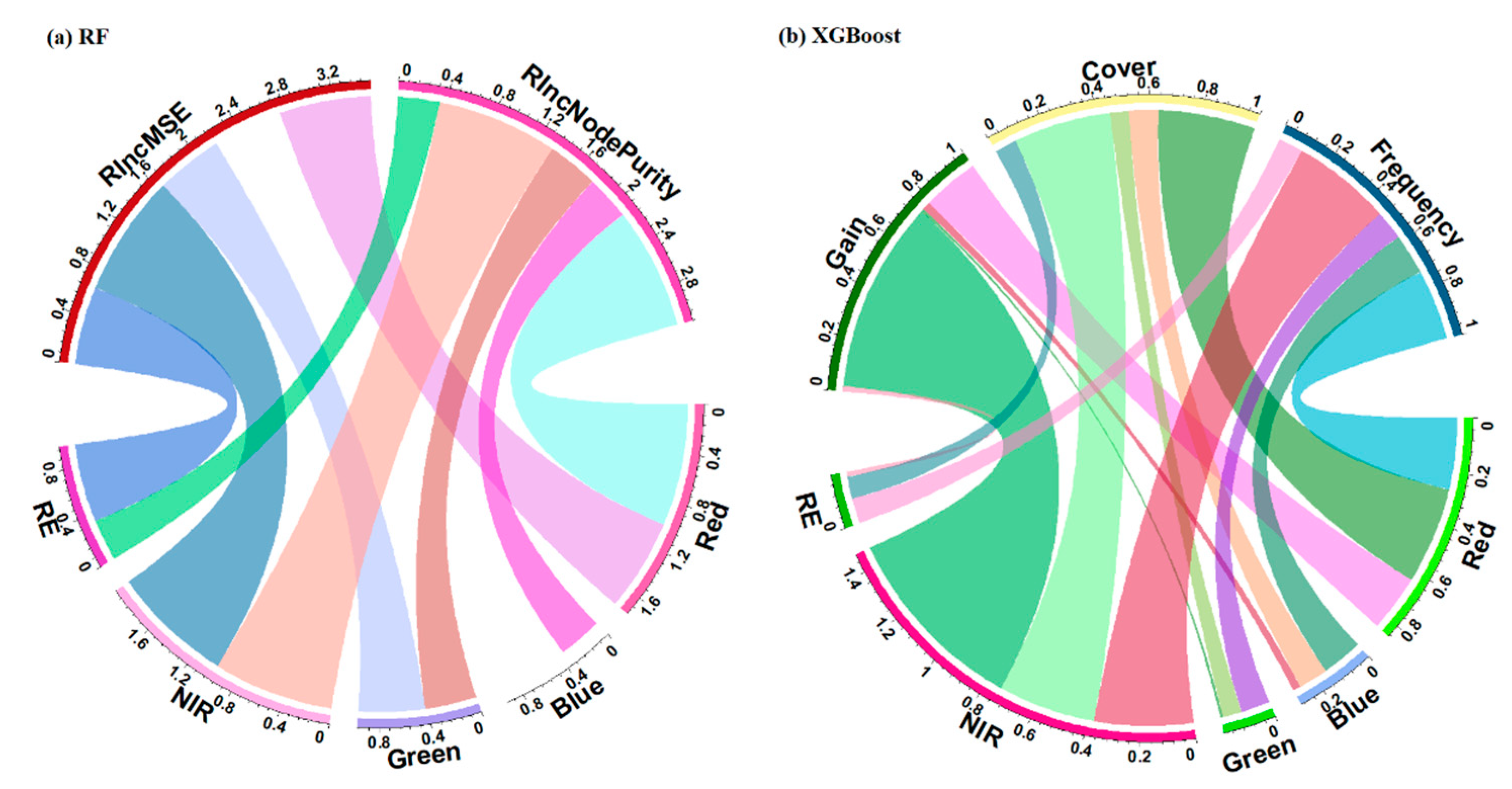
2.4. Random Forest Model (RF)
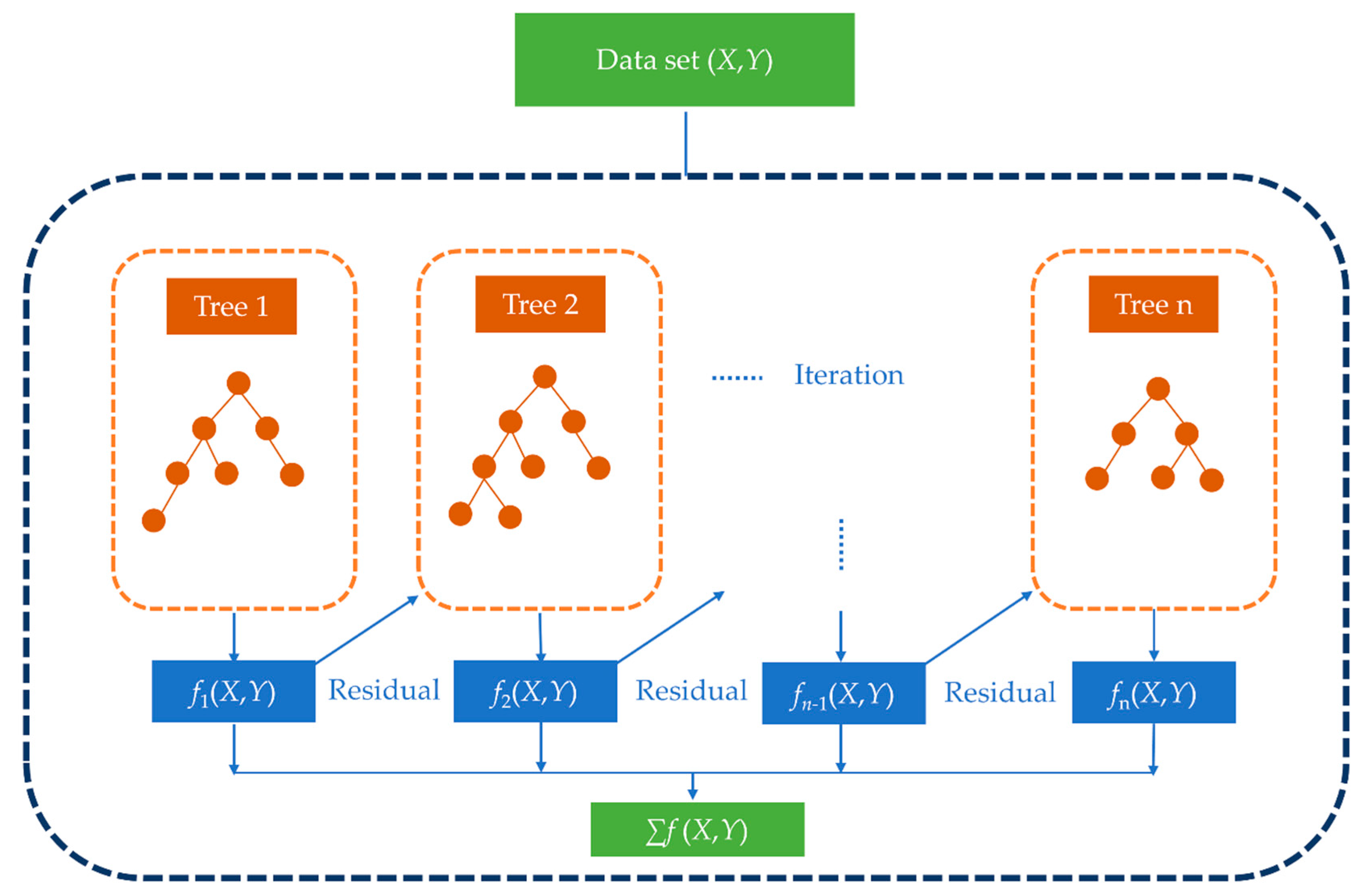
2.5. Extreme Gradient Boosting Model (XGBoost)
2.6. Statistical Evaluation
3. Results and Discussion
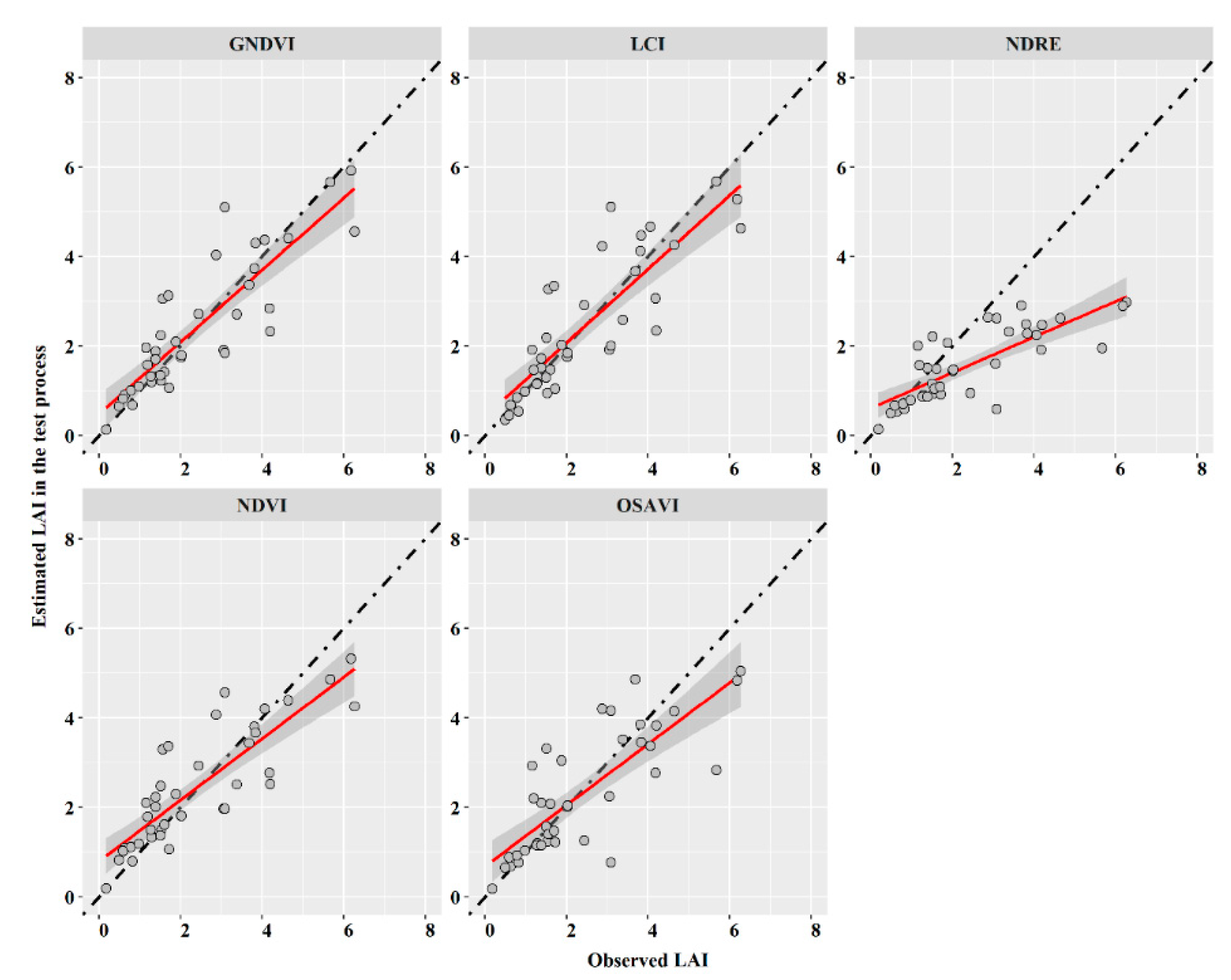
3.1. Performance of the Semi-Empirical Model (SEM)
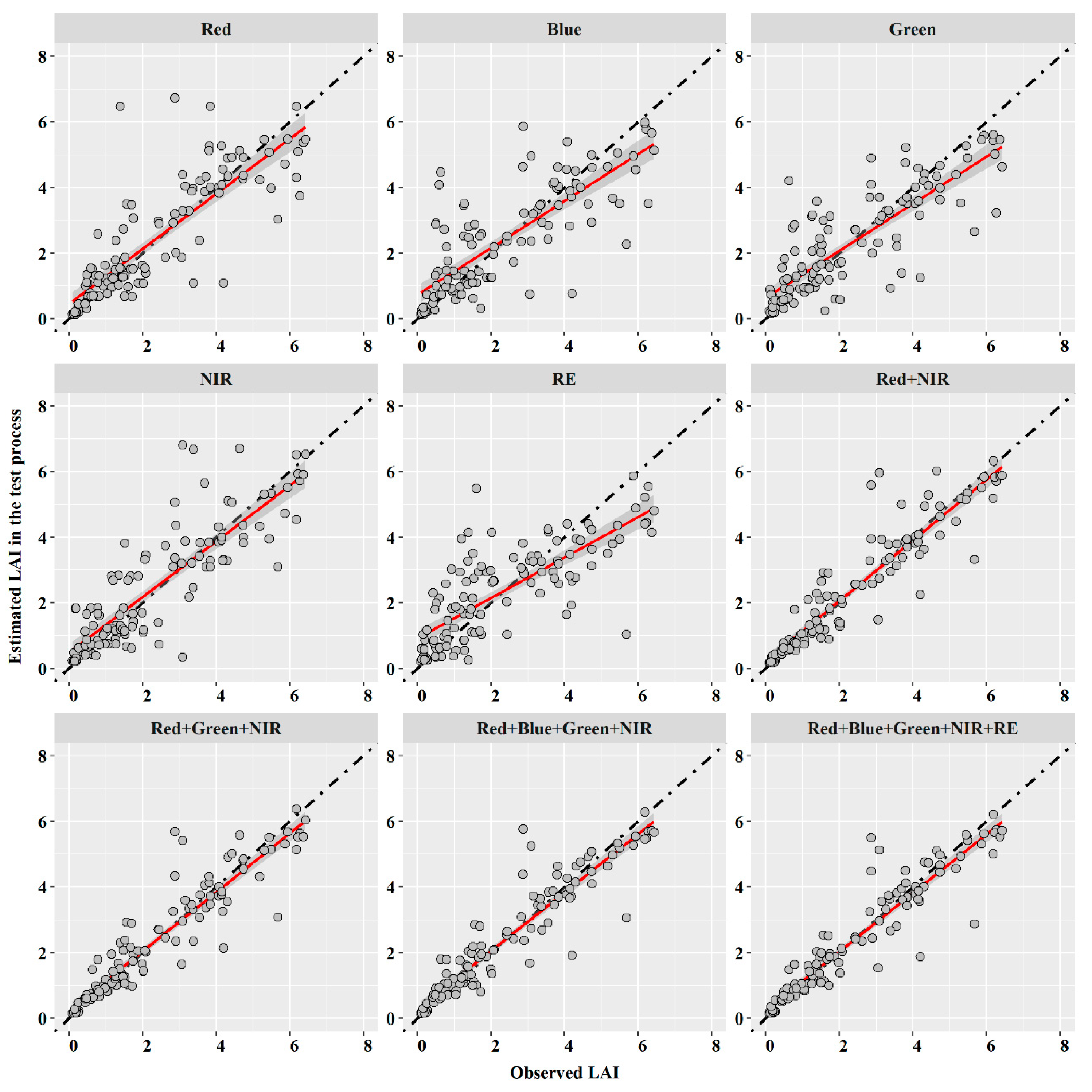
3.2. Machine Learning Models with Multispectral Band
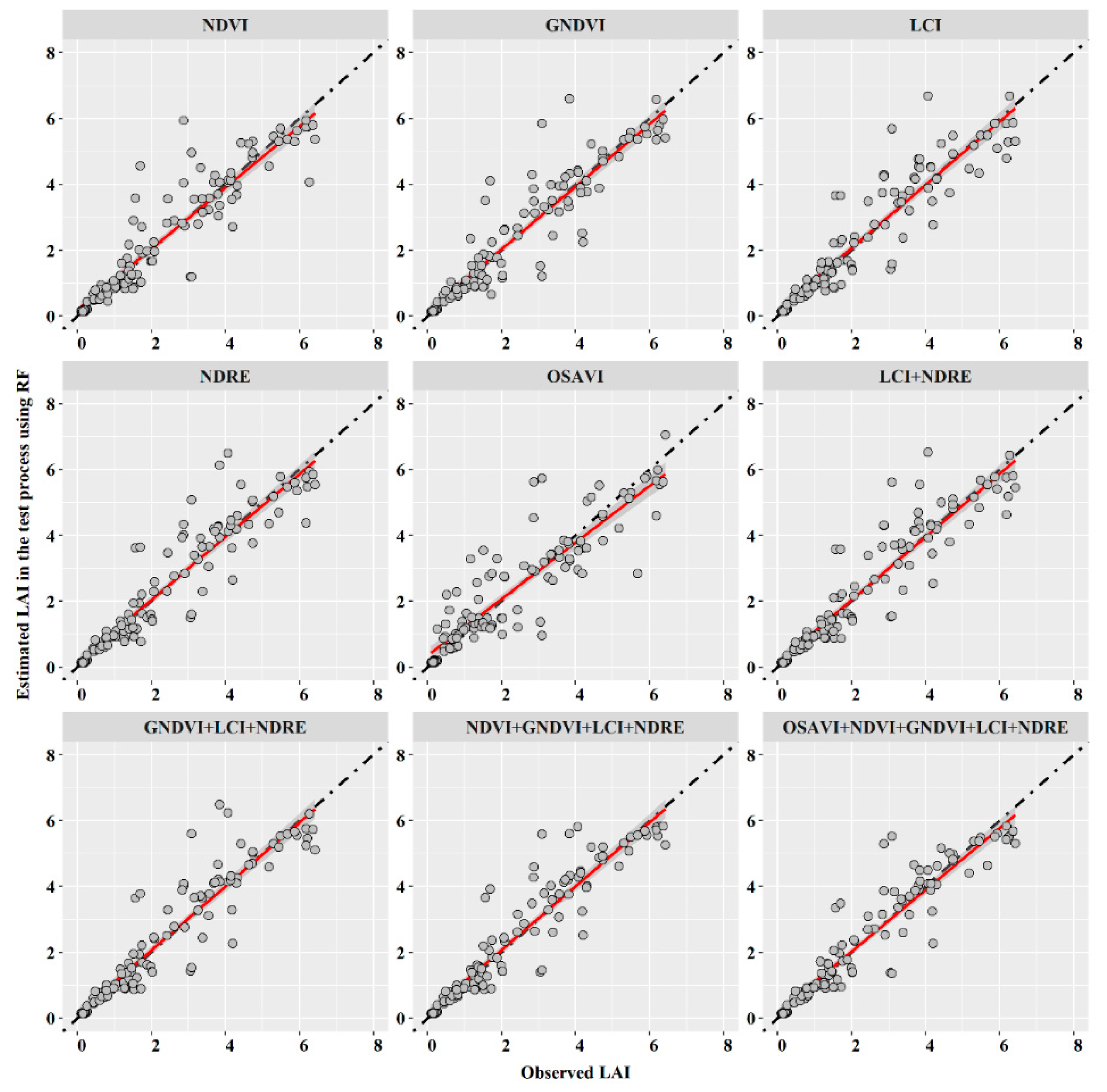
3.3. Machine Learning Models with Vegetation Index
3.4. Machine Learning Models with Multispectral Band and Vegetation Index
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Watson, D.J. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years. Ann. Bot. 1947, 11, 41–76. [Google Scholar] [CrossRef]
- Brown, L.A.; Meier, C.; Morris, H.; Pastor-Guzman, J.; Bai, G.; Lerebourg, C.; Gobron, N.; Lanconelli, C.; Clerici, M.; Dash, J. Evaluation of global leaf area index and fraction of absorbed photosynthetically active radiation products over North America using Copernicus Ground Based Observations for Validation data. Remote Sens. Environ. 2020, 247, 111935. [Google Scholar] [CrossRef]
- Kanniah, K.; Kang, C.; Sharma, S.; Amir, A. Remote Sensing to Study Mangrove Fragmentation and Its Impacts on Leaf Area Index and Gross Primary Productivity in the South of Peninsular Malaysia. Remote Sens. 2021, 13, 1427. [Google Scholar] [CrossRef]
- Gan, R.; Zhang, Y.; Shi, H.; Yang, Y.; Eamus, D.; Cheng, L.; Chiew, F.H.; Yu, Q. Use of satellite leaf area index estimating evapotranspiration and gross assimilation for Australian ecosystems. Ecohydrol 2018, 11, e1974. [Google Scholar] [CrossRef]
- Lei, G.; Zeng, W.; Jiang, Y.; Ao, C.; Wu, J.; Huang, J. Sensitivity analysis of the SWAP (Soil-Water-Atmosphere-Plant) model under different nitrogen applications and root distributions in saline soils. Pedosphere 2021, 31, 807–821. [Google Scholar] [CrossRef]
- Zhu, J.; Zeng, W.; Ma, T.; Lei, G.; Zha, Y.; Fang, Y.; Wu, J.; Huang, J. Testing and Improving the WOFOST Model for Sunflower Simulation on Saline Soils of Inner Mongolia, China. Agronomy 2018, 8, 172. [Google Scholar] [CrossRef] [Green Version]
- Zeng, W.; Xu, C.; Wu, J.; Huang, J. Sunflower seed yield estimation under the interaction of soil salinity and nitrogen application. Field Crop. Res. 2016, 198, 1–15. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part, I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Z.; Tao, F. Improving regional winter wheat yield estimation through assimilation of phenology and leaf area index from remote sensing data. Eur. J. Agron. 2018, 101, 163–173. [Google Scholar] [CrossRef]
- Srinet, R.; Nandy, S.; Patel, N. Estimating leaf area index and light extinction coefficient using Random Forest regression algorithm in a tropical moist deciduous forest, India. Ecol. Informatics 2019, 52, 94–102. [Google Scholar] [CrossRef]
- Bsaibes, A.; Courault, D.; Baret, F.; Weiss, M.; Olioso, A.; Jacob, F.; Hagolle, O.; Marloie, O.; Bertrand, N.; Desfond, V.; et al. Albedo and LAI estimates from FORMOSAT-2 data for crop monitoring. Remote Sens. Environ. 2009, 113, 716–729. [Google Scholar] [CrossRef]
- Qu, Y.; Han, W.; Ma, M. Retrieval of a Temporal High-Resolution Leaf Area Index (LAI) by Combining MODIS LAI and ASTER Reflectance Data. Remote Sens. 2014, 7, 195–210. [Google Scholar] [CrossRef]
- Jafari, M.; Keshavarz, A. Improving CERES-Wheat Yield Forecasts by Assimilating Dynamic Landsat-Based Leaf Area Index: A Case Study in Iran. J. Indian Soc. Remote Sens. 2021, 1–14. [Google Scholar] [CrossRef]
- Dehkordi, R.H.; Denis, A.; Fouche, J.; Burgeon, V.; Cornelis, J.T.; Tychon, B.; Gomez, E.P.; Meersmans, J. Remotely-sensed assessment of the impact of century-old biochar on chicory crop growth using high-resolution UAV-based imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102147. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, J.; Sudduth, K.A.; Kitchen, N.R. Estimation of maize yield and effects of variable-rate nitrogen application using UAV-based RGB imagery. Biosyst. Eng. 2020, 189, 24–35. [Google Scholar] [CrossRef]
- Yuan, M.; Burjel, J.C.; Martin, N.F.; Isermann, J.; Goeser, N.; Pittelkow, C.M. Advancing on-farm research with UAVs: Cover crop effects on crop growth and yield. Agron. J. 2021, 113, 1071–1083. [Google Scholar] [CrossRef]
- Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of Crop Growth Parameters Using UAV-Based Hyperspectral Remote Sensing Data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, B.; Ferraz, G.A.E.S.; dos Santos, L.M.; Santana, L.; Marin, D.B.; Rossi, G.; Conti, L. Application of RGB Images Obtained by UAV in Coffee Farming. Remote Sens. 2021, 13, 2397. [Google Scholar] [CrossRef]
- Apolo-Apolo, O.E.; Pérez-Ruiz, M.; Martínez-Guanter, J.; Egea, G. A Mixed Data-Based Deep Neural Network to Estimate Leaf Area Index in Wheat Breeding Trials. Agronomy 2020, 10, 175. [Google Scholar] [CrossRef] [Green Version]
- Demarez, V.; Duthoit, S.; Baret, F.; Weiss, M.; Dedieu, G. Estimation of leaf area and clumping indexes of crops with hemispherical photographs. Agric. For. Meteorol. 2008, 148, 644–655. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Ali, H.; Ur Rehman, A.; Khan, R.J.Z.; Ahmad, W.; Fatima, Z.; Abbas, G.; Irfan, M.; Ali, H.; Khan, M.A. Measuring leaf area of winter cereals by different techniques: A comparison. Pak. J. Life Soc. Sci 2015, 13, 117–125. [Google Scholar]
- Yao, X.; Wang, N.; Liu, Y.; Cheng, T.; Tian, Y.; Chen, Q.; Zhu, Y. Estimation of Wheat LAI at Middle to High Levels Using Unmanned Aerial Vehicle Narrowband Multispectral Imagery. Remote Sens. 2017, 9, 1304. [Google Scholar] [CrossRef] [Green Version]
- Qi, H.; Zhu, B.; Wu, Z.; Liang, Y.; Li, J.; Wang, L.; Chen, T.; Lan, Y.; Zhang, L. Estimation of Peanut Leaf Area Index from Unmanned Aerial Vehicle Multispectral Images. Sensors 2020, 20, 6732. [Google Scholar] [CrossRef]
- Peñuelas, J.; Isla, R.; Filella, I.; Araus, J.L. Visible and Near-Infrared Reflectance Assessment of Salinity Effects on Barley. Crop. Sci. 1997, 37, 198–202. [Google Scholar] [CrossRef]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Steven, M.D. The Sensitivity of the OSAVI Vegetation Index to Observational Parameters. Remote Sens. Environ. 1998, 63, 49–60. [Google Scholar] [CrossRef]
- Du, C.; Meng, Q.; Qin, Q.; Dong, H. The development of a new model on vegetation water content. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, Australia, 21–26 July 2013. [Google Scholar] [CrossRef]
- Miura, T.; Huete, A.R.; Yoshioka, H.; Holben, B.N. An error and sensitivity analysis of atmospheric resistant vegetation indices derived from dark target-based atmospheric correction. Remote Sens. Environ. 2001, 78, 284–298. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Stamatiadis, S.; Taskos, D.; Tsadilas, C.; Christofides, C.; Tsadila, E.; Schepers, J.S. Relation of Ground-Sensor Canopy Reflectance to Biomass Production and Grape Color in Two Merlot Vineyards. Am. J. Enol. Vitic. 2006, 57, 415–422. [Google Scholar]
- Liu, C.; Shan, Y.; Nepf, H. Impact of Stem Size on Turbulence and Sediment Resuspension Under Unidirectional Flow. Water Resour. Res. 2021, 57, e2020WR028620. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Lama, G.; Crimaldi, M.; Pasquino, V.; Padulano, R.; Chirico, G. Bulk Drag Predictions of Riparian Arundo donax Stands through UAV-Acquired Multispectral Images. Water 2021, 13, 1333. [Google Scholar] [CrossRef]
- Peng, X.; Han, W.; Ao, J.; Wang, Y. Assimilation of LAI Derived from UAV Multispectral Data into the SAFY Model to Estimate Maize Yield. Remote Sens. 2021, 13, 1094. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Gahrouei, O.R.; McNairn, H.; Hosseini, M.; Homayouni, S. Estimation of Crop Biomass and Leaf Area Index from Multitemporal and Multispectral Imagery Using Machine Learning Approaches. Can. J. Remote Sens. 2020, 46, 84–99. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Daloye, A.M.; Erkbol, H.; Fritschi, F.B. Crop Monitoring Using Satellite/UAV Data Fusion and Machine Learning. Remote Sens. 2020, 12, 1357. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Han, Y.; Wu, J.; Zhai, B.; Pan, Y.; Huang, G.; Wu, L.; Zeng, W. Coupling a Bat Algorithm with XGBoost to Estimate Reference Evapotranspiration in the Arid and Semiarid Regions of China. Adv. Meteorol. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Ma, X.; Zhou, H.; Zhang, F. Hybrid support vector machines with heuristic algorithms for prediction of daily diffuse solar radiation in air-polluted regions. Renew. Energy 2020, 145, 2034–2045. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Zeng, W.; Wang, X.; Zou, H. Empirical and machine learning models for predicting daily global solar radiation from sunshine duration: A review and case study in China. Renew. Sustain. Energy Rev. 2019, 100, 186–212. [Google Scholar] [CrossRef]
- Setyawan, T.A.; Riwinanto, S.A.; Suhendro; Helmy; Nursyahid, A.; Nugroho, A.S. Comparison of HSV and LAB Color Spaces for Hydroponic Monitoring System. In Proceedings of the 2018 5th International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Hotel Santika Premier, Indonesia, 26–28 September 2018; pp. 347–352. [Google Scholar]
- Tang, H.; Brolly, M.; Zhao, F.; Strahler, A.H.; Schaaf, C.L.; Ganguly, S.; Zhang, G.; Dubayah, R. Deriving and validating Leaf Area Index (LAI) at multiple spatial scales through lidar remote sensing: A case study in Sierra National Forest, CA. Remote Sens. Environ. 2014, 143, 131–141. [Google Scholar] [CrossRef]
- Myung, J.; Lee, W. Adaptive Binary Splitting: A RFID Tag Collision Arbitration Protocol for Tag Identification. Mob. Networks Appl. 2006, 11, 711–722. [Google Scholar] [CrossRef]
- Dorafshan, S.; Thomas, R.J.; Maguire, M. Comparison of deep convolutional neural networks and edge detectors for image-based crack detection in concrete. Construct. Build. Mater. 2018, 186, 1031–1045. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Jégo, G. Assessment of vegetation indices for regional crop green LAI estimation from Landsat images over multiple growing seasons. Remote Sens. Environ. 2012, 123, 347–358. [Google Scholar] [CrossRef]
- Jin, H.; Eklundh, L. A physically based vegetation index for improved monitoring of plant phenology. Remote Sens. Environ. 2014, 152, 512–525. [Google Scholar] [CrossRef]
- Xiao, J.; Davis, K.J.; Urban, N.M.; Keller, K. Uncertainty in model parameters and regional carbon fluxes: A model-data fusion approach. Agric. For. Meteorol. 2014, 189–190, 175–186. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Dewi, C.; Chen, R.-C. Random forest and support vector machine on features selection for regression analysis. Int. J. Innov. Comput. Inf. Control. 2019, 15, 2027–2037. [Google Scholar] [CrossRef]
- Kearns, M.; Valiant, L. Cryptographic limitations on learning Boolean formulae and finite automata. J. ACM 1994, 41, 67–95. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, D.; Song, C.; Wang, L.; Song, J.; Guan, L.; Zhang, M. Interpretable Learning Algorithm Based on XGBoost for Fault Prediction in Optical Network. In Proceedings of the Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 8–12 March 2020. [Google Scholar]
- Gonsamo, A. Leaf area index retrieval using gap fractions obtained from high resolution satellite data: Comparisons of approaches, scales and atmospheric effects. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 233–248. [Google Scholar] [CrossRef]
- Li, H.; Liu, G.; Liu, Q.; Chen, Z.; Huang, C. Retrieval of Winter Wheat Leaf Area Index from Chinese GF-1 Satellite Data Using the PROSAIL Model. Sensors 2018, 18, 1120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, F.-M.; Huang, J.-F.; Tang, Y.-L.; Wang, X.-Z. New Vegetation Index and Its Application in Estimating Leaf Area Index of Rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Milas, A.S.; Romanko, M.; Reil, P.; Abeysinghe, T.; Marambe, A. The importance of leaf area index in mapping chlorophyll content of corn under different agricultural treatments using UAV images. Int. J. Remote Sens. 2018, 39, 5415–5431. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crop. Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Zhang, K.; Ge, X.; Shen, P.; Li, W.; Liu, X.; Cao, Q.; Zhu, Y.; Cao, W.; Tian, Y. Predicting Rice Grain Yield Based on Dynamic Changes in Vegetation Indexes during Early to Mid-Growth Stages. Remote Sens. 2019, 11, 387. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Nguy-Robertson, A.; Arkebauer, T.; Gitelson, A.A. Assessment of Canopy Chlorophyll Content Retrieval in Maize and Soybean: Implications of Hysteresis on the Development of Generic Algorithms. Remote Sens. 2017, 9, 226. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Molnár, V.É.; Simon, E.; Tóthmérész, B.; Ninsawat, S.; Szabó, S. Air pollution induced vegetation stress—The Air Pollution Tolerance Index as a quick tool for city health evaluation. Ecol. Indic. 2020, 113, 106234. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Myneni, R.; Williams, D. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Antipov, E.A.; Pokryshevskaya, E.B. Mass appraisal of residential apartments: An application of Random forest for valuation and a CART-based approach for model diagnostics. Expert Syst. Appl. 2012, 39, 1772–1778. [Google Scholar] [CrossRef] [Green Version]
- Zarco-Tejada, P.; Miller, J.; Morales, A.; Berjón, A.; Agüera-Vega, J. Hyperspectral indices and model simulation for chlorophyll estimation in open-canopy tree crops. Remote Sens. Environ. 2004, 90, 463–476. [Google Scholar] [CrossRef]
- Wang, H.; Yan, H.; Zeng, W.; Lei, G.; Ao, C.; Zha, Y. A novel nonlinear Arps decline model with salp swarm algorithm for predicting pan evaporation in the arid and semi-arid regions of China. J. Hydrol. 2020, 582, 124545. [Google Scholar] [CrossRef]





| Vegetation Indexes (VIs) | Training Process | Test Process | |||||
|---|---|---|---|---|---|---|---|
| KVI | VI∞ | RMSE | R2 | MAE | NSE | MAPE | |
| GNDVI | 0.899 | 0.95 | 0.77 | 0.78 | 0.54 | 0.78 | 0.24 |
| LCI | 0.731 | 0.86 | 0.8 | 0.77 | 0.56 | 0.76 | 0.25 |
| NDRE | 0.419 | 0.66 | 1.31 | 0.67 | 0.9 | 0.35 | 0.4 |
| NDVI | 0.285 | 0.573 | 0.82 | 0.75 | 0.61 | 0.75 | 0.27 |
| OSAVI | 0.391 | 0.54 | 0.93 | 0.68 | 0.64 | 0.67 | 0.28 |
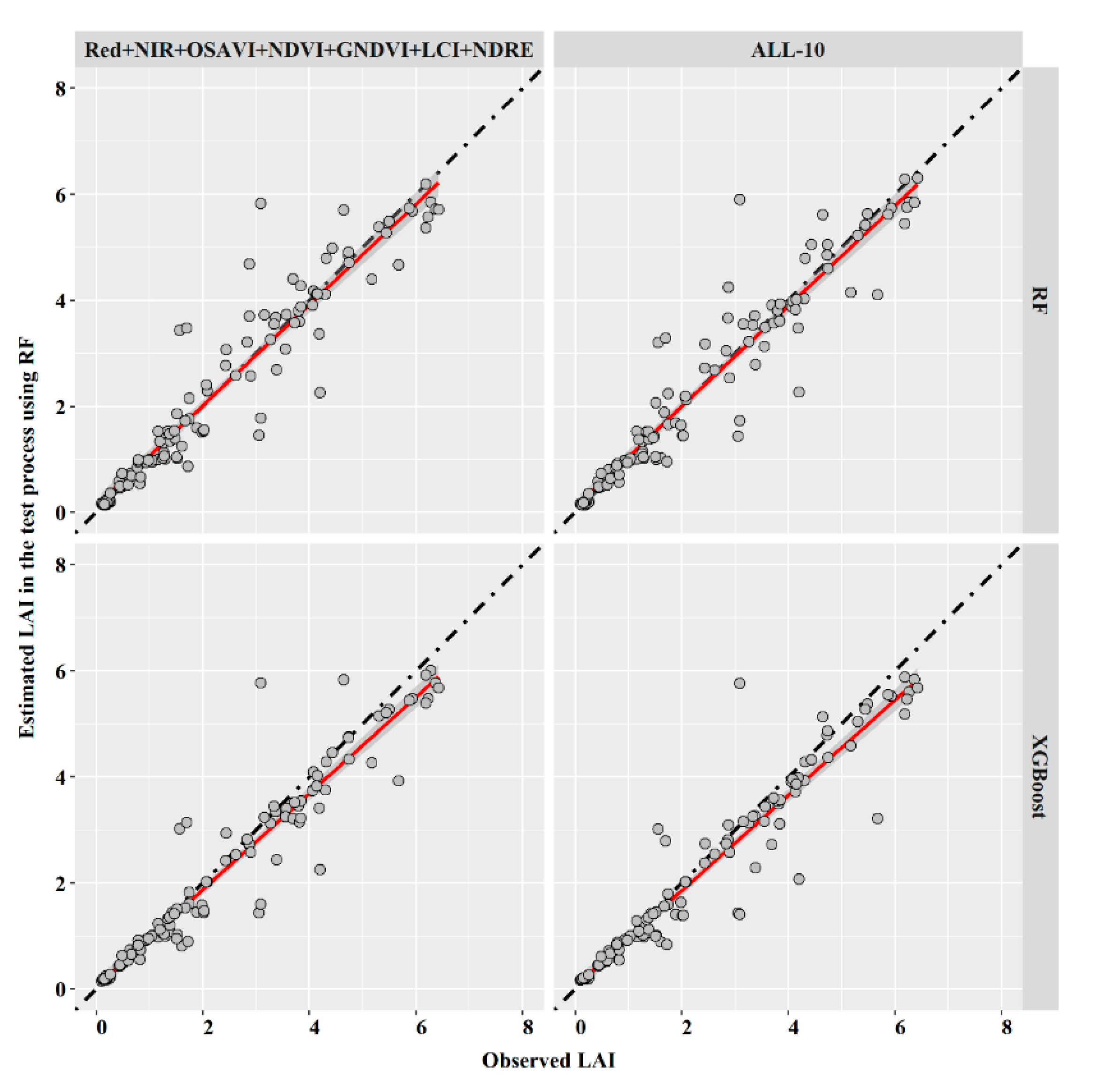
| Model Type | RF | XGBoost | |||
|---|---|---|---|---|---|
| Inputs | Red + NIR + OSAVI + NDVI + GNDVI + LCI + NDRE | ALL-10 | Red + NIR + OSAVI + NDVI + GNDVI + LCI + NDRE | ALL-10 | |
| Evaluation Indices | RMSE | 0.568 | 0.551 | 0.542 | 0.561 |
| R2 | 0.906 | 0.911 | 0.919 | 0.915 | |
| MAE | 0.326 | 0.314 | 0.3 | 0.301 | |
| NSE | 0.904 | 0.909 | 0.912 | 0.906 | |
| MAPE | 0.142 | 0.137 | 0.131 | 0.131 | |
| Bands (B) | RF | XGBoost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | MAE | NSE | MAPE | RMSE | R2 | MAE | NSE | MAPE | |
| Red | 1.039 | 0.706 | 0.652 | 0.679 | 0.284 | 0.980 | 0.720 | 0.622 | 0.714 | 0.271 |
| Blue | 1.136 | 0.629 | 0.761 | 0.616 | 0.332 | 1.119 | 0.630 | 0.756 | 0.627 | 0.330 |
| Green | 1.025 | 0.688 | 0.702 | 0.687 | 0.306 | 1.012 | 0.698 | 0.714 | 0.695 | 0.311 |
| NIR | 0.988 | 0.733 | 0.686 | 0.709 | 0.299 | 0.881 | 0.771 | 0.636 | 0.769 | 0.277 |
| RE | 1.167 | 0.596 | 0.855 | 0.594 | 0.372 | 1.197 | 0.574 | 0.874 | 0.573 | 0.381 |
| Red + NIR | 0.655 | 0.875 | 0.392 | 0.872 | 0.171 | 0.636 | 0.883 | 0.377 | 0.879 | 0.164 |
| Red + Green + NIR | 0.644 | 0.877 | 0.396 | 0.876 | 0.173 | 0.610 | 0.894 | 0.340 | 0.889 | 0.148 |
| Red + Blue + Green + NIR | 0.638 | 0.879 | 0.399 | 0.879 | 0.174 | 0.596 | 0.900 | 0.316 | 0.894 | 0.138 |
| Red + Blue + Green + NIR + RE | 0.612 | 0.889 | 0.369 | 0.889 | 0.161 | 0.603 | 0.896 | 0.307 | 0.892 | 0.134 |
| Vegetation Indexes (VIs) | RF | XGBoost | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | MAE | NSE | MAPE | RMSE | R2 | MAE | NSE | MAPE | |
| NDVI | 0.696 | 0.861 | 0.412 | 0.856 | 0.179 | 0.708 | 0.853 | 0.431 | 0.851 | 0.188 |
| GNDVI | 0.685 | 0.868 | 0.410 | 0.860 | 0.178 | 0.682 | 0.866 | 0.418 | 0.862 | 0.182 |
| LCI | 0.675 | 0.874 | 0.420 | 0.864 | 0.183 | 0.637 | 0.881 | 0.397 | 0.879 | 0.173 |
| NDRE | 0.667 | 0.875 | 0.409 | 0.867 | 0.178 | 0.663 | 0.872 | 0.409 | 0.869 | 0.178 |
| OSAVI | 0.804 | 0.811 | 0.519 | 0.808 | 0.226 | 0.800 | 0.813 | 0.532 | 0.809 | 0.232 |
| LCI + NDRE | 0.661 | 0.878 | 0.400 | 0.870 | 0.174 | 0.643 | 0.879 | 0.388 | 0.877 | 0.169 |
| GNDVI + LCI + NDRE | 0.669 | 0.877 | 0.387 | 0.867 | 0.169 | 0.633 | 0.884 | 0.365 | 0.880 | 0.159 |
| NDVI + GNDVI + LCI + NDRE | 0.640 | 0.887 | 0.391 | 0.878 | 0.170 | 0.617 | 0.890 | 0.341 | 0.886 | 0.148 |
| OSAVI + NDVI + GNDVI + LCI + NDRE | 0.608 | 0.892 | 0.365 | 0.890 | 0.159 | 0.621 | 0.889 | 0.352 | 0.885 | 0.153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Zeng, W.; Wu, L.; Lei, G.; Chen, H.; Gaiser, T.; Srivastava, A.K. Simulating the Leaf Area Index of Rice from Multispectral Images. Remote Sens. 2021, 13, 3663. https://doi.org/10.3390/rs13183663
Liu S, Zeng W, Wu L, Lei G, Chen H, Gaiser T, Srivastava AK. Simulating the Leaf Area Index of Rice from Multispectral Images. Remote Sensing. 2021; 13(18):3663. https://doi.org/10.3390/rs13183663
Chicago/Turabian StyleLiu, Shenzhou, Wenzhi Zeng, Lifeng Wu, Guoqing Lei, Haorui Chen, Thomas Gaiser, and Amit Kumar Srivastava. 2021. "Simulating the Leaf Area Index of Rice from Multispectral Images" Remote Sensing 13, no. 18: 3663. https://doi.org/10.3390/rs13183663
APA StyleLiu, S., Zeng, W., Wu, L., Lei, G., Chen, H., Gaiser, T., & Srivastava, A. K. (2021). Simulating the Leaf Area Index of Rice from Multispectral Images. Remote Sensing, 13(18), 3663. https://doi.org/10.3390/rs13183663