The Potential of Satellite Remote Sensing Time Series to Uncover Wetland Phenology under Unique Challenges of Tidal Setting
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.3. Model Building and Predicting
2.4. Additional Satellites in EVI Histories
2.5. Eddy Covariance Flux Tower Data
2.6. PEPRMT GPP Model
3. Results
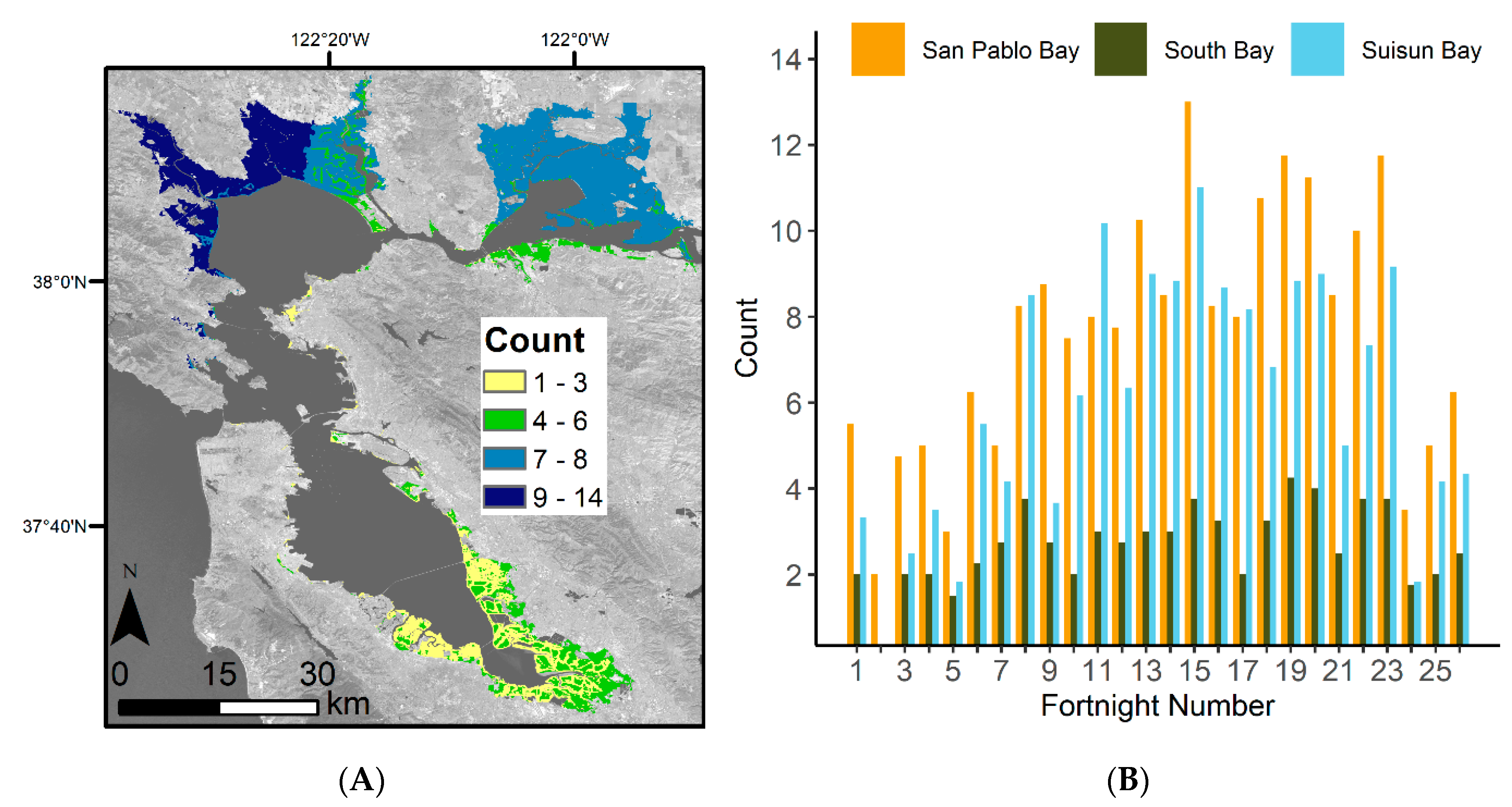
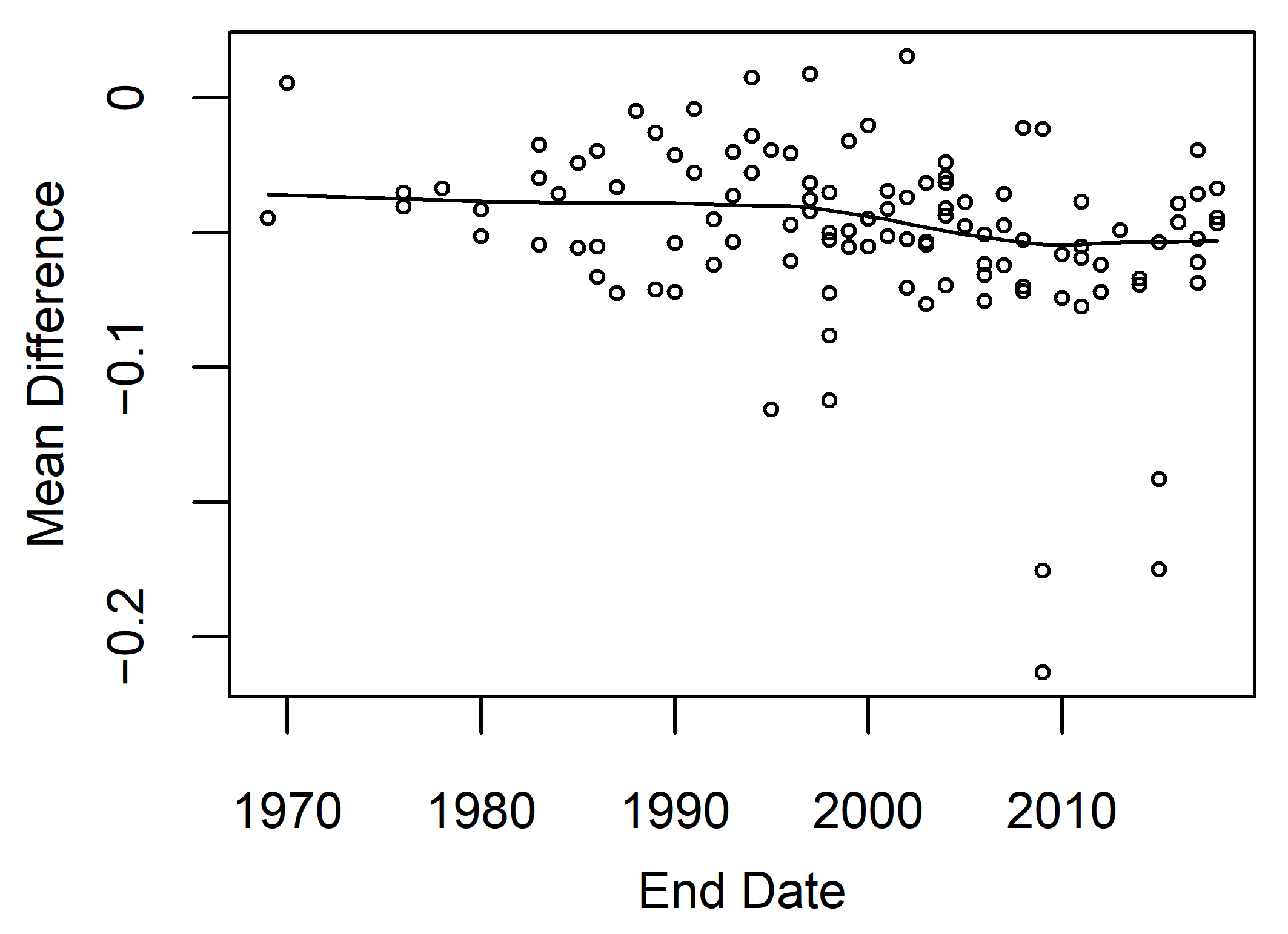
3.1. Satellite Image Count
3.2. Model
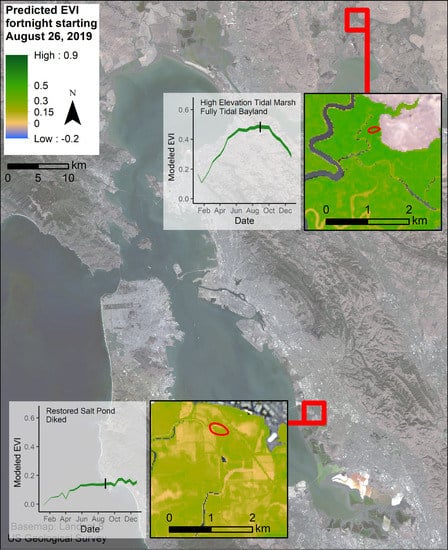
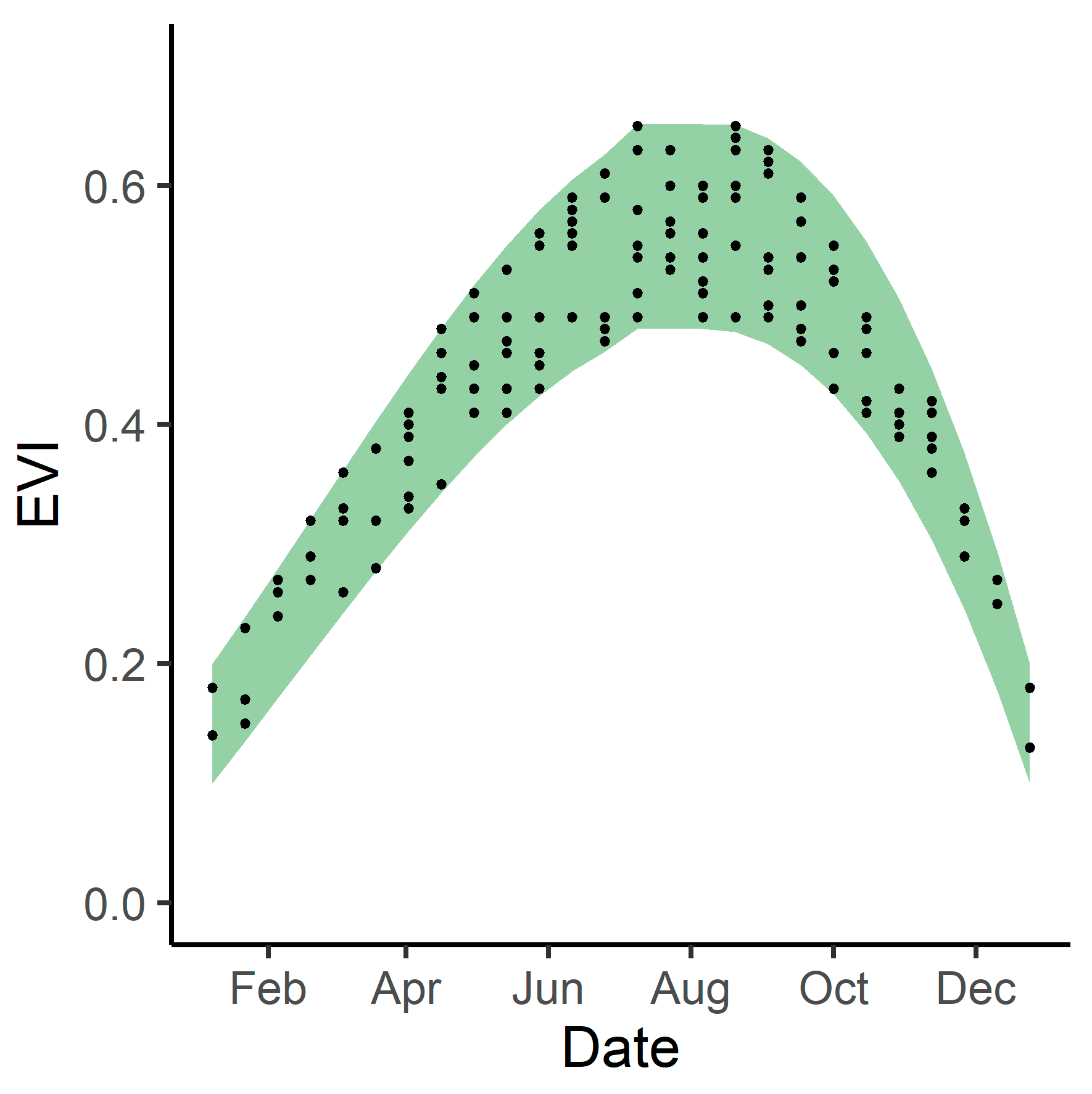
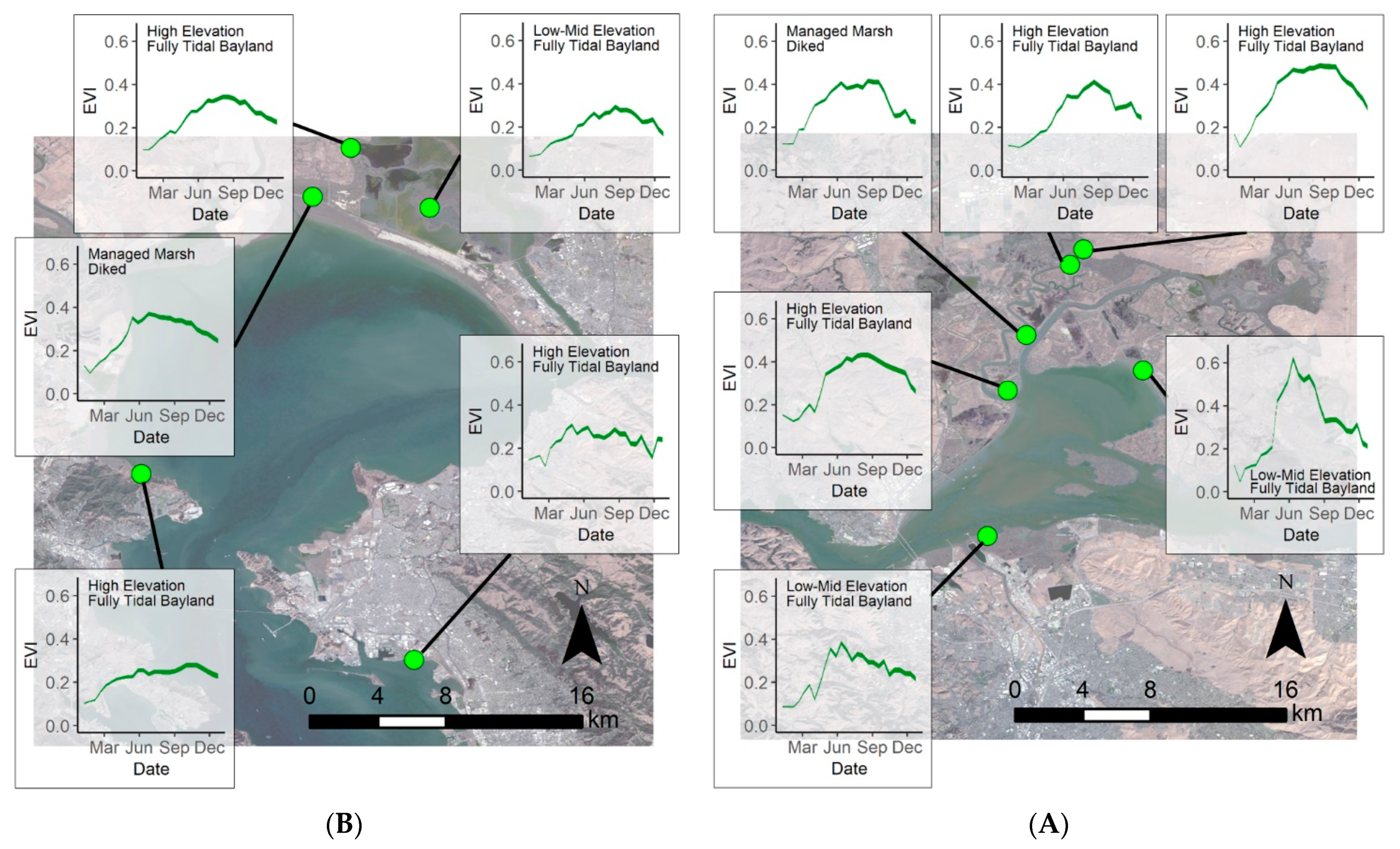
3.3. Phenological Envelope
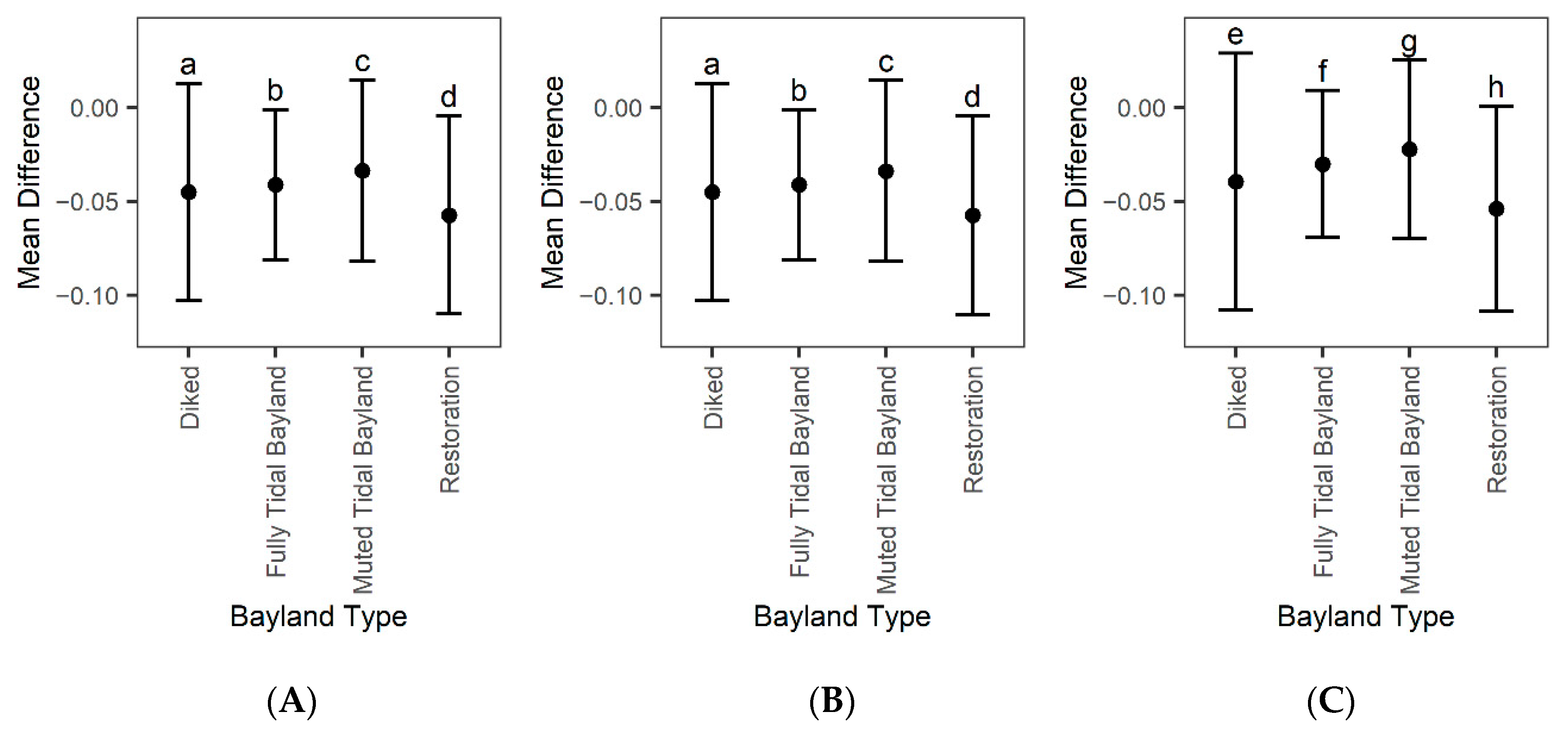
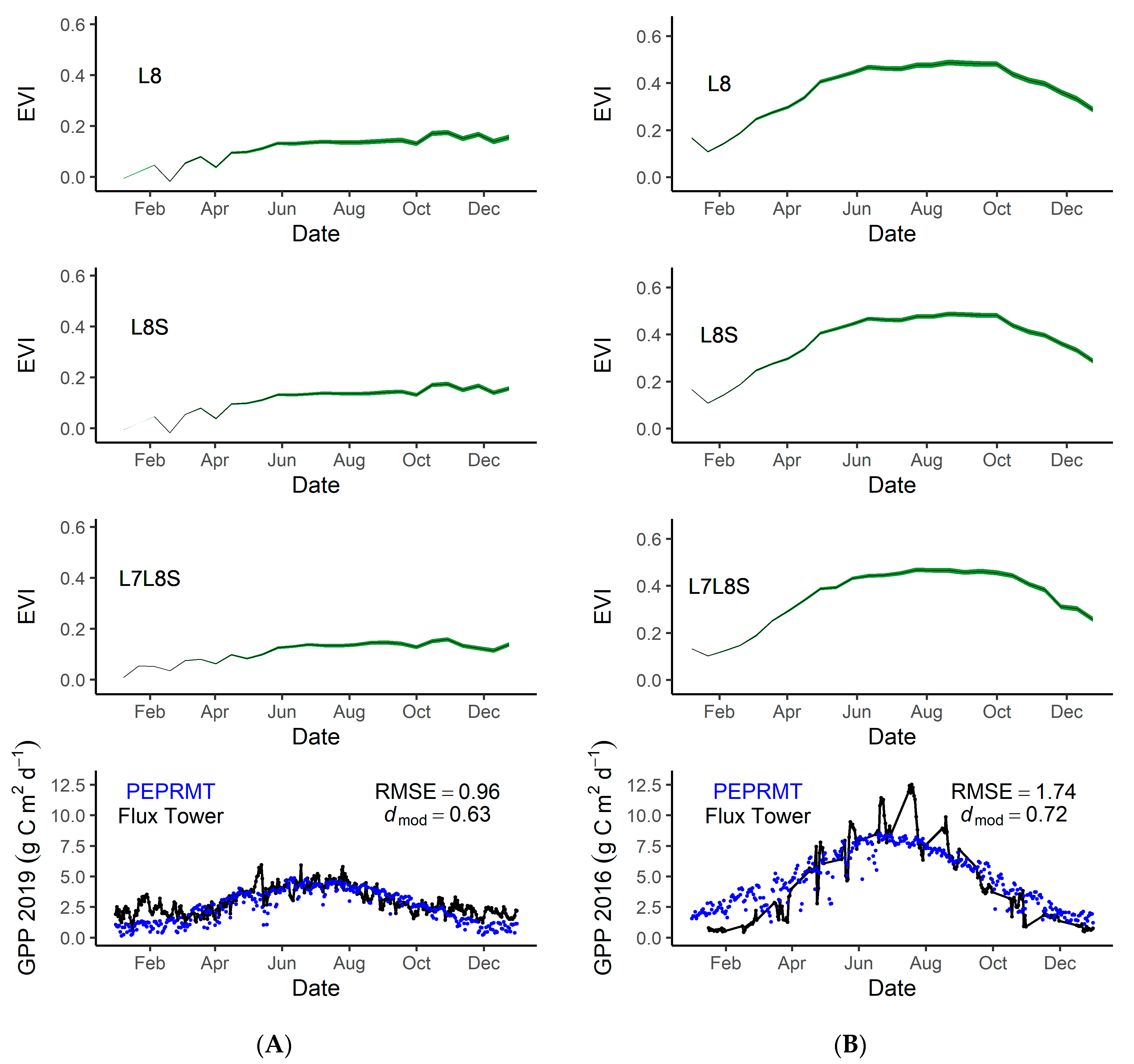
3.4. Model Accuracy
4. Discussion
4.1. The Potential of Multi-Temporal Phenological Information to Facilitate Greenness Interpolation in Tidal Systems
4.2. Model Performance
4.3. Vegetation Greenness throughout the Bay Area
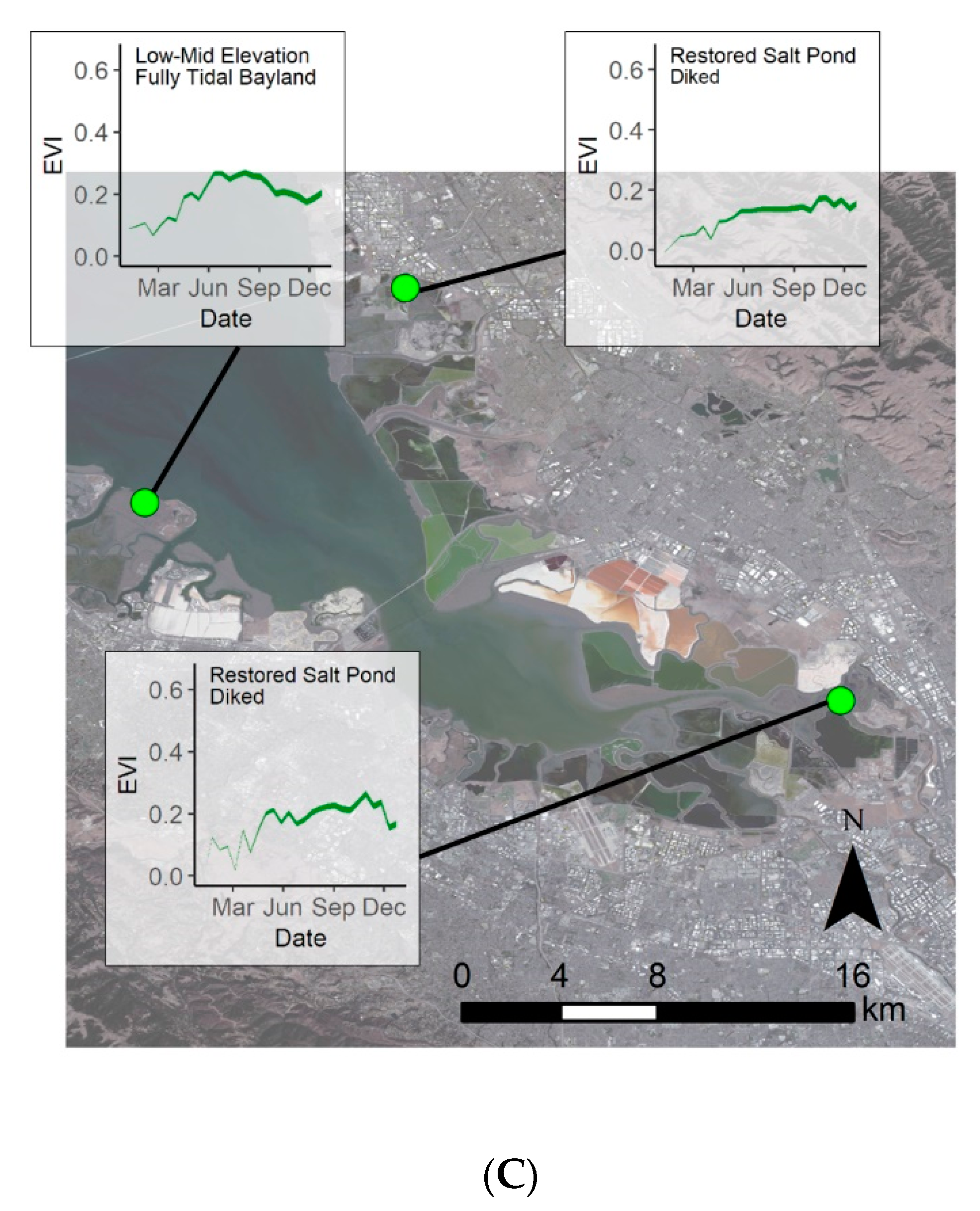
4.4. Restoration Areas
4.5. GPP Modeling
4.6. Limitations and Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Variables | K | AIC | ΔAIC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H24 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmin+ | MHHW+ | MHHW2 | 9 | −201,991 | 0 |
| H14 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmin+ | NAVD+ | NAVD2 | 9 | −201,943 | 48 |
| H25 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | MHHW+ | MHHW2 | 9 | −201,887 | 104 |
| H15 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | NAVD+ | NAVD2 | 9 | −201,861 | 130 |
| H11 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | NAVD | 8 | −201,859 | 132 | |
| H19 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | 7 | −201,855 | 136 | ||
| H16 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | MHHW | 8 | −201,854 | 137 | |
| H26 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmean+ | MHHW+ | MHHW2 | 9 | −201,835 | 156 |
| H12 | DOY+ | DOY2+ | EVIh+ | PDSI+ | NAVD | 7 | −201,815 | 176 | ||
| H10 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmean+ | NAVD | 8 | −201,814 | 176 | |
| H8 | DOY+ | DOY2+ | EVIh+ | PDSI+ | NAVD+ | NAVD2 | 8 | −201,814 | 177 | |
| H9 | DOY+ | DOY2+ | EVIh+ | PDSI+ | 6 | −201,812 | 179 | |||
| H20 | DOY+ | EVIh+ | PDSI+ | Tmin+ | NAVD+ | NAVD2 | 8 | −201,453 | 537 | |
| H17 | EVIh+ | PDSI+ | Tmin+ | NAVD | 6 | −201,437 | 554 | |||
| H18 | DOY+ | DOY2+ | EVIm+ | PDSI+ | Tmax+ | NAVD+ | NAVD2 | 9 | −198,592 | 3399 |
| H23 | DOY+ | DOY2+ | EVIm+ | PDSI+ | Tmax+ | MHHW+ | MHHW2 | 9 | −198,557 | 3434 |
| H7 | EVIh+ | Tmax | 6 | −196,328 | 5662 | |||||
| H21 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | log(NAVD) | 7 | −196,327 | 5664 | |
| H4 | DOY+ | DOY2+ | EVIh+ | NAVD | 6 | −196,326 | 5664 | |||
| H22 | DOY+ | DOY2+ | EVIh+ | PDSI+ | Tmax+ | √NAVD | 7 | −196,326 | 5665 | |
| H3 | DOY+ | DOY2+ | EVIh+ | 5 | −196,324 | 5667 | ||||
| H6 | DOY+ | DOY2+ | EVIh+ | Tmax | 6 | −196,322 | 5669 | |||
| H2 | DOY+ | EVIh+ | 4 | −196,087 | 5904 | |||||
| H13 | DOY+ | DOY2+ | EVIh+ | PDSI+ | NAVD | 6 | −93,559 | 108,432 | ||
| H5 | DOY+ | DOY2+ | PDSI+ | Tmin+ | MHHW+ | MHHW2 | 8 | −93,360 | 108,631 | |
| H1 | DOY+ | DOY2 | 4 | −92,126 | 109,865 | |||||
| H0 | 2 | −76,636 | 125,355 | |||||||
Appendix B


Appendix C

Appendix D
Appendix E

References
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F.; et al. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- McNicol, G.; Sturtevant, C.S.; Knox, S.H.; Dronova, I.; Baldocchi, D.D.; Silver, W.L. Effects of seasonality, transport pathway, and spatial structure on greenhouse gas fluxes in a restored wetland. Glob. Chang. Biol. 2017, 23, 2768–2782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, F.E.; Bergamaschi, B.; Sturtevant, C.; Knox, S.; Hastings, L.; Windham-Myers, L.; Detto, M.; Hestir, E.L.; Drexler, J.; Miller, R.L.; et al. Variation of energy and carbon fluxes from a restored temperate freshwater wetland and implications for carbon market verification protocols. J. Geophys. Res. Biogeosci. 2016, 121, 777–795. [Google Scholar] [CrossRef]
- Wan, R.; Wang, P.; Wang, X.; Yao, X.; Dai, X. Mapping Aboveground Biomass of Four Typical Vegetation Types in the Poyang Lake Wetlands Based on Random Forest Modelling and Landsat Images. Front. Plant Sci. 2019, 1281. [Google Scholar] [CrossRef] [PubMed]
- Knox, S.H.; Dronova, I.; Sturtevant, C.; Oikawa, P.Y.; Matthes, J.H.; Verfaillie, J.; Baldocchi, D. Using digital camera and Landsat imagery with eddy covariance data to model gross primary production in restored wetlands. Agric. For. Meteorol. 2017, 237–238, 233–245. [Google Scholar] [CrossRef] [Green Version]
- Dronova, I.; Taddeo, S.; Hemes, K.S.; Knox, S.H.; Valach, A.; Oikawa, P.Y.; Kasak, K.; Baldocchi, D.D. Remotely sensed phenological heterogeneity of restored wetlands: Linking vegetation structure and function. Agric. For. Meteorol. 2021, 296, 108215. [Google Scholar] [CrossRef]
- Oikawa, P.Y.; Jenerette, G.D.; Knox, S.H.; Sturtevant, C.; Verfaillie, J.; Dronova, I.; Poindexter, C.M.; Eichelmann, E.; Baldocchi, D.D. Evaluation of a hierarchy of models reveals importance of substrate limitation for predicting carbon dioxide and methane exchange in restored wetlands. J. Geophys. Res. Biogeosci. 2017, 122, 145–167. [Google Scholar] [CrossRef]
- Keenan, T.F.; Baker, I.; Barr, A.; Ciais, P.; Davis, K.; Dietze, M.; Dragoni, D.; Gough, C.M.; Grant, R.; Hollinger, D.; et al. Terrestrial biosphere model performance for inter-annual variability of land-atmosphere CO2 exchange. Glob. Chang. Biol. 2012, 18, 1971–1987. [Google Scholar] [CrossRef]
- Keenan, T.F.; Gray, J.; Friedl, M.A.; Toomey, M.; Bohrer, G.; Hollinger, D.Y.; Munger, J.W.; O’Keefe, J.; Schmid, H.P.; Wing, I.S.; et al. Net carbon uptake has increased through warming-induced changes in temperate forest phenology. Nat. Clim. Chang. 2014, 4, 598–604. [Google Scholar] [CrossRef]
- Ramsey, E.W.; Laine, S.C. Comparison of landsat thematic mapper and high resolution photography to identify change in Complex Coastal Wetlands. J. Coast. Res. 1997, 13, 281–292. [Google Scholar]
- Ramsey, E.; Rangoonwala, A.; Chi, Z.; Jones, C.E.; Bannister, T. Marsh Dieback, loss, and recovery mapped with satellite optical, airborne polarimetric radar, and field data. Remote Sens. Environ. 2014, 152, 364–374. [Google Scholar] [CrossRef]
- Byrd, K.B.; O’Connell, J.L.; Di Tommaso, S.; Kelly, M. Evaluation of sensor types and environmental controls on mapping biomass of coastal marsh emergent vegetation. Remote Sens. Environ. 2014, 149, 166–180. [Google Scholar] [CrossRef]
- Mo, Y.; Momen, B.; Kearney, M.S. Quantifying moderate resolution remote sensing phenology of Louisiana coastal marshes. Ecol. Modell. 2015, 312, 191–199. [Google Scholar] [CrossRef]
- Kearney, M.S.; Stutzer, D.; Turpie, K.; Stevenson, J.C. The Effects of Tidal Inundation on the Reflectance Characteristics of Coastal Marsh Vegetation. J. Coast. Res. 2009, 256, 1177–1186. [Google Scholar] [CrossRef]
- Barr, J.G.; Fuentes, J.D.; Delonge, M.S.; O’Halloran, T.L.; Barr, D.; Zieman, J.C. Summertime influences of tidal energy advection on the surface energy balance in a mangrove forest. Biogeosciences 2013, 10, 501–511. [Google Scholar] [CrossRef] [Green Version]
- O’Connell, J.L.; Mishra, D.R.; Cotten, D.L.; Wang, L.; Alber, M. The Tidal Marsh Inundation Index (TMII): An inundation filter to flag flooded pixels and improve MODIS tidal marsh vegetation time-series analysis. Remote Sens. Environ. 2017, 201, 34–46. [Google Scholar] [CrossRef]
- Wedding, L.M.; Moritsch, M.; Verutes, G.; Arkema, K.; Hartge, E.; Reiblich, J.; Douglass, J.; Taylor, S.; Strong, A.L. Incorporating blue carbon sequestration benefits into sub-national climate policies. Glob. Environ. Chang. 2021, 69, 102206. [Google Scholar] [CrossRef]
- Sander, T.; Gerke, H.H.; Rogasik, H. Assessment of Chinese paddy-soil structure using X-ray computed tomography. Geoderma 2008, 145, 303–314. [Google Scholar] [CrossRef]
- Ramsey, E.; Nelson, G.; Baarnes, F.; Spell, R. Light Attenuation Profiling as an Indicator of Structural Changes in Coastal Marshes. In Remote Sensing and GIS Accuracy Assessment; Lunetta, R., Lyon, J., Eds.; CRC Press: New York, NY, USA, 2004; pp. 59–73. [Google Scholar]
- Ju, Y.; Hsu, W.C.; Radke, J.D.; Fourt, W.; Lang, W.; Hoes, O.; Foster, H.; Biging, G.S.; Schmidt-Poolman, M.; Neuhausler, R.; et al. Erratum to: Planning for the Change: Mapping Sea Level Rise and Storm Inundation in Sherman Island Using 3Di Hydrodynamic Model and LiDAR. In Seeing Cities through Big Data; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Buffington, K.J.; Dugger, B.D.; Thorne, K.M.; Takekawa, J.Y. Statistical correction of lidar-derived digital elevation models with multispectral airborne imagery in tidal marshes. Remote Sens. Environ. 2016, 186, 616–625. [Google Scholar] [CrossRef] [Green Version]
- Thorne, K.; MacDonald, G.; Guntenspergen, G.; Ambrose, R.; Buffington, K.; Dugger, B.; Freeman, C.; Janousek, C.; Brown, L.; Rosencranz, J.; et al. U.S. Pacific coastal wetland resilience and vulnerability to sea-level rise. Sci. Adv. 2018, 4, eaao3270. [Google Scholar] [CrossRef] [Green Version]
- Rosso, P.H.; Ustin, S.L.; Hastings, A. Use of lidar to study changes associated with Spartina invasion in San Francisco Bay marshes. Remote Sens. Environ. 2006, 100, 295–306. [Google Scholar] [CrossRef]
- Byrd, K.B.; Ballanti, L.; Thomas, N.; Nguyen, D.; Holmquist, J.R.; Simard, M.; Windham-Myers, L. A remote sensing-based model of tidal marsh aboveground carbon stocks for the conterminous United States. ISPRS J. Photogramm. Remote Sens. 2018, 139, 255–271. [Google Scholar] [CrossRef]
- Miller, G.J.; Morris, J.T.; Wang, C. Estimating Aboveground Biomass and Its Spatial Distribution in Coastal Wetlands Utilizing Planet Multispectral Imagery. Remote Sens. 2019, 11, 2020. [Google Scholar] [CrossRef] [Green Version]
- Feagin, R.A.; Forbrich, I.; Huff, T.P.; Barr, J.G.; Ruiz-Plancarte, J.; Fuentes, J.D.; Najjar, R.G.; Vargas, R.; Vázquez-Lule, A.; Windham-Myers, L.; et al. Tidal Wetland Gross Primary Production Across the Continental United States, 2000–2019. Glob. Biogeochem. Cycles 2020, 34, e2019GB006349. [Google Scholar] [CrossRef]
- Buffington, K.J.; Dugger, B.D.; Thorne, K.M. Climate-related variation in plant peak biomass and growth phenology across Pacific Northwest tidal marshes. Estuar. Coast. Shelf Sci. 2018, 202, 212–221. [Google Scholar] [CrossRef]
- Forbrich, I.; Giblin, A.E.; Hopkinson, C.S. Constraining Marsh Carbon Budgets Using Long-Term C Burial and Contemporary Atmospheric CO2 Fluxes. J. Geophys. Res. Biogeosci. 2018, 123, 867–878. [Google Scholar] [CrossRef] [Green Version]
- Melaas, E.K.; Friedl, M.A.; Zhu, Z. Detecting interannual variation in deciduous broadleaf forest phenology using Landsat TM/ETM+ data. Remote Sens. Environ. 2013, 132, 176–185. [Google Scholar] [CrossRef]
- Melaas, E.K.; Sulla-Menashe, D.; Gray, J.M.; Black, T.A.; Morin, T.H.; Richardson, A.D.; Friedl, M.A. Multisite analysis of land surface phenology in North American temperate and boreal deciduous forests from Landsat. Remote Sens. Environ. 2016, 186, 452–464. [Google Scholar] [CrossRef]
- Chapple, D.; Dronova, I. Vegetation development in a tidal marsh restoration project during a historic drought: A remote sensing approach. Front. Mar. Sci. 2017, 4, 243. [Google Scholar] [CrossRef] [Green Version]
- Taddeo, S.; Dronova, I. Landscape metrics of post-restoration vegetation dynamics in wetland ecosystems. Landsc. Ecol. 2020, 35, 275–292. [Google Scholar] [CrossRef]
- SFEI. Bay Area EcoAtlas V1.50b4 1998: Geographic Information System of Wetland Habitats Past and Present. Available online: https://www.sfei.org/content/ecoatlas-version-150b4-1998#sthash.CycgJ0lr.dpbs (accessed on 10 December 2020).
- Stralberg, D.; Brennan, M.; Callaway, J.C.; Wood, J.K.; Schile, L.M.; Jongsomjit, D.; Kelly, M.; Parker, V.T.; Crooks, S. Evaluating Tidal Marsh Sustainability in the Face of Sea-Level Rise: A Hybrid Modeling Approach Applied to San Francisco Bay. PLoS ONE 2011, 6, e27388. [Google Scholar] [CrossRef] [Green Version]
- Conomos, T.J.; Smith, R.E.; Gartner, J.W. Environmental setting of San Francisco Bay. Hydrobiologia 1985, 129, 1–12. [Google Scholar] [CrossRef]
- MacWilliams, M.L.; Bever, A.J.; Foresman, E. 3-D simulations of the San Francisco estuary with subgrid bathymetry to explore long-term trends in salinity distribution and fish abundance. San Fr. Estuary Watershed Sci. 2016, 14, 2. [Google Scholar] [CrossRef] [Green Version]
- California Wetlands Monitoring Workgroup Habitat Projects. Available online: https://ecoatlas.org/regions/ecoregion/bay-delta (accessed on 21 June 2021).
- Wang, R.; Ateljevich, E.; Fregoso, T.A.; Jaffe, B.E. A Revised Continuous Surface Elevation Model for Modeling (Chapter 5). In Methodology for Flow and Salinity Estimates in the Sacramento-San Joaquin Delta and Suisun Marsh, 38th Annual Progress Report to the State Water Resources Control Board; California Department of Water Resources, Bay-Delta Office: Sacramento, CA, USA, 2018. [Google Scholar]
- Abatzoglou, J.T. Development of gridded surface meteorological data for ecological applications and modelling. Int. J. Climatol. 2013, 33, 121–131. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Tan, Z.; Jiang, J. Spatial-temporal dynamics of wetland vegetation related to water level fluctuations in Poyang Lake, China. Water 2016, 8, 397. [Google Scholar] [CrossRef] [Green Version]
- Kang, X.; Hao, Y.; Cui, X.; Chen, H.; Huang, S.; Du, Y.; Li, W.; Kardol, P.; Xiao, X.; Cui, L. Variability and changes in climate, phenology, and gross primary production of an alpine wetland ecosystem. Remote Sens. 2016, 8, 391. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Jiang, Y.; Tao, J.; Huang, Y.; Zhu, J.; Tian, L.; Zhang, Y. The spatial pattern of grassland aboveground biomass on Xizang Plateau and its climatic controls. J. Plant Ecol. 2015, 8, 30–40. [Google Scholar] [CrossRef] [Green Version]
- Mo, Y.U.; Kearney, M.; Momen, B. Drought-associated phenological changes of coastal marshes in Louisiana. Ecosphere 2017, 8, e01811. [Google Scholar] [CrossRef]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Climatol. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach; Springer Science & Business Media: New York, NY, USA, 2002; ISBN 0387953647. [Google Scholar]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. 1985, 90, 8995. [Google Scholar] [CrossRef] [Green Version]
- Pereira, H.R.; Meschiatti, M.C.; Pires, R.C.D.M.; Blain, G.C. On the performance of three indices of agreement: An easy-to-use r-code for calculating the willmott indices. Bragantia 2018, 77, 394–403. [Google Scholar] [CrossRef] [Green Version]
- Baldocchi, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef] [Green Version]
- Chu, H.; Luo, X.; Ouyang, Z.; Chan, W.S.; Dengel, S.; Biraud, S.C.; Torn, M.S.; Metzger, S.; Kumar, J.; Arain, M.A.; et al. Representativeness of Eddy-Covariance flux footprints for areas surrounding AmeriFlux sites. Agric. For. Meteorol. 2021, 301–302, 108350. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model. Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Knox, S.H.; Windham-Myers, L.; Anderson, F.; Sturtevant, C.; Bergamaschi, B. Direct and Indirect Effects of Tides on Ecosystem-Scale CO2 Exchange in a Brackish Tidal Marsh in Northern California. J. Geophys. Res. Biogeosci. 2018, 123, 787–806. [Google Scholar] [CrossRef]
- Malone, S.L.; Starr, G.; Staudhammer, C.L.; Ryan, M.G. Effects of simulated drought on the carbon balance of Everglades short-hydroperiod marsh. Glob. Chang. Biol. 2013, 19, 2511–2523. [Google Scholar] [CrossRef] [PubMed]
- Jones, S.F.; Janousek, C.N.; Casazza, M.L.; Takekawa, J.Y.; Thorne, K.M. Seasonal impoundment alters patterns of tidal wetland plant diversity across spatial scales. Ecosphere 2021, 12, e03366. [Google Scholar] [CrossRef]
- Moyle, P.B.; Manfree, A.D.; Fiedler, P.L. Suisun Marsh: Ecological History and Possible Futures; University of California Press: Berkeley, CA, USA, 2014. [Google Scholar]
- Pearcy, R.W.; Ustin, S.L. Effects of salinity on growth and photosynthesis of three California tidal marsh species. Oecologia 1984, 62, 68–73. [Google Scholar] [CrossRef] [PubMed]
- Lumbierres, M.; Méndez, P.; Bustamante, J.; Soriguer, R.; Santamaría, L. Modeling Biomass Production in Seasonal Wetlands Using MODIS NDVI Land Surface Phenology. Remote Sens. 2017, 9, 392. [Google Scholar] [CrossRef] [Green Version]
- Takekawa, J.Y.; Lu, C.T.; Pratt, R.T. Avian communities in baylands and artificial salt evaporation ponds of the San Francisco Bay estuary. Hydrobiologia 2001, 466, 317–328. [Google Scholar] [CrossRef]
- Baye, P. Tidal Marsh Vegetation of China Camp, San Pablo Bay, California. San Fr. Estuary Watershed Sci. 2012, 10. [Google Scholar] [CrossRef]
- Boul, R.; Hickson, D.; Keeler-Wolf, T.; Jo, M.; Ougzin, A. 2015 Vegetation Map Update for Suisun Marsh, Solano County, California; California Department of Fish & Wildlife: Sacramento, CA, USA, 2018; p. 104.
- Khanna, S.; Santos, M.J.; Boyer, J.D.; Shapiro, K.D.; Bellvert, J.; Ustin, S.L. Water primrose invasion changes successional pathways in an estuarine ecosystem. Ecosphere 2018, 9, e02418. [Google Scholar] [CrossRef]
- McClure, A.; Liu, X.; Hines, E.; Ferner, M.C. Evaluation of Error Reduction Techniques on a LIDAR-Derived Salt Marsh Digital Elevation Model. J. Coast. Res. 2016, 32, 424–433. [Google Scholar] [CrossRef]
- Fulfrost, B. Habitat Evolution Mapping Project South Bay Salt Pond Restoration Project Final Report Habitat Evolution Mapping Project Final Report South Bay Salt Pond Restoration Project; Brian Fulfrost and Associates: Oakland, CA, USA, 2009. [Google Scholar]
- Curcó, A.; Ibàñez, C.; Day, J.W.; Prat, N. Net primary production and decomposition of salt marshes of the Ebre delta (Catalonia, Spain). Estuaries 2002, 25, 309–324. [Google Scholar] [CrossRef]
- Boyer, K.E.; Fong, P.; Vance, R.R.; Ambrose, R.F. Salicornia virginica in a Southern California salt marsh: Seasonal patterns and a nutrient-enrichment experiment. Wetlands 2001, 21, 315–326. [Google Scholar] [CrossRef]
- Moreno-Mateos, D.; Power, M.E.; Comín, F.A.; Yockteng, R. Structural and functional loss in restored wetland ecosystems. PLoS Biol. 2012, 10, e1001247. [Google Scholar] [CrossRef] [Green Version]
- Hemes, K.S.; Chamberlain, S.D.; Eichelmann, E.; Anthony, T.; Valach, A.; Kasak, K.; Szutu, D.; Verfaillie, J.; Silver, W.L.; Baldocchi, D.D. Assessing the carbon and climate benefit of restoring degraded agricultural peat soils to managed wetlands. Agric. For. Meteorol. 2019, 268, 202–214. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.; Gorelick, N.; Braaten, J.; Cavalcante, L.; Cohen, W.B.; Healey, S. Implementation of the LandTrendr algorithm on Google Earth Engine. Remote Sens. 2018, 10, 691. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, R.E.; Yang, Z.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Brown, L.N.; Rosencranz, J.A.; Willis, K.S.; Ambrose, R.F.; MacDonald, G.M. Multiple Stressors Influence Salt Marsh Recovery after a Spring Fire at Mugu Lagoon, CA. Wetlands 2020, 40, 757–769. [Google Scholar] [CrossRef] [Green Version]
- Neira, C.; Ae, L.A.L.; Grosholz, E.D.; Mendoza, G. Influence of invasive Spartina growth stages on associated macrofaunal communities. Biol. Invasions 2007, 9, 975–993. [Google Scholar] [CrossRef] [Green Version]
- Miller, G.J.; Morris, J.T.; Wang, C. Mapping salt marsh dieback and condition in South Carolina’s North Inlet-Winyah Bay National Estuarine Research Reserve using remote sensing. AIMS Environ. Sci. 2017, 4, 677–689. [Google Scholar] [CrossRef]
- Vrieling, A.; Meroni, M.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Zurita-Milla, R.; Oosterbeek, K.; O’Connor, B.; Paganini, M. Vegetation phenology from Sentinel-2 and field cameras for a Dutch barrier island. Remote Sens. Environ. 2018, 215, 517–529. [Google Scholar] [CrossRef]




| Dataset Name | Description | Source | Type | Resolution |
|---|---|---|---|---|
| Elevation MHHW | Elevation above mean higher high water generated by Point Blue | [34] | Raster | 5 m |
| Elevation NAVD88 | Elevation above NAVD88 derived from various sources | [38] | Raster | 10 m |
| Atmospheric Temperature | GRIDMET: University of Idaho Gridded Surface Meteorological Dataset—daily temperature, including minimum, maximum, and mean temperature. Available on Google Earth Engine | [39] | Raster | 4 km |
| Palmer Drought Severity Index | GRIDMET DROUGHT: CONUS drought indices. Gridded biweekly PDSI based on the modified version of the Palmer Formula. Available on Google Earth Engine | [39] | Raster | 2.5 arc min |
| Landsat 8 | USGS Landsat 8 Surface Reflectance Tier 1. Available on Google Earth Engine | Raster | 30 m | |
| Baylands | San Francisco Bay Area EcoAtlas Modern Baylands type | [33] | Shapefile | |
| Habitat Projects | Locations of restoration projects within San Francisco Bay Area Wetlands | [37] | Shapefile |
| Dependent Variable | Predictor | Standardized β Coefficient [Lower Bound, Upper Bound] | β Coefficient [Lower Bound, Upper Bound] |
|---|---|---|---|
| EVI | Intercept * | 0.2353 [0.2346, 0.2361] | −2.672 [−4.23, −1.11] |
| DOY * | −0.0015 [−0.0018, −0.0011] | 2.871 [2.62, 3.13] | |
| DOY2 * | −0.0060 [−0.0065, −0.0055] | −7.420 [−8.05, −6.79] | |
| EVIh * | 0.1166 [0.1162, 0.1171] | 1.002 [0.998, 1.005] | |
| MHHW * | −0.0008 [−0.0011, −0.0004] | 2.836 [1.68, 3.99] | |
| MHHW2 * | 0.0014 [0.0010, 0.0018] | 5.034 [3.65, 6.42] | |
| PDSI * | 0.0141 [0.0137, 0.0144] | 7.563 [7.37, 7.76 | |
| Tmin * | −0.0035 [−0.0040, −0.0029] | −8.792 [−1.02, −7.42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, G.J.; Dronova, I.; Oikawa, P.Y.; Knox, S.H.; Windham-Myers, L.; Shahan, J.; Stuart-Haëntjens, E. The Potential of Satellite Remote Sensing Time Series to Uncover Wetland Phenology under Unique Challenges of Tidal Setting. Remote Sens. 2021, 13, 3589. https://doi.org/10.3390/rs13183589
Miller GJ, Dronova I, Oikawa PY, Knox SH, Windham-Myers L, Shahan J, Stuart-Haëntjens E. The Potential of Satellite Remote Sensing Time Series to Uncover Wetland Phenology under Unique Challenges of Tidal Setting. Remote Sensing. 2021; 13(18):3589. https://doi.org/10.3390/rs13183589
Chicago/Turabian StyleMiller, Gwen Joelle, Iryna Dronova, Patricia Y. Oikawa, Sara Helen Knox, Lisamarie Windham-Myers, Julie Shahan, and Ellen Stuart-Haëntjens. 2021. "The Potential of Satellite Remote Sensing Time Series to Uncover Wetland Phenology under Unique Challenges of Tidal Setting" Remote Sensing 13, no. 18: 3589. https://doi.org/10.3390/rs13183589
APA StyleMiller, G. J., Dronova, I., Oikawa, P. Y., Knox, S. H., Windham-Myers, L., Shahan, J., & Stuart-Haëntjens, E. (2021). The Potential of Satellite Remote Sensing Time Series to Uncover Wetland Phenology under Unique Challenges of Tidal Setting. Remote Sensing, 13(18), 3589. https://doi.org/10.3390/rs13183589