Abstract
The use of UAV-based laser scanning systems is increasing due to the rapid development in sensor technology, especially in applications such as topographic surveys or forestry. One advantage of these multi-sensor systems is the possibility of direct georeferencing of the derived 3D point clouds in a global reference frame without additional information from Ground Control Points (GCPs). This paper addresses the quality analysis of direct georeferencing of a UAV-based laser scanning system focusing on the absolute accuracy and precision of the system. The system investigated is based on the RIEGL miniVUX-SYS and the evaluation uses the estimated point clouds compared to a reference point cloud from Terrestrial Laser Scanning (TLS) for two different study areas. The precision is estimated by multiple repetitions of the same measurement and the use of artificial objects, such as targets and tables, resulting in a standard deviation of <1.2 cm for the horizontal and vertical directions. The absolute accuracy is determined using a point-based evaluation, which results in the RMSE being <2 cm for the horizontal direction and <4 cm for the vertical direction, compared to the TLS reference. The results are consistent for the two different study areas with similar evaluation approaches but different flight planning and processing. In addition, the influence of different Global Navigation Satellite System (GNSS) master stations is investigated and no significant difference was found between Virtual Reference Stations (VRS) and a dedicated master station. Furthermore, to control the orientation of the point cloud, a parameter-based analysis using planes in object space was performed, which showed a good agreement with the reference within the noise level of the point cloud. The calculated quality parameters are all smaller than the manufacturer’s specifications and can be transferred to other multi-sensor systems.
1. Introduction
1.1. Motivation
Nowadays, the use of mobile mapping systems has become increasingly popular due to the rapid technological development and the resulting increase in the range of applications. As a result, these multi-sensor systems are used on mobile platforms, whether on the ground, on water or in the air, and have been adopted in a wide range of application areas. Typical fields for the use of mobile mapping systems are topographic and bathymetric surveys, road and power line inspections, mining, forestry or precision agriculture [1,2,3,4,5].
The recent development of sensor technology for mobile mapping systems in the field of airborne laser scanning offers the possibility to operate compact profile line scanners on an Unmanned Aerial Vehicle (UAV) [6]. The advantages of using a combination of UAV and laser scanner are numerous compared to traditional airborne laser scanning, and benefit, in particular, from a higher level of detail and more flexible flight planning. In comparison to conventional Terrestrial Laser Scanners (TLS), it also offers a faster acquisition of survey objects with higher coverage. In addition, one of the major benefits of UAV-based laser scanning is the possibility of direct georeferencing, which describes the calculation of a 3D point cloud in a global reference frame [7]. The direct georeferencing relies on the UAV’s trajectory estimation with positions and orientations, using the fusion of sensors such as IMU (Inertial Measurement Unit) and GNSS (Global Navigation Satellite System) receiver. Since the trajectory estimation is the most critical component in the error budget of the UAV-based laser scanning, the overall accuracy of the georeferenced point cloud is highly dependent on the quality of the UAV trajectory [7]. In the following, the error budget is used as a summary of errors included in the measurements or processing of the UAV-based laser scanning system. If direct georeferencing with a sufficient accuracy is provided, different advantages are obvious. The need for overlapping flight strips in data collection is less important, which is a great advantage for applications such as corridor mapping, also resulting in larger areas being covered in the same amount of time. Furthermore, the need for Ground Control Points (GCPs) is less important and potentially not needed anymore [8]. Finally, most of the benefits lead to time and cost savings in the execution of a project. This study aims to provide a reliable strategy for the quality assessment of the direct georeferencing of a UAV-based laser scanning system. The main aspects are the analysis of the absolute accuracy in the horizontal and vertical direction and the precision of the system considering repetitions of the same measurement and, thus, the same flight planning.
This paper is organized as follows: Section 1 focuses on the methodology of UAV-based laser scanning, related work and the research scope. This is followed by Section 2 about materials and methods, which describes the used sensor system, the evaluation strategy and the study areas. Section 3 presents and discusses the results of all experiments conducted in this study. Section 4 concludes the paper.
1.2. Methodology of UAV-Based Laser Scanning
For the analysis of the system accuracy, the influencing parameters and the basic principle of UAV-based laser scanning are relevant. The concept is always based on sensors to localize the UAV with position and orientation, as well as sensors to acquire the environment with a laser scanner and an optional camera. The entire processing, starting with the raw data (blue boxes) and ending with the 3D point cloud (green box), is shown in Figure 1 with additional processing steps (orange boxes) and potential error sources, discussed later.
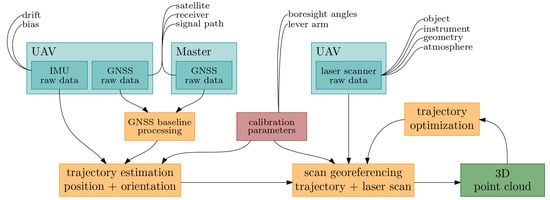
Figure 1.
Processing of UAV-based laser scanning data with major error sources.
For the trajectory estimation with positions and orientations of the system, a combination of GNSS and IMU measurements is used. The GNSS observations from the receiver on the UAV are usually processed in differential mode with the observations from an additional GNSS master station, and then fused with the IMU data using a Kalman filter or similar algorithm [9]. The result is the UAV trajectory described by a set of estimated positions and orientations. With subsequent georeferencing of time-synchronized laser scans based on the estimated trajectory and laser scanner measurements, the georeferenced point cloud is created. Additional information needed in this processing chain are the system calibration parameters describing the relative positions and orientations between the sensors on the platform. The calculation of each 3D point can further be described with the equation
including the parameters for the trajectory, sensor calibration and laser scanner measurements, which contribute to the calculation and, thus, the accuracy [10]. The calibration parameters of the system are defined with the lever arm and the bore-sight angles and between the 2D laser scanner and GNSS/IMU unit. The measurements of the 2D laser scanner are introduced with , with d the measured distance and b the scan angle. Further parameters are the orientation angles of the platform with roll , pitch and yaw and its position with translation vector and ellipsoidal longitude L and latitude B. Based on these parameters and the additional rotation matrices between the sensor , body , navigation and earth -frame, the coordinates of each 3D point can be derived. For a detailed description of the included coordinate frames, calibration parameters and the functional model we refer to [1,11].
For system evaluation, the assumed uncertainty of the point cloud, or rather of the single 3D points, is crucial, which, in turn, is a combination of several systematic and random errors that influence the estimation process [7]. As mentioned before, the major error sources influencing the accuracy of the point cloud are the trajectory estimation of the UAV, the system calibration, the accuracy of the laser scanner itself and further miscellaneous errors like the ones coming from sensor time synchronization [12]. A more detailed list of errors can be found in Table 1, which is assigned to the included parameters in Equation (1).

Table 1.
Major error sources for UAV-based laser scanning systems (refer to [7]).
Typically, the largest errors of mobile mapping systems as well as UAV-based laser scanning come from the GNSS/IMU-based trajectory estimation and they can be expressed in terms of platform position and orientation errors. Both position and orientation errors systematically propagate to errors in the point cloud [12]. Further errors are related to the system calibration with lever arms and the bore-sight angles already described above. These errors influence the point cloud uncertainty also in a systematic manner. In addition, the measurements of the laser scanner may contain errors due to atmospheric refraction, object characteristics, and the range measurement error itself. The error due to object characteristics is given due to different materials of the objects, the reflectivity or even the scan geometry. The remaining errors are caused by the time synchronization and the rigidity of the sensor mounting. To make a qualitative specification of the UAV-based laser scanning error budget and quantify it more concretely, the different sensors of the system used must be considered, which will be done in Section 2.
1.3. Related Work
The assessment of the accuracy of UAV-based laser scanning systems can typically be divided into theoretical and empirical studies. One theoretical approach is described by Pilarska et al. [13], who focus on the propagation of errors in the UAV’s position and orientation on the point cloud. In addition, Glennie [14] also considers the errors introduced by the calibration of the system with bore-sight angles and lever arm. Further studies about the error budget for airborne or UAV-based laser scanning systems are [7,12,15]. The critical aspect for the theoretical investigations is mainly the consideration of all errors that are included in any estimation process for mobile mapping systems with laser scanner [16]. For this reason, most of the quality assessments so far have been done on the empirical approach based on the resulting product, which is usually a georeferenced 3D point cloud with optional RGB information coming from a camera. Examples for the empirical assessment of point cloud accuracy can be found in Tulldahl et al. [17] or investigations with additional optimization strategies by Mandlburger et al. [18].
For the empirical evaluation of point clouds different approaches are recommended, which can be divided into (1) point-based, (2) area-based and (3) parameter-based strategies [11]. Point-based evaluation requires the identification of identical points with a given reference. These reference points are determined by traditional surveying methods such as total stations, GNSS, leveling or TLS. Typical objects for point-based evaluation can be natural objects (e.g., building corners, road markings or manholes) or artificial objects (e.g., targets or checkerboard patterns) [19,20,21,22,23,24,25]. These enable the assessment of the absolute accuracy and the separation of errors into horizontal and vertical components. By measuring points multiple times with the same system, the precision can also be quantified. One challenge with point-based evaluation methods and UAV-based laser scanning is due to the comparatively low point density with increasing flight height and speed, which has to be considered during flight planning.
Besides the point-based evaluation, the area-based strategies are often used for comparison with a known reference point cloud (e.g., TLS) [23,26,27,28]. Also, 3D city models have been used as a reference for evaluation [29]. For the calculation of differences, various algorithms such as the cloud-to-cloud distance or the Multiscale Model to Model Cloud Comparison (M3C2) method are used, which are integrated into common software tools. Since UAV-based laser scanning measurements are typically made with overlapping flight strips to correct the estimated UAV position and orientation [30], area-based comparisons between flight strips can indicate the precision during one flight [31].
The third possibility of the above-mentioned evaluation strategies is the parameter-based evaluation, in which derived parameters from the point cloud are used for the comparison [1,23]. Potential parameters are typically estimated from objects with a defined geometric shape. Fuad et al. [32] for example analyzed the accuracy of estimated DEM models with different flight parameters. Furthermore, several studies investigated the quality for the calculation of forest structural attributes (e.g., stem diameter, volume) in forestry [33,34,35]. In addition, Kucharcyzk et al. [36] analyzed the accuracy of point clouds in vegetated terrain with a focus in the vertical direction. Similar to the previous evaluation methods, parameter-based evaluation can also serve for the analysis of precision.
1.4. Research Scope
The proposed evaluation strategy used in this work intend to evaluate the direct georeferencing quality of the UAV-based laser scanning system by using the calculated point cloud without any additional information or optimization. Since the processing chain recommended by the manufacturer includes point cloud optimization techniques, such as strip adjustment or insertion of GCPs, it is difficult to conclude the accuracy of the direct georeferencing itself. Therefore, the strategy adopted for quality assessment is chosen to evaluate the absolute accuracy and precision of a single measurement without optimization, for example, cross-flight measurements or additional point cloud processing interventions, similar to Torresan et al. [37]. This analysis to derive absolute accuracy is performed by comparing the point cloud obtained with the UAV-based laser scanning system with a TLS reference point cloud using point-based and parameter-based evaluation strategies. The objects for comparison are mainly TLS targets adopted for use with the UAV-based laser scanning system. Furthermore, additional objects are used for the analysis of the height component and, therefore, the accuracy in vertical direction. In addition to absolute accuracy, the precision of the system is also evaluated by performing repeated flights with identical flight planning. This approach allows a proper quantification of the precision of the UAV-based laser scanning system, especially, when the GNSS conditions change, particularly the satellite geometry. Another important factor affecting direct georeferencing is the GNSS master station used. To investigate this aspect in detail, four different master stations are employed: one own master station, one Continuously Operating Reference Station (CORS) and two Virtual Reference Stations (VRS). In addition to the analysis of single strip measurements, a second data set is considered with a cross-flight pattern and extended post-processing as it is commonly done.
2. Materials and Methods
2.1. UAV-Based Laser Scanning System
The UAV-based laser scanning system used for all experiments within this work is shown in flight and on the ground in Figure 2a,b. The platform is based on the DJI Matrice 600 Pro [38] and the lightweight RIEGL miniVUX-SYS designed for the use on UAVs [39]. This system consists of the IMU/GNSS combination Trimble APX-20 UAV [40] for trajectory estimation in post-processing and the full waveform 2D laser scanner RIEGL miniVUX-2UAV for object acquisition.

Figure 2.
DJI Matrice 600 platform with the RIEGL miniVUX-2UAV laser scanner in flight (a) and on the ground (b).
The scanning mechanism is based on a rotating mirror resulting in a field of view of up to and a maximum laser pulse repetition rate of 200 kHz. Furthermore, the laser scanner’s absolute accuracy at 50 m distance is given with cm and the precision with cm [41]. To ensure a precise trajectory estimation and the calculation of the 3D point cloud, the sensor calibration between IMU, GNSS antenna and laser scanner is accurately estimated by the manufacturer RIEGL. Referring to the manufacturer’s specifications in Table 2, it is apparent that also for this UAV-based laser scanning system, the major influence on the accuracy of the estimated point cloud comes from the accuracy of the trajectory.

Table 2.
Error budget of the UAV-based laser scanning system based on RIEGL miniVUX-SYS according to manufacturer’s specification [39,40,41].
The stated accuracy values are typical values that can be expected for trajectory estimation with this platform given short baseline GNSS processing and a sufficient satellite constellation. The sensor and system specifications listed so far are given without trajectory improvements, which are typically provided by strip adjustment approaches or GCPs [30]. To assess the quality of the point cloud in the following, the assumed accuracy of the final product should be within the range of the specified trajectory accuracy.
2.2. Evaluation Strategy
The evaluation approach to analyze the absolute accuracy and precision in this study is generally separated into the analysis based on single strip measurements without additional multi-strip or GCP corrections, and the analysis of measurements with a cross-flight pattern, referred to as multiple strip measurements. Single strip measurements are performed to focus the analysis of system performance without additional GCP input or corrections like strip adjustment, whereas the cross-flight pattern with multiple strips is used to evaluate the full benefit of the post-processing provided by the manufacturer’s software, such as strip adjustment. The limiting factor for the absolute accuracy in the investigation of a single strip is clearly given by the GNSS processing within trajectory estimation. The accuracy achieved in the differential processing of GNSS observations is further dependent on the GNSS master station, the satellite geometry, and the measurement conditions. Since it is almost impossible to evaluate the accuracy of estimated UAV trajectory directly, the calculated point clouds are used for the evaluation of the system. The individual research aspects for the evaluation approach are detailed in the following with the assessment parameters and strategies used, which are investigated for the single strip and the multiple strip measurements.
- (1)
- NoiseThe noise level is analyzed based on different parts of the resulting point clouds. This parameter primarily gives a quantification of the noise of the laser scanner measurements (included in Equation (1)) and an understanding of how much it contributes to the error budget of the system. The noise evaluation parameter is based on a plane fit and the corresponding residuals. Therefore, planar objects with good reflective properties are necessary with an appropriate scan geometry. The noise level is investigated only at the given flight height without a detailed evaluation of the systematic dependence with increasing distance to the object.
- (2)
- Absolute accuracyThe absolute accuracy is the main part of this study. For this, the UAV-based laser scanning point clouds are analyzed in comparison to a georeferenced point cloud measured with TLS. This evaluation is supposed to determine the absolute accuracy of the system in the vertical and horizontal direction using a point-based evaluation approach. Since the accuracy in the vertical direction is in most cases lower than in the horizontal direction [41], a special focus is given on the height component. Besides the point-based evaluation, the orientation of the point cloud in the global reference frame is analyzed using a parameter-based approach. Concerning the parameters in Equation (1), trajectory estimation, laser scanner and system calibration are evaluated simultaneously in this investigation.
- (3)
- PrecisionAdditionally, the precision is evaluated with repeated measurements using the same flight plan for each repetition, spread over several hours. This approach is intended to indicate the precision of the system and, in particular, its performance under changing GNSS conditions and constellations. This investigation uses point-based as well as parameter-based evaluation strategies.
- (4)
- GNSS master stationThis aspect examines the importance of the GNSS master station used for the trajectory estimation of the UAV. In principle, there are different possibilities of master raw data which are used for the relative GNSS processing. The analysis provides a result of the impact of different master stations on the point cloud’s accuracy and a recommendation for the application of UAV-based laser scanning in practice.
2.3. Data Acquisition and Reference Point Cloud
The data acquisition environment was selected according to the different study aspects described in Section 2.2 to generate suitable data sets for the analysis. Since the main part of the investigation relies on a reference point cloud, we selected areas near an existing network of control points that can be used for georeferencing a TLS point cloud. Since the evaluation is performed using artificial objects such as targets or planes, the experiment can be easily implemented in other areas. The two main evaluation strategies are divided into single strip and multiple strip measurements, for which two different study areas were chosen. Since the single strip measurements are the focus, they are discussed in more detail. In the following, the two study areas and the objects contained therein (Section 2.3.1), the procedure for generating the TLS reference (Section 2.3.2) and the UAV-based measurements (Section 2.3.3) are explained.
2.3.1. Study Areas and Objects
The study area used for the single strip measurements is located at the Campus Klein-Altendorf near Bonn and is shown in Figure 3a with additional objects that were arranged over the entire area with a length of about 300 m.
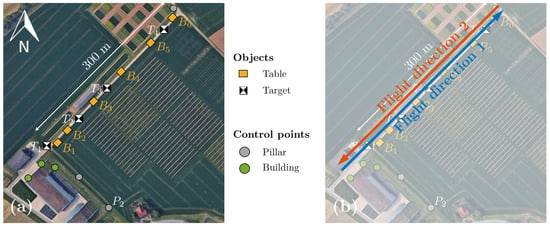
Figure 3.
Study area for the analysis of single strip measurement with included objects (a) and the two flight directions of the individual measurements (b), © https://www.google.de/maps/ (accessed on 14 May 2021).
The location was chosen based on an existing network of high accuracy control points [1], which are shown in Figure 3a and used to georeference the TLS point cloud. The measurement setup was designed in a way that flight planning will be similar to the corridor mapping application with a fixed flight direction, in this case parallel to the road. A measurement with the UAV system, shown in Figure 3b, includes the path along the road in the north–east direction (flight direction 1) and back along the same path (flight direction 2), which means that each object is always measured twice for one data set. The objects within the area used for the quality analysis are six tables (1.2 m × 0.8 m) and four targets (0.3 m × 0.3 m), shown in Figure 4b,c.

Figure 4.
Study area for the analysis of single strip measurement with TLS measurement for the reference point cloud.
The tables have a white and plain surface with high reflective properties and were placed directly below the trajectory. In addition, the tables were aligned horizontally using a spirit level so that each position on the table had the same height.
The second study area used for the evaluation of the multiple strip measurements is a typical urban environment with buildings, streets and vegetation. The principle approach of analyzing the UAV-based laser scanning system is similar by the use of an accurately measured TLS reference point cloud and the following assessment of the UAV point clouds using point-based and parameter-based evaluation techniques. Compared to the data set before, a cross-flight pattern, which is typical for UAV-based laser scanning, is performed.
The study area used for the multiple strip measurements is shown in Figure 5a, where additional targets distributed over the whole area as indicated. The 12 targets are in the same TLS design as before but with a size of 0.8 m × 0.8 m (Example shown in Figure 5b) that targets center could be estimated also with a flight height of 25 m.
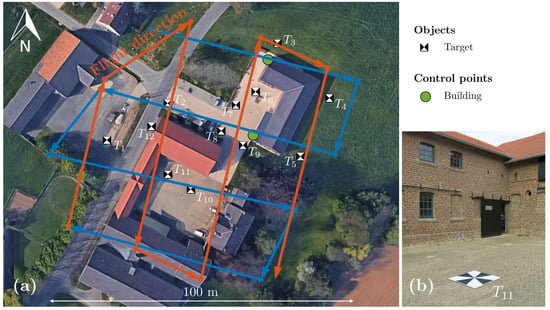
Figure 5.
Second study are for the analysis of multiple strip measurement with included objects and the flight pattern of the individual measurement, © https://www.google.de/maps/ (accessed on 14 May 2021).
2.3.2. Reference Point Cloud from Terrestrial Laser Scanning
A reference point cloud is used for most of the evaluation aspects described in Section 2.2. The point cloud for the first study area was acquired with a Leica ScanStation P50 TLS and a target-based registration using BOTA8 (Bonn Target 8) laser scanning targets [42], shown in Figure 4a. To cover the entire study area, 16 viewpoints with 29 target locations were required, which were measured with the scanner resolution setting of 3.1 mm @ 10 m. In addition, the viewpoints were planned next to the objects along the road and near the control points, which are defined by attached targets (pillar or building) shown in Figure 3. These control points are used for georeferencing the point cloud and are part of an evaluation environment [1], which consists of a dense network of 37 control points in total. The control points are determined in a network adjustment based on measurements from total station, GNSS and leveling, which results in an estimated standard deviation of <0.1 cm. Measurements of the network were carried out in two consecutive years to verify the stability of the control points included. Further information about the measurements and methodology can be found in Heinz [1]. The coordinates of all control points are given in the official German coordinate system ETRS89/UTM32 (European Terrestrial Reference System 1989, Universal Transverse Mercator, Zone 32) for positions. Furthermore, the heights are given in physical heights (DHHN16, German Main Height Network 2016) and also ellipsoidal heights (GRS80, Geodetic Reference System 1980). Subsequently, the control point coordinates are used in the registration of TLS viewpoints to process the georeferenced point cloud. The processing of TLS measurements was done using the Leica Cyclone processing software. The registration error related to control points is given with a RMSE (root mean square error) of 0.5 cm. To control the reference point cloud, additional RTK-GNSS measurements were performed at two different epochs on this day, which showed a RMSE of the reference point cloud <1 cm for the height component. For the second study area with the multiple strip measurements, the creation of the reference point cloud is done quite similar as for the first study area, using a Leica ScanStation P50 and a georeferencing based on known control points as already described. The registration error related to the control points is given with an RMSE of 0.8 cm for the second study area and is further verified by RTK-GNSS measurements of the distributed targets, which are again in a range <1 cm. Therefore, the absolute accuracy described by the RMSE of the georeferenced point cloud in both study areas is much higher than the expected accuracy of the UAV-based laser scanning system measurements and can be used as a reliable reference.
2.3.3. UAV-Based Laser Scanning Measurements and Processing
The UAV measurements are divided into the flights for single and multiple strip measurements. For both approaches we collected data from four identical flights, using the UgCS software for flight planning. Right before and after the measurements, a recommended flight pattern is included, which is later used for sensor initialization in the trajectory estimation process. For the single strip measurements, the flight path is shown in Figure 3 with a straight flight from the start in the north–east direction and on the same path back. The flight plan was chosen due to the challenging conditions for the trajectory estimation with a constant heading of the UAV and, thus, performance evaluation under less optimal conditions similar to corridor mapping. For the measurements with multiple strips, the corresponding flight path is shown in Figure 4. The flight height and speed were chosen according to the buildings and objects to cover the entire area with one flight and the highest possible point density. The corresponding flight parameters for the individual approach are listed in Table 3.

Table 3.
UAV flight parameters for single and multiple strip measurements.
The flight height for the single strip measurements was 10 m, the flight speed was 1 m/s and the line speed of the laser scanner was 55 lines per second. With this configuration, the average point spacing is about 2.2 cm leading to about 2495 points per square meter. With this setting of the flight parameters, the evaluation of the point cloud should mainly include the errors from the trajectory estimation and the system calibration, since the influence of the errors due to the laser scanner is expected to be within the manufacturer’s specification of 1.5 cm. Based on this, the evaluation of the system mainly refers to the aspects of trajectory and system calibration. Thus, the most important aspect is the trajectory accuracy and especially the absolute accuracy resulting from the differential GNSS processing. To evaluate the influence of the choice of the GNSS master station on the result, we compare the different GNSS master stations listed in Table 4.

Table 4.
GNSS master stations used for trajectory estimation of single strip measurements for experiment (4).
The master station mainly used within all experiments is the own master station set to pillar (Figure 3) next to both study areas. The pillar is part of the network of control points and, therefore, known with an accuracy of a few millimeters. The receiver used as the master station is a Leica GS10 with a Leica AS10 multi-GNSS antenna. Besides this own master station, two additional VRS next to the study area and a CORS station from the SAPOS NRW network in 16 km distance are included, which are only used in the comparison between master stations.
The explained measurements are afterward processed using the calculation scheme described in Figure 1 divided in trajectory estimation and the following georeferencing of laser scanner data. The first step of trajectory estimation is done using the software POSPac UAV providing the smoothed trajectory in the same coordinate system as the reference point cloud (ETRS89). The following processing of the point cloud is done with RIEGL’s software RiPROCESS without any additional optimization step or integration of GCPs. The outputs are the georeferenced 3D point clouds for the first study area, which are used in the following section for the evaluation of the system’s performance.
For the second study area, the full processing using RiPRECISION within RIEGL’s RiPROCESS software is used for the optimization of the point cloud product based on overlapping flight strips (Figure 1). This processing corrects the initial UAV trajectory by the alignment of multiple laser scans from the same area and a following reprocessing of the optimized point cloud. The corrections are performed with the point clouds from multiple strips, derived geometric point cloud features, and sensor information such as amplitude or reflectance used in various types of distance minimization to reduce modeling disparities. Within RiPRECISION all flight strips are selected for the optimization with automatic feature detection and a non-rigid adjustment mode with translation. The capability of this additional processing step with RiPRECISION is analyzed shortly with the noise parameter for parts of the point cloud. If the correction of overlapping scans from different flight directions would fail, scan strips are misaligned and the estimated residuals for a plane surface within the point cloud will increase systematically. Since the general accuracy and especially the georeferencing of the UAV system is investigated, no additional GCPs are used.
3. Results
The results are presented in the same order as described in Section 2.2 with the four research aspects related to the single strip measurements separated in Experiment (1)–(4) and the second part of multiple strip measurements described in Experiment (5)–(6). The first results of Experiment (1)–(3) are all based on processing with the own GNSS master station located next to the study area.
3.1. Experiment (1): Noise for Single Strip Measurements
The first experiment analyses the noise of the system using planar surfaces in the study area. The data sets utilized for this are the four repetitions of the single strip measurements. The objects used for the noise analyzes are the six tables shown in Figure 3, which are extracted from the four data sets. For noise evaluation, the residuals with respect to a plane fit are taken, as described in [43]. For the plane estimation, a RANSAC algorithm is first used for plane identification and extraction of the corresponding 3D points . Afterwards, the individual plane can be described with equation
in the three dimensional space. The parameters for the estimation using a Gauß-Helmert model are the orthogonal distance p between origin and plane, and the components of the unit normal vector and [44]. Since the tables are placed horizontally and directly under the flight path, it can be assumed that the angle of incidence for all measurements is close to and deviations due to different incidence angles are therefore negligible. Based on this assumption, the residuals to the plane in z-direction obtained from the adjustment are used for the estimation of the range precision with
where n defines the number of points referring to the plane. An example of the distribution of residuals with respect to the plane fit is shown in Figure 6a for a table from the first data set.
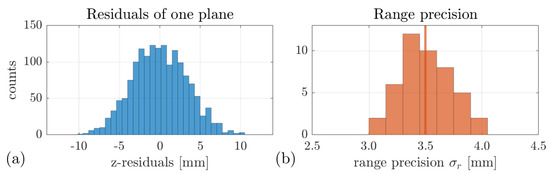
Figure 6.
Evaluation of point cloud noise with residuals regarding plane estimation for an example plane (a) and the histogram of all range precision estimated based on four data sets (b).
Considering all data sets for the single strip measurements, the range precision is estimated for all tables included in each data set and plotted summarized by a histogram in Figure 6b. A total of 48 planes were used for noise evaluation with a mean number of points per plane fit of 1327. The resulting mean range precision for the 10 m flight height is 0.35 cm, which is within the manufacturer’s specification of 1.0 cm [41]. Furthermore, this result describes the impact of scanner precision on the subsequent quality analysis, which is comparatively negligible taking the uncertainty due to trajectory estimation into account. The absolute accuracy of the laser scanner cannot be analyzed with this approach because a systematic offset cannot be separated from errors due to trajectory estimation. For investigations that consider the absolute accuracy of the laser scanner, the sensor should be analyzed without the UAV, while the uncertainties due to trajectory estimation have no influence.
3.2. Experiment (2): Point-Based Absolute Accuracy and Precision for Single Strip Measurements
The second experiment analysis the precision and absolute accuracy based on the comparison to the TLS reference point cloud. The first quantification of accuracy is derived from the target coordinates of four TLS targets divided over the whole study area. The target centers are computed for TLS with and the four flight repetitions with the algorithm by Janßen et al. [42]. This algorithm uses a robust plane estimation for the selected target and subsequent template correlation to detect the target center coordinates with a standard deviation in the millimeter range. The TLS point cloud as well the UAV-based laser scanning point clouds are given in the official German coordinate system ETRS89/UTM32 with ellipsoidal heights. The used relations for quality assessment are shown in Figure 7 simplified for one target and only two dimensions.
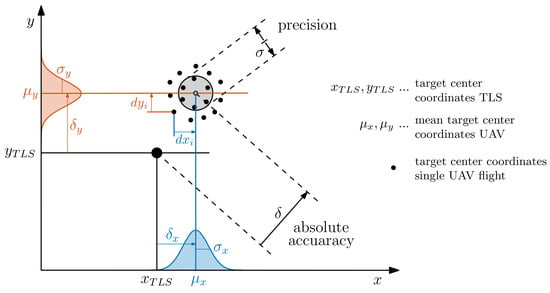
Figure 7.
Relation of target center coordinates from TLS to multiple estimates of the same target from UAV data sets. Included quality parameters are the absolute accuracy and precision.
The coordinates for the target centers from TLS with are assumed to be the reference. Since each target is included multiple times in the four repetitions with the UAV, the precision can be estimated based on the mean target coordinates . The differences between TLS and the UAV-derived target center coordinates are used for the description of the absolute accuracy described with . Considering the differences for all target centers from the UAV data set, a corresponding root mean square error ( RMSE) is calculated.
The histograms in Figure 8 combine the results for four UAV flights and the differences for target coordinates in East, North and height direction. The results are shown together for all targets indicated with the index i for the corresponding data set and index j for the target number.
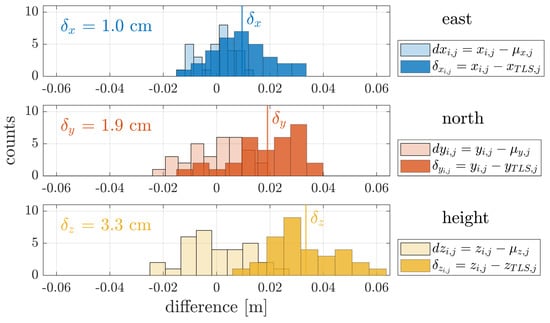
Figure 8.
Histogram for East, North and height difference of estimated target coordinates for four flights. Results are separated in estimates for the precision and absolute accuracy compared to the TLS reference.
The mean absolute difference for the east direction is 0.9 cm with a RMSE of 1.1 cm and for the north direction it is 1.9 cm with 1.2 cm RMSE. The mean absolute difference of target coordinates describes the absolute accuracy of a single measurement without any additional information or correction within the processing. Based on the shown results a systematic error can be seen in the height coordinate by with 3.3 cm, which should be analyzed also by the use of additional objects in the study area. Furthermore, the RMSE for the vertical direction is only 1.2 cm and of a similar order of magnitude compared to the horizontal direction. The precision of the system is determined with the standard deviation using , and . It is lower than 1.2 cm for all directions. Both results are better than the manufacturer’s system specification. Especially the precision shows good results in position and height direction.
Since the uncertainty in the vertical direction is typically worse than the horizontal direction, the tables within the study area are used for the additional analysis of the height component. Therefore, the described plane estimation from Experiment (1) is used for the determination of table heights for a given position on the table. The estimated ellipsoidal heights are compared with the reference from the TLS point cloud. The six tables within the study are measured again twice for one data set as before described for the target evaluation. The results for the individual flights are shown in Figure 9 with a summary of the whole data set in the histogram on the right.
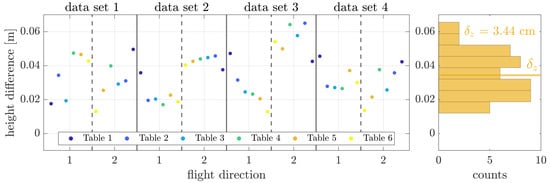
Figure 9.
Height difference of estimated table heights for four flights.
The mean absolute height difference for all table heights are 3.4 cm with a RMSE of 1.3 cm. The systematic offset of about 3 cm is equal to the target-based analysis before, which in general describes a better and consistent absolute accuracy than expected. Also, the RMSE with 1.3 cm provides a good result based on the error budget assumed for the UAV-based laser scanning system. Overall the analysis compared to the TLS reference has shown an absolute accuracy defined by mean difference of <3 cm for the horizontal direction and <4 cm for the vertical direction. In addition, the precision of the system analyzed based on the repeated flights described with the standard deviation is <1.2 cm for the horizontal and vertical direction. These results should serve as a good benchmark for the transfer to other settings and primarily analyze the accuracy of the UAV’s trajectory.
3.3. Experiment (3): Parameter-Based Absolute Accuracy for Single Strip Measurements
The third experiment is an assessment based on the estimated table planes from Experiment (2). Compared to the point-based evaluation of the point clouds, this approach uses a parameter-based evaluation with the estimated plane parameters given in Equation (2). The normal vector defining the orientation of each plane in space is compared to the reference planes from the TLS point cloud. For better interpretation, the tilt is divided into a tilt along and one across the direction of flight. The computation is done using the known heading during the flight. With this tilt parameter, any misalignment of the UAV point cloud could be detected, especially due to errors in the bore-sight angles. The summarized results for the four flights and all included tables are shown in Figure 10 with the tilt across and in the direction of flight.
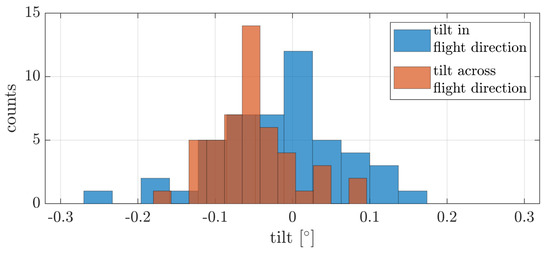
Figure 10.
Tilt of planes estimated from UAV point cloud compared to the TLS reference in flight and across flight direction.
The mean tilt across flight direction is with a RMSE of 0.085 and the mean tilt in flight direction is with a RMSE of . The tilt estimates for the precision are nearly the same and the standard deviation is within the same magnitude.
With these results, various conclusions can be drawn about the precision and absolute accuracy. Due to the scan configuration, the roll angle and the corresponding calibration parameter can be analyzed perfectly. A systematic error in the roll angle would lead to an offset respectively tilt of the point clouds from the flights in the opposite direction. With the histogram of the tilt parameter across the flight direction, a systematic error can be excluded. The small systematic offset with the mean value of can be classified as non-significant. The standard deviation for both tilt directions is another measure of the high precision of the system for multiple flights. Based on the table size, a tilt of would result in a height offset of less than 0.2 cm, which is within the noise level of the UAV-based laser scanning system and also the limitation imposed by the accuracy of the TLS reference.
3.4. Experiment (4): GNSS Master Station
The fourth experiment based on the single strip measurements data set is investigating the impact of different GNSS master stations on the quality of the georeferenced point cloud. In addition to the own master station mounted on a pillar and used for all experiments before, a CORS station and two different VRS are used within the processing. The evaluation parameters are identical to Experiment (2) based on the difference of target center coordinates compared to the TLS reference and the corresponding RMSE of targets centers from four flight repetitions. The calculated differences are shown in Figure 11 for the four different master stations each for the coordinate difference in the east (blue), north (red) and height (yellow) direction.
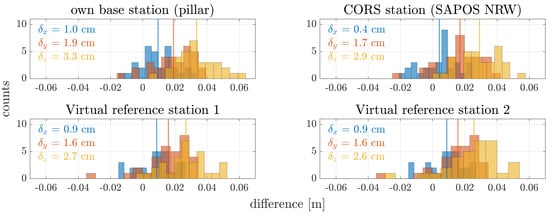
Figure 11.
Difference of the estimated target coordinates compared to the TLS reference when using different master stations for the trajectory estimation. In addition to the own master station used before, a CORS station and two VRS are used. The histograms show the combined results for four flights and all targets included considering the east (blue), north (red) and height (yellow) coordinates.
In addition, the mean absolute difference is indicated in each histogram and in combination with the RMSE given in Table 5. The parameters are estimated based on eight targets for each of the four flights which leads to a total number of 32 targets used for the computation.

Table 5.
Target center difference between TLS reference and UAV point cloud with four different GNSS master stations. The difference is described using the mean value and standard deviation for the East, North and height direction.
In the visual evaluation with Figure 11, the results for the estimated coordinates for different master stations are very similar without much variation. This is stated also with the calculated mean difference as quantification of the absolute accuracy, which only differs in the mm range between different solutions. The expectation beforehand for absolute accuracy was, that results based on own master station would perform best since the pillar coordinates are well known and the conditions for GNSS observations are the same as for the UAV. Comparing the mean difference of the own master station with both VRS and the CORS station, the difference is slightly higher and the results for the RMSE can be rated as equal. Summarizing the absolute accuracy for the comparison of different GNSS master stations, the results are equal on the cm level. The estimated offset is about 1 cm in the horizontal direction and about 3 cm in the vertical direction for all variations of processing. Additionally, the RMSE is used as a measure of the quality, where results are similar or even identical for different master stations. In this case, the own master station provides the best results but without a substantial deviation from the other ones. The conclusion from the evaluation of the Experiment (4) leads to the statement that the use of a VRS and also a CORS station in 16 km distance delivers similar results. Since setting up an own master station always involves additional effort, the two other variants offer a viable alternative that can be recommended. In particular, the use of a VRS is a frequently used approach anyway and is probably the best variant for many applications.
3.5. Experiment (5): Point-Based Absolute Accuracy and Precision for Multiple Strip Measurements
The last Experiments (5) and (6) are investigations based on the second data set already mentioned in Table 3 as multiple strip measurements. Since the analysis of different GNSS master stations in Experiment (4) has shown equal results for all master stations, the processing is only done using a VRS. The first parameter for the precision of the point cloud is given with the noise of different parts in the point cloud. The approach for noise estimation is used as in Experiment (1) and the areas of the 12 targets are extracted for this estimation. The result for the four repetitions and all targets is a mean noise of 0.6 cm. Here, several factors influencing the accuracy of the point cloud can be evaluated simultaneously. First of all, the influence of the laser scanner on the error budget can again be classified as small, since the manufacturer accuracy is even worse specified than the total noise of the resulting point cloud. Of course, the specified distance for the given accuracy is not yet reached with 25 m flight altitude, but the calculated value is still much lower than the given 1.0 cm. Furthermore, the performance of the optimization by RiPRECISION is good for this data set, since no major offsets remain within the point clouds. The further results in this experiment are derived from the estimated target centers and the comparison with the target centers from the TLS reference point cloud. The difference divided in the east (blue), north (red) and height (yellow) coordinates are shown in Figure 12 in histograms summarising all four flight repetitions.
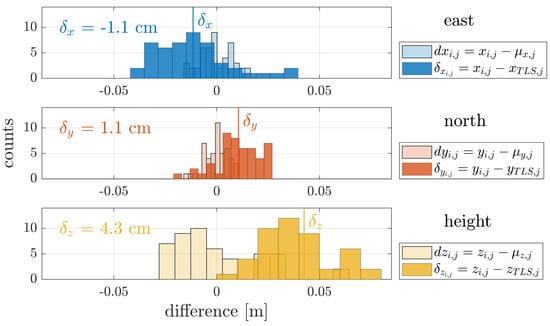
Figure 12.
Difference of the estimated target coordinates compared to the TLS reference considering the east (blue), north (red) and height (yellow) coordinates. A total of 12 targets are estimated for each of the four repeat flights.
The determined mean absolute difference result in cm for the East, cm for the North and cm for the height direction with corresponding RMSE of , cm, and cm. Therefore, the absolute accuracy described by these differences is consistent with the results from Experiment (2) and even a bit smaller for the horizontal direction. The systematic effect in the vertical direction is again similar with a magnitude of 4 cm, which was already recognized in the analysis of the single strip measurement. Since this is only presented as a shift of the point cloud, a simple solution in practice would be the use of one or multiple GCPs. By using a single GCP with precise height information, the entire point cloud can be shifted to the correct height without great effort. The precision described by the standard deviation is given with cm for the East, cm for North and cm for the height component. Both components, horizontal and vertical, are again small and are in accordance with the specification of the manufacturer. Overall, the second data set based on the typical cross-flight pattern with the use of the full processing capability except for the inclusion of ground control information has shown again good results with absolute accuracy described by the mean difference around 1 cm for the horizontal direction and around 4 cm for the vertical direction. Furthermore, the additional processing with RiPRECISION provides a reliable adjustment of the trajectory and so an optimization of the point cloud. The standard deviation as a parameter for the precision provides even better results for the horizontal direction compared to the single strip measurements. This can be explained by the improvement of the point cloud by using multiple measurements from the same area, which are used in the optimization of the point cloud.
3.6. Experiment (6): Parameter-Based Absolute Accuracy for Multiple Strip Measurements
The sixth experiment analyses the orientation of planes within the point cloud according to the parameter-based evaluation as also done in Experiment (3). For the single strip measurements, this approach is capable to detect orientation errors in the trajectory estimation or calibration of the system. The evaluation with the multiple strip measurements in this part will give a general assessment of how well the point cloud is orientated absolutely in space without the ability to trace errors back to their cause due to the complexity of the calculation steps performed. The surfaces of the targets have a size of 0.8 m × 0.8 m and are used for the GHM plane estimation with the normal vector as the parameter. With this normal vector the tilt of the planes can be estimated in relation to the plane parameter derived from the reference point cloud. The tilt is further divided into a tilt between the zenith and north direction and perpendicular between zenith and east direction, which is shown in Figure 13.
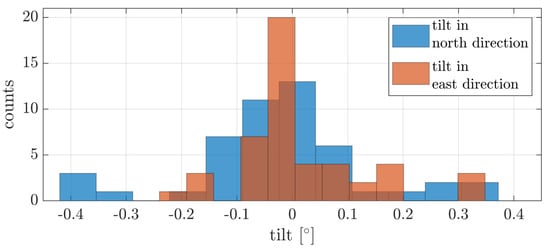
Figure 13.
Tilt of planes estimated from UAV point cloud compared to the TLS reference in north and east direction.
The resulting mean values for the tilt in zenith–north direction is with a RMSE of and in zenith–east direction with a RMSE of . The mean values for both tilt directions indicate that there is no systematic trend or tilting of the entire point cloud compared to the reference. Since the histogram summarizes the estimations based on four separated flights, the distribution can also be used as a measure for the precision. With both RMSE values the precision is a bit higher compared to the first data set but this is explained due to the 25 m flight height. Furthermore, the histogram includes also larger tilt estimates around , which might come from a misalignment in the UAV point cloud but could also be enhanced by the small uncertainty of the TLS point cloud. The tilt of a magnitude of would lead to an error of about 0.6 cm in the height direction considering the object size, which is within the noise level of the point cloud from the UAV-based laser scanning system. The output of the last experiment is a consistent and well orientated point cloud over larger areas and multiple flights. Furthermore, the additional processing for point cloud optimization performs well without manual interaction in the estimation.
4. Conclusions and Outlook
This paper presents an evaluation strategy for the quality assessment of single measurements with a UAV-based laser scanning system and, in particular, the capability for direct georeferencing and the corresponding absolute accuracy and precision. Since the evaluation of a UAV-based laser scanning system is non-trivial due to the complex processing chain and included error sources, the evaluation is performed on the derived point cloud using parameter-based and point-based evaluation strategies. The first study area was designed similar to the challenges within corridor mapping. With this flight planning, systematic errors due to trajectory estimation and especially system calibration are detectable. With the use of a second study area and the different flight plan based on a cross-flight pattern, the capability of RIEGL’s software RiPRECISION was analyzed. The comparison for both study areas is performed with a TLS point cloud reference and the use of different objects like tables and targets. The following results are structured in the same order as the research aspects in Section 2.2 and summarize the results from both study areas.
- (1)
- The first parameter describing the noise and therefore the range precision of the laser scanner resulted in 0.4 cm for the flight height of 10 m for the single strip measurements and 0.6 cm for the flight height of 25 m for the multiple strip measurements. With the second data set, the performance of RiPRECISION is evaluated as well, which performs a proper alignment of several strips from the cross-flight pattern.
- (2)
- The absolute accuracy using the target-based evaluation for four separated flights was given with 0.9 cm in east, 1.9 cm in north and 3.4 cm in height direction for the single strip measurements. The additional focus to the vertical direction using table heights provided nearly the identical height offset of 3.4 cm with a RMSE of 1.3 cm. The results for the multiple strip measurements are consistent with everything concluded from the first data set with a mean difference in the horizontal direction around 1 cm and in vertical direction around 4 cm. The additional parameter-based evaluation was performed for the two different study areas and the tilts between estimated planes are always within the noise level of the point cloud and no systematic effects are observed.
- (3)
- The precision of the UAV system resulted in a standard deviation of 0.7 cm for the east, 1.1 cm for the north and 1.2 cm for height direction. The system provides excellent results over the whole study area for the single strip measurements. The same analysis resulted in a precision of 0.8 cm in the east, 0.5 cm in the north and 2.1 cm in height direction for the multiple strip measurements.
- (4)
- The impact of different master stations is assessed by the use of an own master station, a CORS station and two different VRS. The output of the performed point-based evaluation leads to nearly identical results for the four different GNSS data sets and therefore the conclusion, that strategy should be chosen, which is easiest to handle for the user. Overall, the VRS and the CORS station have shown good results considering the mean absolute difference and are therefore an appropriate alternative for the processing.
Besides the investigations of absolute accuracy, this study shows a new investigation approach for analyzing the precision of UAV-based laser scanning systems. By the use of identical flight planning and repeated measurements, the independent data sets are usable for a precision investigation. This approach can also be performed on a larger scale with different flight parameters and the use of natural objects for similar quality analysis. Overall, the results for the used UAV-based laser scanning system are better than expected based on the manufacturer’s specification. The larger difference in height direction for both study areas might be explained by the uncertainty of the system calibration and especially a systematic error due to the lever arm between sensors. This has to be investigated if a higher accuracy level should be achieved with direct georeferencing. However, it should again be emphasized that for all investigations GCPs were still not used or further manual adjustment in the point cloud optimization is performed. The additional processing step by RiPRECISION has shown a conceivable easy optimization step, which should be part of a standard procedure, but is specifically skipped in parts of this work to analyze the possibilities of the system.
Author Contributions
Conceptualization, A.D., J.J. and L.K.; experiments, A.D. and J.J.; methodology, validation and visualization, A.D.; writing—original draft preparation, A.D.; writing—review and editing, A.D., J.J. and L.K.; supervision, L.K. and H.K.; project administration, L.K.; resources and funding acquisition, H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy–EXC 2070–390732324.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Heinz, E.; Eling, C.; Klingbeil, L.; Kuhlmann, H. On the applicability of a scan-based mobile mapping system for monitoring the planarity and subsidence of road surfaces–Pilot study on the A44n motorway in Germany. J. Appl. Geod. 2020, 14, 39–54. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Guimarães, N.; Pádua, L.; Marques, P.; Silva, N.; Peres, E.; Sousa, J.J. Forestry remote sensing from unmanned aerial vehicles: A review focusing on the data, processing and potentialities. Remote Sens. 2020, 12, 1046. [Google Scholar] [CrossRef] [Green Version]
- Shahmoradi, J.; Talebi, E.; Roghanchi, P.; Hassanalian, M. A Comprehensive Review of Applications of Drone Technology in the Mining Industry. Drones 2020, 4, 34. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Cao, S.; Yu, Y. Use of mobile LiDAR in road information inventory: A review. Int. J. Image Data Fusion 2016, 7, 219–242. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2021, 13, 77. [Google Scholar] [CrossRef]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2018. [Google Scholar]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. Quality assessment of combined IMU/GNSS data for direct georeferencing in the context of UAV-based mapping. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2017, 42, 355. [Google Scholar] [CrossRef] [Green Version]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: Boston, MA, USA; London, UK, 2013. [Google Scholar]
- Vosselman, G.; Maas, H.G. Airborne and Terrestrial Laser Scanning; Whittles Publishing: Dunbeath, Scotland, 2010. [Google Scholar]
- Heinz, E.E. Beiträge zur Kalibrierung und Evaluierung von Multisensorsystemen für Kinematisches Laserscanning. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2021. [Google Scholar]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Pilarska, M.; Ostrowski, W.; Bakuła, K.; Górski, K.; Kurczyński, Z. The potential of light laser scanners developed for unmanned aerial vehicles-the review and accuracy. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 42, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Glennie, C. Rigorous 3D error analysis of kinematic scanning LIDAR systems. J. Appl. Geod. 2007, 1, 147–157. [Google Scholar] [CrossRef]
- Habib, A.; Bang, K.I.; Kersting, A.P.; Lee, D.C. Error budget of LiDAR systems and quality control of the derived data. Photogramm. Eng. Remote Sens. 2009, 75, 1093–1108. [Google Scholar] [CrossRef]
- Vennegeerts, H. Objektraumgestützte kinematische Georeferenzierung für mobile-mapping-systeme. Ph.D. Thesis, Fachrichtung Geodäsie und Geoinformatik der Leibniz-University, Hanover, Germany, 2011. [Google Scholar]
- Tulldahl, H.M.; Bissmarck, F.; Larsson, H.; Grönwall, C.; Tolt, G. Accuracy evaluation of 3D lidar data from small UAV. In Electro-Optical Remote Sensing, Photonic Technologies, and Applications IX; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9649, p. 964903. [Google Scholar]
- Mandlburger, G.; Pfennigbauer, M.; Schwarz, R.; Flöry, S.; Nussbaumer, L. Concept and Performance Evaluation of a Novel UAV-Borne Topo-Bathymetric LiDAR Sensor. Remote Sens. 2020, 12, 986. [Google Scholar] [CrossRef] [Green Version]
- Hesse, C. Hochauflösende Kinematische Objekterfassung mit terrestrischen Laserscannern. Ph.D. Thesis, Leibniz-University, Fachrichtung Geodäsie und Geoinformatik, Hanover, Germany, 2008. [Google Scholar]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform mobile laser scanning: Usability and performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef] [Green Version]
- Lim, S.; Thatcher, C.A.; Brock, J.C.; Kimbrow, D.R.; Danielson, J.J.; Reynolds, B. Accuracy assessment of a mobile terrestrial lidar survey at Padre Island National Seashore. Int. J. Remote Sens. 2013, 34, 6355–6366. [Google Scholar] [CrossRef]
- Barber, D.; Mills, J.; Smith-Voysey, S. Geometric validation of a ground-based mobile laser scanning system. ISPRS J. Photogramm. Remote. Sens. 2008, 63, 128–141. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Kukko, A.; Jaakkola, A.; Hyyppä, H. Benchmarking the performance of mobile laser scanning systems using a permanent test field. Sensors 2012, 12, 12814–12835. [Google Scholar] [CrossRef] [Green Version]
- Schlichting, A.; Brenner, C.; Schön, S. Bewertung von Inertial/GNSS-Modulen mittels Laserscannern und bekannter Landmarken. PFG Photogramm. Fernerkundung Geoinf. 2014, 1, 5–15. [Google Scholar] [CrossRef]
- Pentek, Q.; Kennel, P.; Allouis, T.; Fiorio, C.; Strauss, O. A flexible targetless LiDAR–GNSS/INS–Camera calibration method for UAV platforms. ISPRS J. Photogramm. Remote Sens. 2020, 166, 294–307. [Google Scholar] [CrossRef]
- Tucci, G.; Visintini, D.; Bonora, V.; Parisi, E.I. Examination of indoor mobile mapping systems in a diversified internal/external test field. Appl. Sci. 2018, 8, 401. [Google Scholar] [CrossRef] [Green Version]
- Gräfe, G. Kinematische Anwendungen von Laserscannern im Straßenraum. Ph.D. Thesis, University der Bundeswehr München, Fak. für Bauingenieur-und Vermessenswesen, Hanover, Germany, 2009. [Google Scholar]
- Toschi, I.; Rodríguez-Gonzálvez, P.; Remondino, F.; Minto, S.; Orlandini, S.; Fuller, A. Accuracy evaluation of a mobile mapping system with advanced statistical methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 245. [Google Scholar] [CrossRef] [Green Version]
- Haala, N.; Peter, M.; Kremer, J.; Hunter, G. Mobile LiDAR mapping for 3D point cloud collection in urban areas—A performance test. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 1119–1127. [Google Scholar]
- Glira, P.; Pfeifer, N.; Mandlburger, G. Rigorous Strip adjustment of UAV-based laserscanning data including time-dependent correction of trajectory errors. Photogramm. Eng. Remote Sens. 2016, 82, 945–954. [Google Scholar] [CrossRef] [Green Version]
- Vosselman, G. Analysis of planimetric accuracy of airborne laser scanning surveys. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 99–104. [Google Scholar]
- Fuad, N.; Ismail, Z.; Majid, Z.; Darwin, N.; Ariff, M.; Idris, K.; Yusoff, A. Accuracy evaluation of digital terrain model based on different flying altitudes and conditional of terrain using UAV LiDAR technology. In Proceedings of the IOP Conference Series: Earth and Environmental Science, 9th IGRSM International Conference and Exhibition on Geospatial & Remote Sensing (IGRSM 2018), Kuala Lumpur, Malaysia, 24–25 April 2018; Volume 169, p. 012100. [Google Scholar]
- Brede, B.; Lau, A.; Bartholomeus, H.M.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR derived canopy height and DBH with terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Dalla Corte, A.P.; Rex, F.E.; Almeida, D.R.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Zambrano, A.M.; Cunha Neto, E.M.; Veras, H.F.; et al. Measuring individual tree diameter and height using GatorEye High-Density UAV-Lidar in an integrated crop-livestock-forest system. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef] [Green Version]
- Cao, L.; Liu, H.; Fu, X.; Zhang, Z.; Shen, X.; Ruan, H. Comparison of UAV LiDAR and digital aerial photogrammetry point clouds for estimating forest structural attributes in subtropical planted forests. Forests 2019, 10, 145. [Google Scholar] [CrossRef] [Green Version]
- Kucharczyk, M.; Hugenholtz, C.H.; Zou, X. UAV–LiDAR accuracy in vegetated terrain. J. Unmanned Veh. Syst. 2018, 6, 212–234. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Development and performance assessment of a low-cost UAV laser scanner system (LasUAV). Remote Sens. 2018, 10, 1094. [Google Scholar] [CrossRef] [Green Version]
- Ltd., S.D.T.C. DJI Matrice 600 Pro. 2019. Available online: https://www.dji.com/matrice600-pro/info#downloads (accessed on 21 April 2021).
- GmbH, R.L.M.S. RIEGL miniVUX-SYS. 2020. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/RIEGL_miniVUX-SYS_Datasheet_2020-10-05_01.pdf (accessed on 21 April 2021).
- Corporation, A. APX-20 UAV. 2020. Available online: https://www.applanix.com/products/dg-uavs.htm#specs-and-brochures (accessed on 21 April 2021).
- GmbH, R.L.M.S. RIEGL miniVUX-2UAV. 2021. Available online: http://www.riegl.com/uploads/tx_pxpriegldownloads/RIEGL_miniVUX-2UAV_Datasheet_2021-04-06.pdf (accessed on 21 April 2021).
- Janßen, J.; Medic, T.; Kuhlmann, H.; Holst, C. Decreasing the uncertainty of the target center estimation at terrestrial laser scanning by choosing the best algorithm and by improving the target design. Remote Sens. 2019, 11, 845. [Google Scholar] [CrossRef] [Green Version]
- Schmitz, B.; Holst, C.; Medic, T.; Lichti, D.D.; Kuhlmann, H. How to Efficiently Determine the Range Precision of 3D Terrestrial Laser Scanners. Sensors 2019, 19, 1466. [Google Scholar] [CrossRef] [Green Version]
- Niemeier, W. Ausgleichungsrechnung: Statistische Auswertemethoden; Walter de Gruyter: Berlin, Germany; New York, NY, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).