Fusing Measurements from Wi-Fi Emission-Based and Passive Radar Sensors for Short-Range Surveillance
Abstract
:1. Introduction
2. Wi-Fi-Based Sensor Description
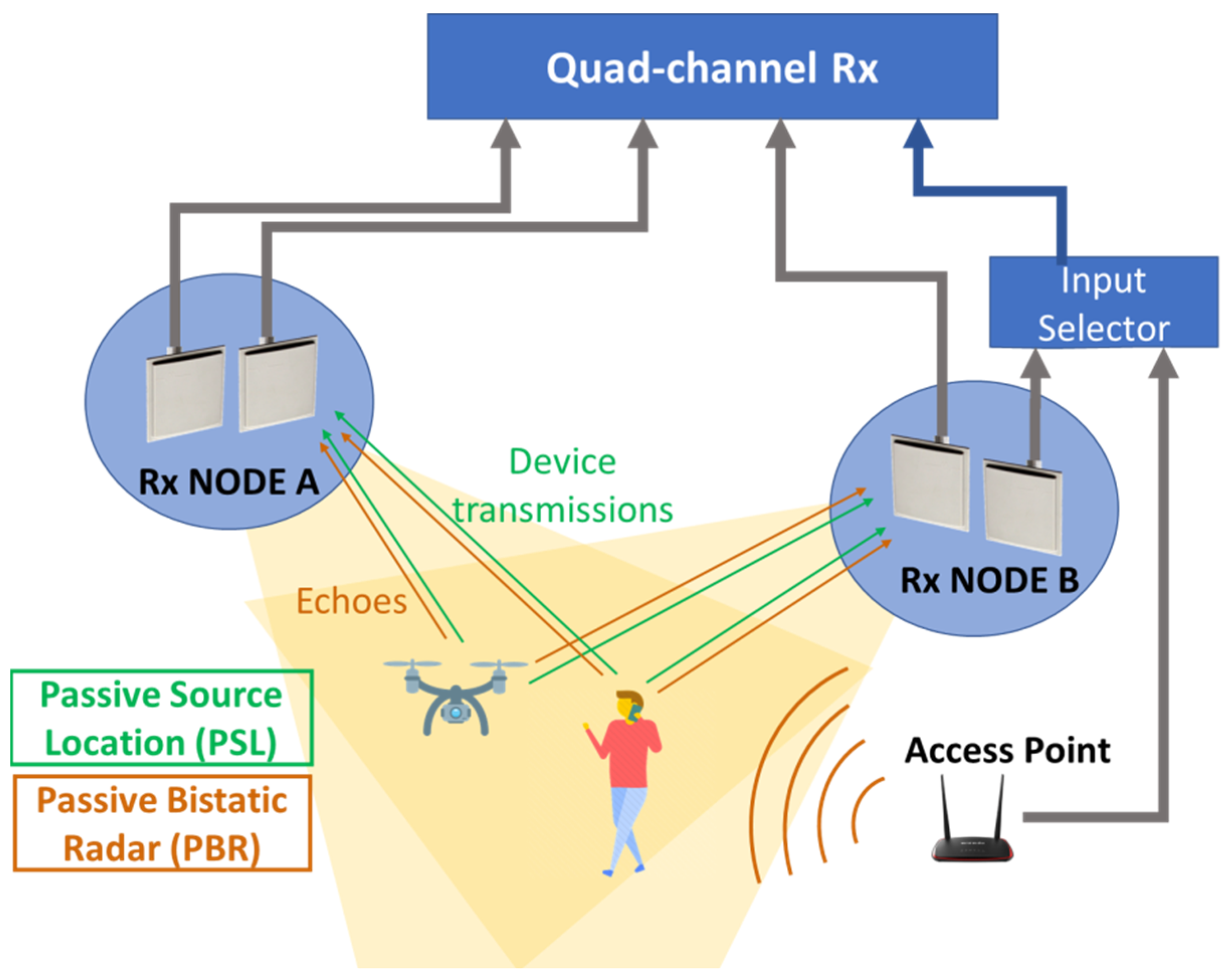
2.1. Multichannel Receiver Architecture and System Setup
- (1)
- If the transmitter of opportunity is directly accessible, and it is possible to introduce a directional coupler between the AP and its antenna, a solution is to connect it to one of the channels of the four-channel Rx. It is worth mentioning that, whilst providing quite a good copy of the signal of opportunity, this approach requires a dedicated receiving channel to be used to collect the reference signal. We explicitly note that, in this case, with the considered setup, the overall system can feature up to three surveillance channels so that node B will employ a single antenna when receiving.
- (2)
- If the Wi-Fi router is not accessible, then the reference waveform must be extracted from the signal collected by one of the surveillance antennas. Specifically, the transmitted signal can be reconstructed by demodulating and remodulating the received signal according to the IEEE 802.11 standard. This approach may suffer from the reconstruction errors, but it avoids the need for a dedicated reference channel. In this case, with the considered hardware setup, it is possible to implement a double-node system where both nodes are equipped with an interferometric pair of surveillance antennas to enable the estimation of the AoA.
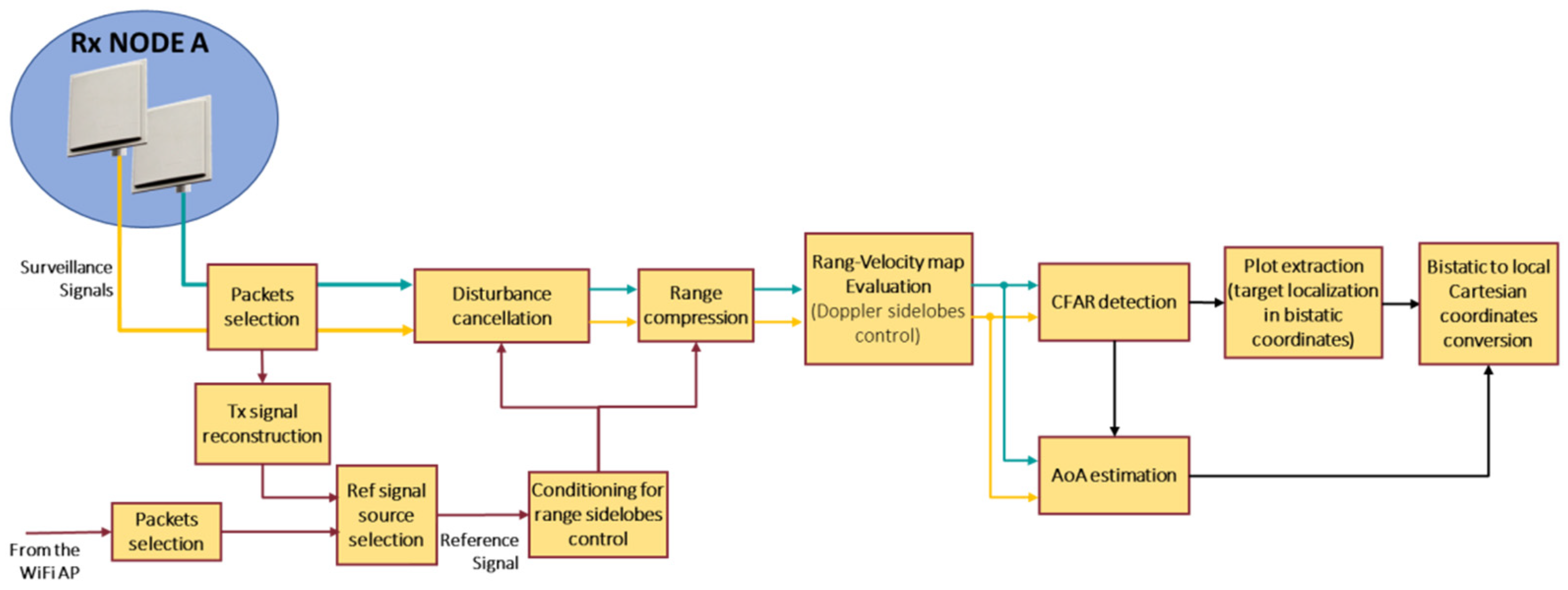
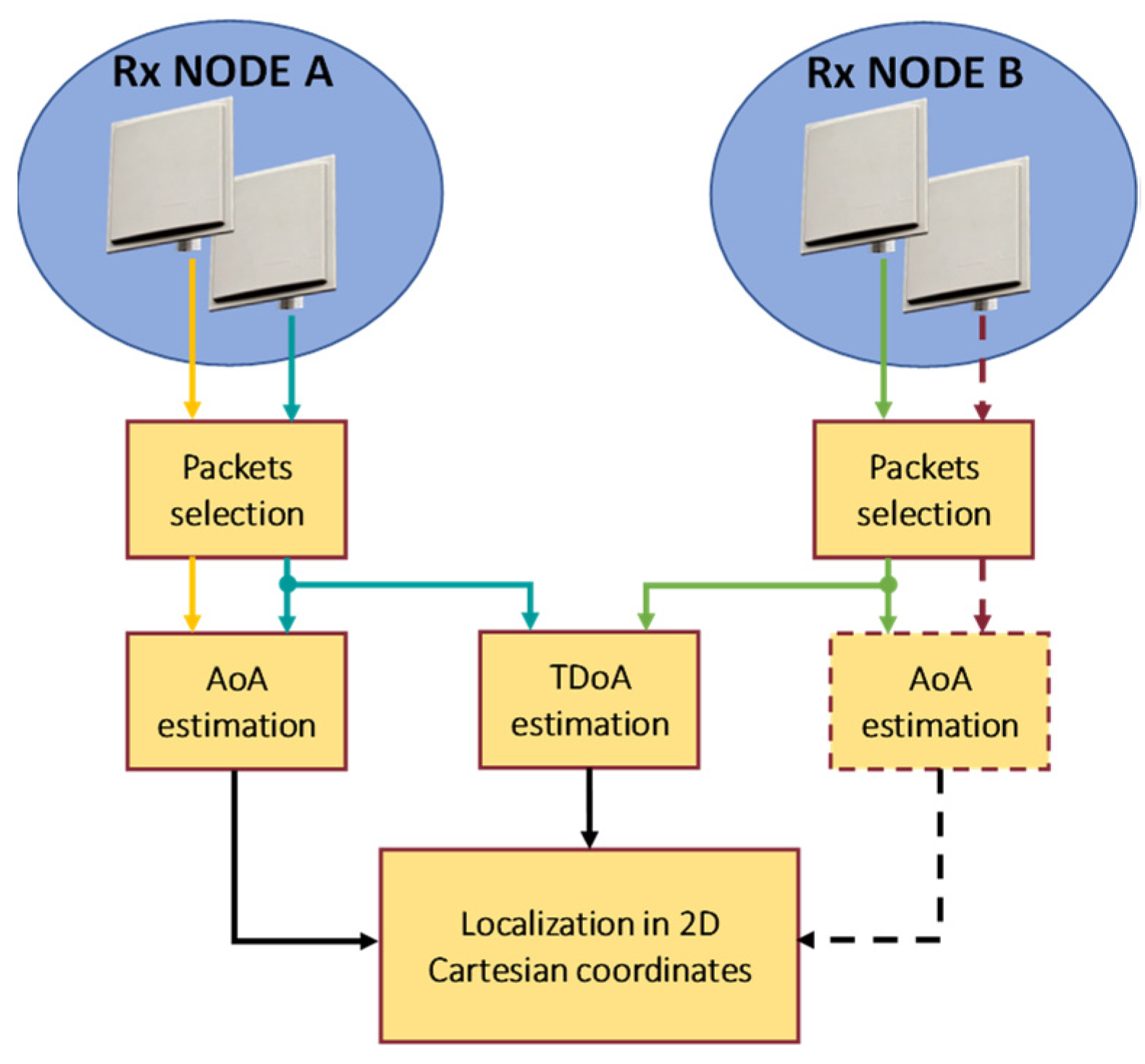
2.2. Passive Bistatic Radar
2.3. Passive Source Location
2.4. Complementarity of PBR and PSL
3. Sensor Fusion for Target Localization
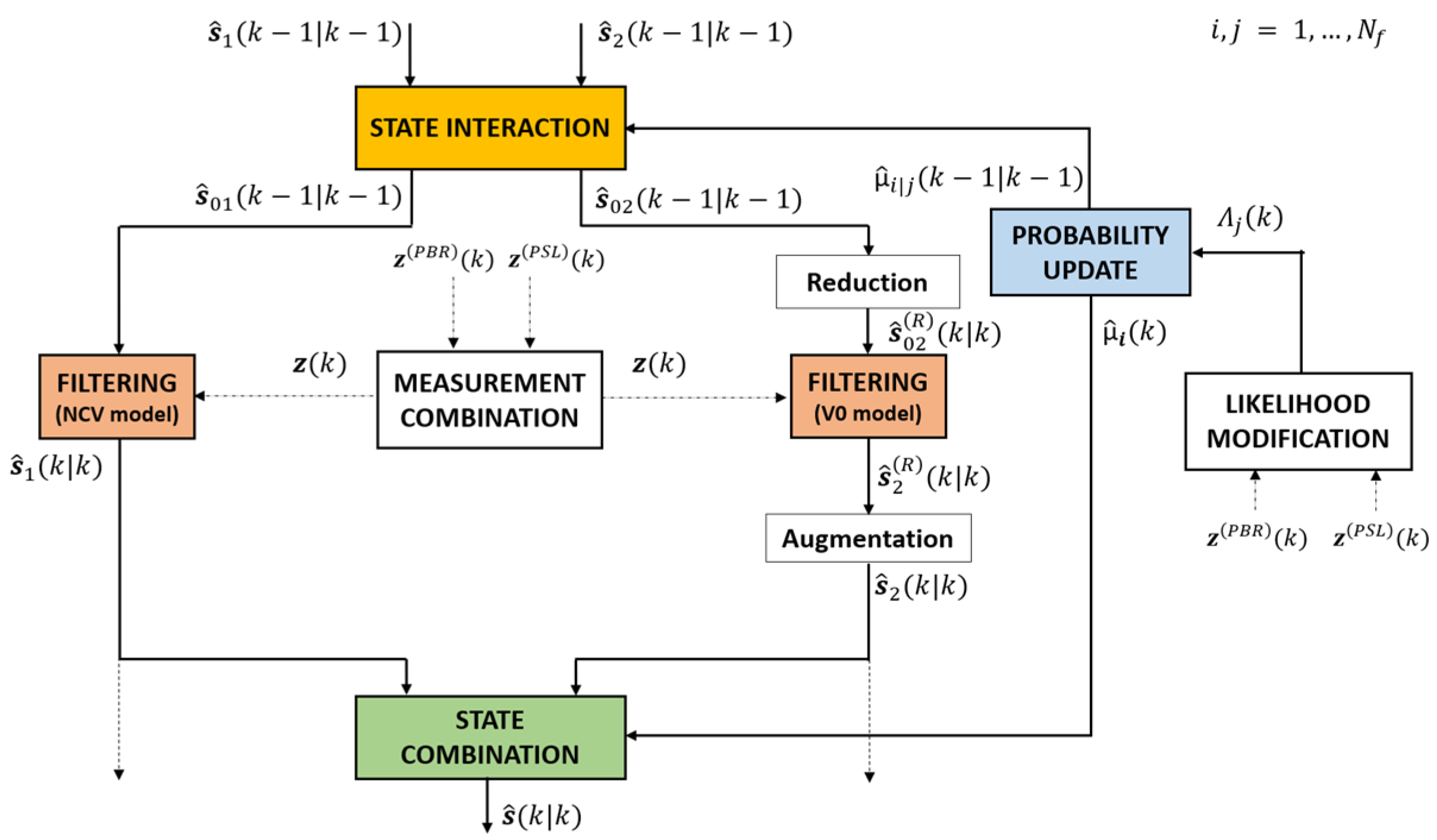
3.1. PBR and PSL-Based Interacting Multiple Model Filter
- (i)
- combines the sensors measurements into a 2 × 1 vector that can be expressed aswhere , is the number of sensors that provide a measurement at time k = 0, 1 or 2 in our case). When = 2, we haveand the error covariance matrix is
- (ii)
- The combined measurement feeds the two Kalman Filters (KF), based on the NCV and the V0 model. The filter outputs ( and ) represent the current filtered estimates of the target state separately provided by the two filters. Notice that the V0 model has a state space of lower dimensions; therefore, its operations inside the IMM require appropriate stages of state augmentation and reduction in order to convert the 2 × 1 vector into a 4 × 1 augmented vector and vice versa.
- (iii)
- The outputs of the two filters are combined in the state combination block in order to provide the final IMM filtered state at time k, , using as weights the mode probabilities provided by the probability update block.
- (iv)
- Eventually, to obtain the required input state for the two filters in the following iterations, the IMM includes a state interaction block that takes as the input the filtered states obtained in the previous iterations: and and produces two mixed states: and . These are obtained by a linear combination of the contributions of each filter, using as coefficients the mixing probabilities calculated in the probability update stage. Similarly, the related state covariance matrices are obtained as inputs to the two filters by mixing the covariance matrices evaluated in each individual KF.The operations performed at each stage are summarized in Table 2.
3.2. Innovation Modification and Probability Update
3.2.1. Absence of PBR Detections
3.2.2. Presence of PBR Detections
4. Tests on Simulated Data
- KF-NCV (Single Sensor): KF with a NCV Model that exploits the measurements of only one sensor.
- KF-NCV (Sensor Fusion): KF with a NCV Model that exploits the measurements of both sensors.
- IMM (Single Sensor): IMM with 2 models (NCV and V0) that exploit the measurements of only one sensor.
- IMM (Sensor Fusion): IMM with 2 models (NCV and V0) that exploit the measurements of both sensors.
- IMM-MI (Sensor Fusion): IMM-MI with 2 models (NCV and V0) that exploit the measurements of both sensors.
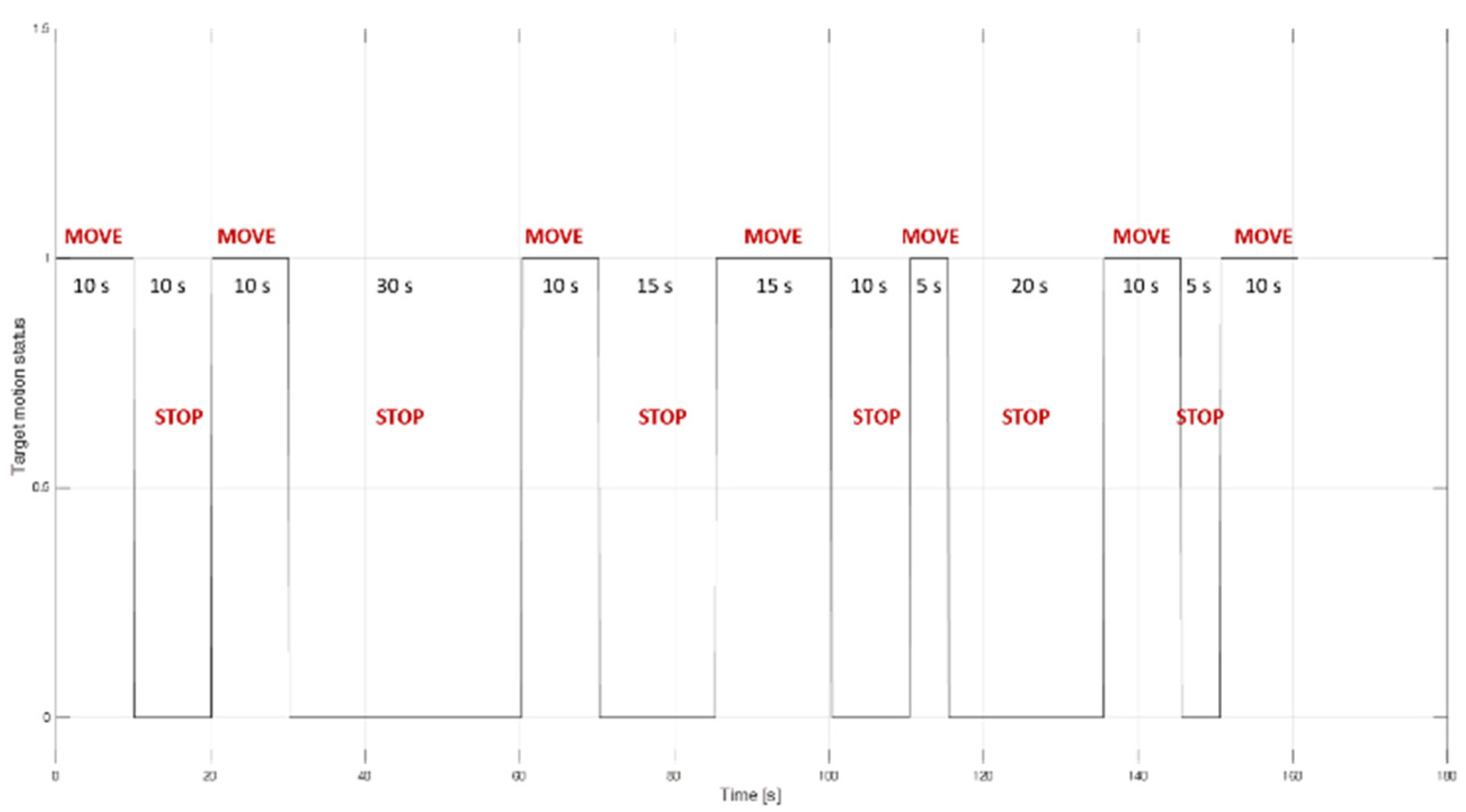
4.1. Case Study Description and Simulation Settings
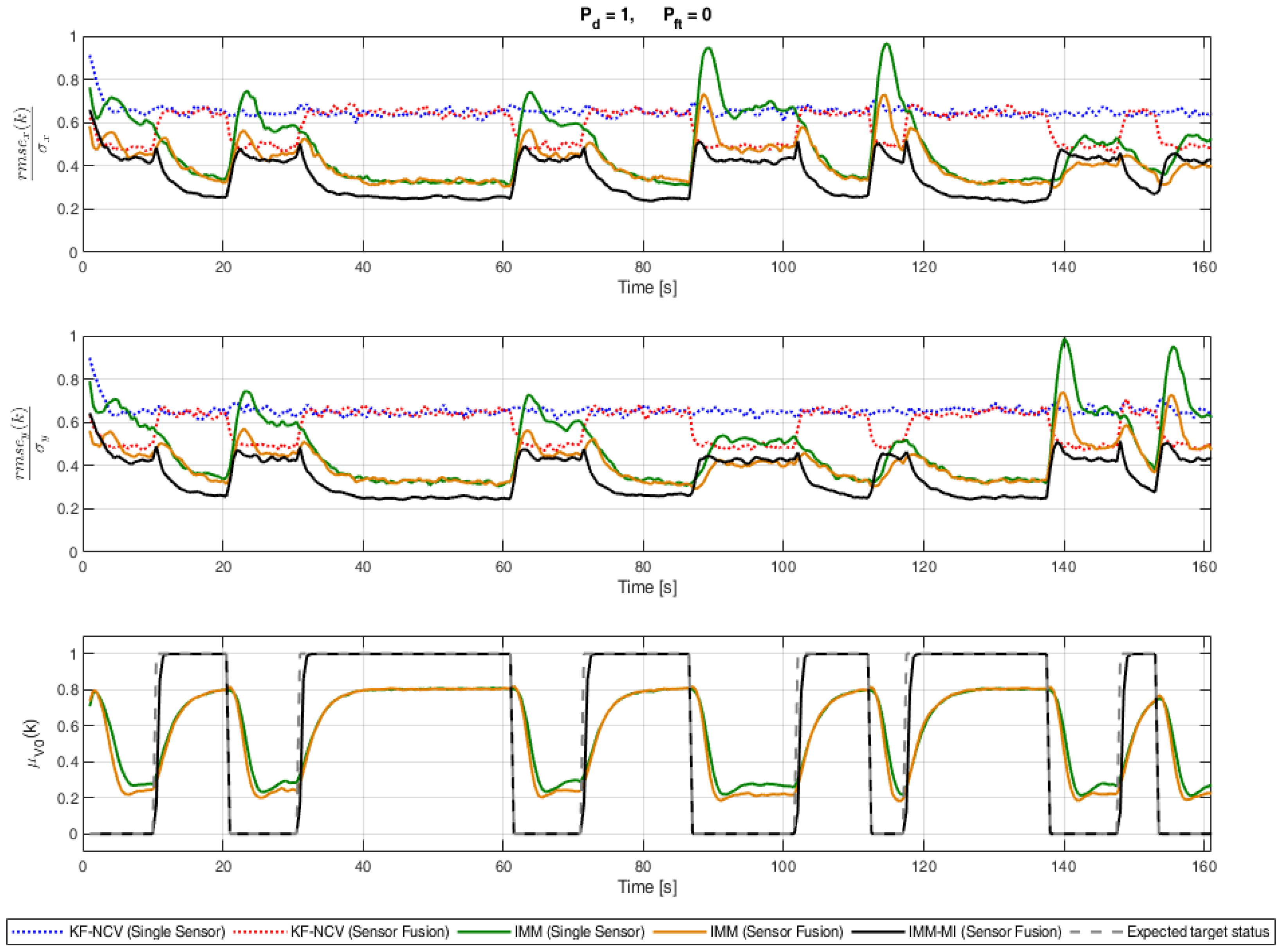
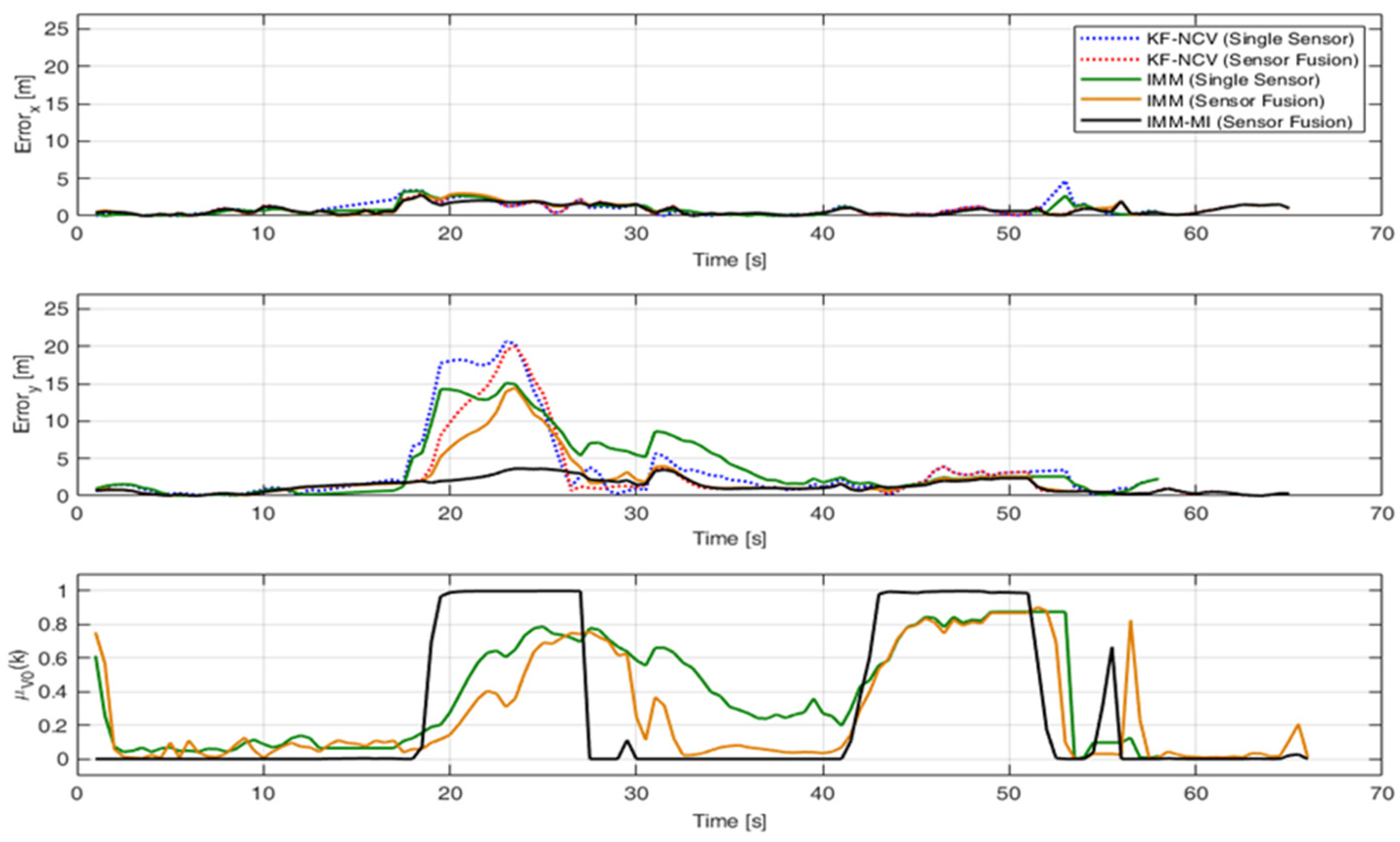
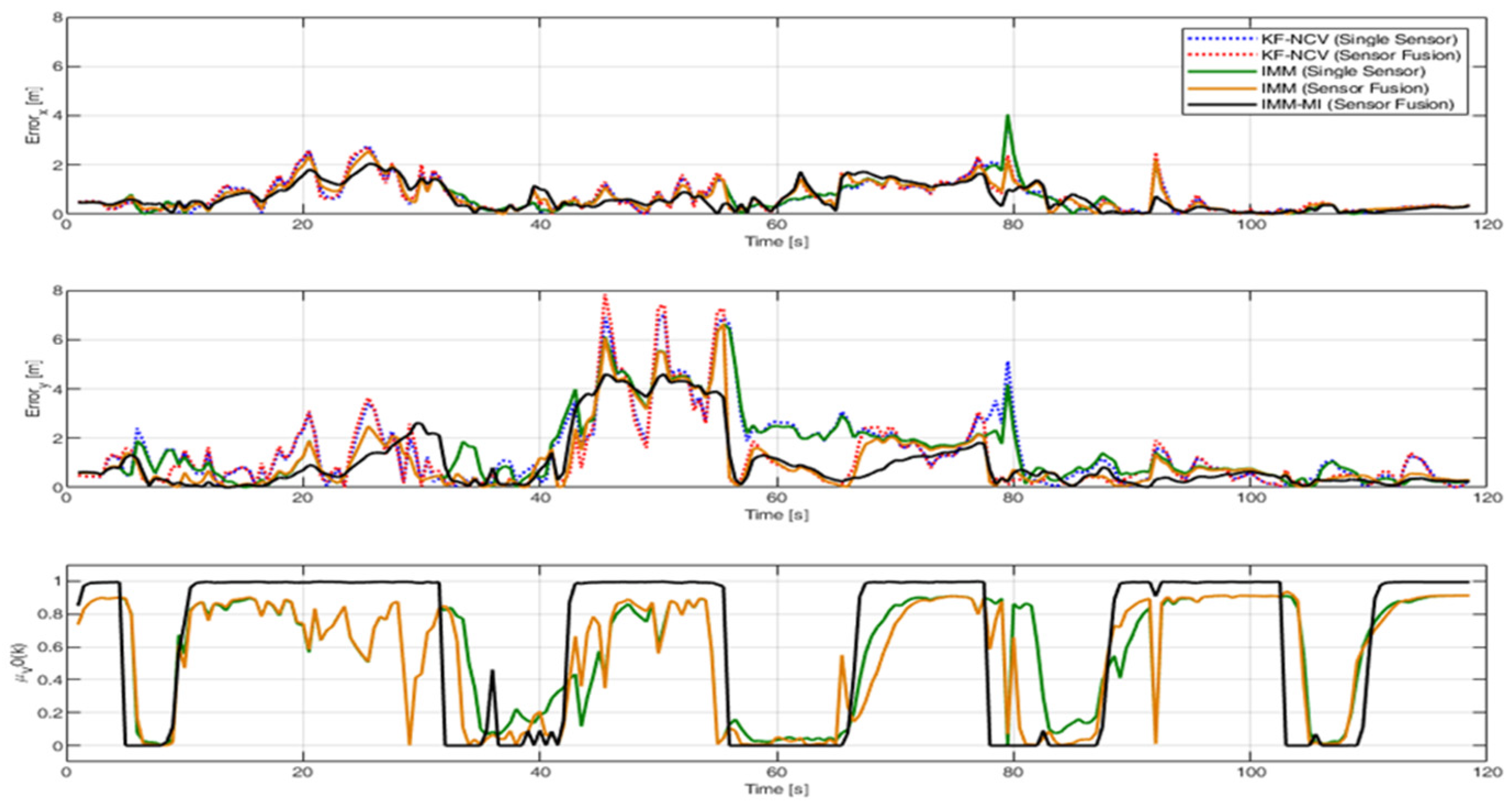
4.2. Evaluation of the RMSE under Ideal Conditions
- (1)
- On average, the sensor fusion version of a specific tracking strategy provides an enhanced performance with respect to the single sensor version of the same strategy.
- (2)
- On average, the IMM filters provide better performances than the KF when the same number of sensors is used.
- (3)
- The IMM-MI filter (black solid line) outperforms the other strategies for almost the entire simulation.
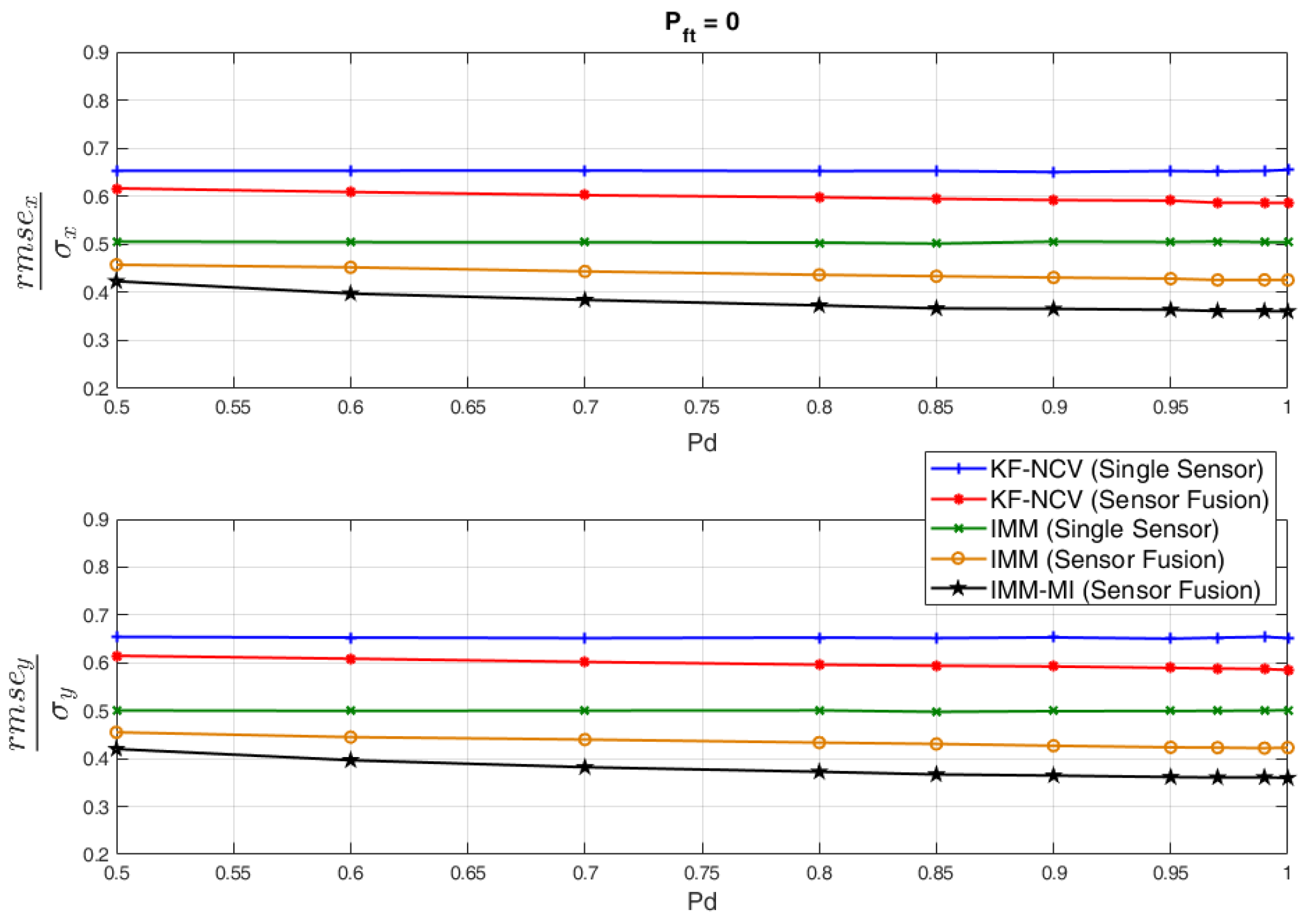
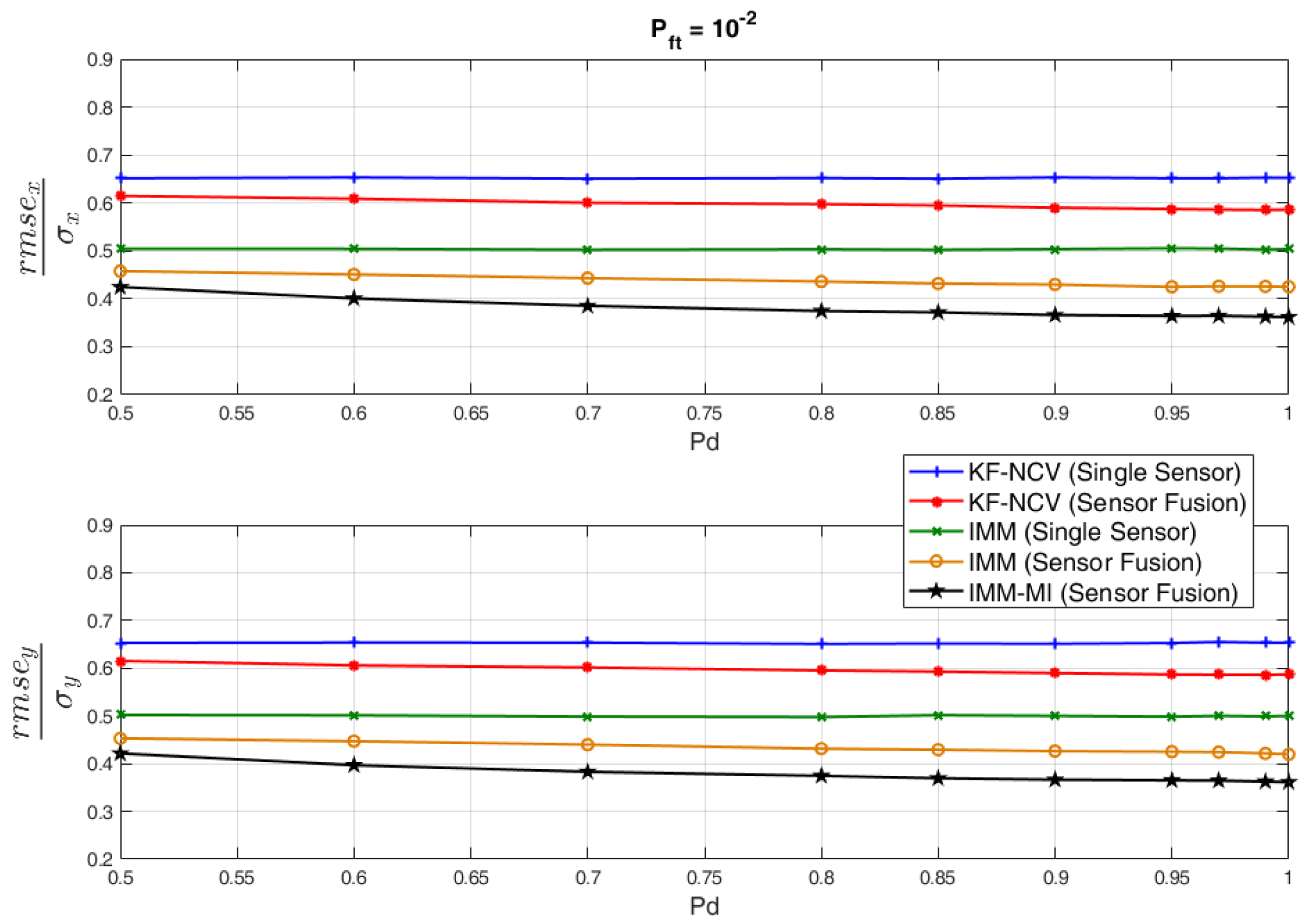
4.3. Evaluation of the RMSE under Non-Ideal Conditions for the PBR Sensor
- Missing PBR measurements when the target is moving are emulated through the definition of the Detection Probability, , which is used for the generation of the radar measurements during the “MOVE” intervals.
- The presence of “False Plots” when the target is stationary that are erroneously associated with the target are emulated by defining the False Target Probability, .
5. Tests on the Experimental Data
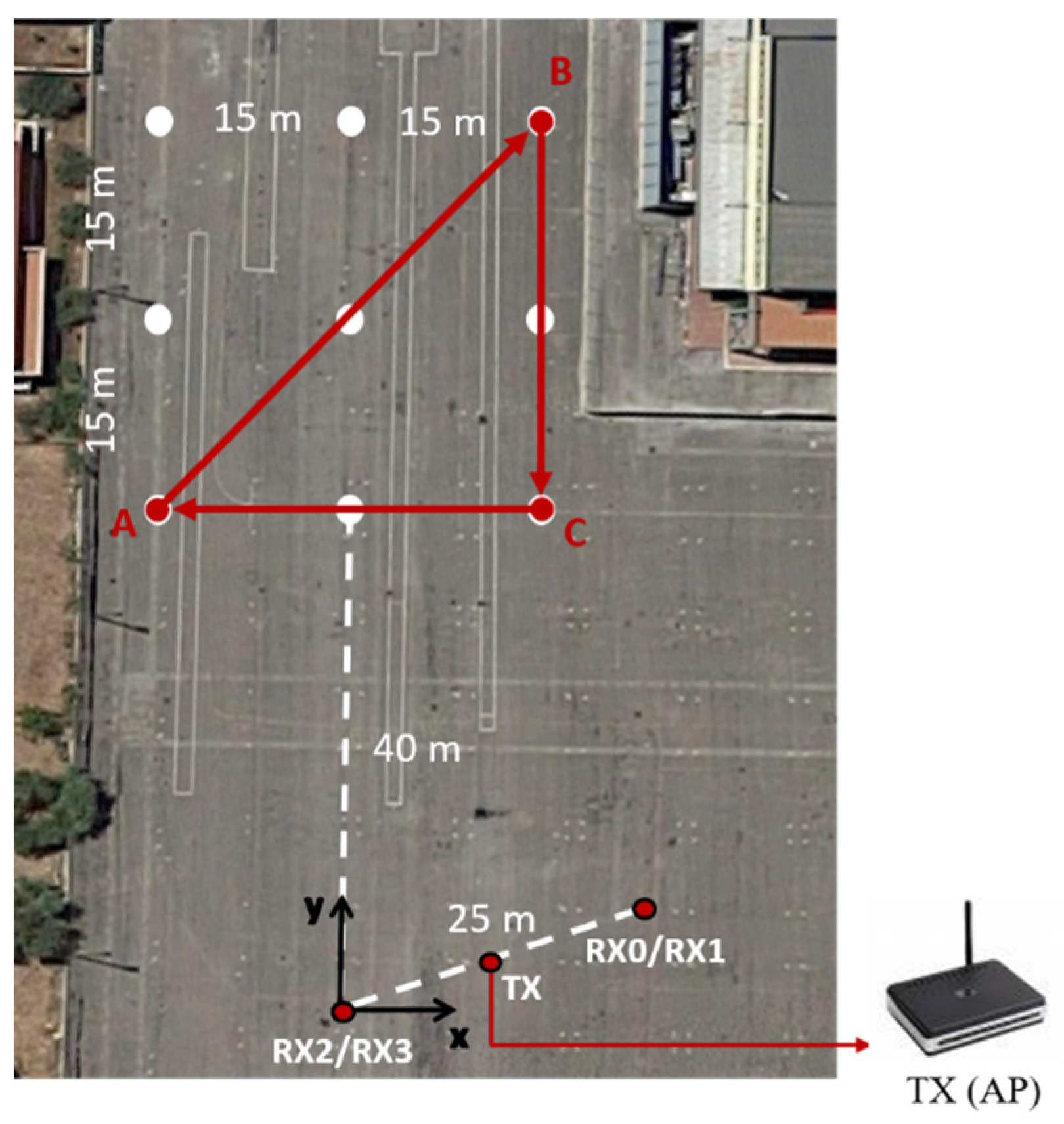
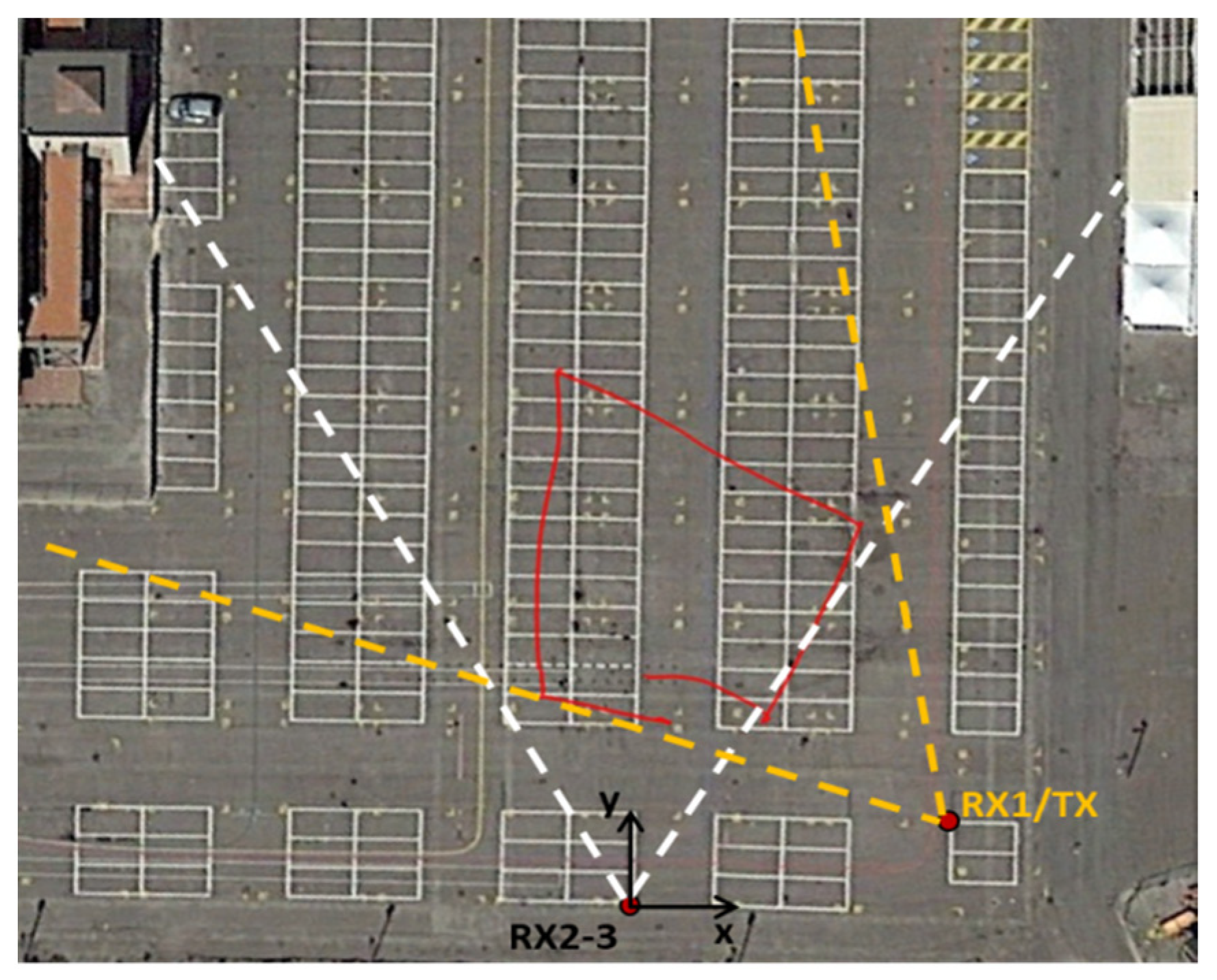
5.1. Experimental Equipment and Operational Conditions
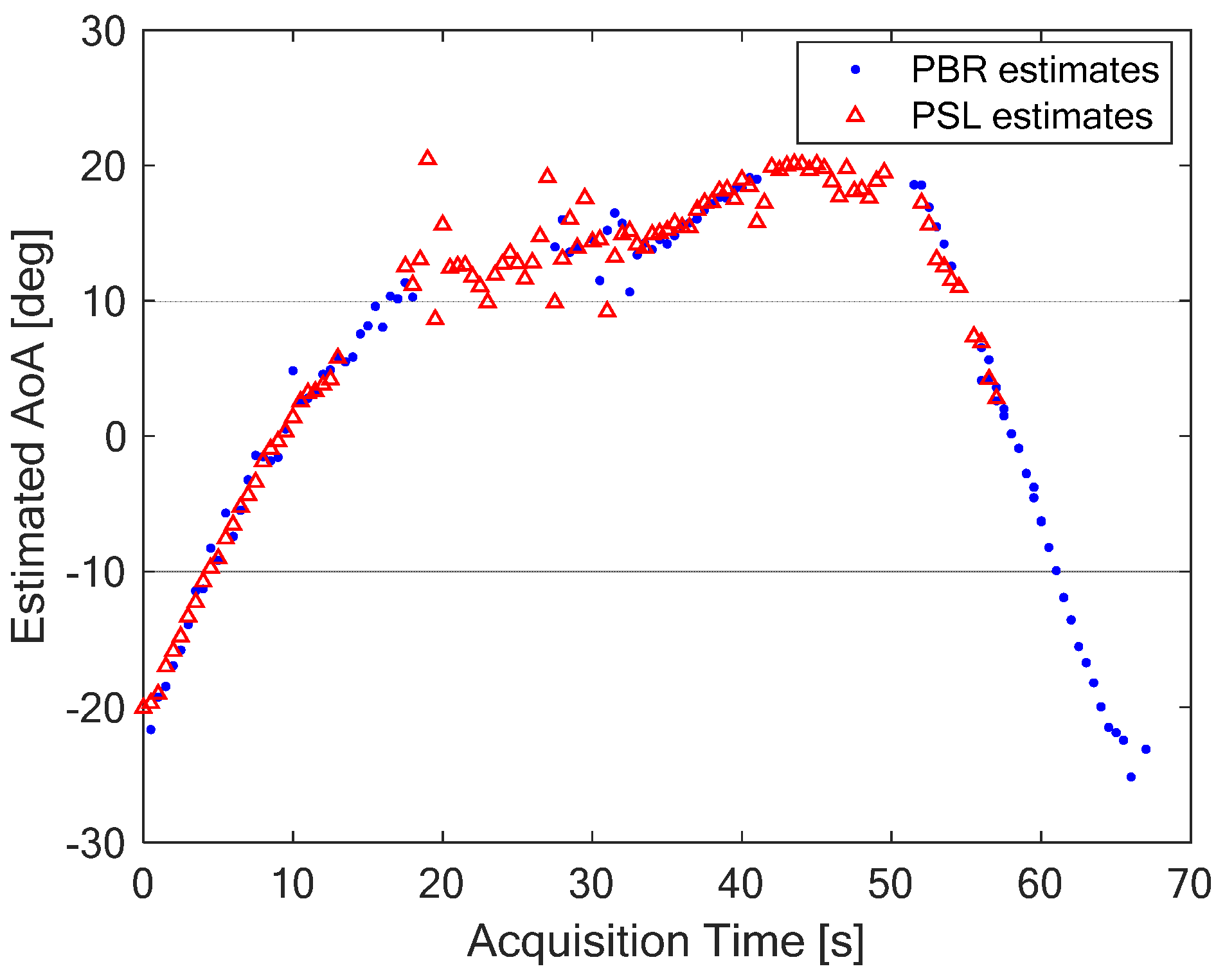
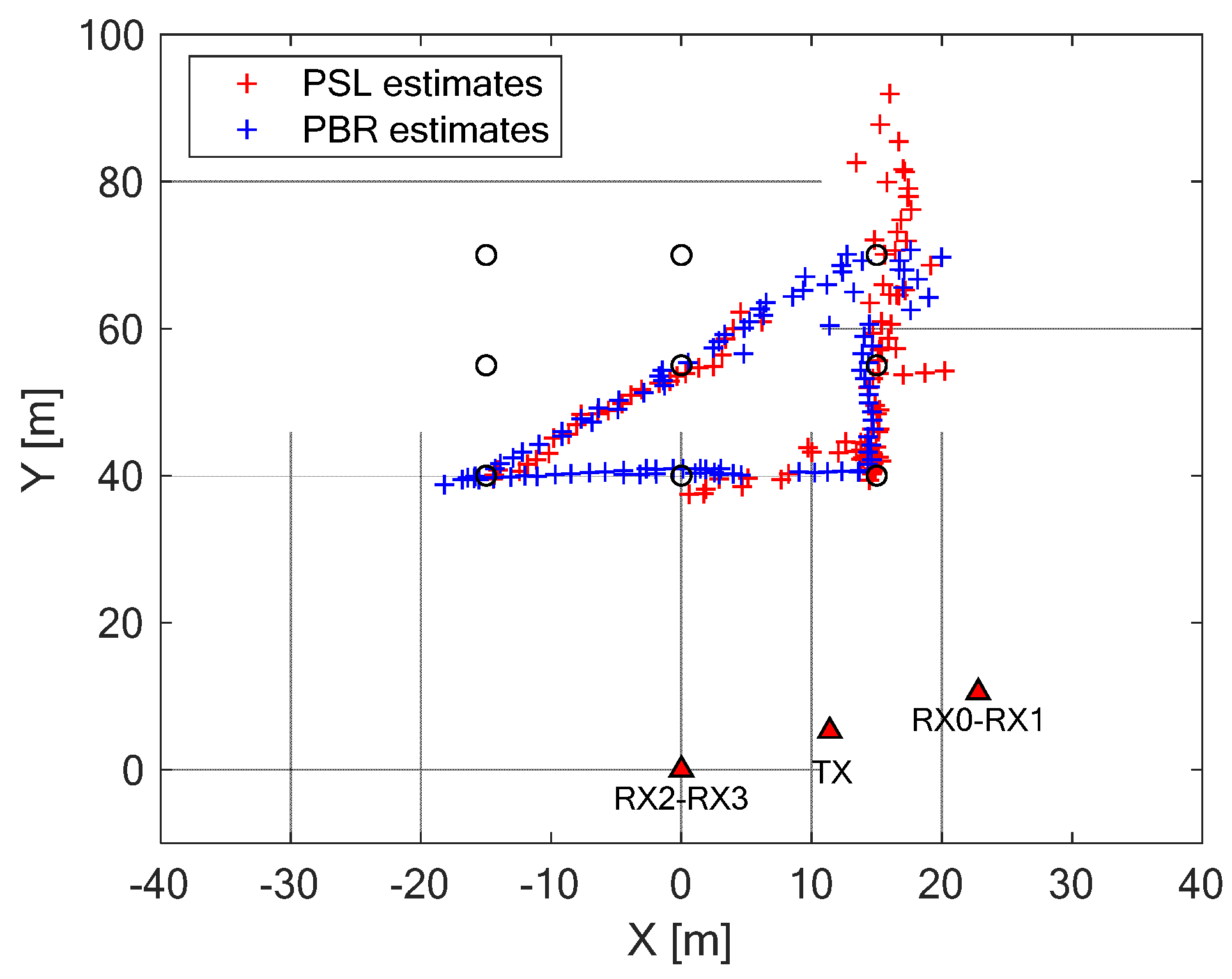
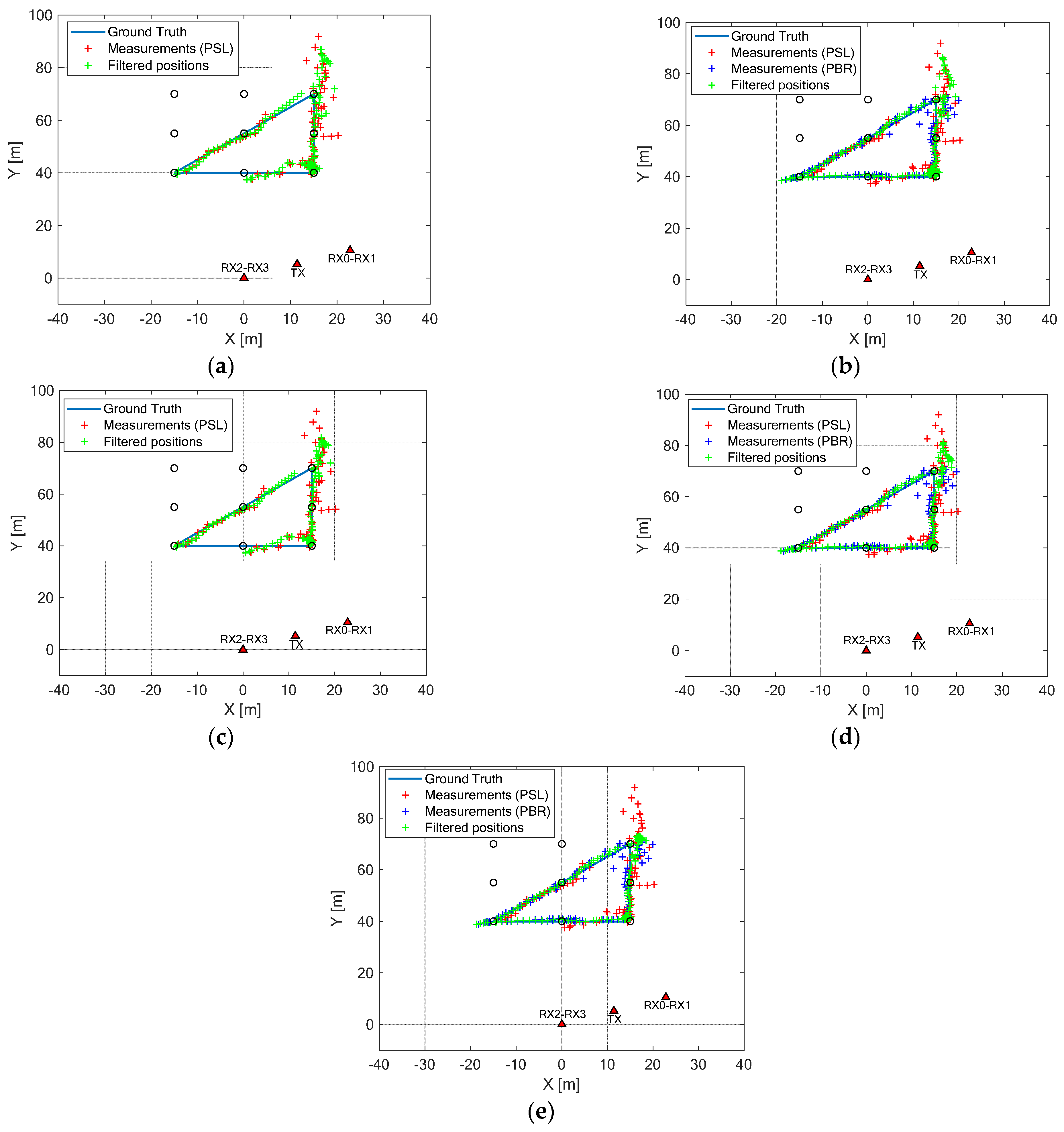
5.2. Experimental Results against Human Targets
- motion from point A (−15 m, 40 m) to point B (15 m, 70 m) in 19 s,
- stop in point B for 8 s,
- motion from point B to point C (15 m, 40 m) in 14 s,
- stop in point C for 10 s and
- motion from point C to point A in 14 s.
- in the motion interval, where smoothed filtered positions are provided, which are very close to the line of the ground truth, and
- in the two stop intervals, where the variations around the points (15 m, 40 m) and (15 m, 70 m) are smaller with respect to those shown for the standard methodologies.
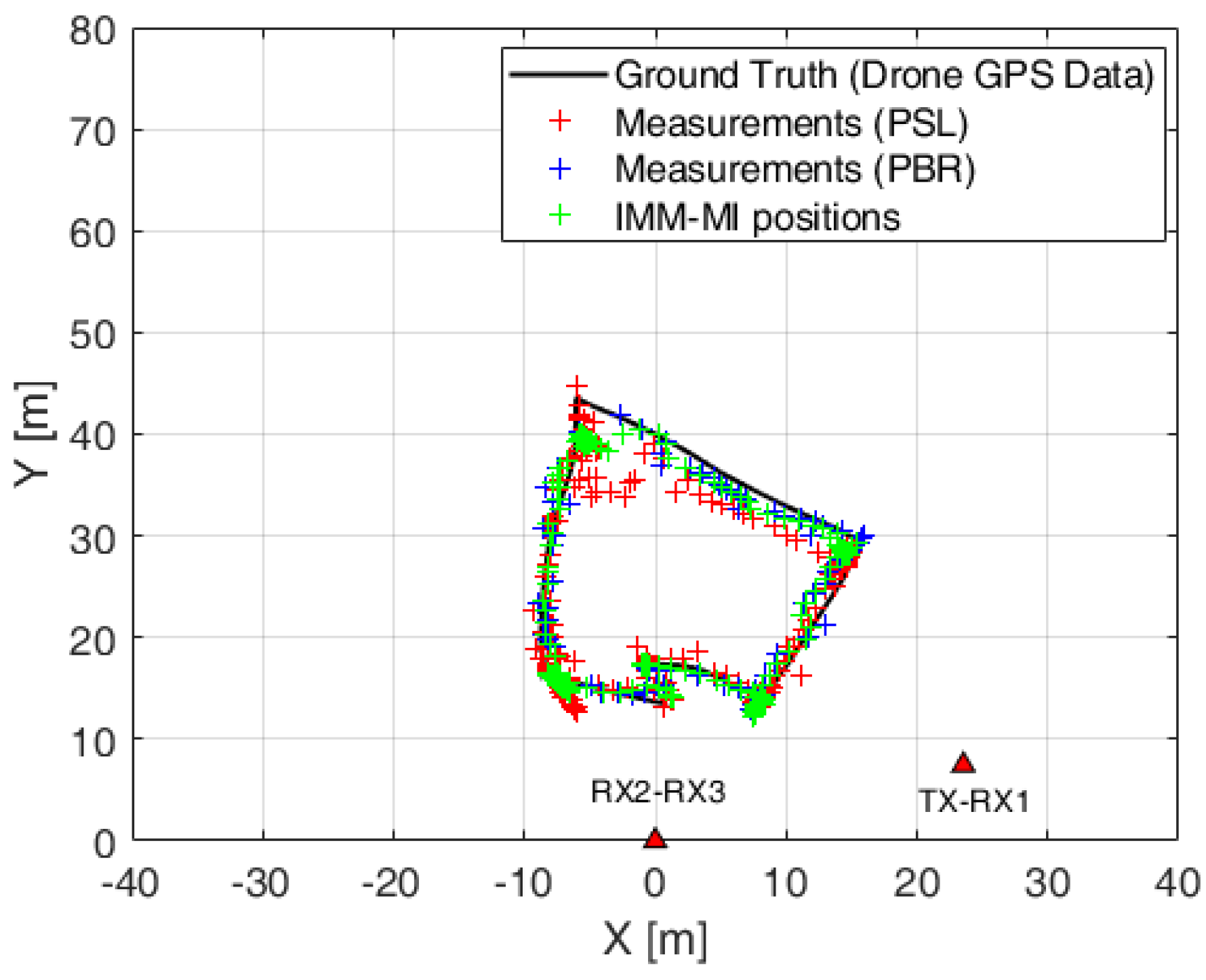
5.3. Experimental Results against Commercial Drones
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Cubber, G. Explosive Drones: How to Deal with this New Threat? In Proceedings of the 9th International Workshop on Measurement, Prevention, Protection and Management of CBRN Risks, International CBRNE Institute, Les Bons Villers, Belgium, 1 April 2019; pp. 1–8. [Google Scholar]
- Ritchie, M.; Fioranelli, F.; Borrion, H. Micro UAV crime prevention: Can we help Princess Leia? In Crime Prevention in the 21st Century; Savona, B.L., Ed.; Springer: New York, NY, USA, 2017; pp. 359–376. [Google Scholar]
- Shi, X.; Yang, C.; Xie, W.; Liang, C.; Shi, Z.; Chen, J. Anti-Drone System with Multiple Surveillance Technologies: Architecture, Implementation, and Challenges. IEEE Commun. Mag. 2018, 56, 68–74. [Google Scholar] [CrossRef]
- Lykou, G.; Moustakas, D.; Gritzalis, D. Defending Airports from UAS: A Survey on Cyber-Attacks and Counter-Drone Sensing Technologies. Sensors 2020, 20, 3537. [Google Scholar] [CrossRef] [PubMed]
- Milani, I.; Colone, F.; Bongioanni, C.; Lombardo, P. WiFi emission-based vs passive radar localization of human targets. IEEE 2018, 1311–1316. [Google Scholar] [CrossRef]
- Milani, I.; Bongioanni, C.; Colone, F.; Lombardo, P. Fusing active and passive measurements for drone localization. IEEE 2020. [Google Scholar] [CrossRef]
- Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications; IEEE: Piscataway Township, NJ, USA, 2016.
- Colone, F.; Falcone, P.; Bongioanni, C.; Lombardo, P. WiFi-Based Passive Bistatic Radar: Data Processing Schemes and Experimental Results. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1061–1079. [Google Scholar] [CrossRef]
- Falcone, P.; Colone, F.; Macera, A.; Lombardo, P. Two-dimensional location of moving targets within local areas using WiFi-based multistatic passive radar. IET Radar Sonar Navig. 2014, 8, 123–131. [Google Scholar] [CrossRef]
- Tan, B.; Woodbridge, K.; Chetty, K. A real-time high resolution passive WiFi Doppler-radar and its applications. In Proceedings of the 2014 International Radar Conference, Lille, France, 13–17 October 2014. [Google Scholar]
- Rzewuski, S.; Kulpa, K.; Samczyński, P. Duty factor impact on WIFIRAD radar image quality. IEEE 2015, 400–405. [Google Scholar] [CrossRef]
- Li, W.; Piechocki, R.J.; Woodbridge, K.; Tang, C.; Chetty, K. Passive WiFi Radar for Human Sensing Using a Stand-Alone Access Point. IEEE Trans. Geosci. Remote. Sens. 2020, 59, 1986–1998. [Google Scholar] [CrossRef]
- Mazor, E.; Averbuch, A.Z.; Barshalom, Y.; Dayan, J. Interacting multiple model methods in target tracking: A survey. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 103–123. [Google Scholar] [CrossRef]
- Kirubarajan, T.; Bar-Shalom, Y. Tracking evasive move-stop-move targets with a GMTI radar using a VS-IMM estimator. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1098–1103. [Google Scholar] [CrossRef]
- Coraluppi, S.; Carthel, C. Multiple-Hypothesis IMM (MH-IMM) Filter for Moving and Stationary Targets. In Proceedings of the 2001 International Conference on Information Fusion, Montreal, QC, Canada, 10 August 2001. [Google Scholar]
- Li, X.-R.; Bar-Shalom, Y. Multiple-model estimation with variable structure. IEEE Trans. Autom. Control. 1996, 41, 478–493. [Google Scholar] [CrossRef]
- Colone, F.; Palmarini, C.; Martelli, T.; Tilli, E. Sliding extensive cancellation algorithm for disturbance removal in passive radar. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1309–1326. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R. Multitarget-Multisensor Tracking: Principles and Techniques; YBS Publishing: Storrs, CT, USA, 1995. [Google Scholar]
- Genovese, A.F. The Interacting Multiple Model Algorithm for Accurate State Estimation of Maneuvering Targets; Johns Hopkins APL Technical Digest: Laurel, MD, USA, 2001; Volume 22, pp. 614–623. [Google Scholar]
- Granstrom, K.; Willett, P.; Bar-Shalom, Y. Systematic approach to IMM mixing for unequal dimension states. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2975–2986. [Google Scholar] [CrossRef]

| Passive Bistatic Radar (PBR) | Passive Source Location (PSL) |
|---|---|
| Higher computational cost | Lower computational cost |
| Closely spaced targets cannot be discriminated | Closely spaced targets can be discriminated based on their MAC address |
| No detection of stationary targets | Stationary targets can be detected and localized |
| Effective for moving targets | Potentially inaccurate for moving targets |
| Device-free localization | Device-based localization |
| Filtering | |
|---|---|
| NCV model-based filter | |
| State prediction | |
| Prediction covariance | |
| Innovation | |
| Innovation Covariance | |
| Kalman Gain | |
| Filtered state | |
| Filtered state covariance | |
| V0 model-based filter | |
| State prediction | |
| Prediction covariance | |
| Innovation | |
| Innovation Covariance | |
| Kalman Gain | |
| Filtered state | |
| Filtered state covariance | |
| Augmentation/Reduction | |
| Augmentation | Uniform distribution augmentation [20]: |
| Reduction | Remove the velocity components from the augmented structures: |
| Interaction ( | |
| State interaction | |
| Delta state | |
| Interaction state Covariance | + |
| Combination | |
| State combination | |
| State difference | ( |
| Combination Covariance | |
| Probability update ( | |
| Mixing probabilities | |
| Normalization factor | |
| Mode probabilities | |
| Likelihood | |
| Approach | P | ||
|---|---|---|---|
| KF-NCV (SINGLE SENSOR) | 2 | - | - |
| KF-NCV (SENSOR FUSION) | 2 | - | - |
| IMM (SINGLE SENSOR) | 1 | 0.5 | |
| IMM (SENSOR FUSION) | 1 | 0.5 | |
| IMM-MI (SENSOR FUSION) | 1 | 0.5 |
| Entire Simulation | Transient State | Steady State | |||||||
|---|---|---|---|---|---|---|---|---|---|
| KF-NCV (SINGLE SENSOR) | 0.66 | 0.65 | 0.65 | 0.66 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 |
| KF-NCV (SENSOR FUSION) | 0.59 | 0.59 | 0.59 | 0.58 | 0.57 | 0.57 | 0.59 | 0.59 | 0.59 |
| IMM (SINGLE SENSOR) | 0.50 | 0.50 | 0.50 | 0.62 | 0.62 | 0.62 | 0.47 | 0.47 | 0.47 |
| IMM (SENSOR FUSION) | 0.43 | 0.42 | 0.42 | 0.51 | 0.50 | 0.51 | 0.41 | 0.40 | 0.41 |
| IMM-MI (SENSOR FUSION) | 0.36 | 0.36 | 0.36 | 0.42 | 0.42 | 0.42 | 0.35 | 0.35 | 0.35 |
| Test Case | Node Used for PBR | PBR Measurements | Nodes Used for PSL | PSL Measurements |
|---|---|---|---|---|
| Human target | Node A, with 2 antenna elements (reference signal reconstructed) | AoA + Bistatic Range | Nodes A & B, each one with 2 antenna elements | AoA + AoA |
| Drone | Node A, with 2 antenna elements (reference signal obtained from the AP) | AoA + Bistatic Range | Nodes A with 2 antenna elements & Node B with 1 antenna element | AoA + TDoA |
| Approach | MEAN ERROR X (m) | STD ERROR X (m) | MEAN ERROR Y (m) | STD ERROR Y (m) | MEAN ERROR POS (m) | STD ERROR POS (m) | MEASUREMENTS AVAILABILITY across the Observation Time |
|---|---|---|---|---|---|---|---|
| PSL MEASURES | 0.89 | 0.99 | 3.78 | 5.38 | 4.02 | 5.37 | 79% |
| PBR MEASURES | 1.03 | 0.92 | 0.91 | 0.70 | 1.49 | 1.01 | 74% |
| KF-NCV (SINGLE SENSOR) | 0.80 | 0.89 | 3.37 | 3.90 | 3.57 | 3.91 | 79% |
| KF-NCV (SENSOR FUSION) | 0.86 | 0.84 | 2.16 | 3.32 | 2.50 | 3.30 | 100% |
| IMM (SINGLE SENSOR) | 0.85 | 0.90 | 3.32 | 3.10 | 3.50 | 3.14 | 79% |
| IMM (SENSOR FUSION) | 0.88 | 0.86 | 1.80 | 2.16 | 2.14 | 2.20 | 100% |
| IMM-MI (SENSOR FUSION) | 0.85 | 0.75 | 1.26 | 0.85 | 1.63 | 0.96 | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milani, I.; Bongioanni, C.; Colone, F.; Lombardo, P. Fusing Measurements from Wi-Fi Emission-Based and Passive Radar Sensors for Short-Range Surveillance. Remote Sens. 2021, 13, 3556. https://doi.org/10.3390/rs13183556
Milani I, Bongioanni C, Colone F, Lombardo P. Fusing Measurements from Wi-Fi Emission-Based and Passive Radar Sensors for Short-Range Surveillance. Remote Sensing. 2021; 13(18):3556. https://doi.org/10.3390/rs13183556
Chicago/Turabian StyleMilani, Ileana, Carlo Bongioanni, Fabiola Colone, and Pierfrancesco Lombardo. 2021. "Fusing Measurements from Wi-Fi Emission-Based and Passive Radar Sensors for Short-Range Surveillance" Remote Sensing 13, no. 18: 3556. https://doi.org/10.3390/rs13183556
APA StyleMilani, I., Bongioanni, C., Colone, F., & Lombardo, P. (2021). Fusing Measurements from Wi-Fi Emission-Based and Passive Radar Sensors for Short-Range Surveillance. Remote Sensing, 13(18), 3556. https://doi.org/10.3390/rs13183556






