Spatiotemporal Monitoring of Soil CO2 Efflux in a Subtropical Forest during the Dry Season Based on Field Observations and Remote Sensing Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Site Description
2.2. Data Acquisition and Preprocessing
2.2.1. Forest Soil CO2 Efflux (FCO2) Measurements
2.2.2. Auxiliary Measurements
2.2.3. Satellite Remote Sensing Data
2.3. Methods for FCO2 Prediction
2.3.1. Random Forest Regression for Modeling FCO2
2.3.2. Evaluation Approaches
3. Results
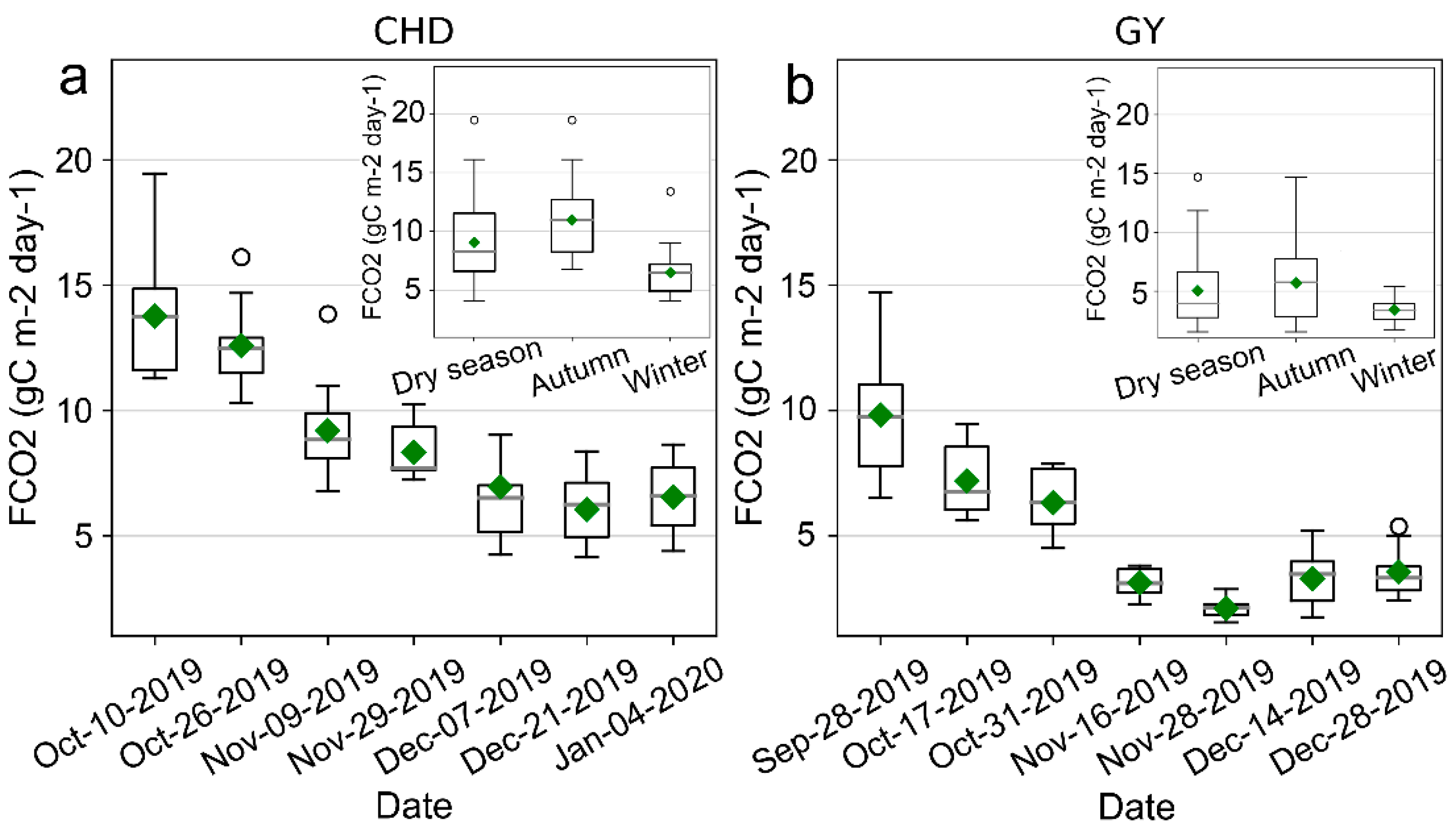
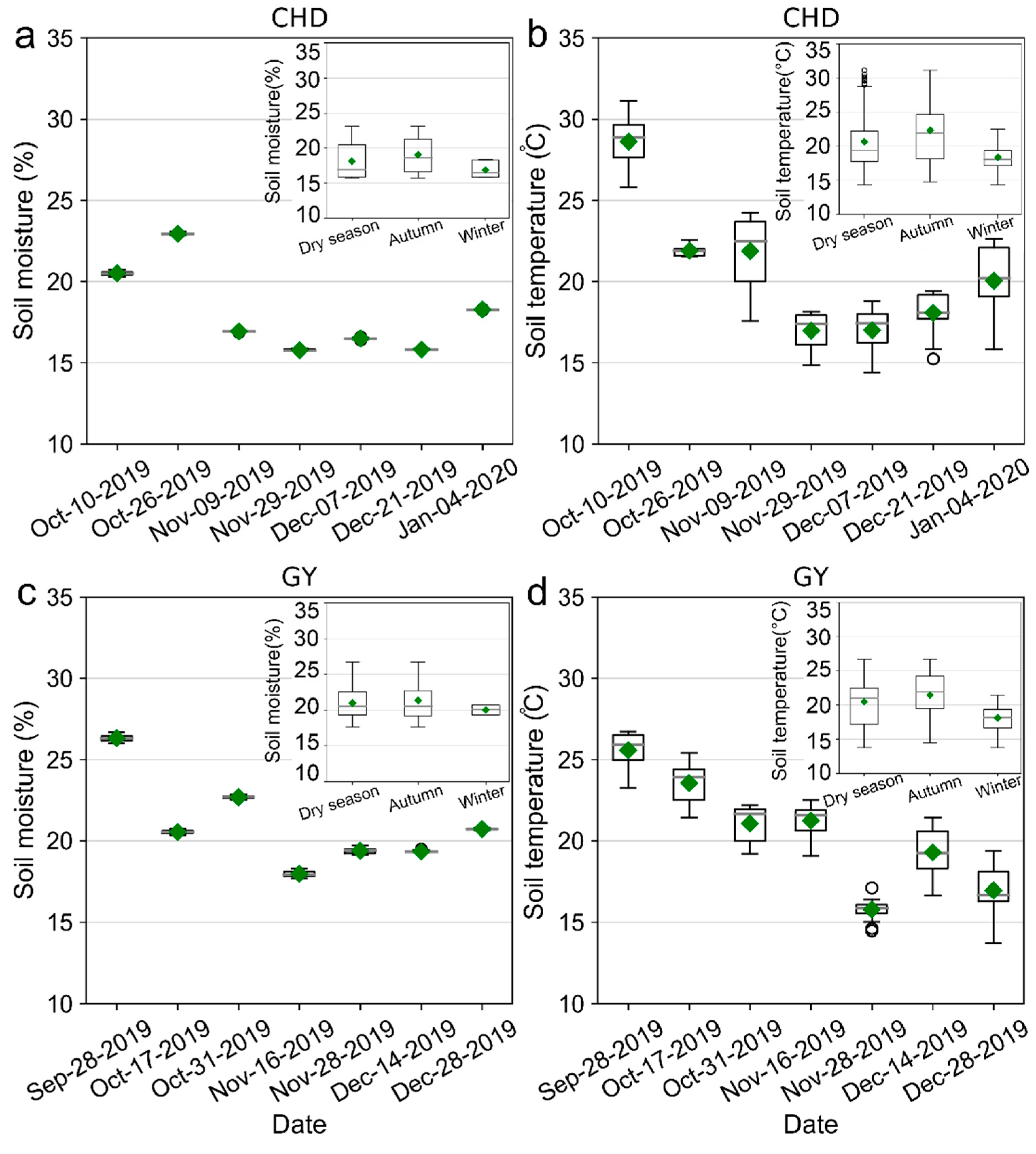
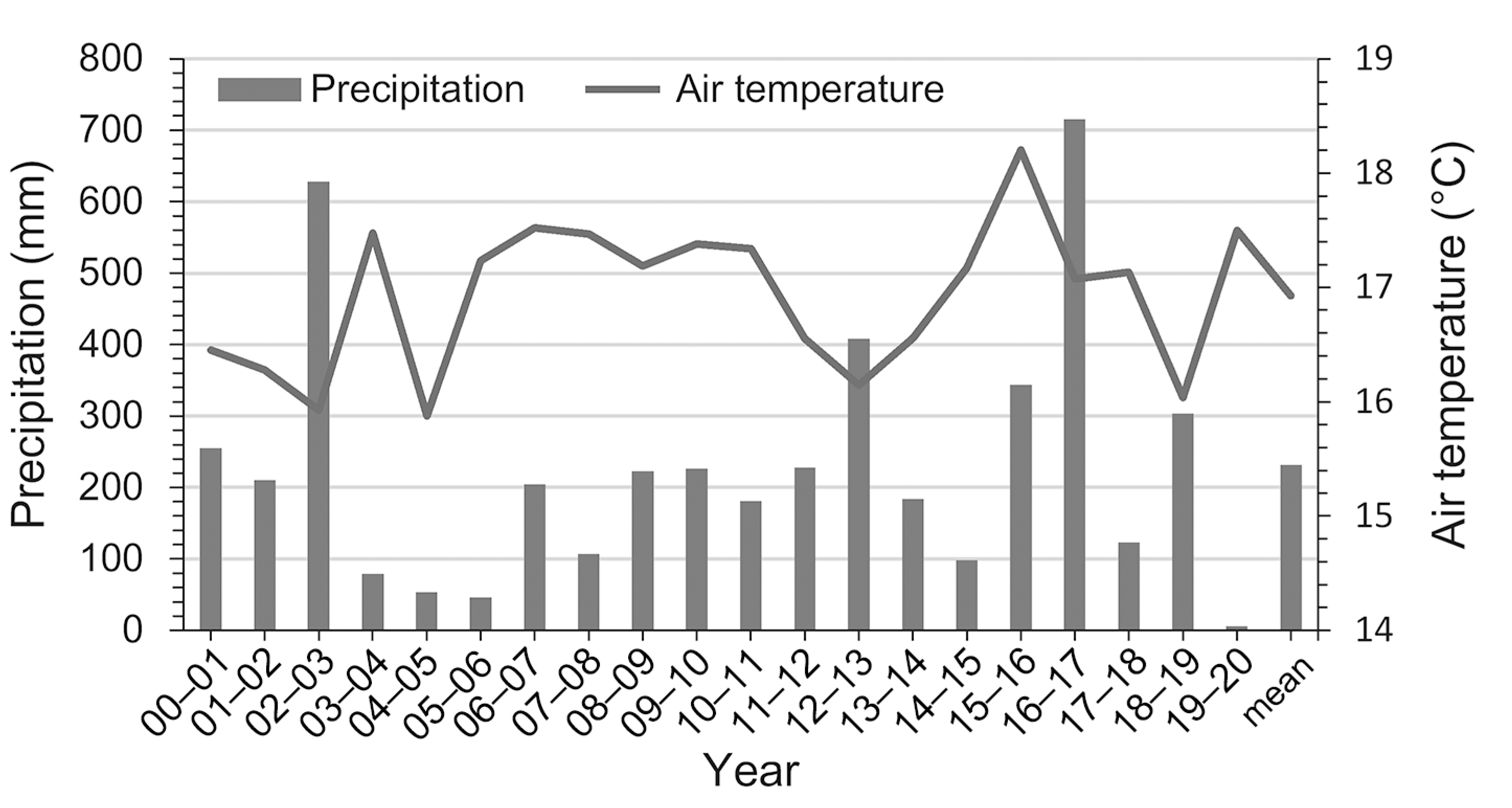
3.1. Temporal Variations of FCO2 and the Corresponding Environmental Variables during the Dry Season
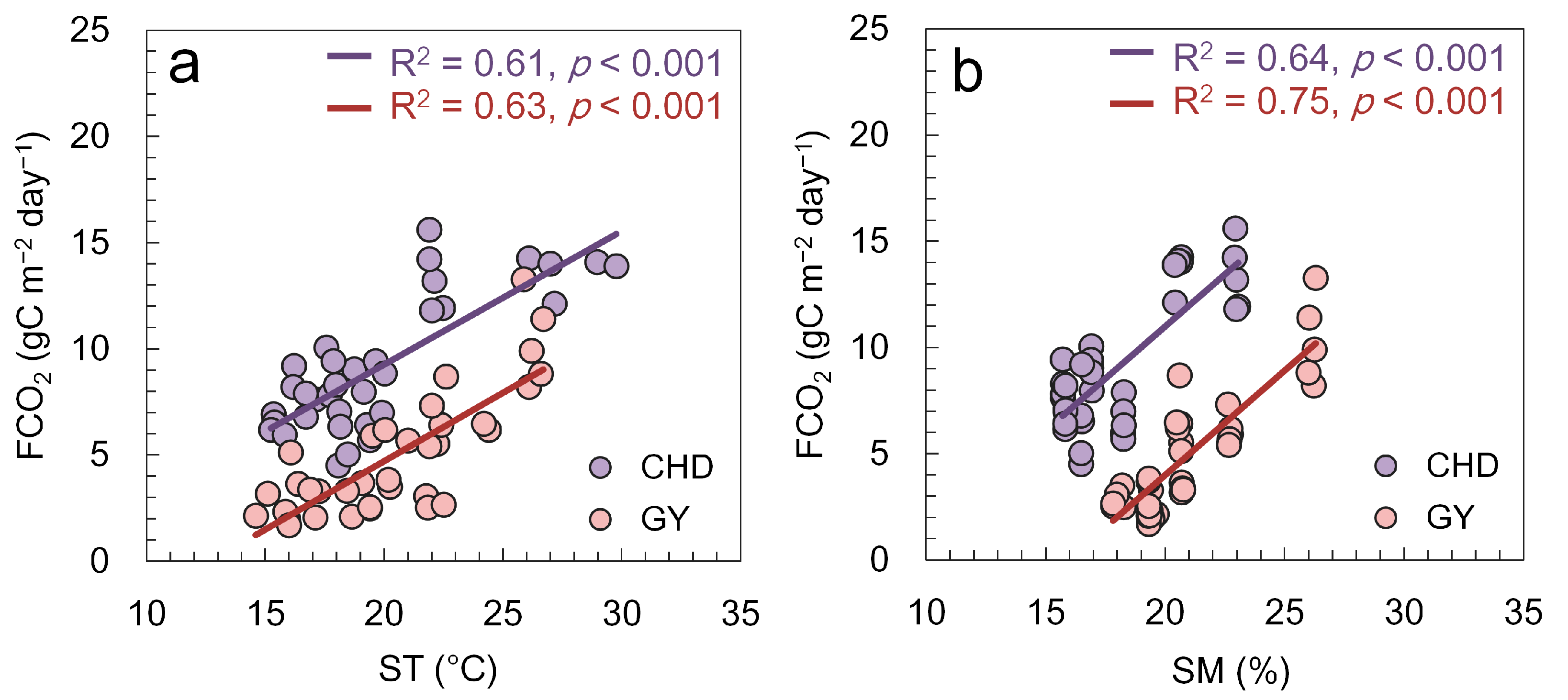
3.2. Relationships between the FCO2 and Environmental Variables and VIs
3.3. Establishing the Model for Estimating FCO2
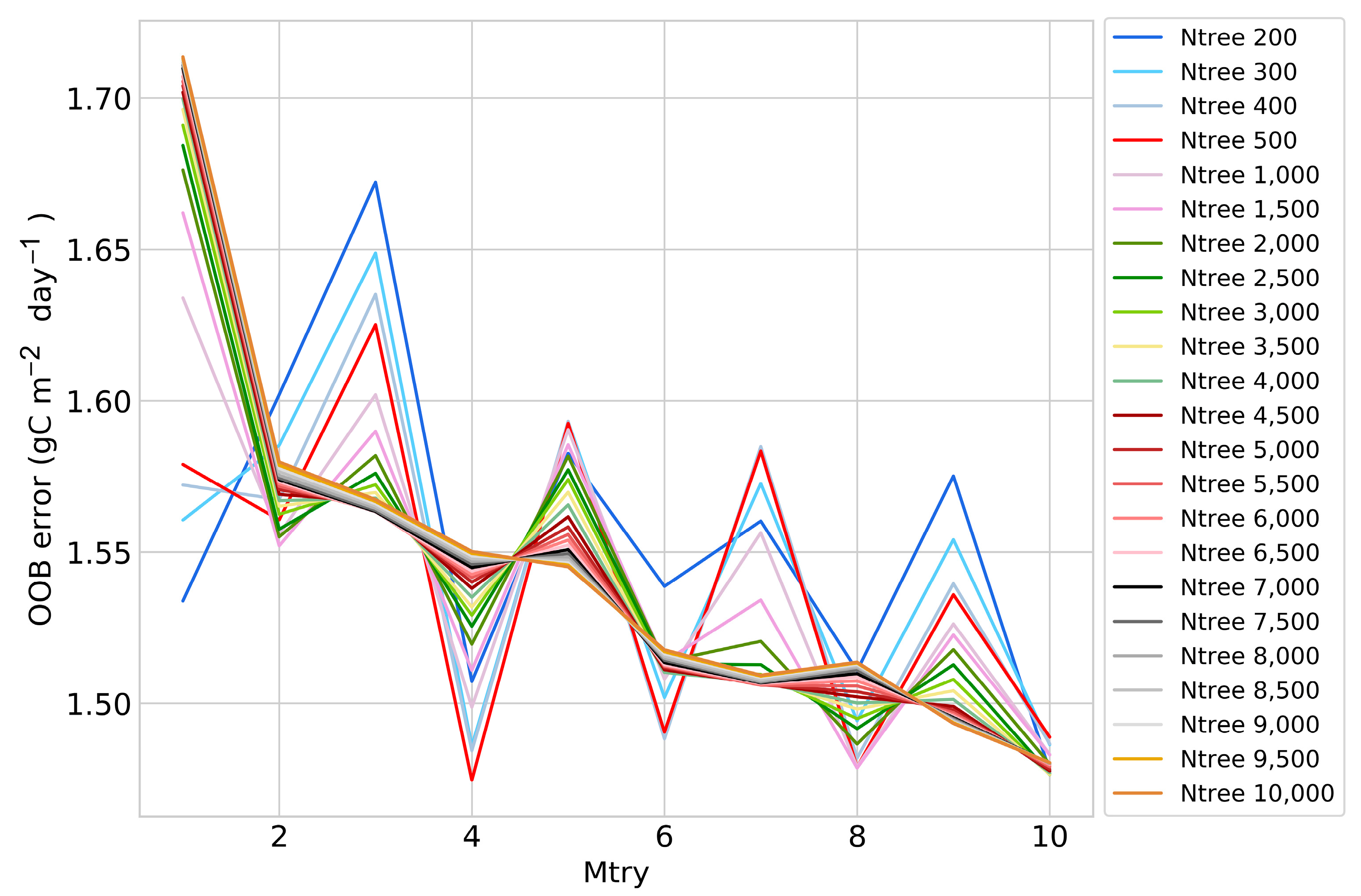
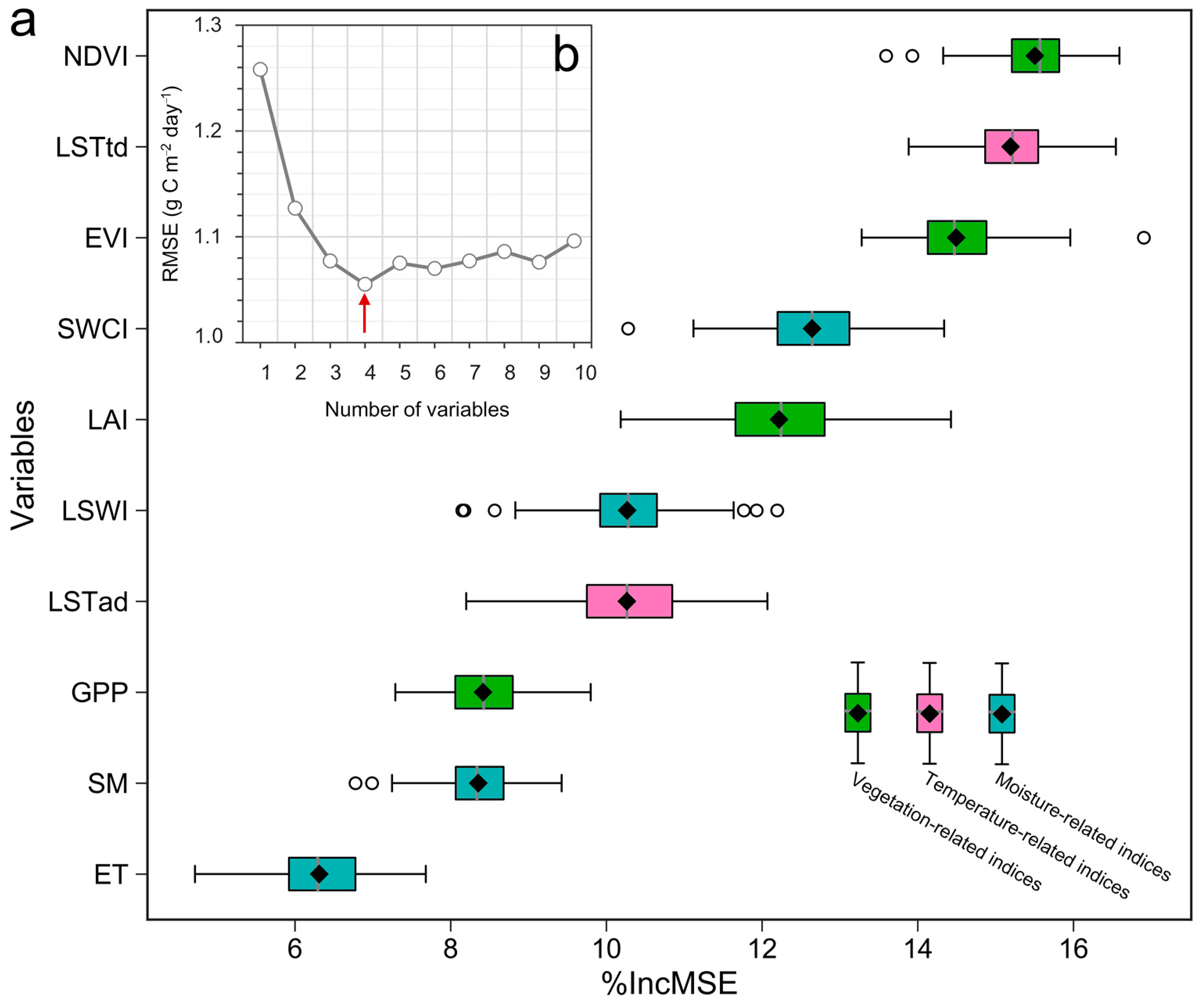
3.3.1. Optimization of Parameters and Selection of Explanatory Variables for FCO2 Estimation
3.3.2. Predicting FCO2 on the Account of RF Model and Model Accuracy
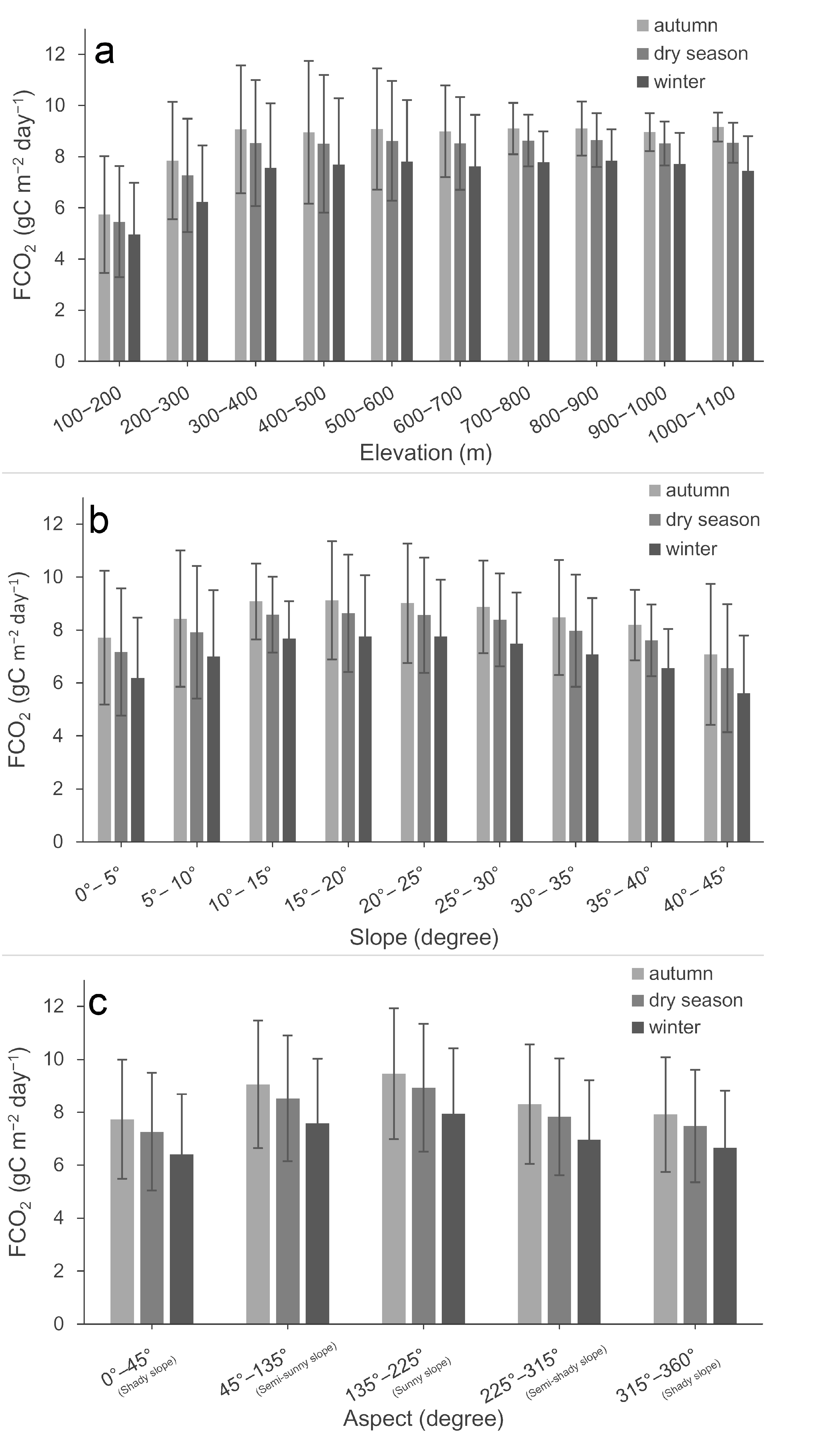
3.4. Mapping the Spatiotemporal Patterns of FCO2 and Exploring Their Topographical Effects
4. Discussion
4.1. Spatiotemporal Variations in FCO2 and Its Driving Factors
4.2. Monitoring and Estimation of the FCO2 Based on Remote Sensing Data
4.3. Advantages, Limitations, and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Bond-Lamberty, B.; Thomson, A. Temperature-associated increases in the global soil respiration record. Nature 2010, 464, 579–582. [Google Scholar] [CrossRef]
- Raich, J.W.; Potter, C.S.; Bhagawati, D. Interannual variability in global soil respiration, 1980–1994. Glob. Chang. Biol. 2010, 8, 800–812. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Wang, C.; Gower, S.T. A global relationship between the heterotrophic and autotrophic components of soil respiration? Glob. Chang. Biol. 2010, 10, 1756–1766. [Google Scholar] [CrossRef]
- Huang, N.; Li, W.; Song, X.-P.; Black, T.A.; Jassal, R.S.; Myneni, R.B.; Wu, C.; Wang, L.; Song, W.; Ji, D.; et al. Spatial and temporal variations in global soil respiration and their relationships with climate and land cover. Sci. Adv. 2020, 6, eabb8508. [Google Scholar] [CrossRef]
- Raich, J.W.; Schlesinger, W.H. The global carbon dioxide flux in soil respiration and its relationship to vegetation and climate. Tellus 1992, 44, 81–99. [Google Scholar] [CrossRef]
- Friedlingstein, P.; Jones, M.W.; O’Sullivan, M.; Andrew, R.M.; Zaehle, S. Global Carbon Budget 2019. Earth Syst. Sci. Data 2019, 11, 1783–1838. [Google Scholar] [CrossRef]
- Crabbe, R.A.; Janouš, D.; Dařenová, E.; Pavelka, M. Exploring the potential of LANDSAT-8 for estimation of forest soil CO2 efflux. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 42–52. [Google Scholar] [CrossRef]
- Bolstad, P.V.; Davis, K.J.; Martin, J.G.; Cook, B.D.; Wang, W.J. Component and whole-system respiration fluxes in northern deciduous forests. Tree Physiol. 2004, 24, 493–504. [Google Scholar] [CrossRef] [PubMed]
- Raich, J.W.; Potter, C.S. Global patterns of carbon dioxide emissions from soils. Glob. Biogeochem. Cycles 1995, 9, 23–36. [Google Scholar] [CrossRef]
- Jian, J.; Steele, M.K.; Thomas, R.Q.; Day, S.D.; Hodges, S.C. Constraining estimates of global soil respiration by quantifying sources of variability. Glob. Chang. Biol. 2018, 24, 4143–4159. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, W.H.; Andrews, J.A. Soil respiration and the global carbon cycle. Biogeochemistry 2000, 48, 7–20. [Google Scholar] [CrossRef]
- Huang, N.; Gu, L.; Niu, Z. Estimating soil respiration using spatial data products: A case study in a deciduous broadleaf forest in the Midwest USA. J. Geophys. Res. Atmos. 2014, 119, 6393–6408. [Google Scholar] [CrossRef]
- Warner, D.L.; Bond-Lamberty, B.; Jian, J.; Stell, E.; Vargas, R. Spatial Predictions and Associated Uncertainty of Annual Soil Respiration at the Global Scale. Glob. Biogeochem. Cycles 2019, 33, 1733–1745. [Google Scholar] [CrossRef]
- Bond-Lamberty, B. New Techniques and Data for Understanding the Global Soil Respiration Flux. Earth’s Future 2018, 6, 1176–1180. [Google Scholar] [CrossRef]
- Tian, Q.; Wang, D.; Tang, Y.; Li, Y.; Wang, M.; Liao, C.; Liu, F. Topographic controls on the variability of soil respiration in a humid subtropical forest. Biogeochemistry 2019, 145, 177–192. [Google Scholar] [CrossRef]
- Zhao, Z.; Peng, C.; Yang, Q.; Meng, F.-R.; Song, X.; Chen, S.; Epule, T.E.; Li, P.; Zhu, Q. Model prediction of biome-specific global soil respiration from 1960 to 2012. Earth’s Future 2017, 5, 715–729. [Google Scholar] [CrossRef]
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Tang, X.; Fan, S.; Qi, L.; Guan, F.; Du, M.; Zhang, H. Soil respiration and net ecosystem production in relation to intensive management in Moso bamboo forests. Catena 2016, 137, 219–228. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B.; Wang, W.; Li, B.; Wu, Z.; Chu, C. Topography and plant community structure contribute to spatial heterogeneity of soil respiration in a subtropical forest. Sci. Total Environ. 2020, 733, 139287. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Chen, Y.; Zhao, J.; Fu, S.; Li, Z.; Xia, H.; Zhou, L. Temperature sensitivity of total soil respiration and its heterotrophic and autotrophic components in six vegetation types of subtropical China. Sci. Total Environ. 2017, 607–608, 160–167. [Google Scholar] [CrossRef]
- Wang, W.; Peng, S.; Wang, T.; Fang, J. Winter soil CO2 efflux and its contribution to annual soil respiration in different ecosystems of a forest-steppe ecotone, north China. Soil Biol. Biochem. 2010, 42, 451–458. [Google Scholar] [CrossRef]
- Schindlbacher, A.; Zechmeister-Boltenstern, S.; Glatzel, G.; Jandl, R. Winter soil respiration from an Austrian mountain forest. Agric. For. Meteorol. 2007, 146, 205–215. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, S.; Zhang, M.; Chen, B.; Xu, Z.; Pan, Y.; Shi, X.; Wu, Z.; Luo, T. Biotic and abiotic properties most closely associated with subtropical forest soil respiration differ in wet and dry seasons: A 10-year in situ study. Agric. For. Meteorol. 2020, 292–293, 108134. [Google Scholar] [CrossRef]
- Monson, R.K.; Lipson, D.L.; Burns, S.P.; Turnipseed, A.A.; Delany, A.C.; Williams, M.W.; Schmidt, S.K. Winter forest soil respiration controlled by climate and microbial community composition. Nature 2006, 439, 711–714. [Google Scholar] [CrossRef]
- Monson, R.K.; Sparks, J.P.; Rosenstiel, T.N.; Scott-Denton, L.E.; Huxman, T.E.; Harley, P.C.; Turnipseed, A.A.; Burns, S.P.; Backlund, B.; Hu, J. Climatic influences on net ecosystem CO2 exchange during the transition from wintertime carbon source to springtime carbon sink in a high-elevation, subalpine forest. Oecologia 2005, 146, 130–147. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, X.; Yang, X.; Drury, C.F.; Mclaughlin, N.B.; Liang, A.; Fan, R.; Jia, S. Contribution of winter soil respiration to annual soil CO2emission in a Mollisol under different tillage practices in northeast China. Glob. Biogeochem. Cycles 2012, 26, GB2007. [Google Scholar] [CrossRef]
- Cleveland, C.C.; Sullivan, B.W. Drought and tropical soil emissions. Nature 2012, 489, 211–212. [Google Scholar] [CrossRef]
- O’Connell, C.S.; Ruan, L.; Silver, W.L. Drought drives rapid shifts in tropical rainforest soil biogeochemistry and greenhouse gas emissions. Nat. Commun. 2018, 9, 1348. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T.; Letoan, T.; Beaudoin, A.; Christensen, N. Dependence of radar backscatter on coniferous forest biomass. IEEE Trans. Geosci. Remote Sens. 1992, 30, 412–415. [Google Scholar] [CrossRef]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating forest biomass to SAR data. IEEE Trans. Geosci. Remote Sens. 1992, 30, 403–411. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, Y.; Li, H.; Yao, L.; Ding, Z.; Ma, M.; Yu, P. Remotely monitoring ecosystem respiration from various grasslands along a large-scale east-west transect across northern China. Carbon Balance Manag. 2020, 15, 6. [Google Scholar] [CrossRef] [PubMed]
- Domínguez, M.T.; Smith, A.R.; Reinsch, S.; Emmett, B.A. Inter-annual Variability of Soil Respiration in Wet Shrublands: Do Plants Modulate Its Sensitivity to Climate? Ecosystems 2016, 20, 796–812. [Google Scholar] [CrossRef]
- Huang, N.; Lianhong, G.; Andrew, B.T.; Li, W.; Zheng, N. Remote sensing-based estimation of annual soil respiration at two contrasting forest sites. J. Geophys. Res. Biogeosci. 2015, 120. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.C.; Nunes, J.P.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Adachi, M.; Ito, A.; Yonemura, S.; Takeuchi, W. Estimation of global soil respiration by accounting for land-use changes derived from remote sensing data. J. Environ. Manag. 2017, 200, 97–104. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Qu, J.J.; Hao, X.; Zhu, Z.; Gutenberg, L. Monitoring soil carbon flux with in-situ measurements and satellite observations in a forested region. Geoderma 2020, 378, 114617. [Google Scholar] [CrossRef]
- Kimball, J.S.; Jones, L.A.; Ke, Z.; Heinsch, F.A.; Oechel, W.C. A satellite approach to estimate land—Atmosphere CO2 exchange for Boreal and Arctic Biomes using MODIS and AMSR-E. IEEE Trans. Geosci. Remote Sens. 2009, 47, 569–587. [Google Scholar] [CrossRef]
- Wu, C.; Gaumont-Guay, D.; Andrew Black, T.; Jassal, R.S.; Xu, S.; Chen, J.M.; Gonsamo, A. Soil respiration mapped by exclusively use of MODIS data for forest landscapes of Saskatchewan, Canada. ISPRS J. Photogramm. Remote Sens. 2014, 94, 80–90. [Google Scholar] [CrossRef]
- Warner, D.L.; Guevara, M.; Inamdar, S.; Vargas, R. Upscaling soil-atmosphere CO2 and CH4 fluxes across a topographically complex forested landscape. Agric. For. Meteorol. 2019, 264, 80–91. [Google Scholar] [CrossRef]
- Hengl, T.; De Jesus Jorge, M.; Macmillan, R.A.; Batjes, N.H.; Heuvelink, G.B.M.; Eloi, R.; Alessandro, S.R.; Bas, K.; Leenaars, J.G.B.; Walsh, M.G. SoilGrids1km—Global Soil Information Based on Automated Mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef]
- Li, X.; Du, H.; Mao, F.; Zhou, G.; Chen, L.; Xing, L.; Fan, W.; Xu, X.; Liu, Y.; Cui, L.; et al. Estimating bamboo forest aboveground biomass using EnKF-assimilated MODIS LAI spatiotemporal data and machine learning algorithms. Agric. For. Meteorol. 2018, 256–257, 445–457. [Google Scholar] [CrossRef]
- Huang, N.; Wang, L.; Guo, Y.; Niu, Z. Upscaling plot-scale soil respiration in winter wheat and summer maize rotation croplands in Julu County, North China. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 169–178. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Wang, S.; Qian, X.; Han, B.-P.; Luo, L.-C.; Ye, R.; Xiong, W. Effects of different operational modes on the flood-induced turbidity current of a canyon-shaped reservoir: Case study on Liuxihe Reservoir, South China. Hydrol. Process. 2013, 27, 4004–4016. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, update 2015 International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2015. [Google Scholar]
- Fleck, D.; He, Y.; Alexander, C.; Jacobson, G.; Cunningham, K.L. Simultaneous Soil Flux Measurements of Five Gases—N2O, CH4, CO2, NH3, and H2O—With the Picarro G2508 1–11; Picarro Inc.: Santa Clara, CA, USA, 2013. Available online: https://picarro.app.box.com/s/z2gpj3hpl11xye9csz6mdpixltc1i5hl (accessed on 26 February 2021).
- Rosentreter, J.A.; Maher, D.T.; Erler, D.V.; Murray, R.H.; Eyre, B.D. Methane emissions partially offset "blue carbon" burial in mangroves. Sci. Adv. 2018, 4, eaao4985. [Google Scholar] [CrossRef]
- Christiansen, J.R.; Outhwaite, J.; Smukler, S.M. Comparison of CO2, CH4 and N2O soil-atmosphere exchange measured in static chambers with cavity ring-down spectroscopy and gas chromatography. Agric. For. Meteorol 2015, 211–212, 48–57. [Google Scholar] [CrossRef]
- Diefenderfer, H.L.; Cullinan, V.I.; Borde, A.B.; Gunn, C.M.; Thom, R.M. High-frequency greenhouse gas flux measurement system detects winter storm surge effects on salt marsh. Glob. Chang. Biol. 2018, 24, 5961–5971. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, Y.; Guo, Y.; Zhai, X.; Wilkes, A.; Han, G.; Jiang, Y.; Liu, K.; Zhou, P.; Wang, K.; et al. Changes of soil CO 2 flux under different stocking rates during spring-thaw period in a northern desert steppe, China. Atmos. Environ. 2015, 122, 343–348. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, X.; Liu, J.; Li, H.; Ding, G. MODIS-Derived Estimation of Soil Respiration within Five Cold Temperate Coniferous Forest Sites in the Eastern Loess Plateau, China. Forests 2020, 11, 131. [Google Scholar] [CrossRef]
- Martin, R.M.; Moseman-Valtierra, S. Effects of transient Phragmites australis removal on brackish marsh greenhouse gas fluxes. Atmos. Environ. 2017, 158, 51–59. [Google Scholar] [CrossRef]
- Thiel, B.; Krzic, M.; Gergel, S.; Terpsma, C.; Black, A.; Jassal, R.; Smukler, S.M. Soil CO2, CH4 and N2O emissions from production fields with planted and remnant hedgerows in the Fraser River Delta of British Columbia. Agrofor. Syst. 2016, 91, 1139–1156. [Google Scholar] [CrossRef]
- Rey, A.; Pegoraro, E.; Tedeschi, V.; Parri, I.D.; Valentini, R. Annual variation in soil respiration and its components in a coppice oak forest in Central Italy. Glob. Chang. Biol. 2002, 8, 851–866. [Google Scholar] [CrossRef]
- Martin, R.M.; Serena, M.V. Greenhouse Gas Fluxes Vary Between Phragmites Australis and Native Vegetation Zones in Coastal Wetlands Along a Salinity Gradient. Wetlands 2015, 35, 1021–1031. [Google Scholar] [CrossRef]
- Tang, S.; Wang, C.; Wilkes, A.; Zhou, P.; Jiang, Y.; Han, G.; Zhao, M.; Huang, D.; Schoenbach, P. Contribution of grazing to soil atmosphere CH4 exchange during the growing season in a continental steppe. Atmos. Environ. 2013, 67, 170–176. [Google Scholar] [CrossRef]
- Ai, J.; Jia, G.; Epstein, H.E.; Wang, H.; Zhang, A.; Hu, Y. MODIS-Based Estimates of Global Terrestrial Ecosystem Respiration. J. Geophys. Res. Biogeosci. 2018, 123, 326–352. [Google Scholar] [CrossRef]
- Reichstein, M.; Rey, A.; Freibauer, A.; Tenhunen, J.; Valentini, R.; Banza, J.; Casals, P.; Cheng, Y.; Grünzweig, J.M.; Irvine, J.; et al. Modeling temporal and large-scale spatial variability of soil respiration from soil water availability, temperature and vegetation productivity indices. Glob. Biogeochem. Cycles 2003, 17, 1104. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodrigueza, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the MODIS Land-Surface Temperature/Emissivity products. Remote Sens. Environ. 2008, 112, 59–74. [Google Scholar] [CrossRef]
- Zhang, L.-W.; Huang, J.-F.; Guo, R.-F.; Li, X.-X.; Sun, W.-B.; Wang, X.-Z. Spatio-temporal reconstruction of air temperature maps and their application to estimate rice growing season heat accumulation using multi-temporal MODIS data. J. Zhejiang Univ. Sci. B 2013, 14, 144–161. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I. Derivation of a shortwave infrared water stress index from MODIS near- and shortwave infrared data in a semiarid environment. Remote Sens. Environ. 2003, 87, 111–121. [Google Scholar] [CrossRef]
- Reitz, O.; Graf, A.; Schmidt, M.; Ketzler, G.; Leuchner, M. Upscaling net ecosystem exchange over heterogeneous landscapes with machine learning. J. Geophys. Res. Biogeosci. 2021, 126, e2020JG005814. [Google Scholar] [CrossRef]
- Acosta, M.; Darenova, E.; Krupková, L.; Pavelka, M. Seasonal and inter-annual variability of soil CO2 efflux in a Norway spruce forest over an eight-year study. Agric. For. Meteorol. 2018, 256–257, 93–103. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Williams, G. Data mining desktop survival guide. Dim Surv. 2008, 1, 15. [Google Scholar]
- Belgiu, M.; Dragut, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Steidinger, B.S.; Crowther, T.W.; Liang, J.; Van Nuland, M.E.; Werner, G.D.A.; Reich, P.B.; Nabuurs, G.J.; de-Miguel, S.; Zhou, M.; Picard, N.; et al. Climatic controls of decomposition drive the global biogeography of forest-tree symbioses. Nature 2019, 569, 404–408. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2–3, 18–22. [Google Scholar]
- R Core Team. R: A language and environment for statistical computing. Computing 2015, 1, 12–21. [Google Scholar]
- Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using RapidEye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Ismail, R.; Mutanga, O. Acomparison ofregression tree ensembles: Predicting Sirex noctilio induced water stress in Pinus patula forests of KwaZulu-Natal, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2010, 12S, S45–S51. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to varaible and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef][Green Version]
- Iqbal, F.; Lucieer, A.; Barry, K. Poppy crop capsule volume estimation using UAS remote sensing and random forest regression. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 362–373. [Google Scholar] [CrossRef]
- Yi, Z.; Fu, S.; Yi, W.; Zhou, G.; Mo, J.; Zhang, D.; Ding, M.; Wang, X.; Zhou, L. Partitioning soil respiration of subtropical forests with different successional stages in south China. For. Ecol. Manag. 2007, 243, 178–186. [Google Scholar] [CrossRef]
- Deng, Q.; Cheng, X.; Zhou, G.; Liu, J.; Liu, S.; Zhang, Q.; Zhang, D. Seasonal responses of soil respiration to elevated CO2 and N addition in young subtropical forest ecosystems in southern China. Ecol. Eng. 2013, 61, 65–73. [Google Scholar] [CrossRef]
- Janssens, I.; Meiresonne, L.; Ceulemans, R. Mean soil CO2 efflux from a mixed forest: Temporal and spatial integration. In Forest Ecosystem Modelling, Upscaling and Remote Sensing; Ceulemans, R., Veroustraete, F., Gond, V., Rensbergen, J., Eds.; SPB Academic Publishing: The Hague, The Netherlands, 1999; pp. 19–33. [Google Scholar]
- Zhou, C.; Zhou, G.; Wang, Y.; Zhang, D.; Liu, S.; Wang, Y.; Sun, Y. Soil respiration of a coniferous and broad-leaved mixed forest in Dinghushan Mountain, Guangdong Province. J. Beijing For. Univ. 2005, 4, 23–27. [Google Scholar]
- Liang, G.H.; Wu, J.P.; Xiong, X.; Wu, X.Y.; Chu, G.W.; Zhou, G.Y.; Zeng, R.S.; Zhang, D.Q. Response of soil respiration to simulated acid rain in three successional subtropical forests in southern China. Chin. J. Ecol. 2016, 35, 125–134. [Google Scholar]
- Zeng, X.; Zhang, W.; Shen, H.; Cao, J.; Zhao, X. Soil respiration response in different vegetation types at Mount Taihang, China. Catena 2014, 116, 78–85. [Google Scholar] [CrossRef]
- Han, T.; Zhou, G.; Li, Y.; Liu, J.; Zhang, D. Partitioning soil respiration in lower subtropical forests at different successional stages in southern China. Chin. J. Plant Ecol. 2011, 35, 946–954. [Google Scholar] [CrossRef]
- Jiang, H.; Deng, Q.; Zhou, G.; Hui, D.; Zhang, D.; Liu, S.; Chu, G.; Li, J. Responses of soil respiration and its temperature/moisture sensitivity to precipitation in three subtropical forests in southern China. Biogeosciences 2013, 10, 3963–3982. [Google Scholar] [CrossRef]
- Pacific, V.J.; McGlynn, B.L.; Riveros-Iregui, D.A.; Welsch, D.L.; Epstein, H.E. Landscape structure, groundwater dynamics, and soil water content influence soil respiration across riparian-hillslope transitions in the Tenderfoot Creek Experimental Forest, Montana. Hydrol. Process. 2011, 25, 811–827. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Sun, Q.; Du, L.; Zhao, M.; Hu, Y.; Guo, S. Soil CO2 emissions from different slope gradients and positions in the semiarid Loess Plateau of China. Ecol. Eng. 2017, 105, 231–239. [Google Scholar] [CrossRef]
- Epron, D.; Bosc, A.; Bonal, D.; Freycon, V. Spatial variation of soil respiration across a topographic gradient in a tropical rain forest in French Guiana. J. Trop. Ecol. 2006, 22, 565–574. [Google Scholar] [CrossRef]
- Hu, M.; Xia, B. A significant increase in the normalized difference vegetation index during the rapid economic development in the Pearl River Delta of China. Land Degrad. Dev. 2018, 30, 359–370. [Google Scholar] [CrossRef]
- Bond-Lamberty, B.; Christianson, D.S.; Malhotra, A. COSORE: A community database for continuous soil respiration and other soil-atmosphere greenhouse gas flux data. Glob. Chang. Biol. 2020, 26, 7268–7283. [Google Scholar] [CrossRef] [PubMed]
- Acosta, M.; Pavelka, M.; Montagnani, L.; Kutsch, W.; Lindroth, A.; Juszczak, R.; Janouš, D. Soil surface CO2 efflux measurements in Norway spruce forests: Comparison between four different sites across Europe—From boreal to alpine forest. Geoderma 2013, 192, 295–303. [Google Scholar] [CrossRef]
- Takahashi, M.; Hirai, K.; Limtong, P.; Leaungvutivirog, C.; Panuthai, S.; Suksawang, S.; Anusontpornperm, S.; Marod, D. Topographic variation in heterotrophic and autotrophic soil respiration in a tropical seasonal forest in Thailand. Soil Sci. Plant Nutr. 2011, 57, 452–465. [Google Scholar] [CrossRef]


| Sites | Guo Yuan (GY) | Chenhe Dong (CHD) |
|---|---|---|
| Location | 23.776°N, 113.851°E | 23.772°N, 113.937°E |
| Aspect | Shady slope | Sunny slope |
| Plant functional type | Coniferous mixed forest | Coniferous mixed forest |
| Dominant species | Pinus massoniana Lamb. | Pinus massoniana Lamb. |
| Soil types 1 | FRh-Haplic Ferralsols | FRh-Haplic Ferralsols |
| Soil organic C (% weight), PH | 0.98, 5.2 | 1.42, 4.8 |
| Soil bulk density (kg/dm3) | 1.4 | 1.25 |
| Drainage class | Moderately well | Moderately well |
| Tree height (m) | 20.50 | 21.33 |
| DBH 2 (cm) | 58.75 | 62.17 |
| Types | Fullname | Indices | Data Source |
|---|---|---|---|
| Plant productivity | Normalized Difference Vegetation Index | NDVI | Calculated from MOD09A1 |
| Enhanced Vegetation Index | EVI | Calculated from MOD09A1 | |
| Leaf Area Index | LAI | MCD15A3H | |
| Gross Primary Production | GPP | MOD17A2H | |
| Soil temperature | Terra MODIS Land Surface Temperature | LSTtd | MOD11A1 |
| Aqua MODIS Land Surface Temperature | LSTad | MYD11A1 | |
| Soil moisture | Evapotranspiration | ET | MOD16A2 |
| Soil Moisture | SM | SMAP Level 4 Global EASE-Grid root zone SM | |
| Land Surface Water Index | LSWI | Calculated from MOD09A1 | |
| Surface Water Capacity Index | SWCI | Calculated from MOD09A1 |
| VIs | CHD (FCO2) | GY (FCO2) | ||
|---|---|---|---|---|
| R2 | p-Value | R2 | p-Value | |
| EVI | 0.71 | p < 0.001 | 0.35 | p < 0.001 |
| GPP | 0.64 | p < 0.001 | 0.49 | p < 0.001 |
| LAI | 0.64 | p < 0.001 | 0.41 | p < 0.001 |
| NDVI | 0.49 | p < 0.001 | 0.52 | p < 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Xu, Z.; Tang, G.; Chen, X.; Fang, H.; Guo, H.; Yuan, Y.; Zheng, G.; Jiang, L.; Niu, X. Spatiotemporal Monitoring of Soil CO2 Efflux in a Subtropical Forest during the Dry Season Based on Field Observations and Remote Sensing Imagery. Remote Sens. 2021, 13, 3481. https://doi.org/10.3390/rs13173481
Chen T, Xu Z, Tang G, Chen X, Fang H, Guo H, Yuan Y, Zheng G, Jiang L, Niu X. Spatiotemporal Monitoring of Soil CO2 Efflux in a Subtropical Forest during the Dry Season Based on Field Observations and Remote Sensing Imagery. Remote Sensing. 2021; 13(17):3481. https://doi.org/10.3390/rs13173481
Chicago/Turabian StyleChen, Tao, Zhenwu Xu, Guoping Tang, Xiaohua Chen, Hong Fang, Hao Guo, Ye Yuan, Guoxiong Zheng, Liangliang Jiang, and Xiangyu Niu. 2021. "Spatiotemporal Monitoring of Soil CO2 Efflux in a Subtropical Forest during the Dry Season Based on Field Observations and Remote Sensing Imagery" Remote Sensing 13, no. 17: 3481. https://doi.org/10.3390/rs13173481
APA StyleChen, T., Xu, Z., Tang, G., Chen, X., Fang, H., Guo, H., Yuan, Y., Zheng, G., Jiang, L., & Niu, X. (2021). Spatiotemporal Monitoring of Soil CO2 Efflux in a Subtropical Forest during the Dry Season Based on Field Observations and Remote Sensing Imagery. Remote Sensing, 13(17), 3481. https://doi.org/10.3390/rs13173481










