Oil Spills or Look-Alikes? Classification Rank of Surface Ocean Slick Signatures in Satellite Data
Abstract
1. Introduction
- Exclusion or inclusion of specific types of data (Experiment 1); and
- Data transformations applied to the attributes (Experiment 2).
- Implementation of stringent knowledge-driven filters;
- Use of simple morphological characteristics (or simply “size information”);
- Exploration of several combinations of Meteorological-Oceanographic parameters (collectively referred to as “metoc variables”);
- Assess the value of the including geo-location parameters (“geo-loc”);
- Application of different data transformations to the attributes in the same analysis.
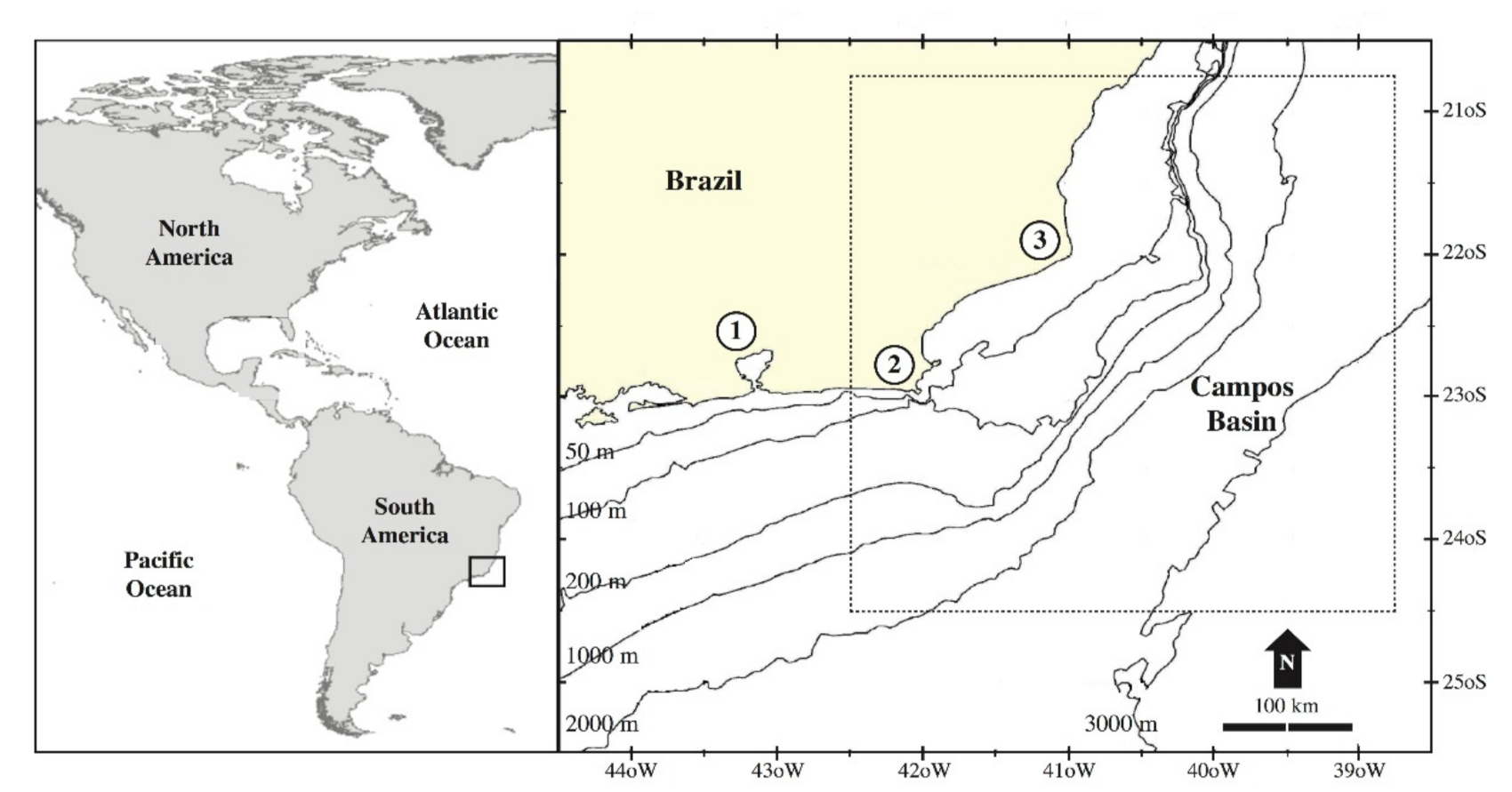
2. Study Area and Data
2.1. Study Region
2.2. Database
- Two textural (i.e., contrast and entropy of the pixels within the features);
- Four related to SAR-signatures (e.g., standard deviation and mean ratios between the pixel values inside and outside of the targets);
- Three scene-related (e.g., quantity of identified features pre-SAR image);
- Nine pieces of size information (e.g., area and perimeter);
- Four metoc variables—cloud cover information, wind speed (WND), sea-surface temperature (SST), and chlorophyll-a concentration (CHL)); and
- Twelve geo-loc parameters (e.g., bathymetry (BAT) and distance to coastline (CST) calculated to the feature centroid).
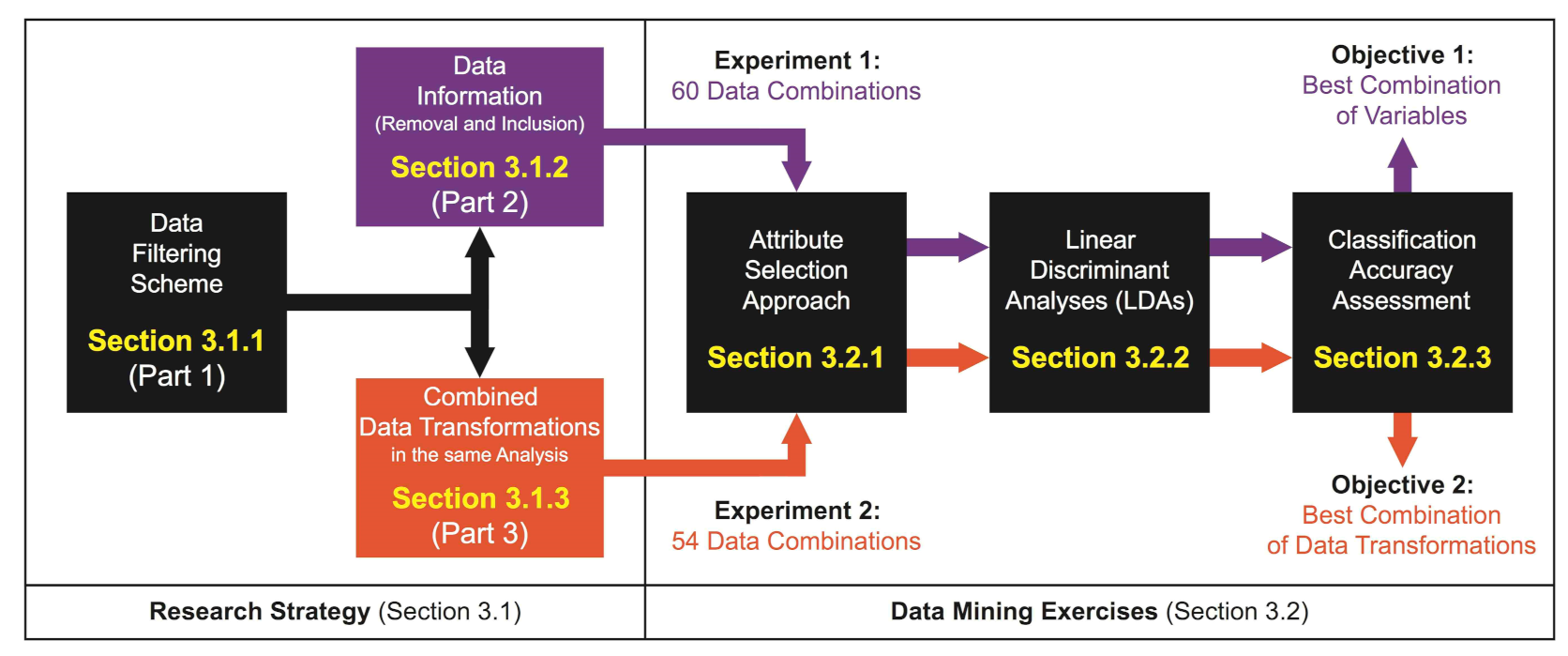
3. Methods
3.1. Research Strategy
3.1.1. Data-Filtering Scheme
3.1.2. Data Information: Removal or Inclusion
3.1.2.1. Size Information
- area;
- CMP;
- LtoW;
- PtoA;
- FRA; and
- NUM.
3.1.2.2. Metoc Variables
- WND, SST, and CHL;
- WND; and
- SST and CHL.
3.1.2.3. Geo-Location Parameters
- bathymetry (BAT); and
- distance to coastline (CST).
3.1.2.4. Data Transformations
- cube root; and
- logarithm base 10 (log10).
3.1.2.5. Data Combinations
3.1.3. Combined Use of Several Data Transformations in the Same Analysis
- “Metoc Assemblage”: WND, SST, and CHL; and
- “Size Assemblage”: area, LtoW, and NUM.
3.2. Data Mining Exercises
3.2.1. Attribute-Selection Approach
- In Experiment 2, a visual identification of correlated groups of variables, from which one attribute is manually selected for each group.
3.2.2. Linear Discriminant Analysis (LDA)
- Advantages: LDA is a supervised classification method that uses the observed values (attribute magnitudes) of the data (samples) to determine the location of a specific boundary (a linear discriminant axis) between each group (in our case, oil and look-alikes). The LDA general concept is to use the data according to two criteria: (i) maximization of the distance between the average value of each group; and (ii) minimization of the scatter within each group. The ratio of these two criteria, mean squared differences to sum of the variances, is projected onto a line (the linear discriminant axis), providing the ability to linearly separate the groups of samples. This projected lower-dimensional space inherently preserves the group discriminatory information, if one exists. A covariance matrix is calculated for each group along with a within-group scatter matrix to create what is called a discriminant function [72]. Numerically, this function, which corresponds to the dependent variable (DF(X)), is the sum of the product of the independent variables’ values (Xn) with a calculated independent variables’ weight (Wn); a constant offset may apply (C): DF(X) = (X1W1 + X2W2 + … + XnWn) − C [73].
- Disadvantages: LDA outcomes tend to support good classification decisions, but there are limitations. The number of variables must not exceed the number of samples [74]. LDAs are restricted to linearly separable groups. In addition, the variables used should have as small a correlation as possible [75]. This was accomplished through the pre-selection of attributes. Another aspect to consider is that the dataset must include a binary labeling that can be used to assess the LDA performance [76]: the accuracies of our supervised learning method were verified against the baseline of the experts’ classifications.
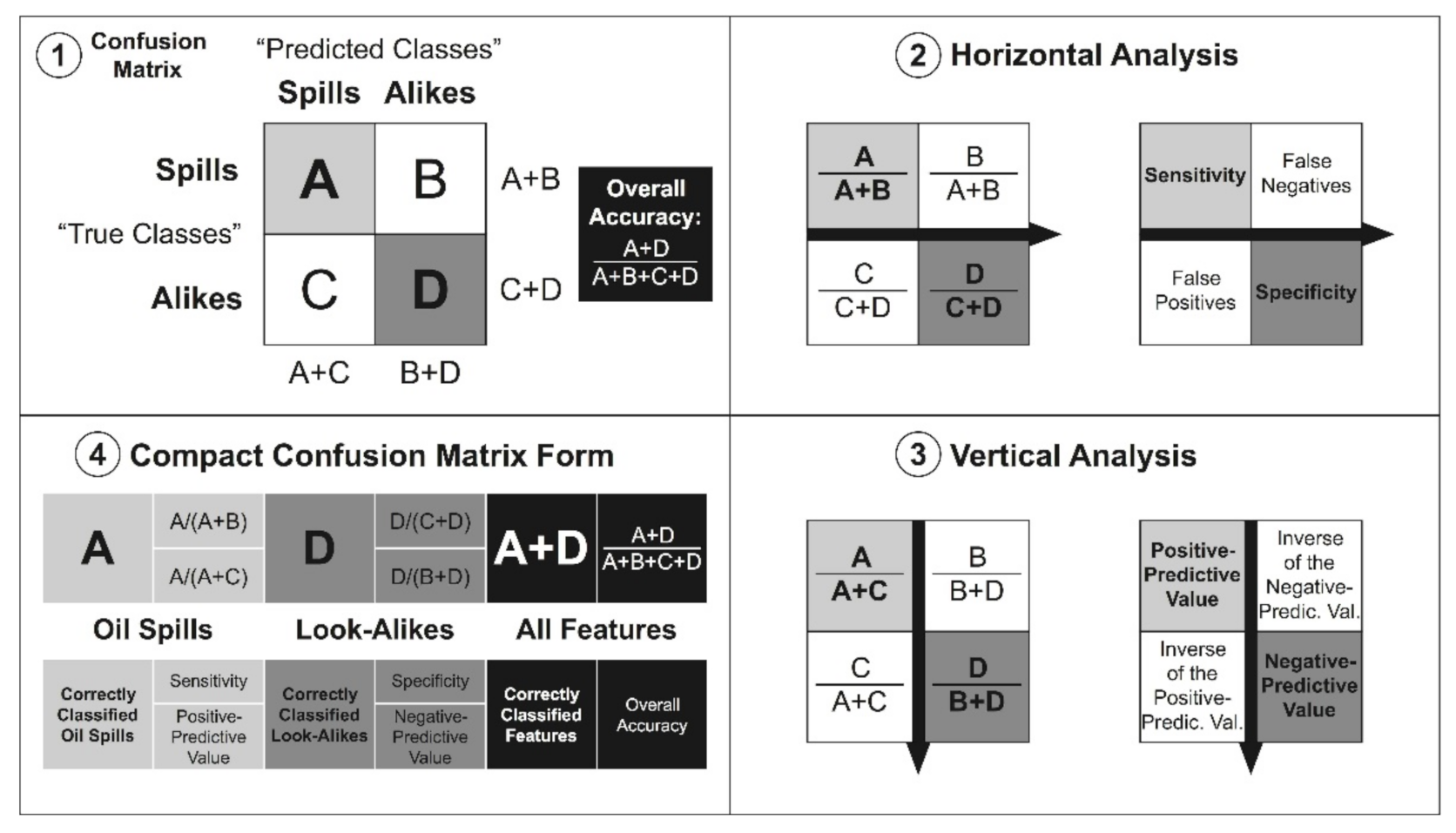
3.2.3. Classification-Accuracy Assessment
- Panel 1: Diagonal analysis produces the overall accuracy;
- Panel 2: Horizontal analysis provides the sensitivities and specificities (the producer’s accuracy), and their complements (false negatives and false positives: Type I error or omission error); and
- Panel 3: Vertical analysis gives the positive- and negative-predictive values (the user’s accuracy) and their counterparts (inverse of the positive- and inverse of negative-predictive values: Type II error or commission error).
4. Results
4.1. Data-Filtering Scheme
- WND Filter: The SAR-detection ability to identify sea-surface features relies on reduced radar backscatter from the sea-surface, which is dependent on the local wind field [80]. However, the wind limits (lower and upper) to identify sea-surface features in SAR images are not agreed upon by the remote sensing community [81,82,83]. Weak wind conditions (<3 m/s) may prevent correct classification of features as the ambient water around them is also smooth [81]. Even though some authors have pointed out that oil slicks can be observed in ~10 m/s or higher winds (e.g., [82]), others have found the upper wind limit is ~6 m/s (e.g., [83]). To eliminate unwanted wind influence on our classifiers, samples having wind speed <3 m/s and >6 m/s were not considered. WND filtering removed 199 features (69 spills and 130 look-alikes) that represent 25.5% of the original dataset (Table 2). A primary concern about the WND variable is the ground resolution disparity between the QuikSCAT wind data and the SAR pixel: ~25 km vs. ~100 m. Although we used the wind information already included in the original dataset [46], finer wind measurements could produce different outcomes. The reader is referred to Remark 5 below, where we discuss the WND variable impact on the LDA classification decision.
- SST Filter: The upwelled cold water that usually surfaces in the Campos Basin region comes from the South Atlantic Central Water and has temperatures between 6 °C and 20 °C [84]. However, an analysis of all AVHRR images from the year 2001 in this basin, 176 cloud-free scenes, did not indicate SSTs <11 °C even in the coldest core of the upwelling between Cabo de São Tomé and Cabo Frio [45]. Thus, all samples with SSTs <11 °C were removed prior to the analysis. This SST filtering did not remove any spill samples but eliminated 10 look-alike slicks amounting to 1.3% of the original dataset (Table 2). The ground resolution discrepancy between the AVHRR SSTs and SAR measurements is not as marked as that with the wind, but may also be a matter to bear in mind: ~1 km vs. ~100 m. As this filter only removed 10 look-alikes (Table 2), it is most likely that it did not exert as much influence as the WND filter on the analysis. Even though our choice of 11 °C was based on an earlier analysis, other SST thresholds could influence the LDA outcomes.
4.2. Experiment 1: Data Information
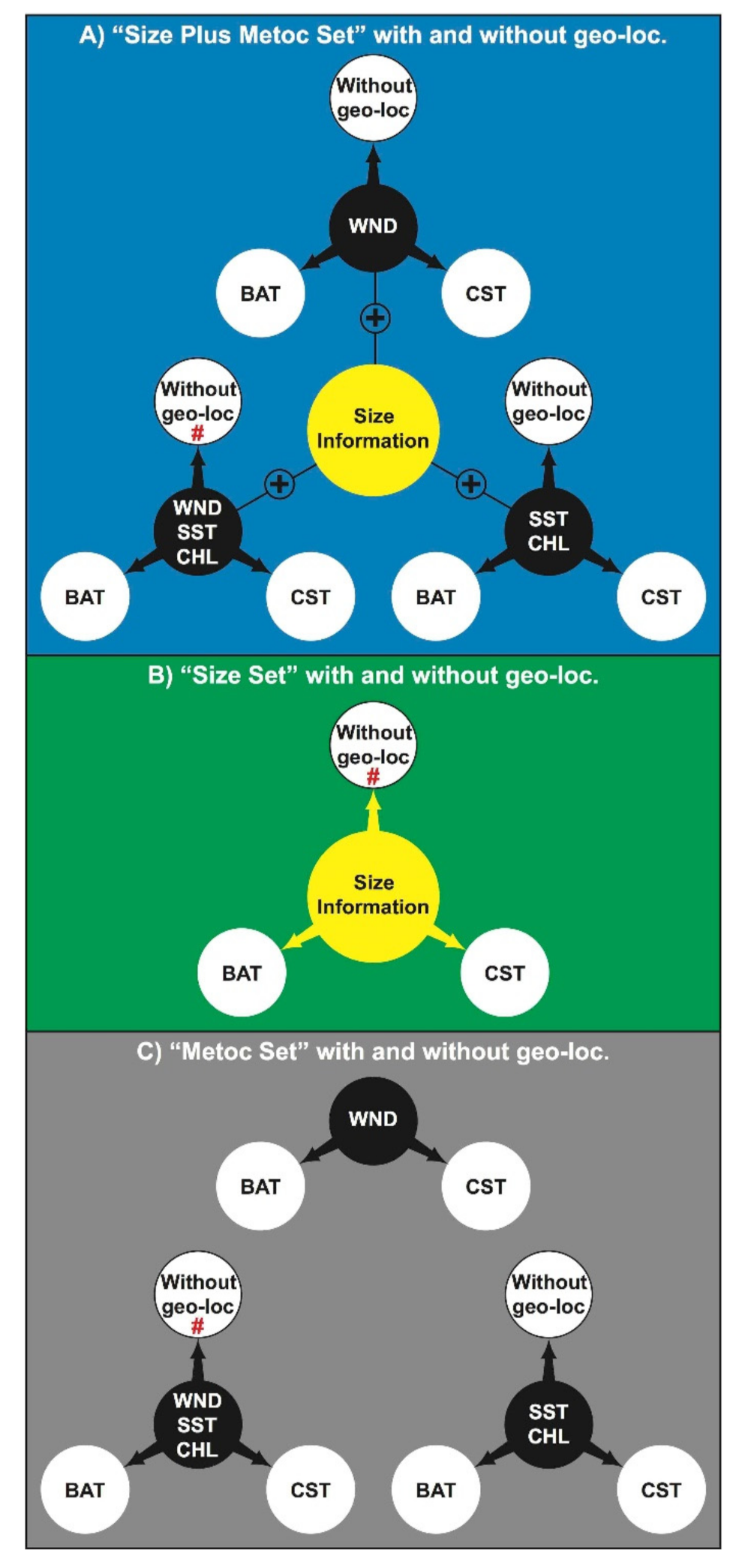
4.2.1. Size Plus Metoc Set, with or without Geo-Location (Blue: 1–27)
4.2.2. Size Set, with or without Geo-Location (Green: 1–9)
4.2.3. Metoc Set, with or without Geo-Location (Gray: 1–24)
4.2.4. Comparative Classification Accuracy
- Comparisons with Earlier Results ofCarvalho et al. [42]: Although the classification accuracy is improved compared with earlier results by using subdivision of the Size Plus Metoc Set in nearly all combinations, there was one exception: log10 without geo-loc (82.5% − 83.0% = −0.5%). Likewise, all accuracies of the Size Set increased (log10 transformation without geo-loc: 80.7% − 78.0% = 2.7%). On the contrary, all combinations of the Metoc Set showed decreased accuracy, and this was independent of the inclusion of geo-loc (no transformation and no geo-loc: 73.4% − 76.9% = −3.5%). See Remark 5 below. Table 5 contains a local ordering of the three data transformations of each attribute-type subdivision. This ordering confirmed that there was no clear consistency to show which data transformation was best; in Table 5, asterisks indicate best accuracies per subdivision. An example of the lack of consistency is seen in the subdivisions of the Size Set that indicated different best transformations in each study: the overall accuracy without any transformation (79.1%) reported by Carvalho et al. [42] surpassed the application of transformations, while here, the most successful transformation without geo-loc was log10 (80.7%), but the best outcome including a geo-loc parameter (BAT) was with the cube-transformed combination (81.4%). See Remark 6 below.
- Including Geo-Location: In nearly all cases, combinations including at least one geo-location parameter had better performance than those without; the exception being the Metoc Set cube-transformed that remained the same with or without geo-loc: 74.5%. The largest overall accuracy increases when geo-loc parameters were considered was ~2%: the Size Set combination with cube root transformation (from 79.6% to 81.4%) and the Size Plus Metoc Set combination with log10 transformation (from 82.5% to 84.3%). See Remark 7 below. In the combinations including geo-loc, BAT was preferable to CST. In only two of nine cases CST achieved superior accuracy. Indeed, among the combinations, the best classifier (cube transformed Size Plus Metoc Set) was improved by ~1% with the use of BAT: from 83.9% to 84.6% (Table 3 and Table 5). See Remark 8 below.
4.3. Experiment 2: Data Transformation
4.3.1. Metoc Assemblage (WND, SST, and CHL) with Different Data Transformations
| Hierarchy | WND | SST | CHL | Oil Spills | Slick-Alikes | All Features | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | None | Cube | log10 | 214 | 76.2% | 205 | 73.5% | 419 | 74.8% |
| 74.3% | 75.4% | ||||||||
| 2 | None | None | log10 | 215 | 76.5% | 203 | 72.8% | 418 | 74.6% |
| 73.9% | 75.5% | ||||||||
| 3 | None | log10 | log10 | 213 | 75.8% | 205 | 73.5% | 418 | 74.6% |
| 74.2% | 75.1% | ||||||||
| 4 | log10 | None | log10 | 218 | 77.6% | 200 | 71.7% | 418 | 74.6% |
| 73.4% | 76.0% | ||||||||
| 5 | log10 | None | Cube | 219 | 77.9% | 199 | 71.3% | 418 | 74.6% |
| 73.2% | 76.2% | ||||||||
| 6 | Cube | Cube | log10 | 218 | 77.6% | 200 | 71.7% | 418 | 74.6% |
| 73.4% | 76.0% | ||||||||
| 7 | Cube | Cube | Cube | 217 | 77.2% | 200 | 71.7% | 417 | 74.5% |
| 73.3% | 75.8% | ||||||||
| 8 | Cube | log10 | log10 | 217 | 77.2% | 200 | 71.7% | 417 | 74.5% |
| 73.3% | 75.8% | ||||||||
| 9 | Cube | log10 | Cube | 217 | 77.2% | 200 | 71.7% | 417 | 74.5% |
| 73.3% | 75.8% | ||||||||
| 10 | log10 | Cube | log10 | 218 | 77.6% | 199 | 71.3% | 417 | 74.5% |
| 73.2% | 76.0% | ||||||||
| 11 | log10 | log10 | log10 | 217 | 77.2% | 199 | 71.3% | 416 | 74.3% |
| 73.1% | 75.7% | ||||||||
| 12 | log10 | None | None | 216 | 76.9% | 200 | 71.7% | 416 | 74.3% |
| 73.2% | 75.5% | ||||||||
| 13 | log10 | Cube | Cube | 218 | 77.6% | 198 | 71.0% | 416 | 74.3% |
| 72.9% | 75.9% | ||||||||
| 14 | Cube | None | log10 | 216 | 76.9% | 200 | 71.7% | 416 | 74.3% |
| 73.2% | 75.5% | ||||||||
| 15 | Cube | None | Cube | 216 | 76.9% | 199 | 71.3% | 415 | 74.1% |
| 73.0% | 75.4% | ||||||||
| 16 | log10 | Cube | None | 214 | 76.2% | 201 | 72.0% | 415 | 74.1% |
| 73.3% | 75.0% | ||||||||
| 17 | None | log10 | Cube | 214 | 76.2% | 201 | 72.0% | 415 | 74.1% |
| 73.3% | 75.0% | ||||||||
| 18 | Cube | None | None | 213 | 75.8% | 201 | 72.0% | 414 | 73.9% |
| 73.2% | 74.7% | ||||||||
| 19 | None | None | Cube | 213 | 75.8% | 201 | 72.0% | 414 | 73.9% |
| 73.2% | 74.7% | ||||||||
| 20 | None | Cube | Cube | 214 | 76.2% | 200 | 71.7% | 414 | 73.9% |
| 73.0% | 74.9% | ||||||||
| 21 | log10 | log10 | Cube | 218 | 77.6% | 196 | 70.3% | 414 | 73.9% |
| 72.4% | 75.7% | ||||||||
| 22 | Cube | Cube | None | 212 | 75.4% | 201 | 72.0% | 413 | 73.8% |
| 73.1% | 74.4% | ||||||||
| 23 | Cube | log10 | None | 211 | 75.1% | 201 | 72.0% | 412 | 73.6% |
| 73.0% | 74.2% | ||||||||
| 24 | None | None | None | 208 | 74.0% | 203 | 72.8% | 411 | 73.4% |
| 73.2% | 73.6% | ||||||||
| 25 | None | Cube | None | 209 | 74.4% | 202 | 72.4% | 411 | 73.4% |
| 73.1% | 73.7% | ||||||||
| 26 | None | log10 | None | 209 | 74.4% | 202 | 72.4% | 411 | 73.4% |
| 73.1% | 73.7% | ||||||||
| 27 | log10 | log10 | None | 213 | 75.8% | 198 | 71.0% | 411 | 73.4% |
| 72.4% | 74.4% | ||||||||
4.3.2. Size Assemblage (Area, LtoW, and NUM) with Different Data Transformations
5. Discussion
| Hierarchy | Area | LtoW | NUM | Oil Spills | Slick-Alikes | All Features | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | log10 | log10 | None | 250 | 89.0% | 203 | 72.8% | 453 | 80.9% | |
| 76.7% | 86.8% | |||||||||
| 2 | log10 | Cube | None | 251 | 89.3% | 202 | 72.4% | 453 | 80.9% | |
| 76.5% | 87.1% | |||||||||
| 3 | log10 | None | None | 250 | 89.0% | 201 | 72.0% | 451 | 80.5% | |
| 76.2% | 86.6% | |||||||||
| 4 | log10 | log10 | Cube | 247 | 87.9% | 200 | 71.7% | 447 | 79.8% | |
| 75.8% | 85.5% | |||||||||
| 5 | log10 | None | Cube | 246 | 87.5% | 199 | 71.3% | 445 | 79.5% | |
| 75.5% | 85.0% | |||||||||
| 6 | log10 | Cube | Cube | 246 | 87.5% | 199 | 71.3% | 445 | 79.5% | |
| 75.5% | 85.0% | |||||||||
| Hierarchy | Area | LtoW | NUM | Oil Spills | Slick-Alikes | All Features | ||||
| * | 7 | Cube | None | None | 269 | 95.7% | 175 | 62.7% | 444 | 79.3% |
| 72.1% | 93.6% | |||||||||
| * | 8 | Cube | log10 | None | 266 | 94.7% | 175 | 62.7% | 441 | 78.8% |
| 71.9% | 92.1% | |||||||||
| * | 9 | Cube | Cube | None | 267 | 95.0% | 174 | 62.4% | 441 | 78.8% |
| 71.8% | 92.6% | |||||||||
| 10 | log10 | log10 | log10 | 239 | 85.1% | 201 | 72.0% | 440 | 78.6% | |
| 75.4% | 82.7% | |||||||||
| 11 | log10 | None | log10 | 240 | 85.4% | 198 | 71.0% | 438 | 78.2% | |
| 74.8% | 82.8% | |||||||||
| 12 | log10 | Cube | log10 | 239 | 85.1% | 199 | 71.3% | 438 | 78.2% | |
| 74.9% | 82.6% | |||||||||
| * | 13 | Cube | log10 | Cube | 251 | 89.3% | 183 | 65.6% | 434 | 77.5% |
| 72.3% | 85.9% | |||||||||
| * | 14 | Cube | Cube | Cube | 251 | 89.3% | 182 | 65.2% | 433 | 77.3% |
| 72.1% | 85.8% | |||||||||
| * | 15 | Cube | None | Cube | 250 | 89.0% | 181 | 64.9% | 431 | 77.0% |
| 71.8% | 85.4% | |||||||||
| 16 | Cube | None | log10 | 243 | 86.5% | 188 | 67.4% | 431 | 77.0% | |
| 72.8% | 83.2% | |||||||||
| 17 | Cube | Cube | log10 | 241 | 85.8% | 185 | 66.3% | 426 | 76.1% | |
| 71.9% | 82.2% | |||||||||
| 18 | Cube | log10 | log10 | 242 | 86.1% | 184 | 65.9% | 426 | 76.1% | |
| 71.8% | 82.5% | |||||||||
| Hierarchy | Area | LtoW | NUM | Oil Spills | Slick-Alikes | All Features | ||||
| *! | 19 | None | log10 | None | 246 | 87.5% | 149 | 53.4% | 395 | 70.5% |
| 65.4% | 81.0% | |||||||||
| *! | 20 | None | None | None | 247 | 87.9% | 146 | 52.3% | 393 | 70.2% |
| 65.0% | 81.1% | |||||||||
| *! | 21 | None | Cube | None | 247 | 87.9% | 146 | 52.3% | 393 | 70.2% |
| 65.0% | 81.1% | |||||||||
| *! | 22 | None | log10 | Cube | 230 | 81.9% | 158 | 56.6% | 388 | 69.3% |
| 65.5% | 75.6% | |||||||||
| *! | 23 | None | None | Cube | 234 | 83.3% | 153 | 54.8% | 387 | 69.1% |
| 65.0% | 76.5% | |||||||||
| *! | 24 | None | Cube | Cube | 230 | 81.9% | 157 | 56.3% | 387 | 69.1% |
| 65.3% | 75.5% | |||||||||
| *! | 25 | None | log10 | log10 | 221 | 78.6% | 158 | 56.6% | 379 | 67.7% |
| 64.6% | 72.5% | |||||||||
| *! | 26 | None | Cube | log10 | 219 | 77.9% | 160 | 57.3% | 379 | 67.7% |
| 64.8% | 72.1% | |||||||||
| *! | 27 | None | None | log10 | 219 | 77.9% | 156 | 55.9% | 375 | 67.0% |
| 64.0% | 71.6% | |||||||||
5.1. Data-Information Experiment
- Remark 1: Considering the hierarchy blocks, when variables from Size Plus Metoc Set were combined, the algorithms were more accurate than those using variables from one type alone. Additionally, when comparing the sole use of size information, the classification accuracies were superior to those using only the metoc variables. A corresponding hierarchical pattern was also observed among the 61 data combinations reported in Carvalho et al. [40]. The hierarchy block formation was only disrupted by two combinations of the Size Set (hierarchies 25 and 28: green group) that were more accurate than a few combinations of the Size Plus Metoc Set (hierarchies 26, 27, and 29: blue group).
- Remark 2: Regarding the subgroups, it is noteworthy that some data combinations achieve classifications better than others (Table 3A,B). Table 4 shows the top-blue (Size Plus Metoc Set) and middle-green (Size Set) blocks have an average difference of ~1% between each of their groups: ~84% to ~80%. The differences between the middle-green and lowest-gray (Metoc Set) blocks were greater, as were those within the groups in the last block.
- Remark 3: Of the many combinations that had the same overall accuracies (to the number of decimal places indicated), most of them did not correctly identify the same samples—this is seen in Table 3A,B: the number of correctly classified oil spills and look-alike slicks. Only hierarchies 34 and 35 (79.6%—Size Set without geo-loc: non-transformed and cube root, respectively) and hierarchies 39 and 40 (74.5%—Metoc Set with and without CST, both cube-transformed) identified the same samples.
5.1.1. Comparative Classification Accuracy
- Remark 4: Although nearly all accuracies were improved in the Size Plus Metoc Set and Size Set subdivisions described by Carvalho et al. [42], the same did not hold for the Metoc Set subdivision that had its overall accuracies reduced (Table 5). While the largest improvements were ~3% in two log-transformed Size Set combinations: without geo-loc (from 78.0% to 80.7%) and with geo-loc (from 78.0% to 81.3%), the best of all combinations (cube transformed Size Plus Metoc Set) had its accuracy increased by ~1% by the inclusion of one geo-loc parameter (BAT): from 83.7% to 84.6% (Table 5). These improvements demonstrate the success of the removal of samples that are unlikely to contribute to the classification and the addition of geo-loc attributes.
5.1.2. Comparisons with Earlier Results
- Remark 5: The Metoc Set combinations did not produce high-ranking accuracies in comparison with the earlier results of Carvalho et al. [42] (Table 5). This may be due to many records having been removed based on the WND thresholds: lower (<3 m/s: 105 samples) and upper (>6 m/s: 94 samples)—i.e., 25.5% of the original dataset (Table 2), even though the exclusion of these cases was based on physical reasoning.
- Remark 6: There was not a clear pattern to indicate which data transformation was best. The non-transformed set and log10 had only two cases each as the best combination among the nine compared, and the cube-transformed combinations were more accurate in five cases (Table 5).
5.1.3. Geo-Location Inclusion
- Remark 7: Two geo-loc parameters available in the original dataset were studied here, but they were not considered together because they are highly correlated. The inclusion of geo-loc parameters results in improved accuracies (Table 5).
- Remark 8: Combinations using Bathymetry (BAT, ranging from 5 m to ~4 km) tended to have improved accuracies compared to those using the distance to coastline (CST, 186 m to ~435 km); Table 5.
5.2. Data-Transformation Experiment
- Remark 9: The investigation of two assemblages of only three variables subjected to three data transformations indicated that the Metoc Assemblage did not show an advantage of using the different transformations, however, the results of using different data transformations within the variables of the Size Assemblage were promising; see below Remarks 12 and 15, and Future Work Recommendations.
5.2.1. Metoc Assemblage: WND, SST, and CHL
- Remark 10: There was a lack of hierarchy blocks in the Metoc Assemblage subjected to different transformations. This may be due to the relatively small range among the analyzed features (WND (3 to 6 m/s), SST (11.44 to 29.43 °C), and CHL (0.003 and 9.7 mg/m3)).
- Remark 11: Even though there was a span of 1.4% (8 samples) between the best and worst accuracy among the 27 combinations of the Metoc Assemblage, if we compare the baseline combinations of three pieces of metoc variables with the same transformation (shown in bold in Table 6), we notice that subjecting variables to different data transformations in the same analysis slightly improved the accuracies of the LDA algorithms.
5.2.2. Size Assemblage: Area, LtoW, and NUM
- Remark 12: The use of three pieces of size information subjected to different transformations (i.e., the two combinations that tied with 80.9%—area (log10), LtoW (log- or cube-transformed), and NUM (non-transformed); hierarchies 1 and 2 in Table 7) reached an equivalent accuracy to the best combination of six pieces of size information log-transformed without geo-loc or metoc (80.7%; hierarchy 31 in Table 3B). Clearly, the combination of various attributes subjected to several data transformations in the same analysis, can lead to improving the LDA algorithm accuracy.
- Remark 13: The combinations using non-transformed areas were void—hierarchies 19 to 27 in Table 7. The lack of data transformation may also be negatively influencing other combinations of variables using the non-transformed area, for example, those among the 60 depicted in Figure 3, and presented in Table 3A,B. As such, other variables may also be suffering from using non-transformed areas, and this should be further investigated. See also Remark 15 below.
- Remark 14: The best of the three baseline combinations of three pieces of size information with the same transformation (shown in bold font in Table 1 and Table 7) was subjected to log10—78.6% (hierarchy 10 in Table 7). However, nine other combinations were better, the best being 80.9% (hierarchies 1 and 2 in Table 7). This improvement of 2.3% is another indication that the combined use of attributes subjected to different data transformations improves the LDA classification accuracy.
- Remark 15: Considering the major hierarchy blocks and secondary groups, among the 27 combinations that use three pieces of size information with three data transformations (Table 7), one reason is given for this ranking: among the 560 analyzed features, areas have a large range of continuous values (from oil spills with 0.45 km2 to look-alikes with 8177.24 km2 cause by upwelling events), whereas the NUM variable with its discrete values had features with only 1 part up to look-alike slicks with 24 different parts caused by biogenic films.
6. Summary and Conclusions
6.1. Objective 1
- if all variables are available, the best accuracy is 84.6% (hierarchy 1; cube-transformed);
- without geo-loc parameters, the best accuracy is 83.9% (hierarchy 6; non-transformed);
- if Oceanographic data are not available, the best accuracy is 83.9% (hierarchy 8; log-transformed);
- if Meteorological data are unavailable, the best accuracy is 83.0% (hierarchy 15; cube-transformed);
- if only size information is given, the best accuracy is 80.7% (hierarchy 31; log-transformed);
- without size information, the best accuracy is 74.8% (hierarchy 37; log-transformed);
- if only Meteorological data and geo-loc are used, the best accuracy is 73.8% (hierarchy 43; cube-transformed); and
- if only Oceanographic data are accounted for (with or without geo-loc), the results are considered void (hierarchies 52–60).
6.2. Objective 2
6.3. Future Work Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- RCC (National Research Council Committee). Oil in the Sea: Inputs, Fates, and Effects; The National Academies Press: Washington, DC, USA, 1985; Available online: https://www.nap.edu/read/314/chapter/1 (accessed on 30 July 2021).
- NRCC (National Research Council Committee). Oil in the Sea III: Inputs, Fates, and Effects; The National Academies Press: Washington, DC, USA, 2003; ISBN 9780309084383. Available online: https://www.nap.edu/read/10388/chapter/1 (accessed on 30 July 2021).
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B.; et al. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Neuparth, T.; Moreira, S.; Santos, M.; Henriques, M.A.R. Review of oil and HNS accidental spills in Europe: Identifying major environmental monitoring gaps and drawing priorities. Mar. Pollut. Bull. 2012, 64, 1085–1095. [Google Scholar] [CrossRef] [PubMed]
- Soares, M.D.O.; Teixeira, C.; Bezerra, L.E.A.; Paiva, S.; Tavares, T.C.L.; Garcia, T.M.; de Araújo, J.T.; Campos, C.C.; Ferreira, S.M.C.; Matthews-Cascon, H.; et al. Oil spill in South Atlantic (Brazil): Environmental and governmental disaster. Mar. Policy 2020, 115, 103879. [Google Scholar] [CrossRef]
- Soares, M.O.; Teixeira, C.; Bezerra, L.E.; Rossi, S.; Tavares, T.; Cavalcante, R. Brazil oil spill response: Time for coordination. Science 2020, 367, 155. [Google Scholar] [CrossRef] [PubMed]
- Coppini, G.; De Dominicis, M.; Zodiatis, G.; Lardner, R.; Pinardi, N.; Santoleri, R.; Colella, S.; Bignami, F.; Hayes, D.R.; Soloviev, D.; et al. Hindcast of oil-spill pollution during the Lebanon crisis in the Eastern Mediterranean, July–August 2006. Mar. Pollut. Bull. 2011, 62, 140–153. [Google Scholar] [CrossRef] [PubMed]
- Stringer, W.J.; Ahlnäs, K.; Royer, T.C.; Dean, K.E.; Groves, J.E. Oil spill shows on satellite image. EOS Trans. 1989, 70, 564. [Google Scholar] [CrossRef]
- Banks, S. SeaWiFS satellite monitoring of oil spill impact on primary production in the Galápagos Marine Reserve. Mar. Pollut. Bull. 2003, 47, 325–330. [Google Scholar] [CrossRef]
- Pisano, A.; Bignami, F.; Santoleri, R. Oil Spill Detection in Glint-Contaminated Near-Infrared MODIS Imagery. Remote Sens. 2015, 7, 1112–1134. [Google Scholar] [CrossRef]
- Jackson, C.R.; Apel, J.R. Synthetic Aperture Radar Marine User’s Manual; NOAA/NESDIS; Office of Research and Applications: Washington, DC, USA, 2004; Available online: http://www.sarusersmanual.com (accessed on 30 July 2021).
- Gens, R. Oceanographic Applications of SAR Remote Sensing. GIScience Remote Sens. 2008, 45, 275–305. [Google Scholar] [CrossRef]
- Espedal, H.A.; Johannessen, O.M.; Knulst, J. Satellite detection of natural films on the ocean surface. Geophys. Res. Lett. 1996, 23, 3151–3154. [Google Scholar] [CrossRef]
- Garcia-Pineda, O.; Zimmer, B.; Howard, M.; Pichel, W.G.; Li, X.; MacDonald, I.R. Using SAR images to delineate ocean oil slicks with a texture-classifying neural network algorithm (TCNNA). Can. J. Remote Sens. 2009, 35, 411–421. [Google Scholar] [CrossRef]
- Yekeen, S.T.; Balogun, A.; Yusof, K.B.W. A novel deep learning instance segmentation model for automated marine oil spill detection. ISPRS J. Photogramm. Remote Sens. 2020, 167, 190–200. [Google Scholar] [CrossRef]
- Ayed, I.B.; Mitiche, A.; Belhadj, Z. Multiregion level-set partitioning of synthetic aperture radar images. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 793–800. [Google Scholar] [CrossRef]
- Topouzelis, K.; Karathanassi, V.; Pavlakis, P.; Rokos, D. Detection and discrimination between oil spills and look-alike phenomena through neural networks. ISPRS J. Photogramm. Remote. Sens. 2007, 62, 264–270. [Google Scholar] [CrossRef]
- Marghany, M. RADARSAT automatic algorithms for detecting coastal oil spill pollution. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 191–196. [Google Scholar] [CrossRef]
- Calabresi, G.; Del Frate, F.; Lichtenegger, I.; Petrocchi, A.; Trivero, P. Neural networks for the oil spill detection using ERS–SAR data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS ‘99), Hamburg, Germany, 28 June–2 July 1999; pp. 215–217. [Google Scholar] [CrossRef]
- Jones, B. A comparison of visual observations of surface oil with Synthetic Aperture Radar imagery of the Sea Empress oil spill. Int. J. Remote Sens. 2001, 22, 1619–1638. [Google Scholar] [CrossRef]
- Fiscella, B.; Giancaspro, A.; Nirchio, F.; Pavese, P.; Trivero, P. Oil spill monitoring in the Mediterranean Sea using ERS SAR data. In Proceedings of the Envisat Symposium, ESA, Göteborg, Sweden, 16–20 October 1998. 9p. [Google Scholar]
- Del Frate, F.; Petrocchi, A.; Lichtenegger, J.; Calabresi, G. Neural networks for oil spill detection using ERS-SAR data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2282–2287. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Cartalis, C.; Kiranoudis, C.T. Automatic identification of oil spills on satellite images. Environ. Model. Softw. 2006, 21, 640–652. [Google Scholar] [CrossRef]
- Topouzelis, K.; Psyllos, A. Oil spill feature selection and classification using decision tree forest on SAR image data. ISPRS J. Photogramm. Remote Sens. 2012, 68, 135–143. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Gibril, M.; Shanableh, A.; Kais, A.; Hamed, O.; Al-Mansoori, S.; Khalil, M. Sensors, Features, and Machine Learning for Oil Spill Detection and Monitoring: A Review. Remote Sens. 2020, 12, 3338. [Google Scholar] [CrossRef]
- Espedal, H.A.; Johannessen, O.M. Cover: Detection of oil spills near offshore installations using synthetic aperture radar (SAR). Int. J. Remote Sens. 2000, 21, 2141–2144. [Google Scholar] [CrossRef]
- Stathakis, D.; Topouzelis, K.; Karathanassi, V. Large-scale feature selection using evolved neural networks. Remote Sens. 2006, 6365, 636513. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Hou, Y.; Wang, X.; Wang, L. Marine Oil Slick Detection Using Improved Polarimetric Feature Parameters Based on Polarimetric Synthetic Aperture Radar Data. Remote Sens. 2021, 13, 1607. [Google Scholar] [CrossRef]
- Alpers, W.; Holt, B.; Zeng, K. Oil spill detection by imaging radars: Challenges and pitfalls. Remote Sens. Environ. 2017, 201, 133–147. [Google Scholar] [CrossRef]
- Fingas, M.F.; Brown, C.E. Review of oil spill remote sensing. Spill Sci. Technol. Bull. 1997, 4, 199–208. [Google Scholar] [CrossRef]
- Fingas, M.; Brown, C. Review of oil spill remote sensing. Mar. Pollut. Bull. 2014, 83, 9–23. [Google Scholar] [CrossRef] [PubMed]
- Fingas, M.; Brown, C.E. A Review of Oil Spill Remote Sensing. Sensors 2017, 18, 91. [Google Scholar] [CrossRef]
- Carvalho, G.A. Multivariate Data Analysis of Satellite-Derived Measurements to Distinguish Natural from Man-Made Oil Slicks on the Sea Surface of Campeche Bay (Mexico). Ph.D. Thesis, COPPE, Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, 2015; 285p. Available online: http://www.coc.ufrj.br/pt/teses-de-doutorado/390-2015/4618-gustavo-de-araujo-carvalho (accessed on 30 July 2021).
- Mattson, J.S.; Mattson, C.S.; Spencer, M.J.; Spencer, F.W. Classification of petroleum pollutants by linear discriminant function analysis of infrared spectral patterns. Anal. Chem. 1977, 49, 500–502. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Li, J.; Brenning, A. A comparative study of different classification techniques for marine oil spill identification using RADARSAT-1 imagery. Remote Sens. Environ. 2014, 141, 14–23. [Google Scholar] [CrossRef]
- Liu, P.; Li, Y.; Liu, B.; Chen, P.; Xu, A.J. Semi-Automatic Oil Spill Detection on X-Band Marine Radar Images Using Texture Analysis, Machine Learning, and Adaptive Thresholding. Remote Sens. 2019, 11, 756. [Google Scholar] [CrossRef]
- Cao, Y.; Xu, L.; Clausi, D. Exploring the Potential of Active Learning for Automatic Identification of Marine Oil Spills Using 10-Year (2004–2013) RADARSAT Data. Remote Sens. 2017, 9, 1041. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; de Miranda, F.P.; Landau, L.; Paes, E.T. Exploratory Data Analysis of Synthetic Aperture Radar (SAR) Measurements to Distinguish the Sea Surface Expressions of Naturally-Occurring Oil Seeps from Human-Related Oil Spills in Campeche Bay (Gulf of Mexico). ISPRS Int. J. Geo-Inf. 2017, 6, 379. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; Paes, E.T.; de Miranda, F.P.; Landau, L. Refined Analysis of RADARSAT-2 Measurements to Discriminate Two Petrogenic Oil-Slick Categories: Seeps versus Spills. J. Mar. Sci. Eng. 2018, 6, 153. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; Paes, E.T.; de Miranda, F.P.; Landau, L. Oil-Slick Category Discrimination (Seeps vs. Spills): A Linear Discriminant Analysis Using RADARSAT-2 Backscatter Coefficients in Campeche Bay (Gulf of Mexico). Remote Sens. 2019, 11, 1652. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; de Miranda, F.P.; Landau, L.; Moreira, F. The Use of a RADARSAT-derived Long-term Dataset to Investigate the Sea Surface Expressions of Human-related Oil spills and Naturally Occurring Oil Seeps in Campeche Bay, Gulf of Mexico. Can. J. Remote Sens. 2016, 42, 307–321. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; Ebecken, N.F.F.; Landau, L. Classification of Oil Slicks and Look-Alike Slicks: A Linear Discriminant Analysis of Microwave, Infrared, and Optical Satellite Measurements. Remote Sens. 2020, 12, 2078. [Google Scholar] [CrossRef]
- ANP (Agência Nacional do Petróleo, Gás Natural e Biocombustíveis). Oil and Natural Gas Production Bulletin, External Circulation; n. 120; ANP (Agência Nacional do Petróleo, Gás Natural e Biocombustíveis): Brasilia, Brazil, 2020; 46p. Available online: http://www.anp.gov.br/publicacoes/boletins-anp/2395-boletim-mensal-da-producao-de-petroleo-e-gas-natural (accessed on 30 July 2021).
- Campos, E.; Gonçalves, J.E.; Ikeda, Y. Water mass characteristics and geostrophic circulation in the South Brazil Bight: Summer of 1991. J. Geophys. Res. Space Phys. 1995, 100, 18537–18550. [Google Scholar] [CrossRef]
- Carvalho, G.A. Wind Influence on the Sea Surface Temperature of the Cabo Frio Upwelling (23° S/42° W—RJ/Brazil) during 2001, through the Analysis of Satellite Measurements (Seawinds-QuikScat/AVHRR-NOAA). Bachelor’s Thesis, UERJ, Rio de Janeiro, Brazil, 2002; 210p. Available online: goo.gl/reqp2H (accessed on 30 July 2021).
- Bentz, C.M. Reconhecimento Automático de Eventos Ambientais Costeiros e Oceânicos em Imagens de Radares Orbitais. Ph.D. Thesis, Universidade Federal do Rio de Janeiro (UFRJ), COPPE, Rio de Janeiro, Brazil, 2006; 115p. Available online: http://www.coc.ufrj.br/index.php?option=com_content&view=article&id=1048:cristina-maria-bentz (accessed on 30 July 2021).
- Moutinho, A.M. Otimização de Sistemas de Detecção de Padrões em Imagens. Ph.D. Thesis, Universidade Federal do Rio de Janeiro (UFRJ), COPPE, Rio de Janeiro, Brazil, 2011; 133p. Available online: http://www.coc.ufrj.br/index.php/teses-de-doutorado/155-2011/1258-adriano-martins-moutinho (accessed on 30 July 2021).
- Fox, P.A.; Luscombe, A.P.; Thompson, A.A. RADARSAT-2 SAR modes development and utilization. Can. J. Remote Sens. 2004, 30, 258–264. [Google Scholar] [CrossRef]
- MDA (MacDonald, Dettwiler and Associates Ltd.). RADARSAT-2 Product Description; Technical Report RN-SP-52-1238, Issue/Revision: 1/13; MDA: Richmond, BC, Canada, 2016; p. 91. [Google Scholar]
- Baatz, M.; Schape, A. Multiresolution segmentation—An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung XI, Beiträge zum AGIT—Symposium 1999; Herbert Wichmann Verlag: Kalsruhe, Germany, 1999. [Google Scholar]
- Chan, Y.K.; Koo, V.C. an introduction to synthetic aperture radar (SAR). Prog. Electromagn. Res. B 2008, 2, 27–60. [Google Scholar] [CrossRef]
- Tang, W.; Liu, W.; Stiles, B. Evaluation of high-resolution ocean surface vector winds measured by QuikSCAT scatterometer in coastal regions. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1762–1769. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.; Evans, R. Overview of the NOAA/NASA advanced very high resolution radiometer Pathfinder algorithm for sea surface temperature and associated matchup database. J. Geophys. Res. Space Phys. 2001, 106, 9179–9197. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.; Walsh, S.; Williams, E.; Halliwell, V.; Szczodrak, M.; Brown, O.B.; Minnett, P.J.; Evans, R. A decade of sea surface temperature from MODIS. Remote Sens. Environ. 2015, 165, 27–41. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Space Phys. 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Esaias, W.; Abbott, M.; Barton, I.; Brown, O.; Campbell, J.; Carder, K.; Clark, D.; Evans, R.; Hoge, F.; Gordon, H.; et al. An overview of MODIS capabilities for ocean science observations. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1250–1265. [Google Scholar] [CrossRef]
- Figueredo, G.P.; Ebecken, N.F.F.; Augusto, D.A.; Barbosa, H.J.C. An immune-inspired instance selection mechanism for supervised classification. Memet. Comput. 2012, 4, 135–147. [Google Scholar] [CrossRef]
- Passini, M.L.C.; Estébanez, K.B.; Figueredo, G.P.; Ebecken, N.F.F. A Strategy for Training Set Selection in Text Classification Problems. Int. J. Adv. Comput. Sci. Appl. 2013, 4, 6. [Google Scholar] [CrossRef][Green Version]
- MDA (MacDonald, Dettwiler and Associates Ltd.). RADARSAT-2 Product Format Definition; Technical Report RN-RP-51–2713, Issue/Revision: 1/10; MDA: Richmond, BC, Canada, 2011; 83p. [Google Scholar]
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological Statistics software package for education and data analysis. Palaeontol. Electron. 2001, 4, 9. [Google Scholar]
- Sneath, P.H.A.; Sokal, R.R. Numerical Taxonomy—The Principles and Practice of Numerical Classification; W.H. Freeman and Company: San Francisco, CA, USA, 1973; 573p, ISBN 0716706970. Available online: http://www.brclasssoc.org.uk/books/Sneath/ (accessed on 30 July 2021).
- Kelley, L.A.; Gardner, S.P.; Sutcliffe, M.J. An automated approach for clustering an ensemble of NMR-derived protein structures into conformationally related subfamilies. Protein Eng. Des. Sel. 1996, 9, 1063–1065. [Google Scholar] [CrossRef] [PubMed]
- Zar, H.J. Biostatistical Analysis, 5th ed.; New International Edition; Pearson: Upper Saddle River, NJ, USA, 2014; ISBN 1292024046. [Google Scholar]
- Rao, C.R. The use and interpretation of principal component analysis in applied research. Sankhyã Indian J. Stat. 1964, 26, 329–358. [Google Scholar]
- Zhang, D.; He, J.; Zhao, Y.; Luo, Z.; Du, M. Global plus local: A complete framework for feature extraction and recognition. Pattern Recognit. 2014, 47, 1433–1442. [Google Scholar] [CrossRef]
- Li, P.; Fu, Y.; Mohammed, U.; Elder, J.H.; Prince, S.J.D. Probabilistic Models for Inference about Identity. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 144–157. [Google Scholar] [CrossRef]
- Wang, X.; Tang, X. 2004, Dual-Space Linear Discriminant Analysis for Face Recognition. In Proceedings of the Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’04), Washington, DC, USA, 27 June–2 July 2004; Volume 2, p. 15. [Google Scholar] [CrossRef]
- Chen, L.-F.; Liao, H.-Y.M.; Ko, M.-T.; Lin, J.-C.; Yu, G.-J. A new LDA-based face recognition system which can solve the small sample size problem. Pattern Recognit. 2000, 33, 1713–1726. [Google Scholar] [CrossRef]
- Hastie, T.; Buja, A.; Tibshirani, R. Penalized Discriminant Analysis. Ann. Stat. 1995, 23, 73–102. [Google Scholar] [CrossRef]
- Tharwat, A.; Gaber, T.; Ibrahim, A.; Hassanien, A.E. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017, 30, 169–190. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Numerical Ecology. In Developments in Environmental Modelling, 3rd English ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2012; Volume 24, 990p, ISBN 978–0444538680. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Morgan Kaufmann: San Francisco, CA, USA, 2016; 654p. [Google Scholar]
- Lohninger, H. Teach/Me Data Analysis; Springer: Berlin, Germany; New York, NY, USA; Tokyo, Japan, 1999; ISBN 3540147438. [Google Scholar]
- Clemmensen, L.K.H. On Discriminant Analysis Techniques and Correlation Structures in High Dimensions; Technical Report-2013 No. 04; Technical University of Denmark: Lyngby, Denmark, 2013; Available online: https://backend.orbit.dtu.dk/ws/portalfiles/portal/53413081/tr13_04_Clemmensen_L.pdf (accessed on 30 July 2021).
- McLachlan, G. Discriminant Analysis and Statistical Pattern Recognition; John Wiley & Sons, Inc.: Milton, Australia, 1992; 534p, ISBN 0-471-61531-5. [Google Scholar]
- Aurelien, G. Hands-On Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent System; O’Reilly Media: Newton, MA, USA, 2017. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Factor to ROC, Informedness, Markedness & Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Christiansen, M.B.; Koch, W.; Horstmann, J.; Hasager, C.B.; Nielsen, M. Wind resource assessment from C-band SAR. Remote Sens. Environ. 2006, 105, 68–81. [Google Scholar] [CrossRef]
- Bern, T.-I.; Wahl, T.; Anderssen, T.; Olsen, R. Oil Spill Detection Using Satellite Based SAR: Experience from a Field Experiment. Photogramm. Eng. Remote Sens. 1993, 59, 423–428. [Google Scholar]
- Johannessen, J.A.; Digranes, G.; Espedal, H.; Johannessen, O.M.; Samuel, P.; Browne, D.; Vachon, P. SAR Ocean Feature Catalogue; ESA Publication Division: Noordwijk, The Netherlands, 1994; 106p. [Google Scholar]
- Staples, G.C.; Hodgins, D.O. RADARSAT-1 emergency response for oil spill monitoring. In Proceedings of the 5th International Conference on Remote Sensing for Marine and Coastal Environments, San Diego, CA, USA, 5–7 October 1998; pp. 163–170. [Google Scholar]
- Silveira, I.C.A.; Schmidt, A.C.K.; Campos, E.J.D.; Godoi, S.S.; Ikeda, Y. The Brazil Current off the Eastern Brazilian Coast. Rev. Bras. De Oceanogr. 2000, 48, 171–183. [Google Scholar] [CrossRef]
- Brown, C.E.; Fingas, M. New Space-Borne Sensors for Oil Spill Response. In Proceedings of the International Oil Spill Conference, Tampa, FL, USA, 26–29 March 2001; pp. 911–916. [Google Scholar]
- Brown, C.E.; Fingas, M. The Latest Developments in Remote Sensing Technology for Oil Spill Detection. In Proceedings of the Interspill Conference and Exhibition, Marseille, France, 12–14 May 2009; p. 13. [Google Scholar]
| Var. 1 | Var. 2 | Var. 3 | Var. 1 | Var. 2 | Var. 3 | Var. 1 | Var. 2 | Var. 3 |
|---|---|---|---|---|---|---|---|---|
| None | None | None | Cube | Cube | Cube | log10 | log10 | log10 |
| None | None | Cube | Cube | Cube | None | log10 | log10 | None |
| None | Cube | Cube | Cube | None | None | log10 | None | None |
| None | Cube | None | Cube | None | Cube | log10 | None | log10 |
| None | None | log10 | Cube | Cube | log10 | log10 | log10 | Cube |
| None | log10 | log10 | Cube | log10 | log10 | log10 | Cube | Cube |
| None | log10 | None | Cube | log10 | Cube | log10 | Cube | log10 |
| None | Cube | log10 | Cube | None | log10 | log10 | None | Cube |
| None | log10 | Cube | Cube | log10 | None | log10 | Cube | None |
| Class/Category | Orginal Dataset | WND Filter | SST Filter | Typo Filter | All Filters | Analyzed Database | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| <3 m/s | >6 m/s | Both | ||||||||
| Formation Tests | 65 | (8.3%) | 0 | −10 | −10 | 0 | −3 | −13 | 52 | (9.3%) |
| Accidental Discards | 149 | (19.1%) | −2 | −19 | −21 | 0 | −3 | −24 | 125 | (22.3%) |
| Ship-Spills | 76 | (9.9%) | −1 | −13 | −14 | 0 | 0 | −14 | 62 | (11.1%) |
| Orphan-Spills | 68 | (8.7%) | −4 | −20 | −24 | 0 | −2 | −26 | 42 | (7.5%) |
| Oil Spills | 358 | (46.0%) | −7 | −62 | −69 | 0 | −8 | −77 | 281 | (50.2%) |
| Biogenic Films | 203 | (26.1%) | −40 | −1 | −41 | −4 | 0 | −45 | 158 | (28.2%) |
| Algal Blooms | 61 | (7.8%) | −18 | 0 | −18 | 0 | 0 | −18 | 43 | (7.7%) |
| Upwelling | 27 | (3.5%) | −2 | −5 | −7 | 0 | −1 | −8 | 19 | (3.4%) |
| Low Wind | 51 | (6.5%) | −38 | 0 | −38 | 0 | −1 | −39 | 12 | (2.1%) |
| Rain Cells | 79 | (10.1%) | 0 | −26 | −26 | −6 | 0 | −32 | 47 | (8.4%) |
| Slick-Alikes | 421 | (54.0%) | −98 | −32 | −130 | −10 | −2 | −142 | 279 | (49.8%) |
| Class/Category | Orginal Dataset | WND filter | SST filter | Typo filter | All Filters | Analyzed Database | ||||
| <3 m/s | >6 m/s | Both | ||||||||
| All Features | 779 | −105 | −94 | −199 | −10 | −10 | −219 | 560 | ||
| 100.0% | −13.5% | −12.0% | −25.5% | −1.3% | −1.3% | −28.1% | 71.9% | |||
| (A) | |||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| 1 | (1) | Size | WND | SST | CHL | BAT | . | Cube | 251 | 89.3% | 223 | 79.9% | 474 | 84.6% | |
| 81.8% | 88.1% | ||||||||||||||
| 2 | (2) | Size | WND | SST | CHL | BAT | . | log10 | 251 | 89.3% | 221 | 79.2% | 472 | 84.3% | |
| 81.2% | 88.0% | ||||||||||||||
| 3 | (3) | Size | WND | SST | CHL | . | CST | Cube | 250 | 89.0% | 222 | 79.6% | 472 | 84.3% | |
| 81.4% | 87.7% | ||||||||||||||
| 4 | (4) | Size | WND | SST | CHL | . | CST | None | 245 | 87.2% | 226 | 81.0% | 471 | 84.1% | |
| 82.2% | 86.3% | ||||||||||||||
| 5 | (5) | Size | WND | SST | CHL | . | CST | log10 | 250 | 89.0% | 221 | 79.2% | 471 | 84.1% | |
| 81.2% | 87.7% | ||||||||||||||
| # | 6 | (6) | Size | WND | SST | CHL | . | . | None | 244 | 86.8% | 226 | 81.0% | 470 | 83.9% |
| 82.2% | 85.9% | ||||||||||||||
| # | 7 | (7) | Size | WND | SST | CHL | . | . | Cube | 250 | 89.0% | 220 | 78.9% | 470 | 83.9% |
| 80.9% | 87.6% | ||||||||||||||
| 8 | (8) | Size | WND | . | . | BAT | . | log10 | 247 | 87.9% | 223 | 79.9% | 470 | 83.9% | |
| 81.5% | 86.8% | ||||||||||||||
| 9 | (9) | Size | WND | SST | CHL | BAT | . | None | 243 | 86.5% | 226 | 81.0% | 469 | 83.8% | |
| 82.1% | 85.6% | ||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| 10 | (10) | Size | WND | . | . | . | CST | Cube | 247 | 87.9% | 220 | 78.9% | 467 | 83.4% | |
| 80.7% | 86.6% | ||||||||||||||
| 11 | (11) | Size | WND | . | . | . | CST | None | 239 | 85.1% | 227 | 81.4% | 466 | 83.2% | |
| 82.1% | 84.4% | ||||||||||||||
| 12 | (12) | Size | WND | . | . | . | CST | log10 | 247 | 87.9% | 219 | 78.5% | 466 | 83.2% | |
| 80.5% | 86.6% | ||||||||||||||
| 13 | (13) | Size | WND | . | . | . | . | Cube | 242 | 86.1% | 223 | 79.9% | 465 | 83.0% | |
| 81.2% | 85.1% | ||||||||||||||
| 14 | (14) | Size | WND | . | . | BAT | . | Cube | 243 | 86.5% | 222 | 79.6% | 465 | 83.0% | |
| 81.0% | 85.4% | ||||||||||||||
| 15 | (15) | Size | . | SST | CHL | BAT | . | Cube | 250 | 89.0% | 215 | 77.1% | 465 | 83.0% | |
| 79.6% | 87.4% | ||||||||||||||
| 16 | (16) | Size | WND | . | . | . | . | None | 237 | 84.3% | 226 | 81.0% | 463 | 82.7% | |
| 81.7% | 83.7% | ||||||||||||||
| 17 | (17) | Size | WND | . | . | BAT | . | None | 237 | 84.3% | 226 | 81.0% | 463 | 82.7% | |
| 81.7% | 83.7% | ||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| # | 18 | (18) | Size | WND | SST | CHL | . | . | log10 | 244 | 86.8% | 218 | 78.1% | 462 | 82.5% |
| 80.0% | 85.5% | ||||||||||||||
| 19 | (19) | Size | . | SST | CHL | . | . | None | 246 | 87.5% | 216 | 77.4% | 462 | 82.5% | |
| 79.6% | 86.1% | ||||||||||||||
| 20 | (20) | Size | . | SST | CHL | . | CST | Cube | 250 | 89.0% | 212 | 76.0% | 462 | 82.5% | |
| 78.9% | 87.2% | ||||||||||||||
| 21 | (21) | Size | . | SST | CHL | . | . | log10 | 246 | 87.5% | 214 | 76.7% | 460 | 82.1% | |
| 79.1% | 85.9% | ||||||||||||||
| 22 | (22) | Size | . | SST | CHL | . | . | Cube | 245 | 87.2% | 213 | 76.3% | 458 | 81.8% | |
| 78.8% | 85.5% | ||||||||||||||
| 23 | (23) | Size | . | SST | CHL | . | CST | None | 244 | 86.8% | 214 | 76.7% | 458 | 81.8% | |
| 79.0% | 85.3% | ||||||||||||||
| 24 | (24) | Size | . | SST | CHL | BAT | . | None | 243 | 86.5% | 215 | 77.1% | 458 | 81.8% | |
| 79.2% | 85.0% | ||||||||||||||
| $ | 26 | (25) | Size | . | SST | CHL | BAT | . | log10 | 247 | 87.9% | 209 | 74.9% | 456 | 81.4% |
| 77.9% | 86.0% | ||||||||||||||
| $ | 27 | (26) | Size | WND | . | . | . | . | log10 | 240 | 85.4% | 216 | 77.4% | 456 | 81.4% |
| 79.2% | 84.0% | ||||||||||||||
| $ | 29 | (27) | Size | . | SST | CHL | . | CST | log10 | 248 | 88.3% | 206 | 73.8% | 454 | 81.1% |
| 77.3% | 86.2% | ||||||||||||||
| (B) | |||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| $ | 25 | (1) | Size | . | . | . | BAT | . | Cube | 245 | 87.2% | 211 | 75.6% | 456 | 81.4% |
| 78.3% | 85.4% | ||||||||||||||
| $ | 28 | (2) | Size | . | . | . | BAT | . | log10 | 245 | 87.2% | 210 | 75.3% | 455 | 81.3% |
| 78.0% | 85.4% | ||||||||||||||
| 30 | (3) | Size | . | . | . | . | CST | Cube | 248 | 88.3% | 205 | 73.5% | 453 | 80.9% | |
| 77.0% | 86.1% | ||||||||||||||
| # | 31 | (4) | Size | . | . | . | . | . | log10 | 237 | 84.3% | 215 | 77.1% | 452 | 80.7% |
| 78.7% | 83.0% | ||||||||||||||
| 32 | (5) | Size | . | . | . | . | CST | log10 | 245 | 87.2% | 205 | 73.5% | 450 | 80.4% | |
| 76.8% | 85.1% | ||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| 33 | (6) | Size | . | . | . | BAT | . | None | 240 | 85.4% | 207 | 74.2% | 447 | 79.8% | |
| 76.9% | 83.5% | ||||||||||||||
| # | 34 | (7) | Size | . | . | . | . | . | None | 233 | 82.9% | 213 | 76.3% | 446 | 79.6% |
| 77.9% | 81.6% | ||||||||||||||
| # | 35 | (8) | Size | . | . | . | . | . | Cube | 233 | 82.9% | 213 | 76.3% | 446 | 79.6% |
| 77.9% | 81.6% | ||||||||||||||
| 36 | (9) | Size | . | . | . | . | CST | None | 241 | 85.8% | 203 | 72.8% | 444 | 79.3% | |
| 76.0% | 83.5% | ||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| 37 | (1) | . | WND | SST | CHL | BAT | . | log10 | 220 | 78.3% | 199 | 71.3% | 419 | 74.8% | |
| 73.3% | 76.5% | ||||||||||||||
| 38 | (2) | . | WND | SST | CHL | . | CST | log10 | 219 | 77.9% | 199 | 71.3% | 418 | 74.6% | |
| 73.2% | 76.2% | ||||||||||||||
| # | 39 | (3) | . | WND | SST | CHL | . | . | Cube | 217 | 77.2% | 200 | 71.7% | 417 | 74.5% |
| 73.3% | 75.8% | ||||||||||||||
| 40 | (4) | . | WND | SST | CHL | . | CST | Cube | 217 | 77.2% | 200 | 71.7% | 417 | 74.5% | |
| 73.3% | 75.8% | ||||||||||||||
| # | 41 | (5) | . | WND | SST | CHL | . | . | log10 | 217 | 77.2% | 199 | 71.3% | 416 | 74.3% |
| 73.1% | 75.7% | ||||||||||||||
| 42 | (6) | . | WND | SST | CHL | BAT | . | Cube | 216 | 76.9% | 198 | 71.0% | 414 | 73.9% | |
| 72.7% | 75.3% | ||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| 43 | (7) | . | WND | . | . | . | CST | Cube | 215 | 76.5% | 198 | 71.0% | 413 | 73.8% | |
| 72.6% | 75.0% | ||||||||||||||
| 44 | (8) | . | WND | SST | CHL | BAT | . | None | 209 | 74.4% | 204 | 73.1% | 413 | 73.8% | |
| 73.6% | 73.9% | ||||||||||||||
| 45 | (9) | . | WND | . | . | BAT | . | log10 | 214 | 76.2% | 198 | 71.0% | 412 | 73.6% | |
| 72.5% | 74.7% | ||||||||||||||
| 46 | (10) | . | WND | SST | CHL | . | CST | None | 210 | 74.7% | 202 | 72.4% | 412 | 73.6% | |
| 73.2% | 74.0% | ||||||||||||||
| # | 47 | (11) | . | WND | SST | CHL | . | . | None | 208 | 74.0% | 203 | 72.8% | 411 | 73.4% |
| 73.2% | 73.6% | ||||||||||||||
| 48 | (12) | . | WND | . | . | . | CST | log10 | 217 | 77.2% | 193 | 69.2% | 410 | 73.2% | |
| 71.6% | 75.1% | ||||||||||||||
| 49 | (13) | . | WND | . | . | BAT | . | Cube | 211 | 75.1% | 197 | 70.6% | 408 | 72.9% | |
| 72.0% | 73.8% | ||||||||||||||
| 50 | (14) | . | WND | . | . | . | CST | None | 208 | 74.0% | 198 | 71.0% | 406 | 72.5% | |
| 72.0% | 73.1% | ||||||||||||||
| 51 | (15) | . | WND | . | . | BAT | . | None | 204 | 72.6% | 197 | 70.6% | 401 | 71.6% | |
| 71.3% | 71.9% | ||||||||||||||
| Hierarchy | (Rank) | Size | Metoc | Geo-Loc | Transf. | Oil Spills | Slick-Alikes | All Features | |||||||
| *! | 52 | (16) | . | . | SST | CHL | BAT | . | Cube | 223 | 79.4% | 152 | 54.5% | 375 | 67.0% |
| 63.7% | 72.4% | ||||||||||||||
| *! | 53 | (17) | . | . | SST | CHL | . | . | Cube | 221 | 78.6% | 153 | 54.8% | 374 | 66.8% |
| 63.7% | 71.8% | ||||||||||||||
| *! | 54 | (18) | . | . | SST | CHL | BAT | . | log10 | 209 | 74.4% | 162 | 58.1% | 371 | 66.3% |
| 64.1% | 69.2% | ||||||||||||||
| *! | 55 | (19) | . | . | SST | CHL | . | CST | log10 | 210 | 74.7% | 159 | 57.0% | 369 | 65.9% |
| 63.6% | 69.1% | ||||||||||||||
| *! | 56 | (20) | . | . | SST | CHL | . | CST | Cube | 216 | 76.9% | 153 | 54.8% | 369 | 65.9% |
| 63.2% | 70.2% | ||||||||||||||
| *! | 57 | (21) | . | . | SST | CHL | . | . | None | 212 | 75.4% | 151 | 54.1% | 363 | 64.8% |
| 62.4% | 68.6% | ||||||||||||||
| *! | 58 | (22) | . | . | SST | CHL | . | CST | None | 211 | 75.1% | 148 | 53.0% | 359 | 64.1% |
| 61.7% | 67.9% | ||||||||||||||
| *! | 59 | (23) | . | . | SST | CHL | . | . | log10 | 197 | 70.1% | 158 | 56.6% | 355 | 63.4% |
| 61.9% | 65.3% | ||||||||||||||
| *! | 60 | (24) | . | . | SST | CHL | BAT | . | None | 206 | 73.3% | 145 | 52.0% | 351 | 62.7% |
| 60.6% | 65.9% | ||||||||||||||
| Blocks | Subdivisions | Percentages | (Samples) | Subgroups | Percentages | (Samples) | |
|---|---|---|---|---|---|---|---|
| Top- Blue (1–29) | Size Plus Metoc Set | 83.0% | (465) | Top Group | WND, SST, and CHL | 84.1% | (471) |
| Middle Group | WND | 83.0% | (465) | ||||
| 3.6% | (20) + | Bottom Group | SST and CHL | 81.9% | (459) | ||
| Middle- Green (25–36) | Size Set | 80.3% | (450) | First Group | log10 or cube root | 80.9% | (453) |
| 2.1% | (12) + | Second Group | Original set | 79.6% | (446) | ||
| Bottom- Gray (37–60) | Metoc Set | 70.5% | (395) | Top Group | WND, SST, and CHL | 74.4% | (417) |
| Middle Group | WND | 73.1% | (410) | ||||
| 12.1% | (68) + | Bottom Group | SST and CHL | 65.2% | (365) *! | ||
| Carvalho et al. [42] | This Paper (without Geo-Loc) | This Paper (with Geo-Loc) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sub Division | Transf. | Overall | Order | Overall | Order | Diff. i | Overall | Order | Diff. ii | Geo- Loc |
| Accuracy | (Hierarchy) | Accuracy | (Hierarchy) | Accuracy | (Hierarchy) | |||||
| Size Plus Metoc Set | None | 83.1% | 2 (5) | 83.9% | * 1 (6) | 0.8% | 84.1% | 3 (4) | 0.2% | CST |
| Cube Root | 83.7% | * 1 (2) | 83.9% | 2 (7) | 0.2% | 84.6% | * 1 (1) | 0.7% | BAT | |
| log10 | 83.0% | 3 (7) | 82.5% | 3 (18) | −0.5% | 84.3% | 2 (2) | 1.8% | BAT | |
| Size Set | None | 79.1% | * 1 (19) | 79.6% | 2 (34) | 0.5% | 79.8% | 3 (33) | 0.2% | BAT |
| Cube Root | 78.9% | 2 (21) | 79.6% | 3 (35) | 0.7% | 81.4% | * 1 (25) | 1.8% | BAT | |
| log10 | 78.0% | 3 (24) | 80.7% | * 1 (31) | 2.7% | 81.3% | 2 (28) | 0.6% | BAT | |
| Metoc Set | None | 76.9% | 2 (27) | 73.4% | 3 (47) | −3.5% | 73.8% | 3 (44) | 0.4% | BAT |
| Cube Root | 77.1% | * 1 (26) | 74.5% | * 1 (39) | −2.6% | 74.5% | 2 (40) | 0.0% | CST | |
| log10 | 76.7% | 3 (29) | 74.3% | 2 (41) | −2.4% | 74.8% | * 1 (37) | 0.5% | BAT | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, G.d.A.; Minnett, P.J.; Ebecken, N.F.F.; Landau, L. Oil Spills or Look-Alikes? Classification Rank of Surface Ocean Slick Signatures in Satellite Data. Remote Sens. 2021, 13, 3466. https://doi.org/10.3390/rs13173466
Carvalho GdA, Minnett PJ, Ebecken NFF, Landau L. Oil Spills or Look-Alikes? Classification Rank of Surface Ocean Slick Signatures in Satellite Data. Remote Sensing. 2021; 13(17):3466. https://doi.org/10.3390/rs13173466
Chicago/Turabian StyleCarvalho, Gustavo de Araújo, Peter J. Minnett, Nelson F. F. Ebecken, and Luiz Landau. 2021. "Oil Spills or Look-Alikes? Classification Rank of Surface Ocean Slick Signatures in Satellite Data" Remote Sensing 13, no. 17: 3466. https://doi.org/10.3390/rs13173466
APA StyleCarvalho, G. d. A., Minnett, P. J., Ebecken, N. F. F., & Landau, L. (2021). Oil Spills or Look-Alikes? Classification Rank of Surface Ocean Slick Signatures in Satellite Data. Remote Sensing, 13(17), 3466. https://doi.org/10.3390/rs13173466







