Modeling the Relationship of ≥2 MeV Electron Fluxes at Different Longitudes in Geostationary Orbit by the Machine Learning Method
Abstract
:1. Introduction
2. Materials and Methods
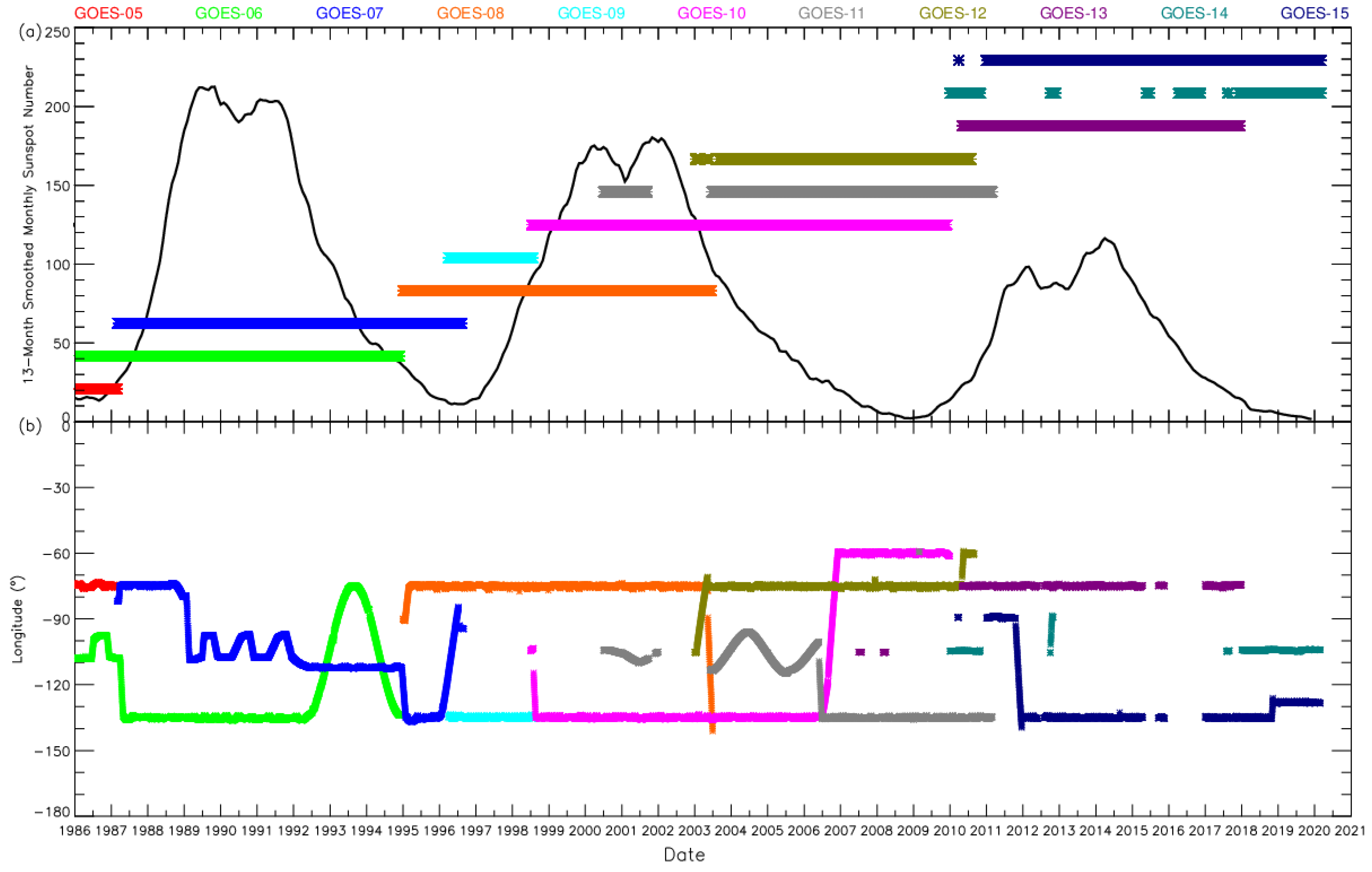
2.1. Data
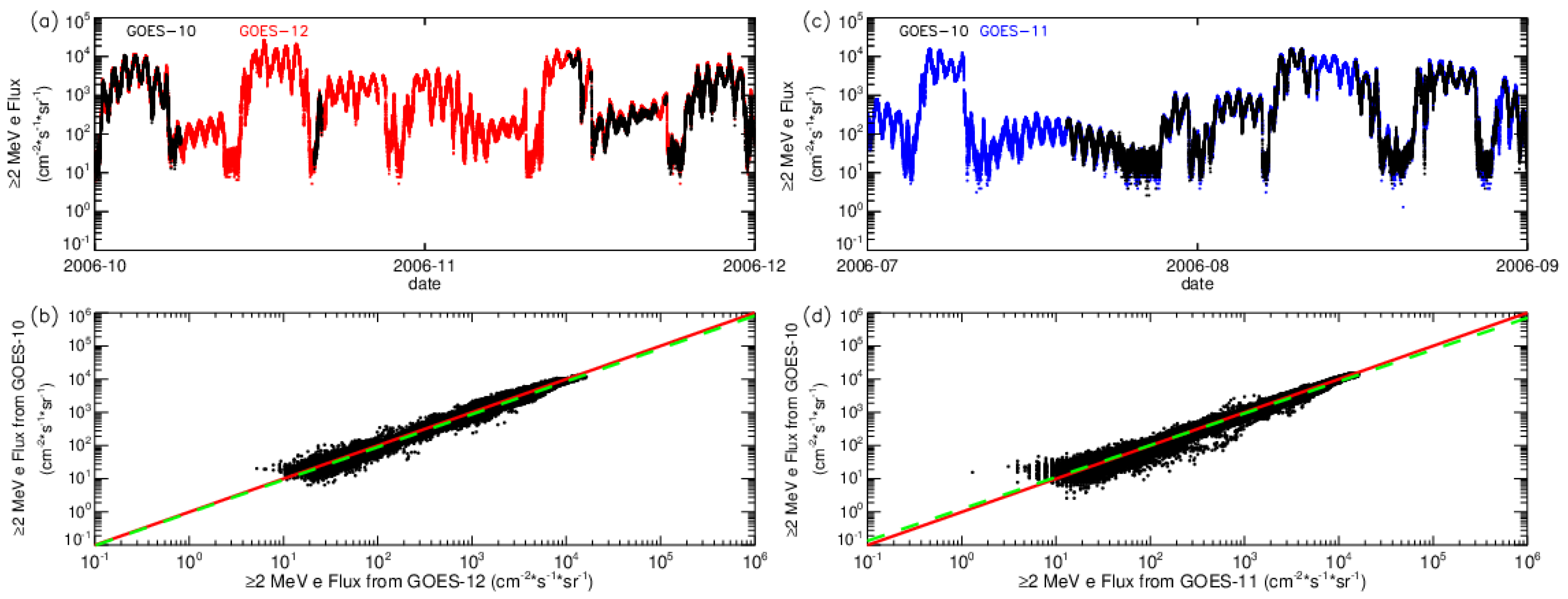
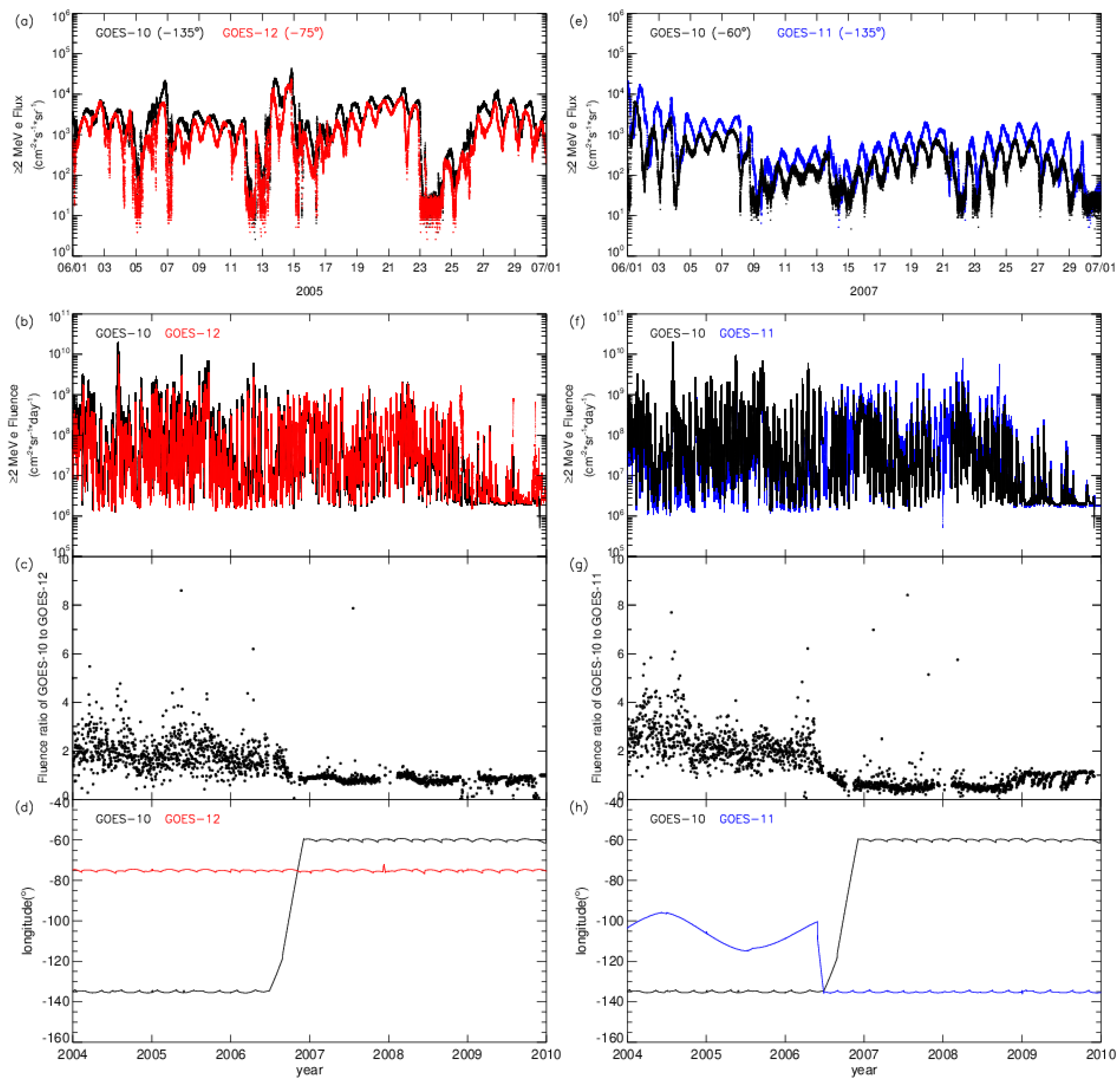
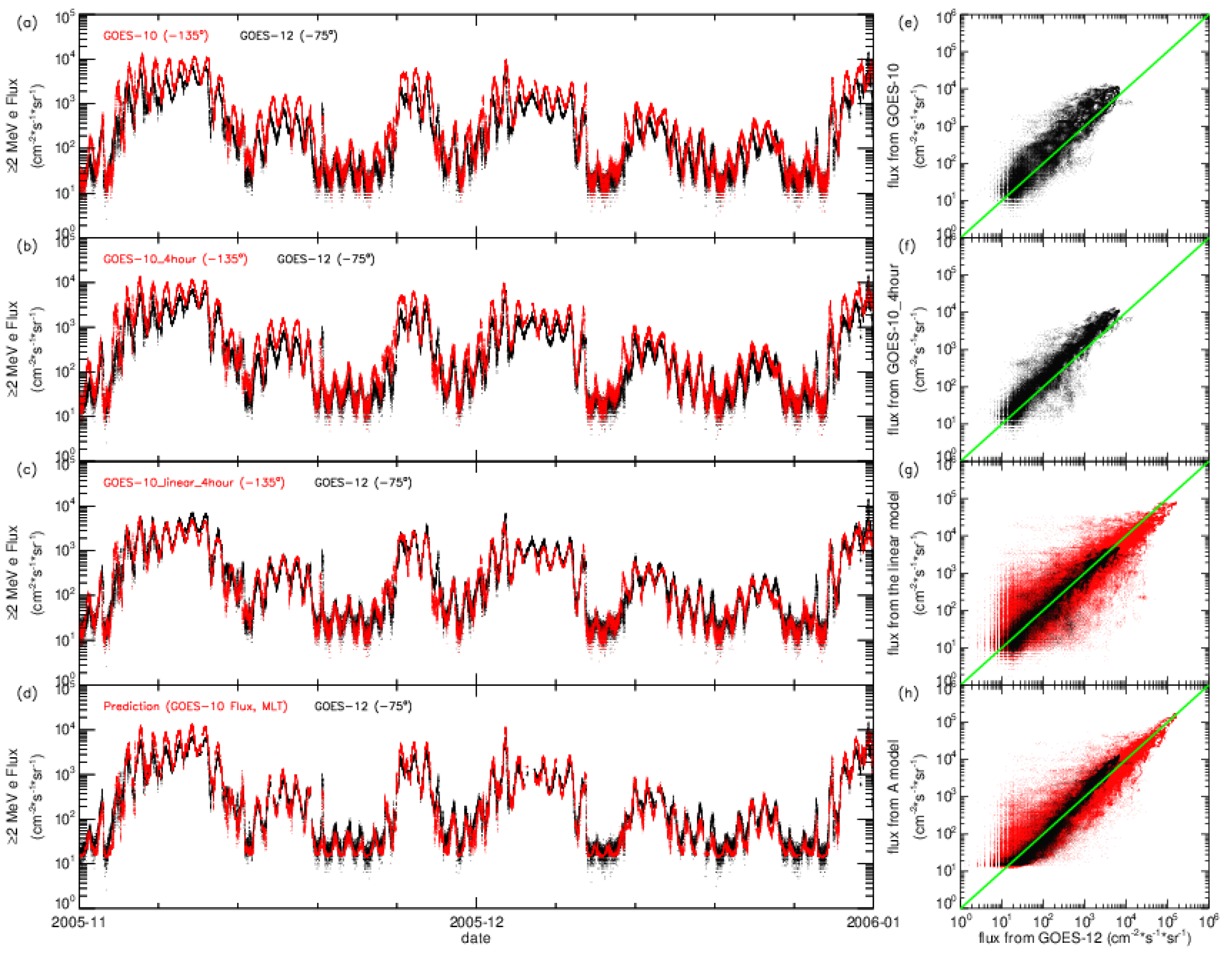
2.2. Calibration Verification and Comparison of ≥2 MeV Electron Distribution at Different Longitudes in GEO Orbit
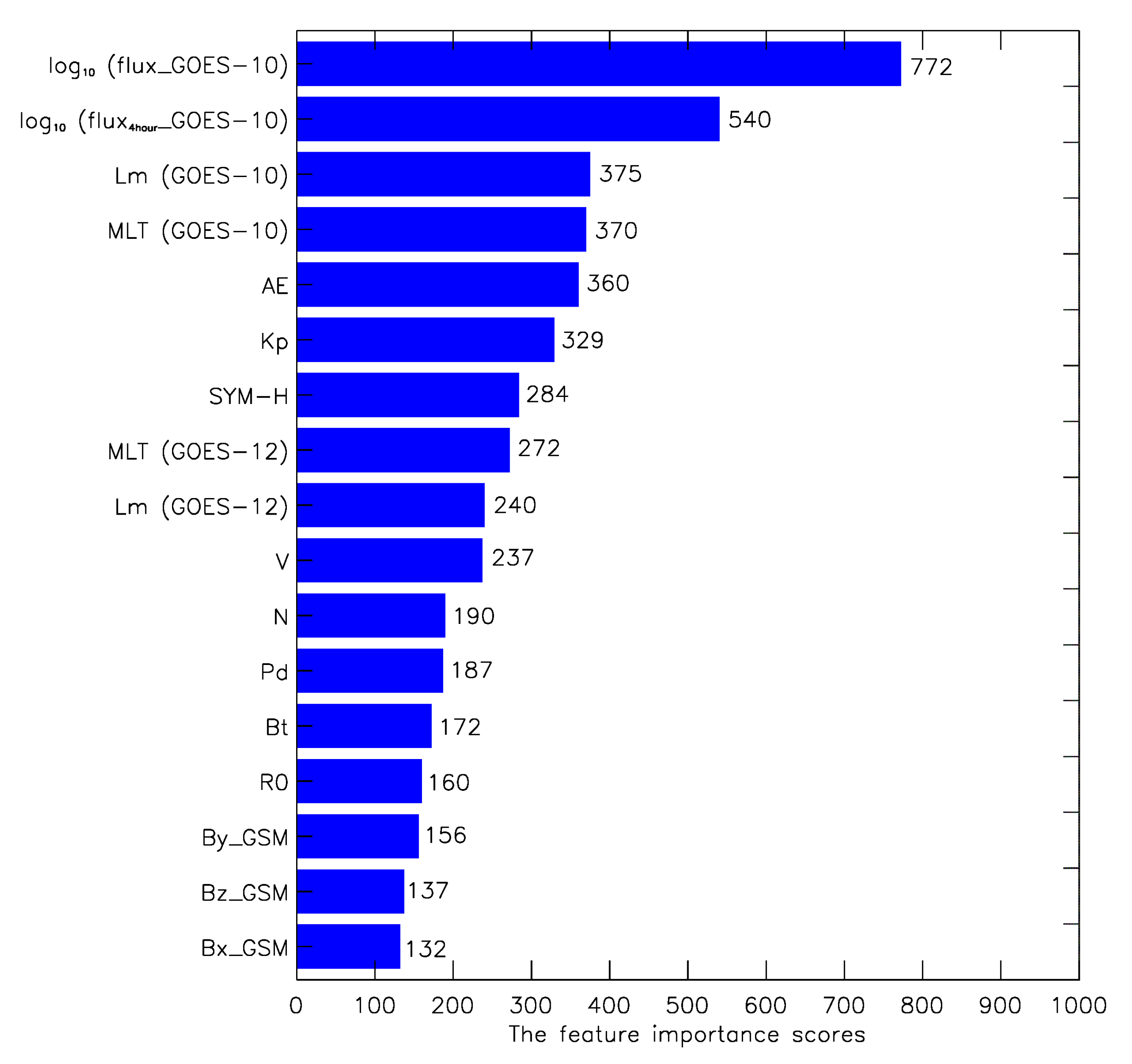
2.3. The Evaluation of Important Parameters for Modeling
2.4. The Fully Connected Neural Network
3. Results and Discussion
3.1. Modeling the Relationship of ≥2 MeV Electron Fluxes at Two Different Longitudes in GEO Orbit
3.1.1. The Models with Different Combinations of Input Parameters
3.1.2. Comparison with the Statistical Model by Linear Fitting
3.2. Modeling the Relationship between ≥2 MeV Electron Fluxes at a Fixed Longitude and at Variable Longitudes in GEO Orbit
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, B. The status and prospect of orbital servicing in the geostationary orbit. J. Astronaut. 2010, 31, 1–13. [Google Scholar]
- Tian, T. Analysis of the Chinese GEO satellite anomaly on 9 March 2012. Chin. J. Space Sci. 2015, 35, 687–695. [Google Scholar]
- Wang, Z. Influence of high energy electrons on geosynchronous orbit satellites. J. Spacecr. TTC Technol. 2017, 36, 201–206. [Google Scholar]
- Violet, M. Spacecraft anomalies on the CRRES satellite correlated with the environment and insulator samples. IEEE Trans. Nucl. Sci. 1993, 40, 1512–1520. [Google Scholar] [CrossRef] [Green Version]
- Lanzerotti, L. Studies of spacecraft charging on a geosynchronous telecommunications satellite. Adv. Space Res. 1998, 22, 79–82. [Google Scholar] [CrossRef]
- Frederickson, A. Measurement of charge storage and leakage in polyimides. Nucl. Instrum. Methods Phys. Res. B 2003, 208, 454–460. [Google Scholar] [CrossRef]
- Baker, D. Characterizing the Earth’s outer Van Allen zone using a radiation belt content index. Space Weather 2004, 2. [Google Scholar] [CrossRef]
- Horne, R. Space weather impacts on satellites and forecasting the Earth’s electron radiation belts with SPACECAST. Space Weather 2013, 11, 169–186. [Google Scholar] [CrossRef] [Green Version]
- Bedingfield, K.; Leach, R.; Alexander, M. NASA Reference Publication 1390; Bedingfield, K.L., Leach, R.D., Alexander, M.B., Eds.; National Aeronautics and Space Administration: Washington, DC, USA, 1996; pp. 1–43. [Google Scholar]
- Koons, H.C.; Mazur, J.E.; Selesnick, R.S.; Blake, J.B. The Impact of the Space Environment on Space Systems. In Proceedings of the 6th Spacecraft Charging Technology Conference, Hanscom AFB, MA, USA, 26–29 October 1998; AFRL Science Center USA, Koons, H.C., Mazur, J.E., Selesnick, R.S., Blake, J.B., Eds.; AFRL Science Cente: Hanscom AFB, OH, USA, 1998. [Google Scholar]
- Lucci, N. Space weather conditions and spacecraft anomalies in different orbits. Space Weather 2013, 3. [Google Scholar] [CrossRef]
- Wrenn, G. A solar cycle of spacecraft anomalies due to internal charging. Ann. Geophys. 2002, 20, 953–956. [Google Scholar] [CrossRef] [Green Version]
- Turner, D. Quantitative forecast of relativistic electron flux at geosynchronous orbit based on low-energy electron flux. Space Weather 2008, 6. [Google Scholar] [CrossRef]
- Baker, D. Deep dielectric charging effects due to high energy electrons in the earth’s outer magnetosphere. J. Electrost. 1987, 20, 3–19. [Google Scholar] [CrossRef]
- Baker, D. Linear prediction filter analysis of relativistic electron properties at 6.6RE. J. Geophys. Res. 1990, 95, 15133–15140. [Google Scholar] [CrossRef]
- Lam, H. Prediction of relativistic electron fluence using magnetic observatory data. COSPAR Colloq. Ser. 2002, 14, 439–442. [Google Scholar]
- Rigler, E. Adaptive linear prediction of radiation belt electrons using the Kalman fillter. Space Weather 2004, 2, S03003. [Google Scholar] [CrossRef]
- Kataoka, R. Flux enhancement of radiation belt electrons during geomagnetic storms driven by coronal mass ejections and corotating interaction regions. Space Weather 2006, 4. [Google Scholar] [CrossRef]
- Miyoshi, Y. Probabilistic space weather forecast of the relativistic electron flux enhancement at geosynchronous orbit. J. Atmos. Sol.-Terr. Phys. 2008, 70, 475–481. [Google Scholar] [CrossRef]
- He, T. Quantitative prediction of relativistic electron flux at geosynchronous orbit with geomagnetic pulsations parameters. Chin. J. Space Sci. 2013, 33, 20–27. [Google Scholar]
- Sakaguchi, K. Relativistic electron flux forecast at geostationary orbit using Kalman filter based on multivariate autoregressive model. Space Weather 2013, 11, 79–89. [Google Scholar] [CrossRef]
- Potapova, A. Solar cycle variation of “killer” electrons at geosynchronous orbit and electron flux correlation with the solar wind parameters and ULF waves intensity. Acta Astronaut. 2014, 95, 55–63. [Google Scholar] [CrossRef]
- Li, S. Dynamic prediction model of relativistic electron differential fluxes at the geosynchronous orbit. Chin. J. Space Sci. 2017, 37, 298–311. [Google Scholar]
- Zhong, Q. Statistical model of the relativistic electron fluence forecast at geostationary orbit. Chin. J. Space Sci. 2019, 39, 18–27. [Google Scholar]
- Qian, Y. An hourly prediction model of relativistic electrons based on empirical mode decomposition. Space Weather 2020, 17. [Google Scholar] [CrossRef]
- Ukhorskiy, A. Data-derived forecasting model for relativistic electron intensity at geosynchronous orbit. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Wei, H. Forecasting relativistic electron flux using dynamic multiple regression models. Ann. Geophys. 2011, 29, 415–420. [Google Scholar] [CrossRef] [Green Version]
- Boynton, R. Online NARMAX model for electron fluxes at GEO. Ann. Geophys. 2015, 33, 405–411. [Google Scholar] [CrossRef]
- Li, X. Quantitative prediction of radiation belt electrons at geostationary orbit based on solar wind measurements. Geophys. Res. Lett. 2001, 28, 1887–1890. [Google Scholar] [CrossRef] [Green Version]
- Li, X. Variations of 0.7–6.0 MeV electrons at geosynchronous orbit as a function of solar wind. Space Weather 2004, 2. [Google Scholar] [CrossRef]
- Li, X. Correlation between the inner edge of outer radiation belt electrons and the innermost plasmapause location. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Li, X. Behavior of MeV electrons at geosynchronous orbit during last two solar cycles. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Fukata, M. Neural network prediction of relativistic electrons at geosynchronous orbit during the storm recovery phase: Effects of recurring substorms. Ann. Geophys. 2002, 20, 947–951. [Google Scholar] [CrossRef] [Green Version]
- Xue, B. Forcast of the enhancement of relativistic eletron at the GEO-synchronous orbit. Chin. J. Space Sci. 2004, 24, 283–288. [Google Scholar]
- Ling, A. A neural network-based geosynchronous relativistic electron flux forecasting model. Space Weather 2010, 8. [Google Scholar] [CrossRef]
- Guo, C. Approach for predicting the energetic electron flux in geosynchronous earth orbit. Chin. J. Space Sci. 2013, 33, 418–426. [Google Scholar]
- Shin, D. Artificial neural network prediction model for geosynchronous electron fluxes: Dependence on satellite position and particle energy. Space Weather 2016, 14, 313–321. [Google Scholar] [CrossRef] [Green Version]
- Wang, R. Study on the forecasting method of relativistic electron flux at geostationary orbit based on support vector machine. Chin. J. Space Sci. 2012, 32, 354–361. [Google Scholar]
- Wei, L.H. Study on the Prediction Model of High-Energy Electron Integral Flux at GEO Based on Deep Learning. Master’s Thesis, National Space Science Center, Chinese Academy of Sciences, Beijing, China, 2018. [Google Scholar]
- Onsager, T. The radial gradient of relativistic electrons at geosynchronous orbit. J. Geophys. Res. 2004, 109, A05221. [Google Scholar] [CrossRef]
- Sun, X. Influence of geomagnetic field structure on ≥2 MeV electron distribution at geostationary orbit. Chin. J. Geophys. 2020, 63, 3604–3625. [Google Scholar]
- Lin, R. A three-dimensional asymmetric magnetopause model. J. Geophys. Res. 2010, 115, A04207. [Google Scholar] [CrossRef]
- Macmillan, S. The international geomagnetic reference field. IAGA Spec. Sopr. Book 2011, 2, 265–276. [Google Scholar]
- Erwan, T. International Geomagnetic Reference Field: The 12th generation. Earth Planets Space 2015, 67, 19. [Google Scholar]
- Tsyganenko, N. A magnetospheric magnetic field model with a warped tail current sheet. Planet. Space Sci. 1989, 37, 5–12. [Google Scholar] [CrossRef]
- Chen, T. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Chen, T.Q., Guestrin, C., Eds.; ACM Press: New York, NY, USA, 2016. [Google Scholar]
- Breiman, L. Classification and Regression Trees. Biometrics 1984, 40, 358. [Google Scholar]
- Schapire, R. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Paulikas, G. Effects of the solar wind on magnetospheric dynamics-Energetic electrons at the synchronous orbit. Geophys. Monogr. Ser. 1979, 1979, 180–202. [Google Scholar]
- Baker, D. Coronal mass ejections, magnetic clouds, and relativistic magnetospheric electron events: ISTP. J. Geophys. Res. 1998, 103, 17279–17291. [Google Scholar] [CrossRef] [Green Version]
- Li, X. The electron radiation belt. Space Sci. Rev. 2001, 95, 569–580. [Google Scholar] [CrossRef]
- Reeves, G. Acceleration and loss of relativistic electron during geomagnetic storms. Geophys. Res. Lett. 2003, 30, 1529. [Google Scholar] [CrossRef]
- Millan, R. Review of radiation belt relativistic electron losses. J. Atmos. Sol.-Terr. Phys. 2007, 69, 362–377. [Google Scholar] [CrossRef]
- Zhang, H. Relative electron flux prediction at geosynchronous orbit based on the neural network and the quantile regression method. Space Weather 2020, 18. [Google Scholar] [CrossRef]
- Rumelhart, D. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Hornik, K. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Glorot, X. Deep sparse rectifier neural networks. J. Mach. Learn. Res. 2011, 15, 315–323. [Google Scholar]
- Li, X. Long term measurements of radiation belts by SAMPEX and their variations. Geophys. Res. Lett. 2001, 28, 3827–3830. [Google Scholar] [CrossRef] [Green Version]
- Li, L. Statistical roles of storms and substorms in changing the entire outer zone relativistic electron population. J. Geophys. Res. 2009, 114, 214. [Google Scholar] [CrossRef] [Green Version]
- Borovsky, J. Electron loss rates from the outer radiation belt caused by the fillvig of the outer plasmaspbere: The calm before the storm. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
| Input Parameters | PE | RMSE |
|---|---|---|
| log (GOES-10 fluxes) + MLT (GOES-10) | 0.920 | 0.2140 |
| log (GOES-10 fluxes) + MLT (GOES-12) | 0.912 | 0.2249 |
| log (GOES-10 fluxes) + Lm (GOES-10) | 0.839 | 0.3042 |
| log (GOES-10 fluxes) + Lm (GOES-12) | 0.810 | 0.3303 |
| log (GOES-10 fluxes)+log (GOES-10 fluxes) | 0.805 | 0.3344 |
| log (GOES-10 fluxes) + N | 0.799 | 0.3394 |
| log (GOES-10 fluxes) + AE | 0.797 | 0.3408 |
| log (GOES-10 fluxes) + log (GOES-10 fluxes (four hours ahead)) | 0.794 | 0.3431 |
| log (GOES-10 fluxes) + V | 0.793 | 0.3446 |
| log (GOES-10 fluxes) + Bz | 0.792 | 0.3455 |
| log (GOES-10 fluxes) + Kp | 0.785 | 0.3510 |
| log (GOES-10 fluxes) + R0 | 0.781 | 0.3542 |
| log (GOES-10 fluxes) + By | 0.769 | 0.3641 |
| log (GOES-10 fluxes) + Bt | 0.754 | 0.3757 |
| log (GOES-10 fluxes) + Pd | 0.753 | 0.3762 |
| log (GOES-10 fluxes) + Bx | 0.723 | 0.3984 |
| log (GOES-10 flux) + SYM-H | 0.707 | 0.4098 |
| Input Parameters | PE | RMSE |
|---|---|---|
| log (GOES-10 fluxes) + MLT (GOES-10) | 0.920 | 0.2140 |
| log (GOES-10 fluxes) + MLT (GOES-10) + MLT (GOES-12) | 0.904 | 0.2348 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Lm (GOES-10) | 0.899 | 0.2402 |
| log (GOES-10 fluxes) + MLT (GOES-10) + N | 0.898 | 0.2414 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Lm (GOES-12) | 0.893 | 0.2476 |
| log (GOES-10 fluxes) + MLT (GOES-10) + R0 | 0.893 | 0.2478 |
| log (GOES-10 fluxes) + MLT (GOES-10) + AE | 0.890 | 0.2509 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Kp | 0.884 | 0.2582 |
| log (GOES-10 fluxes) + MLT (GOES-10) + V | 0.872 | 0.2709 |
| log (GOES-10 fluxes) + MLT (GOES-10) + By | 0.868 | 0.2754 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Bz | 0.864 | 0.2797 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Bt | 0.818 | 0.3234 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Pd | 0.806 | 0.3334 |
| log (GOES-10 fluxes) + MLT (GOES-10) + Bx | 0.797 | 0.3408 |
| log (GOES-10 fluxes) + MLT (GOES-10) + SYM-H | 0.708 | 0.4093 |
| Input Parameters | PE | RMSE |
|---|---|---|
| log (GOES-11 fluxes) + MLT (GOES-11) | 0.903 | 0.2312 |
| log (GOES-11 fluxes) + MLT (GOES-12) | 0.905 | 0.2293 |
| log (GOES-11 fluxes) + MLT (GOES-11) + MLT (GOES-12) | 0.902 | 0.2324 |
| log (GOES-11 fluxes) + MLT (GOES-11) + MLT | 0.907 | 0.2263 |
| log (GOES-11 fluxes) + MLT (GOES-12) + MLT | 0.906 | 0.2277 |
| Input Parameters | PE | RMSE |
|---|---|---|
| log (GOES-12 flux) + MLT (GOES-12) | 0.922 | 0.2121 |
| log (GOES-12 flux) + MLT (GOES-11) | 0.923 | 0.2111 |
| log (GOES-12 flux) + MLT (GOES-12) + MLT (GOES-11) | 0.928 | 0.2034 |
| log (GOES-12 flux) + MLT (GOES-12) + MLT | 0.923 | 0.2108 |
| log (GOES-12 flux) + MLT (GOES-11) + MLT | 0.920 | 0.2191 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Lin, R.; Liu, S.; He, X.; Shi, L.; Luo, B.; Zhong, Q.; Gong, J. Modeling the Relationship of ≥2 MeV Electron Fluxes at Different Longitudes in Geostationary Orbit by the Machine Learning Method. Remote Sens. 2021, 13, 3347. https://doi.org/10.3390/rs13173347
Sun X, Lin R, Liu S, He X, Shi L, Luo B, Zhong Q, Gong J. Modeling the Relationship of ≥2 MeV Electron Fluxes at Different Longitudes in Geostationary Orbit by the Machine Learning Method. Remote Sensing. 2021; 13(17):3347. https://doi.org/10.3390/rs13173347
Chicago/Turabian StyleSun, Xiaojing, Ruilin Lin, Siqing Liu, Xinran He, Liqin Shi, Bingxian Luo, Qiuzhen Zhong, and Jiancun Gong. 2021. "Modeling the Relationship of ≥2 MeV Electron Fluxes at Different Longitudes in Geostationary Orbit by the Machine Learning Method" Remote Sensing 13, no. 17: 3347. https://doi.org/10.3390/rs13173347
APA StyleSun, X., Lin, R., Liu, S., He, X., Shi, L., Luo, B., Zhong, Q., & Gong, J. (2021). Modeling the Relationship of ≥2 MeV Electron Fluxes at Different Longitudes in Geostationary Orbit by the Machine Learning Method. Remote Sensing, 13(17), 3347. https://doi.org/10.3390/rs13173347







