High Speed Maneuvering Platform Squint TOPS SAR Imaging Based on Local Polar Coordinate and Angular Division
Abstract
:1. Introduction
2. Signal Model and Properties
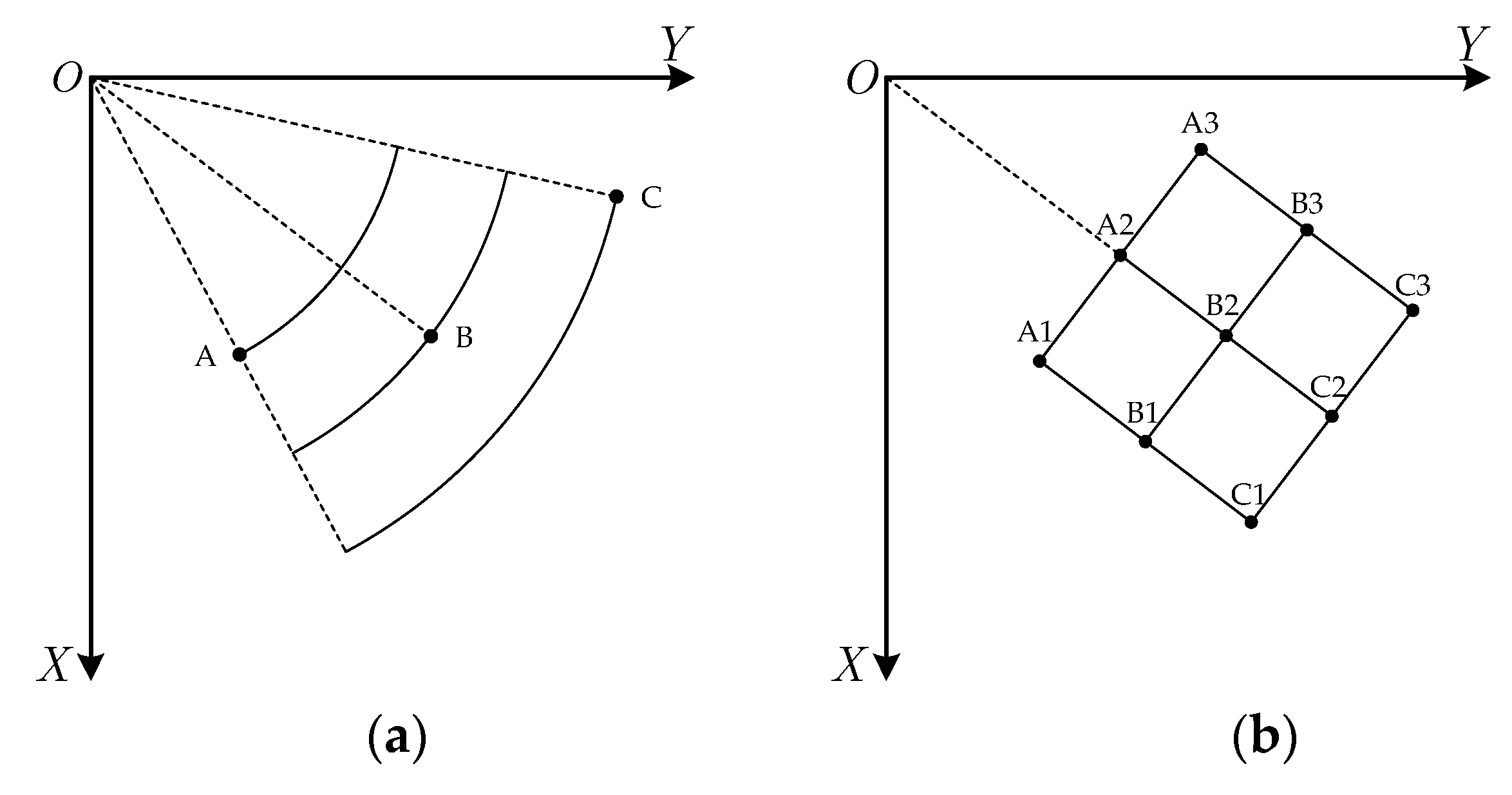
2.1. Range Model in Local Polar Format Coordinate
2.2. Space-Variation of Doppler Parematers
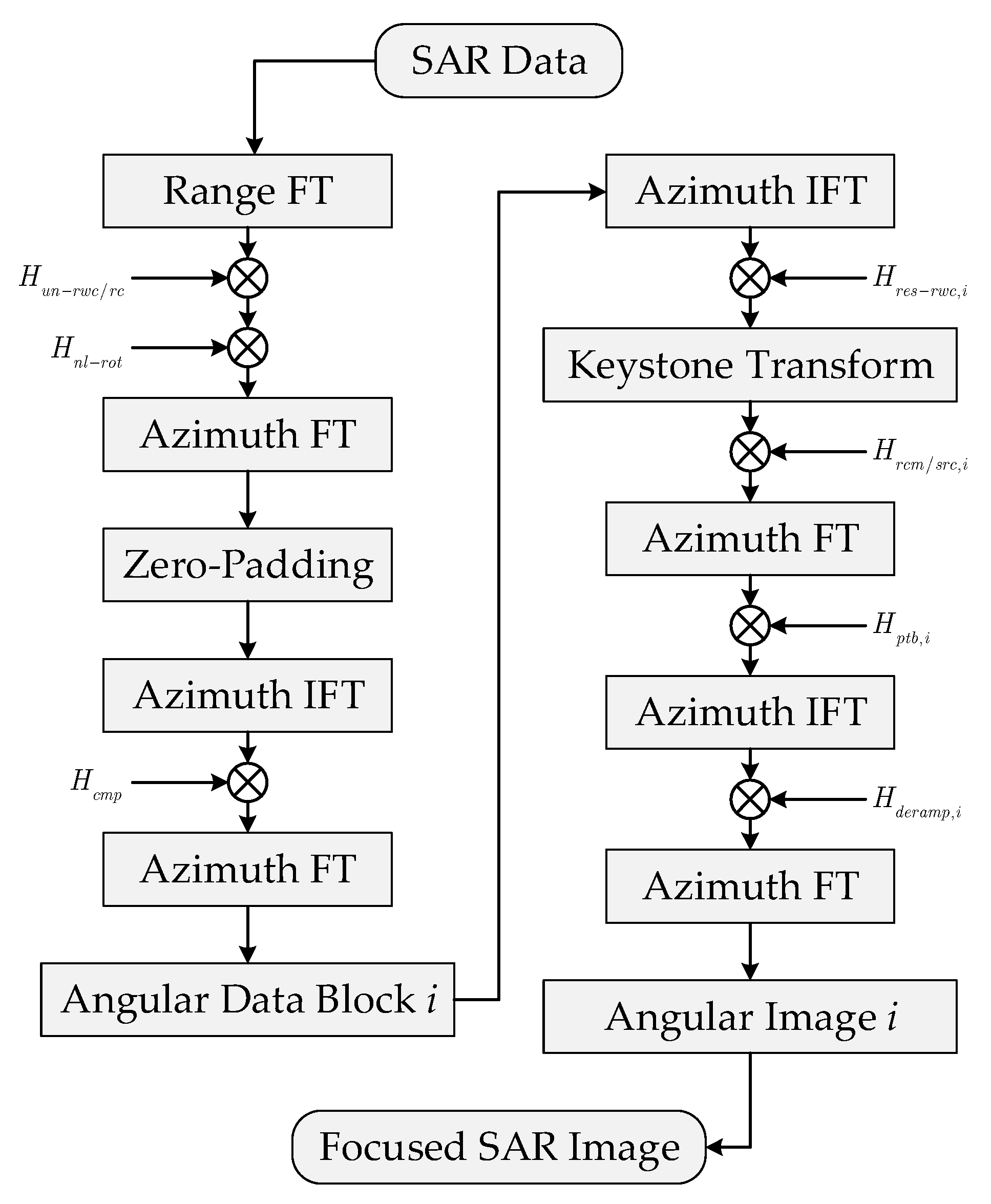
3. Imaging Algorithm
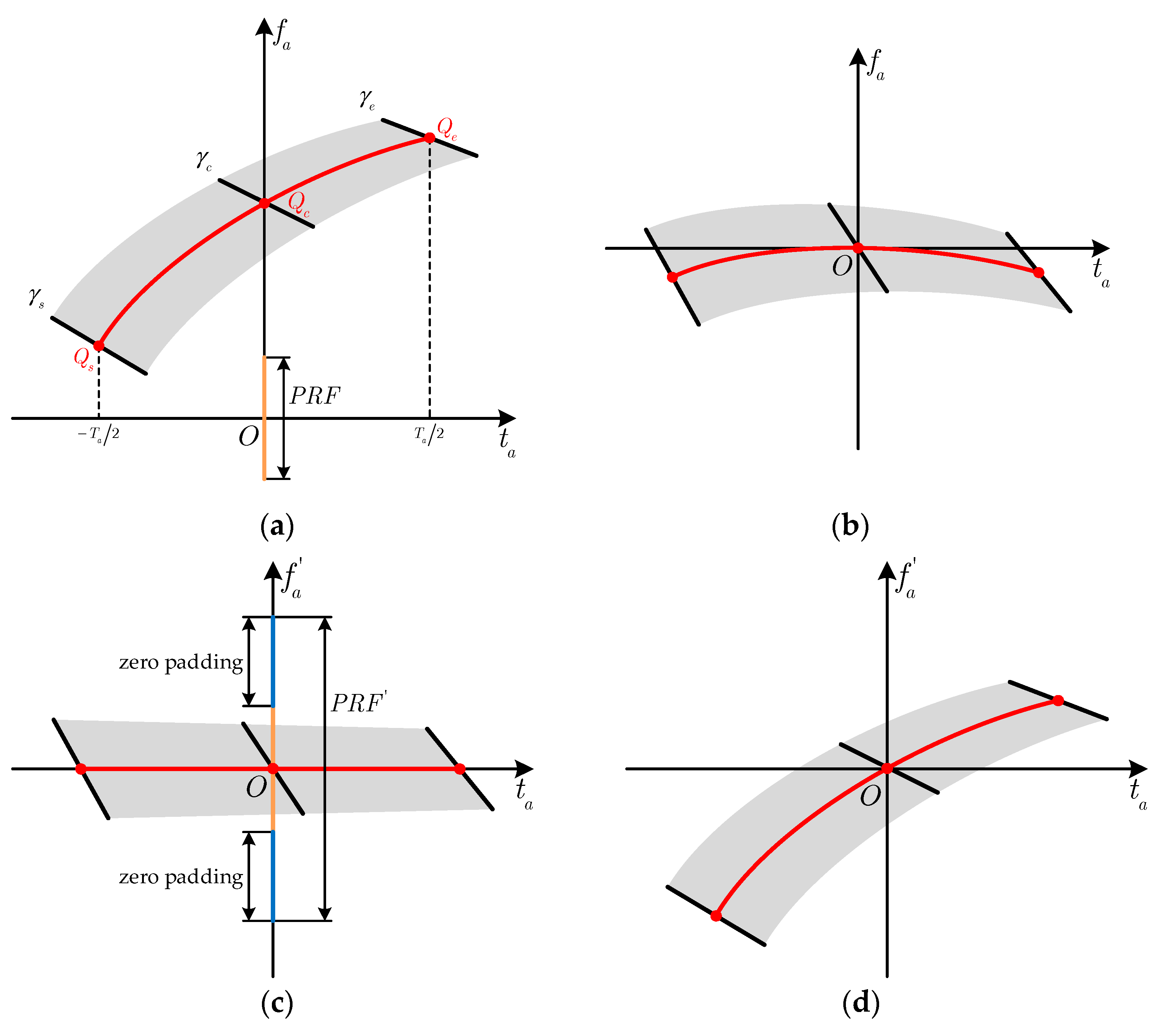
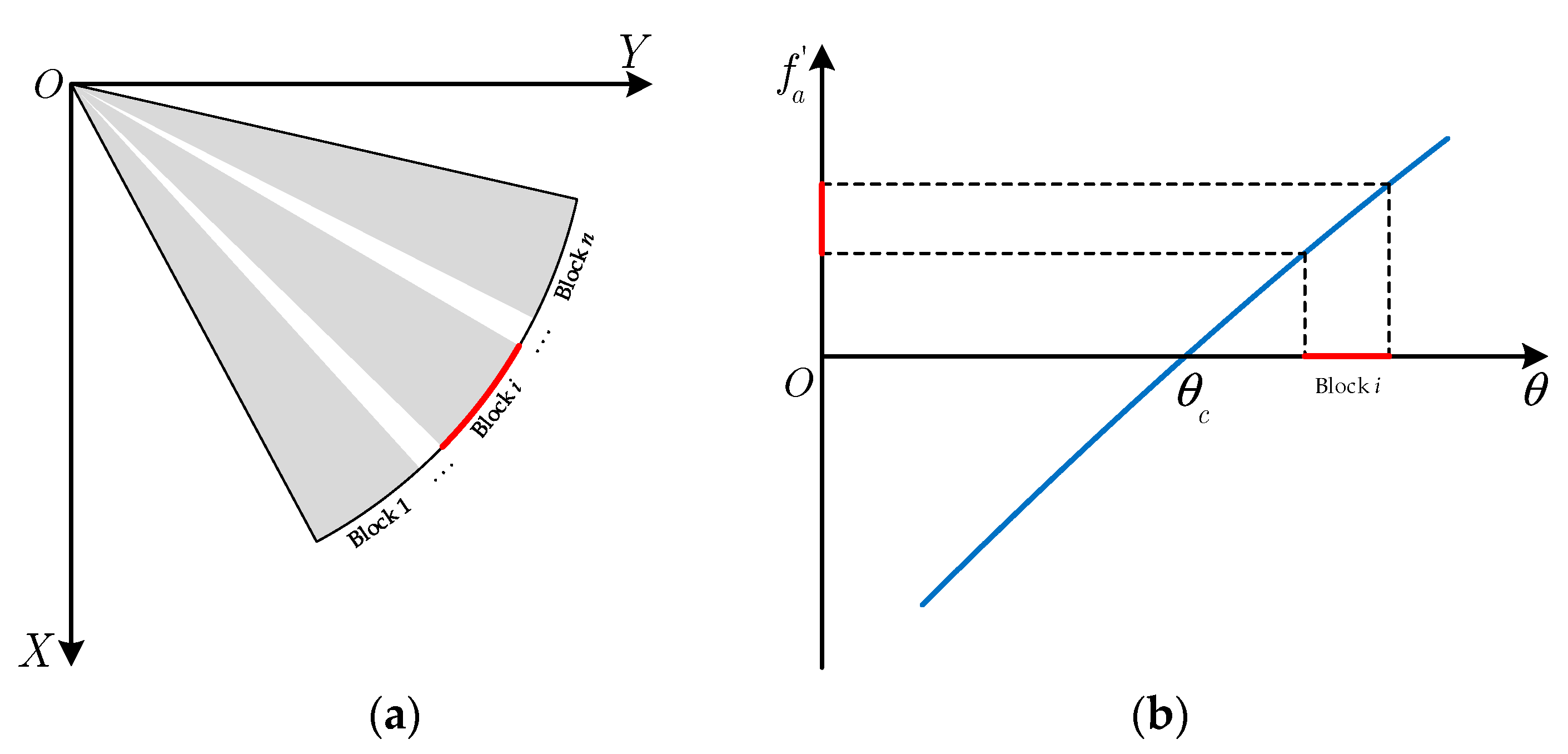
3.1. Spectrum Recovering and Angular Division
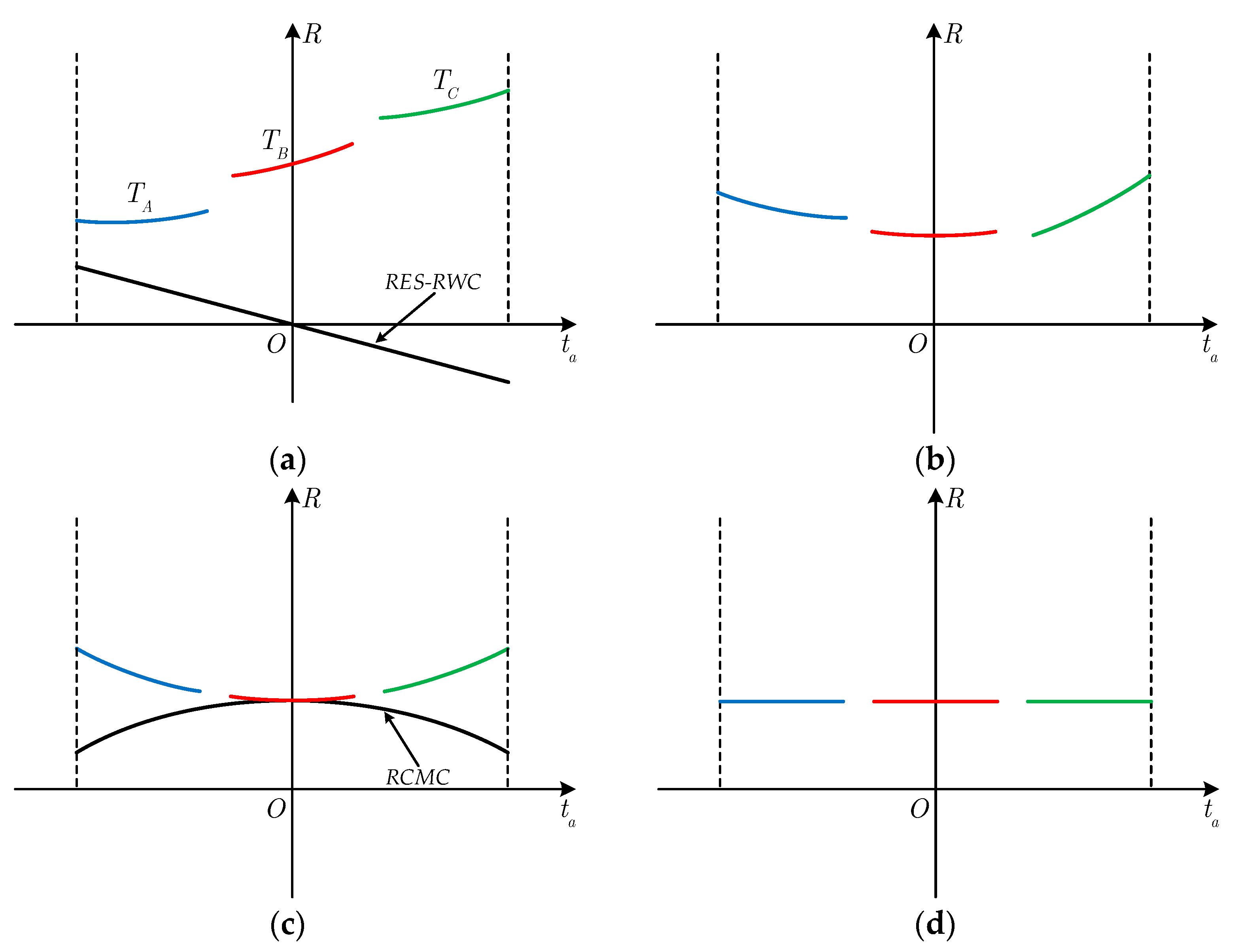
3.2. Residual RWC and Space-Variant RCMC
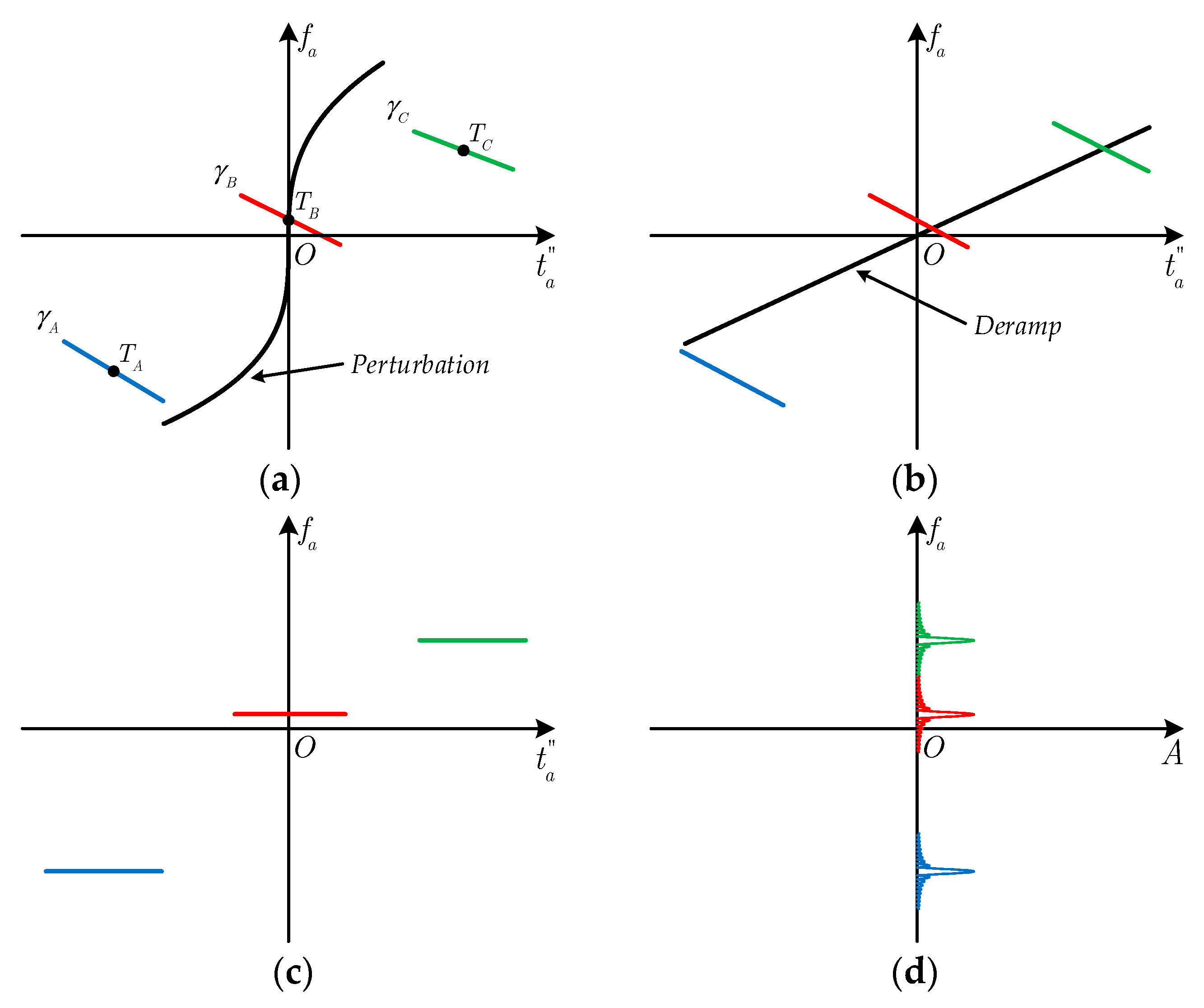
3.3. Aizmuth Fousing
3.4. Geometric Correction
4. Experimental Results
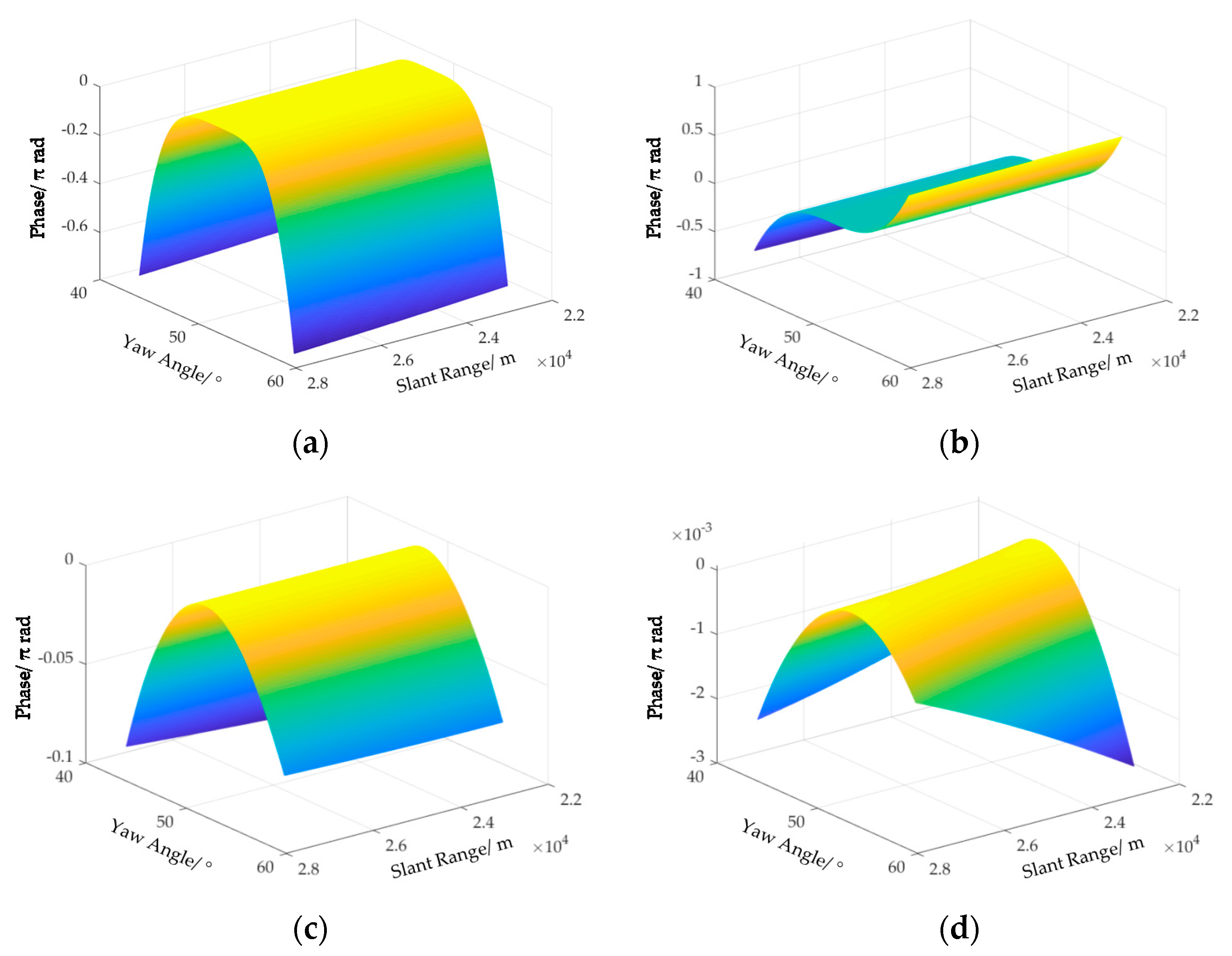
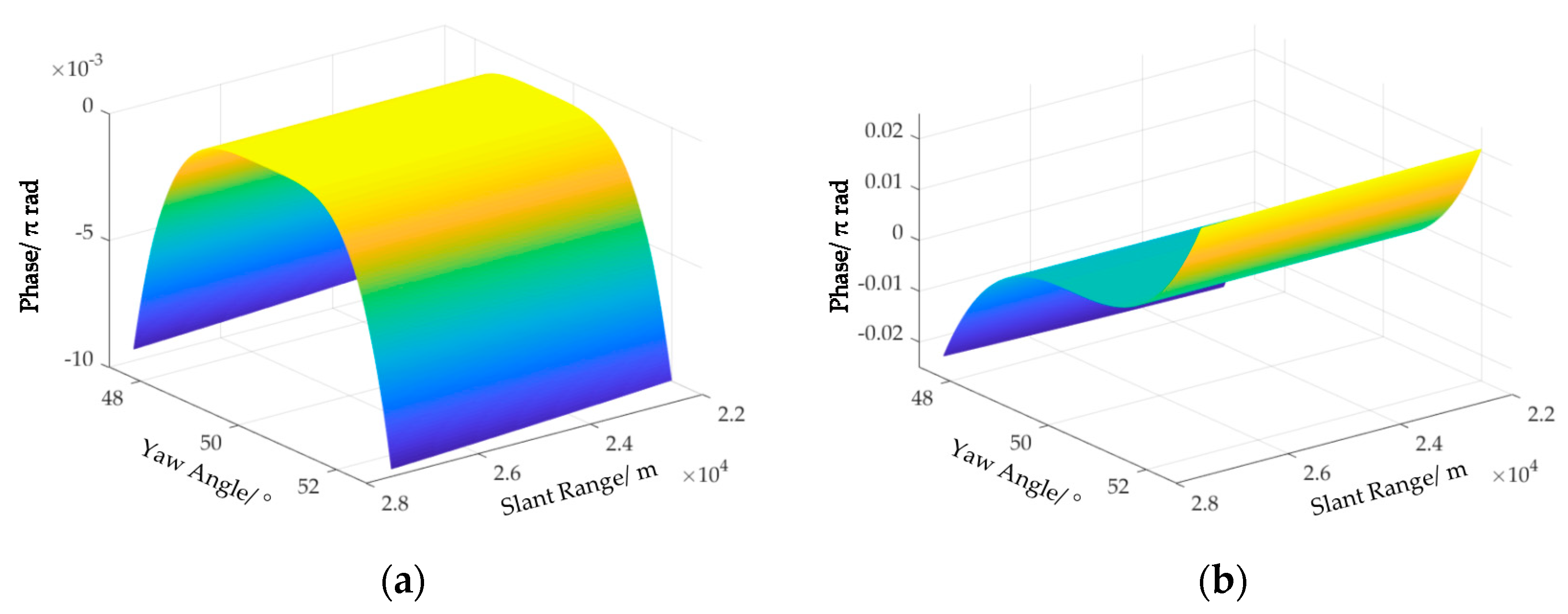
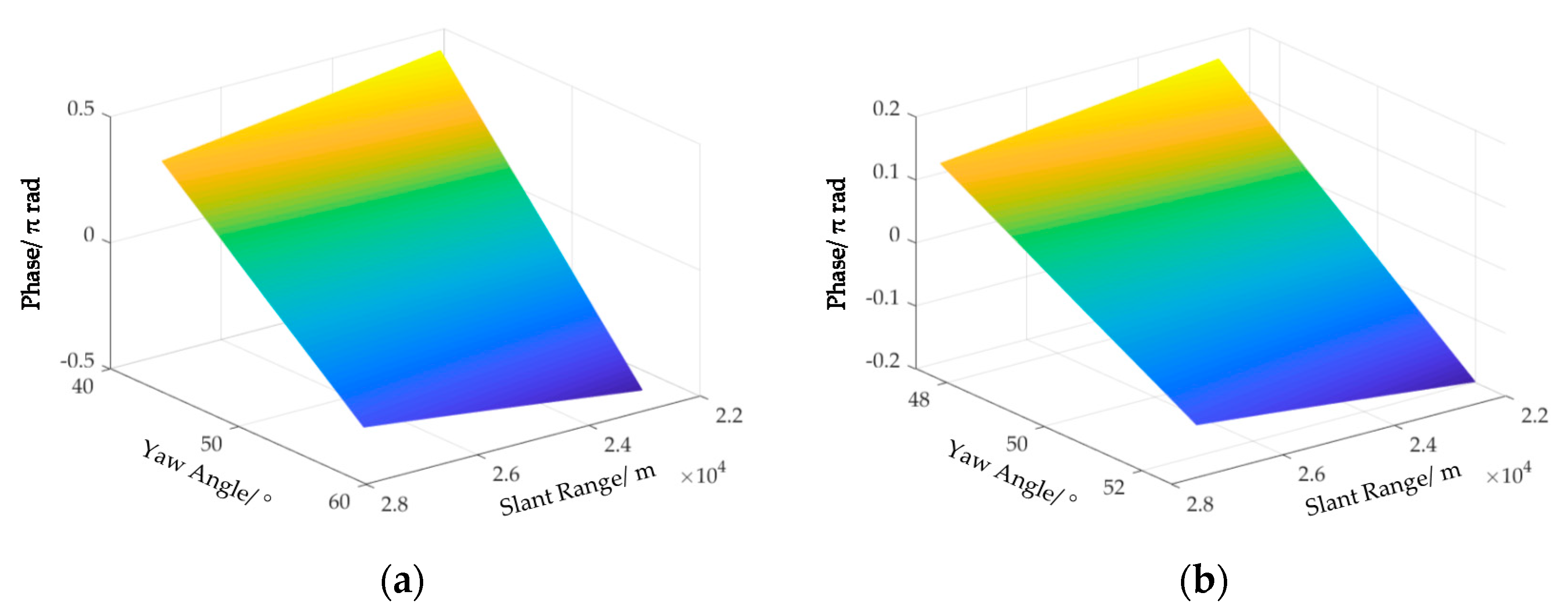
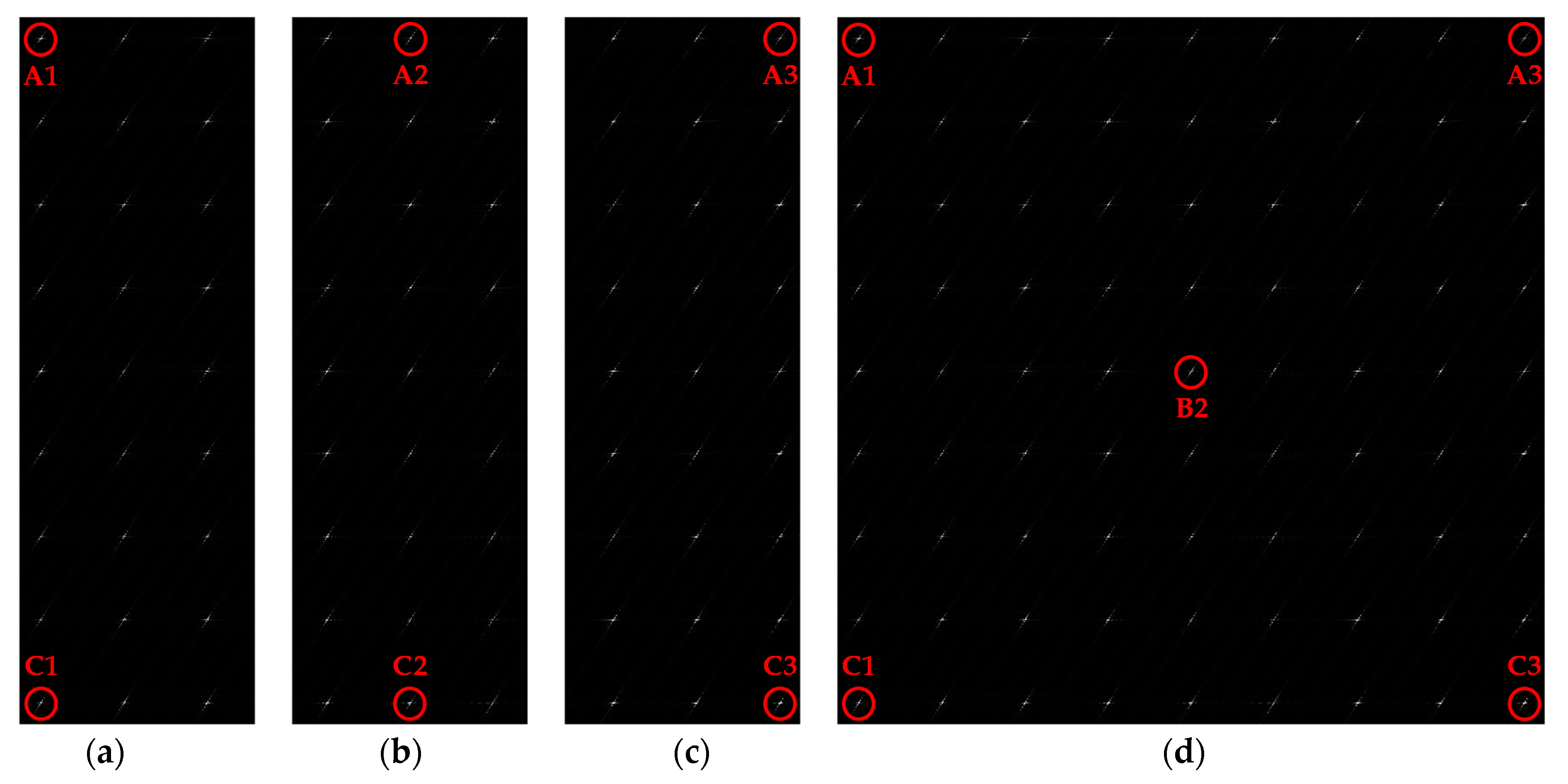
4.1. Correction of Space-Variant RCM
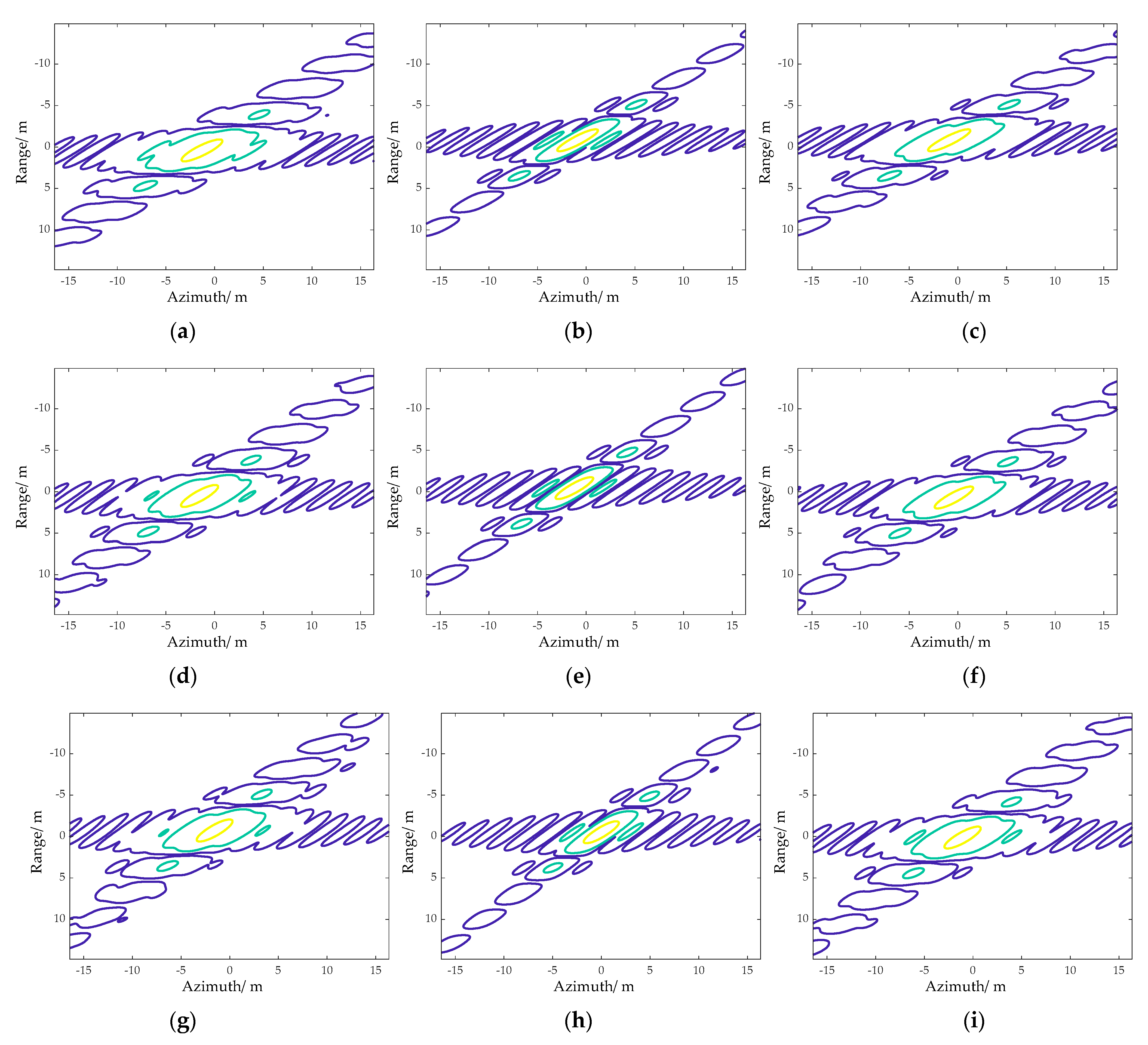
4.2. Performance of Geometric Correction and Azimuth Focusing
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Younis, M.; Lopez-Dekker, P.; Huber, S.; Villano, M.; Pardini, M. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the earth’s surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Carrara, W.G.; Goodman, R.S.; Majewski, R.M. Spotlight Synthetic Radar: Signal Processing Algorithm; Artech House: Boston, MA, USA, 1995. [Google Scholar]
- Cumming, I.G.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Zhang, L.; Qiao, Z.; Xing, M.D.; Yang, L.; Bao, Z. A robust motion compensation approach for UAV SAR imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Zhang, L.; Sheng, J.; Xing, M.; Qiao, Z.; Xiong, T.; Bao, Z. Wavenumber-domain autofocusing for highly squinted UAV SAR imagery. IEEE Sens. J. 2011, 12, 1574–1588. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Huang, Y.; Zhang, L.; Wang, F. Robust two-dimensional spatial-variant map-drift algorithm for UAV SAR autofocusing. Remote Sens. 2019, 11, 340. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Zhang, L.; So, H.C. Focusing high-resolution highly-squinted airborne SAR data with maneuvers. Remote Sens. 2018, 10, 862. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Zhang, L.; Guo, P.; Liu, G.; Sun, G.C. Acceleration model analyses and imaging algorithm for highly squinted airborne spotlight-Mode SAR with maneuvers. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2015, 8, 1120–1131. [Google Scholar] [CrossRef]
- Li, Z.; Xing, M.; Liang, Y.; Gao, Y.; Chen, J.; Huai, Y.; Zeng, L.; Sun, G.-C.; Bao, Z. A frequency-domain imaging algorithm for highly squinted SAR mounted on maneuvering platforms with nonlinear trajectory. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4023–4038. [Google Scholar] [CrossRef]
- Zeng, T.; Li, Y.; Ding, Z. Subaperture approach based on azimuth-dependent range cell migration correction and azimuth focusing parameter equalization for maneuvering high-squint-mode SAR. IEEE Trans. Geosci. Remote Sens. 2015, 52, 6718–6734. [Google Scholar] [CrossRef]
- Sun, G.-C.; Xing, M.; Xia, X.-G.; Wu, Y.; Huang, P.; Wu, Y.; Bao, Z. Multichannel full-aperture azimuth processing for beam steering SAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4761–4778. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, G.-C.; Xia, X.-G.; Xing, M.; Yang, J.; Bao, Z. An azimuth frequency non-linear chirp scaling (FNCS) algorithm for TOPS SAR imaging with high squint angle. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 213–221. [Google Scholar] [CrossRef]
- Bie, B.; Sun, G.; Xia, X.; Xing, M.; Guo, L.; Bao, Z. High-speed maneuvering platforms squint beam-steering SAR imaging without sub-aperture. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6974–6985. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Xie, R.; Zhang, L. Focusing high-squint synthetic aperture radar data based on factorized back-projection and precise spectrum fusion. Remote Sens. 2019, 11, 2885. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Sun, G.-C.; Xing, M.; Xia, X.-G.; Liang, Y.; Bao, Z. Squinted TOPS SAR imaging based on modified range migration algorithm and spectral analysis. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1707–1711. [Google Scholar] [CrossRef]
- Prats, P.; Scheiber, R.; Mittermayer, J.; Meta, A.; Moreira, A. Processing of sliding spotlight and TOPS SAR data using baseband azimuth scaling. IEEE Trans. Geosci. Remote Sens. 2010, 48, 770–780. [Google Scholar] [CrossRef] [Green Version]
- Engen, G.; Larsen, Y. Efficient full aperture processing of TOPS mode data using the moving band chirp Z-transform. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3688–3693. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Wang, Y.; Yang, J.; Bao, Z. A 2-D space-variant chirp scaling algorithm based on the RCM equalization and sub-band synthesis to process geosynchronous SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4868–4880. [Google Scholar]
- Wong, F.H.; Yeo, T.S. New applications of nonlinear chirp scaling in SAR data processing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 946–953. [Google Scholar] [CrossRef]
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing bistatic SAR data using the nonlinear chirp scaling. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.; Xing, M.; Liu, Y.; Sun, L.; Bao, Z.; Wu, Y. Extended NCS based on method of series reversion for imaging of highly squinted SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 446–450. [Google Scholar] [CrossRef]
- Sun, G.; Jiang, X.; Xing, M.; Qiao, Z.-J.; Wu, Y.; Bao, Z. Focus improvement of highly squinted data based on azimuth nonlinear scaling. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2308–2322. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended nonlinear chirp scaling algorithm for high-resolution highly squint SAR data focusing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3595–3609. [Google Scholar] [CrossRef]
- Li, N.; Bie, B.; Sun, G.C.; Xing, M.; Bao, Z. A high-squint TOPS SAR imaging algorithm for maneuvering platforms based on joint time-doppler deramp without subaperture. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1899–1903. [Google Scholar] [CrossRef]
- Xing, M.; Wu, Y.; Zhang, Y.D.; Sun, G.-C.; Bao, Z. Azimuth resampling processing for highly squinted synthetic aperture radar imaging with several modes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4339–4352. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Rodriguez-Cassola, M.; Mittermayer, J.; Wollstadt, S.; De Zan, F.; Brautigam, B.; Schwerdt, M.; Reigber, A.; Moreira, A. On the processing of very high resolution spaceborne SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6003–6016. [Google Scholar] [CrossRef] [Green Version]





| Parameters | Value |
|---|---|
| Carrier frequency | 15 GHz |
| Range bandwidth | 50 MHz |
| Pulse width | 10 μs |
| Height | 16.5 km |
| Center slant range | 30 km |
| Center yaw angle | 50° |
| Center squint angle | 39.8° |
| Time duration | 0.6 s |
| Steering angle | 42.13°~57.87° |
| Range swath | 5 km |
| Azimuth swath | 6.88 km |
| (vx, vy, vz) | (−40, 1300, −600) m/s |
| (ax, ay, az) | (−15, −30, −35) m/s2 |
| Target | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
| PSLR(dB) | ISLR(dB) | IRW(m) | PSLR(dB) | ISLR(dB) | IRW(m) | |
| A1 | −13.26 | −10.97 | 2.68 | −5.74 | −7.02 | 2.18 |
| A2 | −13.23 | −10.98 | 2.68 | −13.10 | −10.52 | 1.85 |
| A3 | −13.21 | −10.92 | 2.68 | −8.48 | −6.59 | 2.01 |
| B1 | −13.23 | −10.98 | 2.68 | −7.65 | −5.89 | 2.01 |
| B2 | −13.14 | −10.89 | 2.67 | −13.24 | −10.70 | 1.89 |
| B3 | −13.24 | −10.97 | 2.68 | −8.43 | −6.34 | 1.97 |
| C1 | −13.19 | −10.95 | 2.68 | −7.37 | −5.73 | 2.06 |
| C2 | −13.18 | −10.97 | 2.68 | −13.21 | −10.65 | 1.85 |
| C3 | −13.25 | −10.96 | 2.68 | −7.04 | −5.28 | 2.10 |
| Target | Range | Azimuth | ||||
|---|---|---|---|---|---|---|
| PSLR(dB) | ISLR(dB) | IRW(m) | PSLR(dB) | ISLR(dB) | IRW(m) | |
| A1 | −13.26 | −10.97 | 2.68 | −12.81 | −10.30 | 1.85 |
| A2 | −13.23 | −10.98 | 2.68 | −13.10 | −10.52 | 1.85 |
| A3 | −13.21 | −10.92 | 2.68 | −13.30 | −10.79 | 1.89 |
| B1 | −13.23 | −10.98 | 2.68 | −13.25 | −10.77 | 1.89 |
| B2 | −13.14 | −10.89 | 2.67 | −13.24 | −10.70 | 1.89 |
| B3 | −13.24 | −10.97 | 2.68 | −13.14 | −10.59 | 1.89 |
| C1 | −13.19 | −10.95 | 2.68 | −13.14 | −10.64 | 1.85 |
| C2 | −13.18 | −10.97 | 2.68 | −13.21 | −10.65 | 1.85 |
| C3 | −13.25 | −10.96 | 2.68 | −12.92 | −10.41 | 1.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bie, B.; Quan, Y.; Xu, K.; Sun, G.; Xing, M. High Speed Maneuvering Platform Squint TOPS SAR Imaging Based on Local Polar Coordinate and Angular Division. Remote Sens. 2021, 13, 3329. https://doi.org/10.3390/rs13163329
Bie B, Quan Y, Xu K, Sun G, Xing M. High Speed Maneuvering Platform Squint TOPS SAR Imaging Based on Local Polar Coordinate and Angular Division. Remote Sensing. 2021; 13(16):3329. https://doi.org/10.3390/rs13163329
Chicago/Turabian StyleBie, Bowen, Yinghui Quan, Kaijie Xu, Guangcai Sun, and Mengdao Xing. 2021. "High Speed Maneuvering Platform Squint TOPS SAR Imaging Based on Local Polar Coordinate and Angular Division" Remote Sensing 13, no. 16: 3329. https://doi.org/10.3390/rs13163329
APA StyleBie, B., Quan, Y., Xu, K., Sun, G., & Xing, M. (2021). High Speed Maneuvering Platform Squint TOPS SAR Imaging Based on Local Polar Coordinate and Angular Division. Remote Sensing, 13(16), 3329. https://doi.org/10.3390/rs13163329








