The MSG Technique: Improving Commercial Microwave Link Rainfall Intensity by Using Rain Area Detection from Meteosat Second Generation
Abstract
1. Introduction
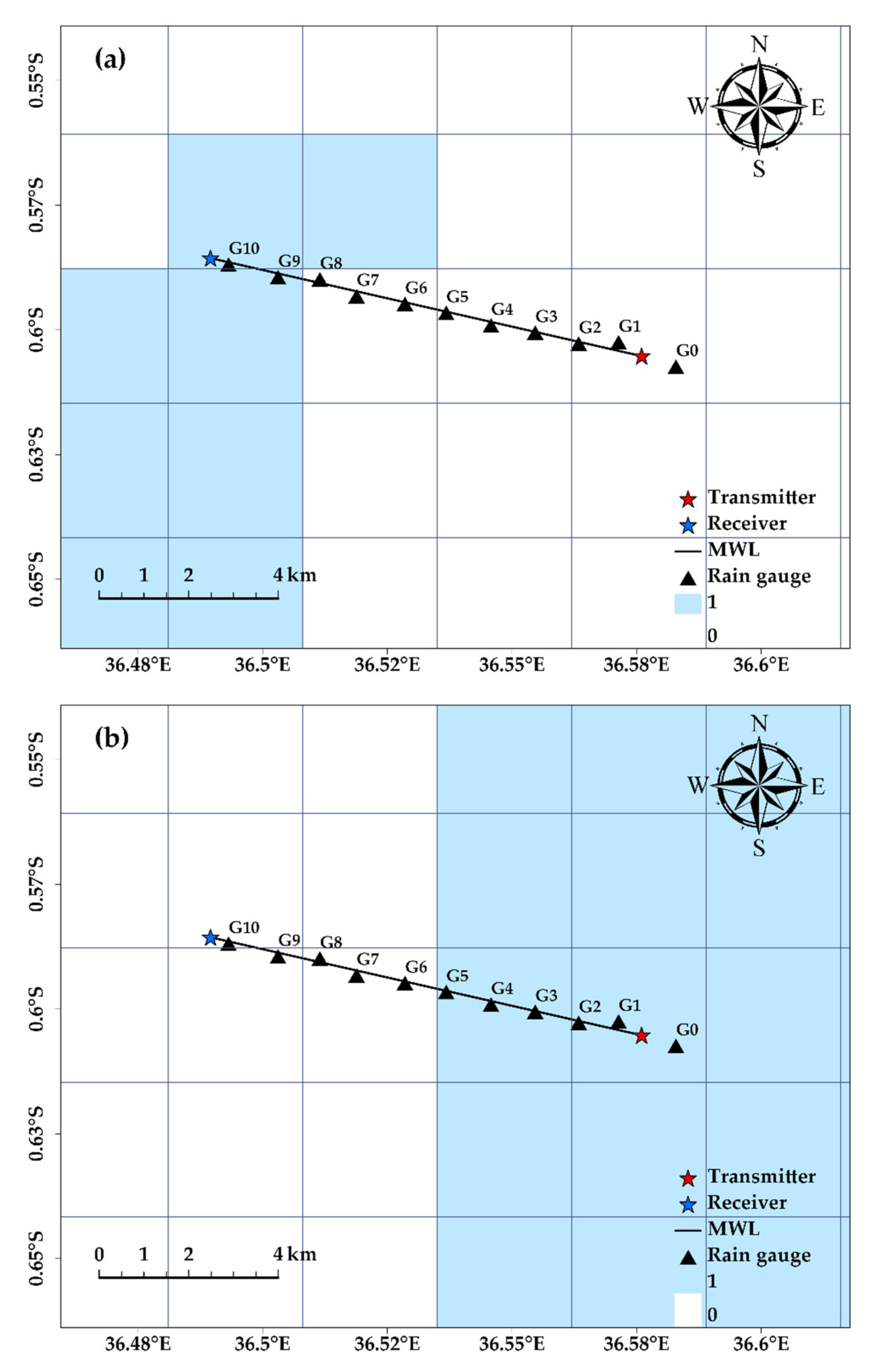
2. Study Area and Dataset
3. Method
3.1. Rainfall Intensities Estimated from Rain Gauges
3.2. Rainfall Intensities Estimated from MWL
3.2.1. The Conventional Technique
3.2.2. The New MSG Technique
3.2.2.1. Conditions and Uncertainties in Estimating the
3.3. Error Metrics
4. Results
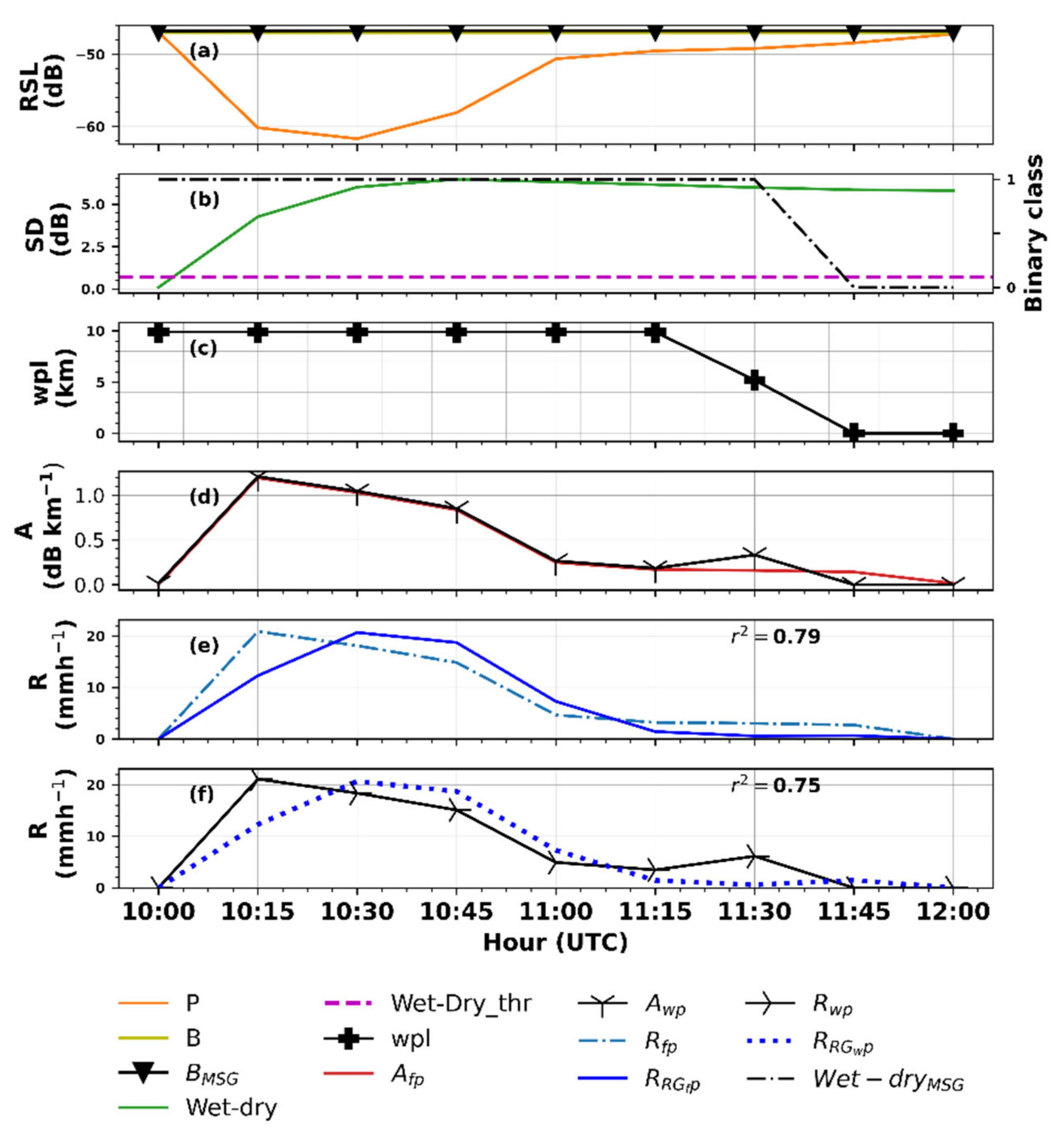
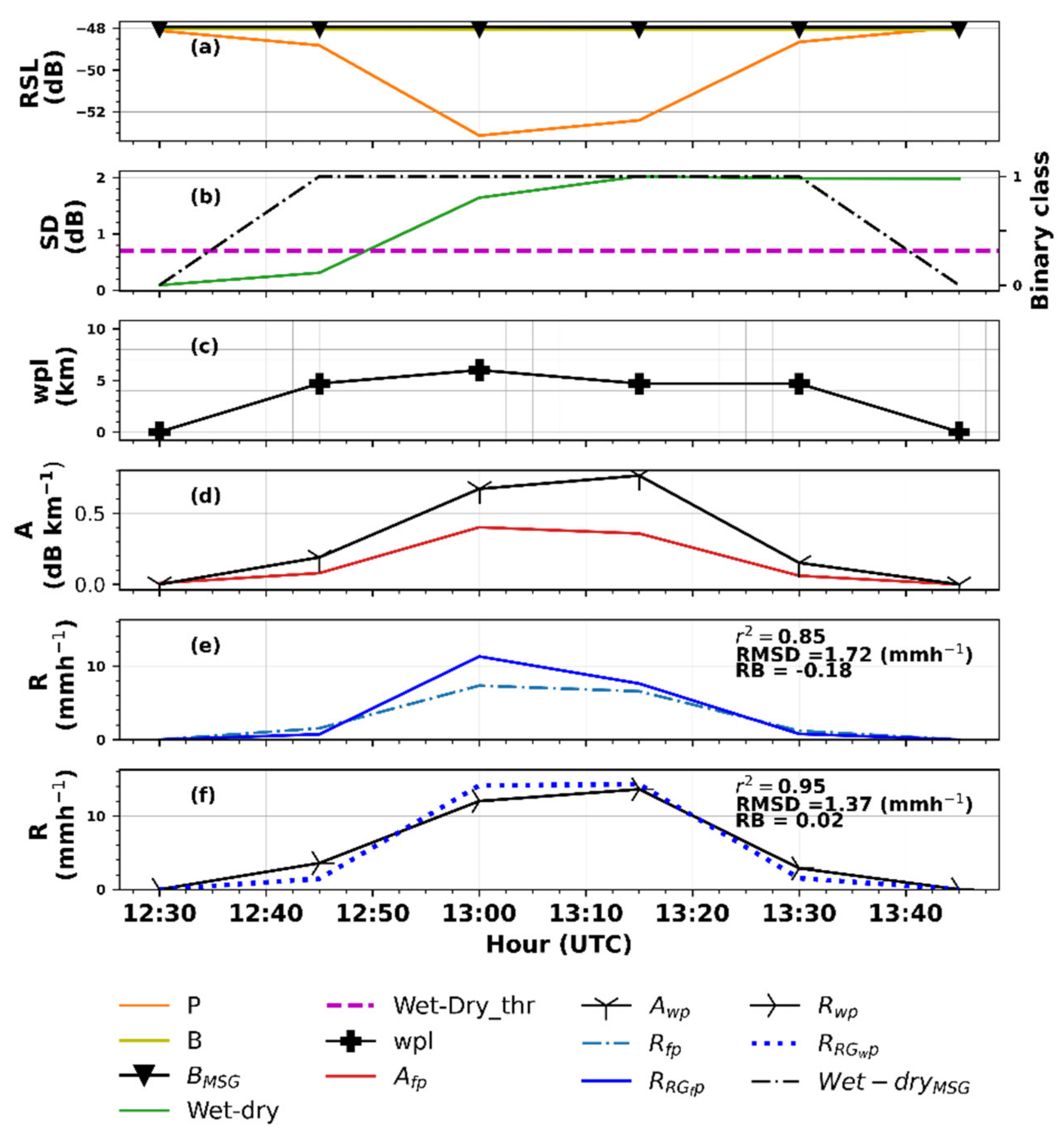
4.1. From Raw RSL to Rainfall Intensity Estimates: A Comparison of the Conventional and MSG Technique
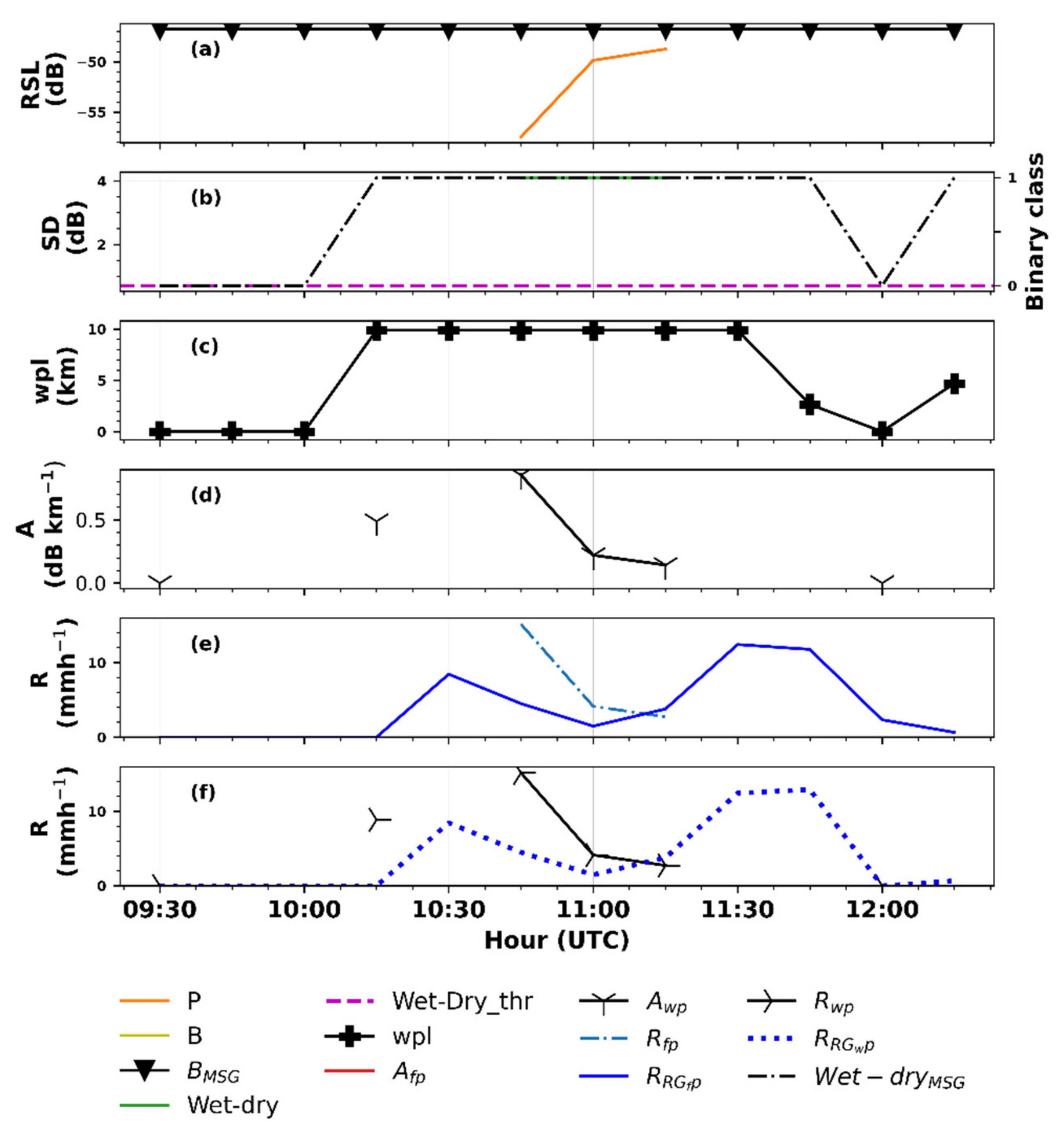
4.2. Appraisal of the MSG and Conventional Technique for MWL Rainfall Intensity Estimation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patrick, S. Microwave Link: Gigabit Microwave Connectivity. Available online: https://www.microwave-link.com/ (accessed on 13 July 2021).
- Ericsson. Ericsson Microwave towards 2020: Delivering High-Capacity and Cost-Efficient Backhaul for Broadband Networks Today and in the Future; Ericsson: Stockholm, Sweden, 2015. [Google Scholar]
- Edstam, J.; Olsson, A.; Flodin, J.; Öhberg, M.; Henriksson, A.; Hansryd, J.; Ahlberg, J. Ericsson Microwave Outlook; Ericsson: Göteborg, Sweden, 2018. [Google Scholar]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Hydrometeorological Application of a Microwave Link: 2. Precipitation. Water Resour. Res. 2007, 43, 1–9. [Google Scholar] [CrossRef]
- Messer, H.; Zinevich, A.; Alpert, P. Environmental monitoring by wireless communication networks. Science 2006, 312, 713. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Measuring urban rainfall using microwave links from commercial cellular communication networks. Water Resour. Res. 2011, 47, 1–16. [Google Scholar] [CrossRef]
- David, N.; Alpert, P.; Messer, H. The potential of cellular network infrastructures for sudden rainfall monitoring in dry climate regions. Atmos. Res. 2013, 131, 13–21. [Google Scholar] [CrossRef]
- David, N.; Liu, Y.; Kumah, K.K.; Hoedjes, J.C.B.; Su, B.Z.; Gao, H.O. On the Power of Microwave Communication Data to Monitor Rain for Agricultural Needs in Africa. Water 2021, 13, 730. [Google Scholar] [CrossRef]
- David, N.; Gao, H.O.; Kumah, K.K.; Hoedjes, J.C.B.; Su, Z.; Liu, Y. Microwave communication networks as a sustainable tool of rainfall monitoring for agriculture needs in Africa. In Proceedings of the 16th International Conference on Environmental Science and Technology, Rhodes, Greece, 4–7 September 2019. [Google Scholar]
- Doumounia, A.; Gosset, M.; Cazenave, F.; Kacou, M.; Zougmore, F. Rainfall monitoring based on microwave links from cellular telecommunication networks: First results from a West African test bed. Geophys. Res. Lett. 2014, 41, 6016–6022. [Google Scholar] [CrossRef]
- Kumah, K.K.; Hoedjes, J.C.B.; David, N.; Maathuis, B.P.; Gao, H.O.; Su, B.Z. Combining MWL and MSG SEVIRI Satellite Signals for Rainfall Detection and Estimation. Atmosphere 2020, 11, 884. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Country-wide rainfall maps from cellular communication networks. Proc. Natl. Acad. Sci. USA 2013, 110, 2741–2745. [Google Scholar] [CrossRef] [PubMed]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Two and a half years of country-wide rainfall maps using radio links from commercial cellular telecommunication networks. Water Resour. Res. 2016, 52, 8039–8065. [Google Scholar] [CrossRef]
- Rahimi, A.R.; Upton, G.J.G.; Holt, A.R. Dual-frequency Links—A Complement to Gauges and Radar for the Measurement of Rain. J. Hydrol. 2004, 288, 3–12. [Google Scholar] [CrossRef]
- Chwala, C.; Kunstmann, H. Commercial microwave link networks for rainfall observation: Assessment of the current status and future challenges. Wires Water 2019, 6, e1337. [Google Scholar] [CrossRef]
- Upton, G.J.G.; Holt, A.R.; Cummings, R.J.; Rahimi, A.R.; Goddard, J.W.F. Microwave Links: The Future for Urban Rainfall Measurement? Atmos. Res. 2005, 77, 300–312. [Google Scholar] [CrossRef]
- Zinevich, A.; Alpert, P.; Messer, H. Estimation of rainfall fields using commercial microwave communication networks of variable density. Adv. Water Resour. 2008, 31, 1470–1480. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Stricker, J.N.M. Microwave link rainfall estimation: Effects of link length and frequency, temporal sampling, power resolution, and wet antenna attenuation. Adv. Water Resour. 2008, 31, 1481–1493. [Google Scholar] [CrossRef]
- Uijlenhoet, R.; Overeem, A.; Leijnse, H. Opportunistic remote sensing of rainfall using microwave links from cellular communication networks. Wires Water 2018, 5, e1289. [Google Scholar] [CrossRef]
- David, N.; Sendik, Q.; Messer, H.; Alpert, P. Cellular network infrastructure: The future of fog monitoring? Bull. Am. Meteorol. Soc. 2015, 96, 1687–1698. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; Uijlenhoet, R. Retrieval algorithm for rainfall mapping from microwave links in a cellular communication network. Atmos. Meas. Tech. 2016, 9, 2425–2444. [Google Scholar] [CrossRef]
- Schleiss, M.; Berne, A. Identification of Dry and Rainy Periods Using Telecommunication Microwave Links. IEEE Geosci. Remote Sens. Lett. 2010, 7, 611–615. [Google Scholar] [CrossRef]
- Gaona, M.F.R.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. Measurement and interpolation uncertainties in rainfall maps from cellular communication networks. Hydrol. Earth Syst. Sci. 2015, 19, 3571–3584. [Google Scholar] [CrossRef]
- Olsen, R.; Rogers, D.; Hodge, D. The aRb Relation in the Calculation of Rain Attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Schleiss, M.; Rieckermann, J.; Berne, A. Quantification and modeling of wet-antenna attenuation for commercial microwave links. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1195–1199. [Google Scholar] [CrossRef]
- Nakamura, M. Method for wet antenna correct at 50 GHz. J. Chem. Inf. Modeling 2013, 53, 1689–1699. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An Introduction to Meteosat Second Generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Kuhnlein, M.; Thies, B.; Nauss, T.; Bendix, J. Rainfall-Rate Assignment Using MSG SEVIRI Data-A Promising Approach to Spaceborne Rainfall-Rate Retrieval for Midlatitudes. J. Appl. Meteorol. Climatol. 2010, 49, 1477–1495. [Google Scholar] [CrossRef]
- Van het Schip, T.I.; Overeem, A.; Leijnse, H.; Uijlenhoet, R.; Meirink, J.F.; van Delden, A.J. Rainfall measurement using cell phone links: Classification of wet and dry periods using geostationary satellites. Hydrol. Sci. J. 2017, 62, 1343–1353. [Google Scholar] [CrossRef]
- Hoedjes, J.C.B.; Kooiman, A.; Maathuis, B.H.P.; Said, M.Y.; Becht, R.; Limo, A.; Mumo, M.; Nduhiu-Mathenge, J.; Shaka, A.; Su, B. A Conceptual Flash Flood Early Warning System for Africa, Based on Terrestrial Microwave Links and Flash Flood Guidance. ISPRS Int. J. Geo Inf. 2014, 3, 584–598. [Google Scholar] [CrossRef]
- Van de Giesen, N.; Hut, R.; Selker, J. The Trans-African Hydro-Meteorological Observatory (TAHMO). Wiley Interdiscip. Rev. Water 2014, 1, 341–348. [Google Scholar] [CrossRef]
- Eumetsat. Meteosat-8 Satellite’s New Position of 41.5E Provides Weather and Climate View over the Indian Ocean. Available online: https://phys.org/news/2016-09-meteosat-satellite-position-415e-weather.html (accessed on 14 July 2020).
- ITU. Specific Attenuation Model for Rain for Use in Prediction Methods; I.T.U. RECOMMENDATION ITU-R P.838-3; ITU: Geneva, Switzerland, 2005. [Google Scholar]
- Kingsley, K.K.; Maathuis, B.H.P.; Hoedjes, J.C.B.; Rwasoka, D.T.; Retsios, B.V.; Su, B.Z. Rain Area Detection in South-Western Kenya by Using Multispectral Satellite Data from Meteosat Second Generation. Sensors 2021, 21, 3547. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: London, UK, 2006; Volume 14, p. 627. [Google Scholar]
- Walther, B.A.; Moore, J.L. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- Barnston, A.G. Correspondence among the Correlation, Rmse, and Heidke Forecast Verification Measures—Refinement of the Heidke Score. Weather Forecast. 1992, 7, 699–709. [Google Scholar] [CrossRef]
- Rowe, R.D. The Effects of Aggregation over Time on T-Ratios and R2’s. Int. Econ. Rev. 1976, 17, 751. [Google Scholar] [CrossRef]
- Leijnse, H.; Uijlenhoet, R.; Berne, A. Errors and Uncertainties in Microwave Link Rainfall Estimation Explored Using Drop Size Measurements and High-Resolution Radar Data. J. Hydrometeorol. 2010, 11, 1330–1344. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; van Leth, T.; Bogerd, L.; Priebe, J.; Tricarico, D.; Droste, A.M.; Uijlenhoet, R. Tropical rainfall monitoring with commercial microwave links in Sri Lanka. Environ. Res. Lett. 2021, 16, 074058. [Google Scholar] [CrossRef]
- Feidas, H.; Giannakos, A. Identifying precipitating clouds in Greece using multispectral infrared Meteosat Second Generation satellite data. Theor. Appl. Climatol. 2011, 104, 25–42. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. Precipitation process and rainfall intensity differentiation using Meteosat Second Generation Spinning Enhanced Visible and Infrared Imager data. J. Geophys. Res. Atmos. 2008, 113, D23206. [Google Scholar] [CrossRef]
- Thies, B.; Nauss, T.; Bendix, J. First results on a process-oriented rain area classification technique using Meteosat Second Generation SEVIRI nighttime data. Adv. Geosci. 2008, 16, 63–72. [Google Scholar] [CrossRef][Green Version]



| G0 | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | G9 | G10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 7.12 | 7.65 | 8.74 | 8.25 | 6.79 | 4.41 | 2.88 | 4.36 | 6.7 | 3.82 | 3.98 |
| Maximum | 43.46 | 23.64 | 72.36 | 49.53 | 27.72 | 43.63 | 5.54 | 27.47 | 19.3 | 12.86 | 28.02 |
| Standard deviation | 9.8 | 7.65 | 15.01 | 12.79 | 8.16 | 8.56 | 1.43 | 5.61 | 7.33 | 3.98 | 5.71 |
| Fraction% | 3.29 | 1.72 | 2.4 | 1.98 | 1.46 | 2.82 | 1.14 | 2.47 | 0.62 | 0.82 | 1.88 |
| N | 70 | 7 | 23 | 19 | 14 | 44 | 11 | 46 | 6 | 8 | 40 |
| n days | 53 | 12 | 26 | 26 | 26 | 39 | 26 | 46 | 26 | 26 | 53 |
| Estimation technique | RMSD mm h−1 | RB | r2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 min | 30 min | 1 h | 3 h | 15 min | 30 min | 1 h | 3 h | 15 min | 30 min | 1 h | 3 h | |
| MSG technique | 0.63 | 0.84 | 1.32 | 2.61 | 0.47 | 0.47 | 0.47 | 0.47 | 0.70 | 0.78 | 0.83 | 0.81 |
| Conventional technique | 0.60 | 0.80 | 1.23 | 2.09 | 0.02 | 0.02 | 0.03 | 0.04 | 0.63 | 0.73 | 0.80 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumah, K.K.; Hoedjes, J.C.B.; David, N.; Maathuis, B.H.P.; Gao, H.O.; Su, B.Z. The MSG Technique: Improving Commercial Microwave Link Rainfall Intensity by Using Rain Area Detection from Meteosat Second Generation. Remote Sens. 2021, 13, 3274. https://doi.org/10.3390/rs13163274
Kumah KK, Hoedjes JCB, David N, Maathuis BHP, Gao HO, Su BZ. The MSG Technique: Improving Commercial Microwave Link Rainfall Intensity by Using Rain Area Detection from Meteosat Second Generation. Remote Sensing. 2021; 13(16):3274. https://doi.org/10.3390/rs13163274
Chicago/Turabian StyleKumah, Kingsley K., Joost C. B. Hoedjes, Noam David, Ben H. P. Maathuis, H. Oliver Gao, and Bob Z. Su. 2021. "The MSG Technique: Improving Commercial Microwave Link Rainfall Intensity by Using Rain Area Detection from Meteosat Second Generation" Remote Sensing 13, no. 16: 3274. https://doi.org/10.3390/rs13163274
APA StyleKumah, K. K., Hoedjes, J. C. B., David, N., Maathuis, B. H. P., Gao, H. O., & Su, B. Z. (2021). The MSG Technique: Improving Commercial Microwave Link Rainfall Intensity by Using Rain Area Detection from Meteosat Second Generation. Remote Sensing, 13(16), 3274. https://doi.org/10.3390/rs13163274









