Abstract
Satellite rainrate estimation is a great challenge, especially in mesoscale convective systems (MCSs), which is mainly due to the absence of a direct physical connection between observable cloud parameters and surface rainrate. The machine learning technique was employed in this study to estimate rainrate in the MCS domain via using cloud top temperature (CTT) derived from a geostationary satellite. Five kinds of machine learning models were investigated, i.e., polynomial regression, support vector machine, decision tree, random forest, and multilayer perceptron, and the precipitation of Climate Prediction Center morphing technique (CMORPH) was used as the reference. A total of 31 CTT related features were designed to be the potential inputs for training an algorithm, and they were all proved to have a positive contribution in modulating the algorithm. Random forest (RF) shows the best performance among the five kinds of models. By combining the classification and regression schemes of the RF model, an RF-based hybrid algorithm was proposed first to discriminate the rainy pixel and then estimate its rainrate. For the MCS samples considered in this study, such an algorithm generates the best estimation, and its accuracy is definitely higher than the operational precipitation product of FY-4A. These results demonstrate the promising feasibility of applying a machine learning technique to solve the satellite precipitation retrieval problem.
1. Introduction
Most vigorous rainstorms are generated by so-called mesoscale convective systems (MCSs) [1,2], which are commonly defined as a cluster of vigorous precipitating clouds with a horizontal scale exceeding 100 km [3]. The combination of high intensity, large area, and long lifetime of such violent precipitation systems tends to produce extremely massive rainfall and possibly leads to various hydrological or geological disasters, such as floods, landslides, etc. The desire for accurate estimation of MCS precipitation has stimulated a large number of studies that were dedicated to the precipitation characteristics of MCSs, as well as those focusing on their spatial structures and dynamics that eventually determine the variation of MCS precipitation [4,5].
In the MCS, there usually are many convective cells that are dependent on each other, appearing as an ensemble of cumulonimbus clouds with particular organizations. Depending on the form of organization, MCS could be classified as a squall line, mesoscale convective complex (MCC), mesoscale convective vortex (MCV), etc. [2,4]. In terms of the precipitation-generating regime, it is notable that convective precipitation and stratiform precipitation coexist in the domain of MCS, corresponding to the developing and decaying stage of the individual convection, respectively. During the mature phase of MCS that is accompanied by heavy precipitation, it is featured by the organized mesoscale circulation [2]. In particular, cloud top temperature was revealed to be an effective indicator for precipitation probability on the local scale within the MCS. It was suggested that the occurrence of extremely heavy precipitation is very likely correlated with both the cloud top temperature and the overall size of the MCS [6].
Precipitation intensity is the most fundamental parameter for quantitatively depicting a precipitating system. In liquid-phase, it is conventionally termed as rainrate that is used to indicate the downward flux of water at the ground level. Precipitation intensity with high spatiotemporal resolution is preferred either for operational or scientific intention. The measurement of instantaneous precipitation intensity in the MCS domain is undoubtedly of great importance since the variabilities of precipitation fields generated by MCSs are far from those produced by a single precipitating cloud, nimbostratus, or cumulonimbus, regardless of its volume or strength [7]. The ground-based rain gauges and microwave radars are extensively equipped, which constitute an effective means for measuring real-time precipitation intensity. However, these ground-based facilities are nearly unavailable over the vast oceans and numerous mountainous regions around the world. Thus far, the areas covered by these conventional facilities are few on the global scale, and, therefore, the representativeness of these precipitation data for depicting MCSs is rather incomplete [8].
Satellite remote sensing provides a unique way, in the top-down perspective, to measure global precipitation. Microwave sensors, including passive radiometers and active radars, aboard low Earth orbiting (LEO) meteorological satellites are used for retrieving precipitation intensity. The microwave radiation has the capability to penetrate clouds and, therefore, is highly sensitive to raindrops below the cloud layer. This feature ensures the basis of physical retrieval for microwave-based measurements. However, microwave sensors have thus far only been able to be carried on LEO satellites due to restrictions on spatial resolution. Among others, such as swath truncation [9], the most notable deficiency of LEO satellites is the very low temporal resolution. Except for the polar region, most locations throughout the globe are merely visited by such satellites twice per day and cannot form temporally continuous observation. Especially for MCSs, a huge cloud system with rapid motion and internal variation, the precipitation information from just an arbitrary snapshot is rather limited.
On the contrary, the geostationary (GEO) satellite is suitable for nearly continuous observation of MCSs, which is largely attributed to its high temporal resolution (1~10 min). For sensors aboard the GEO satellite, the available measurements are from visible and infrared (VIR) bands. Although there is no direct connection between VIR signals and precipitation-sized hydrometers below the cloud layer, the information of cloud top height and cloud layer thickness involved in VIR signals are indicative of the strength of updrafts, which are correlated to the precipitation processes. This fact constitutes the physical basis for precipitation retrieval relying on satellite VIR measurements [10]. Many retrieval algorithms have been accordingly proposed. For instance, given sufficient ground truth of rainrate at a local scale, which is possibly from rain gauges or radar networks, the regression scheme was usually employed for establishing the retrieval algorithm. The selective parameters, such as the infrared brightness temperature of cloud top and the horizontal scale of cloud mass, were used together to regressively estimate rainrate [11]. In fact, all these approaches are semi-empirical and have considerable uncertainties since the physical connection between the several parameters extracted from the measurements and the desired rainrate is rather weak. For the precipitation retrieval in the MCS domain, the situation even deteriorates because there exists a nonlinear relationship between precipitation intensity at individual locations and those selective parameters that reflect specific cloud features [6]. As a result, these semi-empirical methods are not suitable for rainrate retrieval in MCS.
Machine learning has been widely proved to be effective for solving such complicated problems that have nonlinear correlation among their numerous inner components, to which it is extremely difficult to set up simple physical models by using ordinary mathematic analysis or statistical skills [12]. The unique capability of machine learning can be greatly enhanced via ingesting the massive volume of practical data, which is getting more and more available due to the recent development of data-collecting and computing techniques [13]. A good many machine learning algorithms have been proposed that are currently used in nearly all kinds of social and scientific fields. Especially for the meteorological field, the enormous measurements that are routinely collected by various observational platforms, e.g., meteorological sites, radar networks, satellites, provide the feasibility for introducing machine learning as an effective tool. For instance, the convolutional neural network technique was employed to help to estimate the strength of tropical cyclones [14]. The critical environmental factors were sought to identify the transformation from MCS to tropical cyclones [15]. Machine learning techniques were also evaluated and used particularly to categorize convective storms [16].
Machine learning is especially appropriate for the satellite-based precipitation estimation, where massive observations of cloud features are available. By using infrared or vapor channel data, Tao et al. used the fully connected neural network technique to discriminate precipitation events from non-precipitation ones, and in turn to estimate precipitation intensity [17]. Though there were some biases in their results, it seemed to be a feasible way that deserved further improvement. Szunyogh et al. proposed a machine learning-based precipitation model that could be used to estimate global precipitation with low spatial resolution, which showed good performance at middle latitudes [18]. Hirose et al. designed a random forest-based precipitation model that merely used satellite infrared measurements to derive precipitation estimation and achieved a rather high accuracy for warm precipitation [19].
Apparently, the MCS is an even more complicated environment that frequently generates heavy precipitation [2,6]. Given the above successes, the problem of precipitation estimation in such an extreme situation is worthy of examination from the machine learning perspective. To our knowledge, thus far, there is no report on evaluating the feasibility of using a machine learning technique for estimating MCS precipitation based on GEO satellite measurements. Therefore, the present study is devoted to such a problem by using FY-4A satellite measurements, which is a new-generation GEO meteorological satellite managed by China Meteorological Administration (CMA) that provides high-quality real-time VIR observations. Taking the CMORPH (Climate Prediction Center morphing technique) precipitation data as a reference, the many features that are closely relevant to the MCS precipitation characteristics were identified, and then several kinds of machine learning algorithms were trained, and their performances for precipitation intensity estimation were evaluated.
2. Data and Methods
2.1. Data
The geographic region considered in the present study is South China and its adjacent ocean (15° N–30° N, 105° E–120° E). This is the transitional domain connecting the East Asia mainland and the Western Pacific warm pool and is notable for frequent strong convective activities, especially in the warm season [4,5,20,21], supplying abundant MCS samples. The FY-4A cloud top temperature (CTT) data and the CMORPH precipitation data in June and July 2019 were used. The CTT was used to identify and track the individual MCS, while the CMORPH precipitation was used as the true value of precipitation for training and evaluating the machine learning algorithm.
FY-4A is the new generation of GEO meteorological satellites of China, launched on 11 December 2016, and situated over the equator around 104.7° E. Its main payloads are: Advanced Geostationary Radiation Imager (AGRI), Geostationary Interferometric Infrared Sounder (GIIRS), Lightning Mapping Imager (LMI), and Space Environmental Package (SEP) [22]. The AGRI has 14 bands in the visible and infrared bands, with the spatial resolution at visible/near-infrared bands and remaining infrared bands around 0.5 km and 2 km, respectively. The AGRI scans a full-disk Earth image every 15 min and thus is able to provide high-temporal and spatial resolution product data of clouds, water vapor, and aerosols. The Chinese regional dataset of cloud top temperature in FY-4A atmospheric products was in particular used in this study, which has an enhanced spatial resolution of 4 km and a time resolution of about 10 min. As the preliminary exploration for introducing a machine learning algorithm into GEO satellite-based precipitation remote sensing, CTT was especially employed among the many atmospheric parameters provided by FY-4A [23]. CTT provides the most important information that is in principle related to convection intensity as well as the thermodynamic phase of hydrometeors in clouds. Moreover, CTT is mainly retrieved from infrared measurements that are available both daytime and nighttime. This is very beneficial for generating observational data that cover the life cycle of MCS without any break.
The CMORPH data were used to represent the actual rainrate in the present study. It is a global precipitation dataset that is derived based on passive microwave observations from LEO satellites and infrared observations from GEO satellites [24,25,26,27]. The passive microwave measurements were employed to achieve high-quality precipitation estimation, which was then propagated through motion vectors derived from GEO satellite infrared images at 30 min intervals to form a grid precipitation dataset. A set of precipitation features was modified during the time-gap among the scans of microwave sensors by performing time-weighted linear interpolation. The spatial resolution of CMORPH is approximately 8 km and the time resolution is 30 min. Compared with ground-based rain gauges and radars that cover limited regions, CMORPH provides reliable precipitation data around the world. Such a precipitation dataset is preferred for the concerned region that includes both terrestrial and oceanic components, which is necessary for reasonably training the algorithm. Due to the inconsistent resolutions between FY-4A CTT and CMORPH precipitation, they were matched into the 4 km spatial grids and 15 min temporal intervals by using cubic spline interpolation.
It should be noted that all the existent precipitation products, including CMORPH, have their own limits. In fact, there is no ideal precipitation dataset that could really represent the ground truth for training a machine learning algorithm. Nevertheless, as a reference dataset that is required for such a study, CMORPH is the most suitable one considering the abovementioned factors.
2.2. Identifying and Tracking MCS
As the first step in data processing, the MCS snapshot should be identified in each CTT image, and then the MCS object that is continuously deforming and moving should be tracked and recorded in the successive images. The CTT-based criteria were very useful to actualize such an intention. Maddox, for the first time, proposed the definition of MCC (mesoscale convective complexes) that was based on satellite CTT observations [28]. The subsequent studies focused on MCC and MCS and introduced many practical modifications to refine the identification [29]. In general, MCS was identified by applying the thresholds both on CTT and area. Among others, sufficiently low CTT and large area associated with a contiguous cloudy region were the most remarkable features of MCS. The CTT thresholds suggested in these studies were mostly around 230~240 K. For example, Zheng used 241 K to identify mesoscale-α convective system (MαCS) [30], and Goyens et al. used 233 K to identify MCS in the Sahel [31]. In the present study, a relatively loose threshold of 238 K was adopted. Such a CTT threshold adequately screens out strong convection regions while retaining, as far as possible, the whole domain covered by MCS [32]. Overall, the procedure for identifying potential MCS (pMCS) in a CTT image included 3 steps: (1) for CTT data passing through the preprocessing, select those pixels with CTT below 238 K, (2) identify spatially contiguous pixels as belonging to the same cloud cluster, and (3) discard those with an area smaller than 100 km2.
Given the pMCS identified in individual satellite images that have about 15 min intervals, an appropriate tracking technique was employed to adjoin some of them, which constituted the life cycle of an MCS event. The widely used approaches for tracking MCS were the area overlap (AOL) scheme [32,33] and the maximum spatial correlation scheme [34]. The AOL method is based on the principle that there is little change in the position and area of the considered MCS on successive satellite images. A MCS object thus could be tracked by calculating the rate of overlapping (ROL) for pMCS at adjacent moments. If the ROL exceeds a certain threshold, the 2 pMCS belong to the same MCS object. Compared with the complicated calculation required by the maximum spatial correlation scheme, the AOL is rather simple and adaptable to practical applications. Although, in principle, the AOL may miss small MCSs that move very fast, such a deficiency has little effect due to their few quantities in the total sample. As for the threshold of ROL, a too small value may wrongly regard isolated convective clouds as MCS, while a too large one tends to reduce the life cycle of MCS. A medium ROL threshold of 12% was adopted in this study. For a certain pMCS at T moment (referred to as MT), the tracking procedure was to find out the pMCS at T + 1 moment (referred to as NT+1) that had ROL exceeding 12% with respect to MT. Such a qualified NT+1 was deemed to be the successor of MT and this procedure would be iterated until no successor was found. The mathematical definition of ROL between MT and NT+1 is as follows:
It is noteworthy that the AOL scheme performs well for complicated situations, i.e., several small pMCS merge into a large one (referred to as MCS merging), and a large pMCS splits into a number of small ones (referred to as MCS splitting). According to D. Chen et al. [33], when MCS splitting and/or merging occur, only the largest one would be tracked continuously. The others would be regarded as reaching their final stage or as being the origin of the new MCS. Additional two requirements for a qualified MCS are that the duration exceeds 3 h, and the maximum area during the life cycle is at least 10,000 km2. In the region considered, a total of 241 (255) MCS samples were identified in June (July) 2019, and their average life cycle was about 421 (439) min. A total of 39,544,521 (52,198,474) pixels were included in these MCS samples. Non-rainy pixels accounted for over a half in the total, indicating that even in the MCS domain, there were substantial areas without precipitation. Among the rainy pixels, low rainrate ones (below 5 mm/h) were the majority, and the maximum exceeded 50 mm/h. It is notable that the precipitation field of MCS is highly inhomogeneous.
Given the qualified MCS samples, the purpose of applying machine learning algorithms is to estimate precipitation intensity for every pixel within MCSs in the satellite image. Since the concerned precipitation events are mostly in liquid phase at ground surface, their intensities are all referred to as rainrate in the subsequent text.
2.3. Machine Learning Models
In principle, machine learning represents the big-data-based computations to automatically achieve a special objective. In practice, machine learning needs to be actualized through various concrete algorithm models. As an attempt at introducing machine learning techniques into the particular application of precipitation retrieval, we did not have a preferred model beforehand but tried to evaluate the candidates as much as possible. In this study, 5 kinds of typical models were considered, including polynomial regression, support vector machine, decision tree, random forest, and multilayer perceptron. These widely used models have all been experimentally applied in the meteorological field and produced encouraging results [16,35,36,37,38].
Despite various strategies, these 5 machine learning models all ingest the satellite observations and transform them into features, which are then correlated to rainrate. Note that machine learning can be used to solve 2 kinds of problems: classification problem and regression problem. The unknowns for the classification scheme are discrete values, while those for the regression scheme are continuous values. As for rainrate, which is inherently a continuous variable, the regression scheme is undoubtedly preferred. Yet in some cases, the classification scheme could also be used to estimate rainrate with a certain precision. In particular, it is crucial to discriminate the zero rainrate and those nonzero ones, which belongs to a classification problem. Among the 5 models concerned, polynomial regression is merely applicable for solving regression problems, while the other 4 are competent for both kinds of problems. The major principles of these 5 models are briefly described as follows.
- (a)
- Polynomial Regression
Multiple linear regression is a traditional method that has been heavily used in satellite retrieval of rainrate [39]. The key principle is to estimate rainrate by specifying a series of features as distinct weights that form a linear relationship. Polynomial regression is an extension of multiple linear regression, in which high order terms of some features are also contained in the regression formula [15,40]. As shown in Equation (2), means the weight coefficient while indicates each feature. Since nonlinearity is essential in atmospheric dynamics, the consideration of nonlinear factors could lead to improvement in the retrieval. As expected, the expense of such a nonlinear regression is the huge computational load, but fortunately, it could be alleviated by the scikit-learn.
- (b)
- Support Vector Machine
Support vector machine (SVM) is a powerful machine learning model with a good many applications [15]. In the classification problem, linear SVM works by finding a hyperplane in the predictor space that best separates the two classes [16]. However, most practical datasets cannot be linearly separated into two parts. The kernel tricks, i.e., polynomial kernel and Gaussian radial basis function (RBF) kernel, were thus introduced to gain nonlinear classification capability by transforming the original input into a higher dimensional space. In general, the adoption of a kernel trick does not induce an appreciable increase in computational load. As for the regression problem, SVM is designed to find the hyperplane that can make the sample as close as possible, whether for linear or nonlinear datasets. This approach shows good performance in many applications, including those in weather forecasts [35].
- (c)
- Decision Tree/Random Forest
The decision tree is nominated for its branch-like structure of the decision-making flow [36]. The flow for making a decision is quite intuitional, and every decision is explicable. By arranging a set of determinant criteria, a decision tree could be used to implement fitting for very complicated data. However, the decision tree model is highly susceptible to noisy data, resulting in similar training data possibly generating totally different algorithm models. This deficiency could be overcome by introducing integration models [15]. For regression problems, the integration is actualized by weighted averaging of the classifying result from each independent classifier. For classification problems, the classifying result that has the highest probability is retained as the final result of the integration model. Random forest (RF) is such an integration model that is based on the integration of decision trees. In the random forest model, the training dataset for each decision tree is just a subset of the dataset ensemble, which could restrain the effects from noisy data. In addition, random forest is able to train multiple decision trees, supporting parallel computation. This is very useful for reducing computational time, facilitating its application in many problems within the meteorological field [36,37].
- (d)
- Multilayer Perceptron
Multilayer perceptron (MLP) is a subtype of artificial neural networks that is notable for its layer structure. It has an input layer, some hidden layers, and an output layer [38]. In each layer, there are numerous neural nodes that are independent of each other, and all these nodes are connected to those in the next layer [15]. No matter for the classification problem or the regression problem, initial weights are firstly used to obtain estimation during the training process of MLP. Then, these weights are modified according to the differences between estimated values and true values in order to reduce the biases in the next round. Such processes iterate until the accuracy of estimated values reaches the anticipation. The unique advantage of MLP is its ability to solve complicated nonlinear problems [13], which is especially useful in satellite image identification [38].
2.4. Model Configuration
The pixels in June 2019 were randomly divided into a training set (90%) and a test set (10%). The training set was used to determine the optimal configuration of the full set of parameters for each model, while the test set was used to compare the performance of various models and to help form the optimal algorithm. Note that there is not an explicit validation set (a special dataset retained only for validation), which has been mixed with the training set, and they are jointly called the training set (90% of June 2019) in this study. These data constitute a nominal training set since they all participate in the algorithm development. During the operation of 5-fold cross-validation scheme, at each time of the 5 steps, the part for validation (one fifth of the nominal training set) and the part for training (four fifths of the nominal training set) were distinct. In particular, the pixels in July 2019 were entirely retained as an independent dataset to implement an objective evaluation on the final algorithm established.
The package of scikit-learn was especially employed to actualize these algorithm models [41], and hyperparameter tuning was implemented to achieve the final form of each model that reaches its best performance. This ensures an equitable comparison among them. For each model, the full set of configurations could be determined through two steps: determining the hyperparameter setting and determining the specific parameters. In the first step, the methods called random search and grid search were used to provide possible hyperparameter combinations, and the 5-fold cross-validation scheme was used to evaluate the performance. In the 5-fold cross-validation scheme, the training set was randomly divided into 5 equal parts. Each time, one of them was used for evaluating and the other 4 parts for training. Such a process was repeated 5 times and the mean was regarded as representing the overall performance of a certain hyperparameter combination. The best combination was selected as the optimal hyperparameter setting of a certain model. The optimal hyperparameter setting of the five machine learning models is shown in Table 1. In the second step, all the pixels of the training set were input into the model with the best hyperparameter setting to determine its specific parameters. In this way, the optimal configuration of each model was eventually determined, and these models could be fairly compared given the specific problem of rainrate estimation.

Table 1.
The optimal setting of hyperparameters for the five machine learning models. The hyperparameters of each model are classified into two groups. The one (selected) is the key hyperparameters that highly affect the model performance and need to select the optimal values. The other (default) are those with default or specified values. These models are provided by the scikit-learn package. The meaning and function of these hyperparameters are fully described in the reference [41]. The name of hyperparameters is in the odd-numbered lines, while their values are in the even-numbered lines.
3. Results
3.1. Selected Features
For the machine learning algorithm used to implement rainrate retrieval on a pixel scale, the estimated rainrate was the unique output, while inputs for the algorithm are potentially numerous. Any information that is indicative of some characteristics of a certain pixel should be a candidate of the inputs, and it is conventionally nominated as a feature. These features should be more or less physically correlated to the rainrate at this pixel, which is essentially determined by dynamical and microphysical constraints but without an explicit relationship. On the other hand, the satellite-generated MCS samples were practically composed of CTT snapshots with about 15 min intervals, and the rainrate estimation was fulfilled on each pixel for a certain MCS image. Therefore, for a specified pixel at a certain moment, its available features were actually the temporal and spatial variation characteristics of CTT around this pixel. These CTT-based features were deemed to have implications with dynamics and microphysics in the cloud system and, in turn, with precipitation processes, especially across regions adjacent to the pixel. The machine learning algorithms would employ these features as potential inputs for estimating rainrate.
As shown in Table 2, a total of 31 features have been proposed. Since the evolution of MCS and its associated precipitation are actually driven by a dynamic system, the precipitation characteristics at a certain moment for a specific location are correlated to the physical state at current and previous moments and are relevant to those from the concerned location and from its nearby areas. Taking all these into account, two groups of CTT-based features were designed to contain as much information as possible that is probably effective for indicating the desired rainrate.

Table 2.
Summary of features used by the machine learning algorithms to estimate rainrate for a certain pixel within the MCS domain.
The RL reflects the relative location of a certain pixel in the MCS domain. It was defined as a normalized distance and calculated as the distance between the pixel and the MCS center divided by the squared root of the MCS area. The central position of MCS is calculated as follows.
where, latc and lonc are the latitude and longitude of the central position of MCS, respectively. The lati, loni, and CTTi is the latitude, longitude, and CTT of each pixel in the MCS domain. The parameter C is a constant, and its value is 273 K. Such a calculation gives larger weights to colder pixels, and, therefore, the MCS center would locate in the area with the lowest CTT. The graCTT reflects the alteration of CTT around the pixel, considering the fact that strong convective activities are often accompanied by a dramatic change in the CTT field. CTTm,n is the CTT of the concerned pixel, while CTTm±1,n±1 are the CTT of the pixels around it.
The varCTT was especially designed to isolate anvil clouds in the MCS domain that generally do not produce effective surface rainfall. Anvil clouds have alike low CTT but possess much smaller variances compared with areas of strong convection.
By using the contour lines of selected CTT values, the whole domain of MCS was divided into five subdomains: 238–231 K, 230–221 K, 220–216 K, 215–211 K, and <210 K. The area index was defined as the area of a subdomain divided by the area of the whole domain of MCS. The area index and the corresponding temporal variation were deemed to be related to the evolution of MCS, and then be informative to the rainrate.
For the 31 features, the correlations between each one and the rainrate were investigated, as shown in Figure 1. Note that the correlation coefficient was recorded as Rr.f with its absolute value recorded as |Rr.f|. The maximum |Rr.f| was found to be lower than 0.4, indicating that there was no single feature that is closely related to rainrate. This should be the main reason that traditional statistical schemes cannot give reliable estimation via using satellite CTT data. Among these features, CTT0, difCTT, and CTTi,j (i, j = 1, 2, 3; except i = j = 2) had a relatively large |Rr.f|. Note that it was CTT13, rather than CTT0, that had the maximum |Rr.f|. The effects of bCTT15 and bCTT30 were also considerable, which were negatively correlated with rainrate.
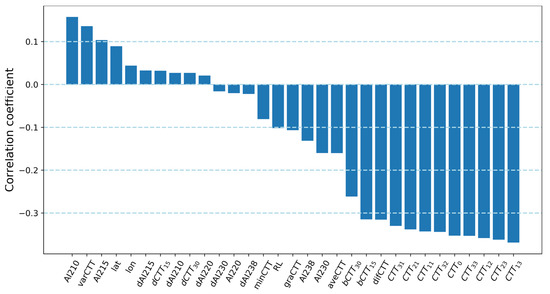
Figure 1.
Correlation coefficients between each of the 31 features and rainrate.
Among these features, CTT0, varCTT, minCTT, and dsize220 were particularly selected to represent those with a strong negative correlation, strong positive correlation, weak correlation, and nearly no correlation, respectively. For each feature of these four, the frequency distribution of rainrate for its varying values within the valid range was calculated, and the results are shown in Figure 2. It is evident that for features with appreciable correlation, the distribution pattern changes to some extent with varying values of the feature, toward an increasing probability of heavy precipitation or weak precipitation. As a contrast, the distribution pattern is almost invariable for the features with nearly no correlation.
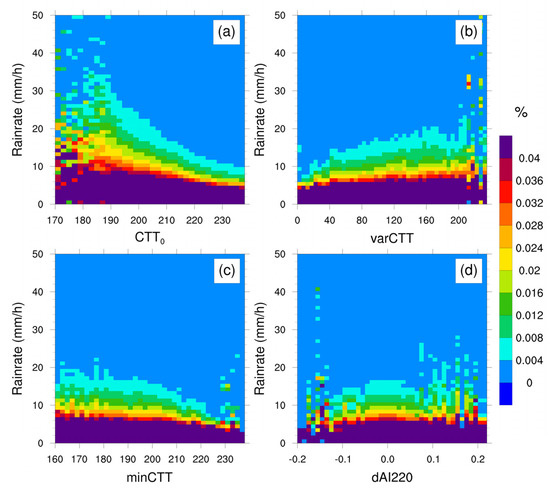
Figure 2.
Frequency distribution of rainrate for varying CTT0 (a), varCTT (b), minCTT (c), and dAI220 (d).
3.2. Comparison among Machine Learning Models
Each machine learning model has its own characteristics, and its applicability to various problems is probably distinct. As for the problem of rainrate estimation in MCS, the performance of these five models was not definite in advance. Thus, given the CTT features available, it is required to determine the model that is able to use these features in an optimal way. Note that the information from the previous statistical analysis is rather limited. Each correlation coefficient merely reflects the apparent relationship between two variables, a certain feature and the rainrate, without excluding possible effects from other features. When these features work together in the algorithm, the larger correlation coefficient of a certain feature by no means ensures its higher contribution to the algorithm improvement. Therefore, regardless of the specific correlation coefficients, all the features were firstly adopted, and the five models were compared by introducing the same configuration of inputs.
By comparing the rainrate estimated from each mode and those from CMORPH that was regarded as the actual value, the performance of each model was examined. Figure 3 shows the comparison as a scatterplot and bias characteristics, with a focus on the overall difference (Bias), correlation coefficient (R), and root mean square error (RMSE). The Bias indicates the average difference between the estimated rainrate and the CMORPH rainrate. The relative bias was calculated by dividing the Bias by the average of the CMORPH rainrate.
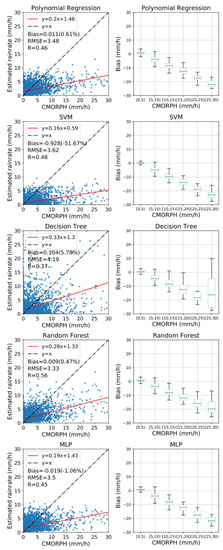
Figure 3.
Scatterplot (left) and boxplot (right) between rainrate from CMORPH and those from the five machine learning models. In the scatterplot, the black dotted line is the diagonal line, while the red solid line is the fitting line of the scattered points. In the boxplot, the box boundary indicates the interquartile, and the inner line means the median. The top and bottom bar are the maximum and minimum.
Among the five models, RF gives the highest consistency of rainrate estimation with respect to the reference, indicated by the minimum Bias, the minimum RMSE as well as the maximum R. According to the detailed bias characteristics shown in the boxplots in Figure 3, the five models have lower biases in estimating weak precipitation. Especially for rainrate less than 5 mm/h, the biases are positive but very small. As rainrate increases, there exist steadily negative biases for these models. Thus for moderate and heavy precipitation, the rainrate tends to be consistently underestimated. Moreover, such an underestimation would be strengthened with increasing rainrate. Overall, RF shows to be the best among these candidates for the specific problem of MCS rainrate estimation and, therefore, is used as the basis in the subsequent algorithm development.
In addition, it was found that there exists a notable difference in the performance between test and training for the RF model. This gap is suspected to be caused by overfitting that is possibly related to the high complexity of the model. Therefore, special work was conducted for this problem, in which the model complexity was adjusted to assess the overall performance (refer to Appendix A). The results show that the gap could only be decreased at the cost of a considerable decline in the accuracy of rainrate estimation. It is thus infeasible to restrain this gap by artificially reducing the model complexity. The hyperparameters derived for the RF model are indeed optimal even if the effect of the gap between test and training is taken into account.
3.3. Contribution of Features to the Algorithm
For a machine learning algorithm, more features used for inputs do not always ensure better performance. This is because the features are extracted from practical observational data, which inevitably have uncertainties. For any feature potentially as an input to an algorithm, it contains information as well as noise that jointly affects the training process. Moreover, possible interactions among features can also have some unknown impacts, which may be negative. Therefore, it is necessary to find out the contribution of each feature and to construct a set of suitable features that acts as the optimal input. Herein, such a particular set of features was called a feature set.
Due to a large number of selected features, it is impractical to analyze the effect of each feature one by one. Considering that Rr.f is the basic index for assessing a single feature, a feature set can be grouped based on the individual Rr.f. The three feature sets examined in this study are shown in Table 3. The performance of the RF model with inputting varying feature sets was thus compared. As shown in Figure 4, among the three feature sets, Feature set 1 provides the best estimation while the feature set proves to be the worst. This contrast suggests that the performance of RF model enhances with increasing features that were selected in this study. Everyone in these 31 features has a definite positive contribution to the algorithm performance, even those features that are weakly correlated with rainrate. Therefore, the full set of 31 features constitute the optimal input for the RF model to estimate rainrate in MCS.

Table 3.
Three feature sets considered in the machine learning algorithm.
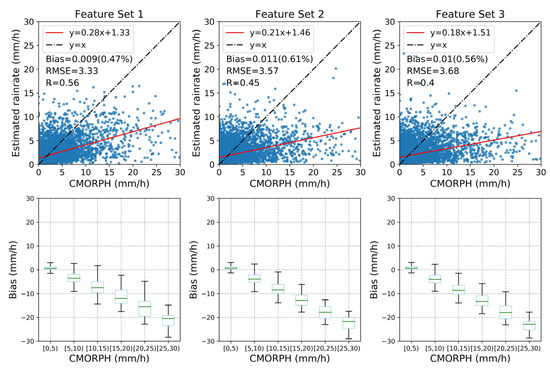
Figure 4.
Scatterplot (upper) and boxplot (bottom) of rainrate from CMORPH and the RF model for Feature set 1 (left), Feature set 2 (middle), and Feature set 3 (right).
In the field of machine learning, the concept of importance is commonly used for quantifying the contribution of a certain feature to the algorithm. As for the decision tree, the most important feature would be selected as the root node in training, while the other features would be used as child nodes occurred at various levels. Therefore, the importance of a feature is readily quantified as the distance between the node of this feature and the root node. RF is virtually composed of many decision trees. Given the same feature, its importance may differ among these decision tree members. Thus the importance of a feature in RF should be evaluated by considering all the decision trees. The Scikit-Learn can provide an absolute value for quantifying the importance of each feature in RF. For comparison, as shown in Figure 5, this absolute value was transformed to a relative value via dividing it by the maxima that are from the most decisive feature, which was referred to as the relative importance for a certain feature.
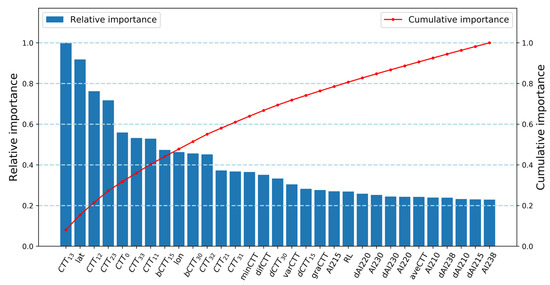
Figure 5.
The relative importance of all the 31 features for the random forest (RF) algorithm. Importance quantifies the contribution of a specific feature to the algorithm. The relative importance is the normalized value with respect to the maximum importance among these features. The cumulative importance is the accumulation of relative importance from the first feature.
In general, the importance of features with large |Rr.f| (such as CTT13, CTT0, and bCTT15) is high, and the importance of features with small |Rr.f| (such as dAI215, dAI210 and AI220) is relatively low. However, there are also many anomalies. For example, the |Rr.f| of lat is less than 0.1, but its importance ranks second among the 31 features. On the contrary, the |Rr.f| of difCTT exceeds 0.3, but its importance is just medium in all these features. Such a comparison on the relative importance indicates that for a certain feature, its |Rr.f| does not necessarily determine its importance in the algorithm. It is the features with quite high importance that dominate the performance of an algorithm. In the case herein, it is revealed that the features that are based on the area of MCS have a rather small contribution to the algorithm. The geographic location of the current pixel and the absolute CTT of this and nearby pixels provide the majority of effective information for rainrate estimation by the RF model, and their cumulative importance is about 50%. Particularly, the high importance of geographic location is probably due to the heterogeneity of the MCS precipitation field. Without appointing a definite geographic location, the rainrate estimation would be declined to some extent.
3.4. RF-Based Hybrid Algorithm
Given the optimal configuration of inner parameters and external inputs, the RF algorithm was proved to perform well in rainrate estimation with the default scheme, i.e., the regression scheme. Furthermore, the classification scheme of RF was taken into account to examine the feasibility of further improving the algorithm. In order to fairly compare the two schemes, regression and classification, the samples were divided into 10 groups according to the rainrate value as defined in Table 4. Since the output of RF-Classification is a group number, its accuracy could be directly evaluated. For the rainrate value retrieved from RF-Regression, it was firstly converted to a group number and then could also be evaluated in this manner.

Table 4.
The 10 groups of samples used in RF-Classification.
As shown in Table 4, the rainrate intervals were specially specified to ensure that the samples in every group were roughly comparable, except for the one of zero rainrate. Note that nearly half of the samples were non-rainy pixels. This fact suggests that there are naturally two categories with comparable samples, zero and non-zero rainrate. It is reasonable to use RF-Classification to solve such a binary classification task. In addition, by excluding such a large number of non-rainy pixels in advance, the efficiency of the training process for rainrate estimation would be enhanced. Therefore, an RF-based hybrid algorithm that combines the classification and regression schemes of the RF model was also examined, referred to as RF-Combine, which was compared with RF-Classification and RF-Regression. In practice, the RF-Combine algorithm has two steps. The status of a pixel, precipitating or not, is firstly determined by using the classification algorithm. Then for the precipitating pixel, its rainrate is estimated by using the regression algorithm.
Based on the 10 groups of rainrate, the confusion matrices were employed to evaluate the performance of each algorithm. As shown in Figure 6, the percentage signed in each box indicates the probability that the algorithm generates a certain rainrate for a given true value labeled on the abscissa. Correspondingly, the sum of percentage values in each column is 1, and the values in the diagonal line mean the percentage of right estimation. Note that compared with RF-Regression and RF-Classification, the RF-Combine algorithm with relatively concentrated estimation is notably better. Its percentage of right estimation raises at every group, and the bias range narrows to a large extent. For example, about 80% of the zero rainrate can be accurately estimated, which is markedly higher than that of RF-Regression or RF-Classification. According to these confusion matrices, the RF-Combine algorithm possesses the strongest feasibility in practical cases of rainrate estimation.
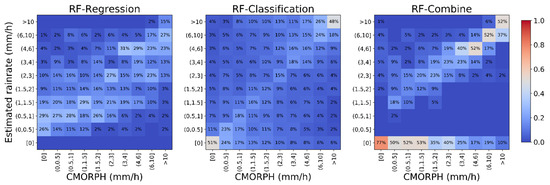
Figure 6.
Confusion matrices of RF-Regression (left), RF-Classification (middle) and RF-Combine (right). The percentage value in each grid means the probability that the algorithm generates a certain estimation for a given true value. The sum of the percentage values in each column is 1.
It is apparent that the grouping of rainrate actually degrades the precision of estimation, which artificially elevates the accuracy. In order to assess the quality of rainrate estimation on higher accuracy, the rainrate values from RF-Regression and RF-Combine, without grouping, were directly compared with CMOPRH rainrate as scatterplots and were shown in Figure 7. The contrast between RF-Regression and RF-Combine is similar to the group-based comparison. Due to the errors in the classification of rainy and non-rainy events, the Bias of the RF-Combine algorithm is slightly higher than that of the RF-Regression algorithm. However, the RF-Combine algorithm becomes much better than the RF-Regression algorithm, with the R increasing from 0.56 to 0.73, and RMSE decreasing from 3.33 to 2.75, respectively. By invoking the classification scheme to specially identify the rainy pixel in advance, the quality of the estimated rainrate by the RF model has been substantially enhanced. Given the practical problem of rainrate retrieval in MCS, such a combination of classification and regression schemes was proved to be beneficial for improving the performance of RF.
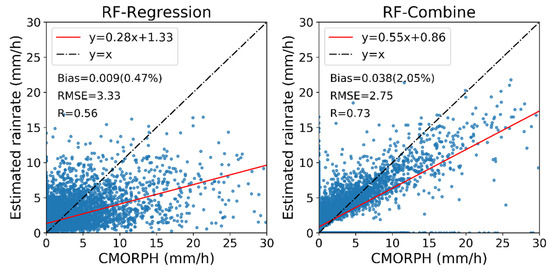
Figure 7.
Scatterplot of rainrate from CMORPH versus those from RF-Regression (left) and RF-Combine (right).
Moreover, three MCS snapshots with ample rainy pixels were selected as the representative cases to verify the capability of the three algorithms (RF-Classification, RF-Regression, and RF-Combine) in actual situations. Correspondingly the comparison on grouped rainrate was adopted. Meanwhile, the operational product of quantitative precipitation estimation (QPE) from FY-4A was also involved in the comparison. According to the 10 groups of rainrate, the spatial distributions are shown in Figure 8 for these datasets. Compared with the CMOPRH, the general patterns of the three cases are roughly captured by all these data, with several cores of maximum precipitation approximately in the right position. However, the detailed discrepancies in the distribution are also notable, which eventually determine the overall accuracy of these rainrate data. Table 5 provides the accuracy of these data for each of the three cases. Herein, the accuracy is defined as the percentage of retrievals that are in the right group according to CMORPH. For such a group-based comparison, the RF-Regression algorithm appears to be the worst, and the RF-Classification algorithm is just comparable with the FY-4A QPE. The RF-Combine algorithm shows to be the best one among the three RF algorithms and is also much better than the FY-4A QPE. Even in two cases, the accuracy of rainrate from RF-Combine exceeds 60%, representing a rather high consistency. This once again suggests that it is the combination of classification and regression schemes that largely improve the performance of RF in rainrate estimation, which results in the superiority of the RF algorithm against the FY-4A QPE.
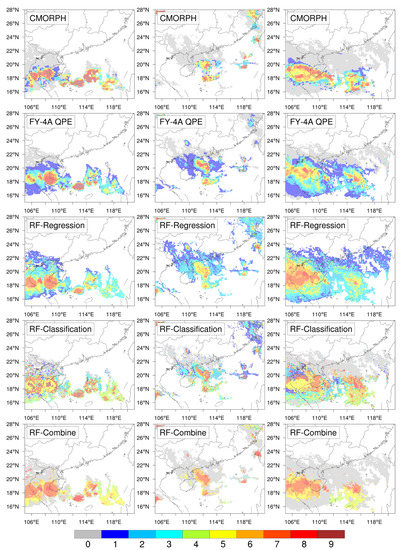
Figure 8.
Rainrate from CMORPH (1st row), FY-4A QPE (2nd row), RF-Regression (3th row), RF-Classification (4th row), and RF-Combine (5th row) for three arbitrary MCS snapshots, 9 June 2019 20:45 (left), 11 June 2019 13:15 (middle), and 23 June 2019 1:00 (right), respectively. The rainrate value was converted to the group number according to the criteria as shown in Table 4.

Table 5.
Accuracy of rainrate from FY-4A QPE (Quantitative Precipitation Estimation), RF-Regression, RF-Classification, and RF-Combine (unit: %) for the three cases in Figure 8. The accuracy is defined as the percentage of retrievals that fall into the right group according to CMORPH.
In the previous analysis, evaluations were mostly based on the test set, which has been randomly selected and accounts for 10% of the MCS samples in June 2019. Although there is no overlapping between the test set and training set, they are extracted from the same month. The potential similarity between these two parts of samples may elevate to some extent the performance of the RF algorithm. In order to ascertain the applicability of the RF-Combine algorithm in the more universal cases, samples in July 2019 that are completely independent of the training samples were especially used to implement a strict evaluation. As shown in Figure 9, for ensuring equitable comparison with the results from the test set, the randomly selected 10% of the samples in July 2019 were used to fulfill the verification. As expected, the performance of the RF-Combine algorithm for samples in July declines evidently, with the correlation coefficient down to below 0.5 and RMSE up to above 3.0, implying that there exist appreciable differences in the MCS samples between these two successive months. It is suggested that even for a given region, much more MCS samples should be taken into account to train a more general machine learning algorithm, which is likely to maintain the high performance in the independent data. The relevant works for further improving the RF-Combine algorithm would be carried out in the future. It is noteworthy that even in July, the quality of the estimated rainrate from the RF-Combine algorithm is definitely better than the FY-4A QPE. Such a result is particularly promising since the RF-Combine algorithm is just a preliminary attempt of introducing machine learning into satellite rainrate retrieval, and there is much space for progress in this way.
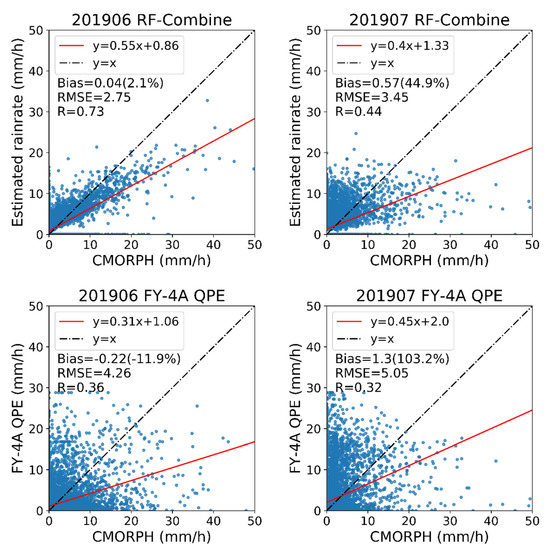
Figure 9.
Scatterplot of rainrate from RF-Combine (upper) and FY-4A QPE (bottom) versus those from CMORPH rainrate in June (left) and July (right) 2019.
4. Summary
Geostationary meteorological satellites provide the most suitable platform for monitoring global precipitation. Benefiting from the high-frequency sampling, nowadays in the order of 10 min, as well as the vast field of view, it is particularly useful for the real-time retrieval of precipitation that is generated by the fast-moving systems in the atmosphere. MCS is the most representative one among these vigorous systems that often produce heavy rainfall. However, the observable parameters from geostationary satellites are inherently limited. Most of them are merely cloud top properties, which do not have a direct physical connection with surface rainfall. This forms the primary difficulty for retrieving precipitation intensity via using geostationary satellite measurements, regardless of the elaborate usage of semi-empirical relationships. Traditional retrieval algorithms are thus incompetent for reliable precipitation retrieval in the MCS domain.
Due to the unique advantage in dealing with complicated problems, especially those with nonlinear kernels, machine learning techniques have been extensively applied in numerous fields for solving various practical problems. It was introduced in this study to implement the rainrate estimation within MCS, and five kinds of machine learning models were considered, including polynomial regression, support vector machine, decision tree, random forest (RF), and multilayer perceptron. Focusing on the abundant MCS activities during summer over South China, one month (June 2019) of FY-4A CTT was used to develop an algorithm based on machine learning, whereas the CMORPH precipitation was used as the reference data. Such an algorithm is expected to be applicable to MCSs in South China.
Based on the CTT that is approximately continuous in both temporal and spatial dimensions, a total of 31 features were designed to act as potential inputs for the algorithm operation. Although the physical connection of a specific feature with the concerned rainrate is not clear, the features as a whole are implicitly related to dynamical and microphysical processes, and in turn, related to the precipitation status at a certain moment for a given location. A reasonable estimation of rainrate is, therefore, expected as these features were adequately digested by the machine learning algorithm through intensive internal calculations.
Given the full set of 31 features, RF was proved to be the best one among the 5 kinds of models. The estimated rainrate from RF has the highest consistency with respect to the CMORPH rainrate. In order to clarify the contribution of individual features to the algorithm performance, three feature sets, each as a subset of the full set by using certain thresholds, were investigated to act as inputs for the RF operation. It was proved that the ensemble of 31 features was the optimal selection, and all of them positively contributed to the algorithm.
Considering the inherent difficulty of the regression algorithm to discriminate rainy and non-rainy pixels that are quantitatively comparable in MCS, an RF-based hybrid algorithm that combines the classification and regression schemes of RF were established. It distinguishes in advance whether the pixel is rainy or not by using the classification scheme while estimating rainrate for those rainy ones by using the regression scheme. Such a combination shows notable improvement compared to either a classification or a regression scheme. This combination also leads to the superiority of the RF algorithm compared with the FY-4A QPE. Based on the samples in July 2019 that are completely independent of training, the evaluation confirms that the accuracy of rainrate from the RF-Combine algorithm is higher than that of the FY-4A QPE.
It is apparent that such an algorithm derived from training is heavily dependent on the training dataset. Although CMORPH performs reasonably well and has been proved to be the most suitable reference dataset for this study, it has inherent defects, which would inevitably affect the present machine learning algorithm. For instance, CMORPH has an evident false alarm rate and tends to overestimate weak precipitation. These are likely to be inherited by the present algorithm. However, it should be pointed out that the objective of this study is to propose an algorithm framework for retrieving rainrate in MCS, rather than to establish an operational precipitation algorithm. It is in the current stage and for the specific region that CMORPH appears to be suitable, but it could be replaced as long as a new precipitation dataset that has much higher quality becomes available. In other words, the framework is meaningful, but the algorithm details could be updated as the reference dataset is updated.
The machine learning-based precipitation retrieval algorithm proposed in this study is just elementary. Such a prototype algorithm undoubtedly needs to be further improved in the future by introducing more MCS samples, adding more observable parameters, taking into account more effective features, and designing a more sophisticated algorithm structure. However, the most important is that it demonstrates a new way of applying machine learning techniques to circumvent classical problems in precipitation remote sensing. In particular, it provides a feasible approach to make full use of the measurements from geostationary meteorological satellites, which were inhibited to some extent in the previous usage due to inadequate information extraction. Machine learning techniques, as an efficient method for processing complicated information, is expected to play a vital role in improving the precipitation retrieval that relies on the high-spatiotemporal resolution observations from geostationary satellite platforms.
Author Contributions
Q.L. proposed the idea. P.L. collected data and made the analysis. P.L. and Q.L. wrote the manuscript. Y.D., Y.W., Y.L. and M.L. helped the data preparation and participated in discussions on the results. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key Research and Development Program of China (Grant 2018YFC1507401), the National Natural Science Foundation of China (41875030, 42075075), and the Fundamental Research Funds for the Central Universities.
Acknowledgments
We would like to thank China Meteorological Administration for sharing FY-4A datasets and Climate Prediction Center for sharing CMORPH data. Thanks are also given to Aurélien Géron for his book “Hands-on Machine Learning with Scikit-Learn and TensorFlow”.
Conflicts of Interest
The authors declare they have no conflict of interest.
Appendix A
As shown in Figure A1, there exists a notable difference in the performance between training and test for the RF model where the RMSE in the test set is much larger than that in the training set. This gap is suspected to be caused by overfitting that is possibly related to high model complexity. By artificially reducing the complexity to restrain this gap, the overall performance of the RF model was analyzed as follows.
Herein, the RMSE in the test set (referred to as TRMSE) represents the model performance, while the RMSE difference between training and test (referred to as DRMSE) represents the performance gap between them. It should be noted that because the hyperparameters derived from the training process are the optimal values that correspond to the minimal TRMSE, adjusting the hyperparameters to change the complexity would inevitably lead to increasing TRMSE and, in turn, the decline of model performance. Considering that the performance is the most important index for assessing a machine learning algorithm, for any artificial adjustment of model complexity, the notable increase in TRMSE is denied. The adjustment is acceptable only when it brings a significant decrease in DRMSE associated with a mild increase in TRMSE. According to this principle, the ratio of weight between TRMSE and DRMSE was designated as 9:1 to jointly determine the optimal hyperparameters. That is, compared with the hyperparameters derived merely according to RMSE, when the decrease rate of DRMSE is more than nine times the increase rate of TRMSE, the impact of DRMSE cannot be neglected and the hyperparameters should be modified to ensure the optimum by taking into account both TRMSE and DRMSE.
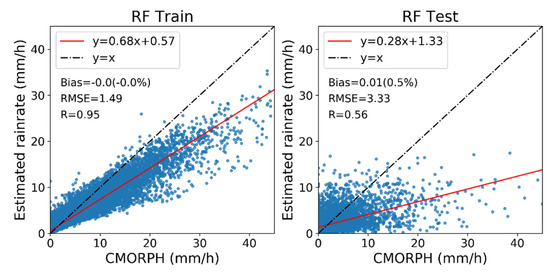
Figure A1.
Scatterplot of rainrate from CMORPH versus those from the RF model in the training set (left) and in the test set (right).
For the RF model, five hyperparameters have a significant impact on the model complexity and they are n_estimators, max_depth, max_features, min_samples_leaf, and min_samples_split. Among these five hyperparameters, the decrease of n_estimators, max_depth, and max_features, or the increase of min_samples_leaf and min_samples_split, leads to the reduction of model complexity. Meanwhile, these hyperparameters are nearly independent of each other, thus they could individually analyze the impact of each of them on the model by adjusting a single hyperparameter at a time. The changes of TRMSE and DRMSE with the model complexity are shown in Figure A2, for each of the five hyperparameters. In order to quantify the change rate of TRMSE and DRMSE, the slope of a straight line that fits the curve near the optimal value was used. The ka represents the slope for rising complexity, while kb represents the slope for reducing complexity. Note that nearly all ka are negative, meaning that both TRMSE and DRMSE increase with rising complexity. This suggests that with rising complexity, the overall performance always declines, which is undesired. For reducing complexity, kb of TRMSE for all the five hyperparameters are positive, and kb of DRMSE are negative for four hyperparameters. The hyperparameter of n_estimators is the only exception, which has a positive kb. Thus for n_estimators, its value has been optimal, whether or not the impact of DRMSE was taken into account. For the other four hyperparameters, as expected, with reducing model complexity, TRMSE increases, and meanwhile DRMSE decreases. Detailed comparisons for the change rate of TRMSE and DRMSE are thus required.
Considering that the performance is the most important index for assessing a machine learning algorithm, a ratio of 9:1 between TRMSE and DRMSE, kb′ was used to represent the weighted slope, as shown in Table A1. Simply, kb′ of TRMSE was defined as nine times kb, while kb′ of DRMSE just equals to kb. In this way, kb′ could be directly compared between TRMSE and DRMSE. If the absolute value of kb′ of DRMSE is larger (smaller) than that of TRMSE, reducing the complexity has a positive (negative) impact. The results in Table A1 show that, for the four hyperparameters that have positive kb and negative kb, for TRMSE and DRMSE, respectively, the absolute value of kb′ of DRMSE keeps consistently smaller than that of TRMSE. It proved that the DRMSE could only be decreased at the cost of considerable increase of TRMSE. Therefore, it is infeasible to restrain the gap between test and training by artificially reducing the model complexity. This result confirms that the hyperparameters derived in this study are indeed optimal, even if the effect of the gap between test and training is taken into account.

Table A1.
The original slope (kb) of the five hyperparameters in Figure A2 and the weighted slope (kb′). According to the ratio of weight between TRMSE and DRMSE, 9:1, kb′ of TRMSE was nine times kb, while kb′ of DRMSE equals to kb.
Table A1.
The original slope (kb) of the five hyperparameters in Figure A2 and the weighted slope (kb′). According to the ratio of weight between TRMSE and DRMSE, 9:1, kb′ of TRMSE was nine times kb, while kb′ of DRMSE equals to kb.
| Order of Magnitude | Original Slope (kb) | Weighted Slope (kb′) | |||
|---|---|---|---|---|---|
| TRMSE | DRMSE | TRMSE | DRMSE | ||
| N_estimators | 10−6 | 2.16 | 1.97 | n/a | n/a |
| Max_depth | 10−3 | 0.32 | −2.38 | 2.88 | −2.38 |
| Max_features | 10−3 | 1.75 | −7.71 | 15.75 | −7.71 |
| Min_samples_leaf | 10−2 | 5.15 | −14.1 | 46.35 | −14.1 |
| Min_samples_split | 10−4 | 1.21 | −4.11 | 10.89 | −4.11 |
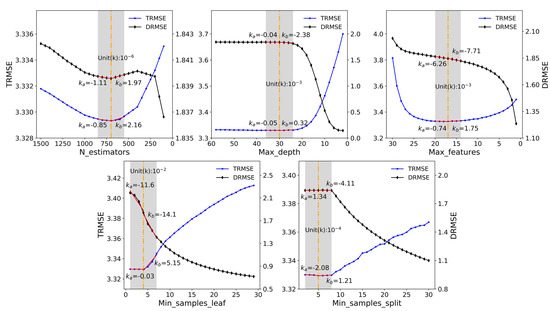
Figure A2.
The response of TRMSE (the RMSE in the test set) and DRMSE (the RMSE difference between the test set and the training set) with varying value for each of the five hyperparameters for the RF model. For all five panels, the complexity consistently reduces from left to right with the varying value of a hyperparameter. The orange dotted line represents the optimal value of a hyperparameter determined uniquely by RMSE. The shadow area is a fitting region centered on the optimal value and its width is 1/5 of the scope of abscissa, in which the curves are fitted by the straight lines. The red solid line is the fitting line. The ka is the slope of fitting line with rising complexity, while the kb is the slope with reducing complexity.
References
- Adachi, A.; Kobayashi, T.; Yamauchi, H.; Onogi, S. Detection of potentially hazardous convective clouds with a dual-polarized C-band radar. Atmos. Meas. Tech. 2013, 6, 2741–2760. [Google Scholar] [CrossRef]
- Houze, R.A. Mesoscale convective systems. Rev. Geophys. 2004, 42. [Google Scholar] [CrossRef]
- Houze, R.A. Cloud cluster and large-scale vertical motions in the trpics. J. Meteorol. Soc. Jpn. 1982, 60, 396–410. [Google Scholar] [CrossRef]
- Luo, Y.L.; Gong, Y.; Zhang, D.L. Initiation and Organizational Modes of an Extreme-Rain-Producing Mesoscale Convective System along a Mei-Yu Front in East China. Mon. Weather Rev. 2014, 142, 203–221. [Google Scholar] [CrossRef]
- Luo, Y.L.; Li, L.Y.; Johnson, R.H.; Chang, C.P.; Chen, L.S.; Wong, W.K.; Chen, J.; Furtado, K.; McBride, J.L.; Tyagi, A.; et al. Science and prediction of monsoon heavy rainfall. Sci. Bull. 2019, 64, 1557–1561. [Google Scholar] [CrossRef]
- Klein, C.; Belušić, D.; Taylor, C.M. Wavelet Scale Analysis of Mesoscale Convective Systems for Detecting Deep Convection from Infrared Imagery. J. Geophys. Res. Atmos. 2018, 123, 3035–3050. [Google Scholar] [CrossRef]
- Migliorini, S.; Dixon, M.; Bannister, R.; Ballard, S. Ensemble prediction for nowcasting with a convection-permitting model-I: Description of the system and the impact of radar-derived surface precipitation rates. Tellus Ser. A-Dyn. Meteorol. Oceanol. 2011, 63, 468–496. [Google Scholar] [CrossRef][Green Version]
- Zeng, Q.L.; Wang, Y.Q.; Chen, L.F.; Wang, Z.F.; Zhu, H.; Li, B. Inter-Comparison and Evaluation of Remote Sensing Precipitation Products over China from 2005 to 2013. Remote Sens. 2018, 10, 168. [Google Scholar] [CrossRef]
- Liu, Q. On the scale estimation using truncated swath measurements from low Earth orbiting satellites. J. Geophys Res. Atmos. 2013, 118, 4816–4833. [Google Scholar] [CrossRef]
- Mishra, A.K.; Rafiq, M. Rainfall estimation techniques over India and adjoining oceanic regions. Curr. Sci. 2019, 116, 56–68. [Google Scholar] [CrossRef]
- Kidd, C.; Bauer, P.; Turk, J.; Huffman, G.J.; Joyce, R.; Hsu, K.L.; Braithwaite, D. Intercomparison of High-Resolution Precipitation Products over Northwest Europe. J. Hydrometeorol. 2012, 13, 67–83. [Google Scholar] [CrossRef]
- El-Alfy, E.M.; Mohammed, S.A. A review of machine learning for big data analytics: Bibliometric approach. Technol. Anal. Strateg. Manag. 2020, 32, 984–1005. [Google Scholar] [CrossRef]
- Petković, V.; Orescanin, M.; Kirstetter, P.; Kummerow, C.; Ferraro, R. Enhancing PMW Satellite Precipitation Estimation: Detecting Convective Class. J. Atmos. Ocean. Technol. 2019, 36, 2349–2363. [Google Scholar] [CrossRef]
- Chen, B.-F.; Chen, B.; Lin, H.-T.; Elsberry, R.L. Estimating Tropical Cyclone Intensity by Satellite Imagery Utilizing Convolutional Neural Networks. Weather Forecast. 2019, 34, 447–465. [Google Scholar] [CrossRef]
- Zhang, T.; Lin, W.Y.; Lin, Y.L.; Zhang, M.H.; Yu, H.Y.; Cao, K.; Xue, W. Prediction of Tropical Cyclone Genesis from Mesoscale Convective Systems Using Machine Learning. Weather Forecast. 2019, 34, 1035–1049. [Google Scholar] [CrossRef]
- Jergensen, G.E.; McGovern, A.; Lagerquist, R.; Smith, T. Classifying Convective Storms Using Machine Learning. Weather Forecast. 2020, 35, 537–559. [Google Scholar] [CrossRef]
- Hsu, K.; Tao, Y.; Ihler, A.; Gao, X.; Sorooshian, S. A Two-Stage Deep Neural Network Framework for Precipitation Estimation from Bispectral Satellite Information. J. Hydrometeorol. 2018, 19, 393–408. [Google Scholar] [CrossRef]
- Szunyogh, I.; Arcomano, T.; Pathak, J.; Wikner, A.; Hunt, B.; Ott, E. A Machine Learning-Based Global Atmospheric Forecast Model. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Hirose, H.; Shige, S.; Yamamoto, M.K.; Higuchi, A. High Temporal Rainfall Estimations from Himawari-8 Multiband Observations Using the Random-Forest Machine-Learning Method. J. Meteorol. Soc. Jpn. 2019, 97, 689–710. [Google Scholar] [CrossRef]
- Yang, X.R.; Fei, J.F.; Huang, X.G.; Cheng, X.P.; Carvalho, L.M.V.; He, H.R. Characteristics of Mesoscale Convective Systems over China and Its Vicinity Using Geostationary Satellite FY2. J. Clim. 2015, 28, 4890–4907. [Google Scholar] [CrossRef]
- Zhang, L.; Min, J.Z.; Zhuang, X.R.; Schumacher, R.S. General Features of Extreme Rainfall Events Produced by MCSs over East China during 2016-17. Mon. Weather Rev. 2019, 147, 2693–2714. [Google Scholar] [CrossRef]
- Min, M.; Wu, C.; Li, C.; Liu, H.; Xu, N.; Wu, X.; Chen, L.; Wang, F.; Sun, F.; Qin, D.; et al. Developing the science product algorithm testbed for Chinese next-generation geostationary meteorological satellites: Fengyun-4 series. J. Meteorol. Res. 2017, 31, 708–719. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.Q.; Wei, C.Y.; Lu, F.; Guo, Q. Introducing the new generation of Chinese geostationary weather satellites, FENGYUN-4, Bull. Amer. Meteor. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R.J. Evaluation of the High-Resolution CMORPH Satellite Rainfall Product Using Dense Rain Gauge Observations and Radar-Based Estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Rao, T.N.; Saikranthi, K.; Rao, M.P. Comprehensive evaluation of multisatellite precipitation estimates over India using gridded rainfall data. J. Geophys. Res. Atmos. 2015, 120, 8987–9005. [Google Scholar] [CrossRef]
- Xu, S.; Niu, Z.; Shen, Y.; Kuang, D. A Research into the Character of CMORPH Remote Sensing Precipitation Error in China. Remote Sens. Technol. Appl. 2015, 29, 189–194. [Google Scholar] [CrossRef]
- Maddox, R.A. Mesoscale convective complexes. B Am. Meteorol. Soc. 1980, 61, 1374–1387. [Google Scholar] [CrossRef]
- Laing, A.G.; Carbone, R.; Levizzani, V.; Tuttle, J. The propagation and diurnal cycles of deep convection in northern tropical Africa. Q. J. Roy. Meteor. Soc. 2008, 134, 93–109. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Chen, J.; Zhu, P.J. Climatological distribution and diurnal variation of mesoscale convective systems over China and its vicinity during summer. Chin. Sci. Bull. 2008, 53, 1574–1586. [Google Scholar] [CrossRef]
- Goyens, C.; Lauwaet, D.; Schroder, M.; Demuzere, M.; Van Lipzig, N.P.M. Tracking mesoscale convective systems in the Sahel: Relation between cloud parameters and precipitation. Int. J. Climatol. 2012, 32, 1921–1934. [Google Scholar] [CrossRef]
- Ai, Y.; Li, W.; Meng, Z.; Li, J. Life Cycle Characteristics of MCSs in Middle East China Tracked by Geostationary Satellite and Precipitation Estimates. Mon. Weather Rev. 2016, 144, 2517–2530. [Google Scholar] [CrossRef]
- Chen, D.; Guo, J.; Yao, D.; Lin, Y.; Zhao, C.; Min, M.; Xu, H.; Liu, L.; Huang, X.; Chen, T.; et al. Mesoscale Convective Systems in the Asian Monsoon Region from Advanced Himawari Imager: Algorithms and Preliminary Results. J. Geophys. Res. Atmos. 2019, 124, 2210–2234. [Google Scholar] [CrossRef]
- Carvalho, L.M.V.; Jones, C. A satellite method to identify structural properties of mesoscale convective systems based on the maximum spatial correlation tracking technique (MASCOTTE). J. Appl. Meteorol. 2001, 40, 1683–1701. [Google Scholar] [CrossRef]
- Radhika, Y.; Shashi, M. Atmospheric Temperature Prediction using Support Vector Machines. Int. J. Comput. Theory Eng. 2009, 1, 55–58. [Google Scholar] [CrossRef]
- Haberlie, A.M.; Ashley, W.S. A Method for Identifying Midlatitude Mesoscale Convective Systems in Radar Mosaics. Part I: Segmentation and Classification. J. Appl. Meteorol. Climatol. 2018, 57, 1575–1598. [Google Scholar] [CrossRef]
- Ko, B.C.; Kim, H.H.; Nam, J.Y. Classification of Potential Water Bodies Using Landsat 8 OLI and a Combination of Two Boosted Random Forest Classifiers. Sensors 2015, 15, 13763–13777. [Google Scholar] [CrossRef] [PubMed]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates with Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Martin, D.W.; Howland, M.R. Grid history—A geostaionary satellite technique for estimating daily rainfall in the tropics. J. Clim. Appl. Meteorol. 1986, 25, 184–195. [Google Scholar] [CrossRef]
- Liao, B.; Zhang, T.; Yu, J.; Guo, B.; Li, M.; Liu, Y. QPR-NN: A New Recommendation Algorithm Combining Quadric Polynomial Regression and Neural Network. J. Xi’an Jiaotong Univ. 2019, 53, 79–87, 136. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).