Abstract
Strong geometric and radiometric distortions often exist in optical wide-baseline stereo images, and some local regions can include surface discontinuities and occlusions. Digital photogrammetry and computer vision researchers have focused on automatic matching for such images. Deep convolutional neural networks, which can express high-level features and their correlation, have received increasing attention for the task of wide-baseline image matching, and learning-based methods have the potential to surpass methods based on handcrafted features. Therefore, we focus on the dynamic study of wide-baseline image matching and review the main approaches of learning-based feature detection, description, and end-to-end image matching. Moreover, we summarize the current representative research using stepwise inspection and dissection. We present the results of comprehensive experiments on actual wide-baseline stereo images, which we use to contrast and discuss the advantages and disadvantages of several state-of-the-art deep-learning algorithms. Finally, we conclude with a description of the state-of-the-art methods and forecast developing trends with unresolved challenges, providing a guide for future work.
1. Introduction
Wide-baseline image matching is the process of automatically extracting corresponding features from stereo images with substantial changes in viewpoint. It is the key technology for reconstructing realistic three-dimensional (3D) models [1,2,3] based on two-dimensional (2D) images [4,5,6]. Wide-baseline stereo images provide rich spectral, real texture, shape, and context information for detailed 3D reconstruction. Moreover, they have advantages with respect to spatial geometric configuration and 3D reconstruction accuracy [7]. However, because of the significant change in image viewpoint, there are complex distortions and missing content between corresponding objects in regard to scale, azimuth, surface brightness, and neighborhood information, which make image matching very challenging [8]. Hence, many scholars in the fields of digital photogrammetry and computer vision have intensely explored the deep-rooted perception mechanism [9] for wide-baseline images, and have successively proposed many classic image-matching algorithms [10].
Based on the recognition mechanism, existing wide-baseline image-matching methods can be divided into two categories [11,12,13]: Handcrafted matching and deep-learning matching. Inspired by professional knowledge and intuitive experience, several researchers have proposed handcrafted matching methods that can be implemented by intuitive computational models and their empirical parameters according to the image-matching task [14,15,16,17,18].This category of methods is also referred to as traditional matching, the classical representative of which is the scale invariant feature transform (SIFT) algorithm [14].Traditional matching has many problems [15,16,17,18] such as repetition in wide-baseline image feature extraction or the reliability of the feature descriptors and matching measures. Using multi-level convolutional neural network (CNN) architecture, learning-based methods perform iterative optimization by back-propagation and model parameter learning from a large amount of annotated matching data to develop the trained image-matching CNN model [19]. A representative deep-learning model under this category can be chosen, such as MatchNet [20]. Methods under this category offer a different approach to solving the problem of wide-baseline image matching, but they are currently limited by the number and scope of training samples, and it is difficult to learn the optimal model parameters that are suitable for practical applications [21,22,23,24,25]. Learning-based image matching is essentially a method that is driven by prior knowledge. In contrast to the traditional handcrafted methods, it can avoid the need for many manual interventions with respect to feature detection [26], feature description [27], model design [28], and network parameter assignment [29]. Moreover, it can adaptively learn the deep representation and correlation of the topographic features directly from large-scale sample data. According to the scheme used for model training, the wide-baseline matching methods can be further divided into two types [30]: Multi-stage training with (1) step-by-step [31] and (2) end-to-end training [32]. The former focuses on the concrete issues of each stage, such as feature detection, neighborhood direction estimation, and descriptor construction, and it can be freely integrated with handcrafted methods [33]; whereas the latter considers the multiple stages of feature extraction, description, and matching as a whole and achieves the global optimum by jointly training with various matching stages [34]. In recent years, with the growth of training datasets and the introduction of transfer learning [35], deep-learning-based image matching has been able to perform most wide-baseline image-matching tasks [36], and its performance can, in some cases, surpass that of traditional handcrafted algorithms. However, the existing methods still need to be further studied in terms of network structure [37], loss function [38], matching metric [39], and generalization ability [40], especially for typical image-matching problems such as large viewpoint changes [41], surface discontinuities [42], terrain occlusion [43], shadows [44], and repetitive patterns [45,46,47].
On the basis of a review of the image-matching process, we incrementally organize, analyze, and summarize the characteristics of proposed methods in the existing research, including the essence of the methods as well as their advantages and disadvantages. Then, the classical deep-learning models are trained and tested on numerous public datasets and wide-baseline stereo images. Furthermore, we compare and evaluate the state-of-the-art methods and determine their unsolved challenges. Finally, possible future trends in the key techniques are discussed. We hope that research into wide-baseline image matching will be stimulated by the review work of this article.
The main contributions of this article are summarized as follows. First, we conduct a complete review for the learning-based matching methods, from the feature detection to end-to-end matching, which involves the essences, merits, and defects of each method for wide-baseline images. Second, we construct various combined methods to evaluate the representative modules fairly and uniformly by using numerous qualitative and quantitative tests. Third, we reveal the root cause for struggling to produce high-quality matches across wide-baseline stereo images and present some feasible solutions for the future work.
In Section 2, this article reviews the most popular learning-based matching methods, including the feature detection, feature description, and end-to-end strategies. The results and discussion are presented in Section 3. The following summary and outlook are given in Section 4. Finally, Section 5 draws the conclusions of this article.
2. Deep-Learning Image-Matching Methodologies
At present, the research on deep-learning methods for wide-baseline image matching mainly focuses on three topics: Feature detection, feature description, and end-to-end matching (see Figure 1). Therefore, this section provides a review and summary of the related work in these research topics below.
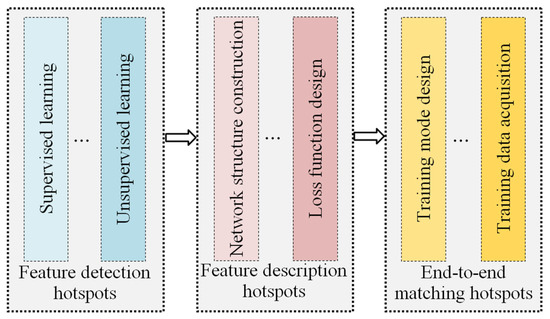
Figure 1.
Focus of this review: Topics of deep-learning methods for wide-baseline stereo image matching.
2.1. Deep-Learning-Based Feature Detection
Figure 2 summarizes the progress in deep-learning feature-detection methods. Based on the implemented learning mode, the mainstream deep-learning feature-detection algorithms can be divided into two types: Supervised learning [48] and unsupervised learning [49]. Supervised learning feature detection takes the feature points extracted by traditional methods as “anchor points”, and then trains a regression neural network to predict the location of more feature points; whereas the unsupervised learning strategy uses a neural network directly to train the candidate points and their response-values, and then takes the candidate points at the top or bottom of the ranking as the final feature points.
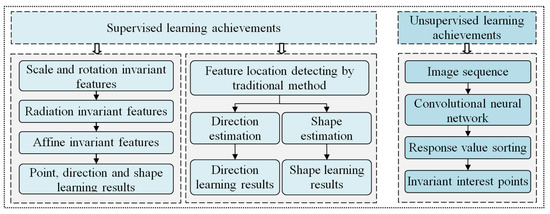
Figure 2.
Development of feature detection with deep learning.
The basis of wide-baseline image matching is the extraction of local invariant features, which are local features that remains table between the stereo images under geometric or radiometric distortions, such as viewpoint change or illumination variation. In recent years, researchers have focused on exploring feature detection schemes for deep learning with enhancing network [50]. Using the supervised learning strategy as an example, Lenc et al. first proposed a local invariant feature loss function [51].
where is F-norm, x is the image block to be processed, g is the random geometric transformation, gx is the random transformation result of x, is the transformation matrix output by the neural network, and q is the complementary residual transformation of g. On this basis, this algorithm employs the Siamese neural network DetNet to learn the invariant feature geometric transformations. Moreover, it uses image control points as anchor points and treats potential feature points as certain transformation forms of these anchor points. In the training phase, the images with anchor points are input to the regression neural network, and the optimal transformation is learned iteratively. Then, the weights of the regression neural network are adjusted according to the loss function and finally interpolated to obtain more feature positions, directions, and shapes. This method created a precedent for deep-learning invariant feature detection, and the detected features are equipped with good scale and rotation invariance.
Zhang et al. [52] used the illumination-invariant feature TILDE [30] of deep learning as an anchor point, which solved the problem of image matching under strong illumination changes; on this basis, Doiphode et al. [53] used a triple network [54] and introduced an affine invariant constraint to learn stable and reliable affine invariant features. The above methods give the target features a certain geometric and radiation invariance, but the geometric relationship between the image blocks must be roughly known before training the model; this invisibly increases the workload of the training dataset production.
Yi et al. [55] further studied the Edge Foci (EF) [56] and SIFT [14] features to detect the location of key points and learned the neighborhood direction of features based on a CNN; Mishkin et al. [57] used a multi-scale Hessian to detect the initial feature points and estimate the affine invariant region based on the triplet network AffNet. This method combines traditional feature extraction algorithms with deep-learning invariant features, which substantially improves the efficiency and reliability of feature detection.
In addition to the above-mentioned features for supervised learning, Savinov et al. [58] also proposed a classic feature-learning strategy with unsupervised idea. This method transforms the learning problem of feature detection into a learning problem of response-value sorting of image interest points. The response function of the image point is denoted by , where p represents the image point, and H and w represent the CNN to be trained and the weight vector of the network, respectively. The image point response-value sorting model is then expressed as follows:
where represents one scene target in the image and is located on ; and are the indexes of , and ; and are generated respectively by transformation of and . Therefore, all points on target are sorted according to the response-value function and Equation (2), and the image points with the response-values in the top or bottom ranks are retained as feature points. The key purpose of this method is to learn the invariant response function of the image point using the neural network. The feature points maintain good invariance to the perspective transformation of the images; additional experiments in Reference [58] demonstrate that the proposed method may outperform the Difference of Gaussian (DoG) strategy [14] regarding feature repeatability for view-change images. However, the existing methods still have many shortcomings with respect to feature point detection repeatability and stability for wide-baseline images with large view changes.
As mentioned above, the most learning-based methods for feature detection are categorized as supervised learning achievements. Such mainstream methods can handily surpass the unsupervised strategies in invariant feature learning because the supervised methods may directly and separately produce the geometric covariant frames for wide-baseline images, while the unsupervised methods need to simultaneously cope with the locations of interest points and their invariance during learning process.
2.2. Deep-Learning Feature Description
Deep-learning feature description [59] has been widely applied in professional tasks [60] such as image retrieval, 3D reconstruction, face recognition, interest point detection, and target positioning and tracking. Specific research on this topic mainly focuses on network structure construction and loss function design, as shown in Figure 3. Among them, the network structure of deep learning directly determines the discrimination and reliability of the feature descriptors, while the loss function affects the training performance of the model by controlling the iterative update frequency of the model parameters and optimizing the quantity and quality of the sample input.
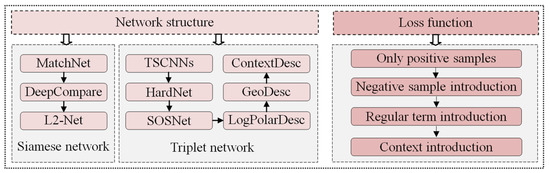
Figure 3.
Development of deep-learning feature description.
The key to high-quality feature description is to consider both similarity and discrimination. “Similarity” refers to the ability of corresponding feature descriptors to maintain good invariance to signal noise, geometric distortion, and radiation distortion, thereby retaining a high degree of similarity. In contrast, “discrimination” refers to the idea that there should be a large difference between any non-matching feature descriptors. To generate high-quality descriptors, the learning-based method departs from the paradigm of traditional algorithms and builds Siamese network or triplet network, which emulates the cognitive structure of human visual nerves. The Siamese network, also known as the dual-channel network, is a coupled architecture based on a binary branch network, whereas the triple network has one more branch than the Siamese network, and thus it can be adapted to a scenario in which three samples are input simultaneously.
Figure 4 shows the evolution of several typical feature-description networks. Among them, a representative approach is MatchNet [20], which uses the original Siamese network and is composed of two main parts: A feature coding network and a similarity measurement network. The two branches of the feature network maintain dynamic weight sharing and extract the feature patches from stereo images through a convolution layer [58], a maximum pooling layer [61], and other layers. Furthermore, it calculates the similarity between image blocks though a series connecting to the top fully connected network [62], and then determines the matching blocks based on the similarity score. Subsequently, Zagoruyko et al. [63] further explored the role of the central-surround two-stream network (CSTSNet) [64] and the spatial pyramid pooling net (SPPNet) [65] in the feature description. CSTSNet combines a low-resolution surround stream with a high-resolution center stream, which not only use the multi-resolution information of the image, but also emphasize the information of the center pixels, thus substantially improving the matching performance. In contrast, SPPNet inherits the good characteristics of the Siamese network, then it enhances the adaption to image block data of different sizes by introducing a spatial pyramid pooling layer. To apply SPPNetto the description of features in satellite images, Fan et al. [66] designed a dual-channel description network based on a spatial-scale convolutional layer to improve the accuracy of satellite image matching.
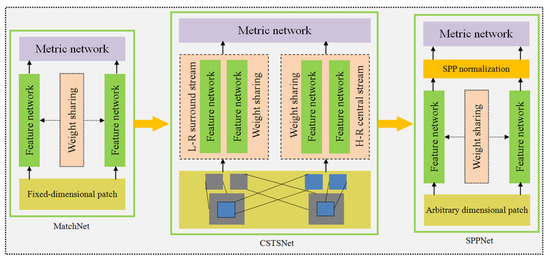
Figure 4.
Evolution of representativefeature description networks.
These descriptor measurement networks belong to the fully connected category of networks, which consume a large amount of computing resources during training and testing, and hence have low matching efficiency. To address this, Tian et al. proposed a feature description model called L2-Net [67] with a full convolutional network representation. This method inherits the idea of SIFT descriptors, namely, it adjusts the dimension of network output to 128 and uses the L2 norm measure of Euclidean distance instead of a metric network to evaluate the similarity of the feature descriptors. The basic structure of the L2-Net network is shown in Figure 5. This network consists of seven convolutional layers and a local response normalization layer (LRN). In the figure, the term “3 × 3 Conv” in the convolutional layer refers to convolution, batch normalization, and linear activation operations in the series, and “8 × 8 Conv” represents the convolution and batch normalization processing operations. Moreover, “32” represents a 32-dimensional convolution with a step size of 1 and “64/2” refers to a 64-dimensional convolution operation with a step size of 2. The final output layer LRN is used to generate unit descriptor vectors while accelerating network convergence and enhancing model generalization.
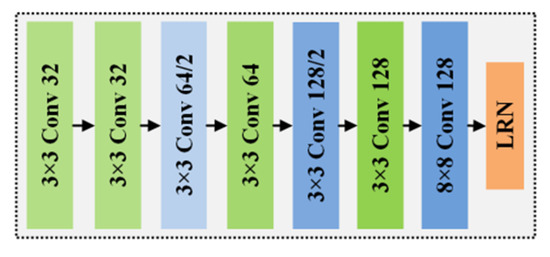
Figure 5.
Basic architecture of L2-Net.
The results on the open-source dataset Brown [68], Oxford [10], and HPatches [69] training and testing datasets show that L2-Net has good generalization ability, and its performance is better than the existing traditional descriptors. Moreover, L2-Net performs well with respect to image feature classification as well as wide-baseline stereo image feature description and matching, and thus many researchers regard it as a classic feature description network and have extended it with improvements in network structure. Balntas et al. [34] found that one disadvantage of L2-Net is that it ignores the contribution of negative samples to the loss function value. Hence, they proposed the triplets and shallow CNN (TSCNN). This method simplifies the L2-Net network layer and the number of channels, then incorporates negative samples into the network training, and hence that the modified model can reduce the distance between matching feature descriptors while increasing the distance between non-matching feature descriptors. However, the negative samples are input into TSCNNs using random sampling strategy, and as a result, most negative samples do not sufficiently contribute to the model training, which limits the improvements in descriptor discrimination. In view of this, HardNet [70] incorporates the most difficult negative sample, namely the nearest non-matching descriptor, into the training of the model, which substantially enhances the training efficiency and matching performance. The triplet margin loss (TML) function used by this model is as follows:
where m is the batch size, is the Euclidean distance between two descriptors, and are an arbitrary pair of matching descriptors, and and represent the closest non-matching descriptors to and , respectively.
On the basis of the L2-Net network structure, the HardNet descriptor model employs the nearest neighbor negative sample sampling strategy and the TML loss function, which is another important advance in the descriptor network model. Inspired by HardNet, some notable deep-learning models for feature description have been further explored. For example, LogPolarDesc [71] uses a polar transform network to extract corresponding image blocks with higher similarity to improve the quality and efficiency of model training; SOSNet [72] introduces the second-order similarity regularization into the loss function to prevent over-fitting of the model and substantially improve the utilization of the descriptors. To generate a descriptor with both global and local geometric invariance, some researchers have proposed making full use of the geometry or the visual context information of an image. The representative approach GeoDesc [73] employs cosine similarity to measure the matching degree of descriptors. It also sets self-adaptive distance thresholds to handle different training image blocks and then introduces a geometric loss function to enhance the geometric invariance of the descriptor, which is expressed by the following equation:
where represents the adaptive threshold; represents the cosine similarity between corresponding features descriptors; and represents the similarity of the correspondingimage blocks. On this basis, ContextDesc [74] integrates geometry and visual context perception into the process of network model construction, thus improving the utilization of image geometry and visual context information. Finally, many data tests show that the ContextDesc adapts well to the geometric and radiation distortions of different scenes.
In short, feature description plays a vital role in image matching, as the high-quality descriptor can absorb the local and global information from the feature neighborhoods, which may provide adequate knowledge for recognizing the unique feature from extensive false candidates. Based on the aforementioned, the triple networks can perform better than the Siamese or sole model, because multi-branch networks can be efficient in learning the uniqueness of features and make full use of context information.
2.3. Deep-Learning End-to-End Matching
The end-to-end matching strategy integrates three different stages of image feature extraction, description, and matching into one system for training, which is beneficial for learning the globally optimal model parameters, and adaptively improves the performance of each stage [75]. Figure 6 summarizes the development of end-to-end deep-learning matching. Most end-to-end methods focus on the design of training modes and the automatic acquisition of training data [76]. The design of training modes is intended to obtain high-quality image features and descriptors in a more concise and efficient way; the aim of automatic acquisition of data is to achieve fully automatic training by means of a classical feature detection algorithm and spatial multi-scale sampling strategy.
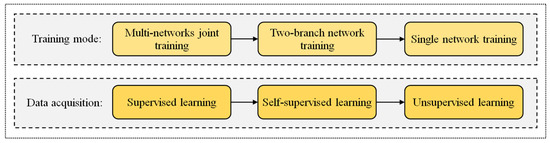
Figure 6.
Development of end-to-end matching with learning-based methods.
Yi et al. proposed the learned invariant feature transform (LIFT) network structure [77]. This network first integrates feature detection, direction estimation, and feature description into one pipeline based on the Transformer (ST) [78] and softargmax algorithm [79]. The end-to-end training is carried out by back propagation. The complete training and testing process of this method is shown in Figure 7.
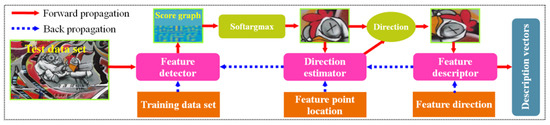
Figure 7.
Training and testing of the LIFT pipeline.
The back propagation-based training process of LIFT can be briefly described as follows. First, the feature location and principal direction can be extracted using the structure from motion (SFM) algorithm [80], and then the feature descriptor is trained. Second, guided by the feature descriptor, the direction estimator is trained based on the feature location and its neighborhood ST. Finally, the feature descriptor and direction estimator are united to train the feature detector based on the training dataset. After the LIFT has been trained, the corresponding test process proceeds as follows. First, the feature score map of a multi-scale image is obtained based on the feature detector. Second, scale-space non-maximum suppression is performed using the softargmax function and then the scale invariant feature region is extracted. Finally, the feature region is further normalized and then the description vectors are extracted by the feature descriptor.
Although LIFT belongs to the category of end-to-end network models, a back propagation-based multi-stage training mode is adopted in the network training, which reduces the training efficiency and practicality of the model; additionally, LIFT employs an SFM strategy and random spatial transformation to provide matching image blocks for training, which limits the discrimination of descriptors. In view of this, DeTone et al. [81] proposed a self-supervised network model called MagicPoint instead of SFM to label training data. They then use the SuperPoint model to learn feature points and extract their descriptors for end-to-end training.
SuperPoint realizes the joint training of feature detection and description through the encoding structure [82] and decoding structure [83]. The encoding structure is used for image feature extraction, whereas the decoding structure can not only output the position of the feature point, but also output the descriptor vector. Similarly, Revaud et al. [84] proposed the Siamese decoding structure R2D2, which focuses more on the repetitive and discriminative expression of training features than SuperPoint.
The learning-based method of MagicPoint can replace the handcrafted labeling of feature points, but a small amount of handcrafted labeling data is still required when obtaining the pre-trained model. Ono et al. [85] proposed LF-Net, which is an end-to-end model that uses unsupervised training. This method directly uses the stereo images obtained by a metric camera, an image depth map, the camera position, and orientation data, and other prior information to complete the end-to-end model training, which greatly reduces the need for manual intervention and promotes the automated process of deep-learning matching. In addition, Dusmanu et al. proposed a combination of feature detection and descriptor extraction that can make more effective use of high-level semantic information. They then proposed a simplified end-to-end model D2Net [86]. The difference between this model and the traditional model is depicted in Figure 8. Figure 8a shows the traditional “detect-then-describe” model, that is, SuperPoint [81], which is a representative model of this type, and Figure 8b shows the D2Net “describe-and-detect” model. In contrast to a Siamese or multi-branch network structure [87], D2Net adopts a single-branch network architecture, and the feature location and descriptor information of the image are stored in high-dimensional feature channels, which is thus more conducive to obtaining stable and efficient matches. However, D2Net must extract dense descriptors in the process of using high-level semantic information, which reduces the accuracy and efficiency of feature detection.
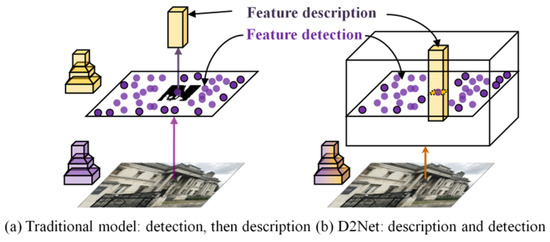
Figure 8.
Difference between D2Net and the traditional model.
All in all, the end-to-end strategy is prone to train the optimal parameters for image matching. Multi-networks with complex architecture need to input more training samples than a single network. Considering the available scale of training data [76], the self-supervised learning mode is the best choice for current practical applications.
3. Results and Discussion
3.1. Representative Algorithms and Experimental Data
To evaluate the performance, advantages, and disadvantages of deep-learning stereo matching algorithms, we selected a total five categories of 10 well-performed algorithms for the experiments, including deep-learning end-to-end matching, deep-learning feature detection and description, deep-learning feature detection and handcrafted feature description, handcrafted feature detection and deep-learning feature description, and handcrafted image matching, as shown in Table 1. In addition, the key source code of each algorithm can be obtained from the corresponding link in this table. The above methods were selected due to the following reasons. First, as the representatives of deep-learning end-to-end matching, SuperPoint [81] and D2Net [86] were published recently, and they have been widely applied [88,89,90] in the fields of photogrammetry and computer vision. Second, the deep-learning feature detectors AffNet [57] andDetNet [51], deep-learning feature descriptors HardNet [70], SOSNet [72], and ContextDesc [74], were all proposed for wide-baseline image matching, and were often used as benchmarks [12]. Third, the classical handcrafted methods are used here to verify the strength of deep-learning methods. Finally, all selected methods are effective and well-performed in previous reports, and the source codes are open to public.

Table 1.
Representative algorithms and their references.
The datasets used to train each deep-learning algorithm are as follows: SuperPoint using MSCOCO [91]; D2Net using MegaDepth [92]; AffNet using UBC Phototour [68]; both HardNet and SOSNet using HPatches [69]; ContextDesc using GL3D [93]; DetNet using DTU-Robots [94]. According to their corresponding literatures [68,69,91,92,93,94], the characters of each dataset would be discussed and summarized as follows. MSCOCO was proposed with the goal of advancing the state-of-the-art in scene understanding and object detection. In contrast to the popular datasets, MSCOCO involves fewer common object categories but more instances per category, which would be useful for learning complex scenes. MegaDepth was created to exploit multi-view internet images and produce a large amount of training data by the SFM method. It performs well for challenging environments such as offices and close-ups, but MegaDepth is biased towards outdoor scenes. UBC Phototour initially proposed patch verification as an evaluation protocol. There is large number of patches available in this dataset, which is particularity suited for deep-learning-based detectors. The images in this dataset have notable variations in illumination and view changes, but most of these images only focus on three scenes: Liberty, Notre-Dame, and Yosemite. HPatches presented a new large-scale dataset special for training local descriptors, aiming to eliminate the ambiguities and inconsistencies in scene understanding. It has the superiorities of diverse scenes and notable viewpoint changes. GL3D designed a large-scale database for 3D surface reconstruction and geometry-related learning issues. This dataset covered many different scenes, including rural area, urban, and scenic spots taken from multiple scales and viewpoints. The DTU-Robots dataset involves real images of 3D scenes, shot using a robotic arm in rigorous laboratory conditions, which is suitable for certain application but of limited size and variety in the data.
The representative wide-baseline test data are presented in Figure 9, and the corresponding data descriptions are listed in Table 2. Algorithms ①, ②, and ⑩ can directly output the corresponding features, and for the descriptors output by algorithms ③–⑨, we adopt the nearest-neighbor and second nearest-neighbor distance ratio to obtain the matches. Finally, each algorithm employs the random sample consensus (RANSAC) strategy to eliminate outliers. The performance of the algorithms is objectively evaluated according to the number of matching points, matching accuracy, and matching spatial distribution indexes.

Figure 9.
(a–m) Wide-baseline test data. These data are carefully selected from different platforms of ground close-range, UAV, and satellite, respectively. They cover various terrains and have significant viewpoint changes.

Table 2.
Description of the wide-baseline test data.
3.2. Experimental Results
For the 13 sets of wide-baseline stereo images and 10 representative algorithms, the results are as follows: Table 3 presents the number of image matches obtained by each algorithm, and the bold number is the maximum number of matches in each group of test data; Figure 10 shows the matching errors of each algorithm, where the matching error is estimated by the following equations [95]:
where N is the number of matches, and are an arbitrary pair of matching point coordinates, and H and F are the known true perspective transformation matrix and true fundamental matrix, respectively. The matching errors of test data (a)–(f),which consist of planar or approximately planar scenes, are evaluated by εH (pixel), and the matching errors of test data (g)–(m), which consist of non-planar scenes, are evaluated by εF (pixel). Figure 11 shows the image-matching results of each algorithm. Because of the limited space, this figure only exhibits the matching results of algorithms ①, ③, ④, ⑤, and ⑩ based on test data (a), (f), (g), (i), (j), and (m), where the matching points are indicated by red dots and joined by yellow lines, and the most matches in each row of the figure are marked by a green frame. For each algorithm, Figure 12 shows the matching distribution quality Dis, which is estimated by the following equation [96]:
where n represents the total number of Delaunay triangles generated by the matching points, denotes the area of the i-th triangle, represents the radian value of the maximum internal angle, and represents the average area of the triangle. The value of Dis can reveal the consistency and uniformity of the spatial distribution of the triangle network, and a smaller Dis value indicates that the matches have a higher spatial distribution quality.

Table 3.
The contrast of ten algorithms in the aspect of number of matches. Bold font denotes the best results.
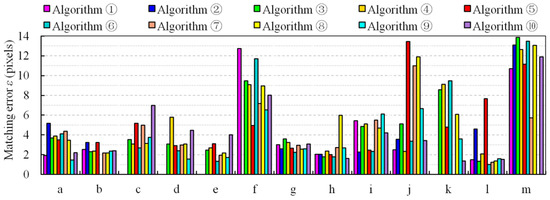
Figure 10.
Comparison of the matching error results of the ten algorithms.
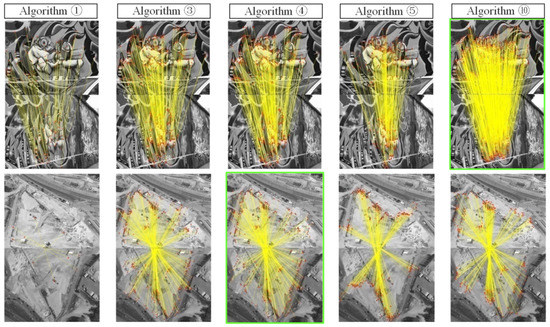

Figure 11.
Matching results of algorithms ①, ③, ④, ⑤, and ⑩ on test data (a), (f), (g), (i), (j), and (m).
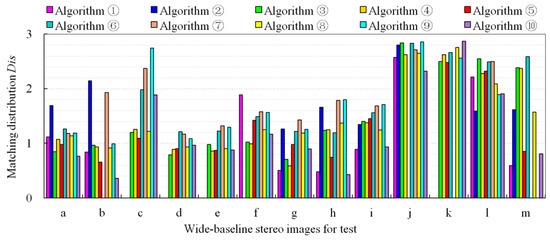
Figure 12.
Comparison of the matching distribution quality of the ten algorithms.
3.3. Analysis and Discussion
First, we discuss the test results of compared methods as a whole. The results in Table 3 and Figure 11 and Figure 12 show that no single algorithm always obtains the best performance on stereo images with different platform types, different viewpoint changes, and various texture structures. As a typical representative of handcrafted algorithms, ASIFT can achieve affine invariant stereo matching through a multi-level sampling strategy in 3D space; however, compared with the deep-learning algorithms, the test results of ASIFT show that its advantageis in the number of matches in close-range images with planar scene or satellite images. In contrast, the deep-learning algorithms DetNet + Contexdesc, AffNet + SOSNet, and SuperPointcan perform better on close-range stereo images with large rotations and scale changes, low-altitude stereo images with approximately planar scenes, and high-altitude stereo images with complex 3D scenes. This is because handcrafted algorithms tend to adopt the global spatial geometry rectification or a single segmentation model, which is more suitable for simple stereo images with planar scenes; whereas deep-learning algorithms build deep convolutional layers or fully connected neural network models from the perspective of emulating human visual cognition, and they iteratively learn the optimal network model parameters based on a large number of training samples, which can theoretically approximate any complex geometric or radiometric transform model, and hence this type of algorithm is more suitable for matching wide-baseline images with complex scenes. For test data (a), (b), (h), and (j), ASIFT yields better matching distribution quality; the algorithms DetNet + Contexdesc and AffNet + HardNet respectively perform well on data (c) and (d) with respect to matching distribution, whereas SuperPoint performs well on data (g) and (m) with respect to matching distribution. All compared algorithms consistently achieve poor matching distribution quality for data (c), (j), (k), and (l). This is mainly because the traditional problems of digital photogrammetry, such as large-scale deformation of images, lack of texture, terrain occlusion, and surface discontinuity, are still difficult for the available algorithms to handle. On this topic, we suggest that handcrafted algorithms may expand the search range of geometric transform parameters to enhance adaptability to large-scale deformation data, whereas deep-learning algorithms may also improve the matching compatibility of complex terrain by increasing the number of samples in such areas.
Second, we discuss the CNN architectures combining the used training datasets. Deep-learning wide-baseline image matching is mainly limited by the structure of the neural network model and the size of the training dataset. Table 3 and Figure 11 show that the SuperPoint algorithm can obtain the most matches from the complex 3D scene (data (g)–(j) and (m)) for UAV oblique stereo images (data (d)–(i), (j), and (k)) or satellite wide-baseline images (data (l) and (m)), but it almost fails on simple ground scenes (data (d)–(f)). Although the MSCOCO training dataset used by SuperPoint contains large-scale independent structural objects, it lacks ground scene annotation instances with a single texture, and hence this training dataset limits the matching performance of SuperPoint on the ground scenes. The AffNet+SOSNet algorithm can obtain a sufficient number of matches from wide-baseline images (data (d)–(f)) with ground scenes and poor texture, where the spatial distribution of the matches is relatively uniform, as presented in Figure 11 and Figure 12. The reason is that the UBC Phototour and HPatches datasets cover a large number of homogeneous structures such as ground, wall, and sculpture structures, which enables the algorithm to enhance its perception of some scenes with a single texture. A comparison of the matching results of algorithms 3 and 4 shows that, even with the same training dataset, the feature description performance of SOSNet is substantially better than that of HardNet. Reviewing the structures of the two networks shows that on the basis of the HardNet, SOSNet embeds a second-order similarity regularization term in the loss function to avoid over-fitting problems in the model training and further improve the similarity and discrimination of the descriptors. The ContextDesc algorithm integrates visual and geometric context encoding structures into the network model to improve the use of image context information. The test results show that it is particularly suitable for image matching in scenes with cluttered background (data (c)) or large radiometric distortion (data (e)).
Third, we further discuss the strengths and weaknesses of integrating methods for the difficult test data. Although algorithms ③, ④, and ⑦ all adopt AffNet to extract affine invariant features, the test results of algorithms ③ and ④ are substantially better. We speculate the reason is that the deep-learning descriptors of algorithms ③ and ④ perform better than the handcrafted descriptor SIFT of algorithm 7. Figure 10 shows that the matching of both the deep learning and handcrafted algorithms is not able to achieve sub-pixel accuracy. The main reason is that the two stages of feature detection and feature matching are relatively independent, which makes it difficult for the corresponding points to be accurately aligned. The complete UAV dataset, which is larger in size and resolution (data (j) and (k)) was also used for testing. It should theoretically be beneficial for each algorithm to obtain more matches; however, Table 3 shows that the number of matches did not increase substantially as a result. We believe that a high resolution will exacerbate the lack of local texture in the image, and larger images tend to introduce more occluded regions. Specifically, data (j) contain more occluded scenes and homogenous textures, whereas data (k) involve a large area of water and scenes with viewpoint changes. Additionally, the ratio of the corresponding regions in the larger images is lower. Thus, it would become more difficult to obtain the corresponding features in the absence of prior knowledge or initial matches. For satellite wide-baseline images with various mountainous and urban areas, both the deep-learning approach SuperPoint and the handcrafted ASIFT method can obtain a significant number of matches.
4. Summary and Outlook
For wide-baseline image-matching problems, this paper systematically organized, analyzed, and summarized the existing deep-learning image invariant feature detection, description, and end-to-end matching models. In addition, the matching performances of the representative algorithms were evaluated and compared through comprehensive experiments on wide-baseline images. According to the above test results and discussion, future research and challenges can be summarized as follows.
(1) The current deep-learning invariant feature detection approach continues to reveal its potential, and the research on invariant features and their applications has increasingly developed, from the scale invariant feature learning of Reference [52] to the affine invariant feature training of Reference [53]. Experiments have shown that learning-based methods have better potential than handcrafted detection algorithms such as DoG [14] and pixel watershed [17]. In addition, the strategy of combining handcrafted methods with learning-based methods [55] to extract invariant features has become a good option, but this type of method obviously depends on the accurate extraction of the image features by the handcrafted algorithms. In short, although the feature detection methods based on deep learning tend to show abilities beyond the traditional methods, this approach is not yet fully mature, especially for the matching problem of wide-baseline images with complex scenes and various textures, and it still faces great challenges. Therefore, extracting invariant features with high repeatability and stability needs further study.
(2) Deep-learning feature description is essentially metric learning; this kind of method is mainly focused on network model construction and loss function design. From the MatchNet Siamese network [20] to the SOSNet triplet structure [72], the model parameters are gradually simplified, and the performance is correspondingly improved. However, most network backbones still inherit the structure of the classic L2-Net [67]. Especially for the affine invariant feature description network structure, we suggest introducing a viewpoint transform module, which could enhance the transparency, perception, and generalization capabilities of existing models for wide-baseline images. Moreover, the loss function design is mainly used to select reasonable training samples. Although the existing functions focus on traditional problems such as the selection of positive and negative samples, they do not consider the inherent characteristics of wide-baseline images. Therefore, to improve the performance of the descriptors, future work could involve the construction of novel wide-baseline network structures or the design of universal loss functions.
(3) Recently, end-to-end learning-based methods such as back propagation-trained LIFT [77] and feature description-and-detection D2Net [86] have received increasing attention. This type of method has led to numerous innovations in terms of training mode and the automatic acquisition of training data. The research shows that the end-to-end method has a faster computation speed than other learning-based methods and can meet the performance requirements for simultaneous localization and mapping (SLAM) [68], SFM [80], and other real-time vision tasks. However, for wide-baseline image-matching tasks, it is difficult for this type of method to extract sufficient feature points. Therefore, in the field of wide-baseline image matching, we should further explore the end-to-end learning of unconventional and complex distortions as well as the image features of various textures and structures.
(4) Image matching based on deep learning is a data-driven image-matching method that must automatically learn the deep expression mechanism of ground surface features from a large amount of image data. Therefore, the key for deep-learning image matching is to build a diverse and massive training dataset. At present, the main training datasets for deep-learning wide-baseline image matching are UBC Phototour [68] and HPatches [69]. The UBC Phototour dataset contains a large number of artificial statues, whereas the HPatches dataset mainly consists of simple facade configurations. These available training datasets are very different from the data captured by aerial photography or satellite remote sensing, which stop the affine invariant network models, such as AffNet [57], HardNet [70], and SOSNet [72], from achieving the optimal matches in wide-baseline remote sensing images. Therefore, it is an urgent task to establish a large wide-baseline dataset of multi-source, multi-platform, and multi-spectrum data through crowd sourcing or sharing mechanisms.
(5) The existing studies have shown that the comprehensive performance of a model can be substantially improved through transfer learning, which has been widely applied in the fields of target recognition, image classification, and change detection. However, there are few published reports on transfer learning in the field of deep-learning wide-baseline image matching, specifically for feature detection, feature description, and end-to-end methods. Therefore, on the basis of establishing a wide-baseline image dataset, further work should focus on training a network for wide-baseline matching using a transfer learning strategy to achieve high-quality matching for wide-baseline images. In addition, for the original observation of matching points, the positioning errors must be fully considered in the field of digital photogrammetry. However, the corresponding points across wide-baseline images cannot be registered precisely by learning-based methods. Hence, the matching accuracy could be improved by some optimization strategies, such as least-squares image matching or the Newton iteration method, which remains as future work.
5. Conclusions
In this paper, based on a review of the image-matching stages, we organized and summarized the development status and trends of existing learning-based methods. Moreover, the matching performance, advantages, and disadvantages of typical algorithms were evaluated through comprehensive experiments on the representative wide-baseline images. The results reveal that there is no algorithm that can adapt to all types of wide-baseline images with various viewpoint changes and texture structures. Therefore, the currently urgent task is to enhance the generalization ability of the models by combining a mixed model with more extensive training datasets. Moreover, it was suggested that a critical task is to construct deep network models with elastic receptive field and self-adaptive loss functions based on wide-baseline imaging properties and typical problems in image matching. It is our hope that the review work of this paper will act as a reference for future research.
Author Contributions
Conceptualization, A.Y. and G.Y.; data curation, L.Z. and G.Y.; validation, G.Y. and F.M.; writing—original draft preparation, G.Y.; writing—review and editing, A.Y.; supervision, A.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China with Project No. 41601489, the Shandong Provincial Natural Science Foundation with Project No. ZR2015DQ007, the Postgraduate Education and Teaching Reform Foundation of Shandong Province with Project No. SDYJG19115, and the Open Fund of Key Laboratory of Geographic Information Science (Ministry of Education, East China Normal University) with Project No. KLGIS2021A02.
Acknowledgments
The authors would like to thank Karel Lenc, Dmytro Mishkin, and Daniel DeTonefor providing their key algorithms. We are very grateful also for the valuable comments and contributions of anonymous reviewers and members of the editorial team.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, M.; Gao, H.; Jia, W. Stable image matching for 3D reconstruction in outdoor. Int. J. Circuit Theory Appl. 2021, 49, 2274–2289. [Google Scholar] [CrossRef]
- Yao, J.; Qi, D.; Yao, Y.; Cao, F.; He, Y.; Ding, P.; Jin, C.; Jia, T.; Liang, J.; Deng, L.; et al. Total variation and block-matching 3D filtering-based image reconstruction for single-shot compressed ultrafast photography. Opt. Lasers Eng. 2020, 139, 106475. [Google Scholar] [CrossRef]
- Park, S.-W.; Yoon, R.; Lee, H.; Lee, H.-J.; Choi, Y.-D.; Lee, D.-H. Impacts of Thresholds of Gray Value for Cone-Beam Computed Tomography 3D Reconstruction on the Accuracy of Image Matching with Optical Scan. Int. J. Environ. Res. Public Health 2020, 17, 6375. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, Z.; Gong, J. Generalized photogrammetry of spaceborne, airborne and terrestrial multi-source remote sensing datasets. Acta Geod. Cartogr. Sin. 2021, 50, 1–11. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, Q.; He, H.; Yan, S.; Zhao, Y. Structure adaptive feature point matching for urban area wide-baseline images with viewpoint variation. Acta Geod. Cartogr. Sin. 2019, 48, 1129–1140. [Google Scholar] [CrossRef]
- Zhang, L.; Ai, H.; Xu, B.; Sun, Y.; Dong, Y. Automatic tie-point extraction based on multiple-image matching and bundle adjustment of large block of oblique aerial images. Acta Geod. Cartogr. Sin. 2017, 46, 554–564. [Google Scholar] [CrossRef]
- Yao, G.; Deng, K.; Zhang, L.; Ai, H.; Du, Q. An algorithm of automatic quasi-dense matching and three-dimensional recon-struction for oblique stereo images. Geomat. Informat. Sci. Wuhan Univ. 2014, 39, 843–849. [Google Scholar]
- Jin, Y.; Mishkin, D.; Mishchuk, A.; Matas, J.; Fua, P.; Yi, K.M.; Trulls, E. Image Matching across Wide Baselines: From Paper to Practice. Int. J. Comput. Vis. 2020, 129, 517–547. [Google Scholar] [CrossRef]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperGlue: Learning Feature Matching with Graph Neural Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Van Gool, L. A Comparison of Affine Region Detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef] [Green Version]
- Kasongo, S.M.; Sun, Y. A deep learning method with wrapper based feature extraction for wireless intrusion detection system. Comput. Secur. 2020, 92, 101752. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image Matching from Handcrafted to Deep Features: A Survey. Int. J. Comput. Vis. 2020, 129, 23–79. [Google Scholar] [CrossRef]
- Chen, L.; Rottensteiner, F.; Heipke, C. Feature detection and description for image matching: From hand-crafted design to deep learning. Geo-Spat. Inf. Sci. 2020, 24, 58–74. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Yao, G.; Cui, J.; Deng, K.; Zhang, L. Robust Harris Corner Matching Based on the Quasi-Homography Transform and Self-Adaptive Window for Wide-Baseline Stereo Images. IEEE Trans. Geosci. Remote Sens. 2017, 56, 559–574. [Google Scholar] [CrossRef]
- Mikolajczyk, K. Scale & Affine Invariant Interest Point Detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar] [CrossRef]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Morel, J.-M.; Yu, G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison. SIAM J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, G.; Wang, J.; Lha, D. A Multiple Feature Fully Convolutional Network for Road Extraction from High-Resolution Remote Sensing Image Over Mountainous Areas. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1600–1604. [Google Scholar] [CrossRef]
- Han, X.; Leung, T.; Jia, Y.; Sukthankar, R.; Berg, A.C. MatchNet: Unifying feature and metric learning for patch-based matching. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3279–3286. [Google Scholar] [CrossRef] [Green Version]
- Sangwan, D.; Biswas, R.; Ghattamaraju, N. An effective analysis of deep learning based approaches for audio based feature extraction and its visualization. Multimedia Tools Appl. 2018, 78, 23949–23972. [Google Scholar] [CrossRef]
- Yu, Y.; Li, X.; Liu, F. Attention GANs: Unsupervised Deep Feature Learning for Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2019, 58, 519–531. [Google Scholar] [CrossRef]
- Alshaikhli, T.; Liu, W.; Maruyama, Y. Automated Method of Road Extraction from Aerial Images Using a Deep Convolutional Neural Network. Appl. Sci. 2019, 9, 4825. [Google Scholar] [CrossRef] [Green Version]
- Saeedimoghaddam, M.; Stepinski, T.F. Automatic extraction of road intersection points from USGS historical map series using deep convolutional neural networks. Int. J. Geogr. Inf. Sci. 2019, 34, 947–968. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Xiao, G.; Shao, Z.; Guo, X. A review of multimodal image matching: Methods and applications. Inf. Fusion 2021, 73, 22–71. [Google Scholar] [CrossRef]
- Cosgriff, C.V.; Celi, L.A. Deep learning for risk assessment: All about automatic feature extraction. Br. J. Anaesth. 2020, 124, 131–133. [Google Scholar] [CrossRef] [PubMed]
- Maggipinto, M.; Beghi, A.; McLoone, S.; Susto, G.A. DeepVM: A Deep Learning-based approach with automatic feature extraction for 2D input data Virtual Metrology. J. Process. Control 2019, 84, 24–34. [Google Scholar] [CrossRef]
- Sun, Y.; Yen, G.G.; Yi, Z. Evolving Unsupervised Deep Neural Networks for Learning Meaningful Representations. IEEE Trans. Evol. Comput. 2018, 23, 89–103. [Google Scholar] [CrossRef]
- Lee, K.; Lim, J.; Ahn, S.; Kim, J. Feature extraction using a deep learning algorithm for uncertainty quantification of channelized reservoirs. J. Pet. Sci. Eng. 2018, 171, 1007–1022. [Google Scholar] [CrossRef]
- Verdie, Y.; Yi, K.M.; Fua, P.; Lepetit, V. TILDE: A Temporally Invariant Learned DEtector. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5279–5288. [Google Scholar] [CrossRef] [Green Version]
- Shukla, S.; Arac, A. A Step-by-Step Implementation of DeepBehavior, Deep Learning Toolbox for Automated Behavior Analysis. J. Vis. Exp. 2020, e60763. [Google Scholar] [CrossRef]
- Yan, M.; Li, Z.; Yu, X.; Jin, C. An End-to-End Deep Learning Network for 3D Object Detection From RGB-D Data Based on Hough Voting. IEEE Access 2020, 8, 138810–138822. [Google Scholar] [CrossRef]
- Laguna, A.B.; Riba, E.; Ponsa, D.; Mikolajczyk, K. Key.Net: Keypoint Detection by Handcrafted and Learned CNN Filters. In Proceedings of the IEEECVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–29 October 2019. [Google Scholar] [CrossRef] [Green Version]
- Balntas, V.; Riba, E.; Ponsa, D.; Mikolajczyk, K. Learning local feature descriptors with triplets and shallow convolutional neural networks. In Proceedings of the British Machine Vision Conference, York, UK, 19–22 September 2016. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Pan, B.; Zhang, J. Power tower detection in remote sensing imagery based on deformable network and transfer learning. Acta Geod. Cartogr. Sin. 2020, 49, 1042–1050. [Google Scholar] [CrossRef]
- Yao, Y.; Park, H.S. Multiview co-segmentation for wide baseline images using cross-view supervision. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Snowmass, CL, USA, 1–5 March 2020; pp. 1942–1951. [Google Scholar]
- Liu, J.; Wang, S.; Hou, X.; Song, W. A deep residual learning serial segmentation network for extracting buildings from remote sensing imagery. Int. J. Remote Sens. 2020, 41, 5573–5587. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Z.; Liao, G.; Yuan, K. New loss functions for medical image registration based on VoxelMorph. In Image Processing of Medical Imaging, Proceedings of the SPIE Medical Imaging, Houston, TX, USA, 15–20 February 2020; p. 11313. [CrossRef]
- Cao, Y.; Wang, Y.; Peng, J.; Zhang, L.; Xu, L.; Yan, K.; Li, L. DML-GANR: Deep Metric Learning with Generative Adversarial Network Regularization for High Spatial Resolution Remote Sensing Image Retrieval. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8888–8904. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C. Quantitative analysis of the generalization ability of deep feedforward neural networks. J. Intell. Fuzzy Syst. 2021, 40, 4867–4876. [Google Scholar] [CrossRef]
- Wang, L.; Qian, Y.; Kong, X. Line and point matching based on the maximum number of consecutive matching edge segment pairs for large viewpoint changing images. Signal Image Video Process. 2021, 1–8. [Google Scholar] [CrossRef]
- Zheng, B.; Qi, S.; Luo, G.; Liu, F.; Huang, X.; Guo, S. Characterization of discontinuity surface morphology based on 3D fractal dimension by integrating laser scanning with ArcGIS. Bull. Int. Assoc. Eng. Geol. 2021, 80, 2261–2281. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, S.; Jia, Y.; Liu, S. Prediction of terrain occlusion in Change-4 mission. Measures 2020, 152. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, X. Efficient and de-shadowing approach for multiple vehicle tracking in aerial video via image segmentation and local region matching. J. Appl. Remote Sens. 2020, 14, 014503. [Google Scholar] [CrossRef]
- Yuan, X.; Yuan, W.; Xu, S.; Ji, Y. Research developments and prospects on dense image matching in photogrammetry. Acta Geod. Cartogr. Sin. 2019, 48, 1542–1550. [Google Scholar]
- Liu, J.; Ji, S. Deep learning based dense matching for aerial remote sensing images. Acta Geod. Cartogr. Sin. 2019, 48, 1141–1150. [Google Scholar] [CrossRef]
- Chen, X.; He, H.; Zhou, J.; An, P.; Chen, T. Progress and future of image matching in low-altitude photogrammetry. Acta Geod. Cartogr. Sin. 2019, 48, 1595–1603. [Google Scholar] [CrossRef]
- Li, Y.; Huang, X.; Liu, H. Unsupervised Deep Feature Learning for Urban Village Detection from High-Resolution Remote Sensing Images. Photogramm. Eng. Remote Sens. 2017, 83, 567–579. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, T.; Shang, Y.; Shao, Z.; Ding, H. Salient Object Detection: Integrate Salient Features in the Deep Learning Framework. IEEE Access 2019, 7, 152483–152492. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Y. FE-YOLO: A Feature Enhancement Network for Remote Sensing Target Detection. Remote Sens. 2021, 13, 1311. [Google Scholar] [CrossRef]
- Lenc, K.; Vedaldi, A. Learning Covariant Feature Detectors. In Proceedings of the ECCV Workshop on Geometry Meets Deep Learning, Amsterdam, The Netherlands, 31 August–1 September 2016; pp. 100–117. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yu, F.X.; Karaman, S.; Chang, S.-F. Learning Discriminative and Transformation Covariant Local Feature Detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4923–4931. [Google Scholar] [CrossRef]
- Doiphode, N.; Mitra, R.; Ahmed, S.; Jain, A. An Improved Learning Framework for Covariant Local Feature Detection. In Proceedings of the Asian Conference on Computer Vision (ACCV), Perth, Australia, 2–6 December 2019; pp. 262–276. [Google Scholar] [CrossRef] [Green Version]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015; pp. 84–92. [Google Scholar] [CrossRef] [Green Version]
- Yi, K.M.; Verdie, Y.; Fua, P.; Lepetit, V. Learning to Assign Orientations to Feature Points. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 107–116. [Google Scholar] [CrossRef] [Green Version]
- Zitnick, C.L.; Ramnath, K. Edge foci interest points. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 359–366. [Google Scholar] [CrossRef]
- Mishkin, D.; Radenović, F.; Matas, J. Repeatability Is Not Enough: Learning Affine Regions via Discriminability. In European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2018; pp. 287–304. [Google Scholar] [CrossRef] [Green Version]
- Savinov, N.; Seki, A.; Ladicky, L.; Sattler, T.; Plooeleys, M. Quad-networks: Unsupervised learning to rank for interest point detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1822–1830. [Google Scholar]
- De Vos, B.D.; Berendsen, F.F.; Viergever, M.A.; Sokooti, H.; Staring, M.; Išgum, I. A deep learning framework for unsupervised affine and deformable image registration. Med. Image Anal. 2019, 52, 128–143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abdullah, T.; Bazi, Y.; Al Rahhal, M.M.; Mekhalfi, M.L.; Rangarajan, L.; Zuair, M. TextRS: Deep Bidirectional Triplet Network for Matching Text to Remote Sensing Images. Remote Sens. 2020, 12, 405. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Zhang, Y.; Gong, Y.; Zheng, N. Kernelized subspace pooling for deep local descriptors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Simo-Serra, E.; Trulls, E.; Ferraz, L.; Kokkinos, I.; Fua, P.; Moreno-Noguer, F. Discriminative Learning of Deep Convolutional Feature Point Descriptors. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 118–126. [Google Scholar] [CrossRef] [Green Version]
- Zagoruyko, S.; Komodakis, N. Learning to compare image patches via convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4353–4361. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 346–361. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE T. Pattern. Anal. 2014, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, D.; Dong, Y.; Zhang, Y. Satellite image matching method based on deep convolution neural network. Acta Geod. Cartogr. Sin. 2018, 47, 844–853. [Google Scholar] [CrossRef]
- Tian, Y.; Fan, B.; Wu, F. L2-Net: Deep Learning of Discriminative Patch Descriptor in Euclidean Space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6128–6136. [Google Scholar] [CrossRef]
- A Brown, M.; Hua, G.; Winder, S. Discriminative Learning of Local Image Descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 43–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balntas, V.; Lenc, K.; Vedaldi, A.; Mikolajczyk, K. HPatches: A Benchmark and Evaluation of Handcrafted and Learned Local Descriptors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3852–3861. [Google Scholar] [CrossRef] [Green Version]
- Mishchuk, A.; Mishkin, D.; Radenovic, F. Working hard to know your neighbor’s margins: Local descriptor learning loss. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4826–4837. [Google Scholar]
- Ebel, P.; Mishchuk, A.; Yi, K.M.; Fua, P.; Trulls, E. Beyond cartesian representations for local descriptors. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 253–262. [Google Scholar]
- Tian, Y.; Yu, X.; Fan, B.; Wu, F.; Heijnen, H.; Balntas, V. SOSNet: Second Order Similarity Regularization for Local Descriptor Learning. In Proceedings of the Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11008–11017. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Shen, T.; Zhou, L.; Zhu, S.; Zhang, R.; Yao, Y.; Fang, T.; Quan, L. GeoDesc: Learning Local Descriptors by Integrating Geometry Constraints. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 170–185. [Google Scholar] [CrossRef] [Green Version]
- Luo, Z.; Shen, T.; Zhou, L.; Zhang, J.; Yao, Y.; Li, S.; Fang, T.; Quan, L. ContextDesc: Local Descriptor Augmentation with Cross-Modality Context. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 2522–2531. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; Yilmaz, A.; Zhang, L.; Meng, F.; Ai, H.; Jin, F. Matching Large Baseline Oblique Stereo Images Using an End-To-End Convolutional Neural Network. Remote Sens. 2021, 13, 274. [Google Scholar] [CrossRef]
- Mahapatra, D.; Ge, Z. Training data independent image registration using generative adversarial networks and domain adaptation. Pattern Recognit. 2019, 100, 107109. [Google Scholar] [CrossRef]
- Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. LIFT: Learned Invariant Feature Transform. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; pp. 467–483. [Google Scholar] [CrossRef] [Green Version]
- Jaderberg, M.; Simonyan, K.; Zisserman, A. Spatial transformer networks. Adv. Neural Inf. Process. Syst. 2015, 28, 2017–2025. [Google Scholar]
- Chapelle, O.; Wu, M. Gradient descent optimization of smoothed information retrieval metrics. Inf. Retr. 2009, 13, 216–235. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, R.; Zhou, L.; Shen, T.; Fang, T.; Tan, P.; Quan, L. Very Large-Scale Global SfM by Distributed Motion Averaging. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4568–4577. [Google Scholar] [CrossRef]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperPoint: Self-Supervised Interest Point Detection and Description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 337–33712. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Li, F. Image Encode Method Based on IFS with Probabilities Applying in Image Retrieval. In Proceedings of the Fourth Global Congress on Intelligent Systems (GCIS), Hong Kong, China, 2–3 December 2013; pp. 291–295. [Google Scholar] [CrossRef]
- Lie, W.-N.; Gao, Z.-W. Video Error Concealment by Integrating Greedy Suboptimization and Kalman Filtering Techniques. IEEE Trans. Circuits Syst. Video Technol. 2006, 16, 982–992. [Google Scholar] [CrossRef]
- Revaud, J.; Weinzaepfel, P.; De, S. R2D2: Repeatable and reliable detector and descriptor. arXiv 2019, arXiv:1906.06195. [Google Scholar]
- Ono, Y.; Trulls, E.; Fua, P.; Mooyi, K. LF-Net: Learning local features from images. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 6234–6244. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-Net: A Trainable CNN for Joint Description and Detection of Local Features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 8084–8093. [Google Scholar] [CrossRef]
- Xu, X.-F.; Zhang, L.; Duan, C.-D.; Lu, Y. Research on Inception Module Incorporated Siamese Convolutional Neural Networks to Realize Face Recognition. IEEE Access 2019, 8, 12168–12178. [Google Scholar] [CrossRef]
- Li, J.; Xie, Y.; Li, C.; Dai, Y.; Ma, J.; Dong, Z.; Yang, T. UAV-Assisted Wide Area Multi-Camera Space Alignment Based on Spatiotemporal Feature Map. Remote Sens. 2021, 13, 1117. [Google Scholar] [CrossRef]
- Hasheminasab, S.M.; Zhou, T.; Habib, A. GNSS/INS-Assisted Structure from Motion Strategies for UAV-Based Imagery over Mechanized Agricultural Fields. Remote Sens. 2020, 12, 351. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.-H.; Yoo, J.; Park, M.; Kim, J.; Kwon, S. Robust Extrinsic Calibration of Multiple RGB-D Cameras with Body Tracking and Feature Matching. Sensors 2021, 21, 1013. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Cham, Switzerland; pp. 740–755. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Snavely, N. MegaDepth: Learning Single-View Depth Prediction from Internet Photos. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 2041–2050. [Google Scholar] [CrossRef] [Green Version]
- Shen, T.; Luo, Z.; Zhou, L.; Zhang, R.; Zhu, S.; Fang, T.; Quan, L. Matchable Image Retrieval by Learning from Surface Reconstruction. In Computer Vision–ACCV, Proceedings of the 14th Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 415–431. [Google Scholar] [CrossRef] [Green Version]
- Aanæs, H.; Jensen, R.R.; Vogiatzis, G.; Tola, E.; Dahl, A.B. Large-Scale Data for Multiple-View Stereopsis. Int. J. Comput. Vis. 2016, 120, 153–168. [Google Scholar] [CrossRef] [Green Version]
- Yao, G.; Deng, K.; Zhang, L.; Yang, H.; Ai, H. An automated registration method with high accuracy for oblique stereo images based on complementary affine invariant features. Acta Geod. Cartogr. Sin. 2013, 42, 869–876. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Q.; Wu, B.; Xu, Z.-X.; Qing, Z. Seed Point Selection Method for Triangle Constrained Image Matching Propagation. IEEE Geosci. Remote Sens. Lett. 2006, 3, 207–211. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).