Validation of FY-3D MERSI-2 Precipitable Water Vapor (PWV) Datasets Using Ground-Based PWV Data from AERONET
Abstract
1. Introduction
2. Materials and Methods
2.1. FY-3D MERSI-2 PWV Data
2.2. Ground-Based PWV Data
2.3. Validation of Remote Sensing Data Using Ground-Based Data
3. Results
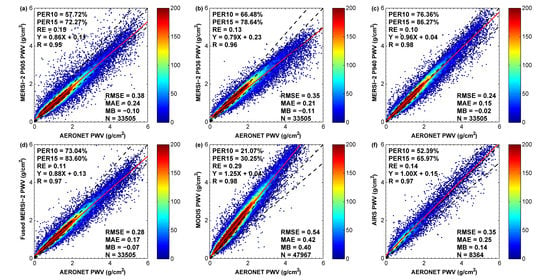
3.1. Overall Accuracy Assessment and Comparison of Four MERSI-2 PWV Datasets
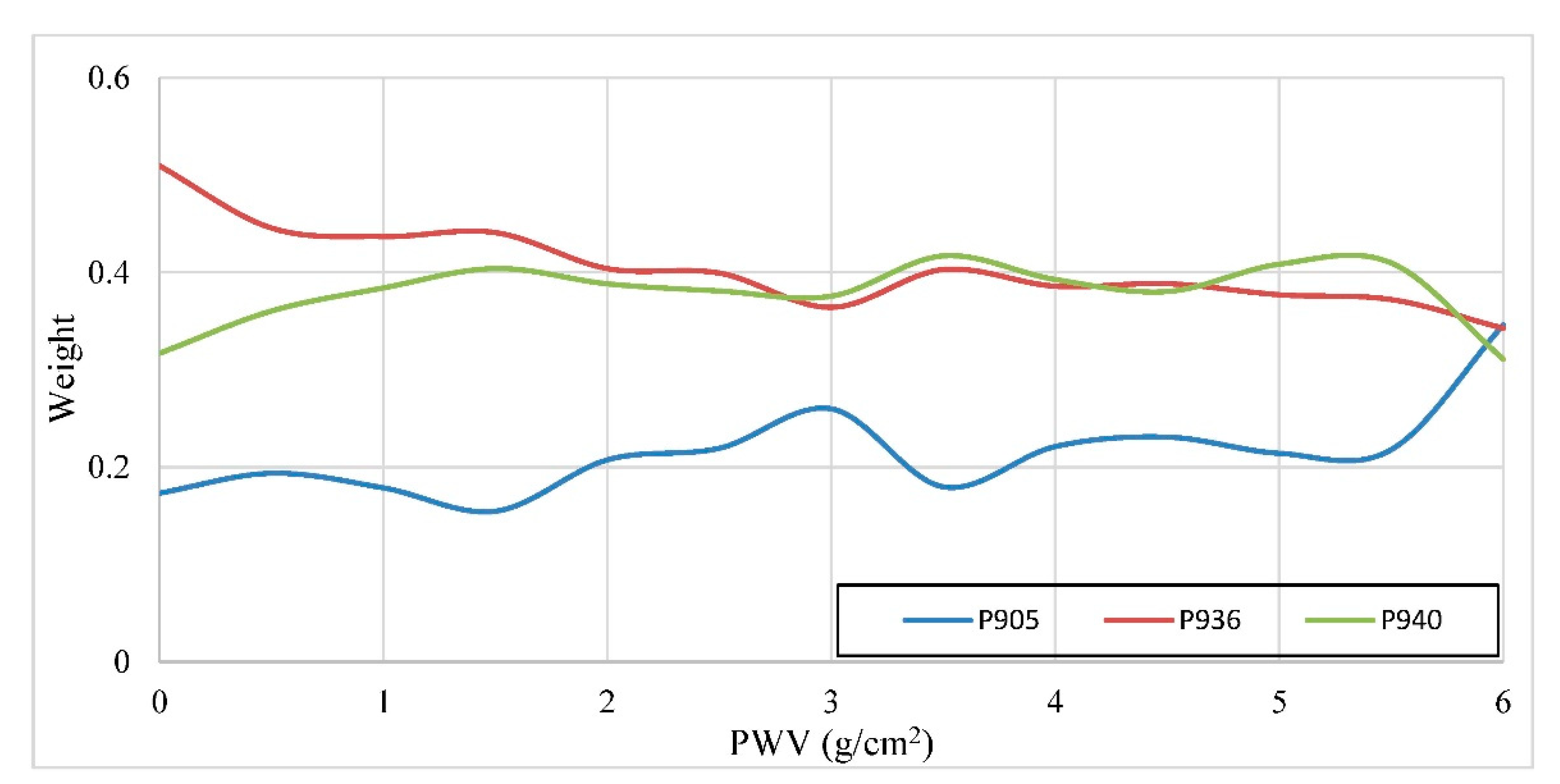
3.2. Error Analysis of MERSI-2 PWV Products under Different Water Vapor Content
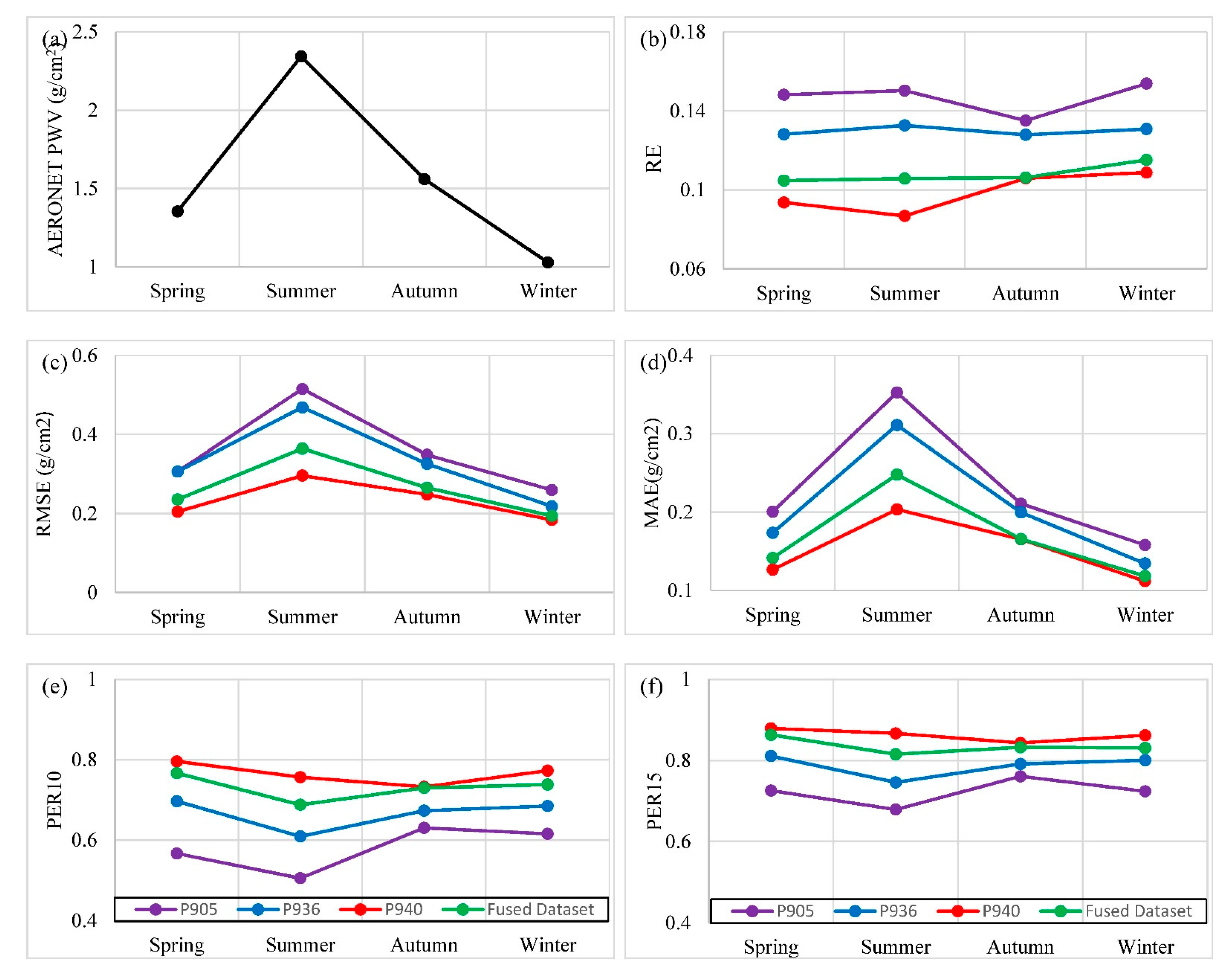
3.3. Validation Results of MERSI-2 PWV Datasets in Different Seasons
3.4. Validation Results of MERSI-2 PWV Datasets in Different Locations
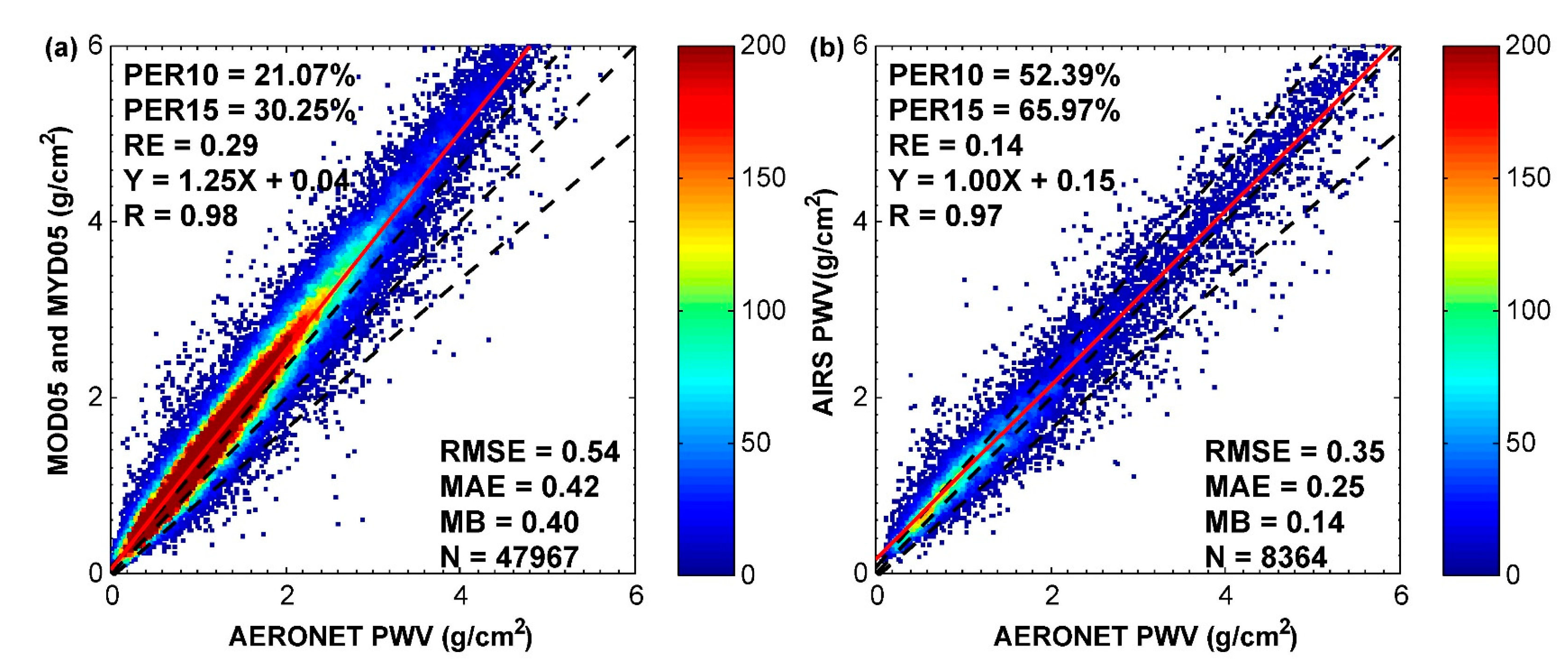
3.5. Accuracy Comparision between Four MERSI-2 PWV Datasets, AIRS PWV Dataset and MODIS PWV Dataset
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Held, I.M.; Soden, B.J. Water Vapor Feedback and Global Warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef]
- Lyngwa, R.V.; Nayak, M.A. Atmospheric river linked to extreme rainfall events over Kerala in August 2018. Atmos. Res. 2021, 253, 13. [Google Scholar] [CrossRef]
- Reid, K.J.; Rosier, S.M.; Harrington, L.J.; King, A.D.; Lane, T.P. Extreme rainfall in New Zealand and its association with Atmospheric Rivers. Environ. Res. Lett. 2021, 16, 044012. [Google Scholar] [CrossRef]
- Ziskin Ziv, S.; Alpert, P.; Reuveni, Y. Long-term variability and trends of precipitable water vapour derived from GPS tropospheric path delays over the Eastern Mediterranean. Int. J. Climatol. 2021, 1–22. [Google Scholar] [CrossRef]
- Zheng, Y.T.; Ren, H.Z.; Guo, J.X.; Ghent, D.; Tansey, K.; Hu, X.B.; Nie, J.; Chen, S.S. Land Surface Temperature Retrieval from Sentinel-3A Sea and Land Surface Temperature Radiometer, Using a Split-Window Algorithm. Remote Sens. 2019, 11, 650. [Google Scholar] [CrossRef]
- Choi, Y.Y.; Suh, M.S. Development of Himawari-8/Advanced Himawari Imager (AHI) Land Surface Temperature Retrieval Algorithm. Remote Sens. 2018, 10, 2013. [Google Scholar] [CrossRef]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef]
- Xue, Y.; He, X.W.; Xu, H.; Guang, J.; Guo, J.P.; Mei, L.L. China Collection 2.0: The aerosol optical depth dataset from the synergetic retrieval of aerosol properties algorithm. Atmos. Environ. 2014, 95, 45–58. [Google Scholar] [CrossRef]
- Koulali, A.; Ouazar, D.; Bock, O.; Fadil, A. Study of seasonal-scale atmospheric water cycle with ground-based GPS receivers, radiosondes and NWP models over Morocco. Atmos. Res. 2012, 104, 273–291. [Google Scholar] [CrossRef]
- Renju, R.; Raju, C.S.; Mathew, N.; Antony, T.; Moorthy, K.K. Microwave radiometer observations of interannual water vapor variability and vertical structure over a tropical station. J. Geophys. Res. Atmos. 2015, 120, 4585–4599. [Google Scholar] [CrossRef]
- Hu, H.; Yang, R.K.; Lee, W.C.; Cao, Y.C.; Mao, J.J.; Gao, L.N. Multi-sensor study of precipitable water vapor and atmospheric profiling from microwave radiometer, GNSS/MET, radiosonde, and ECMWF reanalysis in Beijing. J. Appl. Remote Sens. 2020, 14, 18. [Google Scholar] [CrossRef]
- Li, Z.Q.; Xu, H.; Li, K.T.; Li, D.H.; Xie, Y.S.; Li, L.; Zhang, Y.; Gu, X.F.; Zhao, W.; Tian, Q.J.; et al. Comprehensive Study of Optical, Physical, Chemical, and Radiative Properties of Total Columnar Atmospheric Aerosols over China: An Overview of Sun-Sky Radiometer Observation Network (SONET) Measurements. Bull. Am. Meteorol. Soc. 2018, 99, 739–755. [Google Scholar] [CrossRef]
- Campmany, E.; Bech, J.; Rodríguez-Marcos, J.; Sola, Y.; Lorente, J. A comparison of total precipitable water measurements from radiosonde and sunphotometers. Atmos. Res. 2010, 97, 385–392. [Google Scholar] [CrossRef]
- Wu, Z.L.; Liu, Y.X.; Liu, Y.; Wang, J.G.; He, X.F.; Xu, W.X.; Ge, M.R.; Schuh, H. Validating HY-2A CMR precipitable water vapor using ground-based and shipborne GNSS observations. Atmos. Meas. Tech. 2020, 13, 4963–4972. [Google Scholar] [CrossRef]
- Gao, B.C.; Kaufman, Y.J. Water vapor retrievals using moderate resolution Imaging spectroradiometer (MODIS) near-infrared channels. J. Geophys. Res. Atmos. 2003, 108, 10. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Y.X.; Chen, G.X.; Wu, Z.L. Evaluation of HY-2A satellite-borne water vapor radiometer with shipborne GPS and GLONASS observations over the Indian Ocean. GPS Solut. 2019, 23, 9. [Google Scholar] [CrossRef]
- He, J.; Liu, Z.Z. Water Vapor Retrieval From MODIS NIR Channels Using Ground-Based GPS Data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3726–3737. [Google Scholar] [CrossRef]
- Liu, H.L.; Li, H.P.; Tang, S.H.; Duan, M.Z.; Zhang, S.L.; Deng, X.B.; Hu, J.Y. A physical algorithm for precipitable water vapour retrieval over land using passive microwave observations. Int. J. Remote Sens. 2020, 41, 6288–6306. [Google Scholar] [CrossRef]
- Gangwar, R.K.; Thapliyal, P.K. Retrieval of total precipitable water from thermal infrared observations of INSAT-3D imager over the ocean. Curr. Sci. 2020, 119, 382–389. [Google Scholar] [CrossRef]
- Li, Z.L.; Jia, L.; Su, Z.B.; Wan, Z.M.; Zhang, R.H. A new approach for retrieving precipitable water from ATSR2 split-window channel data over land area. Int. J. Remote Sens. 2003, 24, 5095–5117. [Google Scholar] [CrossRef]
- Abbasi, B.; Qin, Z.H.; Du, W.H.; Fan, J.L.; Zhao, C.L.; Hang, Q.Y.; Zhao, S.H.; Li, S.F. An Algorithm to Retrieve Total Precipitable Water Vapor in the Atmosphere from FengYun 3D Medium Resolution Spectral Imager 2 (FY-3D MERSI-2) Data. Remote Sens. 2020, 12, 3469. [Google Scholar] [CrossRef]
- Wang, L.; Hu, X.Q.; Xu, N.; Chen, L. Water Vapor Retrievals from Near-infrared Channels of the Advanced Medium Resolution Spectral Imager Instrument onboard the Fengyun-3D Satellite. Adv. Atmos. Sci. 2020, 38, 1351–1366. [Google Scholar] [CrossRef]
- Merrikhpour, M.H.; Rahimzadegan, M. Improving the Algorithm of Extracting Regional Total Precipitable Water Vapor Over Land From MODIS Images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5889–5898. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Pang, J. A comparison between atmospheric water vapour content retrieval methods using MSG2-SEVIRI thermal-IR data. Int. J. Remote Sens. 2015, 36, 5075–5086. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Drews, A.; Heise, S. Total water vapor column retrieval from MSG-SEVIRI split window measurements exploiting the daily cycle of land surface temperatures. Remote Sens. Environ. 2008, 112, 249–258. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Romaguera, M. Water-vapour retrieval from Meteosat 8/SEVIRI observations. Int. J. Remote Sens. 2008, 29, 741–754. [Google Scholar] [CrossRef]
- Eck, T.F.; Holben, B.N. AVHRR split window temperature differences and total precipitable water over land surfaces. Int. J. Remote Sens. 1994, 15, 567–582. [Google Scholar] [CrossRef]
- Du, B.L.; Ji, D.B.; Shi, J.C.; Wang, Y.Q.; Lei, T.J.; Zhang, P.; Letu, H. The Retrieval of Total Precipitable Water over Global Land Based on FY-3D/MWRI Data. Remote Sens. 2020, 12, 1508. [Google Scholar] [CrossRef]
- Wu, Q.; Dou, F.; Guo, Y.; Gu, S. Validation of FY-3C MWRI Total Precipitable Water Products. Meteorol. Mon. 2020, 46, 73–79. [Google Scholar]
- Chen, S.L.; Zheng, X.B.; Li, X.; Wei, W.; Du, S.D.; Guo, F.X. Vicarious Radiometric Calibration of Ocean Color Bands for FY-3D/MERSI-II at Lake Qinghai, China. Sensors 2021, 21, 139. [Google Scholar] [CrossRef]
- Martins, V.S.; Lyapustin, A.; Wang, Y.J.; Giles, D.M.; Smirnov, A.; Slutsker, I.; Korkin, S. Global validation of columnar water vapor derived from EOS MODIS-MAIAC algorithm against the ground-based AERONET observations. Atmos. Res. 2019, 225, 181–192. [Google Scholar] [CrossRef]
- Xu, N.; Niu, X.H.; Hu, X.Q.; Wang, X.H.; Wu, R.H.; Chen, S.S.; Chen, L.; Sun, L.; Ding, L.; Yang, Z.D.; et al. Prelaunch Calibration and Radiometric Performance of the Advanced MERSI II on FengYun-3D. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4866–4875. [Google Scholar] [CrossRef]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. MODTRAN: A Moderate Resolution Model for LOWTRAN. Technical Report, 12 May 1986–11 May 1987; Spectral Sciences, Inc.: Burlington, MA, USA, 1987. [Google Scholar]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Michalsky, J.J.; Min, Q.L.; Kiedron, P.W.; Slater, D.W.; Barnard, J.C. A differential technique to retrieve column water vapor using sun radiometry. J. Geophys. Res. Atmos. 2001, 106, 17433–17442. [Google Scholar] [CrossRef][Green Version]
- Halthore, R.N.; Eck, T.F.; Holben, B.N.; Markham, B.L. Sun photometric measurements of atmospheric water vapor column abundance in the 940-nm band. J. Geophys. Res. Atmos. 1997, 102, 4343–4352. [Google Scholar] [CrossRef]
- Shi, F.L.; Xin, J.Y.; Yang, L.K.; Cong, Z.Y.; Liu, R.X.; Ma, Y.N.; Wang, Y.S.; Lu, X.F.; Zhao, L. The first validation of the precipitable water vapor of multisensor satellites over the typical regions in China. Remote Sens. Environ. 2018, 206, 107–122. [Google Scholar] [CrossRef]
- Makarau, A.; Richter, R.; Schlapfer, D.; Reinartz, P. APDA Water Vapor Retrieval Validation for Sentinel-2 Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 227–231. [Google Scholar] [CrossRef]
- Giles, D.M.; Sinyuk, A.; Sorokin, M.G.; Schafer, J.S.; Smirnov, A.; Slutsker, I.; Eck, T.F.; Holben, B.N.; Lewis, J.R.; Campbell, J.R.; et al. Advancements in the Aerosol Robotic Network (AERONET) Version 3 database—Automated near-real-time quality control algorithm with improved cloud screening for Sun photometer aerosol optical depth (AOD) measurements. Atmos. Meas. Tech. 2019, 12, 169–209. [Google Scholar] [CrossRef]
- Ichoku, C.; Chu, D.A.; Mattoo, S.; Kaufman, Y.J.; Remer, L.A.; Tanre, D.; Slutsker, I.; Holben, B.N. A spatio-temporal approach for global validation and analysis of MODIS aerosol products. Geophys. Res. Lett. 2002, 29, MOD1-1–MOD1-4. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Mattoo, S.; Vermote, E.F.; Kaufman, Y.J. Second-generation operational algorithm: Retrieval of aerosol properties over land from inversion of Moderate Resolution Imaging Spectroradiometer spectral reflectance. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, H.L.; Zhang, Y.; Duan, M.Z.; Tang, S.H.; Deng, X.B. Validation of FY-4A AGRI layer precipitable water products using radiosonde data. Atmos. Res. 2021, 253, 14. [Google Scholar] [CrossRef]
- Vaquero-Martinez, J.; Anton, M.; de Galisteo, J.P.O.; Cachorro, V.E.; Alvarez-Zapatero, P.; Roman, R.; Loyola, D.; Costa, M.J.; Wang, H.Q.; Abad, G.G.; et al. Inter-comparison of integrated water vapor from satellite instruments using reference GPS data at the Iberian Peninsula. Remote Sens. Environ. 2018, 204, 729–740. [Google Scholar] [CrossRef]
- Xie, Y.Q.; Xue, Y.; Che, Y.H.; Guang, J.; Mei, L.L.; Voorhis, D.; Fan, C.; She, L.; Xu, H. Ensemble of ESA/AATSR Aerosol Optical Depth Products Based on the Likelihood Estimate Method With Uncertainties. IEEE Trans. Geosci. Remote Sens. 2018, 56, 997–1007. [Google Scholar] [CrossRef]
- Ningombam, S.S.; Jade, S.; Shrungeshwara, T.S.; Song, H.J. Validation of water vapor retrieval from Moderate Resolution Imaging Spectro-radiometer (MODIS) in near infrared channels using GPS data over IAO-Hanle, in the trans-Himalayan region. J. Atmos. Sol. Terr. Phys. 2016, 137, 76–85. [Google Scholar] [CrossRef]
- Wang, R.N.; Liu, Y.B. Recent declines in global water vapor from MODIS products: Artifact or real trend? Remote Sens. Environ. 2020, 247, 18. [Google Scholar] [CrossRef]
- Roman, J.; Knuteson, R.; August, T.; Hultberg, T.; Ackerman, S.; Revercomb, H. A global assessment of NASA AIRS v6 and EUMETSAT IASI v6 precipitable water vapor using ground-based GPS SuomiNet stations. J. Geophys. Res. Atmos. 2016, 121, 8925–8948. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, T. Asian water tower evinced in total column water vapor: A comparison among multiple satellite and reanalysis data sets. Clim. Dyn. 2020, 54, 231–245. [Google Scholar] [CrossRef]
- Bright, J.M.; Gueymard, C.A.; Killinger, S.; Lingfors, D.; Sun, X.X.; Wang, P.; Engerer, N.A. Climatic and Global Validation of Daily MODIS Precipitable Water Data at AERONET Sites for Clear-Sky Irradiance Modelling; International Solar Energy Society: Freiburg, Germany, 2018; pp. 1490–1501. [Google Scholar] [CrossRef]
- Tang, Q.X.; Bo, Y.C.; Zhu, Y.X. Spatiotemporal fusion of multiple-satellite aerosol optical depth (AOD) products using Bayesian maximum entropy method. J. Geophys. Res. Atmos. 2016, 121, 4034–4048. [Google Scholar] [CrossRef]
- Xu, H.; Guang, J.; Xue, Y.; de Leeuw, G.; Che, Y.H.; Guo, J.P.; He, X.W.; Wang, T.K. A consistent aerosol optical depth (AOD) dataset over mainland China by integration of several AOD products. Atmos. Environ. 2015, 114, 48–56. [Google Scholar] [CrossRef]
- Xie, Y.; Xue, Y.; Guang, J.; Mei, L.; Fan, C.; Che, Y.; She, L. Image fusion of MODIS AOD (collection 6) in China based on uncertainty. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3365–3368. [Google Scholar]
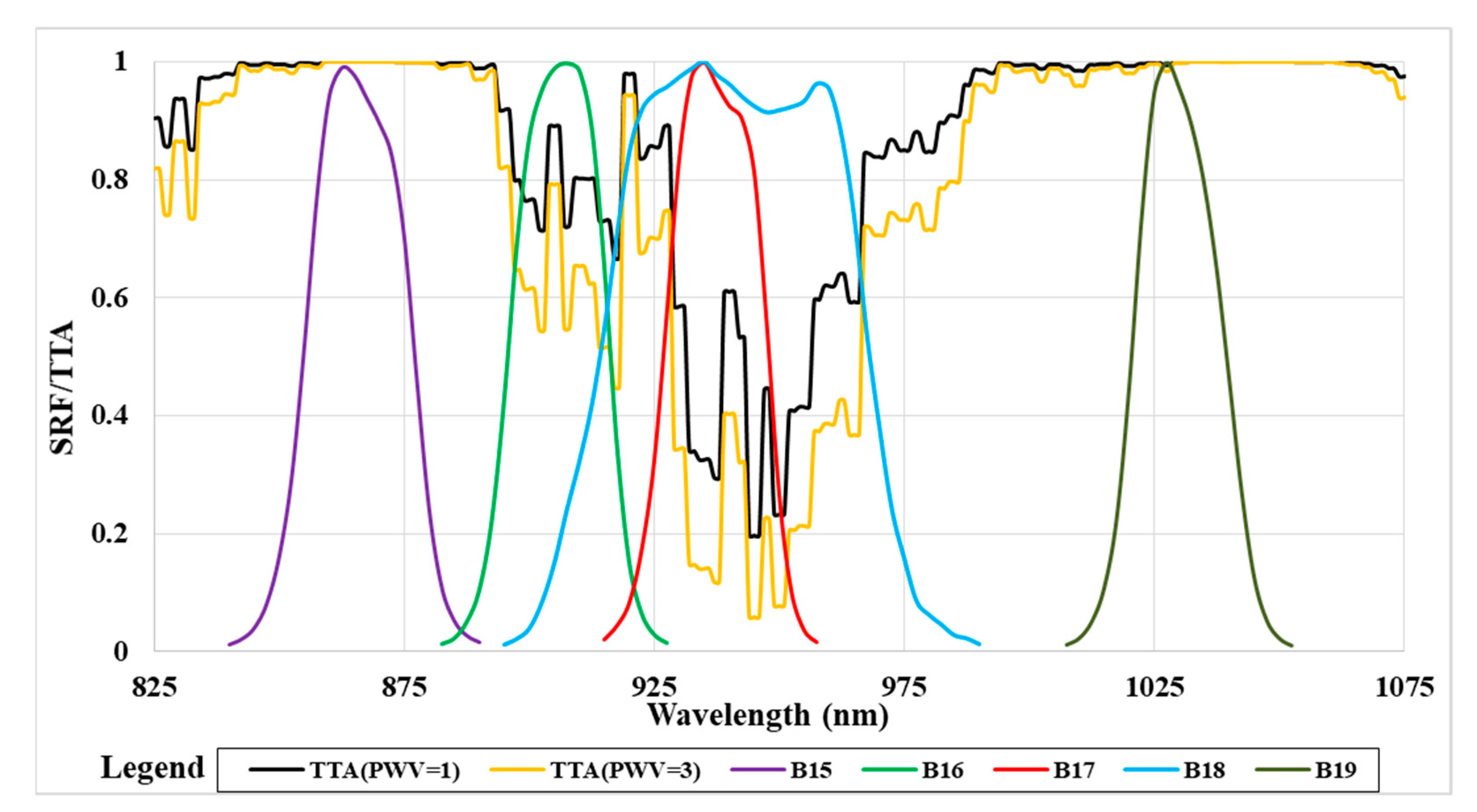



| Band No. | Center Wavelength (μm) | Band Width (nm) | Signal-to-Noise Ratio | Spatial Resolution (m) | Atmospheric Window |
|---|---|---|---|---|---|
| 15 | 0.865 | 20 | 500 | 1000 | Yes |
| 16 | 0.905 | 20 | 200 | 1000 | No |
| 17 | 0.936 | 20 | 100 | 1000 | No |
| 18 | 0.940 | 50 | 200 | 1000 | No |
| 19 | 1.03 | 20 | 100 | 1000 | Yes |
| Statistical Parameters | P905 Dataset | P936 Dataset | P940 Dataset | Fused Dataset |
|---|---|---|---|---|
| RMSE (g/cm2) | 0.38 | 0.35 | 0.24 | 0.28 |
| MAE (g/cm2) | 0.24 | 0.21 | 0.15 | 0.17 |
| MB (g/cm2) | −0.10 | −0.11 | −0.02 | −0.07 |
| PER10 | 57.72% | 66.48% | 76.36% | 73.04% |
| PER15 | 72.27% | 78.64% | 86.27% | 83.60% |
| RE | 0.15 | 0.13 | 0.10 | 0.11 |
| Slope | 0.86 | 0.79 | 0.96 | 0.88 |
| Bias (g/cm2) | 0.11 | 0.23 | 0.04 | 0.13 |
| R | 0.95 | 0.96 | 0.98 | 0.97 |
| Dataset | PWV Range (g/cm2) | MB (g/cm2) | STD (g/cm2) | RMSE (g/cm2) | MAE (g/cm2) | PER10 (%) | PER15 (%) | RE | N |
|---|---|---|---|---|---|---|---|---|---|
| P905 dataset | [0, 1) | 0.04 | 0.19 | 0.20 | 0.12 | 61.75 | 72.05 | 0.19 | 12,024 |
| [1, 2) | −0.09 | 0.30 | 0.32 | 0.21 | 58.32 | 73.65 | 0.14 | 11,967 | |
| [2, 3) | −0.24 | 0.38 | 0.45 | 0.34 | 52.91 | 70.70 | 0.14 | 5506 | |
| [3, 4) | −0.35 | 0.51 | 0.62 | 0.47 | 49.45 | 69.88 | 0.14 | 2457 | |
| [4, 5) | −0.41 | 0.65 | 0.77 | 0.57 | 52.45 | 73.77 | 0.13 | 1243 | |
| [5, 6] | −0.58 | 0.75 | 0.95 | 0.71 | 50.32 | 68.18 | 0.13 | 308 | |
| P936 dataset | [0, 1) | 0.07 | 0.12 | 0.14 | 0.10 | 67.91 | 79.04 | 0.16 | 12,024 |
| [1, 2) | −0.04 | 0.19 | 0.20 | 0.14 | 76.29 | 86.31 | 0.10 | 11,967 | |
| [2, 3) | −0.23 | 0.29 | 0.37 | 0.28 | 63.71 | 77.50 | 0.11 | 5506 | |
| [3, 4) | −0.49 | 0.38 | 0.62 | 0.51 | 43.96 | 62.68 | 0.15 | 2457 | |
| [4, 5) | −0.81 | 0.50 | 0.95 | 0.81 | 28.32 | 49.88 | 0.18 | 1243 | |
| [5, 6] | −1.19 | 0.57 | 1.32 | 1.19 | 12.34 | 29.22 | 0.23 | 308 | |
| P940 dataset | [0, 1) | 0.02 | 0.13 | 0.14 | 0.08 | 78.48 | 85.59 | 0.13 | 12,024 |
| [1, 2) | −0.01 | 0.20 | 0.20 | 0.14 | 75.68 | 86.28 | 0.10 | 11,967 | |
| [2, 3) | −0.05 | 0.29 | 0.29 | 0.22 | 75.43 | 87.32 | 0.09 | 5506 | |
| [3, 4) | −0.11 | 0.37 | 0.39 | 0.29 | 73.02 | 86.53 | 0.08 | 2457 | |
| [4, 5) | −0.11 | 0.48 | 0.50 | 0.37 | 73.85 | 87.21 | 0.08 | 1243 | |
| [5, 6] | −0.15 | 0.54 | 0.56 | 0.43 | 73.05 | 87.66 | 0.08 | 308 | |
| Fused dataset | [0, 1) | 0.05 | 0.14 | 0.14 | 0.09 | 74.72 | 82.84 | 0.14 | 12,024 |
| [1, 2) | −0.04 | 0.20 | 0.20 | 0.14 | 76.44 | 86.86 | 0.10 | 11,967 | |
| [2, 3) | −0.17 | 0.28 | 0.33 | 0.24 | 70.34 | 82.93 | 0.10 | 5506 | |
| [3, 4) | −0.30 | 0.36 | 0.47 | 0.37 | 63.21 | 78.14 | 0.11 | 2457 | |
| [4, 5) | −0.42 | 0.46 | 0.62 | 0.48 | 60.82 | 76.83 | 0.11 | 1243 | |
| [5, 6] | −0.60 | 0.53 | 0.80 | 0.64 | 51.62 | 69.16 | 0.12 | 308 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Li, Z.; Hou, W.; Guang, J.; Ma, Y.; Wang, Y.; Wang, S.; Yang, D. Validation of FY-3D MERSI-2 Precipitable Water Vapor (PWV) Datasets Using Ground-Based PWV Data from AERONET. Remote Sens. 2021, 13, 3246. https://doi.org/10.3390/rs13163246
Xie Y, Li Z, Hou W, Guang J, Ma Y, Wang Y, Wang S, Yang D. Validation of FY-3D MERSI-2 Precipitable Water Vapor (PWV) Datasets Using Ground-Based PWV Data from AERONET. Remote Sensing. 2021; 13(16):3246. https://doi.org/10.3390/rs13163246
Chicago/Turabian StyleXie, Yanqing, Zhengqiang Li, Weizhen Hou, Jie Guang, Yan Ma, Yuyang Wang, Siheng Wang, and Dong Yang. 2021. "Validation of FY-3D MERSI-2 Precipitable Water Vapor (PWV) Datasets Using Ground-Based PWV Data from AERONET" Remote Sensing 13, no. 16: 3246. https://doi.org/10.3390/rs13163246
APA StyleXie, Y., Li, Z., Hou, W., Guang, J., Ma, Y., Wang, Y., Wang, S., & Yang, D. (2021). Validation of FY-3D MERSI-2 Precipitable Water Vapor (PWV) Datasets Using Ground-Based PWV Data from AERONET. Remote Sensing, 13(16), 3246. https://doi.org/10.3390/rs13163246