Retrieving Precipitable Water Vapor from Real-Time Precise Point Positioning Using VMF1/VMF3 Forecasting Products
Abstract
:1. Introduction
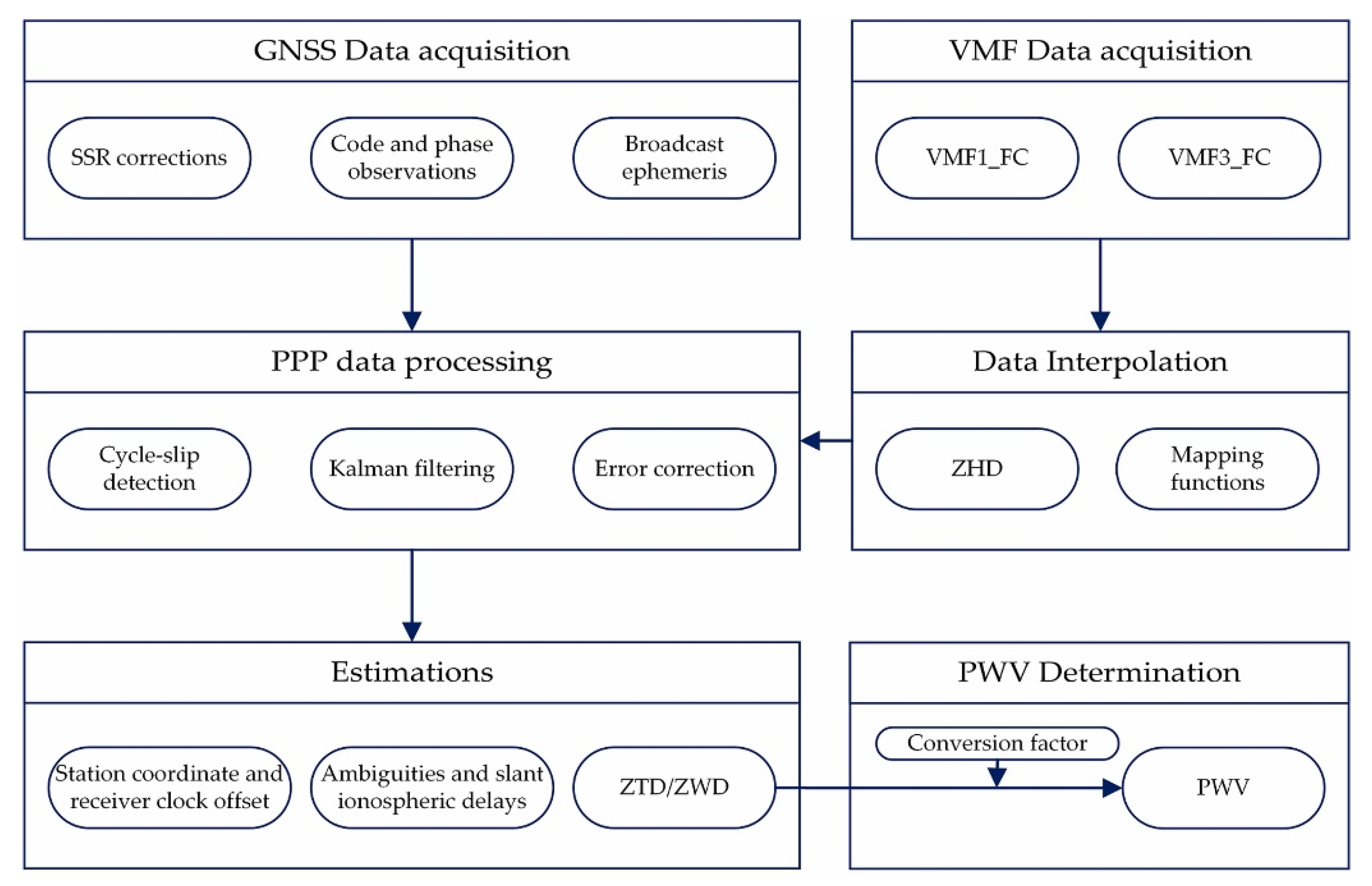
2. Materials and Methods
2.1. Real-Time Orbits and Clocks
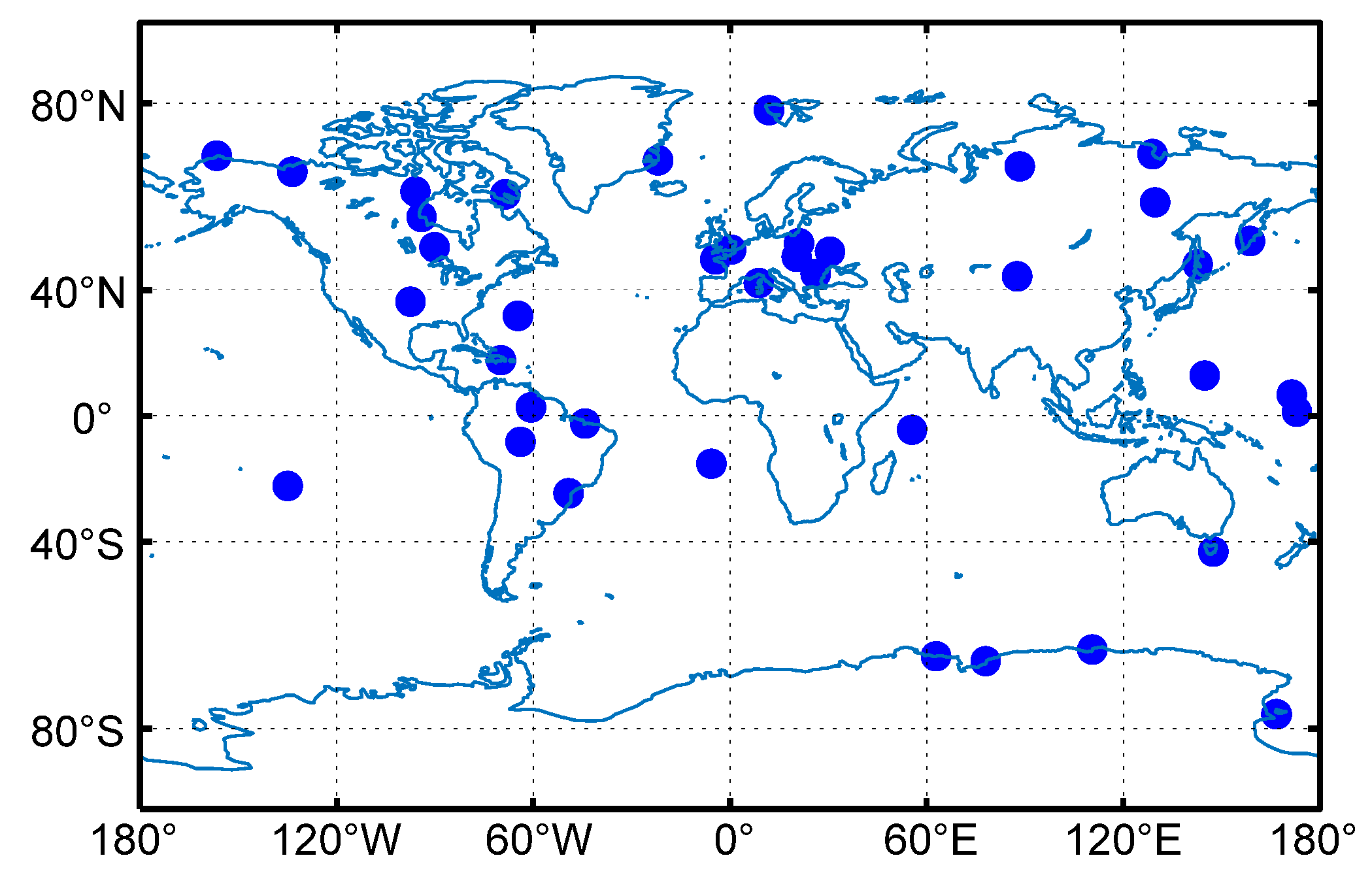
2.2. GPS Data and Processing Strategies
2.3. VMF Forecasting Data
2.4. Radiosonde Data for Evaluating VMF1/VMF3 Forecasting ZHD
2.5. Radiosonde Data for Evaluating RT-PPP-Based PWV
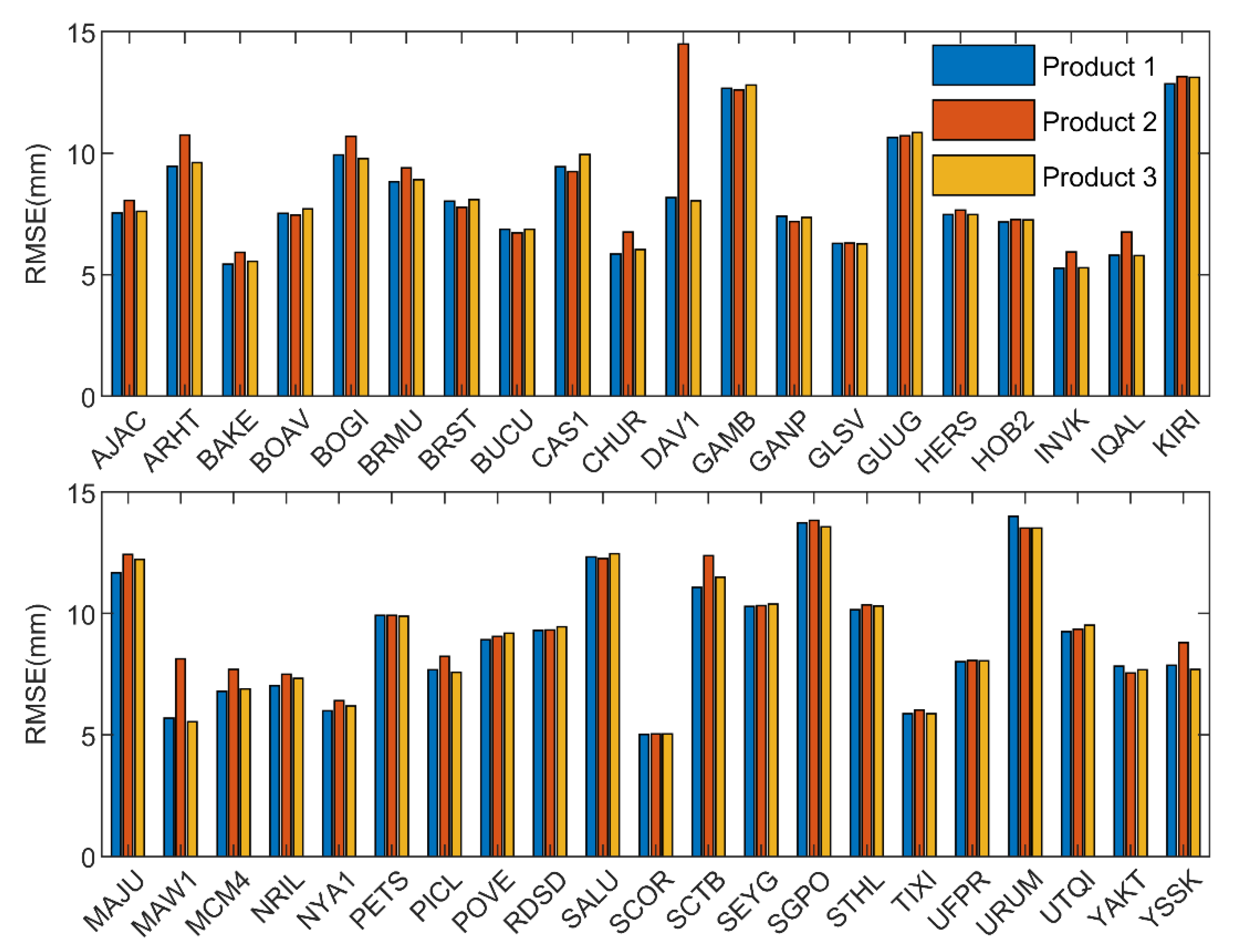
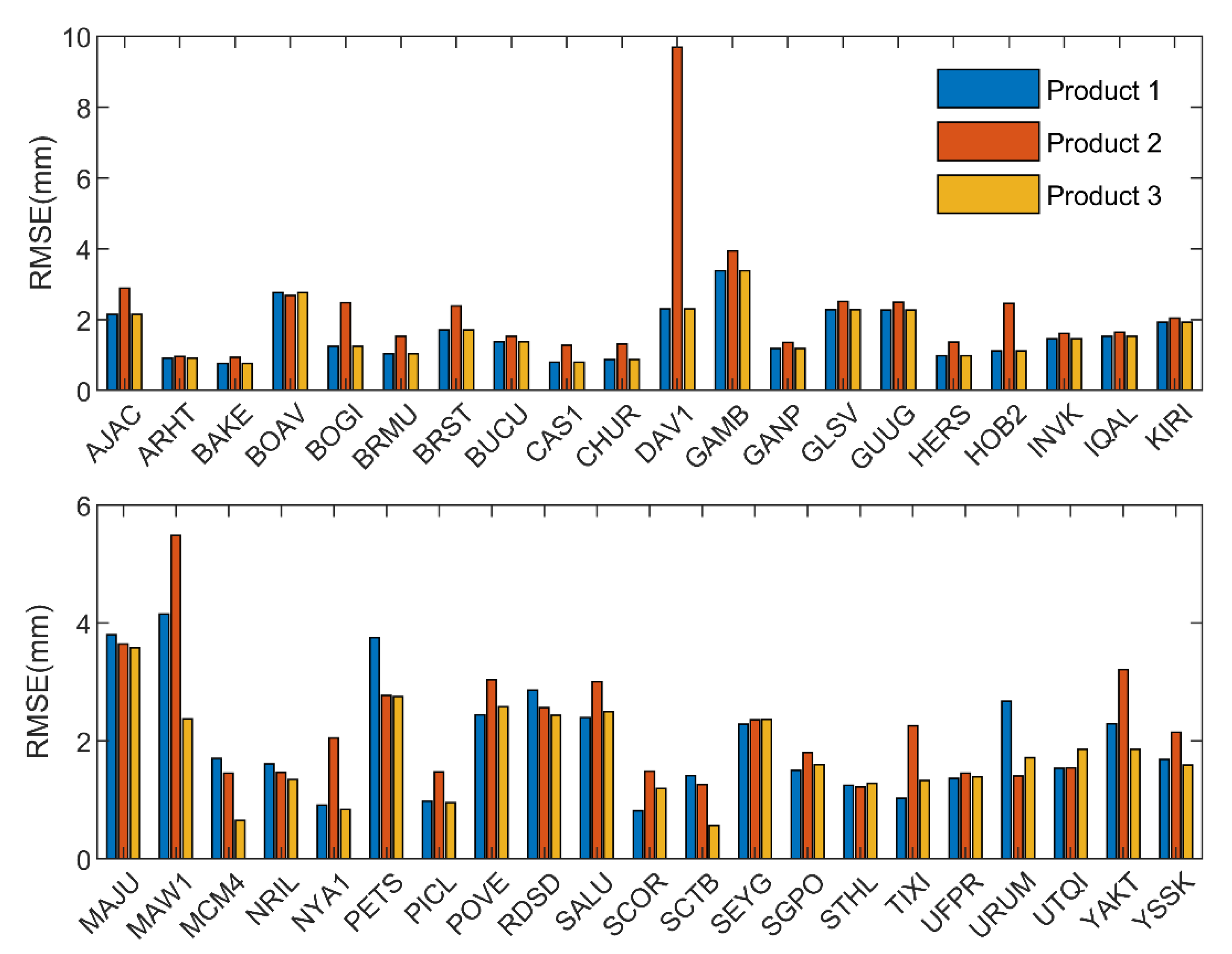
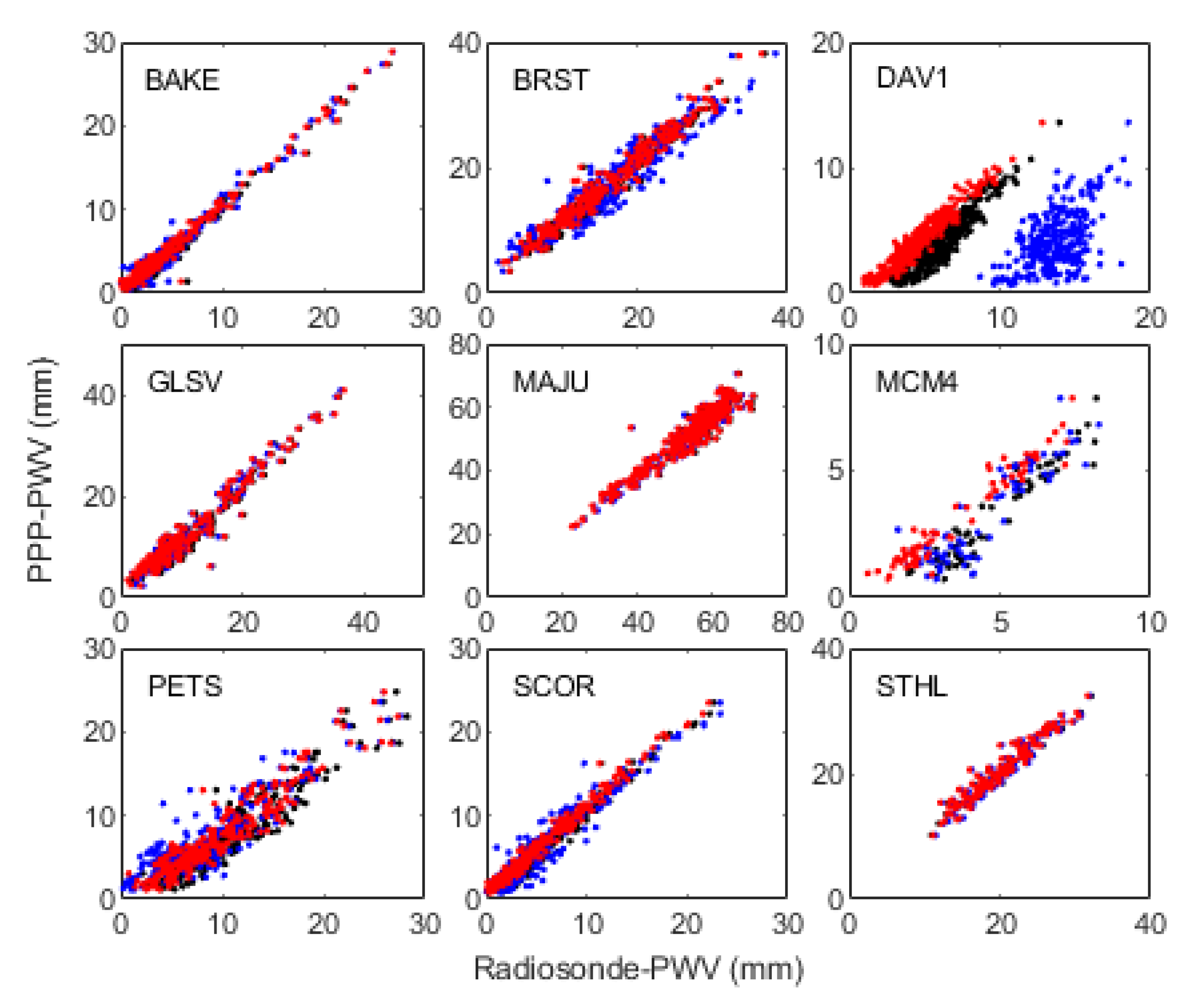
3. Results and Discussion
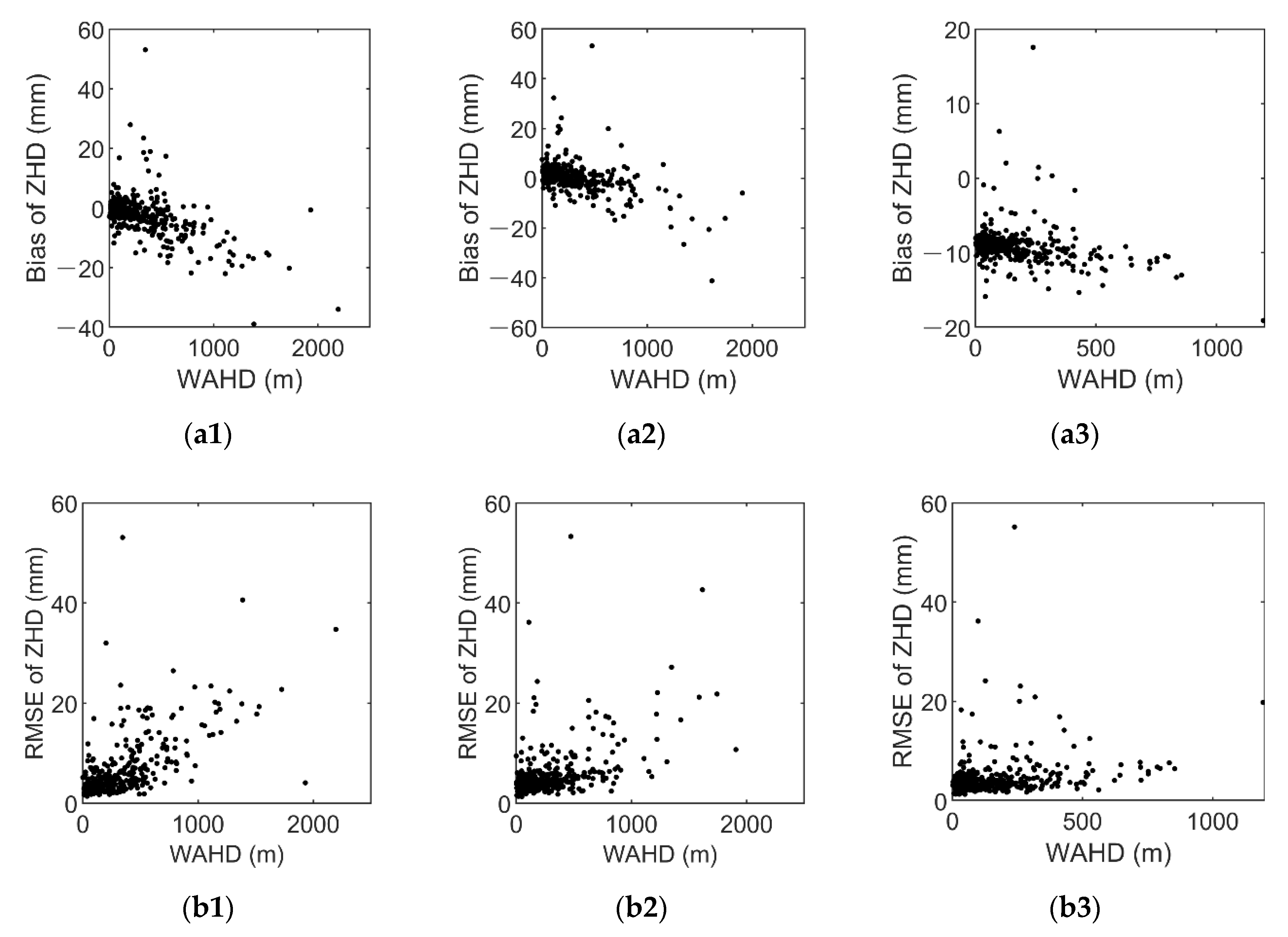
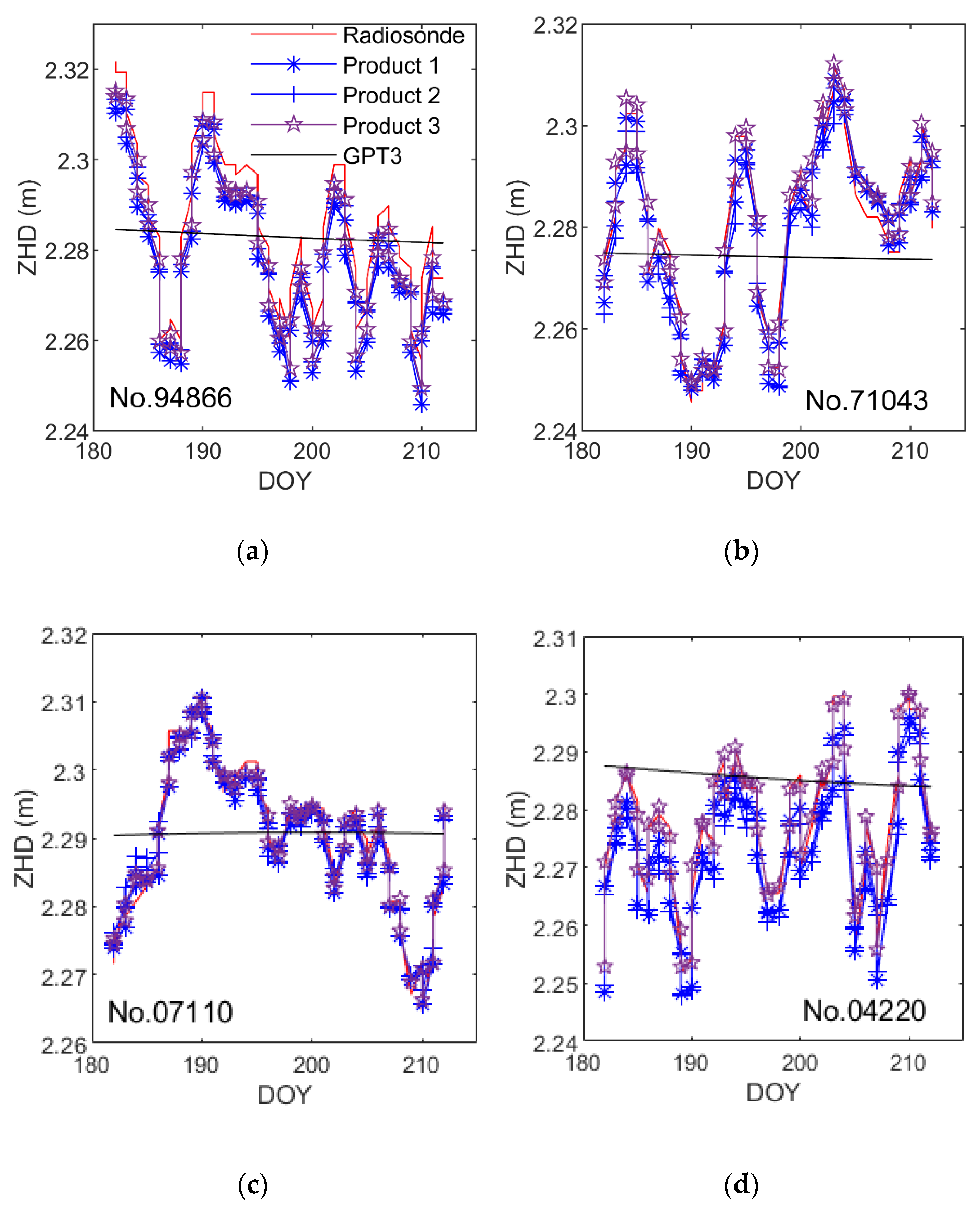
3.1. A Priori ZHD from VMF1_FC and VMF3_FC
3.2. RT-ZTD Estimated from PPP
3.3. RT-PWV Estimated from PPP
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Model for GPS Uncombined PPP
References
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. The Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere Mapping Functions for GPS and Very Long Baseline Interferometry from European Centre for Medium-Range Weather Forecasts Operational Analysis Data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. Refined Discrete and Empirical Horizontal Gradients in VLBI Analysis. J. Geod. 2018, 92, 1387–1399. [Google Scholar] [CrossRef] [Green Version]
- Guerova, G.; Jones, J.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; Elgered, G.; Vedel, H.; et al. Review of the State of the Art and Future Prospects of the Ground-Based GNSS Meteorology in Europe. Atmos. Meas. Tech. 2016, 9, 5385–5406. [Google Scholar] [CrossRef] [Green Version]
- Gutman, S.I.; Sahm, S.R.; Benjamin, S.G.; Schwartz, B.E.; Holub, K.L.; Stewart, J.Q.; Smith, T.L. Rapid Retrieval and Assimilation of Ground Based GPS Precipitable Water Observations at the NOAA Forecast Systems Laboratory: Impact on Weather Forecasts. J. Meteorol. Soc. Jpn. 2004, 82, 351–360. [Google Scholar] [CrossRef] [Green Version]
- Mile, M.; Benáček, P.; Rózsa, S. The Use of GNSS Zenith Total Delays in Operational AROME/Hungary 3D-Var over a Central European Domain. Atmos. Meas. Tech. 2019, 12, 1569–1579. [Google Scholar] [CrossRef] [Green Version]
- Rohm, W.; Yuan, Y.; Biadeglgne, B.; Zhang, K.; Marshall, J.L. Ground-Based GNSS ZTD/IWV Estimation System for Numerical Weather Prediction in Challenging Weather Conditions. Atmos. Res. 2014, 138, 414–426. [Google Scholar] [CrossRef]
- Ahmed, F.; Václavovic, P.; Teferle, F.N.; Douša, J.; Bingley, R.; Laurichesse, D. Comparative Analysis of Real-Time Precise Point Positioning Zenith Total Delay Estimates. GPS Solut. 2016, 20, 187–199. [Google Scholar] [CrossRef] [Green Version]
- Dousa, J.; Vaclavovic, P. Real-Time Zenith Tropospheric Delays in Support of Numerical Weather Prediction Applications. Adv. Space Res. 2014, 53, 1347–1358. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Ge, M.; Heise, S.; Wickert, J.; Bender, M. Real-Time GPS Sensing of Atmospheric Water Vapor: Precise Point Positioning with Orbit, Clock, and Phase Delay Corrections. Geophys. Res. Lett. 2014, 41, 3615–3621. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Real-Time GPS Precise Point Positioning-Based Precipitable Water Vapor Estimation for Rainfall Monitoring and Forecasting. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3452–3459. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, K.; Rohm, W.; Choy, S.; Norman, R.; Wang, C.-S. Real-Time Retrieval of Precipitable Water Vapor from GPS Precise Point Positioning: Real-Time Retrieval of PWV from GPS PPP. J. Geophys. Res. Atmos. 2014, 119, 10044–10057. [Google Scholar] [CrossRef]
- Hadas, T.; Hobiger, T. Benefits of Using Galileo for Real-Time GNSS Meteorology. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Lu, C.; Ge, M.; Nilsson, T.; Ning, T.; Wickert, J.; Schuh, H. Multi-GNSS Meteorology: Real-Time Retrieving of Atmospheric Water Vapor from BeiDou, Galileo, GLONASS, and GPS Observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6385–6393. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tan, H.; Li, X.; Dick, G.; Wickert, J.; Schuh, H. Real-Time Sensing of Precipitable Water Vapor from BeiDou Observations: Hong Kong and CMONOC Networks. J. Geophys. Res. Atmos. 2018, 123, 7897–7909. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Nilsson, T.; Ning, T.; Heinkelmann, R.; Ge, M.; Glaser, S.; Schuh, H. Real-Time Retrieval of Precipitable Water Vapor from GPS and BeiDou Observations. J. Geod. 2015, 89, 843–856. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Ge, M.; Heinkelmann, R.; Nilsson, T.; Soja, B.; Dick, G.; Schuh, H. Estimation and Evaluation of Real-Time Precipitable Water Vapor from GLONASS and GPS. GPS Solut. 2016, 20, 703–713. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Chen, X.; Liu, G.; Dick, G.; Wickert, J.; Jiang, X.; Zheng, K.; Schuh, H. Real-Time Tropospheric Delays Retrieved from Multi-GNSS Observations and IGS Real-Time Product Streams. Remote Sens. 2017, 9, 1317. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Feng, G.; Zheng, Y.; Zhang, K.; Tan, H.; Dick, G.; Wickert, J. Real-Time Retrieval of Precipitable Water Vapor from Galileo Observations by Using the MGEX Network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4743–4753. [Google Scholar] [CrossRef]
- Pan, L.; Guo, F. Real-Time Tropospheric Delay Retrieval with GPS, GLONASS, Galileo and BDS Data. Sci. Rep. 2018, 8, 17067. [Google Scholar] [CrossRef] [Green Version]
- Ding, W.; Teferle, F.N.; Kazmierski, K.; Laurichesse, D.; Yuan, Y. An Evaluation of Real-Time Troposphere Estimation Based on GNSS Precise Point Positioning. J. Geophys. Res. Atmos. 2017, 122, 2779–2790. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Cheng, J.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Real-Time Tropospheric Delay Retrieval from Multi-GNSS PPP Ambiguity Resolution: Validation with Final Troposphere Products and a Numerical Weather Model. Remote Sens. 2018, 10, 481. [Google Scholar] [CrossRef] [Green Version]
- Hadas, T.; Teferle, F.N.; Kazmierski, K.; Hordyniec, P.; Bosy, J. Optimum Stochastic Modeling for GNSS Tropospheric Delay Estimation in Real-Time. GPS Solut. 2017, 21, 1069–1081. [Google Scholar] [CrossRef] [Green Version]
- Hadas, T.; Hobiger, T.; Hordyniec, P. Considering Different Recent Advancements in GNSS on Real-Time Zenith Troposphere Estimates. GPS Solut. 2020, 24, 99. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Li, Y.; Gao, Y. Impacts of Real-Time Satellite Clock Errors on GPS Precise Point Positioning-Based Troposphere Zenith Delay Estimation. J. Geod. 2015, 89, 747–756. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, L.; Wang, G.; Li, W. The Impact of Second-Order Ionospheric Delays on the ZWD Estimation with GPS and BDS Measurements. GPS Solut. 2020, 24, 41. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, F.; Zhang, X. The Effects of Higher-Order Ionospheric Terms on GPS Tropospheric Delay and Gradient Estimates. Remote Sens. 2018, 10, 1561. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Václavovic, P.; Douša, J. Performance Evaluation of Troposphere Estimated from Galileo-Only Multi-Frequency Observations. Remote Sens. 2020, 12, 373. [Google Scholar] [CrossRef] [Green Version]
- Zus, F.; Deng, Z.; Wickert, J. The Impact of Higher-Order Ionospheric Effects on Estimated Tropospheric Parameters in Precise Point Positioning: Higher-Order Ionospheric Effects. Radio Sci. 2017, 52, 963–971. [Google Scholar] [CrossRef] [Green Version]
- Kouba, J. Implementation and Testing of the Gridded Vienna Mapping Function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Tregoning, P.; Herring, T.A. Impact of a Priori Zenith Hydrostatic Delay Errors on GPS Estimates of Station Heights and Zenith Total Delays. Geophys. Res. Lett. 2006, 33, L23303. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging satellites. In The Use of Artificial Satellites for Geodesy; American Geophysical Union (AGU): Washington, DC, USA, 1972; pp. 247–251. ISBN 978-1-118-66364-6. [Google Scholar]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical Slant Delay Model for Radio Space Geodetic Techniques. Geophys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Zhang, K.; Wu, S.; He, C.; Cheng, Y.; Li, X. Determination of Zenith Hydrostatic Delay and Its Impact on GNSS-Derived Integrated Water Vapor. Atmos. Meas. Tech. 2017, 10, 2807–2820. [Google Scholar] [CrossRef] [Green Version]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Re3data.org: VMF Data Server Editing Status 2020-12-14; Re3data.Org-Registry of Research Data Repositories. Available online: https://vmf.geo.tuwien.ac.at (accessed on 26 July 2021).
- Yao, Y.; Xu, X.; Xu, C.; Peng, W.; Wan, Y. GGOS Tropospheric Delay Forecast Product Performance Evaluation and Its Application in Real-Time PPP. J. Atmos. Sol.-Terr. Phys. 2018, 175, 1–17. [Google Scholar] [CrossRef]
- Yuan, Y.; Holden, L.; Kealy, A.; Choy, S.; Hordyniec, P. Assessment of Forecast Vienna Mapping Function 1 for Real-Time Tropospheric Delay Modeling in GNSS. J. Geod. 2019, 93, 1501–1514. [Google Scholar] [CrossRef]
- Weber, G.; Mervart, L.; Stürze, A. BKG Ntrip Client (BNC): Version 2.12; Verlag des Bundesamtes für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2016; Volume 49. [Google Scholar]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W. An Analysis of Multisource Tropospheric Hydrostatic Delays and Their Implications for GPS/GLONASS PPP-Based Zenith Tropospheric Delay and Height Estimations. J. Geod. 2021, 95, 83. [Google Scholar] [CrossRef]
- Sun, P.; Wu, S.; Zhang, K.; Wan, M.; Wang, R. A New Global Grid-Based Weighted Mean Temperature Model Considering Vertical Nonlinear Variation. Atmos. Meas. Tech. 2021, 14, 2529–2542. [Google Scholar] [CrossRef]

| Item | Strategy |
|---|---|
| Frequency | GPS: L1, L2 |
| Sampling interval | 30 s |
| Elevation cut-off angle | 5° |
| PPP model | Uncombined PPP (see Appendix A) |
| Receiver phase center | Corrected |
| Solid earth tide | Corrected |
| Ocean tide | Corrected |
| Phase wind-up | Corrected |
| Estimation method | Kalman filtering |
| Station coordinate | Estimated, constant was assumed |
| ZHD | Corrected with VMF1_FC/VMF3_FC grid |
| ZWD | Estimated, random-walk process was assumed (0.02 m), and the initial value of the first epoch was set to the ZWD derived from VMF1_FC/VMF3_FC grid. |
| Tropospheric gradient | Neglected |
| Mapping function | VMF1/VMF3 |
| Receiver clock error | Estimated, white noise was assumed |
| Ambiguity | Estimated, float constant was assumed |
| Slant ionospheric delay | Estimated, random-walk process was assumed (0.04 ) |
| Product No. | VMF Product | Resolution | Mapping Function |
|---|---|---|---|
| 1 | VMF1_FC | 2.5° × 2° | VMF1 |
| 2 | VMF3_FC | 5° × 5° | VMF3 |
| 3 | VMF3_FC | 1° × 1° | VMF3 |
| Product No. | Bias (mm) Mean [Min, Max] | RMSE (mm) Mean [Min, Max] | ||
|---|---|---|---|---|
| 1 | −2.2 | [−38.9, 53.0] | 5.9 | [1.4, 53.1] |
| 2 | 0.5 | [−41.3, 53.2] | 5.4 | [1.3, 53.3] |
| 3 | 1.7 | [−18.2, 55.1] | 4.3 | [1.3, 55.1] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Zhang, K.; Wu, S.; Wan, M.; Lin, Y. Retrieving Precipitable Water Vapor from Real-Time Precise Point Positioning Using VMF1/VMF3 Forecasting Products. Remote Sens. 2021, 13, 3245. https://doi.org/10.3390/rs13163245
Sun P, Zhang K, Wu S, Wan M, Lin Y. Retrieving Precipitable Water Vapor from Real-Time Precise Point Positioning Using VMF1/VMF3 Forecasting Products. Remote Sensing. 2021; 13(16):3245. https://doi.org/10.3390/rs13163245
Chicago/Turabian StyleSun, Peng, Kefei Zhang, Suqin Wu, Moufeng Wan, and Yun Lin. 2021. "Retrieving Precipitable Water Vapor from Real-Time Precise Point Positioning Using VMF1/VMF3 Forecasting Products" Remote Sensing 13, no. 16: 3245. https://doi.org/10.3390/rs13163245
APA StyleSun, P., Zhang, K., Wu, S., Wan, M., & Lin, Y. (2021). Retrieving Precipitable Water Vapor from Real-Time Precise Point Positioning Using VMF1/VMF3 Forecasting Products. Remote Sensing, 13(16), 3245. https://doi.org/10.3390/rs13163245







