Automated Rain Detection by Dual-Polarization Sentinel-1 Data
Abstract
1. Introduction
2. Dataset
2.1. Sentinel-1
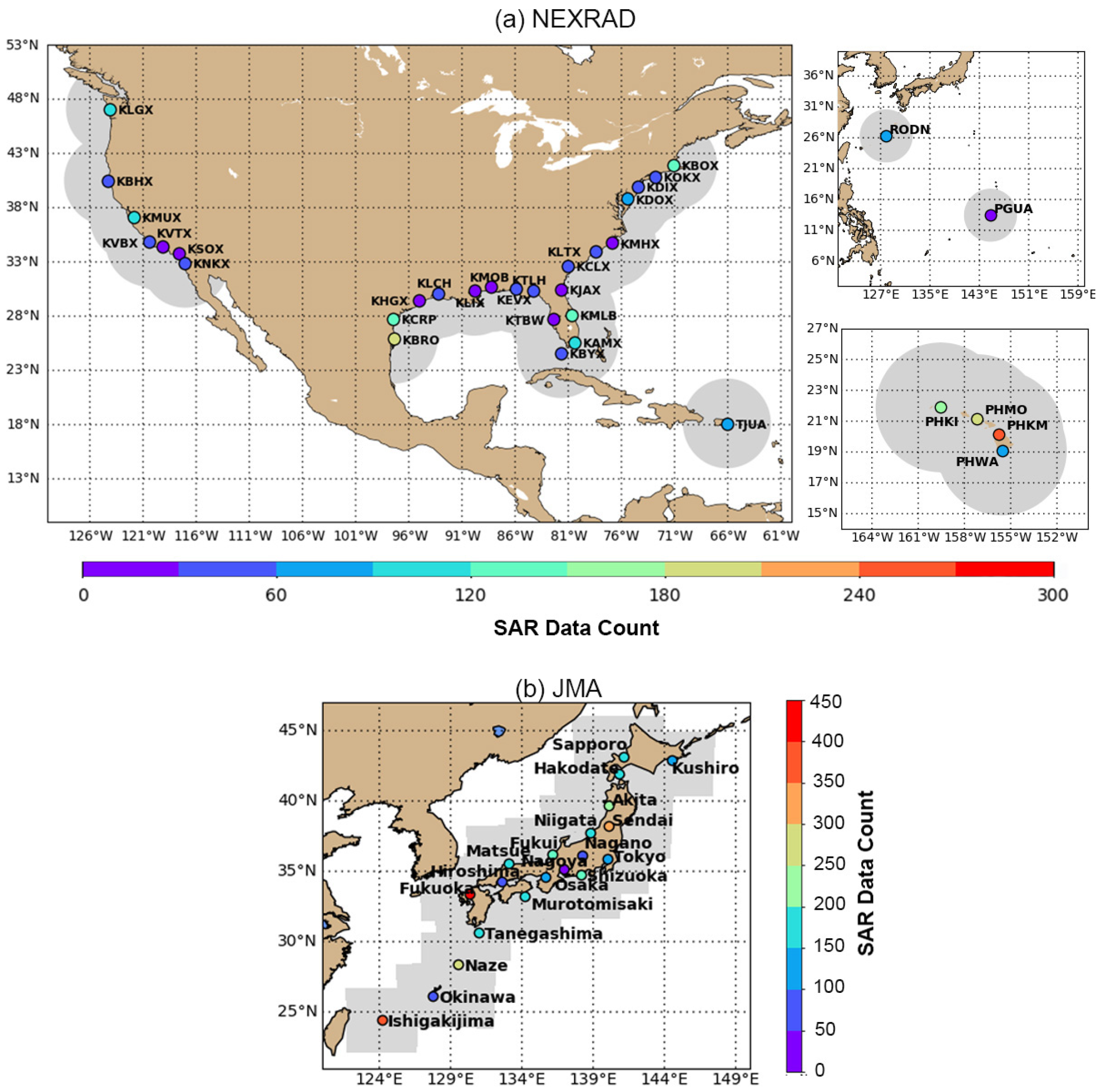
2.2. Weather Radar
2.3. Match-Up Database with Sentinel-1 and Weather Radar Data
3. Co-Analysis of Rain Rate and C-Band SAR Backscattering
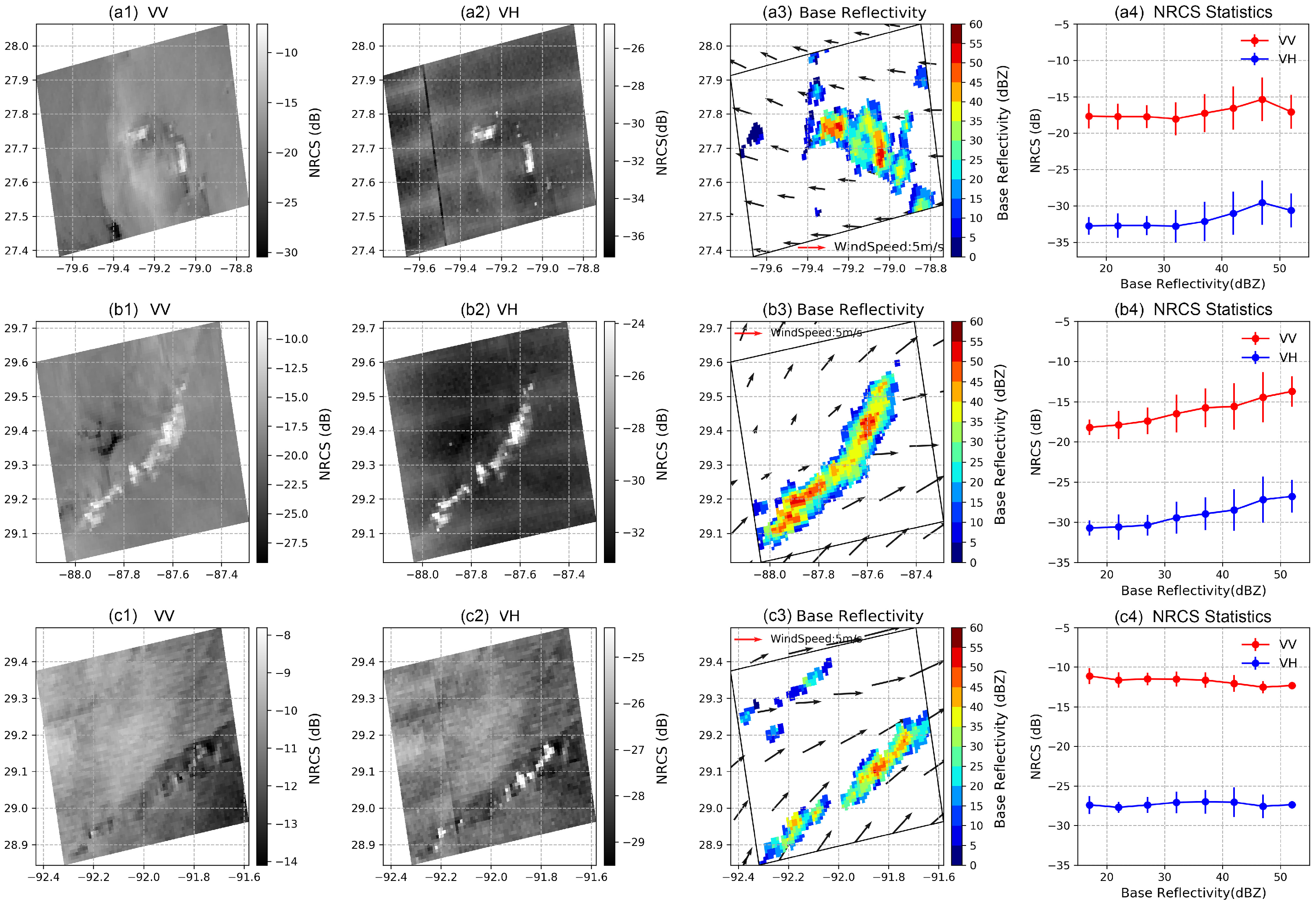
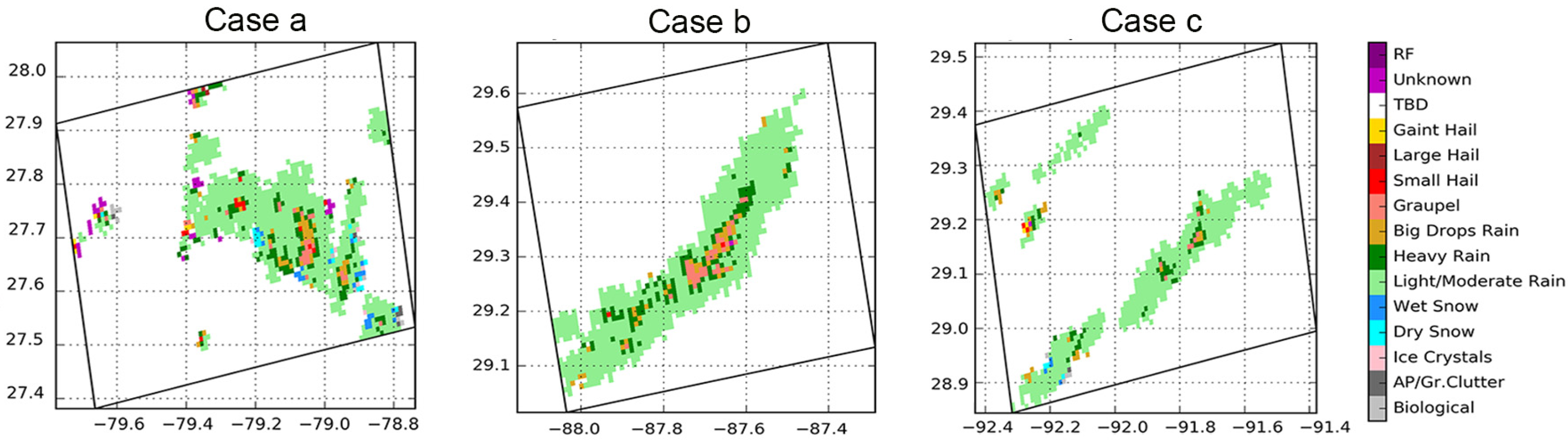
3.1. A First Qualitative Assessment
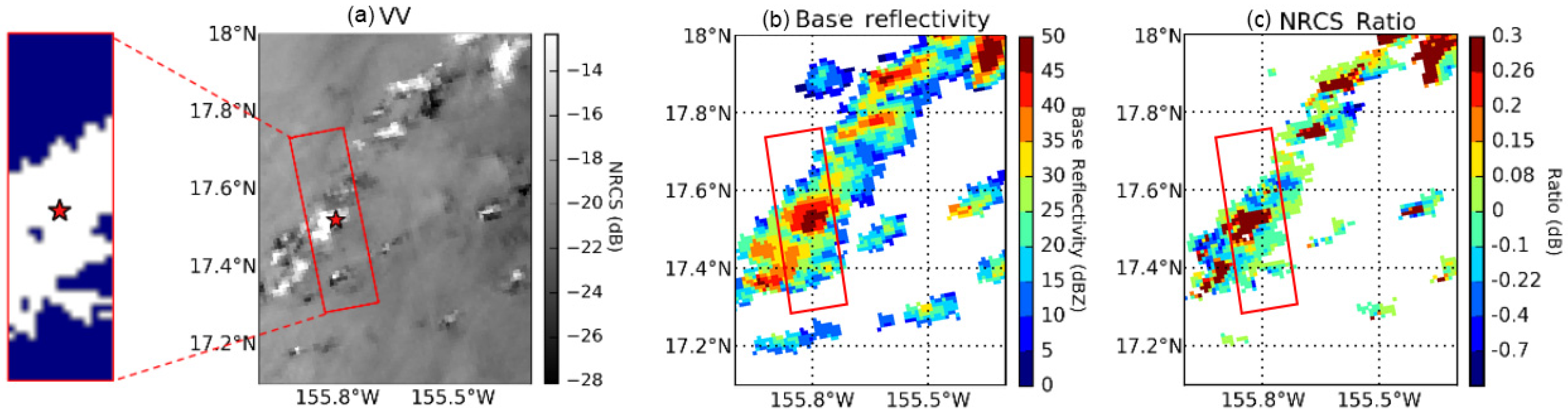
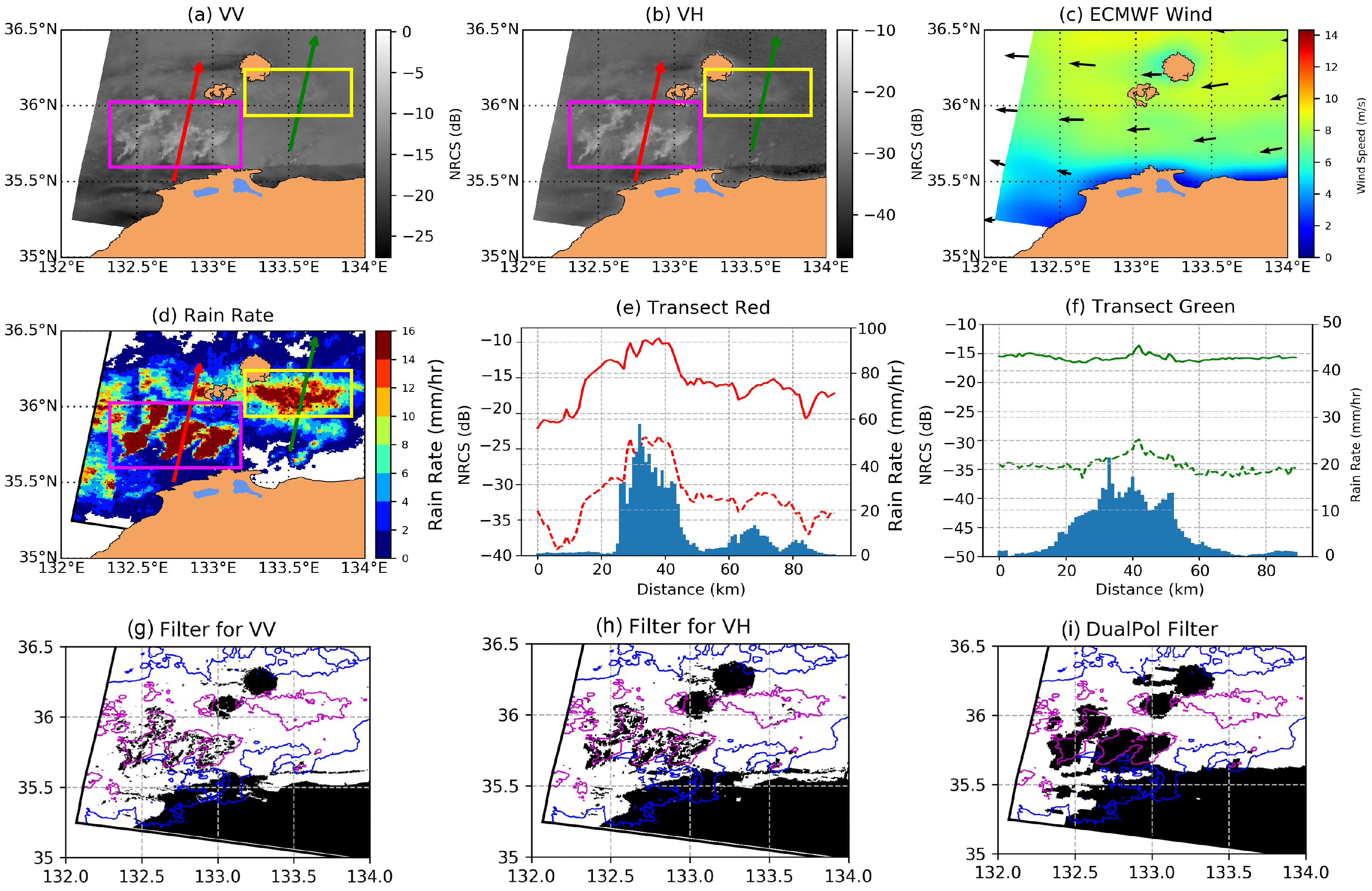
- Case a (Top in Figure 2): This is a typical example of storm cell footprint as discussed by Atlas [28]. Both VV- and VH-polarized images show two rain areas with concurrent bright and dark patches within the cell, the downdraft area and the wind gust. Here the surrounding wind speed is about 3 m/s. Collocated NEXRAD measurements presented in Figure 2(a3) indicate two separate rain cells. Bright patches are located at the same location in VV and VH images and correspond to NEXRAD base reflectivity measurements higher than 40 dBZ. This suggests an increase of C-band radar backscattering at high rain rates. As also noted by Melsheimer et al. [23], the extent of base reflectivity is less than the storm cell signature in the SAR image as rain radar is not sensitive to the wind acceleration due to downdraft or its associated wind gust. In this case, the relationship between NRCS and base reflectivity confirms the NRCS increases with base reflectivity for values larger than 40 dBZ.
- Case b (Middle in Figure 2): This case acquired in the Gulf of Mexico corresponds to a stationary front with stratiform precipitation without intense vertical convection. As indicated by Figure 2(b3), wind speed is significantly different on each side of the atmospheric front with ambient background wind speed lower than 2 m/s in the western area and higher than 6 m/s in the eastern area. In this case, there is also a good match between bright patches observed on both co- and cross-polarization channels and the highest values of base reflectivity (see Figure 2(b3)). The relationship between NRCS and base reflectivity also confirms that for values larger than 25 dBZ, the NRCS increases with base reflectivity.
- Case c (Bottom in Figure 2): Here, the background ambient wind is stronger than in the previous cases, about 13 m/s from the model. As observed, the distribution, size and intensity of the bright patches are not the same in co- and cross-polarization. More bright patches are observed in VH than in VV. In particular, dark areas are observed in the VV image where the VH image exhibits bright patches associated with high base reflectivity. As a result, in this case, the VV NRCS shows decreases when the base reflectivity increases whereas the VH NRCS stays almost constant.
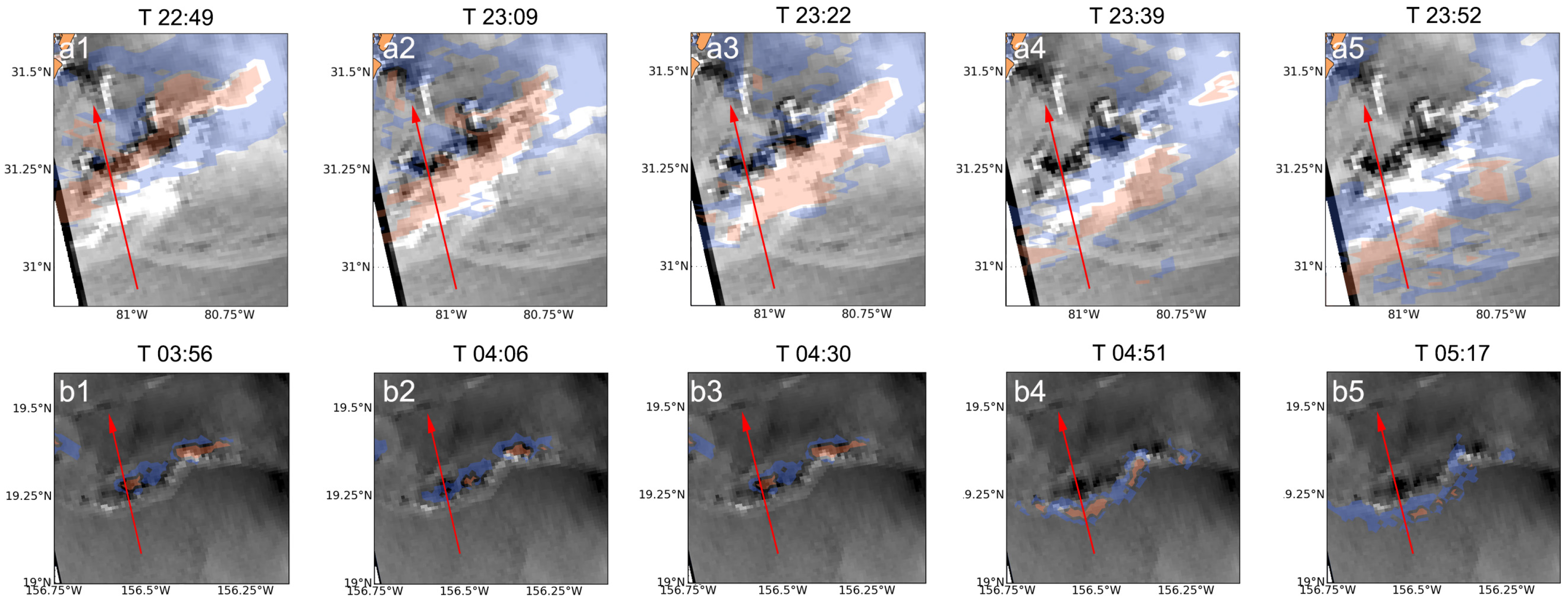
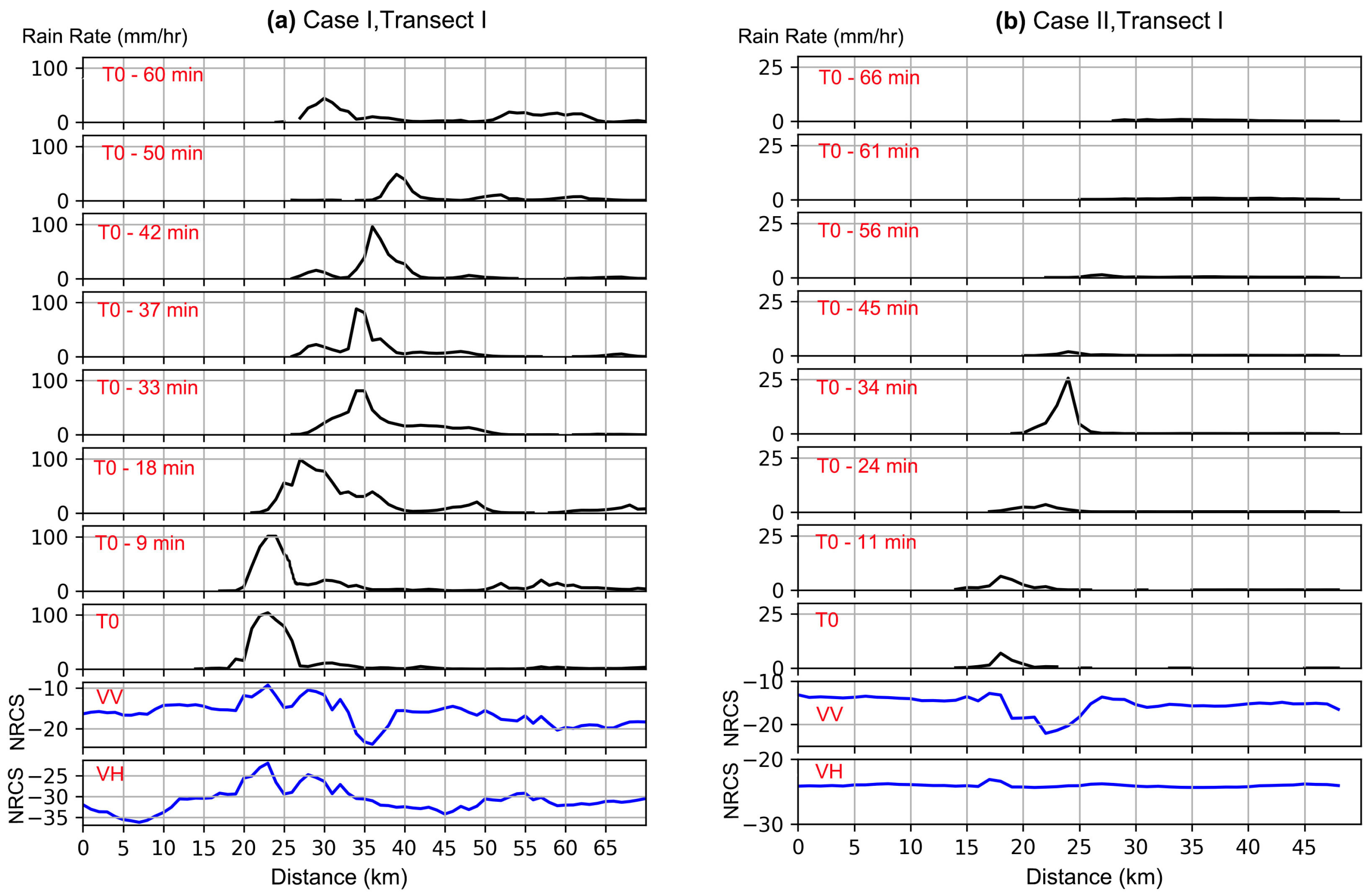
3.2. Timeliness of the Data
3.3. Scattering by the Melting Layer
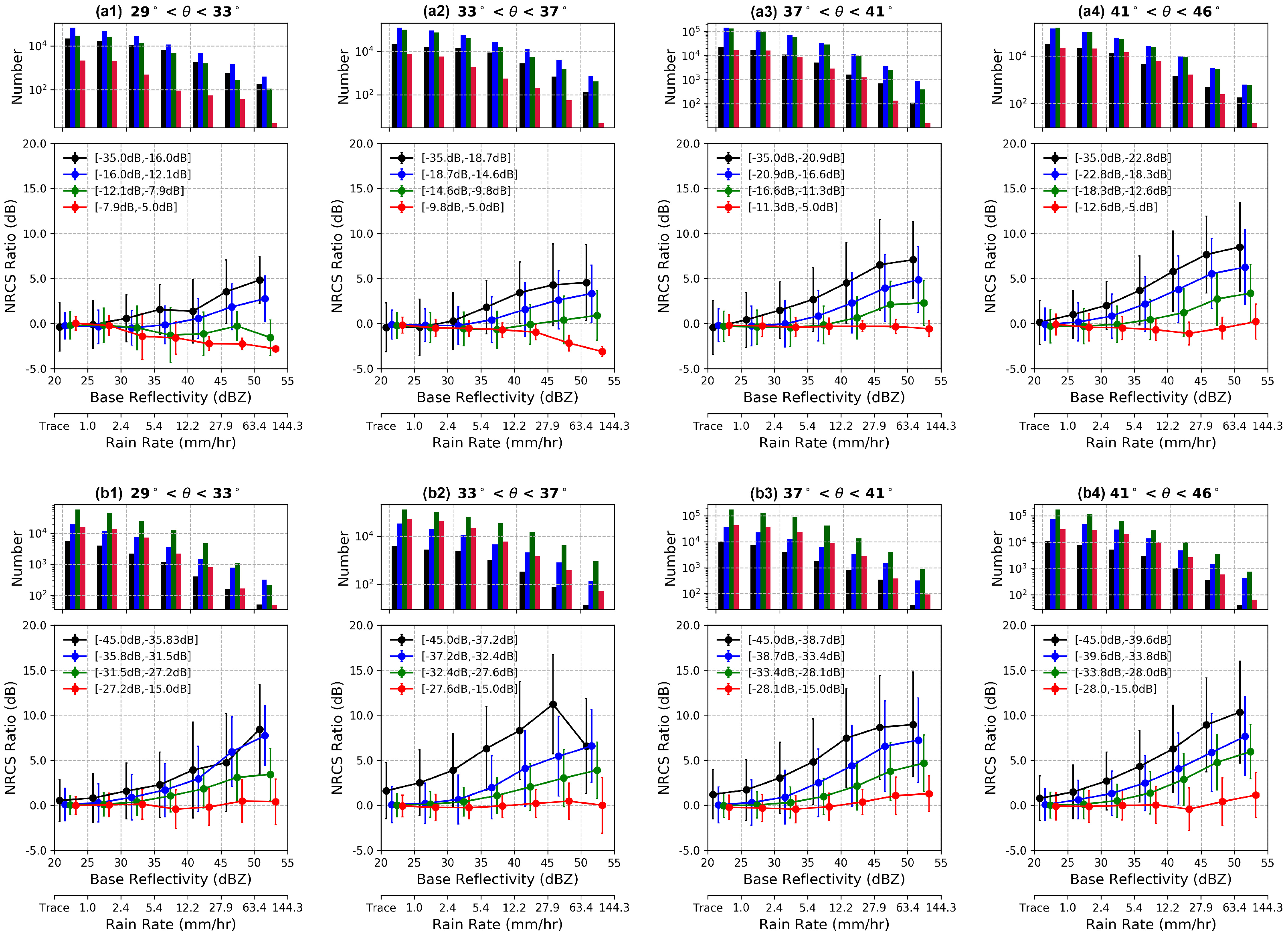
3.4. Statistical Analysis
4. Rain Detection
4.1. Optimization of the Heterogeneity Filter(s) for Rain Detection
- : The ratio between the standard deviation and the average computed for each pixel using a sliding bounding box of the smoothed/reduced image. It is computed using a convolutive averaging bounding box over the amplitude (square root of NRCS) and its second moment. This parameter is particularly useful to decipher open water surface from other extended areas (land, tidal zones, sea ice, etc.)
- : The second parameter is built on a Laplace pyramid filter with the difference between images at adjacent levels in the pyramid. It is based on the squared ratio of the high-pass-filtered image and its local average. It has the capability of detecting narrow image features, as slicks, internal waves, or fronts.
- : The third parameter is the ratio of the magnitude of the squared local Sobel-based gradient and its local average. A Sobel operator is basically involved to do spatial gradient measurement on 2-dimensional images. It is generally adapted to detect edges and point targets.
- : The ratio between the reduced/smoothed version of the squared local gradient and its absolute squared gradient: it can be considered to be a measure of directional coherence. It should detect the edges such as ”slicks, internal waves, or fronts” [25].
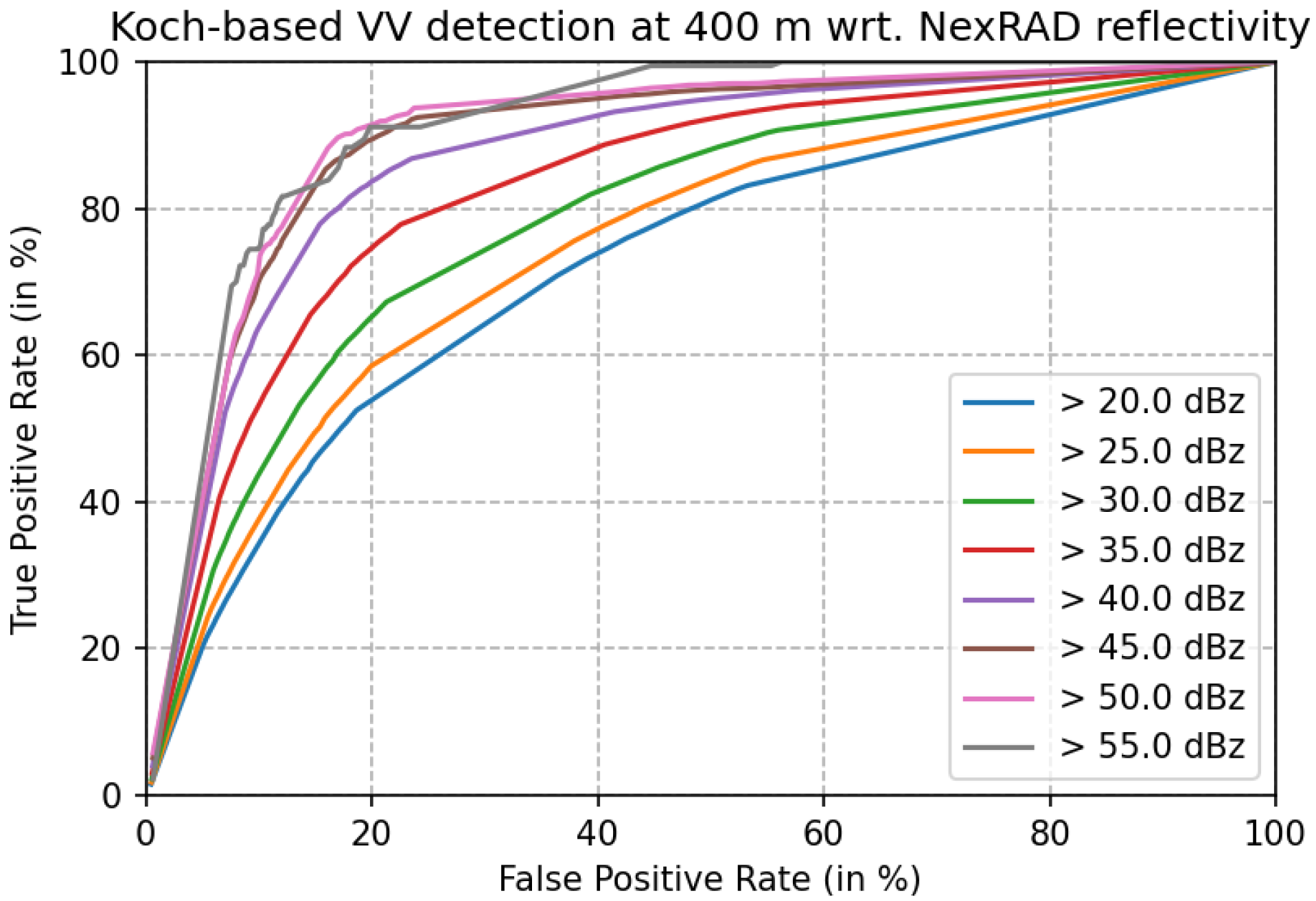
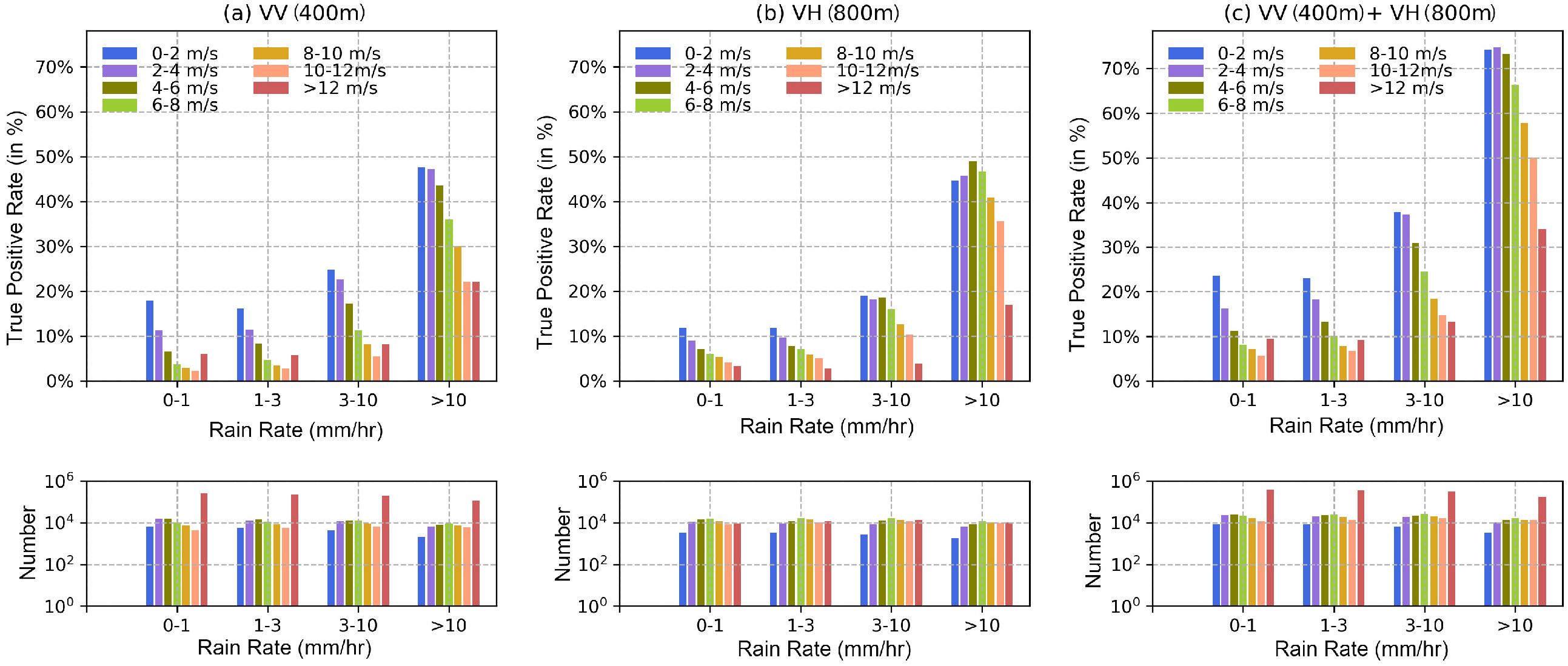
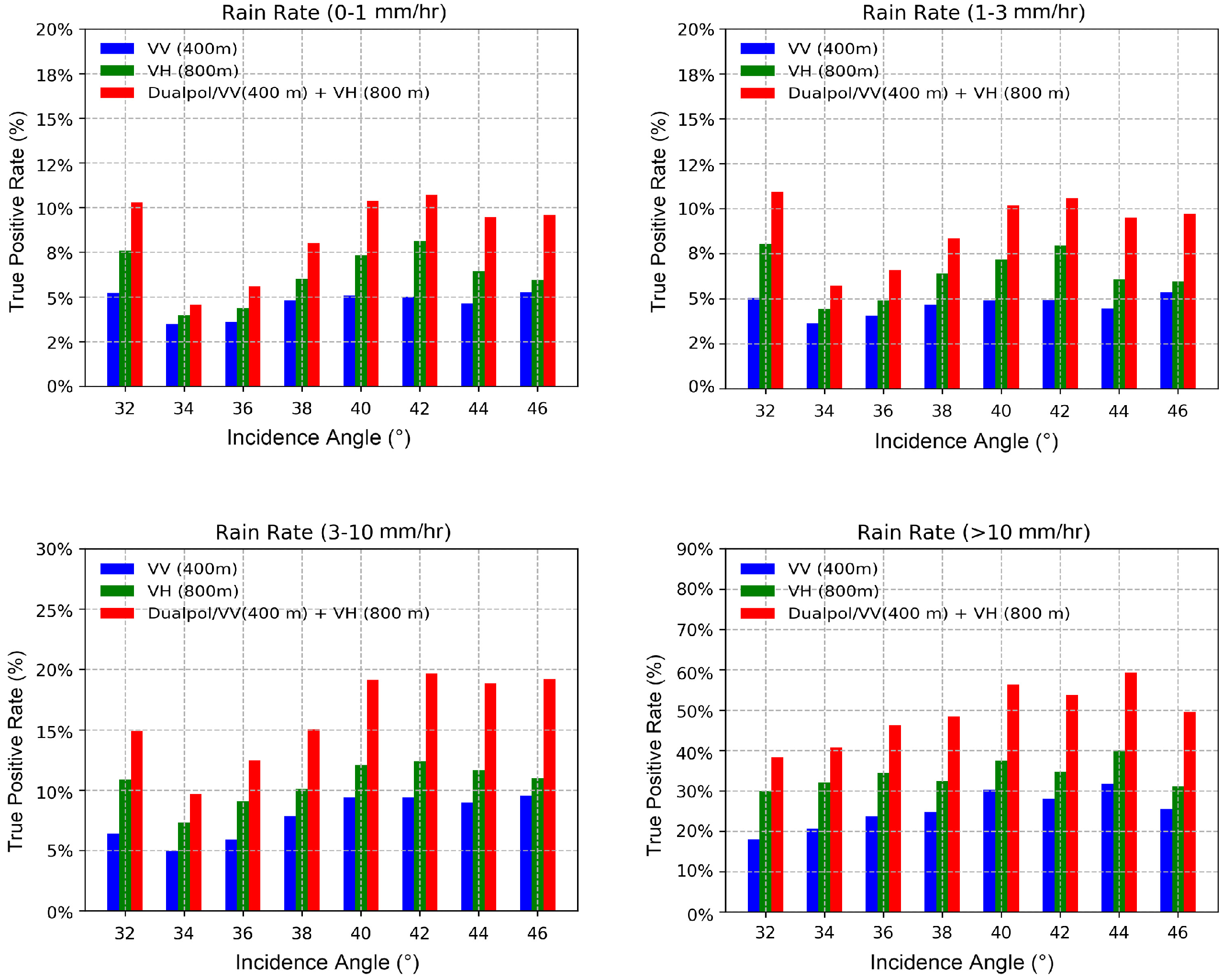
4.2. Validation of the Performance of the Filters
4.3. Application of Dual-Pol Filter on Different Rain Types
5. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, L.L.; Holt, B. Seasat Views Oceans and Sea Ice with Synthetic-Aperture Radar; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1982; Volume 81. [Google Scholar]
- Wang, C.; Vandemark, D.; Mouche, A.; Chapron, B.; Li, H.; Foster, R.C. An assessment of marine atmospheric boundary layer roll detection using Sentinel-1 SAR data. Remote Sens. Environ. 2020, 250, 112031. [Google Scholar] [CrossRef]
- Fan, S.; Kudryavtsev, V.; Zhang, B.; Perrie, W.; Chapron, B.; Mouche, A. On C-Band Quad-Polarized Synthetic Aperture Radar Properties of Ocean Surface Currents. Remote Sens. 2019, 11, 2321. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Fan, S.; Zhang, B.; Mouche, A.A.; Chapron, B. On quad-polarized SAR measurements of the ocean surface. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8362–8370. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Kozlov, I.; Chapron, B.; Johannessen, J. Quad-polarization SAR features of ocean currents. J. Geophys. Res. Ocean. 2014, 119, 6046–6065. [Google Scholar] [CrossRef]
- Horstmann, J.; Wackerman, C.; Falchetti, S.; Maresca, S. Tropical cyclone winds retrieved from synthetic aperture radar. Oceanography 2013, 26, 46–57. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Zhang, J.A.; Uhlhorn, E.W.; He, Y. High-resolution hurricane vector winds from C-band dual-polarization SAR observations. J. Atmos. Ocean. Technol. 2014, 31, 272–286. [Google Scholar] [CrossRef]
- Mouche, A.A.; Chapron, B.; Zhang, B.; Husson, R. Combined co-and cross-polarized SAR measurements under extreme wind conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Brekke, C.; Johannessen, J.A. Wave breaking in slicks: Impacts on C-band quad-polarized SAR measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4929–4940. [Google Scholar] [CrossRef]
- Johansson, A.M.; Brekke, C.; Spreen, G.; King, J.A. X-, C-, and L-band SAR signatures of newly formed sea ice in Arctic leads during winter and spring. Remote Sens. Environ. 2018, 204, 162–180. [Google Scholar] [CrossRef]
- Longépé, N.; Thibaut, P.; Vadaine, R.; Poisson, J.C.; Guillot, A.; Boy, F.; Picot, N.; Borde, F. Comparative evaluation of sea ice lead detection based on SAR imagery and altimeter data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4050–4061. [Google Scholar] [CrossRef]
- Li, X.M.; Sun, Y.; Zhang, Q. Extraction of Sea Ice Cover by Sentinel-1 SAR Based on Support Vector Machine With Unsupervised Generation of Training Data. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3040–3053. [Google Scholar] [CrossRef]
- Gelis, I.D.; Colin, A.; Longépé, N. Prediction of categorized Sea Ice Concentration from Sentinel-1 SAR images based on a Fully Convolutional Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5831–5841. [Google Scholar] [CrossRef]
- Melsheimer, C.; Alpers, W.; Gade, M. Investigation of multifrequency/multipolarization radar signatures of rain cells over the ocean using SIR-C/X-SAR data. J. Geophys. Res. Ocean. 1998, 103, 18867–18884. [Google Scholar] [CrossRef]
- Lin, I.I.; Alpers, W.; Khoo, V.; Lim, H.; Lim, T.K.; Kasilingam, D. An ERS-1 synthetic aperture radar image of a tropical squall line compared with weather radar data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 937–945. [Google Scholar] [CrossRef]
- Danklmayer, A.; Doring, B.J.; Schwerdt, M.; Chandra, M. Assessment of Atmospheric Propagation Effects in SAR Images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3507–3518. [Google Scholar] [CrossRef]
- Alpers, W.; Zhang, B.; Mouche, A.; Zeng, K.; Chan, P.W. Rain footprints on C-band synthetic aperture radar images of the ocean-Revisited. Remote Sens. Environ. 2016, 187, 169–185. [Google Scholar] [CrossRef]
- Braun, N.; Gade, M. Multi-frequency scatterometer measurements on water surfaces agitated by artificial and natural rain. Int. J. Remote Sens. 2006, 27, 27–39. [Google Scholar] [CrossRef]
- Tournadre, J.; Morland, J.C. The effects of rain on TOPEX/Poseidon altimeter data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1117–1135. [Google Scholar] [CrossRef]
- Olsen, R.; Rogers, D.V.; Hodge, D. The aR b relation in the calculation of rain attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Alpers, W.; Zhao, Y.; Mouche, A.A.; Chan, P.W. A note on radar signatures of hydrometeors in the melting layer as inferred from Sentinel-1 SAR data acquired over the ocean. Remote Sens. Environ. 2020, 253, 112177. [Google Scholar] [CrossRef]
- Lin, W.; Portabella, M.; Stoffelen, A.; Turiel, A.; Verhoef, A. Rain identification in ASCAT winds using singularity analysis. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1519–1523. [Google Scholar] [CrossRef][Green Version]
- Melsheimer, C.; Alpers, W.; Gade, M. Simultaneous observations of rain cells over the ocean by the synthetic aperture radar aboard the ERS satellites and by surface-based weather radars. J. Geophys. Res. Ocean. 2001, 106, 4665–4677. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, Q.; Liu, R.; Wang, D.; Duncan, J.H.; Huang, S.J. A study of radar backscattering from water surface in response to rainfall. J. Geophys. Res. Ocean. 2016, 121, 1546–1562. [Google Scholar] [CrossRef]
- Koch, W. Directional analysis of SAR images aiming at wind direction. IEEE Trans. Geosci. Remote Sens. 2004, 42, 702–710. [Google Scholar] [CrossRef]
- Longépé, N.; Mouche, A.; Ferro-Famil, L.; Husson, R. Co-Cross Polarization Coherence over the Sea Surface from Sentinel-1 SAR Data: Perspectives for Mission Calibration and Wind Field Retrieval. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrops with size. J. Meteor. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Atlas, D. Origin of storm footprints on the sea seen by synthetic aperture radar. Science 1994, 266, 1364–1366. [Google Scholar] [CrossRef]
- Moore, R.; Yu, Y.; Fung, A.; Kaneko, D.; Dome, G.; Werp, R. Preliminary study of rain effects on radar scattering from water surfaces. IEEE J. Ocean. Eng. 1979, 4, 31–32. [Google Scholar] [CrossRef]
- Bliven, L.; Sobieski, P.; Craeye, C. Rain generated ring-waves: Measurements and modelling for remote sensing. Int. J. Remote Sens. 1997, 18, 221–228. [Google Scholar] [CrossRef]
- Jameson, A.R.; Li, F.K.; Durden, S.L.; Haddad, Z.S.; Holt, B.; Fogarty, T.; Im, E.; Moore, R.K. SIR-C/X-SAR observations of rain storms. Remote Sens. Environ. 1997, 59, 267–279. [Google Scholar] [CrossRef]
- Katsaros, K.B.; Paris, W.; Vachon, P.G.B.; Dodge, P.P.; Uhlhorn, E.W. Wind fields from SAR: Could they improve our understanding of storm dynamics? Johns Hopkins Apl Tech. Dig. 2000, 21, 86–93. [Google Scholar]
- Browne, I.C.; Robinson, N. Cross-polarization of the radar melting-band. Nature 1952, 170, 1078–1079. [Google Scholar] [CrossRef]
- Jameson, A. The interpretation and meteorological application of radar backscatter amplitude ratios at linear polarizations. J. Atmos. Ocean. Technol. 1989, 6, 908–919. [Google Scholar] [CrossRef][Green Version]
- Federal Meteorologica Handbook No. 11. In Doppler Radar Meteorological Observations. Part B, Doppler Radar Theory and Meteorology; Technical Report; FCM-H11B-2005; Office of the Federal Coordinator for Meteorological Services and Supporting Research: Washington, DC, USA, 2005.
- Vachon, P.W.; Wolfe, J. C-band cross-polarization wind speed retrieval. IEEE Geosci. Remote Sens. Lett. 2010, 8, 456–459. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B. Global C-Band Envisat, RADARSAT-2 and Sentinel-1 SAR measurements in copolarization and cross-polarization. J. Geophys. Res. Ocean. 2015, 120, 7195–7207. [Google Scholar] [CrossRef]
- Tilbury, J.B.; Van Eetvelt, W.; Garibaldi, J.M.; Curnsw, J.; Ifeachor, E.C. Receiver operating characteristic analysis for intelligent medical systems-a new approach for finding confidence intervals. IEEE Trans. Biomed. Eng. 2000, 47, 952–963. [Google Scholar] [CrossRef] [PubMed]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Atlas, D. Footprints of storms on the sea: A view from spaceborne synthetic aperture radar. J. Geophys. Res. Ocean. 1994, 99, 7961–7969. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Longépé, N.; Mouche, A.; Husson, R. Automated Rain Detection by Dual-Polarization Sentinel-1 Data. Remote Sens. 2021, 13, 3155. https://doi.org/10.3390/rs13163155
Zhao Y, Longépé N, Mouche A, Husson R. Automated Rain Detection by Dual-Polarization Sentinel-1 Data. Remote Sensing. 2021; 13(16):3155. https://doi.org/10.3390/rs13163155
Chicago/Turabian StyleZhao, Yuan, Nicolas Longépé, Alexis Mouche, and Romain Husson. 2021. "Automated Rain Detection by Dual-Polarization Sentinel-1 Data" Remote Sensing 13, no. 16: 3155. https://doi.org/10.3390/rs13163155
APA StyleZhao, Y., Longépé, N., Mouche, A., & Husson, R. (2021). Automated Rain Detection by Dual-Polarization Sentinel-1 Data. Remote Sensing, 13(16), 3155. https://doi.org/10.3390/rs13163155





