Assimilating FY-4A Lightning and Radar Data for Improving Short-Term Forecasts of a High-Impact Convective Event with a Dual-Resolution Hybrid 3DEnVAR Method
Abstract
:1. Introduction
2. Data and Methods
2.1. Lightning Data
2.2. Radar Data
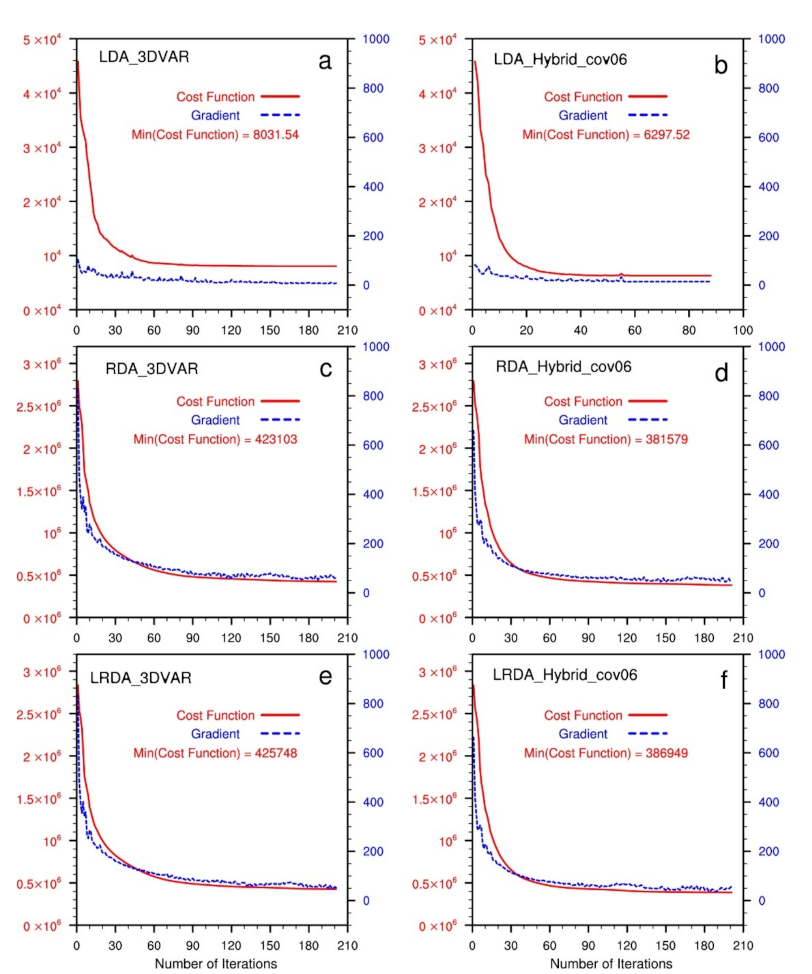
2.3. Data Assimilation Methods
2.3.1. DVAR Method
2.3.2. Dual-Resolution Hybrid 3DEnVAR Method
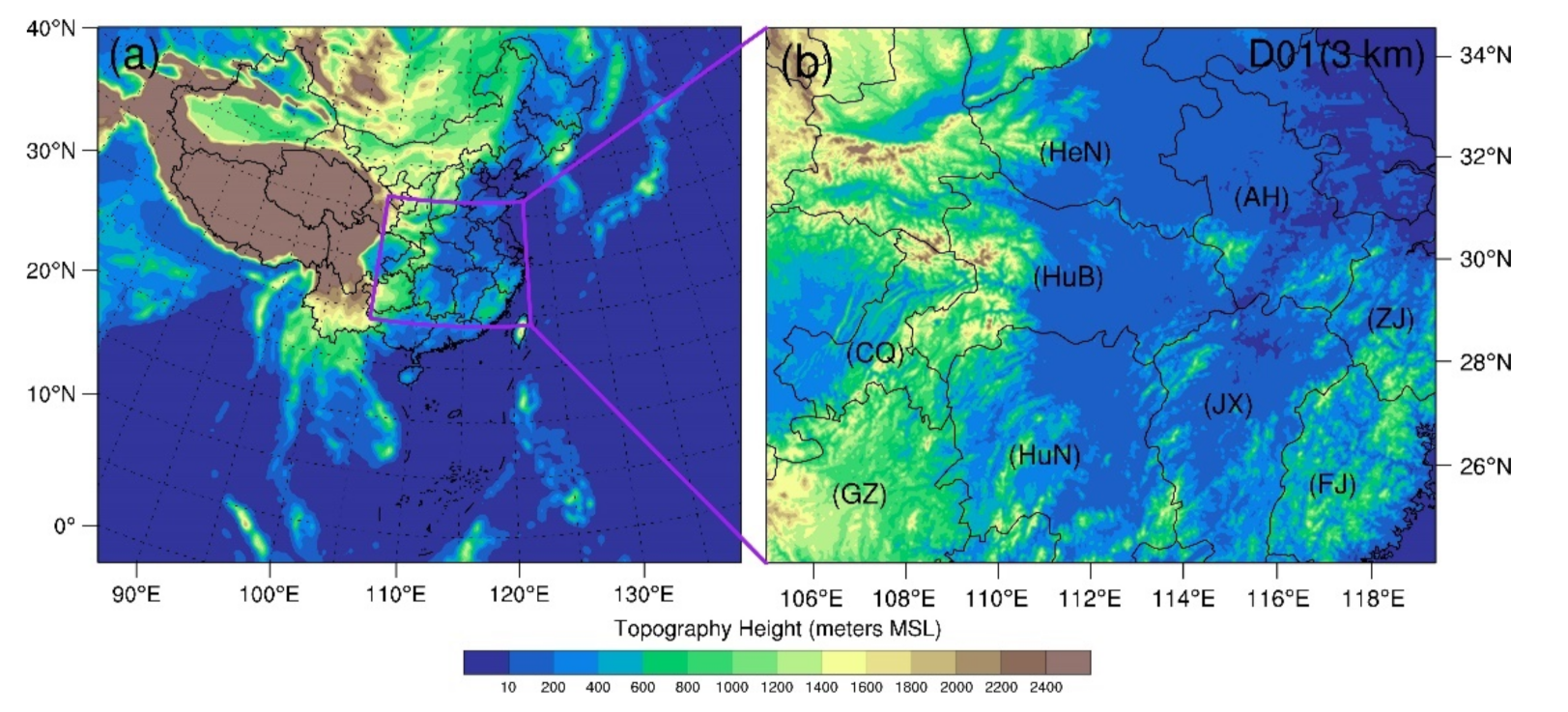
3. Experimental Design and Model Description
3.1. Experimental Design
3.2. Model Description
4. Results
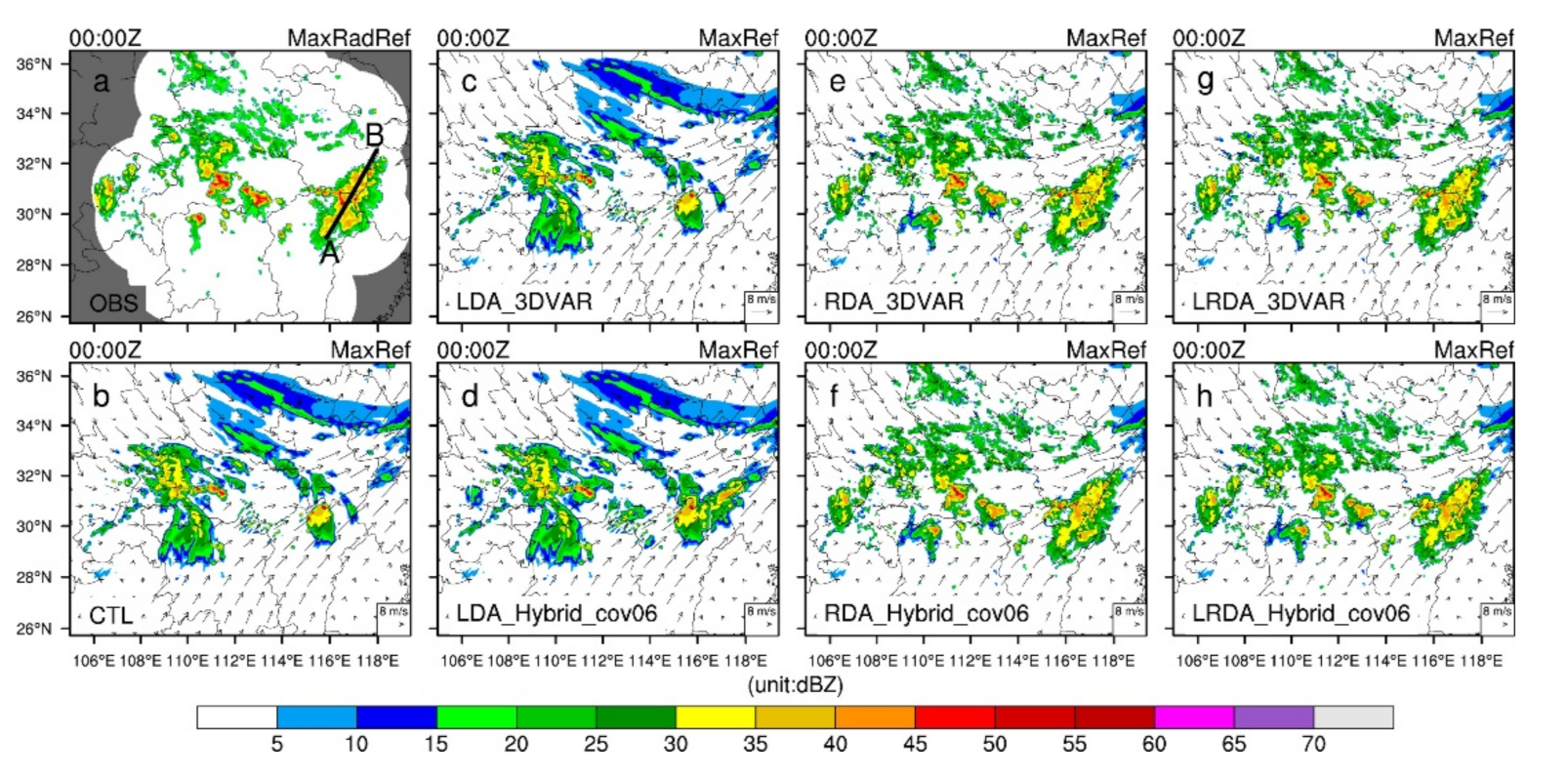
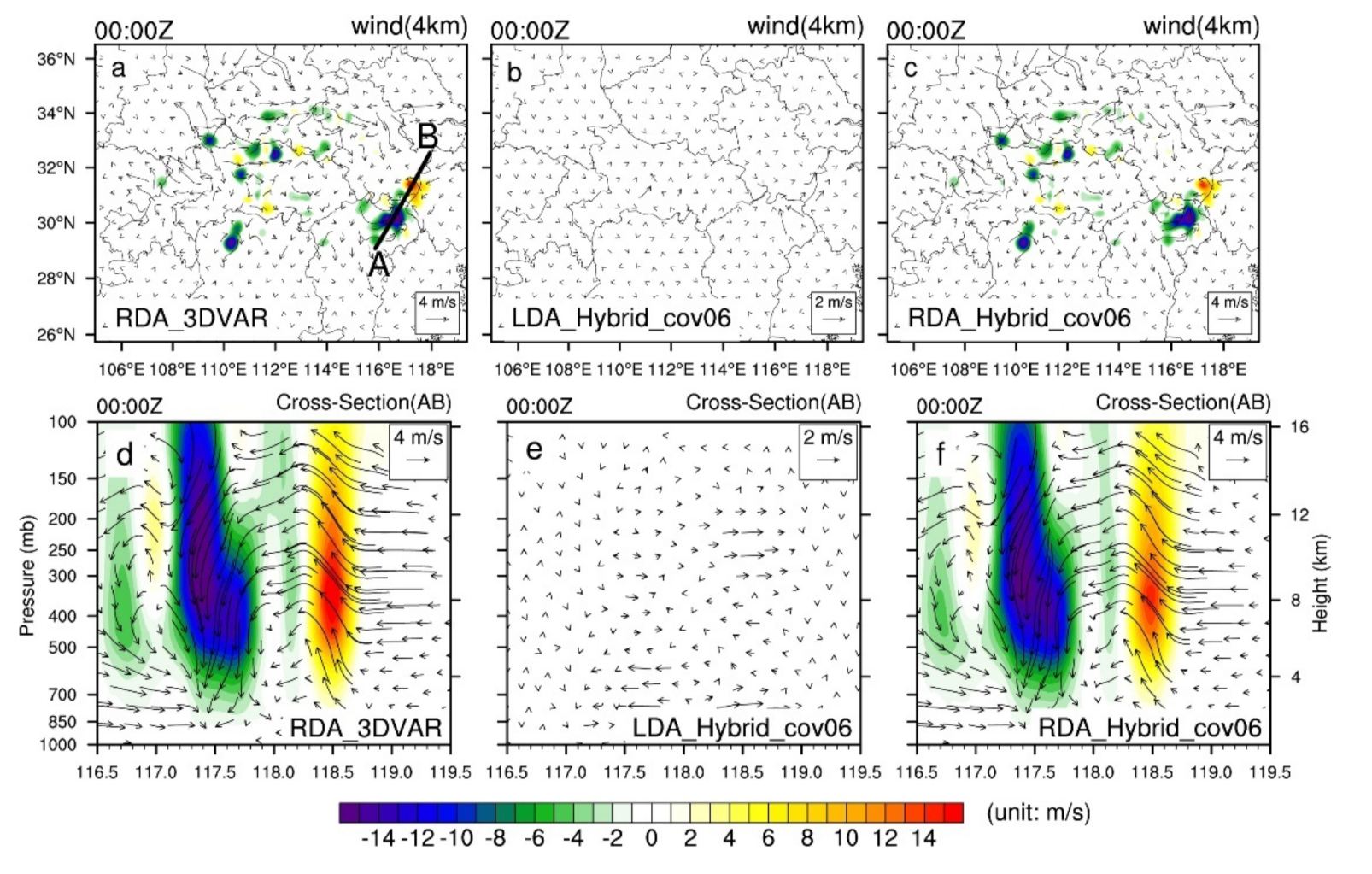
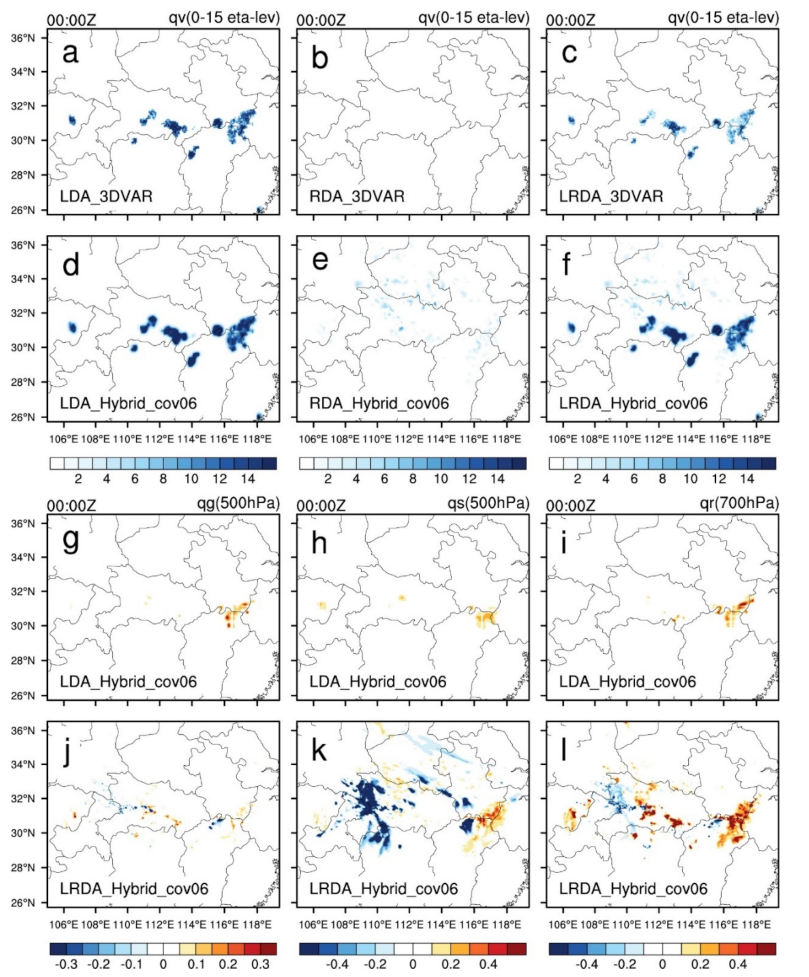
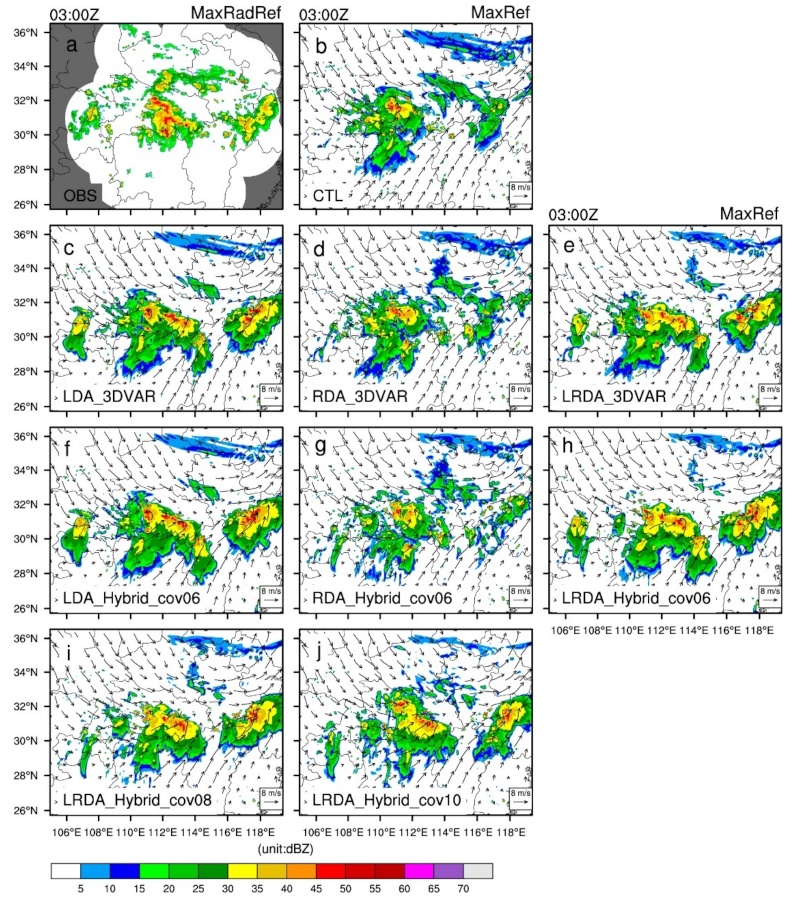
4.1. Analysis Field of Single-analysis Experiments
4.1.1. Radar Reflectivity and Wind Field
4.1.2. Water Vapor and Hydrometers
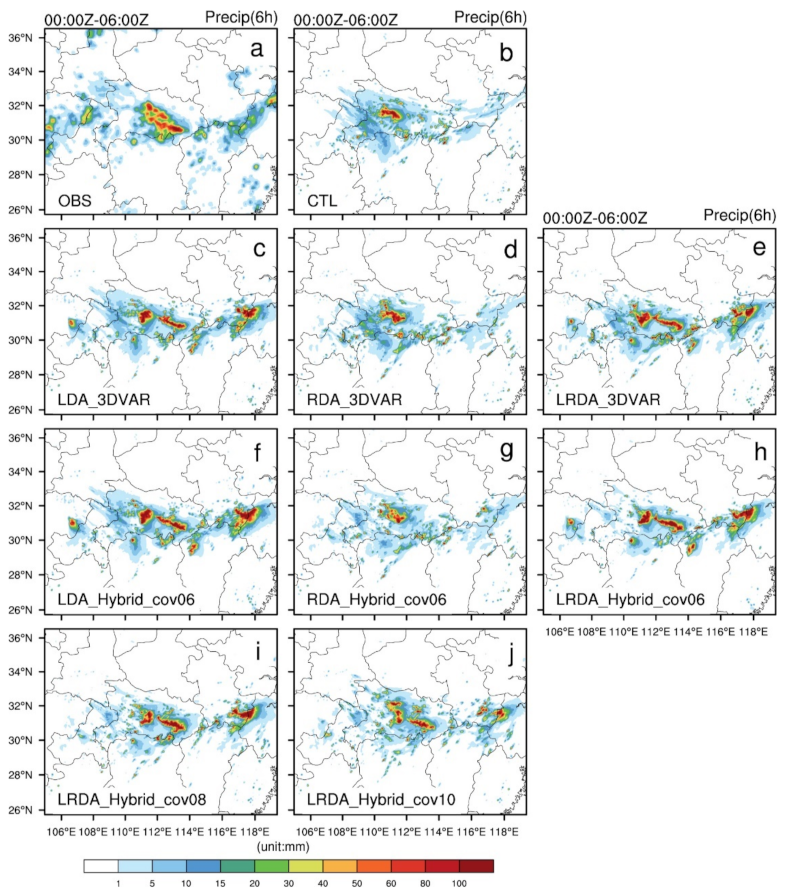
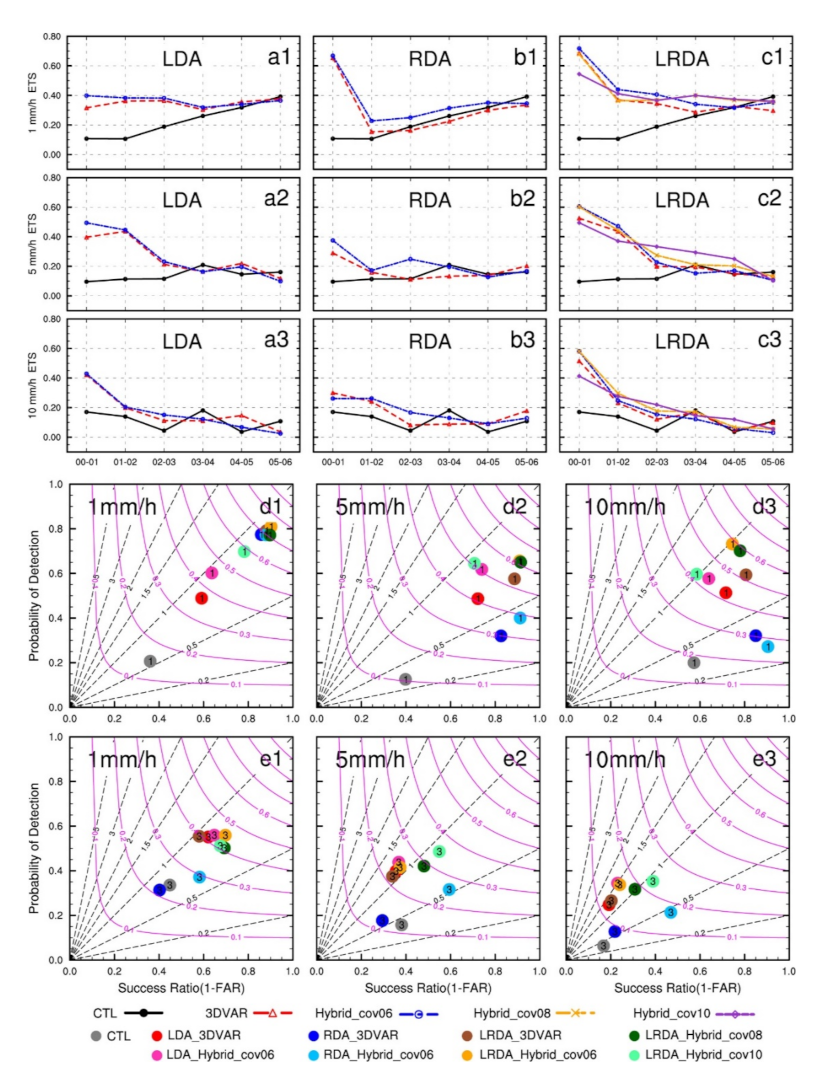
4.2. Forecast Field
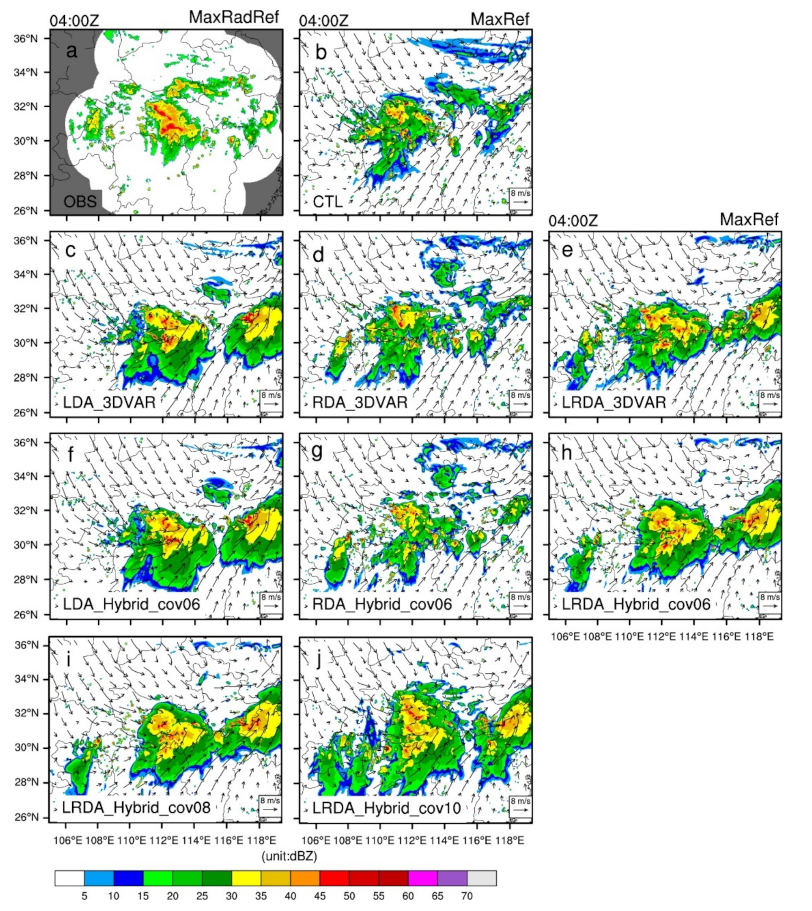
4.2.1. The Single-analysis Experiments
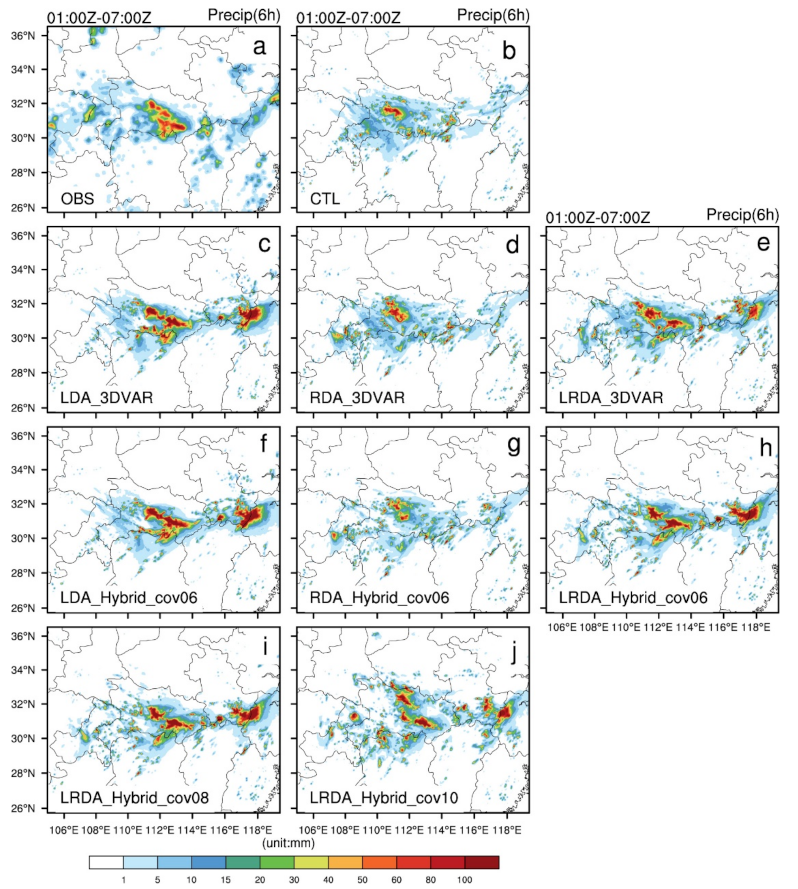
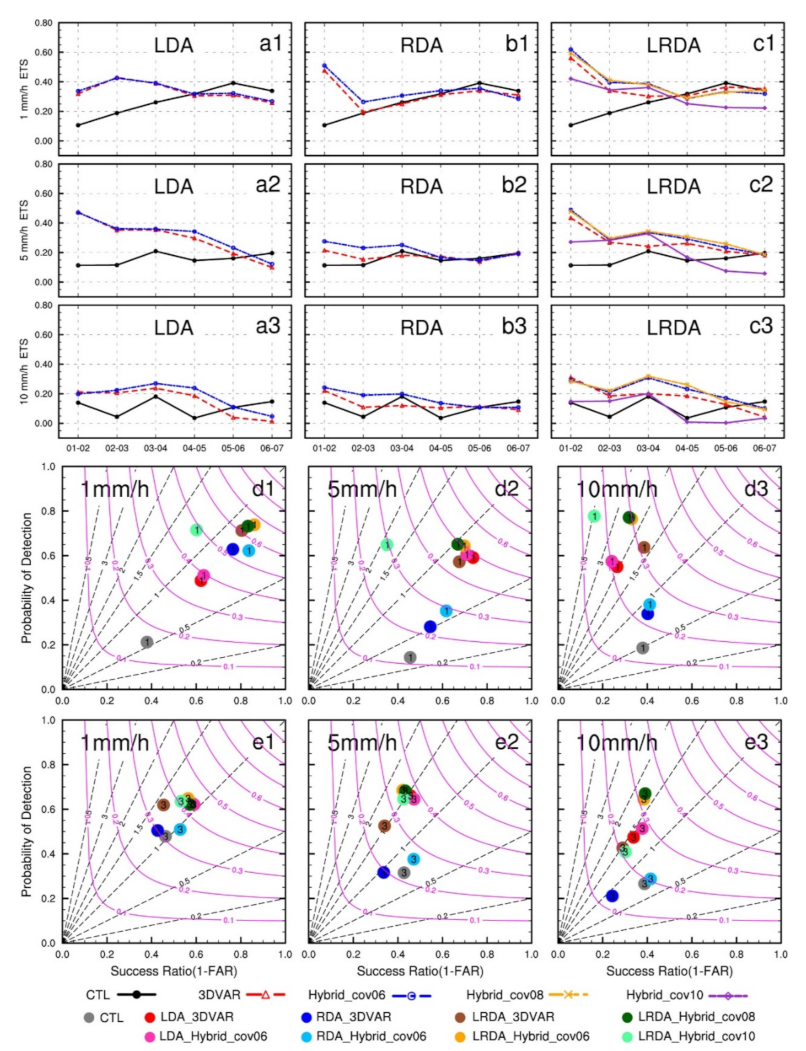
4.2.2. The Cycling Analysis Experiments
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Stensrud, D.J.; Xue, M.; Wicker, L.J.; Kelleher, K.E.; Foster, M.P.; Schaefer, J.T.; Schneider, R.S.; Benjamin, S.; Weygandt, S.S.; Ferree, J.T.; et al. Convective-scale Warn-On-Forecast system: A vision for 2020. Bull. Am. Meteorol. Soc. 2009, 90, 1487–1499. [Google Scholar] [CrossRef]
- Sun, J.; Wang, H. Radar data assimilation with WRF 4D-Var. PartII: Comparison with 3D-Var for a squall line over the U.S. Great plains. Mon. Weather Rev. 2013, 141, 2245–2264. [Google Scholar] [CrossRef]
- Sun, J. Convective-scale assimilation of radar data: Progress and challenges. Q. J. R. Meteorol. Soc. 2005, 131, 3439–3463. [Google Scholar] [CrossRef]
- Pu, Z.; Li, X.; Sun, J. Impact of airborne doppler radar data assimilation on the numerical simulation of intensity changes of hurricane dennis near a landfall. J. Atmos. Sci. 2009, 66, 3351–3365. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Sun, J.; Fan, S.; Huang, X.-Y. Indirect assimilation of radar reflectivity with wrf 3d-var and its impact on prediction of four summertime convective events. J. Appl. Meteorol. Climatol. 2013, 52, 889–902. [Google Scholar] [CrossRef]
- MacGorman, D.R.; Burgess, D.W.; Mazur, V.; Rust, W.D.; Taylor, W.L.; Johnson, B.C. Lightning Rates Relative to Tornadic Storm Evolution on 22 May 1981. J. Atmos. Sci. 1989, 46, 221–251. [Google Scholar] [CrossRef] [Green Version]
- Qie, X.; Guo, C.; Yan, M.; Zhang, G. Lightning data and study of thunderstorm nowcasting. Acta Meteorol. Sin. 1993, 7, 244–256. [Google Scholar]
- Schultz, C.J.; Petersen, W.A.; Carey, L.D. Lightning and Severe Weather: A Comparison between Total and Cloud-to-Ground Lightning Trends. Weather. Forecast. 2011, 26, 744–755. [Google Scholar] [CrossRef]
- Goodman, S.J. The GOES-R Geostationary Lightning Mapper (GLM). Atmos. Res. 2013, 125–126, 34–49. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the new generation of chinese geostationary weather satellites, fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Xu, W.; Adler, R.F.; Wang, N.-Y. Improving Geostationary Satellite Rainfall Estimates Using Lightning Observations: Underlying Lightning–Rainfall–Cloud Relationships. J. Appl. Meteorol. Climatol. 2013, 52, 213–229. [Google Scholar] [CrossRef]
- Minjarez-Sosa, C.M.; Castro, C.L.; Cummins, K.L.; Waissmann, J.; Adams, D.K. An Improved QPE over Complex Terrain Employing Cloud-to-Ground Lightning Occurrences. J. Appl. Meteorol. Climatol. 2017, 56, 2489–2507. [Google Scholar] [CrossRef]
- Minjarez-Sosa, C.; Waissman, J.; Castro, C.; Adams, D. Algorithm for Improved QPE over Complex Terrain Using Cloud-to-Ground Lightning Occurrences. Atmosphere 2019, 10, 85. [Google Scholar] [CrossRef] [Green Version]
- Alexander, G.D.; Weinman, J.A.; Karyampudi, V.; Olson, W.S.; Lee, A.C.L. The effect of assimilating rain rates derived from satellites and lightning on forecasts of the 1993 superstorm. Mon. Weather Rev. 1999, 127, 1433–1457. [Google Scholar] [CrossRef]
- Chang, D.E.; Weinman, J.A.; Morales, C.A.; Olson, W.S. The effect of spaceborne microwave and ground-based continuous lightning measurements on forecasts of the 1998 Groundhog Day storm. Mon. Weather Rev. 2001, 129, 1809–1833. [Google Scholar] [CrossRef]
- Pessi, A.T.; Businger, S. The Impact of Lightning Data Assimilation on a Winter Storm Simulation over the North Pacific Ocean. Mon. Weather Rev. 2009, 137, 3177–3195. [Google Scholar] [CrossRef] [Green Version]
- Marchand, M.R.; Fuelberg, H.E. Assimilation of Lightning data using a nudging method involving low-level warming. Mon. Weather Rev. 2014, 142, 4850–4871. [Google Scholar] [CrossRef]
- Williams, E.R. Large-scale charge separation in thunderclouds. J. Geophys. Res. 1985, 90, 6013. [Google Scholar] [CrossRef]
- Price, C.; Rind, D. A simple lightning parameterization for calculating global lightning distributions. J. Geophys. Res. Atmos. 1992, 97, 9919–9933. [Google Scholar] [CrossRef]
- Wang, H.; Chen, D.; Yin, J.; Daosheng, X.; Dai, G.; Chen, L. An improvement of convective precipitation nowcasting through lightning data dynamic nudging in a cloud-resolving scale forecasting system. Atmos. Res. 2020, 242, 104994. [Google Scholar] [CrossRef]
- Gan, R.; Yang, Y.; Qiu, X.; Wang, R.; Qiu, X.; Zhu, L. Assimilation of the Maximum Vertical Velocity Converted from Total Lightning Data through the EnSRF Method. J. Geophys. Res. Atmos. 2021, 126, e2020JD034300. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Chronis, T.G.; Anagnostou, E.N. Improving convective precipitation forecasting through assimilation of regional lightning measurements in a mesoscale model. Mon. Weather Rev. 2005, 133, 1961–1977. [Google Scholar] [CrossRef] [Green Version]
- Papadopoulos, A.; Serpetzoglou, E.; Anagnostou, E.N. Evaluating the impact of lightning data assimilation on mesoscale model simulations of a flash flood inducing storm. Atmos. Res. 2009, 94, 715–725. [Google Scholar] [CrossRef]
- Mansell, E.R.; Ziegler, C.L.; MacGorman, D.R. A lightning data assimilation technique for mesoscale forecast models. Mon. Weather Rev. 2007, 135, 1732–1748. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Kotroni, V.; Defer, E.; Bousquet, O. Study of a heavy precipitation event over southern France, in the frame of HYMEX project:observational analysis and model results using assimilation of lightning. Atmos. Res. 2013, 134, 45–55. [Google Scholar] [CrossRef]
- Giannaros, T.M.; Kotroni, V.; Lagouvardos, K. WRF-LTNGDA: A lightning data assimilation technique implemented in the WRF model for improving precipitation forecasts. Environ. Model. Softw. 2016, 76, 54–68. [Google Scholar] [CrossRef]
- Fierro, A.O.; Reisner, J.M. High resolution simulation of the electrification and lightning of Hurricane Rita during the period of rapid intensification. J. Atmos. Sci. 2011, 68, 477–494. [Google Scholar] [CrossRef]
- Fierro, A.O.; Mansell, E.R.; Ziegler, C.L.; MacGorman, D. Application of a lightning data assimilation technique in the WRF-ARW Model at cloud-resolving scales for the tornado outbreak of 24 May 2011. Mon. Weather Rev. 2012, 140, 2609–2627. [Google Scholar] [CrossRef]
- Fierro, A.; Gao, J.; Ziegler, C.L.; Mansell, E.R.; MacGorman, D.; Dembek, S.R. Evaluation of a cloud scale lightning data assimilation technique and a 3DVAR method for the analysis and short term forecast of the 29 June 2012 derecho event. Mon. Weather Rev. 2014, 142, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Fierro, A.; Clark, A.J.; Mansell, E.R.; MacGorman, D.; Dembek, S.R.; Ziegler, C.L. Impact of storm-scale lightning data assimilation on WRF-ARW precipitation forecasts during the 2013 warm season over the contiguous United States. Mon. Weather Rev. 2015, 143, 757–777. [Google Scholar] [CrossRef]
- Fierro, A.O.; Gao, J.; Ziegler, C.L.; Calhoun, K.M.; Mansell, E.R.; MacGorman, D.R. MacGorman. Assimilation of flash extent data in the variational framework at convection-allowing scales: Proofof-concept and evaluation for the short term forecast of the 24 May 2011 tornado outbreak. Mon. Weather Rev. 2016, 144, 4373–4393. [Google Scholar] [CrossRef]
- Fierro, A.O.; Wang, Y.; Gao, J.; Mansell, E.R. Variational assimilation of radar data and GLM lightning-derived water vapor for the short-term forecasts of high-impact convective events. Mon. Weather Rev. 2019, 147, 4045–4069. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Liu, D.; Zhang, D.; Yao, W.; Wang, C. A case study of assimilating lightning-proxy relative humidity with WRF-3DVAR. Atmosphere 2017, 8, 55. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Fierro, A.O.; Wang, Y.; Gao, J.; Mansell, E.R. Exploring the Assimilation of GLM Derived Water Vapor Mass in a Cycled 3DVAR Framework for the Short-term Forecasts of High Impact Convective Events. Mon. Weather Rev. 2019, 148, 1005–1028. [Google Scholar] [CrossRef]
- Liu, P.; Yang, Y.; Gao, J.; Wang, Y.; Wang, C. An Approach for Assimilating FY4 Lightning and Cloud Top Height Data Using 3DVAR. Front. Earth Sci. 2020, 8, 288. [Google Scholar] [CrossRef]
- Gan, R.; Yang, Y.; Xie, Q.; Lin, E.; Wang, Y.; Liu, P. Assimilation of radar and cloud-to-ground lightning data using WRF-3DVar combined with the physical initialization method A case study of a mesoscale convective system. J. Meteorol. Res. 2020, 35, 329–342. [Google Scholar] [CrossRef]
- Qie, X.; Zhu, R.; Yuan, T.; Wu, X.; Li, W.; Liu, D. Application of totallightning data assimilation in a mesoscale convective system based on the WRF model. Atmos. Res. 2014, 14, 255–266. [Google Scholar] [CrossRef]
- Mansell, E.R. Storm-scale ensemble kalman filter assimilation of total lightning flash-extent data. Mon. Weather Rev. 2014, 142, 3683–3695. [Google Scholar] [CrossRef]
- Allen, B.J.; Mansell, E.R.; Dowell, D.C.; Deierling, W. Assimilation of pseudo-GLM data using the ensemble Kalman filter. Mon. Weather Rev. 2016, 144, 3465–3486. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Cheng, W.Y.Y.; Zhao, T.; Xu, M.; Liu, Y.; Shen, S.; Calhoun, K.M.; Fierro, A.O. Improving lightning and precipitation prediction of severe convection using lightning data Assimilation with NCAR WRF-RTFDDA. J. Geophys. Res. Atmos. 2017, 122, 12–296. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Zhao, T.; Liu, Y.; Xu, M.; Shen, S.; Jiang, Y.; Yang, H.; Feng, S. Continuous assimilation of lightning data using time-lagged ensembles for a convection allowing numerical weather prediction model. J. Geophys. Res. Atmos. 2018, 123, 9652–9673. [Google Scholar] [CrossRef]
- Chen, Z.; Qie, X.; Liu, D.; Xiong, Y. Lightning data assimilation with comprehensively nudging water contents at cloud-resolving scale using WRF model. Atmos. Res. 2019, 221, 72–87. [Google Scholar] [CrossRef]
- Kong, R.; Xue, M.; Fierro, A.O.; Jung, Y.; Liu, C.; Mansell, E.R.; MacGorman, D.R. Assimilation of GOES-R Geostationary Lightning Mapper Flash Extent Density Data in GSI EnKF for the Analysis and Short-Term Forecast of a Mesoscale Convective System. Mon. Weather Rev. 2020, 148, 2111–2133. [Google Scholar] [CrossRef] [Green Version]
- Benjamin, S.G.; Dévényi, D.; Weygandt, S.S.; Brundage, K.J.; Brown, J.M.; Grell, G.A.; Manikin, G.S. An Hourly Assimilation–Forecast Cycle: The RUC. Mon. Weather. Rev. 2004, 132, 495–518. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Wang, C. Improving forecasting of strong convection by assimilating cloud-to-ground lightning data using the physical initialization method. Atmos. Res. 2014, 150, 31–41. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Zhu, K. Assimilation of chinese doppler radar and lightning data using WRF-GSI: A Case study of mesoscale convective system. Adv. Meteorol. 2015, 2015, 763919. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, Z.; Han, W.; He, J.; Chen, M. Case Study of a Retrieval Method of 3D Proxy Reflectivity from FY-4A Lightning Data and Its Impact on the Assimilation and Forecasting for Severe Rainfall Storms. Remote Sens. 2020, 12, 1165. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, T. Riming electrification as a charge generation mechanism in thunderstorms. J. Atmos. Sci. 1978, 35, 1536–1548. [Google Scholar] [CrossRef]
- Saunders, C.P.R.; Keith, W.D.; Mitzeva, R.P. The effect of liquid water on thunderstorm charging. J. Geophys. Res. 1991, 96, 11007–11017. [Google Scholar] [CrossRef]
- Yuan, T.; Qie, X. Study on lightning activity and precipitation characteristics before and after the onset of the South China Sea summer monsoon. J. Geophys. Res. 2008, 113, D14101. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Some observing system simulation experiments with a hybrid 3DEnVAR system for storm-scale radar data assimilation. Mon. Weather Rev. 2014, 142, 3326–3346. [Google Scholar] [CrossRef]
- Gao, J.; Fu, C.; Stensrud, D.J.; Kain, J.S. OSSEs for an ensemble 3DVAR data assimilation system with radar observations of convective storms. J. Atmos. Sci. 2016, 73, 2403–2426. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, J.; Skinner, P.S.; Knopfmeier, K.; Jones, T.; Creager, G.; Wicker, L.J. Test of a Weather-Adaptive Dual-Resolution Hybrid Warn-on-Forecast Analysis and Forecast System for Several Severe Weather Events. Weather Forecast. 2019, 73, 2403–2426. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M.; Shapiro, A.; Droegemeier, K.K. A variational analysis for the retrieval of three-dimensional mesoscale wind fields from two Doppler radars. Mon. Weather Rev. 1999, 127, 2128–2142. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part I: Model development and simulated data experiments. J. Atmos. Sci. 1997, 54, 1642–1661. [Google Scholar] [CrossRef]
- Tong, M.J.; Xue, M. Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef] [Green Version]
- Stensrud, D.J.; Gao, J.D. Importance of horizontally inhomogeneous environmental initial conditions to ensemble storm-scale radar data assimilation and very short-range forecasts. Mon. Weather Rev. 2010, 138, 1250–1272. [Google Scholar] [CrossRef]
- Lai, A.; Gao, J.; Koch, S.E.; Wang, Y.; Pan, S.; Fierro, A.O.; Min, J. Assimilation of Radar Radial Velocity, Reflectivity and Pseudo Water Vapor for Convective-scale NWP in a Variational Framework. Mon. Weather Rev. 2019, 147, 2877–2900. [Google Scholar] [CrossRef]
- Lai, A.; Min, J.; Gao, J.; Ma, H.; Cui, C.; Xiao, Y.; Wang, Z. Assimilation of Radar Data, Pseudo Water Vapor, and Potential Temperature in a 3DVAR Framework for Improving Precipitation Forecast of Severe Weather Events. Atmosphere 2020, 11, 182. [Google Scholar] [CrossRef] [Green Version]
- Lai, A.; Min, J.; Gao, J.; Ma, H.; Cui, C.; Xiao, Y.; Wang, Z. Impacts of the radar data assimilation frequency and large-scale constraint on the short-term precipitation forecast of a severe convection case. Atmos. Res. 2021, 257, 105590. [Google Scholar] [CrossRef]
- Peterson, M. Research applications for the Geostationary Lightning Mapper operational lightning flash data product. J. Geophys. Res. Atmos. 2019, 124, 10205–10231. [Google Scholar] [CrossRef]
- Xu, Q.; Nai, K. An Adaptive Dealiasing Method Based on Variational Analysis for Radar Radial Velocities Scanned with Small Nyquist Velocities. J. Atmos. Ocean. Technol. 2012, 29, 1723–1729. [Google Scholar] [CrossRef]
- Xu, Q.; Nai, K.; Wei, L.; Zhang, P.; Liu, S.; Parrish, D. A VAD-Based Dealiasing Method for Radar Velocity Data Quality Control. J. Atmos. Ocean. Technol. 2011, 28, 50–62. [Google Scholar] [CrossRef]
- Gao, J.; Stensrud, D.J. Assimilation of reflectivity data in a convective-scale, cycled 3DVAR framework with hydrometeor classification. J. Atmos. Sci. 2012, 69, 1054–1065. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M. An efficient dual-resolution approach for ensemble DA and tests with assimilated Doppler radar data. Mon. Weather Rev. 2008, 136, 945–963. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M.; Brewster, K.; Droegemeier, K.K. A threedimensional data analysis method with recursive filter for Doppler radars. J. Atmos. Ocean. Technol. 2004, 21, 457–469. [Google Scholar] [CrossRef]
- Gao, J.; Smith, T.M.; Stensrud, D.J.; Fu, C.; Calhoun, K.; Manross, K.L.; Brogden, J.; Lakshmanan, V.; Wang, Y.; Thomas, K.W.; et al. A Real-Time Weather-Adaptive 3DVAR Analysis System for Severe Weather Detections and Warnings. Weather Forecast. 2013, 28, 727–745. [Google Scholar] [CrossRef]
- Xie, Q.; Yang, Y.; Qiu, X.; Ma, Y.; Lai, A.; Lin, E.; Mai, X. 3D-Var Assimilation of GTS observation with the gravity wave drag scheme improves summer high resolution climate simulation over the Tibetan Plateau. Clim. Dyn. 2021. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.R. Explicit forecasts of winter precipitation using an improved bulk microphysics scheme. Part II: Implementation of a new snow parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.-Y. A new stable boundary-layer mixing scheme and its impact on the simulated East Asian summer monsoon. Q. J. R. Meteorol. Soc. 2010, 136, 1481–1496. [Google Scholar] [CrossRef]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Brill, K.F.; Mesinger, F. Applying a general analytic method for assessing bias sensitivity to bias-adjusted threat and equitable threat scores. Weather Forecast. 2009, 24, 1748–1754. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather. Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef] [Green Version]
- Clark, A.J.; Gallus, W.A.; Weisman, M.L. eighborhoodbased verification of precipitation forecasts from convectionallowing NCAR WRF Model simulations and the operational NAM. Weather Forecast. 2010, 25, 1495–1509. [Google Scholar] [CrossRef]

| Experiments | Data Assimilated | Data Assimilation Methods |
|---|---|---|
| CTL | None | None |
| LDA_3DVAR | FY-4A LMI | 3DVAR method |
| LDA_Hybrid_cov06 | Hybrid 3DEnVAR method, , | |
| RDA_3DVAR | Radar reflectivity and radial velocity | 3DVAR method |
| RDA_Hybrid_cov06 | Hybrid 3DEnVAR method, , | |
| LRDA_3DVAR | FY-4A LMI, radar reflectivity, and radial velocity | 3DVAR method |
| LRDA_Hybrid_cov06 | Hybrid 3DEnVAR method, , ) | |
| LRDA_Hybrid_cov08 | Hybrid 3DEnVAR method, (, | |
| LRDA_Hybrid_cov10 | Hybrid 3DEnVAR method, , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Yang, Y.; Lai, A.; Wang, Y.; Fierro, A.O.; Gao, J.; Wang, C. Assimilating FY-4A Lightning and Radar Data for Improving Short-Term Forecasts of a High-Impact Convective Event with a Dual-Resolution Hybrid 3DEnVAR Method. Remote Sens. 2021, 13, 3090. https://doi.org/10.3390/rs13163090
Liu P, Yang Y, Lai A, Wang Y, Fierro AO, Gao J, Wang C. Assimilating FY-4A Lightning and Radar Data for Improving Short-Term Forecasts of a High-Impact Convective Event with a Dual-Resolution Hybrid 3DEnVAR Method. Remote Sensing. 2021; 13(16):3090. https://doi.org/10.3390/rs13163090
Chicago/Turabian StyleLiu, Peng, Yi Yang, Anwei Lai, Yunheng Wang, Alexandre O. Fierro, Jidong Gao, and Chenghai Wang. 2021. "Assimilating FY-4A Lightning and Radar Data for Improving Short-Term Forecasts of a High-Impact Convective Event with a Dual-Resolution Hybrid 3DEnVAR Method" Remote Sensing 13, no. 16: 3090. https://doi.org/10.3390/rs13163090
APA StyleLiu, P., Yang, Y., Lai, A., Wang, Y., Fierro, A. O., Gao, J., & Wang, C. (2021). Assimilating FY-4A Lightning and Radar Data for Improving Short-Term Forecasts of a High-Impact Convective Event with a Dual-Resolution Hybrid 3DEnVAR Method. Remote Sensing, 13(16), 3090. https://doi.org/10.3390/rs13163090







