A Second-Order Time-Difference Position Constrained Reduced-Dynamic Technique for the Precise Orbit Determination of LEOs Using GPS
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Preparation
2.2. Kinematic Observation Equation
2.3. New Dynamic Pseudo-Observation Equation
2.4. Function Model of the RD_STP Method
2.5. Characteristics of the RD_STP Method
2.6. Steps of the RD_STP Method for POD
3. Results
3.1. Accuracy Analysis of the Integrated STP Pseudo-Observations
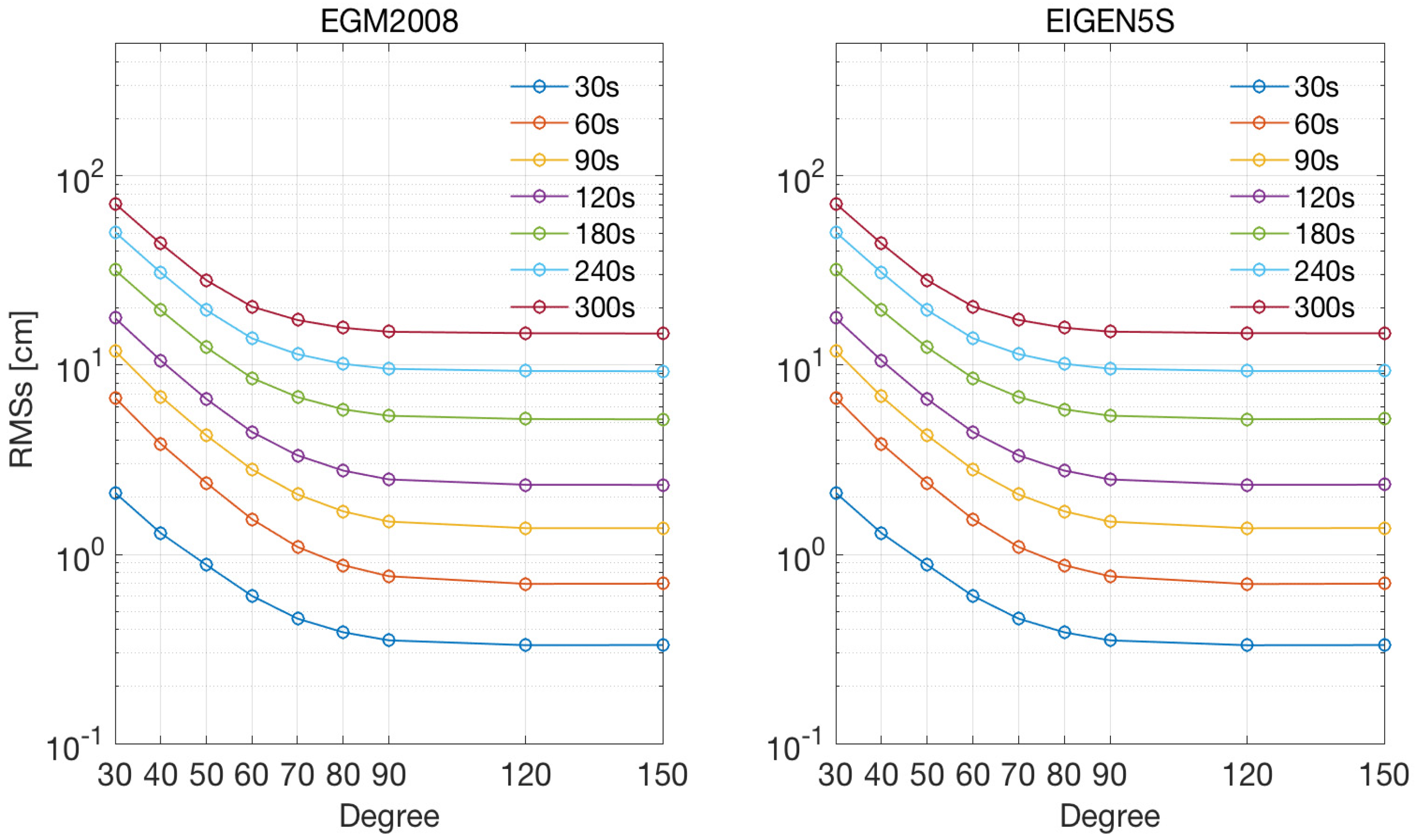
3.1.1. Influence of the Sampling Interval
3.1.2. Magnitude and Error of the a Priori Dynamic Models
3.1.3. Accuracy Analysis of Integrating the STPs of GOCE and GRACE
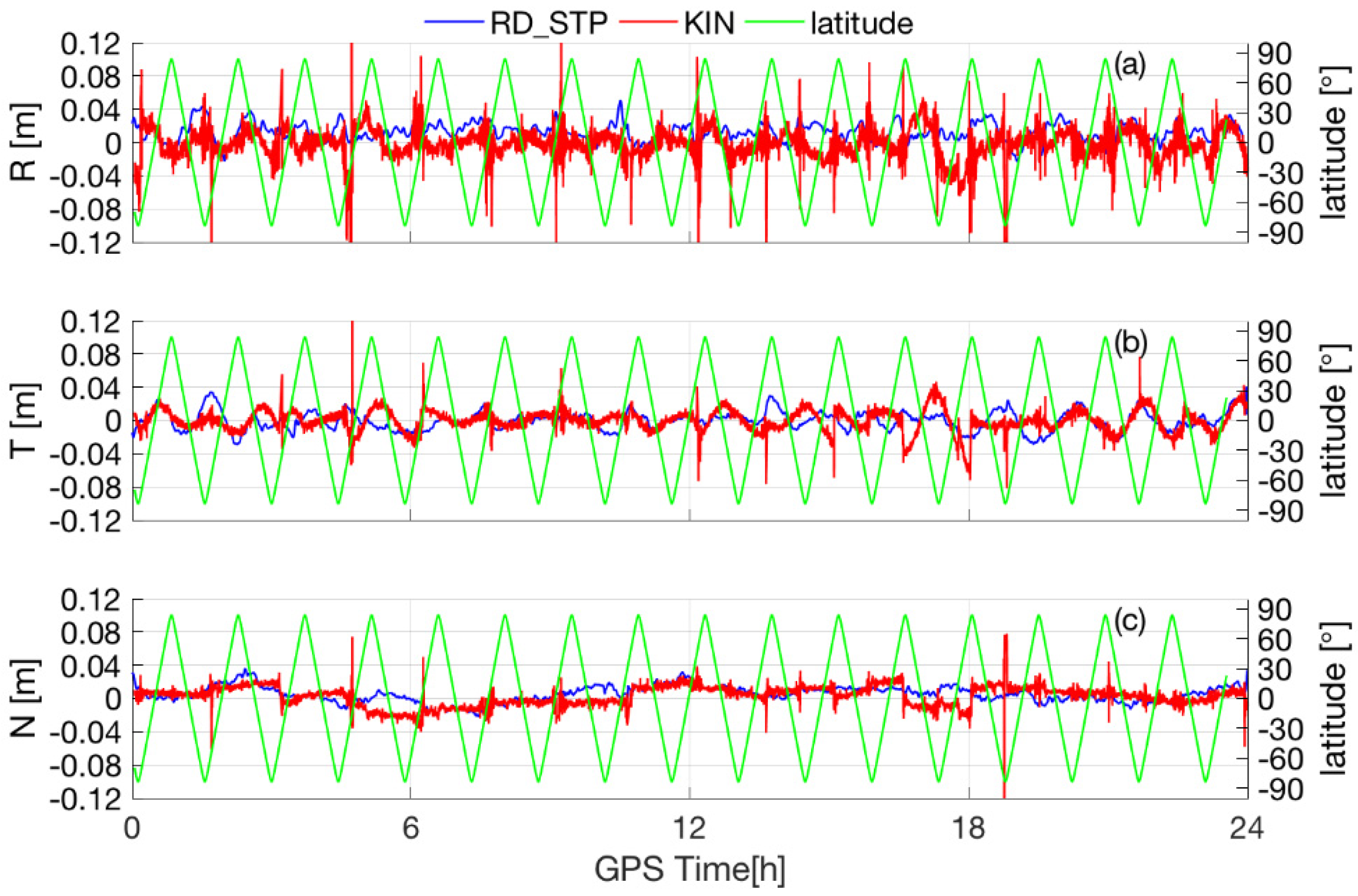
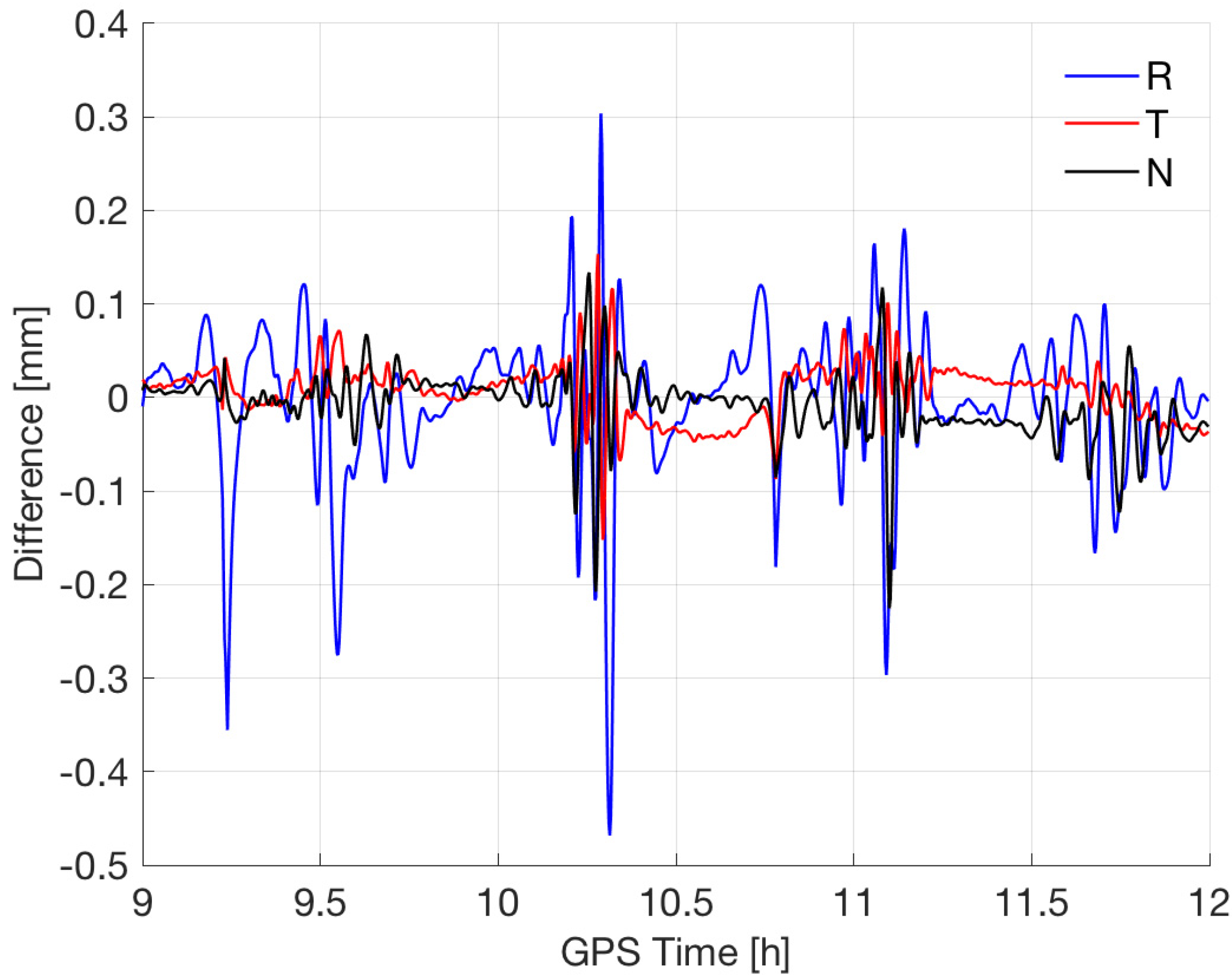
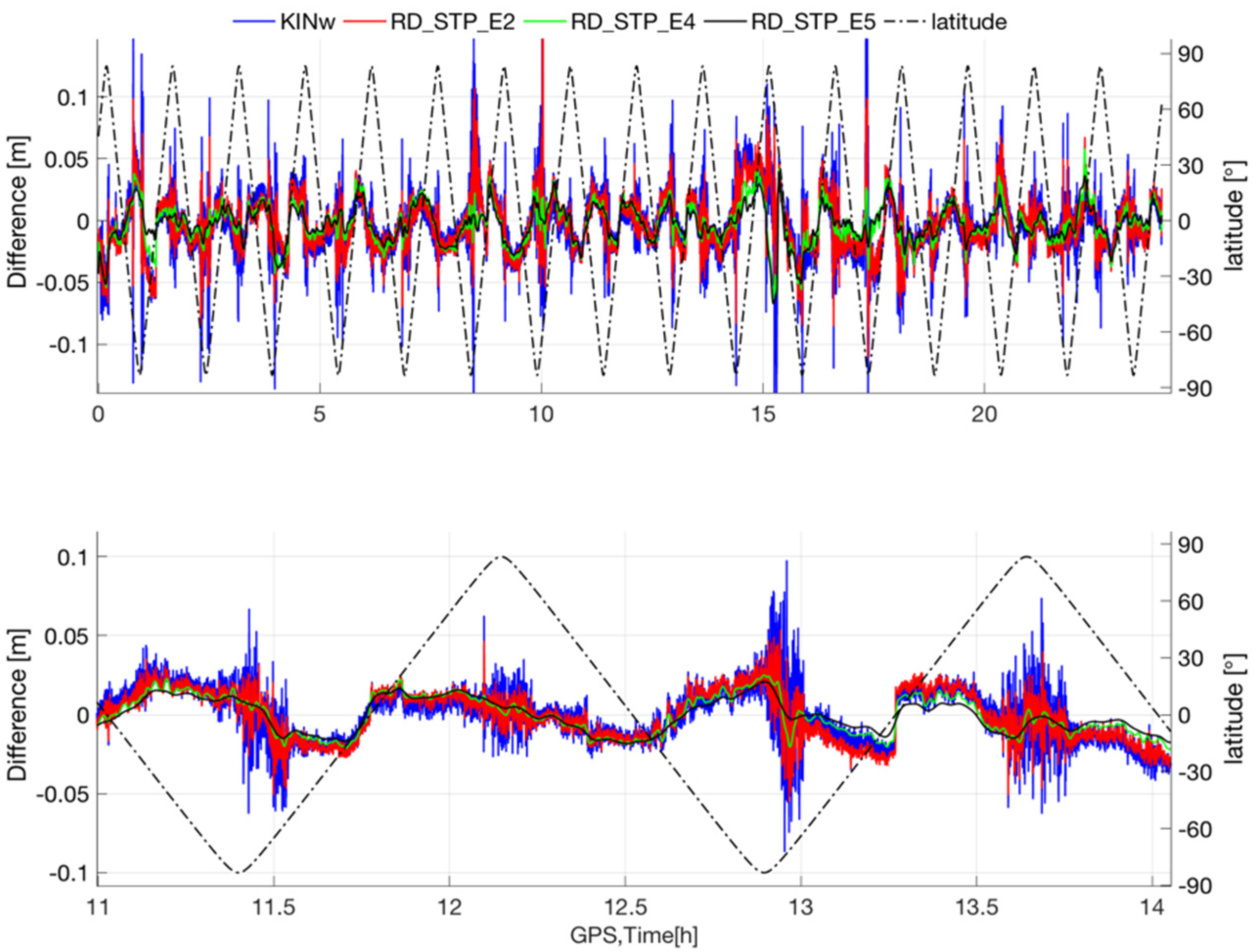
3.2. POD of GOCE Satellite Based on the RD_STP Method
POD Results and Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bertiger, W.I.; Bar-Sever, Y.E.; Christensen, E.J.; Davis, E.S.; Guinn, J.R.; Haines, B.J.; Ibanez-Meier, R.W.; Jee, J.R.; Lichten, S.M.; Melbourne, W.G.; et al. GPS precise tracking of TOPEX/POSEIDON: Results and implications. J. Geophys. Res. Space Phys. 1994, 99, 24449–24464. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Zelensky, N.P.; Rowlands, D.D.; Lemoine, F.G.; Williams, T.A. The 1-Centimeter Orbit: Jason-1 Precision Orbit Determination Using GPS, SLR, DORIS, and Altimeter Data Special Issue: Jason-1 Calibration/Validation. Mar. Geod. 2003, 26, 399–421. [Google Scholar] [CrossRef]
- Cerri, L.; Berthias, J.P.; Bertiger, W.I.; Haines, B.J.; Lemoine, F.G.; Mercier, F.; Ries, J.C.; Willis, P.; Zelensky, N.P.; Ziebart, M. Precision Orbit Determination Standards for the Jason Series of Altimeter Missions. Mar. Geod. 2010, 33, 379–418. [Google Scholar] [CrossRef]
- Flohrer, C.; Otten, M.; Springer, T.; Dow, J. Generating precise and homogeneous orbits for Jason-1 and Jason-2. Adv. Space Res. 2011, 48, 152–172. [Google Scholar] [CrossRef]
- Bisnath, S. Precise Orbit Determination of Low Earth Orbiters with a Single GPS Receiver-Based. Geometric Strategy. Ph.D. Dissertation, Department of Geodesy and Geomatics Engineering, University of New Brunswick, Fredericton, NB, Canada, 2004; 143p. [Google Scholar]
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-Stochastic Orbit Modeling Techniques for Low-Earth Orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Beutler, G.; Bock, H.; Hugentobler, U. Kinematic and highly reduced-dynamic LEO orbit determination for gravity field estimation. In International Symposium on Earth and Environmental Sciences for Future Generations; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2008; pp. 354–361. [Google Scholar]
- Jäggi, A.; Hugentobler, U.; Bock, H.; Beutler, G. Precise orbit determination for GRACE using undifferenced or doubly differenced GPS data. Adv. Space Res. 2007, 39, 1612–1619. [Google Scholar] [CrossRef]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Andres, Y.; Bock, H.; Van Helleputte, T.; Ijssel, J.V.D.; Loiselet, M.; Marquardt, C.; Silvestrin, P.; Visser, P.; Yoon, Y. Tracking and orbit determination performance of the GRAS instrument on MetOp-A. GPS Solut. 2008, 12, 289–299. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Jäggi, A.; Meyer, U.; Visser, P.; Ijssel, J.V.D.; Van Helleputte, T.; Heinze, M.; Hugentobler, U. GPS-derived orbits for the GOCE satellite. J. Geod. 2011, 85, 807–818. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Jaggi, A.; Beutler, G.; Meyer, U. GOCE: Precise orbit determination for the entire mission. J. Geod. 2014, 88, 1047–1060. [Google Scholar] [CrossRef]
- Ijssel, J.V.D.; da Encarnacao, J.T.; Doornbos, E.; Visser, P. Precise science orbits for the Swarm satellite constellation. Adv. Space Res. 2015, 56, 1042–1055. [Google Scholar] [CrossRef]
- Jäggi, A.; Dahle, C.; Arnold, D.; Bock, H.; Meyer, U.; Beutler, G.; Ijssel, J.V.D. Swarm kinematic orbits and gravity fields from 18 months of GPS data. Adv. Space Res. 2016, 57, 218–233. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Ijssel, J.V.D.; Arnold, D. Reduced dynamic and kinematic precise orbit determination for the Swarm mission from 4 years of GPS tracking. GPS Solut. 2018, 22, 79. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hackel, S.; Jäggi, A. Precise orbit determination of the Sentinel-3A altimetry satellite using ambiguity-fixed GPS carrier phase observations. J. Geod. 2018, 92, 711–726. [Google Scholar] [CrossRef] [Green Version]
- Švehla, D.; Rothacher, M. Kinematic positioning of LEO and GPS satellites and IGS stations on the ground. Adv. Space Res. 2005, 36, 376–381. [Google Scholar] [CrossRef]
- Geng, J.; Teferle, F.N.; Meng, X.; Dodson, A.H. Kinematic precise point positioning at remote marine platforms. GPS Solut. 2010, 14, 343–350. [Google Scholar] [CrossRef]
- Li, J.; Zhang, S.; Zou, X.; Jiang, W. Precise orbit determination for GRACE with zero-difference kinematic method. Chin. Sci. Bull. 2010, 55, 600–606. [Google Scholar] [CrossRef]
- Weinbach, U.; Schön, S. Improved GRACE kinematic orbit determination using GPS receiver clock modeling. GPS Solut. 2013, 17, 511–520. [Google Scholar] [CrossRef]
- Baur, O.; Bock, H.; Höck, E.; Jäggi, A.; Krauss, S.; Mayer-Gürr, T.; Reubelt, T.; Siemes, C.; Zehentner, N. Comparison of GOCE-GPS gravity fields derived by different approaches. J. Geod. 2014, 88, 959–973. [Google Scholar] [CrossRef]
- Zehentner, N.; Mayer-Gürr, T. Precise orbit determination based on raw GPS measurements. J. Geod. 2016, 90, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; van Helleputte, T.; Kroes, R.; Gill, E. Reduced dynamic orbit determination using GPS code and carrier measurements. Aerosp. Sci. Technol. 2005, 9, 261–271. [Google Scholar] [CrossRef]
- Švehla, D.; Rothacher, M. Kinematic and reduced-dynamic precise orbit determination of low earth orbiters. Adv. Geosci. 2003, 1, 47–56. [Google Scholar] [CrossRef] [Green Version]
- Colombo, O.L. The dynamics of global positioning system orbits and the determination of precise ephemerides. J. Geophys. Res. Space Phys. 1989, 94, 9167. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E.; Gurtner, W.; Hugentobler, U.; Mervart, L.; Rothacher, M. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and Initial Re-sults. Manuscr. Geod. 1994, 19, 367–386. [Google Scholar]
- Yunck, T.; Wu, S.-C.; Wu, J.-T.; Thornton, C. Precise tracking of remote sensing satellites with the Global Positioning System. IEEE Trans. Geosci. Remote Sens. 1990, 28, 108–116. [Google Scholar] [CrossRef]
- Wu, S.C.; Yunck, T.P.; Thornton, C.L. Reduced-dynamic technique for precise orbit determination of low earth satel-lites. J. Guid. Control Dyn. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Bruinsma, S.; Loyer, S.; Lemoine, J.M.; Perosanz, F.; Tamagnan, D. The impact of accelerometry on CHAMP orbit determination. J. Geod. 2003, 77, 86–93. [Google Scholar] [CrossRef]
- Visser, P.; Ijssel, J.V.D. Aiming at a 1-cm Orbit for Low Earth Orbiters: Reduced-Dynamic and Kinematic Precise Orbit Determination. Space Sci. Rev. 2003, 108, 27–36. [Google Scholar] [CrossRef]
- ESA. GOCE l1b Products User Handbook; GOCE-GSEG-EOPGTN-06-0137; Tech. Rep.; 2008. Available online: https://earth.esa.int/c/document_library/get_file?folderId=14168&name=DLFE-772.pdf (accessed on 13 April 2018).
- ESA. GOCE Level 2 Product Data Handbook; go-ma-hpf-gs-0110; Tech. Rep.; 2014. Available online: https://earth.esa.int/documents/10174/1650485/GOCE_Product_Data_Handbook_Level-2 (accessed on 13 April 2018).
- Hauschild, A. Basic observation equations. In Springer Handbook of Global Navigation Satellite Systems, Chapter 19; Teunissen, P., Montenbruck, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 561–582. [Google Scholar]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 1, pp. 967–982. [Google Scholar] [CrossRef]
- Ditmar, P.; Sluijs, A.A.V.E.V.D. A technique for modeling the Earths gravity field on the basis of satellite accelerations. J. Geod. 2004, 78, 12–33. [Google Scholar] [CrossRef]
- Beutler, G. Methods of Celestial Mechanics; Springer: Berlin/Heidelberg, Germny, 2004. [Google Scholar]
- Bock, H.; Jäggi, A.; Švehla, D.; Beutler, G.; Hugentobler, U.; Visser, P. Precise orbit determination for the GOCE satellite using GPS. Adv. Space Res. 2007, 39, 1638–1647. [Google Scholar] [CrossRef]
- Case, K.; Kruizinga, G.; Wu, S.C. GRACE Level 1B Data Product User Handbook JPL Publication D-22027. 2010. Available online: https://earth.esa.int/c/document_library/get_file?folderId=123371&name=DLFE-1408.pdf (accessed on 17 April 2018).
- Montenbruck, O.; Garcia-Fernandez, M.; Williams, J. Performance comparison of semicodeless GPS receivers for LEO satellites. GPS Solut. 2006, 10, 249–261. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010) (No. IERS-TN-36); Bureau International Des Poids Et Mesures Sevres: Sèvres, France, 2010. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Ijssel, J.V.D.; Visser, P. Determination of non-gravitational accelerations from GPS satellite-to-satellite tracking of CHAMP. Adv. Space Res. 2005, 36, 418–423. [Google Scholar] [CrossRef]
- Beutler, G.; Jäggi, A.; Mervart, L.; Meyer, U. The celestial mechanics approach: Application to data of the GRACE mission. J. Geod. 2010, 84, 661–681. [Google Scholar] [CrossRef] [Green Version]
- Förste, C.; Flechtner, F.; Schmidt, R.; Stubenvoll, R.; Rothacher, M.; Kusche, J.; Neumayer, H.; Biancale, R.; Lemoine, J.M.; Barthelmes, F.; et al. EIGEN-GL05C—A New Global Combined High-Resolution GRACE-Based Gravity Field Model of the GFZ-GRGS Cooperation; General Assembly European Geosciences Union: Vienna, Austria, April 2008; Geophys Res Abstr 10: EGU2008-A-03426. [Google Scholar]

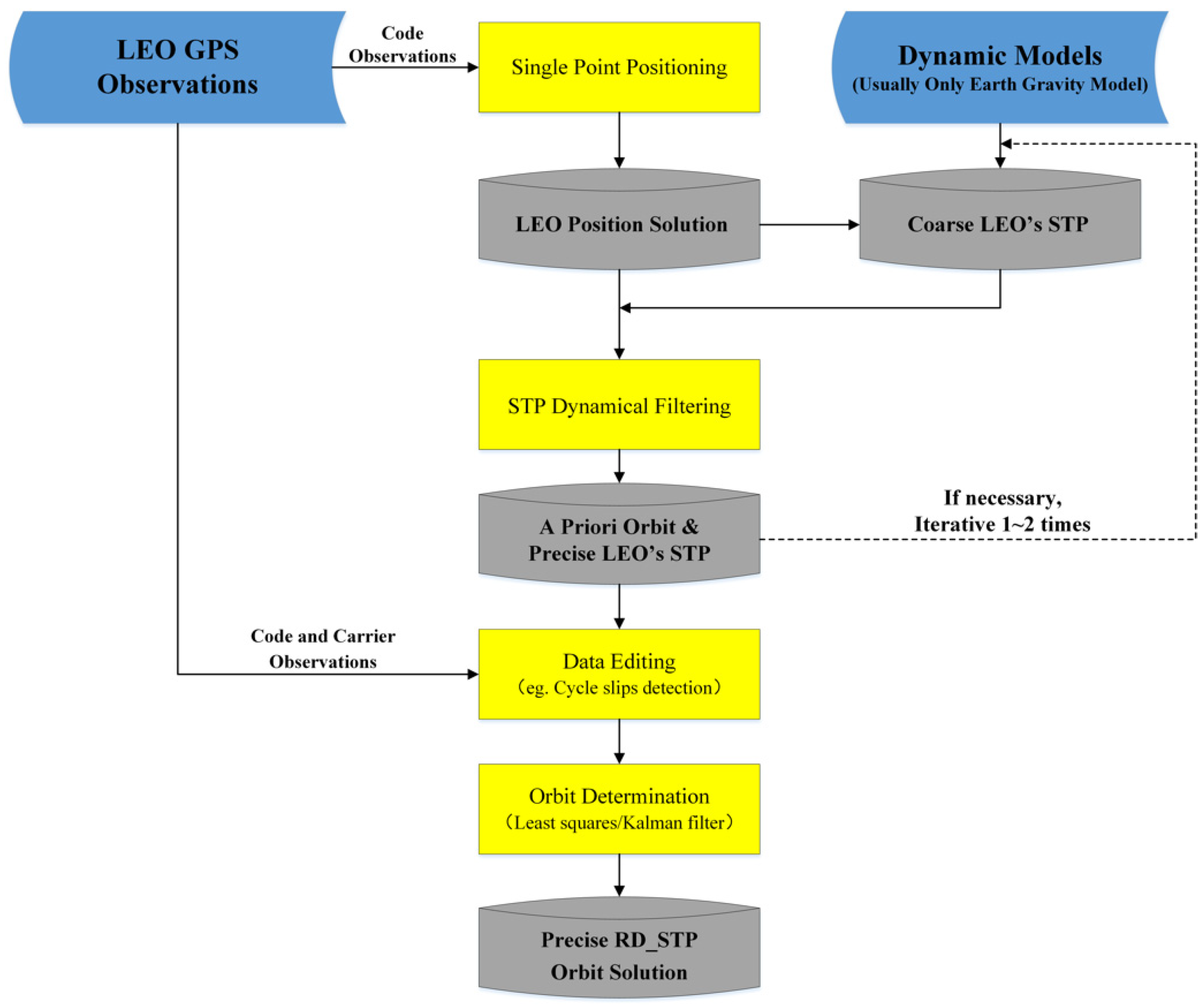
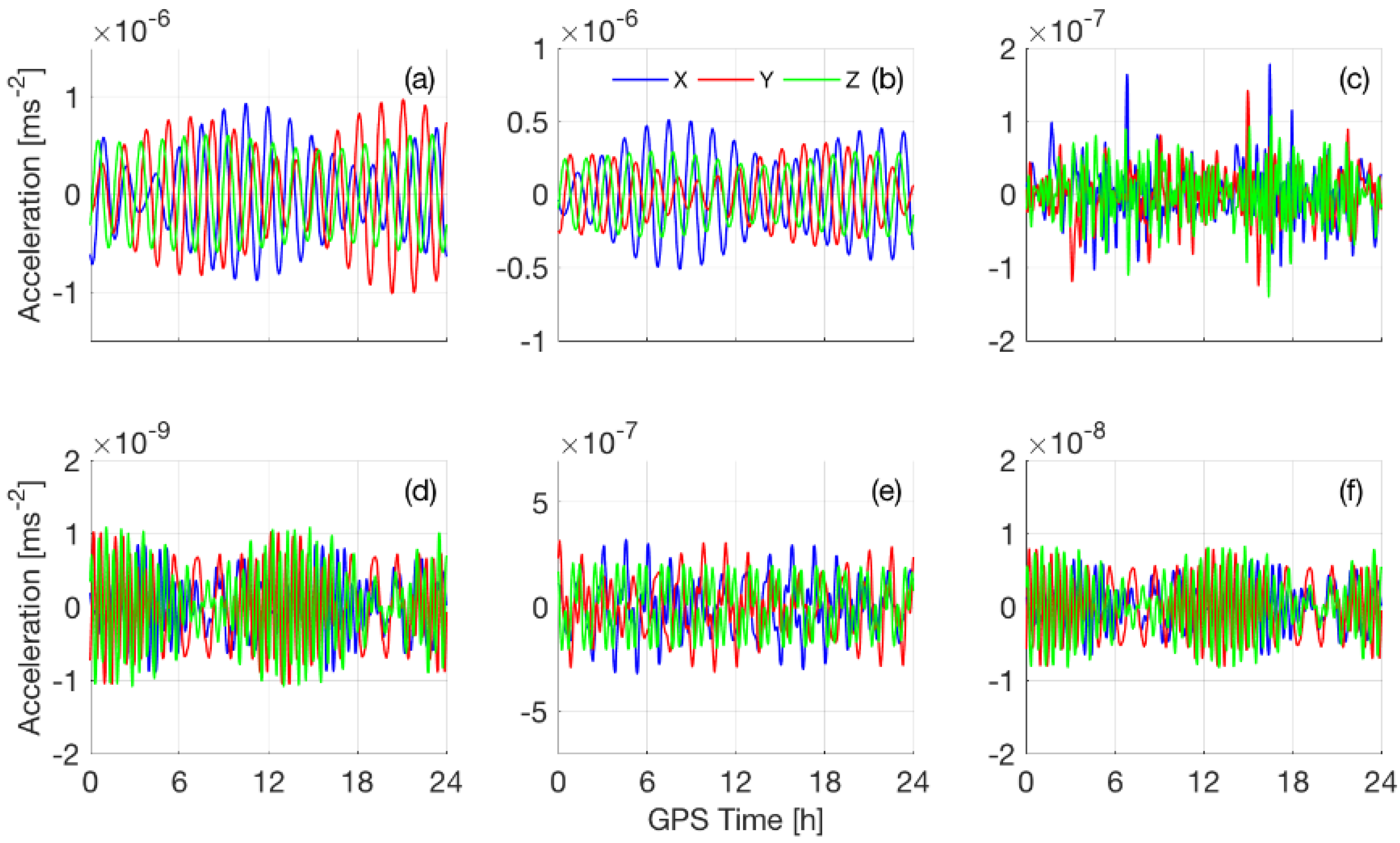
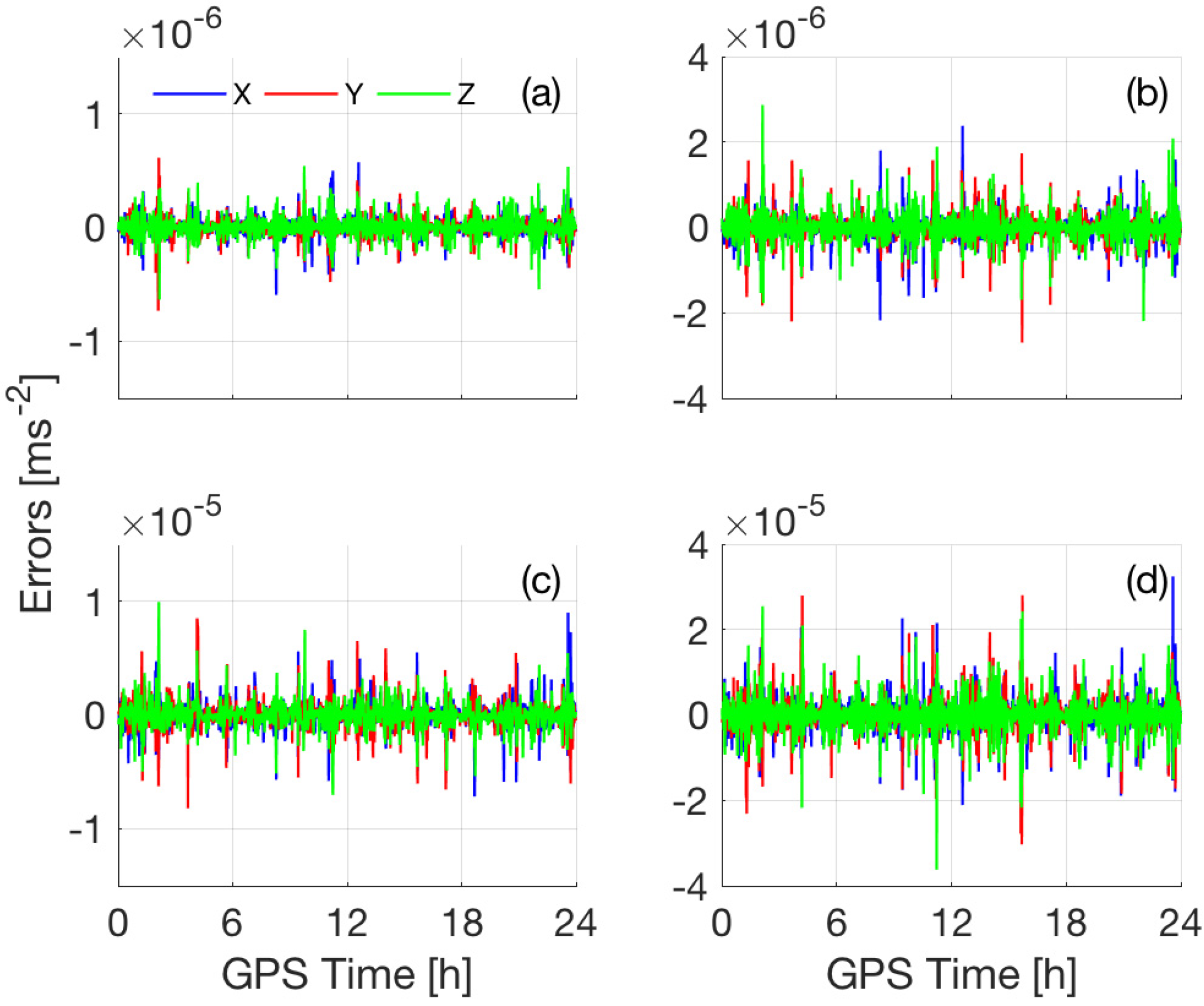
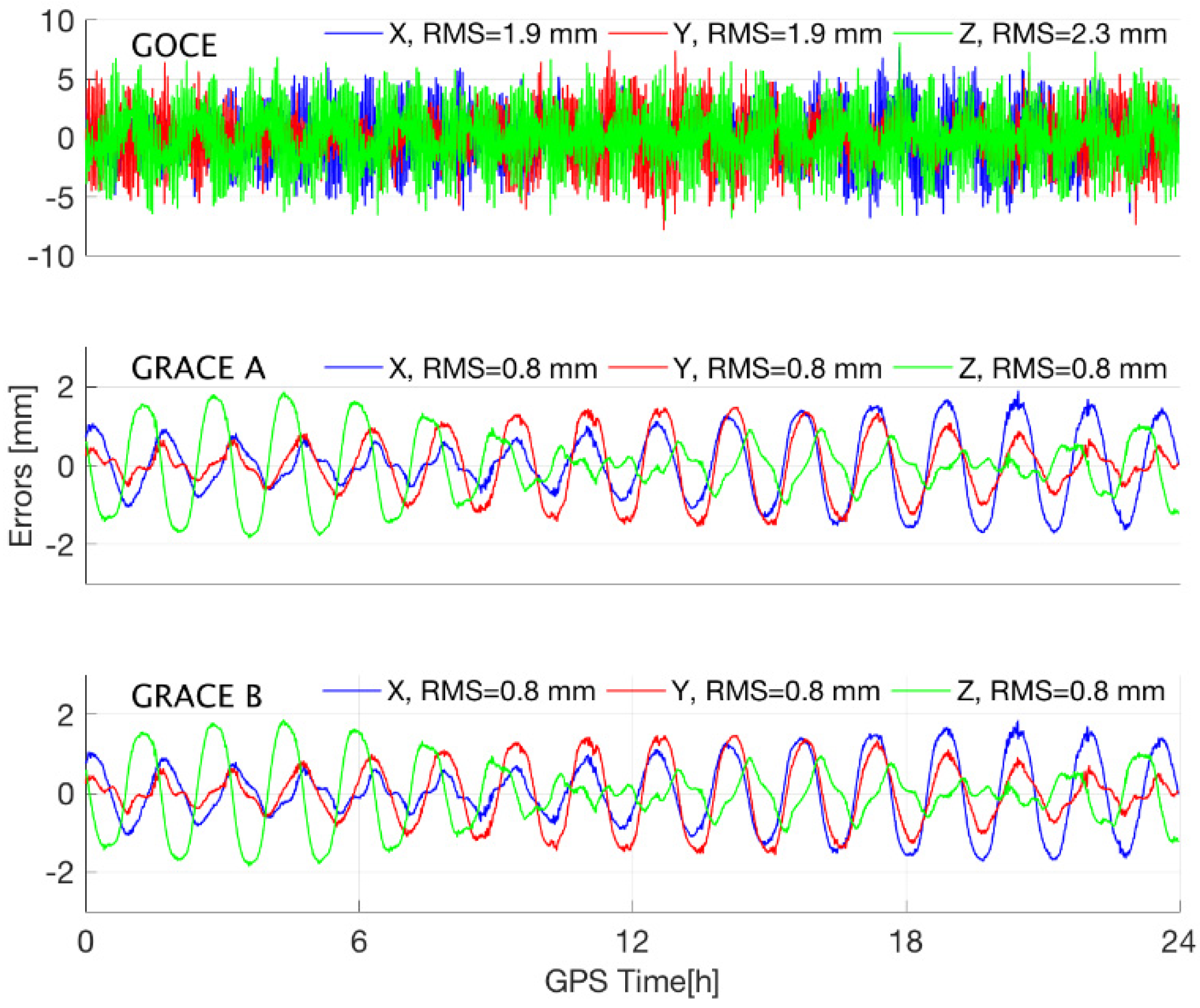

| Kinematic | Dynamic | RD | RD_STP | |
|---|---|---|---|---|
| GPS observations | Yes | Yes | Yes | Yes |
| Integration and integral arc length | No | Yes | Yes, usually 30 h [11] | Yes, 60 s or less |
| Minor perturbation force models | No | Yes | Yes | Usually no |
| Earth’s gravity field model | No | Yes | Yes | Yes, lower-degree |
| Pseudo-stochastic/dynamical parameters | No | Yes | Yes | No |
| Items | Bernese GPS Software KIN and RD POD [11] | RD_STP POD |
|---|---|---|
| GPS measurement model | Undifferenced ionosphere-free phase | Undifferenced ionosphere-free phase |
| igs05.atx | igs05.atx | |
| GOCE PCOs + PCVs | GOCE PCOs + PCVs | |
| CODE final GPS ephemerides and 5 s clocks | CODE final GPS ephemerides and 5 s clocks | |
| Elevation cut-off 0° | Elevation cut-off 0° | |
| 10 s/1 s (RD/KIN) sampling | 1 s sampling | |
| Gravitational forces | EIGEN-5S (120 × 120) [44] Solid Earth, pole and ocean tides luni-solar-planetary gravity N/A for KIN PSO | EGM2008(90 × 90) [41] |
| Non-gravitational forces | Empirical constant N/A for KIN PSO | N/A |
| Estimation | Batch least squares | Batch least squares |
| Mean-RMS (cm) | R | T | N | 3D |
|---|---|---|---|---|
| KIN-10 s | 2.63 | 2.28 | 2.42 | 4.25 |
| KIN-30 s | 2.74 | 2.42 | 2.55 | 4.47 |
| STPRD-10 s | 1.52 | 1.33 | 1.50 | 2.53 |
| STPRD-30 s | 1.69 | 1.46 | 1.63 | 2.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Li, J.; Xu, X.; Zhang, S.; Kuang, K. A Second-Order Time-Difference Position Constrained Reduced-Dynamic Technique for the Precise Orbit Determination of LEOs Using GPS. Remote Sens. 2021, 13, 3033. https://doi.org/10.3390/rs13153033
Wei H, Li J, Xu X, Zhang S, Kuang K. A Second-Order Time-Difference Position Constrained Reduced-Dynamic Technique for the Precise Orbit Determination of LEOs Using GPS. Remote Sensing. 2021; 13(15):3033. https://doi.org/10.3390/rs13153033
Chicago/Turabian StyleWei, Hui, Jiancheng Li, Xinyu Xu, Shoujian Zhang, and Kaifa Kuang. 2021. "A Second-Order Time-Difference Position Constrained Reduced-Dynamic Technique for the Precise Orbit Determination of LEOs Using GPS" Remote Sensing 13, no. 15: 3033. https://doi.org/10.3390/rs13153033
APA StyleWei, H., Li, J., Xu, X., Zhang, S., & Kuang, K. (2021). A Second-Order Time-Difference Position Constrained Reduced-Dynamic Technique for the Precise Orbit Determination of LEOs Using GPS. Remote Sensing, 13(15), 3033. https://doi.org/10.3390/rs13153033






