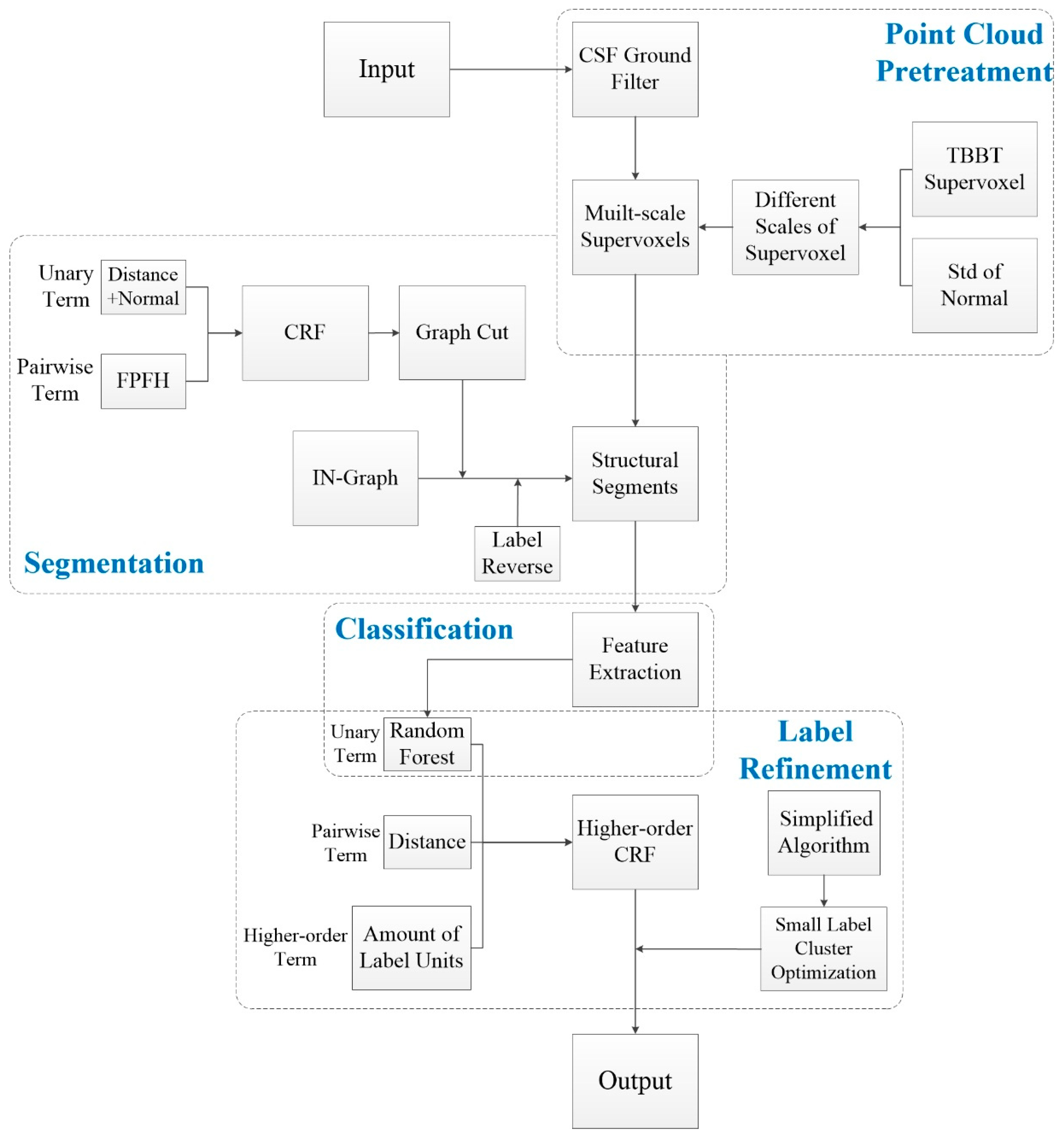
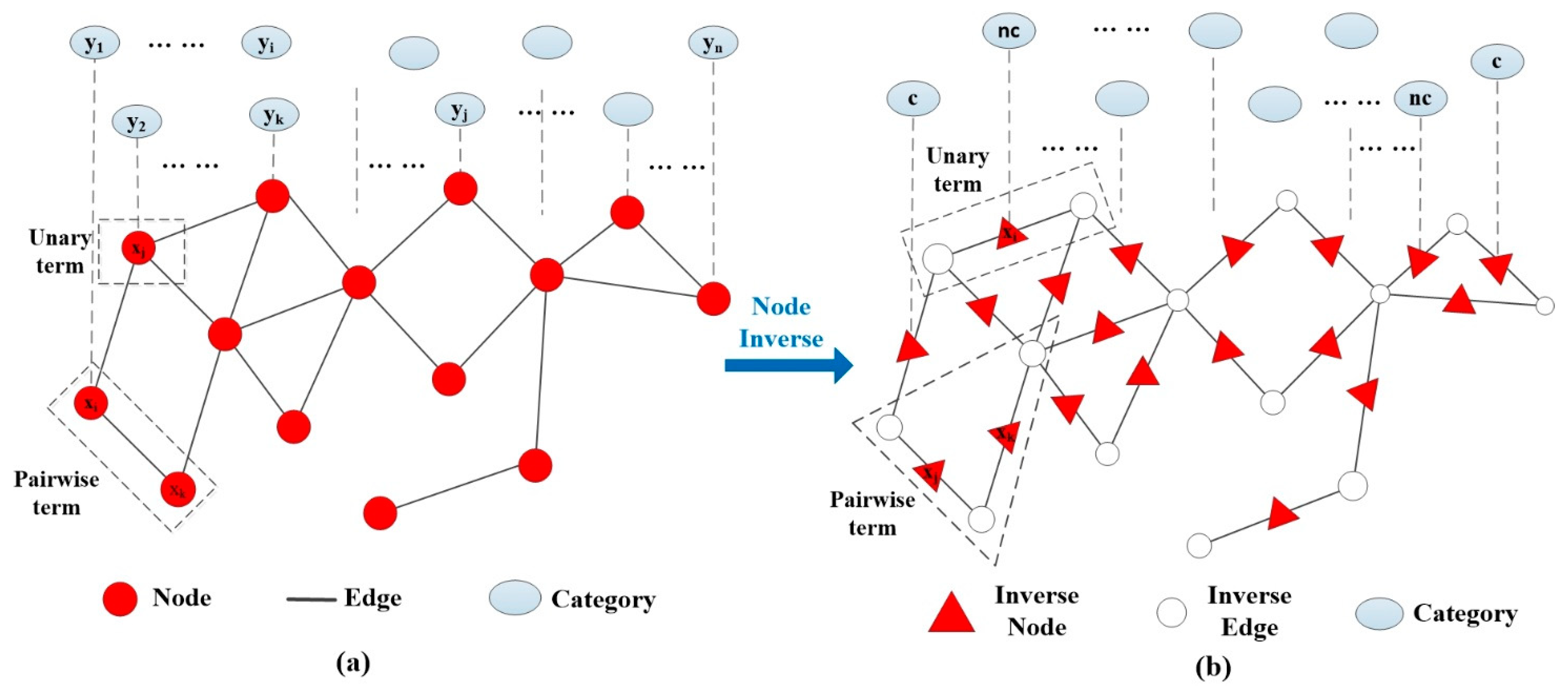
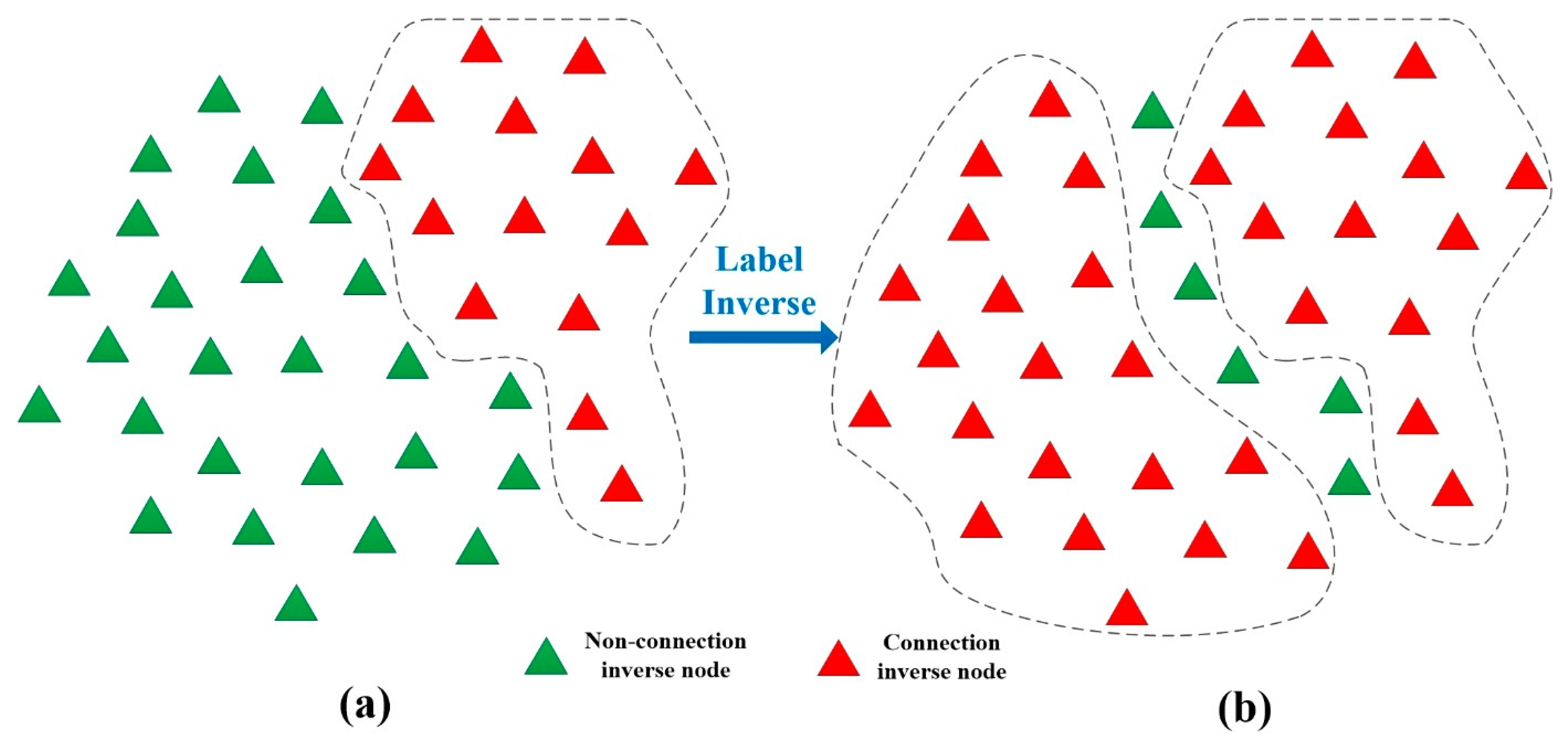
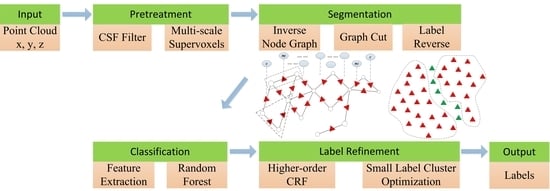
3.1. Dataset Illustration
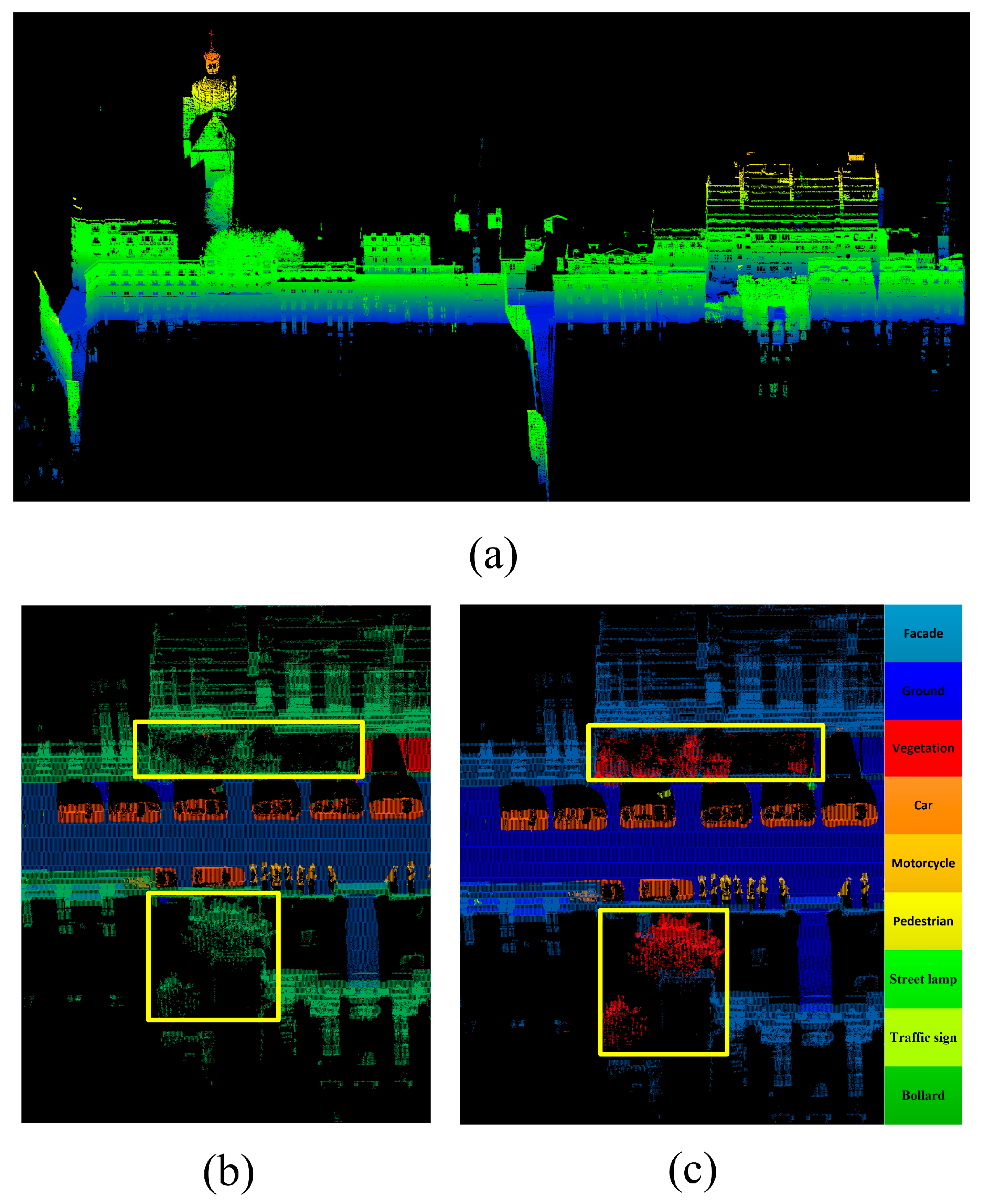
To evaluate the performance of the proposed classification method, this study conducted the experiments on two different urban scene datasets. The first one was a benchmark MLS dataset Paris-rue-Cassette [
39], which is widely used to test the performance of semantic segmentation methods, as shown in
Figure 6. In the original label, some vegetation close to the wall was marked as façade, as shown in the yellow box in
Figure 6b—it has been revised to vegetation, as shown in
Figure 6c. The second dataset was a multi-station TLS dataset which was collected at Wuhan University, as shown in
Figure 7. The descriptions of the two datasets are given in
Table 2. These two datasets were collected by different platforms, so they have different qualities of the point cloud; the difference between the Wuhan University dataset and Paris-rue-Cassette dataset is that the density of the Wuhan University dataset is uniformly distributed. This study tested our semantic segmentation method with different kinds of point cloud.
The parameter configurations of the proposed method in two datasets are shown in
Table 3. It seems that many parameters need to be set, which could influence the stability of the method. In actual application, the parameters of the supervoxel can fit most situations, the distance threshold
of adjacent units can depend on the density of data, and the scalar threshold
n and
of each category are set as empirical values. The parameters that need to be adjusted mainly focus on the weight of distance differences and normal difference in the IN-Graph method, and the weights of the unary term, pairwise term and higher-order term in graph cut optimization.
3.2. Experiment on Paris-Rue-Cassette MLS Dataset
The Paris-rue-Cassette dataset was collected by MLS, and it includes nine categories, which are ground, façade, vegetation, car, motorcycle, pedestrian, traffic sign, street lamp and bollard. The most remarkable property of the dataset is that in the direction of the vehicle, the sampling interval is 0.1 m, and in the direction of the scanner line, the sampling interval is 0.03 m; therefore, the challenge of this dataset is the different densities in different directions, which influences the segmentation of the structural segments. In the supervised classification training data, objects of the same category with different density are chosen for comprehensive training.
Figure 8 shows some objects with the same category but with different densities or shapes from the training datasets: due to the missing data and differently shaped, the same category could have different structural segment components. Considering the fewer samples of some categories in the dataset, the algorithm took half of the samples of some categories, such as pedestrian, traffic sign and street lamp, as training data, and tested the other remaining half of the samples.
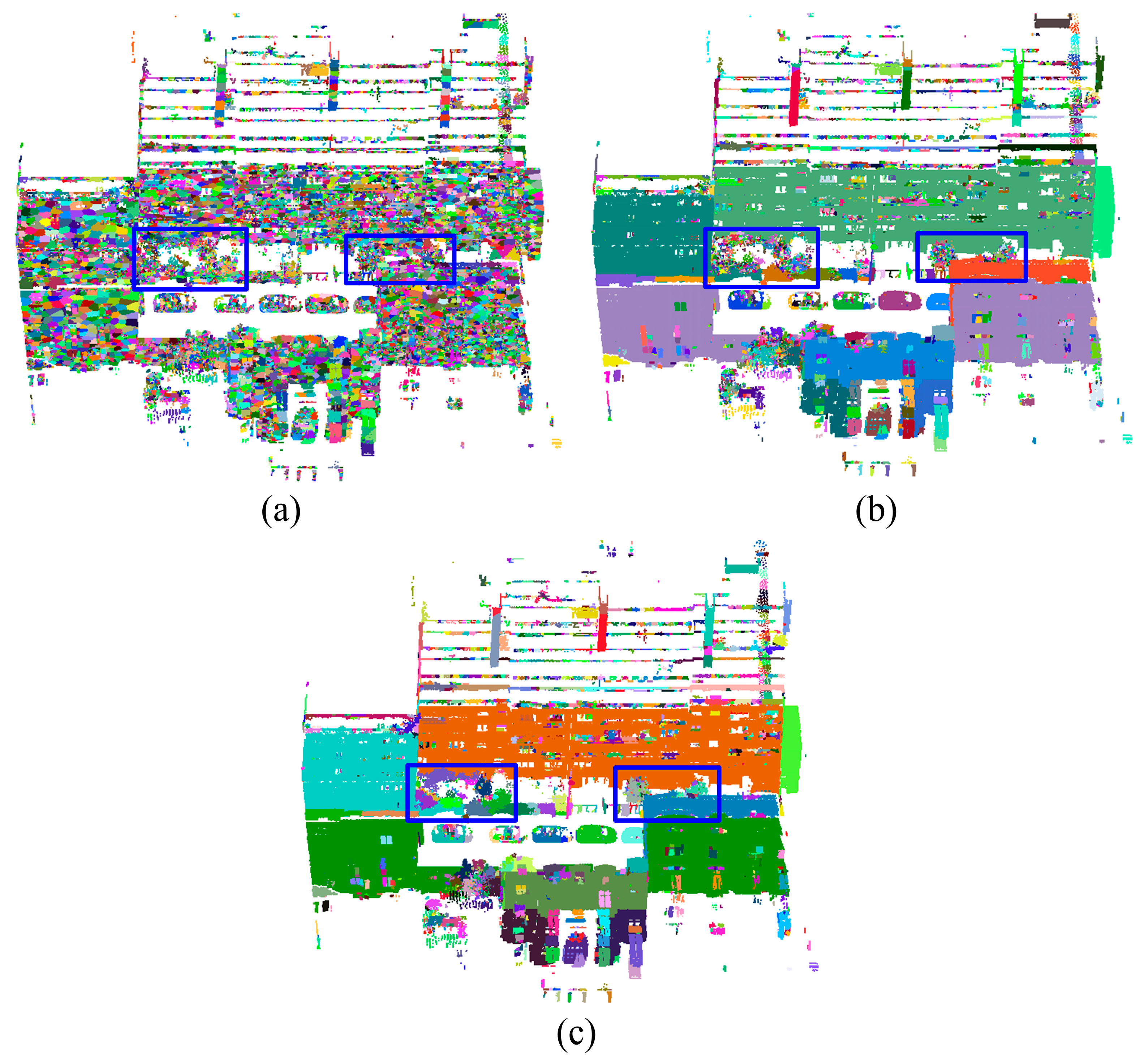
First, the result was qualitatively analyzed by the views of classification. The whole view of the ground-truth of the category is shown in
Figure 9a, and the classification results of the proposed method are shown in
Figure 9b. It can be seen that most of the objects were recognized correctly by the proposed method, compared with ground-truth data: the main façade and vegetation achieved the best classification results. The incorrect classifications are shown in
Figure 9c—the incorrect points are shown in red. Notably, the incorrect points appeared in small structural segments from the façade’s fragment, as show in the green box in
Figure 9c. In the yellow box of
Figure 9c, because the collected points are too sparse in this region, the quality of the point cloud is too low to retain the shape of the bollard; therefore, misclassification is concentrated in this region.
Figure 10 shows three scenes where incorrect points are concentrated.
Figure 10a shows a façade scene where many disperse fragments exist. Due to the discreteness of the fragments, the pairwise term and higher-order term cannot smooth or correct the incorrect classification, which can then easily be mis-identified as other small objects which have similar-shaped features. This situation often occurs in façades because the scanner line generates isolated block point clouds behind the façade, or some irregular objects are attached to the façade. However, it can be seen that the proposed method successfully identified a large number of objects with relatively complete structure, because the method in this paper takes advantage of the structural segments as classification units, which can retain the shape features of objects.
Figure 10b represents an intersection situation between vegetation and façade, with the intersection position marked by a blue box in
Figure 4 in
Section 2.3.3. It can be seen that the over-segmented structural segments generated by the inverse node graph strategy retained lots of boundaries in
Figure 4c, and obtained good classification results even when they were close, as shown in
Figure 10b. The main vegetation has been well recognized in
Figure 10b. Due to the mixture of walls and vegetation, it is inevitable that a few façade structural segments with vegetation have been classified as vegetation.
Figure 10c shows the classification results of small objects, such as cars, motorcycles and pedestrians. It can be seen that the proposed method has a good ability to recognize cars, but incorrectly recognizes motorcycles as cars or pedestrians because of some similarities between them. As marked in the green box in
Figure 10c, some points of the motorcycles are discontinuous; therefore, parts of the structural segments can easily be incorrectly categorized.
Next, the method in this paper was quantitatively analyzed by basic classification metrics, overall accuracy, recall, precision and F1-score. Three existing semantic classification methods [
23,
33,
40] which were successfully tested on the Paris-rue-Cassette dataset are taken as comparative items. The quantified classification results are shown in
Table 4, where the accuracy calculation of the proposed method excluded the training dataset, and the best results in each table are marked in bold. The overall accuracy and mean F1-score of the proposed method were 97.57% and 77.06%, which were 0.44% and 4.86% better than method 3, respectively. Regarding category classifications in
Table 5, the proposed method obtained the best recall in the categories façade, vegetation and car, which all have special geometric features, indicating that the proposed method is good for recognizing these common objects in urban scenes. However, for the smaller categories, the proposed method is weaker than others in recognizing motorcycles, pedestrians and traffic signs. One reason is the lack of training data of objects in the small category, which is why the worst result occurred for traffic signs. Another reason is because the low quality of points generates small fragments in these objects, which may mislead the classifier. Motorcycles and pedestrians have similar geometric features; therefore, it is easy to confuse them, which results in a poor recall result.
In terms of precision, as shown in
Table 6, the proposed method achieved the best performance, which indicates that structural segments segmented from the IN-Graph can retain more typical geometric features for recognizing different categories, reducing the probability of one category being wrongly identified as the other. Although the categories of motorcycle and pedestrian had smaller recall than other methods, they had higher precision than other methods, which means that the proposed method rarely incorrectly recognized other categories as them, but these categories could easily be recognized as other categories. Precision indicates that the proposed method has a good correctness of classification but is not reliable as other methods in recognizing these categories. It infers that due to uneven density, the similar structural segments between different categories can influence the completeness of classification of the proposed method. When the proposed method allocates the correct label as part of structural segments of an object, it can recognize the whole object by higher-order CRF with small-label cluster refinement; therefore, it can improve the precision of identifying objects by recognizing parts of them from the classifier. The F1-scores in
Table 7 indicate that the classification results of some categories in the proposed method are superior to other methods when comprehensively considering both the recall and precision.
Table 8 demonstrates the efficiency of different classification methods. It can be seen that the pointwise classification [
23] takes more time than other methods because it takes points as units, resulting in much more computational complexity. The proposed segment-based classification method is slower than the supervoxel-based classification method [
33], because the proposed method involves the generation of multi-scale supervoxels, running the voxelization program multiple times; the proposed method also involves structural segment generation, which takes some time for segmentation. Supervoxel-based classification does not mention the time cost of higher-order CRF; therefore, the time costs of this step cannot be compared. However, due to the small-label cluster optimization step, the overall time cost of the proposed method will be lower than the supervoxel-based method. It can be concluded that the efficiency of our segment-based method is better than the pointwise method but slower than the supervoxel-based method: the proposed method improves the classification accuracy at the cost of certain efficiency loss.
3.3. Experiment on the Wuhan University TLS Dataset
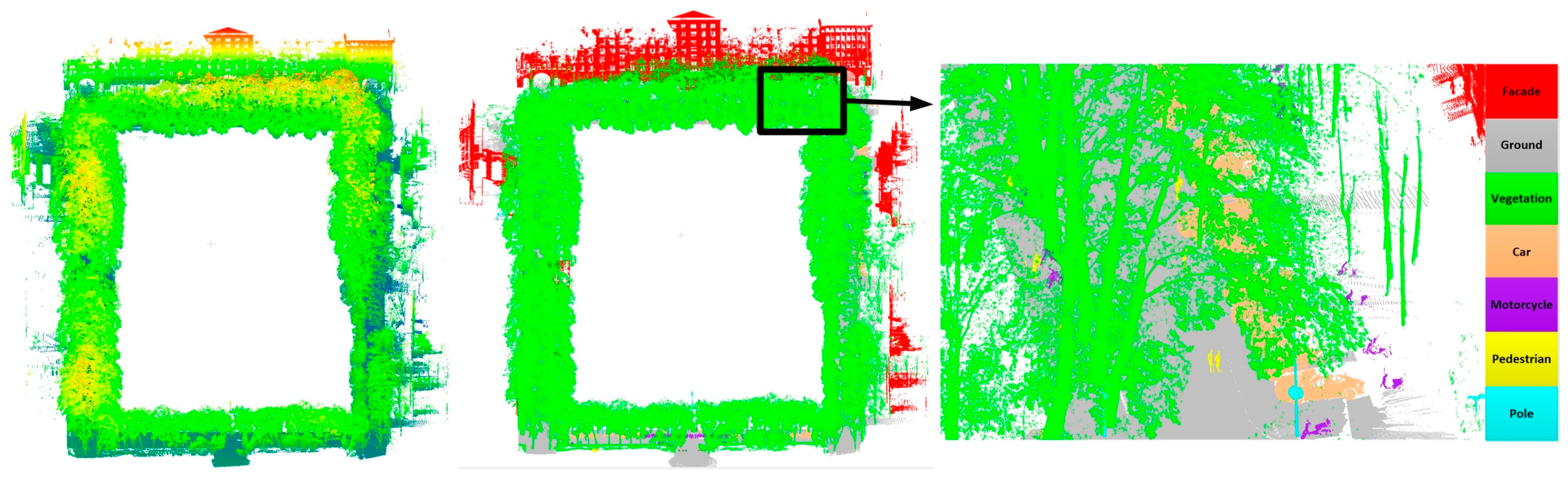
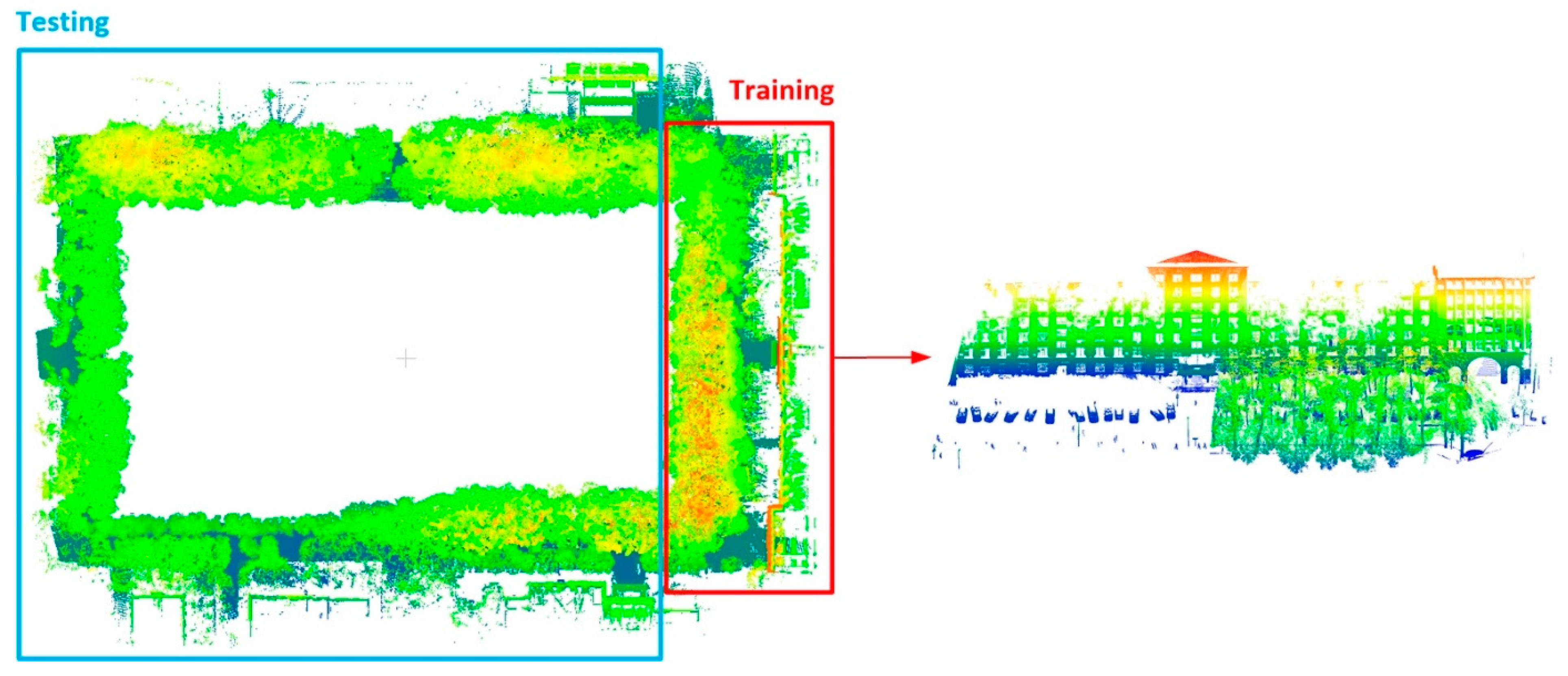
There were seven categories in the Wuhan University dataset: ground, façade, vegetation, car, motorcycle, pedestrian and artificial pole. As
Figure 11 shows, the main category existing in the Wuhan University dataset is vegetation, including a large number of tree crowns and trunks, which makes it a challenge to distinguish between trees and artificial poles. The range of the Wuhan University dataset was large; therefore, the training dataset was obtained from part of the whole dataset, as shown in the red box in
Figure 11 and for balancing the composition between different categories, it reduced the amount of vegetation and façades to prevent overfitting. The remaining region of the Wuhan University dataset was taken as the testing dataset, as shown in the blue box in
Figure 11.
The classification results of Wuhan University dataset are shown in
Figure 12. The first row in
Figure 12 is the classification results by the proposed method, the middle row is the ground-truth of the dataset, and the last row is a binary image which shows the correctly classified points (in blue) and incorrectly classified points (in red).
Figure 12a is a complete view of the classification results, indicating that the proposed method correctly identified most of the targets in this scene, and worked well in identifying the vegetation, façade and ground, which were among the major components in the dataset.
Figure 12b,c show the detailed scenes in which small objects are present; cars, motorcycles and pedestrians were identified well by the proposed method, even though they were close to each other. The results indicate that the proposed method performs well in identifying the objects with distinct structures. The reason is that the proposed method over-segments points into structural segments using IN-Graph, which retains part of the structural features of the objects, and preserves the individuality of single targets. Thus, it can not only identify the target well, but also prevents under-segmentation. As shown in the black box in
Figure 13, a bicycle is parked very close to a tree:
Figure 13a shows the segmentation results. It can be observed that even though they were very close to each other, the segmentation by IN-Graph still divided them well. The skeleton of the bicycle was extracted relatively completely, which preserved distinct features to help with classification, as shown in
Figure 13b.
In the Wuhan University dataset, there were lots of pole-like objects: these were natural poles such as trees and artificial poles such as lamps and traffic signs.
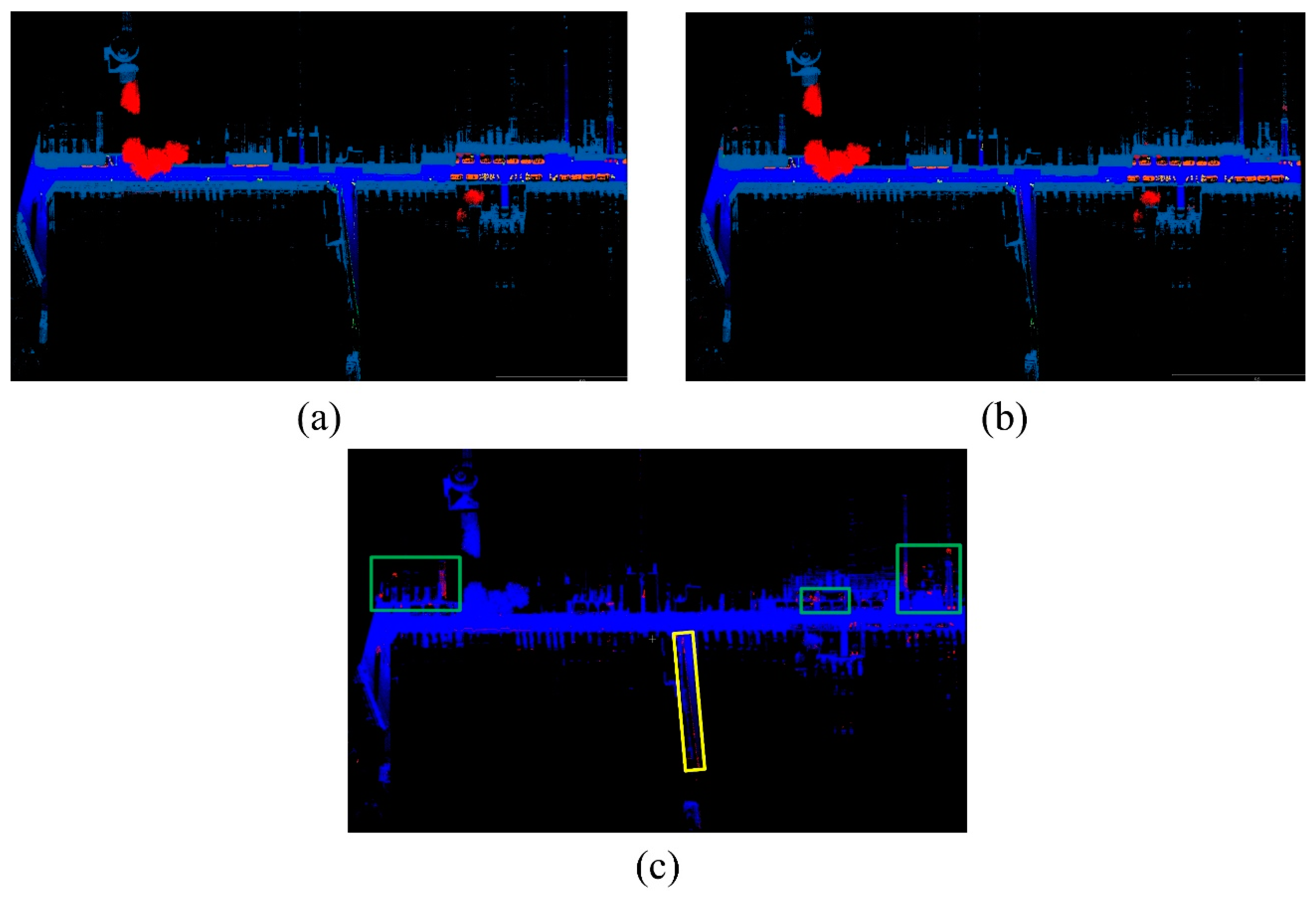
Figure 14 illustrates the recognition capability for distinguishing natural poles and artificial poles. From
Figure 14a, it can be seen that most trees have been identified, and artificial poles have also been successfully identified in many regions, as shown in the blue box in
Figure 14a. This illustrates that the proposed method has some ability to recognize pole-like objects. However, in
Figure 14b,c, misidentification occurred.
Figure 14b misidentified a tree as an artificial pole object because the diameter of tree is rather close to the artificial pole-like object.
Figure 14c shows a situation where a traffic sign is misidentified as a tree, and the reason could be that the upper-half of this traffic sign stretched to the side, which means it could easily be misidentified as a tree. The examples shown in
Figure 14 illustrate that the proposed method has some ability to recognize pole-like objects, but improvements are needed to deal with some special situations.
Next, the performance of each step in the label refinement phase is discussed.
Table 9,
Table 10,
Table 11 and
Table 12 quantitatively evaluate the performance of RF, higher-order CRF and higher-order CRF considering small-label clusters; the quantitative evaluation metrics were the same as in
Section 3.2. As seen from
Table 9, random forest achieved a good overall accuracy of 93.64%, which illustrates that the extracted structural segments provide good materials for classification, indicating the advantages of the segmentation method in this paper and most objects could be directly identified by the classifier; the higher-order CRF improved overall accuracy by 2.02% over the random forest, illustrating that higher-order CRF works well in refining the classification results. The last test was the small-label cluster optimization based on previous steps, which improved overall accuracy by 0.63% and the mean F1-score by 3.26% compared with normal higher-order CRF, indicating that optimization considering small-label clusters can help higher-order CRF to better refine classification results.
Figure 15 presents examples illustrating the optimization of each step in the classification. From the orange box in
Figure 15a,b, the individual targets have been smoothed by higher-order CRF, and from the blue box in
Figure 15b,c, some small, misidentified clusters have been refined by small-label cluster optimization.
Table 10,
Table 11 and
Table 12 present more specific evaluations about different categories in recall, precision and F1-score.
Table 10 indicates that the proposed method had a good ability to identify the ground, façades, vegetation, cars and motorcycles in the Wuhan University dataset, and it was relatively insensitive to pedestrians and artificial poles. However, it can be seen that the higher-order CRF considering small-label clusters contributed to greatly improving the recall accuracy for pedestrians and artificial poles, achieving improvements of 9.38% for pedestrians and 17.42% for artificial poles over RF, and 5.75% and 6.78% over higher-order CRF, indicating that our refined step can improve the recognition rate of each category.
Table 11 presents the precision of each category, and it can be found that pedestrians and artificial poles have better precision than recall, which are 93.58% and 73.99%, respectively, illustrating that the proposed method can identify categories accurately, and the misrecognition of other categories as pedestrians and artificial poles seldom occurs. At the same time, it can be seen that the optimization steps can improve the precision for most targets, and
Table 12 shows the same phenomenon in F1-score; the necessity of optimization steps is verified again.
Table 9,
Table 10,
Table 11 and
Table 12 successfully verify that the proposed method achieved good performance in the Wuhan University dataset, and the contribution of higher-order CRF and further refinements of small-label cluster optimization are also demonstrated.
From
Table 9,
Table 10,
Table 11 and
Table 12, it can be seen that small-label cluster optimization is useful to refine the label of small clusters in one clique; in theory, it needs to run higher-order CRF for each small cluster to obtain their new labels. This means it refines the label of one small cluster, along with allocating the labels of all segments again, consuming lots of computation time. The simplified algorithm is aimed at the target label cluster, which can reduce the time in label refining more than using higher-order CRF directly.
Table 13 provides the time cost of the small-label cluster process in one clique by higher-order CRF and the simplified algorithm; it can be seen that the simplified algorithm can reduce the consumption time.
3.4. Discussions
From the experiments on the Paris-rue-Cassette dataset and Wuhan University dataset, the proposed classification method has been evaluated by qualitative and quantitative analysis, which has proven that the proposed method can work for MLS and TLS point clouds. Through the comparison between the different methods, the proposed method obtained the best overall accuracy of 97.57% in the Paris-rue-Cassette dataset, and it had a better recall in façade, vegetation and car categories, but it achieved lower recall for motorcycles, pedestrians and traffic signs. The overall precision of the proposed method is better than other methods, illustrating that the classification bias is small in the proposed method. Through the results based on the Wuhan University dataset, the contribution of higher-order CRF and small-label optimization in the classification phase have been verified. From
Figure 10b and
Figure 13, it can be seen that the intersecting objects have been divided, illustrating the advantage of segmentation in the method.
The good performance of the proposed method is attributed to the following two reasons:
Segmentation by IN-Graph: In our method, segments are taken as the smallest units of classification, because the structural segments can retain the original shape features, which is beneficial for category recognition. The proposed IN-Graph extracts the segments by cutting off the edge between two objects: this is really segmentation rather than clustering. It is not the same as a normal graph which needs to know the properties of a node. The IN-Graph decides the connection state of two objects by exchanging the decision-making position from node to edge without any prior information or definition of the node; therefore, it has more applicability. Additionally, it realizes the optimal segmentation by graph cutting, so the boundaries between objects are retained while preserving as many of the shape features as possible. This is the reason why segmentation by IN-Graph contributes to improving the classification accuracy, as well as its ability to distinguish adjacent objects;
Higher-order CRF considering small-label clusters: In the refinement step of the classification results, as described above, higher-order CRF works well in small region refinement, but it does not work well in separate clusters in one clique with the same label. In this study, it dealt with these separate clusters with the same label separately, and this paper has proposed a simplified algorithm for a local optimum to allocate labels of these small-label clusters. Thus, it can accurately eliminate small-label clusters in the clique and speed up the operation process. The classification results based on higher-order CRF are further optimized to obtain higher classification accuracy by small-label cluster optimization.
However, some problems need to be fixed in future work. First, comparing the time cost, the efficiency of the proposed method is lower than the supervoxel-based method; the operation time mainly concentrates on the generation of multi-scale supervoxels and structural segments, and small-label cluster optimization also takes some time to refine the classification. This method sacrifices some time efficiency to obtain higher precision units. Secondly, the ability to identify objects with similar shape needs to improve. As shown in
Figure 14b,c, the trees and the artificial poles were misidentified, probably due to the fact that the same category has different forms, and the shapes of items in different categories could be very similar, which confuses the classifier. It would be useful to carry out subdivisions of shape features in the future.