Abstract
Optimal crop emergence is an important trait in crop breeding for genotypic screening and for achieving potential growth and yield. Emergence is conventionally quantified manually by counting the sub-sections of field plots or scoring; these are less reliable, laborious and inefficient. Remote sensing technology is being increasingly used for high-throughput estimation of agronomic traits in field crops. This study developed a method for estimating wheat seedlings using multispectral images captured from an unmanned aerial vehicle. A machine learning regression (MLR) analysis was used by combining spectral and morphological information extracted from the multispectral images. The approach was tested on diverse wheat genotypes varying in seedling emergence. In this study, three supervised MLR models including regression trees, support vector regression and Gaussian process regression (GPR) were evaluated for estimating wheat seedling emergence. The GPR model was the most effective compared to the other methods, with R2 = 0.86, RMSE = 4.07 and MAE = 3.21 when correlated to the manual seedling count. In addition, imagery data collected at multiple flight altitudes and different wheat growth stages suggested that 10 m altitude and 20 days after sowing were desirable for optimal spatial resolution and image analysis. The method is deployable on larger field trials and other crops for effective and reliable seedling emergence estimates.
1. Introduction
Desired plant density is an important agronomic factor for optimal crop growth and yield. Plant density is generally measured by the estimation of crop emergence at early growth stages [1,2,3]. The timely and accurate estimation of emergence or stand count at early growth stages could help farmers in making important field management decisions (e.g., replanting) in order to reduce production loss [4]. Moreover, an accurate measure of crop emergence estimate can be used to understand the impact of soil and environment on crop emergence [5,6]. In crop breeding research for developing improved crop varieties, emergence count is important to screen genotypes for comparative analysis, which is a basis of yield formation in wheat [7]. Conventionally, emergence is assessed by manually counting sub-section of field plots or visual scoring at early growth stages [8]. This is time consuming, labour intensive, not suited to cover large field trials and a cumbersome activity for farmers and plant scientists [4,7,9]. Furthermore, soil conditions, particularly after rainfall or frost, may limit the available time slots when walking in the field for manual observations without damaging the crop. Therefore, an automated high-throughput method for the objective and precise estimation of wheat seedlings emergence will benefit researchers and growers [10,11].
Remote sensing technologies have evolved significantly in the recent past to aid in high-throughput phenotyping for various crop traits including crop emergence. For instance, a ground vehicle imaging systems was used to measure wheat stand count in field conditions [2]. However, these ground-based vehicle systems have limited coverage as they are slow and affected by ground conditions (e.g., wet soil or narrow-row cropping systems), which is not ideal in the case of full-scale crop production or large experimental trials. More recently, unmanned aerial vehicle (UAV)-based sensing technology has evolved manifolds in conjunction with versatile, lightweight and low-cost portable sensors. Such UAV based imaging systems are ideal remote sensing platforms for obtaining images with high spatial resolution and flexibility of frequency in imaging. UAVs are increasingly becoming a standard tool in crop production, monitoring and phenotyping research [12,13]. The technology has been tested as a high-throughput phenotyping tool for crop emergence assessment in different crops [4].
Different image processing methods to measure or estimate crop emergence has been proposed with a focus on stand count and uniformity. At early stages, seedling could be segmented using morphological features (such as canopy area, leaf polygons and length of major axis) from high-resolution images to estimate emergence in rows or over a defined length or area, which is the overall most adopted technique [1,2,3,14]. A seedling template matching approach based on the statistical analysis of seedling geometric shape is another method to count seedlings [15,16]. However, the geometric shape size and overlap of seedlings tend to vary with germination due to variation in soil conditions (moisture, temperature and nutrients), crop management, planting depth and seed quality [3,17,18]. Therefore, simple image features or their combinations are not always sufficient to identify seedlings emergence accurately. Methods based on machine learning or deep learning artificial neural network (ANN) architectures are typically employed directly on images to detect individual seedlings. A range of network architectures are employed for plant emergence counting in different crop types such as CNN in Rapeseed [1], AlexNet in Spinach [19], YOLOv3 in cotton [20] and corn [21], DL in cotton [4], YoloV3 and VGGNet in ornamental plants [22], TasselNetV2+ in Shorgum [23] and TasselNetV3 in maize, wheat and rice [24]. These methods have the inherent requirement of very high spatial resolution and computation resources. Other studies have used seedling clusters (overlapped seedlings) as separate regions-of-interest (RoIs) to develop dedicated classification models to estimate emergence in each RoI. Often these RoIs contain an unbalanced number of seedlings [18], which can potentially affect estimation accuracy [25]. Regression based models can be useful [26] and applied to estimate the emergence in various crops, including maize [27] and cotton [4].
A majority of the previous studies used RGB cameras to estimate plant count [3,9,11,14,19,27]. However, crop color is affected by background soil reflectance and is distorted when the proportion of bare soil in the images is high [28]. The decrease in radiometric contrast between crops and soil creates challenges for segmenting and identifying wheat seedlings. High-resolution cameras with a 4K or 8K sensor size are often used to improve image quality in emergence estimations [27,29]. A UAV mounted 20 M pixel RGB camera system has been used for seedling detection [30,31]. However, previous research also indicated that visible images were potentially affected by sunlight conditions [3,32] and are sensitive to illumination variation, which are identified as challenges in segmenting seedlings [3]. Therefore, multispectral images with near-infrared (NIR) spectral bands could be more effective for crop segmentation. Multispectral imaging has been used to estimate crop emergence using vegetation indices (VIs), such as the normalized difference vegetation index (NDVI) and green normalized difference vegetation index (GNDVI) [33,34]. However, compared to RGB cameras, most commercially available multispectral sensors have a smaller sensor size of 1–2 M pixels, which limits the image resolution [35]. Modified multispectral imaging systems made from high-resolution RGB cameras, by substituting one of the bands filters with a near-infrared filter, are able to provide relatively higher resolutions (e.g., 12 M pixel) at lower costs [33,34]. These modified multispectral imaging systems have been used in high-throughput phenotyping for crop yield estimation [36] and crop stress monitoring [37,38]. However, these sensors have broad spectral bands similar to those of the original cameras, with issues of color distortion, susceptibility to illumination changes, variation in focus with sensor movement and small dynamic range [36] that limit their applicability for seedling emergence estimate. A selection of suitable multispectral VIs was found to improve crop detection accuracies, e.g., green-red vegetation index (GRVI) [39,40] and the wide-dynamic-range vegetation index (WDRVI) [41]. Characteristically, high-resolution RGB cameras use morphological or textural information, whereas multispectral sensors emphasize spectral methods for seedling estimations.
In plant phenotyping, very high-resolution (>40 M pixel CMOS sensor) RGB imaging systems such as DSLR cameras [14,42] currently require additional integration for image geotagging and could be heavy in payload weight which limits the aerial acquisition time for UAV operations. Fully-integrated high-resolution (<20 M pixel CMOS sensor) UAV imaging systems such as the DJI Mavic Pro [24] and Phantom 4 [43] and high-end integrated systems such as Zenmuse P1 [44] are commercially available, although these are yet to be applied in phenotyping applications. On the contrary, off-the-shelf available multispectral sensors for UAV operations are lightweight and integrated with geotagging and irradiance sensor for seamless operation under varying illumination conditions, which are suitable for phenotyping application [45]. Despite this, multispectral imaging systems remain to be appropriately utilized for seedling emergence estimates. This is typically because moderate resolution sensors suffer from the lack of necessary spatial resolution to neatly resolve the geometries of emerged seedlings. Nevertheless, multispectral imaging brings secondary benefits of spectral dimensionality needed to compute multiple VIs, which can then be used to develop multivariate regression models for parametric estimation of plant phenotypic traits [46]. Several approaches such as random forests (RFs) and support vector machines (SVMs) have been developed for fast image processing, particularly for classification [47]. In such multivariate methods, spectral, morphological or textural information can be used individually or in combination with one another [48]. Spectral and textural features have been employed using the SVM model to classify wheat and to estimate seedling count and density [14]. To this end, this study focused on developing an efficient imagery data processing and analysis framework for timely evaluation of wheat emergence by using UAV-based multispectral imagery. This research uniquely applies a machine learning regression (MLR) analysis approach to estimate seedling emergence on combined spectral and morphological data as being efficient and cost-effective. The approach was tested on a diverse number of wheat genotypes with a variation in seedling growth in field conditions. Three supervised MLR models including regression trees (RT), support vector regression (SVR) and Gaussian process regression (GPR) were evaluated and the GPR model was observed to be most effective compared to other MLR methods in estimating seedling emergence.
2. Materials and Methods
2.1. Field Experiment and Data Collection
The wheat field experiment was conducted at the Agriculture Victoria’s Plant Breeding Centre, Horsham, Victoria, Australia (Figure 1a). This location possesses temperate climate with an annual average rainfall of 448 mm and has vertisol soil with predominant clay content. The experiment consisted of 20 wheat genotypes planted in four replications. The seeds for these genotypes were obtained from the Plant Phenomics’ Grains Accession Storage Facility at the Grains Innovation Park, Horsham. The list of wheat genotypes is provided in Supplementary Table S1. The experiment was sown in 5 m × 1 m plots with 5 rows at 25 cm apart (Figure 1b,d). The mechanical seeder places seeds in the row trenches at 2–3 cm deep and covers up the trenches with soil. The normal distance between the seeds was about 1 cm to 4 cm in one line. The seeding pattern was designed to explore the implementation and the evaluation of the emergence estimation model under typical sowing patterns experienced by grain growers.
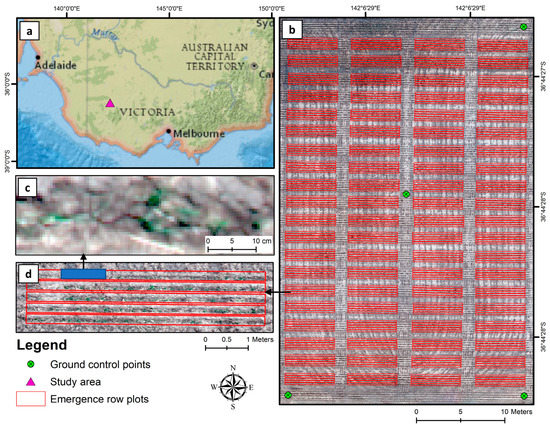
Figure 1.
Location and layout of wheat field trial. (a) Location of the study area in Victoria, Australia; (b) orthomosaic of the study area with row-plot boundaries; (c) an enlarged section of a patch to depict the structural profile of wheat plants obtained at a moderate resolution of 0.69 cm ground sampling distance when flying at 10 m above ground level (agl.); (d) an enlarged section showing a single plot with five row-plots. All presented orthomosaics in figures (b–d) are true color composites (RGBs) created from RedEdge Micasence sensor.
In situ field measurements for emergence counts were collected manually for all experimental row-plots, i.e., 20 genotypes × 4 replications × 5 rows = 400 row-plots (Figure 1b,d). The field measurements technique was exercised at the individual row-plot level rather than at the plot level to increase the number of data points, which is important for the herein used machine learning algorithms to develop robust models. Due diligence was exercised to distinctly count closely placed seedlings with overlapping leaves. The emergence counts were performed by two expert technical staffs and cross-verified for an accurate measurement. The field data was collected at 25 days after sowing (DAS) when seedlings in all field plots were completely germinated. The number of plants in individual row plots ranged between 18 and 94, with a total of 27,892 emergence plant counts over the entire field trial. The statistical average of plant counts per row plot was 60.6. A composite RGB image from UAV multispectral imaging acquired at 20 DAS and operated from a flying height of 10 m is shown in Figure 1c and portrays the level of detail captured in multispectral imaging mode.
2.2. Aerial Data Acquisition
This research used a custom multispectral data acquisition system for phenotypic research integrated at SmartSense iHub, Agriculture Victoria. The system consists of a MicaSense RedEdge-M multispectral camera (MicaSense, Seattle, WA, USA) integrated with a DJI Matrice 100 quadcopter. The complementary metal-oxide-semiconductor (CMOS) sensor of the camera has a size of 4.8 mm × 3.6 mm and captures images with 1,280 × 960 pixels. The multispectral sensor records the position values, i.e., latitude, longitude and altitude onto the camera tags by using the included 3DR uBlox global positioning system (GPS) module. Additionally, the multispectral camera also logs dynamic changes in incident irradiance levels by using a downwelling light sensor (DLS). A radiometric calibration panel with known radiometric coefficients for individual multispectral bands was used. Radiometric calibration measurements were recorded with the multispectral sensor before individual flight missions for image correction.
Meticulous flight planning is important for proper UAV aerial data acquisition campaign, which is critical in high-throughput phenotyping. The UAV trajectory was designed using Ground Station Pro (DJI, Shenzhen, China) and the multispectral sensor was set to trigger the acquisition of images at a specified forward and side overlap of 85%. The UAV multispectral data were obtained on different DAS to identify the time of imaging suitable for the estimation of seedling emergence with higher accuracy. Additionally, the UAV-multispectral system was operated in different flying height configurations to test the effect of different ground sampling distances GSDs useful for identifying the optimal flying height required for emergence estimation. The details for UAV flights and imagery over the experimental site are described in Table 1. The ground control points (GCPs) were installed and the corresponding position was recorded using a multi-band global navigation satellite system (GNSS) based real-time kinetic (RTK) positioning receiver (Reach RS2, Emlid Ltd., Hong Kong) with centimeter level precision, i.e., 2 cm in planimetry and 3 cm in altimetry.

Table 1.
Details of UAV flight parameters.
2.3. Image Processing
The methodology of aerial image processing is included in the overall workflow, shown in Figure 2. The images acquired from UAV aerial mission were processed using a photogrammetry software, Pix4D Mapper (Pix4D SA, Lausanne, Switzerland) [50]. Digital corrections were applied to resolve optical (filters and lenses) aberrations and vignetting effects to maintain consistent spectral response [51,52]. The software used the Structure from Motion (SfM) technique, which is well-suited for processing UAV data to generate reflectance orthomosaic layers. The mosaicked layers were then exported to individual (.tif) files with a spatial resolution as defined in Table 1. The GCPs’ locations collected during the aerial survey were used to geometrically register the orthomosaic datasets. The generated orthomosaic layers were referenced in the Universal Transverse Mercator (UTM) coordinate system with World Geodetic System 1984 (WGS84) as the geodetic datum.
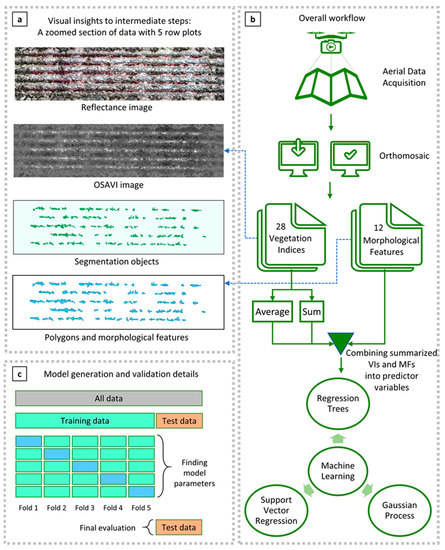
Figure 2.
Workflow for image processing and analysis. (a) Visual insights of intermediate steps in the workflow showing reflectance, OSAVI image, segmented objects and extracted polygons and morphological features; (b) overall workflow adopted in this study covering data acquisition, orthomosaicking, vegetation index, morphological features, summarization of the image layers into predictor variables and used machine learning regressors; (c) model generation and validation details covering both cross-validation and dedicated testing.
2.4. Vegetation Indices
The MicaSense RedEdge multispectral camera records reflectance in blue (475 nm), green (560 nm), red (668 nm), red edge (717 nm) and near-infrared (840 nm) bands. These surface reflectance values were used to compute a comprehensive list of 28 VIs that are commonly used in agriculture plant phenotyping research (Supplementary Table S2). The list includes VIs which are effective in enhancing the contribution of spectral properties of vegetation to correct for confounding factors such as reflectance of soil background in a crop, particularly during the early stages of the growth cycle [53]. VIs involving the mathematical transformation of two or more bands are inherently immune to operator bias or assumptions regarding land cover class, soil type or climatic conditions [45] and are, therefore, promising for phenotyping of crop emergence. For each row-plot, the VI layers were summarized as the average (VImean) and summation (VIsum) of the entire pixel values in the row-plot.
2.5. Vegetation Morphological Features
The key to generating effective morphological features (MFs) for emergence estimation is to separate the emerged plant objects from the background soil. VIs are widely used in identifying crop area [54]. In this study, optimized soil adjusted vegetation index (OSAVI) was selected to suppress background soil reflectance to enhance the detection of vegetation (Figure 2a). The Otsu thresholding method was used to separate the emerged wheat seedlings from soil background because of its advantages of quick operation [55]. The field scene was relatively simple, with brown bare soil and green wheat plants. Color-based Otsu thresholding was previously found to achieve an optimal threshold to sperate background and target with an overall classification accuracy of 99% for the same scene [45]. A watershed delineation algorithm was used to separate image regions into distinct objects by assigning pixels into marked objects [56]. A total of 12 MFs related to the geometrical properties of the delineated image objects were computed (Supplementary Table S3). Although it is difficult to separate wheat plants using the segmentation techniques because of the complex overlap of closely placed seedling canopies, the number of seedlings contained in each object still influence its MFs. For instance, an object with more wheat seedlings contains more pixels than an object with a single wheat seedling. Such differences produce key variations in MFs between the two objects. This was the basis of using MFs to estimate wheat seedling emergence count in addition to VIs. All the MF variables (Supplementary Table S3) were summarized at the row-plot level.
2.6. Emergence Modelling Using Machine Learning Regression
Machine learning regression (MLR) based analysis was used to estimate emergence counts of wheat seedlings. MLR analysis or non-parametric nonlinear regression algorithms combines one or more predictor variables (or input parameter) to establish a significant relationship with a certain response variable (or output parameter), i.e., seedling emergence estimates over a training database. The underlying kernel method provides the flexibility in transforming the original data into a higher dimensional space. The kernel method also provides a dependable theoretical framework and involves few tunable hyper parameters to develop a flexible nonlinear mapping between the predictor and response variable, which is useful in the case of limited training data [57]. Although these methods are widely recognized, some questions on model strength, dependency on training and testing data distribution still remain open. In this study, three supervised MLR models including regression tree (RT) [58], support vector regression (SVR) [59] and Gaussian process regression (GPR) [60] were evaluated to identify the best performing model in estimating wheat seedling emergence.
2.6.1. Regression Trees (RT)
RT is a decision tree based algorithm applied in predictive modeling used in statistics, data mining and machine learning [61]. The models are obtained by recursively partitioning the data space and fitting a simple prediction model within each partition, which helps in dealing with data heterogeneity. It is an ensemble learning method based on multiple decision trees that are widely popular in remote sensing studies [62,63,64]. The method combines bagging and the random selection of features. The data are partitioned into homogeneous subsets called the number of trees (n-trees) and each tree is developed to its maximum extent by selecting random samples and variables from the training dataset. The number of variables (x) and the number of n-trees are used to split the nodes (mtry) by using the best split variable among randomly selected variables and the optimization of both parameters (x and n-trees) is performed in the process [65]. The RT algorithm measures the error for each variable by calculating the mean square error difference between out of bag data against the data used to grow the tree. Unlike decision tree models, RT is resistant to over fitting without losing information and always results in the convergence of generalization error. As the rule of splitting using randomization improves the performance [66], therefore, only three parameters, i.e., ntree, mtry and node size requires optimization using k-fold cross validation to achieve good results [67].
2.6.2. Support Vector Regression (SVR)
SVR is an efficient machine learning algorithm for modeling; it is developed and introduced for versatile-type structural identification [68]. It is widely used for fitting an optimized hyperplane to a set of input features to develop a linear dependency between n-dimensional input variables and 1-dimesional response variable, which can be used for classification, regression and outlier detection [51]. The algorithm achieves optimized fitting of the hyperplane for SVR formulation by minimizing ɛ-insensitive loss function. The training samples are mapped into a higher dimensional feature space that is non-linearly related with the original feature space using kernel functions [69], which enables data distribution to be fitted with a linear model [70,71,72].
2.6.3. Gaussian Process Regression (GPR)
GPR is a nonparametric kernel-based Bayesian probabilistic approach for solving regression and classification problems. It is a stochastic process that results in good performance in terms of the development of a calibration model for both linear and non-linear datasets with the ability to provide uncertainty measurements on the predictions. The Bayesian model, GPR, does not require any intermediate model parameters. The algorithmic execution is somewhat equivalent to neural networks (NN) without being a black-box. Additionally, it alleviates some shortcomings of handling few sample points and feature and sample rankings are based on predictive mean and variance. Another advantage with GPR is the availability of modern kernel functions; therefore, hyperparameters can be adapted efficiently by boosting the marginal likelihood in the training set [73]. Although the approach poses large computational complexity [60,74], this could be easily addressed with modern computational resource or by summarizing layers into a set of input parameters, as is adopted in this study.
2.6.4. Hyperparameter Optimization, Accuracy Assessment and Evaluation
In order to evaluate the repeatability of the developed method, the prediction accuracy for the MLR models (RT, SVR and GPR) was evaluated by implementing a k-fold CV, with k = 5, where 80% of the data was included in the training population (i.e., for 320 plots) and 20% of the remaining data (i.e., for 80 plots) was used as a dedicated testing set; the data partitioning was performed randomly (Figure 2c). A Bayesian hyperparameter optimization [75] approach was used with all the MLR models. The objective of Bayesian optimization and optimization in general is to find a point (xi) in the bounded domain for x such that it minimizes the objective function f(x). In the context of hyperparameter tuning, a point (xi) is a set of hyperparameter values and the objective function is the loss function or the mean squared error (MSE). In short, the algorithm selects the appropriate kernel function from the pool, box constraints, sets the kernel scale, sigma (σ), epsilon (ε) and standardizes the data for suitable MLR methods during the k-fold training and cross-validation.
The cross-validation consisted of five iterations (five-folds) where the dataset was split into five groups and a different testing set was used for each iteration (Figure 2c). Instant accuracy was calculated where the coefficient of determination (R2), root mean square error (RMSE) and mean absolute error (MAE) for each testing set was obtained (Equations (1), (2) and (3), respectively) and an average of five iterations was reported. For the best performing MLR model, a dedicated validation was adopted on the 20% testing data (exclusive to any training data) with the calculation of R2, RMSE and MAE. Additionally, residuals between the estimates and true emergence counts were measured to generate plots of histogram of residuals and the normal probability of residuals:
where is the true value for i-th observation, is the mean of true value of observations, is the predicted value for i-th observation and N is the number of observations.
Meanwhile, the total seedling emergence counts at the plot level was calculated using the sum of corresponding row-plots emergence counts. The estimated count sum was rounded to integers.
3. Results
3.1. Evaluation of Machine Learning Regression Techniques and Model Development
Rigorous experimentation was caried out to develop and investigate a suitable method for estimating the emergence of wheat seedlings by using multispectral imaging. Detecting individual seedling in moderate resolution multispectral imaging is challenging due to complexity arising from closely emerged seedlings with overlapping leaves. Therefore, multimodal explanatory variables such as VIs and MFs derived from aerially acquired multispectral images were used to develop a MLR based emergence estimation model. A comprehensive list of 28 VIs (Supplementary Table S2) and 12 MFs (Supplementary Table S3) was used to produce a reliable and robust model. Furthermore, VIs were categorically summarized as VImean and VIsum to further increase statistical dimensionality. The rationale for this was to investigate the contribution of different summarizations, in particular, VIsum was identified to be potentially significant for quantifying the total emergence in each field plot. Although it is difficult to separate wheat plants using the segmentation techniques because of the complex overlap of closely placed seedling canopies, the number of seedlings contained in each object still influence its MFs. For instance, an object with more wheat seedlings contains more pixels than an object with a single wheat seedling. Such differences produce the key variations in MFs between the two objects. This was the basis of using MFs to estimate wheat seedling emergence count in addition to VIs. The derived 28 VImean, 28 VIsum and 12 MFs were combined into a total set of 68 variables for each of the 400 row-plots and used in MLR models.
Three MLR models RT, SVR and GPR were evaluated in the process to identify the best model (Figure 3). A k-fold (k = 5) cross-validation strategy was used wherein 80% of the available number of observations were used in model training, i.e., the training data were sub-divided into 5-folds (Figure 2c). Each of the iteration data from four folds was used in model training and the data from the remaining one fold were used in testing. With k = 5, the iterations were repeated five times such that a different fold is always selected as a testing set each time. The RT based modelling achieved the lowest accuracy in predicting emergence counts with R2 = 0.66, the SVR based modelling achieved a reasonable accuracy with R2 = 0.76. The GPR based modelling outperformed both RT and SVR with R2 = 0.81, RMSE = 4.97 and MAE = 3.90. Therefore, GPR was selected as the optimal regressor for further testing and analysis in this study.
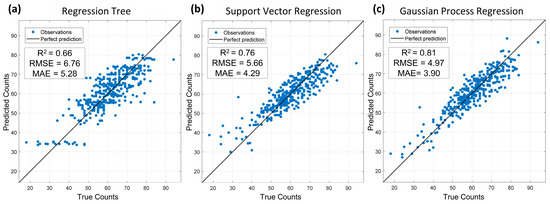
Figure 3.
Cross-validation of machine learning model results. Three machine learning regression models (a) Regression tree, (b) Support vector regression and (c) Gaussian process regression models were applied on the training dataset. True counts are manually measured seedling emergences and predicted counts use a given model.
3.2. Estimation of Wheat Seedling Emergence
The best performing estimation model was GPR. GPR was tested on 20% of the exclusive data, which was originally kept aside from model development. This provides a basis to undertake dedicated testing using the exclusive set of data, which is important to determine the repeatability of the developed GPR model on new data potentially collected from different environments. The selected trained model employed a Matern5/2 Gaussian kernel [60] with a constant basis function and sigma (σ) of 4.613. As the input predictors contained widely different scales variable, scaling or normalization was applied to improve the model fitting. The results of dedicated validation on exclusive data portion demonstrate agreement with the k-fold cross-validation, with R2 = 0.86, RMSE = 4.07 and MAE = 3.21 (Figure 4a). The histogram of the residual plot was used to verify the variance of residual error around zero, i.e., no error (Figure 4b). The histogram shows that the residuals are slightly skewed towards the right (Figure 4b). The histogram of the residual is a frequency plot obtained by placing the error residuals in regularly spaced cells and plotting each cell frequency versus the center of the cell. In this case, the bin width for display was set to three. Furthermore, the normal probability plot of the residuals was used to determine whether it is reasonable to assume that the error terms are normally distributed for the GPR model (Figure 4c). Small departures from the characteristic straight line in the normal probability plot are common, with a coherent unimodal distribution of residuals. The breaks near the ends of this graph are also indications of minor abnormalities in the residual distribution, which in this case is due to slight non-uniform distribution of emergence count observations more towards the center compared to the edges. However, a little variability in residuals was possible due to genotypic variability in the seedling estimation process.
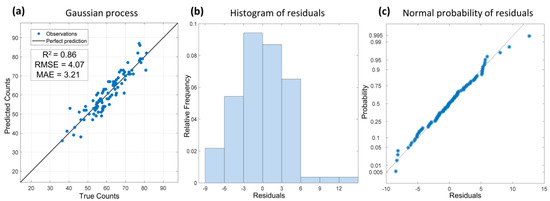
Figure 4.
Dedicated validation of Gaussian processed regression (GPR) model results: (a) GPR model relationship, (b) Histogram of residuals plot and (c) Normal probability of residuals. True counts are manually measured seedling emergences and predicted counts use a given model.
3.3. Effect of Time of Aerial Survey and Flying Altitude on Performance
The timing of aerial imaging is critical in acquiring suitable data for emergence modelling using image processing and MLR based methods. The effect of time of aerial imaging on the accuracy of the GPR model in predicting emergence counts is shown in Figure 5a. The accuracy term is represented with R2 in k-fold cross-validation testing during model development. The model accuracy at 10 DAS was critically low, which increased at 15 and peaked at 20 DAS, and then started reducing with further growth of plants from 30 DAS onwards (Figure 5a). The best time point of imaging with the highest R2 was at 20 DAS, which was selected in this study for all other analysis. A higher number of leaves corresponding to these later vegetative stages in wheat makes more overlap with adjacent plants, resulting in the decrease in seedling emergence estimation accuracy.
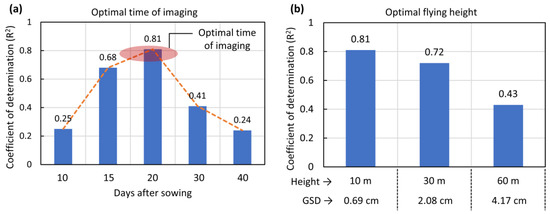
Figure 5.
Cross-validation accuracy in GPR model development in terms of the coefficient of determination (R2). (a) R2 at different timing of aerial survey; (b) flying altitude of UAV. Note: the x-axis of bar graph plots is not linear.
The altitude of aerial surveying governs the resolution of captured images, which tends to influence the modelling approach and accuracy in estimation of emergence. A comparison of the R2 in the k-fold cross-validation testing support that the performance of GPR based estimator decreases with flying altitude, i.e., finer GSD (Figure 5b). The R2 = 0.81 was the highest at a flying height of 10 m and produced a resolution of 0.69 cm GSD, which slightly decreased at 30 m to R2 = 0.72 and substantially reduced to R2 = 0.43 at 60 m with a resolution of 4.17 cm. The accuracy of the regression model was consistently penalized when the spatial resolution reduced.
3.4. Genotypic Screening for Wheat Seedling Emergence
In plant breeding research, genotypic screening and the selection of better performing genotypes for growth and yield are key objectives. Where seedling emergence estimates in field plots comprise several genotypes, it is important to have similar or known numbers of plant density in order to obtain yield comparisons of genotypes. The aim of this study was to develop an accurate, non-invasive and UAV-multispectral based analytical framework to estimate variation amongst wheat genotypes. The seedling emergence counts across 20 genotypes showed a variation between 250 and 475 plants per field plot (Figure 6a). The error bar plot also represents the uncertainty of variation within each genotype among four replications (Figure 6). There are substantial variations in the spread of seedling emergence values around the mean for a few wheat genotypes, including Bolac, Carnamah, Derrimut, EGA Gregory, Ellison, Gladius, Peake and Sunzell; this could be due to variation in the germination rate governed by genotypic performance and seed quality, as well as localized soil moisture characteristics in field conditions. Nevertheless, the predicted values from the proposed UAV-based sensing workflow correlated with ground truth observed values at the plot level (Figure 4a). Overall, the genotype Ellison achieved the highest and Crusader achieved the lowest average emergence.
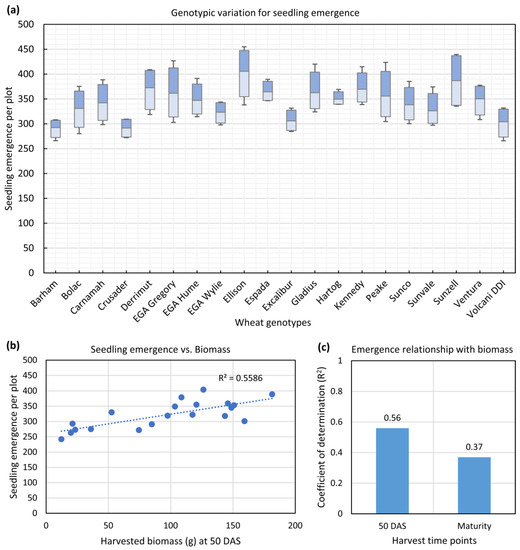
Figure 6.
Seedling emergence profile of wheat genotypes and its effects on biomass in terms of the coefficient of determination (R2). (a) Variation of emergence between different genotypes of wheat as estimated from the method. Each of the floating column summarizes the variability among four replications; maxima and minima are represented by the top and bottom whiskers, respectively, 25th and 75th quartile represented by the second lower and second upper whiskers, respectively, and the average is represented by the middle whisker; (b) R2 of seedling emergence with the harvested biomass at vegetative growth stage of 50 DAS shown using a linear regression plot; (c) R2 of seedling emergence on harvested biomass at 50 DAS and maturity.
The genotypes with better seedling emergence rate have the potential of faster crop establishment with higher biomass at early growth stages. The harvested biomass measured at an early vegetative stage of 50 DAS showed an R2 of 0.56 with seedling emergence (Figure 6b). On the other hand, the harvested biomass measured at maturity produced a low R2 of 0.37 with seedling emergence (Figure 6c).
4. Discussion
High-throughput plant phenotyping enables faster measurement of various crop traits during the development. Among these traits, the timely and accurate estimations of emergence are critical for farmers to make informed field management decisions and plant scientists for genotypic and treatment comparisons [4]. Additionally, seedling emergence estimate is useful for understanding the impact of soil and environment on crop emergence [5,6]. Therefore, emergence is an important agronomic parameter for developing improved crop varieties in plant breeding. Manual seedling emergence counting under field conditions is tedious and time-consuming [4,7,9]. Therefore, in-field emergence counting is often operationally impractical for large breeding trials. This is conducted by visually estimating or scoring the number of seedling emergence, which is quicker but less accurate. Imaging based methods on field system are operationally practical and suitable for larger field trials. Employing UAV-based multispectral imaging in seedling emergence counting is appealing, as the technology is being widely used in plant breeding research and precision agriculture. Multispectral sensor systems are relatively lightweight compared to high-resolution RGB imaging systems, which otherwise necessitates a much larger UAV with heavier payload lifting capabilities and poses operational constraints.
The estimation of seedling emergence using UAV multispectral imaging system in field conditions is challenging, especially when a wide range of genotypes are present with varying emergence rates and densities. Complexities arising due to the emergence of closely placed seeds resulting in overlapping leaves and this poses further problems in separating seedlings. Furthermore, the limited resolution of a multispectral imaging system renders it very difficult to distinguish individual wheat seedlings. Therefore, previous studies have recommended that the accurate extraction of seedlings should combine color indices and mathematical morphology operation [11]. In this study, an MLR analysis on a multi-variable dataset including VImean, VIsum and MFs was a suitable, robust and computationally efficient method for seedling emergence counting in wheat. A comprehensive number of 28 VIs was used to implement a robust MLR model for emergence estimation (Supplementary Table S2) to avoid omitted variable bias, which occurs when a model leaves out confounding variables [76]. Additionally, two sets of summarized VI variables—VImean and VIsum—were used, as both add dimensional modalities which assist in improving the estimation accuracy of the MLR models. The VIsum variables, in particular representing the algebraic sum of the VI pixel values within each plot, provided a conceptual basis for linearly predicting the emergence counts. At the early emergence stage with the seedlings being significantly small, the value of VIs for each pixel is typically low corresponding to distinct seedlings where a linear addition is more explanatory for counting seedlings. The plot variables summarized as VIsum, such as NDVIsum, have been effective in investigating the emergence of wheat seedlings [34]. The complementary information provided by the MFs against VIs is essential for a reliable assessment of emergence counts. Previous studies have also shown MF assisted counts suitable in wheat seedlings, while including more MFs and training data in the future is suggested for improving the estimation performance [29]. In this line, this study aimed to use a set of 12 MFs for counting seedlings emergence for 20 wheat genotypes with a large total of 400 individual row-plot measurements in model training and evaluation. Furthermore, the accuracy of MFs could be subjected to low imaging sensor resolution affecting the extraction of fine plant features. In order to compensate, the UAV was operated at multiple altitudes, with the flight at the lowest altitude of 10 m being found most suitable.
The MLR technique used here was trained repeatedly by using the five-fold cross-validation. This provides the best performances because it considers the genotypic variability influencing the plant structure as well as the possible influence of the environmental conditions, especially in rain and wind. The method was tested on a dedicated dataset to validate the performance of the selected GPR based machine learning model. This ensures promising deployment in other field trials. However, for operational deployment of the method, it is better to re-calibrate the model over the new experimental site. With the passage of time, further training datasets would provide sufficient training encompassing all the possible situations and further variability of genotypes; this is deemed as the future scope of this study. Nevertheless, existing studies have demonstrated continued interest in employing modelling for seedling emergence estimation [2,11,14,33,34]. The method and selected GPR model could be potentially applied to cereal crop species.
Seedling growth is a dynamic process [34,77]. Identifying the suitable time of aerial imaging is an essential prerequisite in image processing for computing spectral VIs and structural MFs have an explanatory association with seedling emergence counts. Compared to a few wheat seedling estimation studies based on single dates of imaging [14,78], this study used the images captured at five time points during the early stages of plant growth. The results indicate that there were significant differences among the estimation models at different time-points with the development of complex leaf architectures. The plant growth stage at the time of imaging is critical for obtaining an accurate estimation of seedling numbers [2,14]. Other methods involving direct seedling recognition have also reported a strong influence of growth stages in revealing the relationship between the count and the number of leaves per seedling and the eventual estimation of seedling stand count [1,77].
By examining the modelling results, data collected at 20 DAS (Z13) were optimal imaging timepoints whereas earlier and later time points were less suitable. This is justified since wheat seedling emergence differs between genotypes and, in the field experiment, there were certain genotypes which had not emerged fully at earlier timepoints, i.e., at 10 to 15 DAS (Z11 to Z12). Additionally, wheat plants are too small at early emergence stages making it difficult to measure quantifiable VIs and MFs. On the other hand, at later vegetative stages of 30 and 40 DAS (Z14 and Z15), canopies of the wheat plant started to significantly overlap, which lowers the effective VI value sensed by the multispectral sensor and prevents the extraction of MFs since plants tend to remain in a single large cluster. These results are in line with previous findings, where R2 estimation accuracy reached a peak at a certain timepoint and declined with an increase in density or plant growth in wheat [11]. The timing of seed germination could be delayed due to environmental factors such as soil moisture status and temperature. Therefore, the germination of seedling needs to be considered under the influence of the environmental condition affecting seed germination. Fundamentally, a timepoint with plots achieving maximum germination and wheat seedlings canopies that are not significantly overlapping each other is ideal for multispectral imaging.
The ground resolution obtained by using UAV-multispectral imaging decreased with flying height. A lower resolution reduced the accuracy in estimating seedling emergence. A flying height of 10 m tested in this study was most suitable compared to flying heights of 30 m and 60 m. This observation is consistent with previous studies advising acquiring data from a lower altitude to improve image quality [79]. However, a lower imaging height is deemed to invariably increase the flight time. Furthermore, small and irregular spacing makes wheat seedlings clustered in low spatial resolutions [3]. As a result, it is hard to detect and estimate wheat seedling counts. A low spatial resolution increases GSD, meaning that a larger area on the ground is sensed per unit pixel. Thus, it becomes difficult to precisely delineate the transitional line between the green wheat seedling and grey background soil due to mixed pixels. Shaky leaves due to wind during the time of imaging perhaps add to the mixed pixel noise in multispectral images, which also reduce delineation of seedlings. Additionally, the existence of in-field weed should be given attention as this may potentially add noise in the computed VIs and confuse the crop segmentation operator that is relied on for generating MFs. The weeds were well-managed in this study with the timely application of herbicides and manual control. Incorporating a weed detection algorithm could potentially apply as a backup solution to mask weed cover before extracting VIs or MFs.
5. Conclusions
A high-throughput phenotyping method to estimate seedling emergence is needed to simplify the otherwise tedious and time-consuming in-field manual counting. The main contribution of this study is to develop a simple procedure to estimate wheat seedling emergence that is important for farmers and plant scientists. The foundation of the method relies on combining spectral and morphological information from multispectral imaging by using UAVs. An MLR based estimator was used to predict the number of seedling emergence at early growth stages of crop. A variety of spectral and morphological parameters were generated from the UAV data to add to dimensional modalities and to best examine the efficacy of tested MLR approaches. Additionally, the research design incorporates investigation of multiple attributes of a UAV mission and analytics, including identifying an optimal flying height and time of imaging to suit wheat seedling emergence. The approach was tested on diverse wheat genotypes with variation in seedling emergence under field conditions. Multispectral imagery with the application of GPR model analytics was identified as a potential alternative to in-field manual emergence counting in wheat. In addition, the desirable options for optimal flight altitude and suitable wheat growth stage were identified, with higher resolution or low flying height providing benefits in estimating wheat germination counts. Early growth stage where germination was complete in all genotypes, but minimal canopy overlap was present was also beneficial. The method is simple to adopt for large research trials and farmers field in wheat and it can be deployed in other crop species.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/rs13152918/s1, Table S1: Wheat genotypes used in the field trial, Table S2: List of vegetation indices relating to physiology and canopy structure used in this study, Table S3: List of vegetation morphological features used in this study.
Author Contributions
B.P.B. and S.K. conceived the experiment. B.P.B. and V.S. conducted the experiments, data analysis and writing original draft. S.K. performed investigation, resources, writing and supervision. S.K. and G.S. conducted project administration, funding acquisition and manuscript review and editing. All authors reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Acknowledgments
We thank Nathan Good for conducting some UAV flights and pre-processing the multispectral data and Denise M Barbulescu, Emily Thoday-Kennedy and Sandra Maybery for their help in managing the field trial and the manual measurement of crop height and biomass harvest.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, J.; Zhao, B.; Yang, C.; Shi, Y.; Liao, Q.; Zhou, G.; Wang, C.; Xie, T.; Jiang, Z.; Zhang, D.; et al. Rapeseed Stand Count Estimation at Leaf Development Stages With UAV Imagery and Convolutional Neural Networks. Front. Plant Sci. 2020, 11, 617. [Google Scholar] [CrossRef]
- Liu, S.; Baret, F.; Andrieu, B.; Burger, P.; Hemmerlé, M. Estimation of Wheat Plant Density at Early Stages Using High Resolution Imagery. Front. Plant Sci. 2017, 8. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Zhang, J.; Yang, C.; Zhou, G.; Ding, Y.; Shi, Y.; Zhang, D.; Xie, J.; Liao, Q. Rapeseed Seedling Stand Counting and Seeding Performance Evaluation at Two Early Growth Stages Based on Unmanned Aerial Vehicle Imagery. Front. Plant Sci. 2018, 9, 1362. [Google Scholar] [CrossRef]
- Feng, A.; Zhou, J.; Vories, E.; Sudduth, K.A. Evaluation of cotton emergence using UAV-based imagery and deep learning. Comput. Electron. Agric. 2020, 177, 105711. [Google Scholar] [CrossRef]
- Forcella, F.; Benech Arnold, R.L.; Sanchez, R.; Ghersa, C.M. Modeling seedling emergence. Field Crop. Res. 2000, 67, 123–139. [Google Scholar] [CrossRef]
- Ghassemi-Golezani, K.; Dalil, B. Effects of seed vigor on growth and grain yield of maize. Plant Breed. Seed Sci. 2014, 70, 81–90. [Google Scholar] [CrossRef]
- Kipp, S.; Mistele, B.; Baresel, P.; Schmidhalter, U. High-throughput phenotyping early plant vigour of winter wheat. Eur. J. Agron. 2014, 52, 271–278. [Google Scholar] [CrossRef]
- Wiles, L.J.; Schweizer, E.E. The cost of counting and identifying weed seeds and seedlings. Weed Sci. 1999, 667–673. [Google Scholar] [CrossRef]
- Varela, S.; Dhodda, P.R.; Hsu, W.H.; Prasad, P.V.V.; Assefa, Y.; Peralta, N.R.; Griffin, T.; Sharda, A.; Ferguson, A.; Ciampitti, I.A. Early-Season Stand Count Determination in Corn via Integration of Imagery from Unmanned Aerial Systems (UAS) and Supervised Learning Techniques. Remote Sens. 2018, 10, 343. [Google Scholar] [CrossRef] [Green Version]
- Araus, J.L.; Cairns, J.E. Field high-throughput phenotyping: The new crop breeding frontier. Trends Plant Sci. 2014, 19, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Yang, T.; Li, C.; Li, R.; Wu, W.; Zhong, X.; Sun, C.; Guo, W. A method to calculate the number of wheat seedlings in the 1st to the 3rd leaf growth stages. Plant Methods 2018, 14, 101. [Google Scholar] [CrossRef]
- Ehsani, R.; Mari Maja, J. The Rise of Small UAVs in Precision Agriculture. Resour. Mag. 2013, 20, 18–19. [Google Scholar]
- Gómez-Candón, D.; De Castro, A.I.; López-Granados, F. Assessing the accuracy of mosaics from unmanned aerial vehicle (UAV) imagery for precision agriculture purposes in wheat. Precis. Agric. 2014, 15, 44–56. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Koh, J.C.O.; Hayden, M.; Daetwyler, H.; Kant, S. Estimation of crop plant density at early mixed growth stages using UAV imagery. Plant Methods 2019, 15, 64. [Google Scholar] [CrossRef]
- García-Martínez, H.; Flores-Magdaleno, H.; Khalil-Gardezi, A.; Ascencio-Hernández, R.; Tijerina-Chávez, L.; Vázquez-Peña, M.A.; Mancilla-Villa, O.R. Digital Count of Corn Plants Using Images Taken by Unmanned Aerial Vehicles and Cross Correlation of Templates. Agronomy 2020, 10, 469. [Google Scholar] [CrossRef] [Green Version]
- Egli, D.B.; Rucker, M. Seed Vigor and the Uniformity of Emergence of Corn Seedlings. Crop Sci. 2012, 52, 2774–2782. [Google Scholar] [CrossRef]
- Feng, A.; Zhou, J.; Vories, E.; Sudduth, K.A. Evaluation of Cotton Emergence Using UAV-Based Narrow-Band Spectral Imagery with Customized Image Alignment and Stitching Algorithms. Remote Sens. 2020, 12, 1764. [Google Scholar] [CrossRef]
- Valente, J.; Sari, B.; Kooistra, L.; Kramer, H.; Mücher, S. Automated crop plant counting from very high-resolution aerial imagery. Precis. Agric. 2020, 21, 1366–1384. [Google Scholar] [CrossRef]
- Oh, S.; Chang, A.; Ashapure, A.; Jung, J.; Dube, N.; Maeda, M.; Gonzalez, D.; Landivar, J. Plant Counting of Cotton from UAS Imagery Using Deep Learning-Based Object Detection Framework. Remote Sens. 2020, 12, 2981. [Google Scholar] [CrossRef]
- Wang, L.; Xiang, L.; Tang, L.; Jiang, H. A Convolutional Neural Network-Based Method for Corn Stand Counting in the Field. Sensors 2021, 21, 507. [Google Scholar] [CrossRef] [PubMed]
- Bayraktar, E.; Basarkan, M.E.; Celebi, N. A low-cost UAV framework towards ornamental plant detection and counting in the wild. ISPRS J. Photogramm. Remote Sens. 2020, 167, 1–11. [Google Scholar] [CrossRef]
- Lu, H.; Cao, Z. TasselNetV2+: A Fast Implementation for High-Throughput Plant Counting From High-Resolution RGB Imagery. Front. Plant Sci. 2020, 11. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Liu, L.; Li, Y.N.; Zhao, X.M.; Wang, X.Q.; Cao, Z.G. TasselNetV3: Explainable Plant Counting With Guided Upsampling and Background Suppression. IEEE Trans. Geosci. Remote Sens. 2021, 1–15. [Google Scholar] [CrossRef]
- Chawla, N.V. Data Mining for Imbalanced Datasets: An Overview. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2010; pp. 875–886. [Google Scholar] [CrossRef] [Green Version]
- Ribera, J.; Chen, Y.; Boomsma, C.; Delp, E. Counting plants using deep learning. In Proceedings of the 2017 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Montreal, QC, Canada, 14–16 November 2017; pp. 1344–1348. [Google Scholar]
- Gnädinger, F.; Schmidhalter, U. Digital Counts of Maize Plants by Unmanned Aerial Vehicles (UAVs). Remote Sens. 2017, 9, 544. [Google Scholar] [CrossRef] [Green Version]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Li, B.; Xu, X.; Han, J.; Zhang, L.; Bian, C.; Jin, L.; Liu, J. The estimation of crop emergence in potatoes by UAV RGB imagery. Plant Methods 2019, 15, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buters, T.M.; Belton, D.; Cross, A.T. Multi-Sensor UAV Tracking of Individual Seedlings and Seedling Communities at Millimetre Accuracy. Drones 2019, 3, 81. [Google Scholar] [CrossRef] [Green Version]
- Buters, T.; Belton, D.; Cross, A. Seed and Seedling Detection Using Unmanned Aerial Vehicles and Automated Image Classification in the Monitoring of Ecological Recovery. Drones 2019, 3, 53. [Google Scholar] [CrossRef] [Green Version]
- Teixeira Crusiol, L.G.; Nanni, M.R.; Furlanetto, R.H.; Cezar, E.; Silva, G.F.C. Reflectance calibration of UAV-based visible and near-infrared digital images acquired under variant altitude and illumination conditions. Remote Sens. Appl. Soc. Environ. 2020, 18, 100312. [Google Scholar] [CrossRef]
- Sankaran, S.; Khot, L.R.; Carter, A.H. Field-based crop phenotyping: Multispectral aerial imaging for evaluation of winter wheat emergence and spring stand. Comput. Electron. Agric. 2015, 118, 372–379. [Google Scholar] [CrossRef]
- Sankaran, S.; Quirós, J.J.; Knowles, N.R.; Knowles, L.O. High-Resolution Aerial Imaging Based Estimation of Crop Emergence in Potatoes. Am. J. Potato Res. 2017, 94, 658–663. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative remote sensing at ultra-high resolution with UAV spectroscopy: A review of sensor technology, measurement procedures, and data correction workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef] [Green Version]
- Feng, A.; Zhou, J.; Vories, E.D.; Sudduth, K.A.; Zhang, M. Yield estimation in cotton using UAV-based multi-sensor imagery. Biosyst. Eng. 2020, 193, 101–114. [Google Scholar] [CrossRef]
- Zhou, J.; Khot, L.R.; Boydston, R.A.; Miklas, P.N.; Porter, L. Low altitude remote sensing technologies for crop stress monitoring: A case study on spatial and temporal monitoring of irrigated pinto bean. Precis. Agric. 2018, 19, 555–569. [Google Scholar] [CrossRef]
- Choudhury, B.; Webster, R.; Sharma, V.; Goswami, J.; Meetei, T.; Krishnappa, R.; Raju, P.L. Frost damage to maize in northeast India: Assessment and estimated loss of yield by hyperspectral proximal remote sensing. J. Appl. Remote Sens. 2019, 13, 044527. [Google Scholar] [CrossRef]
- Chen, A.; Orlov-Levin, V.; Meron, M. Applying High-Resolution Visible-Channel Aerial Scan of Crop Canopy to Precision Irrigation Management. Proceedings 2018, 2, 335. [Google Scholar] [CrossRef] [Green Version]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of Green-Red Vegetation Index for Remote Sensing of Vegetation Phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Li, G.L.; Luo, Y.K.; Pan, Q.; Zhang, S.Y. Monitoring of sugar beet growth indicators using wide-dynamic-range vegetation index (WDRVI) derived from UAV multispectral images. Comput. Electron. Agric. 2020, 171, 105331. [Google Scholar] [CrossRef]
- Peng, X.; Zhong, X.; Zhao, C.; Chen, A.; Zhang, T. A UAV-based machine vision method for bridge crack recognition and width quantification through hybrid feature learning. Constr. Build. Mater. 2021, 299, 123896. [Google Scholar] [CrossRef]
- Lin, Z.; Guo, W. Sorghum Panicle Detection and Counting Using Unmanned Aerial System Images and Deep Learning. Front. Plant Sci. 2020, 11. [Google Scholar] [CrossRef]
- DJI. Zenmuse P1 Specification. Available online: https://www.dji.com/au/zenmuse-p1/specs (accessed on 17 July 2021).
- Banerjee, B.P.; Spangenberg, G.; Kant, S. Fusion of Spectral and Structural Information from Aerial Images for Improved Biomass Estimation. Remote Sens. 2020, 12, 3164. [Google Scholar] [CrossRef]
- Lee, H.; Wang, J.; Leblon, B. Using Linear Regression, Random Forests, and Support Vector Machine with Unmanned Aerial Vehicle Multispectral Images to Predict Canopy Nitrogen Weight in Corn. Remote Sens. 2020, 12, 2071. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. Techniques for Image Processing and Classifications in Remote Sensing; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Linker, R.; Cohen, O.; Naor, A. Determination of the number of green apples in RGB images recorded in orchards. Comput. Electron. Agric. 2012, 81, 45–57. [Google Scholar] [CrossRef]
- Joshi, S.; Choukimath, A.; Isenegger, D.; Panozzo, J.; Spangenberg, G.; Kant, S. Improved Wheat Growth and Yield by Delayed Leaf Senescence Using Developmentally Regulated Expression of a Cytokinin Biosynthesis Gene. Front. Plant Sci. 2019, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.Y.; Lenz-Wiedemann, V.; Miao, Y.X.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]
- Wang, C.Y.; Myint, S.W. A Simplified Empirical Line Method of Radiometric Calibration for Small Unmanned Aircraft Systems-Based Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1876–1885. [Google Scholar] [CrossRef]
- Kelcey, J.; Lucieer, A. Sensor correction of a 6-band multispectral imaging sensor for UAV remote sensing. Remote Sens. 2012, 4, 1462–1493. [Google Scholar] [CrossRef] [Green Version]
- Gnyp, M.L.; Yu, K.; Aasen, H.; Yao, Y.; Huang, S.; Miao, Y.; Bareth, G. Analysis of Crop Reflectance for Estimating Biomass in Rice Canopies at Different Phenological Stages Reflexionsanalyse zur Abschätzung der Biomasse von Reis in unterschiedlichen phänologischen Stadien. Photogramm. Fernerkund. Geoinf. 2013, 351–365. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef] [Green Version]
- Vala, H.J.; Baxi, A. A review on Otsu image segmentation algorithm. Int. J. Adv. Res. Comput. Eng. Technol. 2013, 2, 387–389. [Google Scholar]
- Soille, P.J.; Ansoult, M.M. Automated basin delineation from digital elevation models using mathematical morphology. Signal Process. 1990, 20, 171–182. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Loh, W.-Y. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Ishwaran, H. The effect of splitting on random forests. Mach. Learn. 2015, 99, 75–118. [Google Scholar] [CrossRef] [PubMed]
- Singhal, G.; Bansod, B.; Mathew, L.; Goswami, J.; Choudhury, B.U.; Raju, P.L.N. Chlorophyll estimation using multi-spectral unmanned aerial system based on machine learning techniques. Remote Sens. Appl. Soc. Environ. 2019, 15, 100235. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support Vector Regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar] [CrossRef] [Green Version]
- Chatziantoniou, A.; Psomiadis, E.; Petropoulos, G.P. Co-Orbital Sentinel 1 and 2 for LULC Mapping with Emphasis on Wetlands in a Mediterranean Setting Based on Machine Learning. Remote Sens. 2017, 9, 1259. [Google Scholar] [CrossRef] [Green Version]
- Basak, D.; Pal, S.; Chandra Patranabis, D. Support vector regression. Neural Inf. Process. Lett. Rev. 2007, 203–224. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Gitelson, A.; Delegido, J.; Moreno, J.; Camps-Valls, G. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Verrelst, J.; Munoz-Mari, J.; Laparra, V.; Mateo-Jimenez, F.; Gomez-Dans, J. A Survey on Gaussian Processes for Earth-Observation Data Analysis: A Comprehensive Investigation. IEEE Geosci. Remote Sens. Mag. 2016, 4, 58–78. [Google Scholar] [CrossRef] [Green Version]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25. [Google Scholar]
- Bloom, H.S.; Zhu, P.; Unlu, F. Finite Sample Bias from Instrumental Variables Analysis in Randomized Trials; MDRC Working Paper; MDRC: New York, NY, USA, 2010. [Google Scholar]
- Chen, R.; Chu, T.; Landivar, J.A.; Yang, C.; Maeda, M.M. Monitoring cotton (Gossypium hirsutum L.) germination using ultrahigh-resolution UAS images. Precis. Agric. 2018, 19, 161–177. [Google Scholar] [CrossRef]
- Liu, S.; Baret, F.; Allard, D.; Jin, X.; Andrieu, B.; Burger, P.; Hemmerlé, M.; Comar, A. A method to estimate plant density and plant spacing heterogeneity: Application to wheat crops. Plant Methods 2017, 13, 38. [Google Scholar] [CrossRef] [Green Version]
- Yang, C. Detection of Rape Canopy SPAD Based on Multispectral Images of Low Altitude Remote Sensing Platform. In Proceedings of the 2017 ASABE Annual International Meeting, Spokane, WA, USA, 16–19 July 2017; p. 1. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).