1. Introduction
Due to the powerful capability to detect, recognize, and track targets under the conditions of all weather, radar is widely used in many weapon systems, and it has become an indispensable electronic equipment in military [
1]. With the continuous development of radar jamming technology, many radar jamming technologies have been developed to attack radar systems in order to reduce their target detection, recognition, and tracking capabilities [
2]. In addition to various radar jamming methods, more and more electromagnetic signal use in the battlefield environment also seriously affects the effectiveness of the radar system. Radar anti-jamming technology is used for protecting the radar from jamming [
3]. As an important prerequisite for effective anti-jamming measures, radar jamming signal recognition has received more and more attention.
Recently, many recognition approaches of radar jamming signals have been proposed, including likelihood-based methods [
4,
5,
6] and feature-based methods [
7,
8,
9,
10,
11,
12,
13]. Based on the prior information, the likelihood-based methods identify the type of jamming signal by matching the likelihood function of the jamming signal with some determined thresholds. For instance, based on the adaptive coherent estimator and the generalized likelihood ratio test (GLRT), Greco et al. [
4] proposed a deception jamming recognition method. Moreover, in [
5], an adaptive detection algorithm based on the GLRT implementation of a generalized Neyman–Pearson rule was proposed to discriminate radar targets and electronic countermeasure (ECM) signals. In addition, Zhao et al. [
6] utilized the conventional linear model to discriminate the target and radar jamming signal. Unfortunately, neither the necessary prior information nor the appropriate threshold can be guaranteed in reality, which limits the application of likelihood-based methods for radar jamming signal recognition.
Compared with the signal in the original domain, the extracted features in the transformation domain are usually more separable. Therefore, some jamming signal recognition methods based on feature extraction were proposed. The feature-based method consists of feature extraction and classifier selection. Many researchers extract distinguishing features from jamming signal based on multi-domains, including the time domain [
7], frequency domain [
8], time–frequency domain [
9], and so on. For example, using the product spectrum matrix (SPM), Tian et al. [
10] proposed a deception jamming recognition method. Moreover, in [
11], support vector machine (SVM) was selected as a classifier to recognize chaff jamming. In [
12], based on the AdaBoost.M1 algorithm, a radar jamming recognition algorithm that selected SVM as the component classifiers was proposed. In addition, based on different classifiers (i.e., decision tree, neural network, and support vector machine), Meng et al. [
13] extracted five features of jamming signals, including three time-domain features and two frequency-domain features, which could increase the robustness of the recognition system. Nevertheless, the aforementioned methods require a lot of manpower, and high time costs still remain for these approaches based on feature extraction.
Recently, CNN, which is one of the popular deep learning models, has achieved great performance in many fields, including image, text, and speech processing [
14]. Due to the uniqueness of the network structure of CNN (e.g., local connections and shared weights), CNN-based methods can automatically extract the invariant and discriminant features of data [
15]. Moreover, a growing number of CNN-based methods have been proposed in the field of jamming recognition [
16,
17,
18,
19]. In [
16], a well-designed CNN was utilized to recognize active jamming, and the results indicated that CNNs had the power and ability to distinguish active jamming. In addition, in [
17], a CNN-based method was proposed for the recognition of radar jamming, which could recognize nine typical radar jamming signal. By integrating residual block and asymmetric convolution block, Qu et al. [
18] proposed a jamming recognition network, which could better extract the features of jamming signals. Moreover, based on the CNN, Wu et al. [
19] proposed an automatic radar jamming signal recognition method, which could recognize five kinds of radar jamming signal. Andriyanov et al. used CNN in radar image processing, and they analyzed the construction process of CNN in detail [
20]. The recognition rate and recall rate of radar images could reach more than 90%, which illustrated the effectiveness of CNN in processing radar data. Recently, Shao et al. designed a 1D-CNN for radar jamming signal recognition that can identify 12 types of radar jamming with a recognition accuracy of up to 97% [
21], which also illustrated the effectiveness of the CNN-based method in processing radar jamming signals.
Radar signals, including radar jamming signals, are naturally complex-valued (CV) based data, including real part and imaginary part. CV data contain more information than RV data, i.e., amplitude and phase . When processing the CV signal, neither the phase nor amplitude information should be ignored.
In order to make full use of the phase and amplitude information of radar jamming signals, a bispectrum analysis was used to keep the phase and amplitude information of the CV signal [
22]. Moreover, some researchers have proposed several methods for CV jamming signal recognition [
23,
24]. For example, based on the amplitude fluctuation, high-order cumulant, and bispectrum, Li et at. studied the feature extraction to analyze and compare the features of deception jamming and target echo [
23]. In [
24], an algorithm that utilized the bispectrum transformation to extract the amplitude and phase features was proposed to identify deception jamming.
However, most of the existing RV-CNN-based jamming recognition methods mentioned above converted the CV jamming signal into RV and would then input them into RV-CNN for jamming recognition. Since the input and model parameters of the RV-CNN-based methods are RV, they have insufficient significance for phase and amplitude information and are more suitable for processing RV data. For this reason, the loss of phase and amplitude information caused by RV-CNN-based methods is unavoidable, and the problem that RV-CNN cannot fully extract the features of CV data still exists.
Apparently, it is better to extract the CV jamming signal in a complex domain, which can make better use of the unique information of the CV signal, such as phase and amplitude. Therefore, in our work, a radar jamming signal recognition approach based on CV-CNN is proposed. The proposed CV-CNN consists of multiple CV layers, including a CV input layer, several alternations of CV convolutional layers, CV pooling layers, and so on. By extending the entire network parameters to a complex domain, the proposed CV-CNN is able to extract CV features from the jamming signal more efficiently than the aforementioned RV-CNN.
Although a CV-CNN can deal with the CV jamming signal perfectly, due to the complex expansion of the entire model, the CV-CNN still suffers from high computational complexity. Unfortunately, jamming signal recognition tasks have strict requirements for real-time performance, making it difficult to deploy a CV-CNN in the resource-constrained battlefield environments. For deep learning model compression, model pruning [
25] is a quite effective method by eliminating redundant parameters. Most model pruning methods [
26,
27,
28] pruned the less important weight of the model in the filter. Therefore, in our work, motivated by filter pruning, a simple yet effective F-CV-CNN algorithm is proposed for accelerating the CV-CNN.
The main contributions of this study are listed as followed:
To address the issue that the existing RV-CNN cannot make good use of CV jamming signal, a CV-CNN is proposed to simultaneously extract the features of real and imagery radar signals, which improves the recognition accuracy of a radar jamming signal.
In addition, in view of the high real-time requirements of radar jamming recognition tasks, the fast CV-CNN algorithm is proposed to accelerate the recognition speed of the CV-CNN.
The rest of this paper is organized as follows. The proposed methodology of the CV-CNN for CV jamming signal recognition is provided in
Section 2. The proposed fast CV-CNN algorithm process is then shown in
Section 3. The details of the experiment, the experimental results and the analysis of results are presented in
Section 4, followed by the conclusion presented in
Section 5.
3. F-CV-CNN for Radar Jamming Signal Recognition
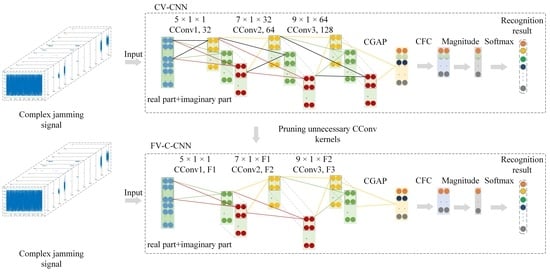
The CV-CNN model can make full use of the information of a radar CV jamming signal. Unfortunately, it is difficult to meet the real-time requirements of radar jamming signal recognition due to the high computational complexity. In order to address this issue, a simple yet effective pruning-based fast CV-CNN (F-CV-CNN) method is proposed; the framework of the F-CV-CNN is shown in
Figure 4.
As shown in
Figure 4, for CV-CNN, some unnecessary CConv kernels that have less impact on the output can be pruned. This can reduce the complexity of the model, so that the CV-CNN can meet the real-time requirement of jamming signal recognition tasks.
Suppose that is an over-parameter CV-CNN model for radar jamming signal recognition, where denotes the CConv kernel, and is the number of CConv layers. On the given CV jamming dataset , the difference between the output of CV-CNN and the true label y can be evaluated by the loss function . Therefore, we need to find the subnetwork based on the given over-parameter model , and make meet the minimum increase in .
In order to obtain , we can eliminate the unnecessary parameters of the CV-CNN based on model pruning, which is a simple yet effective method to compress and accelerate the deep learning model.
For model pruning, a suitable CConv kernel importance evaluation method is vitally important. In this work, considering the parameters of the CV-CNN being in complex form and the real-time requirement of the jamming recognition task, the magnitude of CConv is utilized as the importance evaluation criterion. In actual engineering applications, the computational complexity of the magnitude is low, which is more suitable for engineering implementation. The calculation formula of the magnitude is as follows:
where
is the magnitude of the i-th CConv kernel of layer
. A smaller
means the less importance of the CConv kernel
, and the impact on the CV-CNN is smaller, so it can be eliminated.
By removing the CConv kernel together with their connection feature maps, the computational cost is significantly reduced. Suppose the input jamming feature map for the l-th CConv layer is . Through the CConv operation in the -th CConv layer, the input CV jamming feature map is then converted into the CV output jamming feature map . In the -th CConv layer, the total number of multiplication operations of CConv is . When a certain CConv kernel is eliminated, multiplication operations are reduced in the -th CConv layer. In addition, the corresponding output feature maps are also removed, which further reduces multiplications in the +1-th CConv layer.
The F-CV-CNN algorithm is a “train, prune, and fine-tune” algorithm, which means that F-CV-CNN can be summarized into three steps: training, pruning, and fine-tuning.
Figure 1 is divided into three parts: training set, validation set, and test set. The training set and validation set are fed into the over-parameter CV-CNN for model training.
Secondly, in the process of pruning, considering that the layer-by-layer iterative fine-tuning pruning strategy is time-consuming, which is not suitable for real-time jamming signal recognition task, a one-shot pruning and fine-tuning is adopted to prune the over-parameter CV-CNN . The magnitude of the CConv kernel is calculated layer by layer. Next, in the l-th layer, CConv kernels are sorted according to the value of . Then, CConv kernels with the smallest value of are pruned, and the corresponding feature maps are removed simultaneously. The pruning algorithm is iteratively carried out layer by layer until all the CConv layers are pruned, and the simplified model is obtained.
Finally, in most cases, due to the model pruning, the simplified model
will have a performance loss compared to the over-parameter model
. Therefore, in order to recover the accuracy loss caused by pruning, we need to fine-tune
. In our work, we adopted a fine-tune measure to train the simplified model
for fewer epochs at a lower learning rate. Algorithm 1 shows the workflow of the proposed fast CV-CNN.
| Algorithm 1: F-CV-CNN method for radar jamming recognition. |
| 1. begin |
| 2. divide the jamming signal set into training set, validation set, and test set, |
| 3. input training set and validation set into CV-CNN to train an over-parameterized model , |
| 4. iteratively pruning over-parameterized model layer by layer: |
| 5. for do |
| 6. calculate the magnitude of each CConv kernel of -th layer |
| 7. sort all CCon kernels of the -th layer, according to . |
| 8. remove CConv kernels with smaller magnitude in -th layer, |
| 9. remove the feature maps generated by . |
| 10. end |
| 11. fine-tune the obtain the pruned model . |
| 12. end |
4. Experiments and Results
4.1. Datasets Description
Because linear frequency modulation (line frequency modulation, LFM) signal has the advantages of low peak power and simple modulation method, it has been widely used in the current pulse compression radar system. The expression of the LFM signal is as follows:
Then, 12 kinds of expert-simulated radar jamming signal as experimental datasets were considered to verify the effectiveness of the proposed method, including pure noise, active jamming, and passive jamming. Among them, active jamming includes typical suppression jamming, such as aiming jamming, blocking jamming, sweeping jamming; typical deception jamming such as interrupted sampling repeater jamming (ISRJ) [
29]; distance deception jamming [
30]; dense false target jamming [
31]; smart noise jamming; and passive jamming, such as chaff jamming [
11]. In addition, we also considered some composite jamming, such as ISRJ and chaff compound jamming, dense false target and smart noise compound jamming, and distance deception and sweeping compound jamming.
For the simulated radar jamming signal set, each type of radar jamming signal had 500 simulated samples. Each sample had 2000 sampling points, and each sampling point was composed of a real part and imaginary part.
Figure 5 shows the waveform of the radar jamming signal in the time domain. The pulse width T of the simulated LFM signal we used was 20
, the bandwidth
was 10 MHz, and the sampling frequency
was 20 MHz. The simulation parameters of the jamming signal were shown in
Table 1.
At the same time, we constructed the expert statistical feature (SF) dataset of the radar jamming signal for the comparative experiment, including four time domain features (i.e., skewness, kurtosis, instantaneous amplitude reciprocal, and envelope fluctuation) and four frequency domain features (i.e., additive gaussian white noise factor, maximum value of normalized instantaneous amplitude and frequency, instantaneous phase correlation coefficient, and frequency stability).
4.2. Experimental Setup
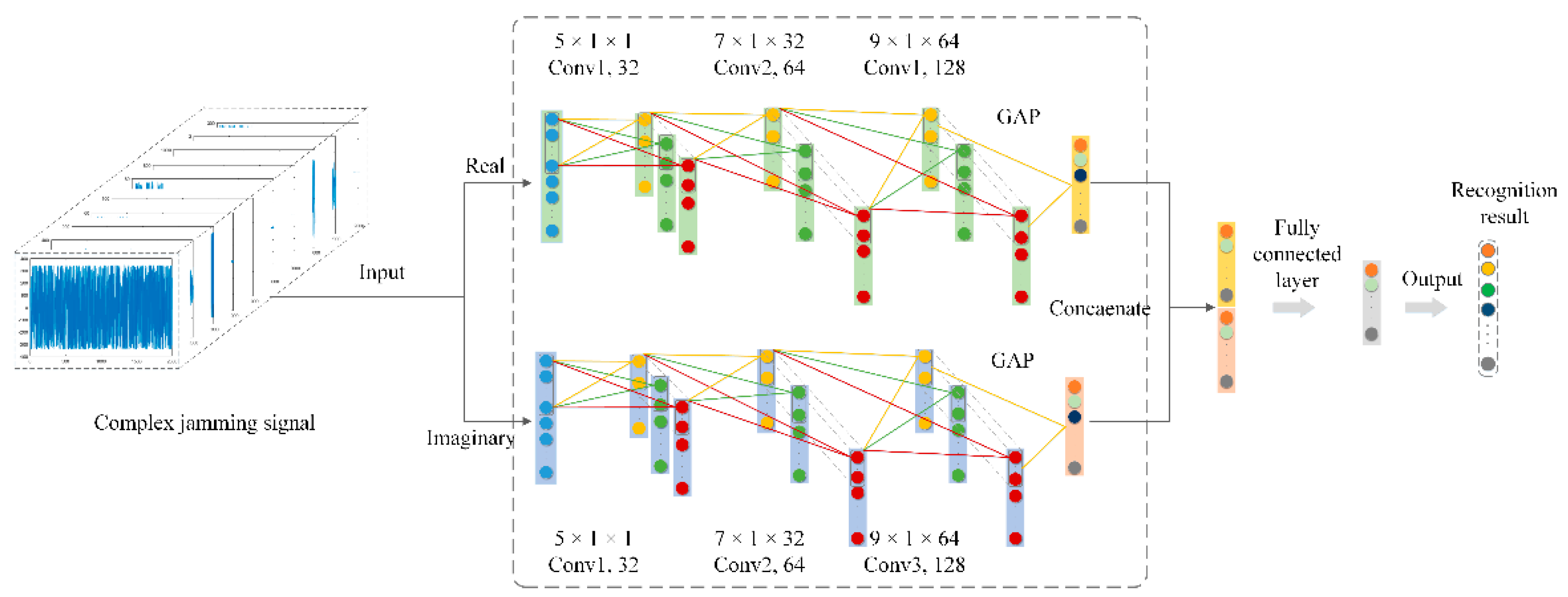
In this study, in order to fully verify the effectiveness of the proposed CV-CNN, the well-designed S-RV-CNN and D-RV-CNN were used for the comparative experiments. The D-RV-CNN consisted of two identical S-RV-CNNs that could extract the real and imaginary features of the CV jamming signal separately. The detailed network structure of RV-CNN is shown in
Table 2.
The S-RV-CNN contained three convolutional layers, three pooling layers, a dropout layer, a BN layer, and a GAP layer. The activation function adopted the ReLU activation function. The convolution step lengths were all set to 1, and the pooling operation adopted a max-pooling operation.
The D-RV-CNN consisted of two identical S-RV-CNNs. The inputs of the two S-RV-CNNs were the real and imaginary parts of the CV jamming signal, which were used to extract the features of the real and imaginary parts separately. The concatenation layer was used to concatenate the real and imaginary part features extracted by two S-RV-CNNs, and then sent the concatenated feature vector as input into the FC layer for feature integration. Finally, the recognition result was obtained by Softmax.
For the proposed CV-CNN, its specific network structure is shown in
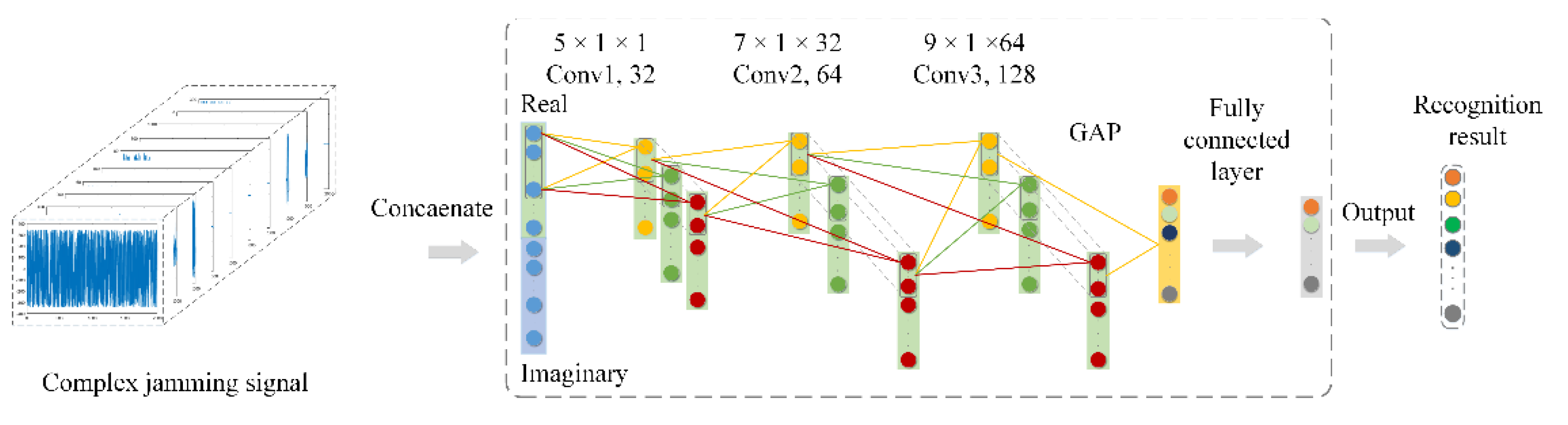
Table 3. Extending the RV-CNN to the complex domain, the CV-CNN included three CConv layers and CPooling layers, one CDropout layers, a CBN layer, and a CGAP layer. The activation function was also extended from the real domain to the complex domain, adopting the ReLU activation function in complex form.
We divided the CV radar jamming signal used in the experiment into three subsets: training set, validation set, and test set. For each class of radar jamming, we randomly selected 25, 50, 75, 100, and 150 samples per class as the training set, 50 samples per class as the validation set, and the remaining data as the test set.
For the S-RV-CNN, D-RV-CNN, and the CV-CNN, we kept the same hyperparameter settings during the experiment. The learning rate was annealed down from 0.009 to 0.0008, and the batch size and training epochs were set to 64 and 100, respectively.
In addition, we used the SF dataset to train different classifiers as the comparison experiment, i.e., support vector machine (SVM), random forest (RF) [
32], decision tree (DT) [
33], and K-nearest neighbors (KNN) [
34]. The kernel function of the SVM was a radial basis kernel function, the maximum tree depth of the DT was set to 6, the size of the RF was set to 300, and K in KNN was set to 10.
To evaluate the effectiveness of the proposed methods, we used two evaluation metrics, i.e., overall accuracy (OA) and kappa coefficient (K), to evaluate the recognition effect of different methods. OA could be calculated as:
The kappa coefficient could be calculated as:
where
denoted the number of test samples for each class jamming signal, and
denoted the number of correct recognitions of each class jamming signal.
In our work, CV-CNN training and testing, pruning, and other comparative experiments were run on a computer equipped with a 3.4-GHz CPU and a NVIDIA GeForce GTX 1070ti card. All deep learning methods were implemented on the PyCharm Community 2019.1 platform with Pytorch 1.1.0 and CUDA 9.0. In addition, F-CV-CNN was also verified on the NVIDIA Jetson Nano development kit.
4.3. Experimental Results and Performance Analysis
4.3.1. The Recognition Results of CV-CNN
For the proposed CV-CNN, we first considered the impact of different activation function layers and different BN layers on its recognition effect. In this work, three CV activation functions were utilized to explore the influence of different activation functions on the recognition effect of the CV-CNN.
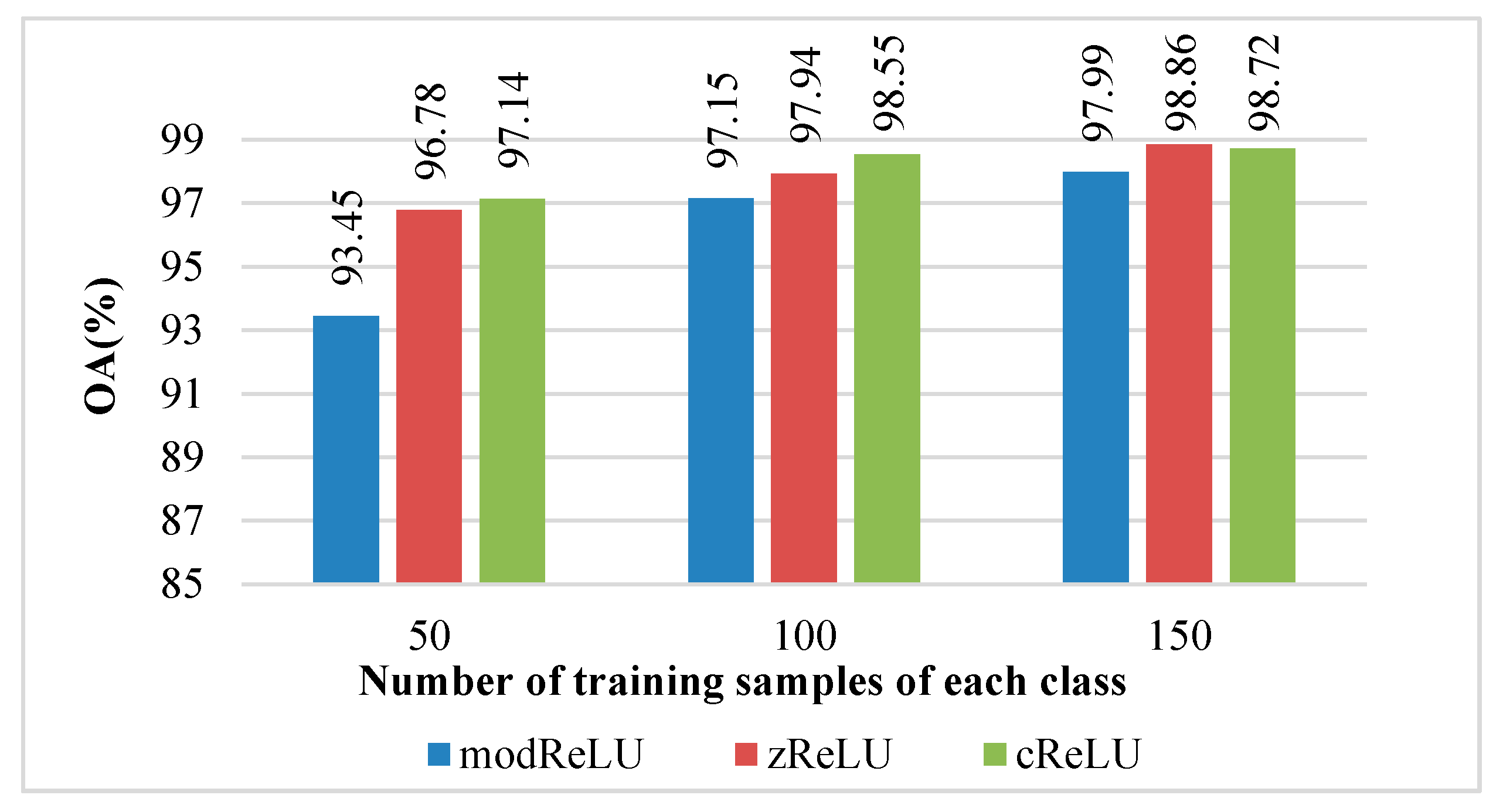
Figure 6 shows the recognition effect of the CV-CNN with different activation functions, i.e., modReLU, zReLU, and cReLU. As shown in
Figure 6, under the condition of 50 training samples of each class, the CV-CNN could obtain the recognition accuracy of 93.45%, 96.78%, and 97.14% when using the modReLU, zReLU, and cReLU activation functions, respectively. When the activation function was cReLU, the proposed CV-CNN could achieve the best recognition performance.
The recognition effect of the CV-CNN when adopting different BN layers is shown in
Table 4. As shown in
Table 4, when the BN layer was not introduced in CV-CNN, and when RBN and CBN were used with CNN separately, recognition accuracies of 96.75%, 96.92% and 97.14% can be obtained, respectively. When using the CBN layer, CV-CNN could achieve the best recognition effect.
Similar experimental results could be obtained when each class of training sample was 100 and 150. For CV-CNN, using the cReLU activation function and a CBN layer could achieve better recognition accuracy.
Table 5 shows the detailed results of the proposed CV-CNN, and the best recognition accuracy is highlighted in bold. In
Table 4, C1–C12 represent pure noise, ISRJ, aiming jamming, blocking jamming, sweeping jamming, distance deception jamming, dense false target jamming, smart noise, chaff jamming, chaff and ISRJ compound jamming, dense false target and smart noise compound jamming, distance deception, and sweeping compound jamming, respectively. From
Table 4, one can see that CV-CNN demonstrated its best recognition performance in terms of OA and K.
Under the condition of 25 training samples of each class, the CV-CNN improved the OA by 10.11% compared to the D-RV-CNN. In addition, the CV-CNN also outperformed the SF-classifier methods. In the case of 50 training samples per class, the CV-CNN exhibited the OA over D-RV-CNN and SF-RF, with improvements of 5.73% and 6.64%.
In addition, experiments with 75, 100, and 150 training samples of each class were also conducted to further demonstrate the effectiveness of our method, the results are also shown in
Table 5. It could be seen from
Table 5 that the CV-CNN achieved the best recognition performance, with 75, 100, and 150 training samples per class, which fully demonstrated the effectiveness of our proposed CV-CNN.
Table 6 shows the results of the proposed method and some previous CNN-based comparative methods. For the detailed network structure of 2D-CNN and 1D-CNN, please refer to [
21].
With 50 training samples per class, the CV-CNN achieved a recognition accuracy of 97.16%, which improved by 9.33% and 5.21% in terms of OA compared with the 2D-CNN and 1D-CNN, respectively. With 100 training samples per class, the CV-CNN could achieve a recognition accuracy of 98.24%. Compared with the 2D-CNN (89.88%) and 1D-CNN (96.97%) in [
21], the CV-CNN achieved an improvement of 8.36% and 1.27%, respectively. In the case of 150 training samples per class, CV-CNN also achieved the highest recognition accuracy. Compared with 2D-CNN and 1D-CNN, the proposed CV-CNN improved the recognition accuracy of 7.43% and 1.43%, respectively.
Under different Dropout rates, the recognition accuracy of CV-CNN was shown in the
Table 7. It could be found that when the dropout rate was small, there was an over-fitting phenomenon for CV-CNN, which led to a decrease in the recognition accuracy of CV-CNN. When the dropout rate was high, the recognition accuracy of CV-CNN would also decrease due to the high proportion of randomly discarded neurons. Therefore, a moderate Dropout rate should be selected. In our experiment, we set the dropout rate to 0.5.
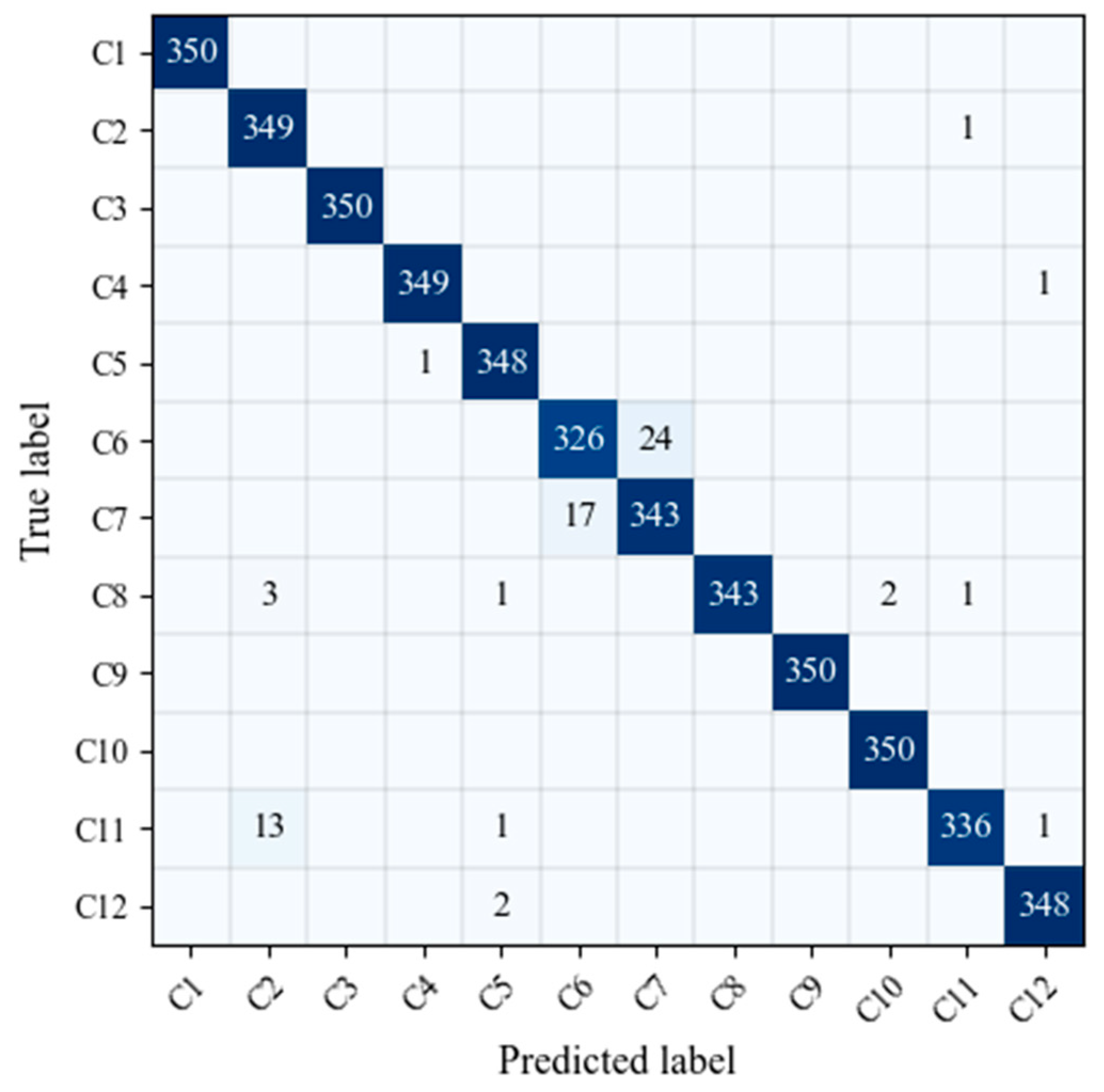
It could be found from
Figure 7 that CV-CNN can achieve a better recognition of jamming signal, but it is easy to confuse C6 (distance false targets) and C7 (dense false targets). The reason for the above phenomenon was mainly due to the fact that the simulation parameters of distance false targets and dense false targets were the same except for the number of false targets. As a result, the two types of jamming signal had a certain degree of similarity, and it is easy to confuse the two.
4.3.2. The Recognition Results of F-CV-CNN
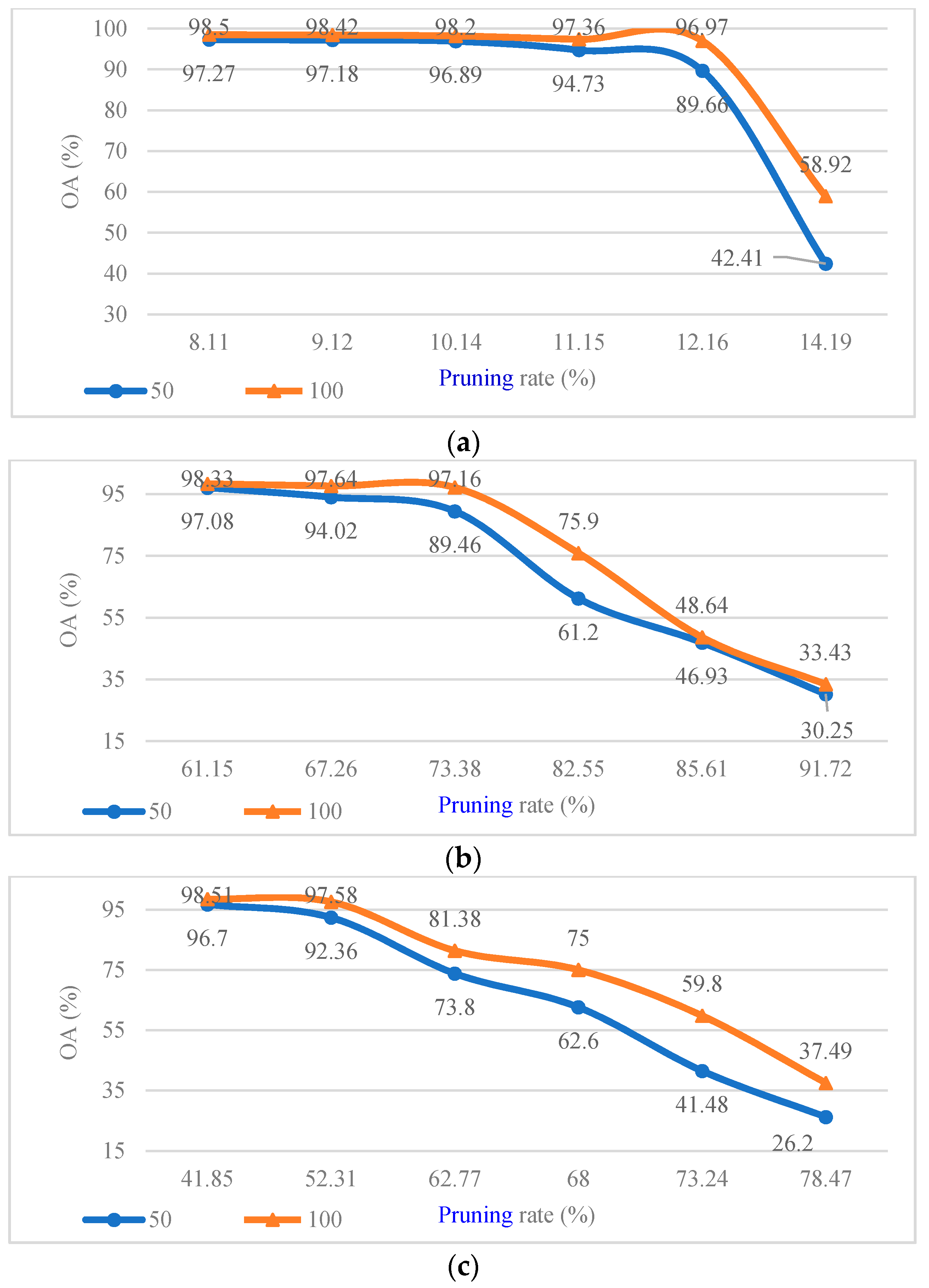
Considering that the CConv kernels in different layers of CV-CNN had different sensitivity to pruning, we first analyzed the pruning sensitivity of CV-CNN. The pruning sensitivity curves of different CConv layers in CV-CNN are shown in
Figure 8, with 50 and 100 training samples per class. As shown in
Figure 8, for the first layer of CConv, when the pruning rate was 14.19%, the model performance after pruning began to decline; for the third layer, when the pruning rate reached 62.77%, the model performance after pruning began to decline. In summary, for the CV-CNN used in the experiment, the pruning sensitivity of the second layer was smaller than that of the first and third layers. In the same CConv layer, the CV-CNN that was trained by more training samples had stronger pruning robustness.
In this subsection, the over-parameter CV-CNN and the simplified model obtained by the F-CV-CNN algorithm were expressed as and , respectively. First, with 50, 100, and 150 training samples for each class, was trained separately. Then the F-CV-CNN algorithm was carried out on the to obtain .
Table 8 shows the recognition results of
under different pruning rates. As shown in
Table 8, when the pruning ratio is low, the performance loss caused by model pruning can be ignored. However, with the increase of the pruning rate, the recognition performance of
continues to decline. When there are 50 training sample for each class and the pruning ratio is 85%, the recognition accuracy of
was reduced from 97.14% to 73.75% compared with
. Similarly, when the number of training samples for each class was 100 and 150, the recognition accuracy of
also dropped to 81.25% and 94.42%, respectively. From
Table 8, one could also find the same conclusions as the previous analysis, i.e., the more training samples, the smaller performance loss of
.
In order to restore the performance of
, a fine-tune post-processing operation was required. The specific operation was to train 15 epochs at a low learning rate of 0.0001. The experimental results of fine-tune post-processing on
are also shown in
Table 8. As shown in
Table 8, the fine-tune post-processing could restore the recognition performance of
to a certain extent.
With a pruning rate of 92% and 50 training samples per class, the recognition performance of after fine-tune processing was restored to 90.66%. Compared with , the performance of had dropped by 6.48%. However, in the case of 100 and 150 training samples per class, the performance of at a pruning rate of 92% could also be restored well through fine-tune processing. The results also showed that for the deep learning model, the more training samples, the stronger the robustness of the model.
In order to better show the effectiveness of the F-CV-CNN algorithm, we tested the inference time of
on NVIDIA Jetson Nano, which is used for real-time jamming recognition in our work.
Table 9 showed the floating-point operations (FLOPs) and inference time.
With the increase of the pruning rate, the FLOPs of continued to decrease, and the inference time also continued to decrease. When the pruning rate was 92%, the FLOPs of were reduced by 91% compared with the , and the inference time was also reduced by 67%. The experimental results also fully illustrated the effectiveness of the F-CV-CNN algorithm.
4.3.3. The Recognition of Radar Jamming and Normal Signal
In real application, it is necessary to recognize the radar normal signal and jamming signal at the same time. Therefore, in this subsection, the effectiveness of the proposed CV-CNN was tested on a dataset which contained radar jamming and normal signals.
The radar jamming signals were the signals in
Section 4.1, which contained twelve types of radar jamming signals. Furthermore, the normal radar signals were generated based on Equation (20), and they were used as the 13th type of the radar jamming and normal signal dataset. The pulse width T was 20 μs, and bandwidth B was 10 MHz, and the sampling rate was 20 MHz. For the normal radar signals, there were 500 simulated samples. Each sample had 2000 sampling points, and each sampling point was composed of a real part and an imaginary part.
Table 10 shows the experimental results of the proposed method to perform recognition for normal radar signals and jamming signals, where C13 represents the normal radar signal. From
Table 10, one can see that CNN-based methods (i.e., S-RV-CNN, D-RV-CNN, and CV-CNN) obtained better recognition performance compared with tradition machine learning methods (i.e., random forest and decision tree). For CNN-based methods, with 50 training samples for each class, the recognition accuracy of the CV-CNN for normal radar signals was 89.60%, which was 5.6% and 3.75% higher than that of the S-RV-CNN (84.00%) and D-RV-CNN (85.85%), respectively.
Moreover, with 100 training samples per class, the CV-CNN improved the recognition accuracy by 3.77% and 1.26% compared with the S-RV-CNN and D-RV-CNN, respectively. With 150 training samples per class, the CV-CNN also achieved the highest recognition accuracy, and the recognition accuracy for normal radar signals reached 94.80%, which further verified the effectiveness of the proposed CV-CNN.
5. Conclusions
In this paper, we proposed a CV-CNN for radar jamming signal recognition which extends the network parameters from real number to complex number. Through CConv, CPooling, CBN layer, and so on, the unique information of the CV jamming data can be better utilized. Experimental results show that our proposed method can better identify CV jamming signals, and its recognition performance was further improved, with the improvements of 11.44% in terms of OA when there are 25 training samples per class.
In addition, in order to deal with the issue of over parameters and poor real-time performance, the F-CV-CNN algorithm was proposed. Based on filter-level filter pruning, unnecessary CConv kernels were pruned to reduce the number of parameters and calculations of CV-CNN so that the CV-CNN meets the real-time requirements of interference signal recognition tasks. After pruning the F-CV-CNN, FLOPs can be reduced by up to 91% compared with CV-CNN, and the inference time can be reduced by 67%.
Furthermore, the effectiveness of the proposed CV-CNN was also tested on a dataset which contained radar jamming and normal signals. The results showed that the CV-CNN worked well on the recognition of radar jamming and normal signals at the same time.
For radar jamming signal recognition, we usually face a problem of limited training samples. Due to a large number of learnable parameters, this problem is serious when deep learning-based methods are used for radar jamming signal recognition. Therefore, in the near future, deep CV CNN-based recognition with limited training samples is the next move of our research.