Global Ocean Studies from CALIOP/CALIPSO by Removing Polarization Crosstalk Effects
Abstract
:1. Introduction
2. Methods
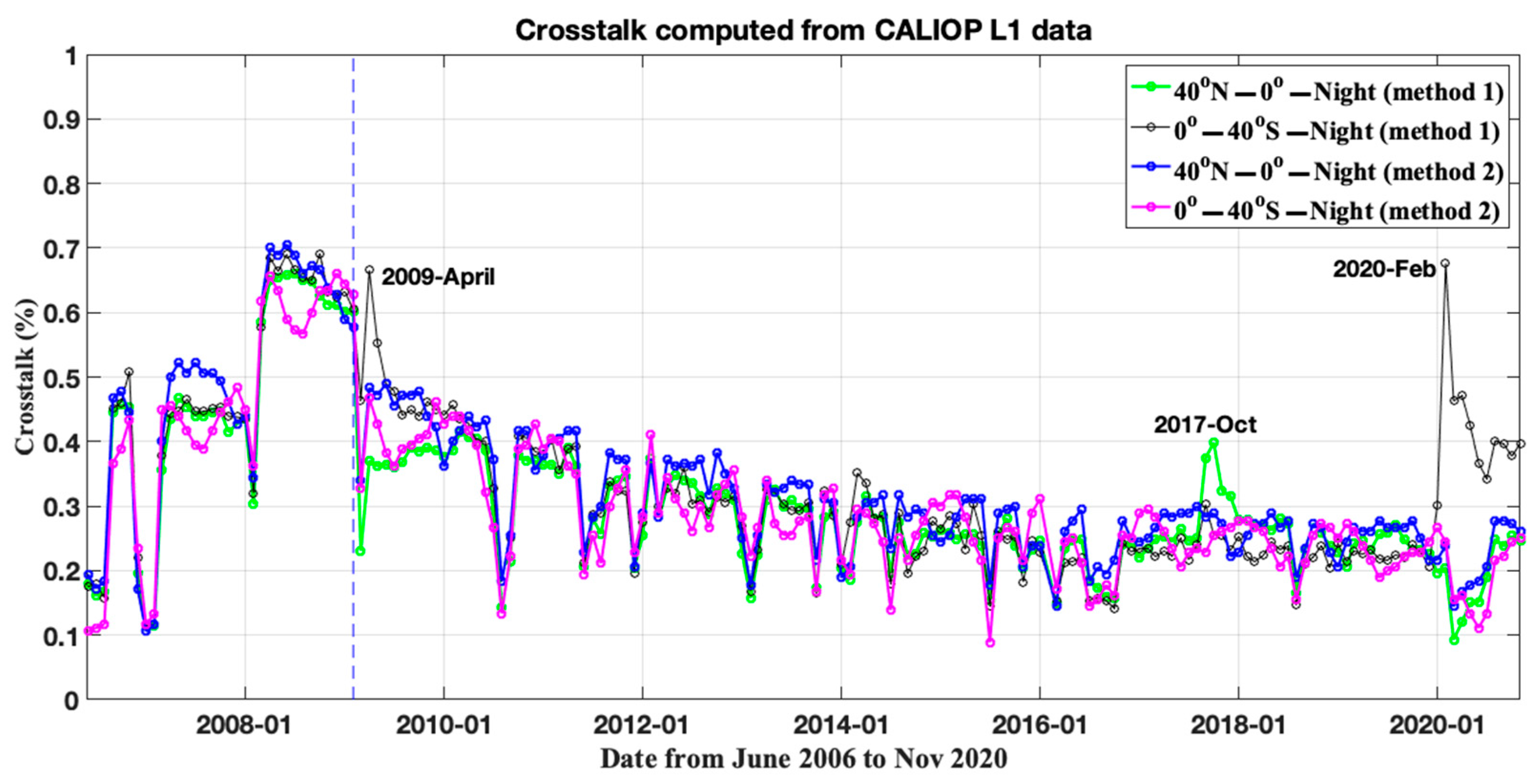
2.1. Crosstalk Estimation from Clear Air Depolarization Ratio (Method 1)
2.2. Crosstalk Estimation from Ocean Surface Return (Method 2)
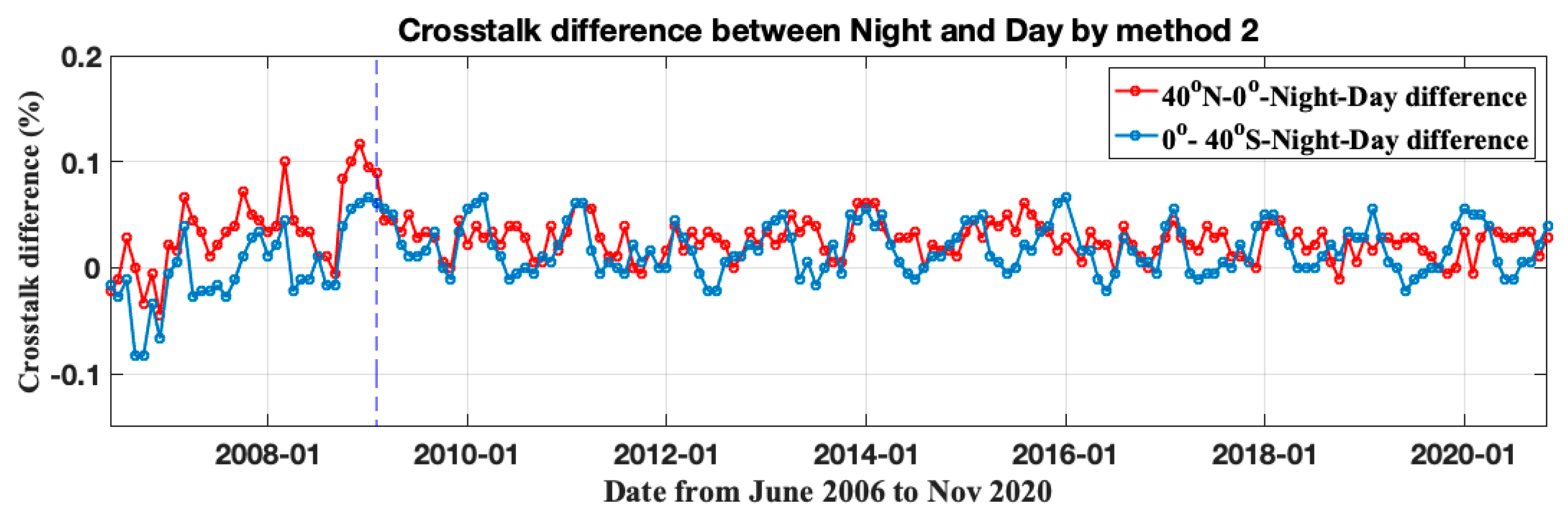
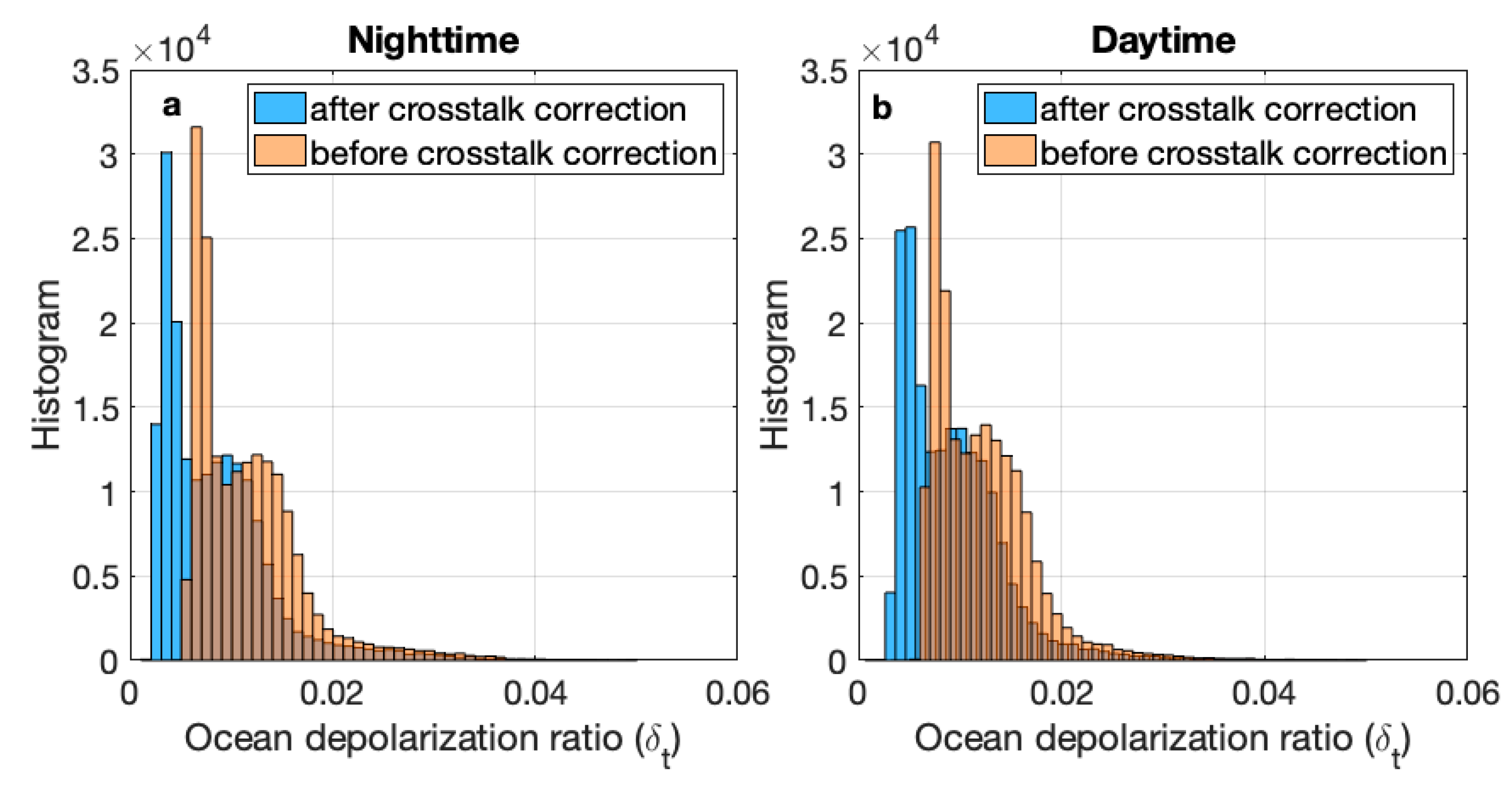
2.3. Effects of Crosstalk on Measured Ocean Backscattered Signals
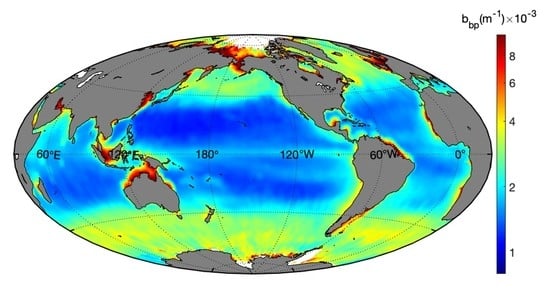
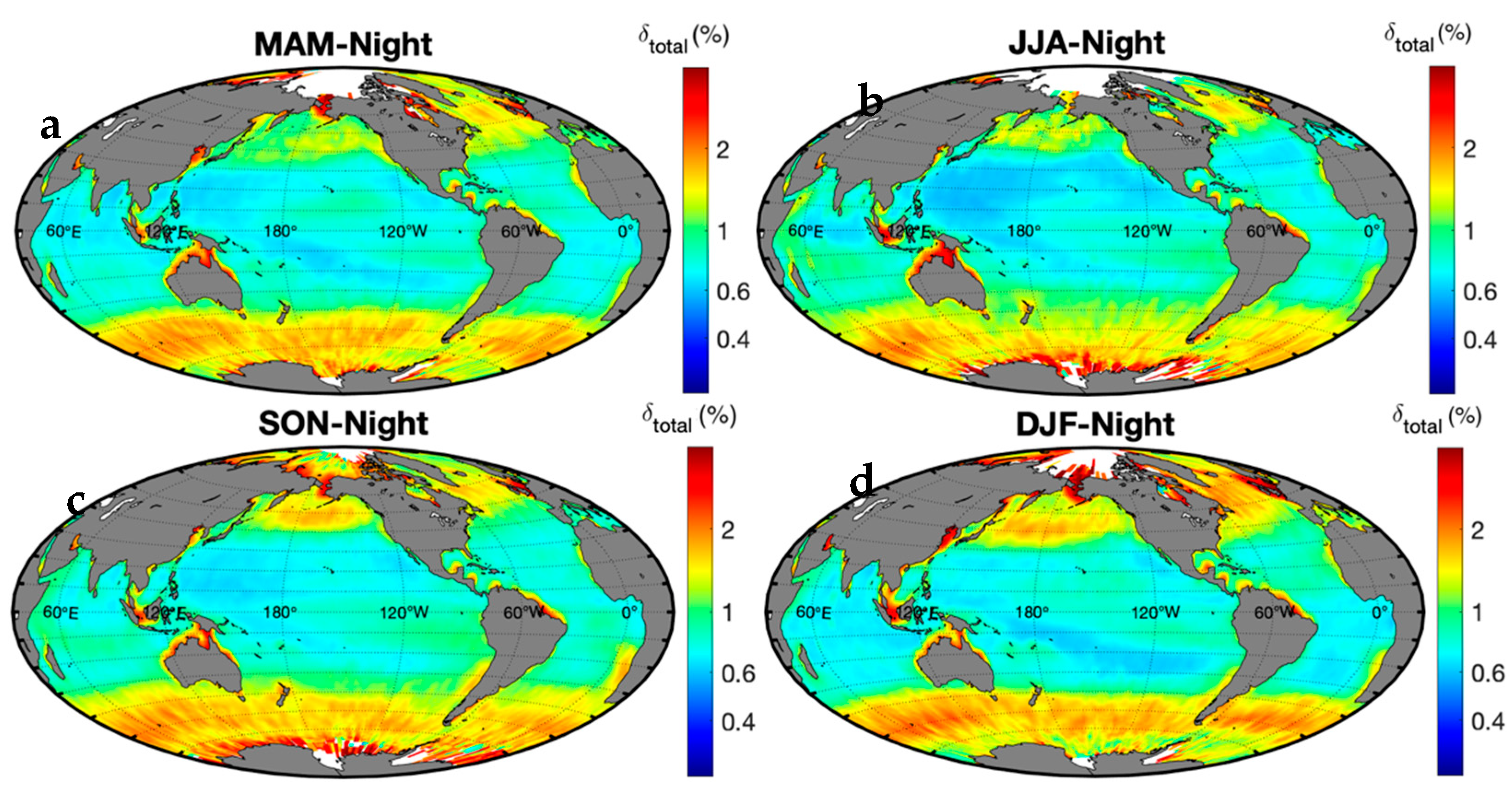
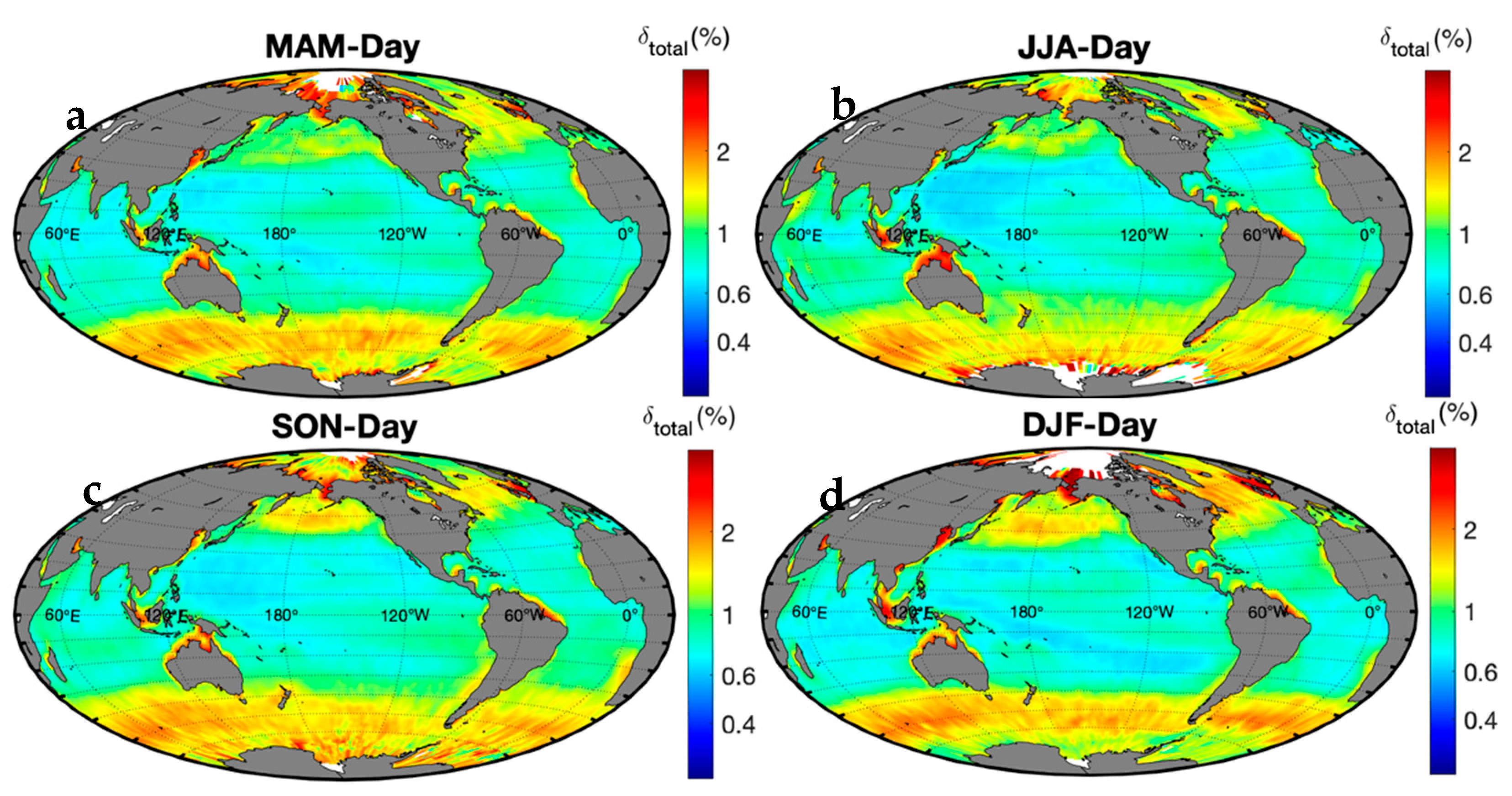
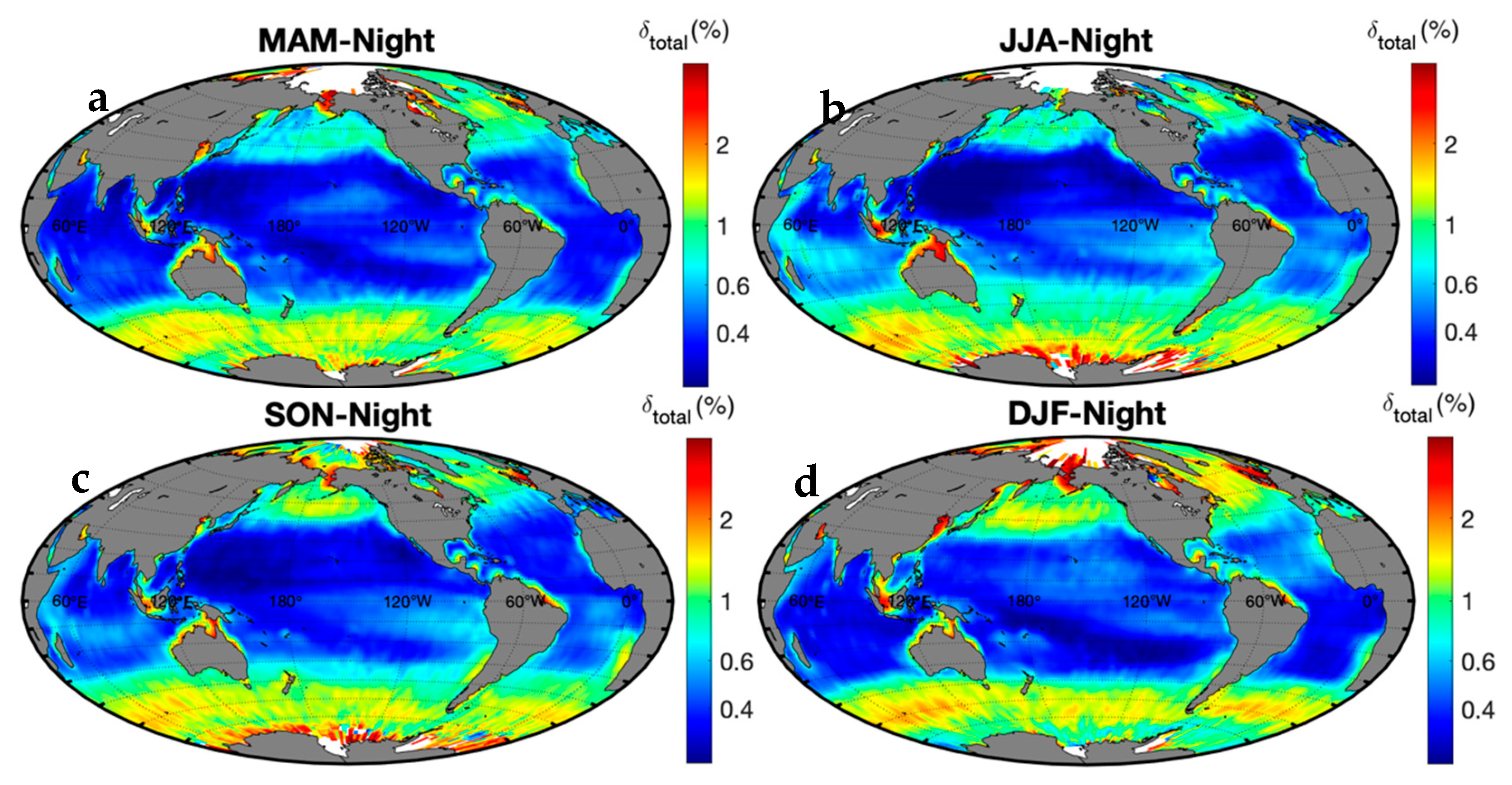
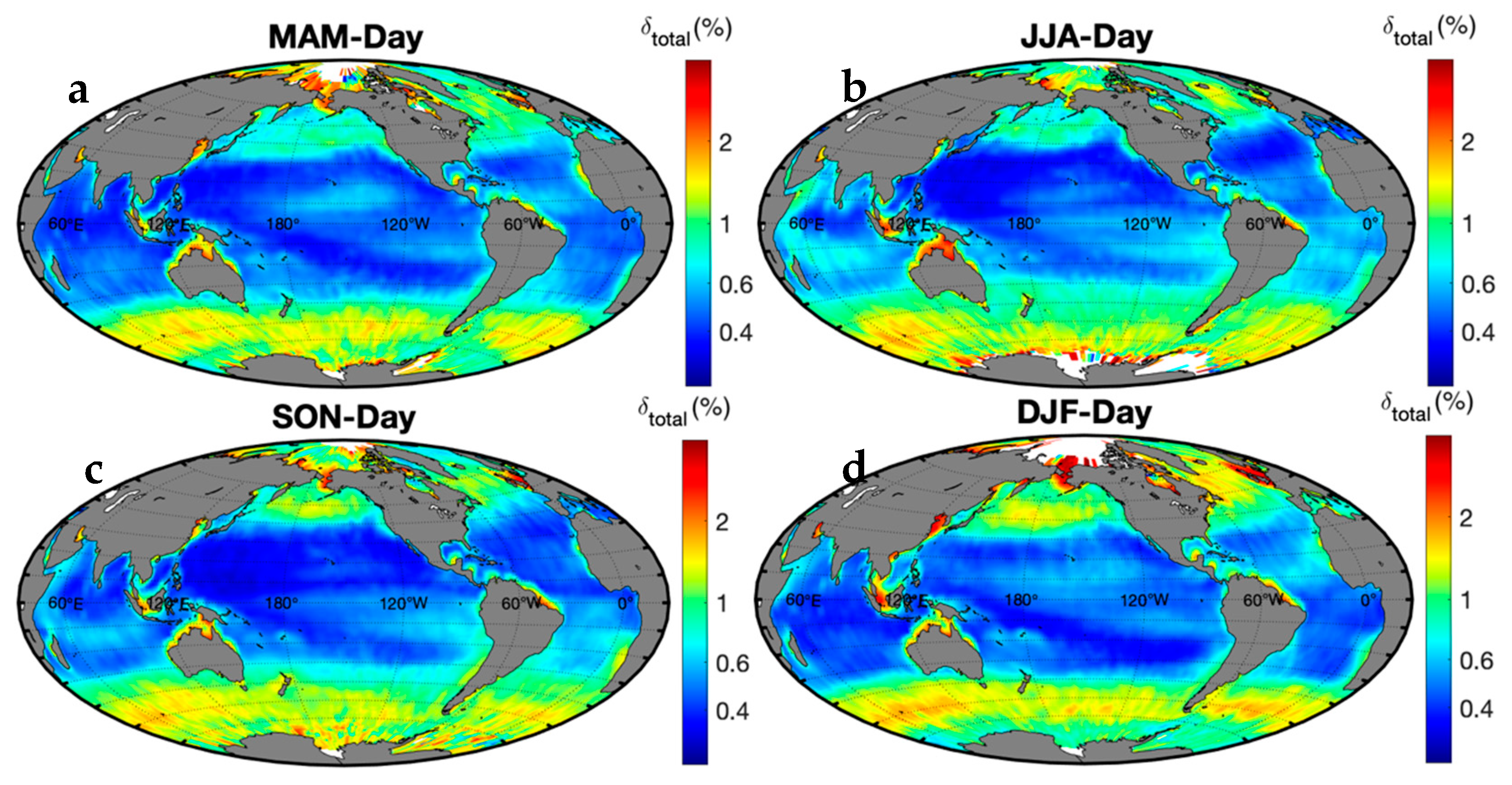
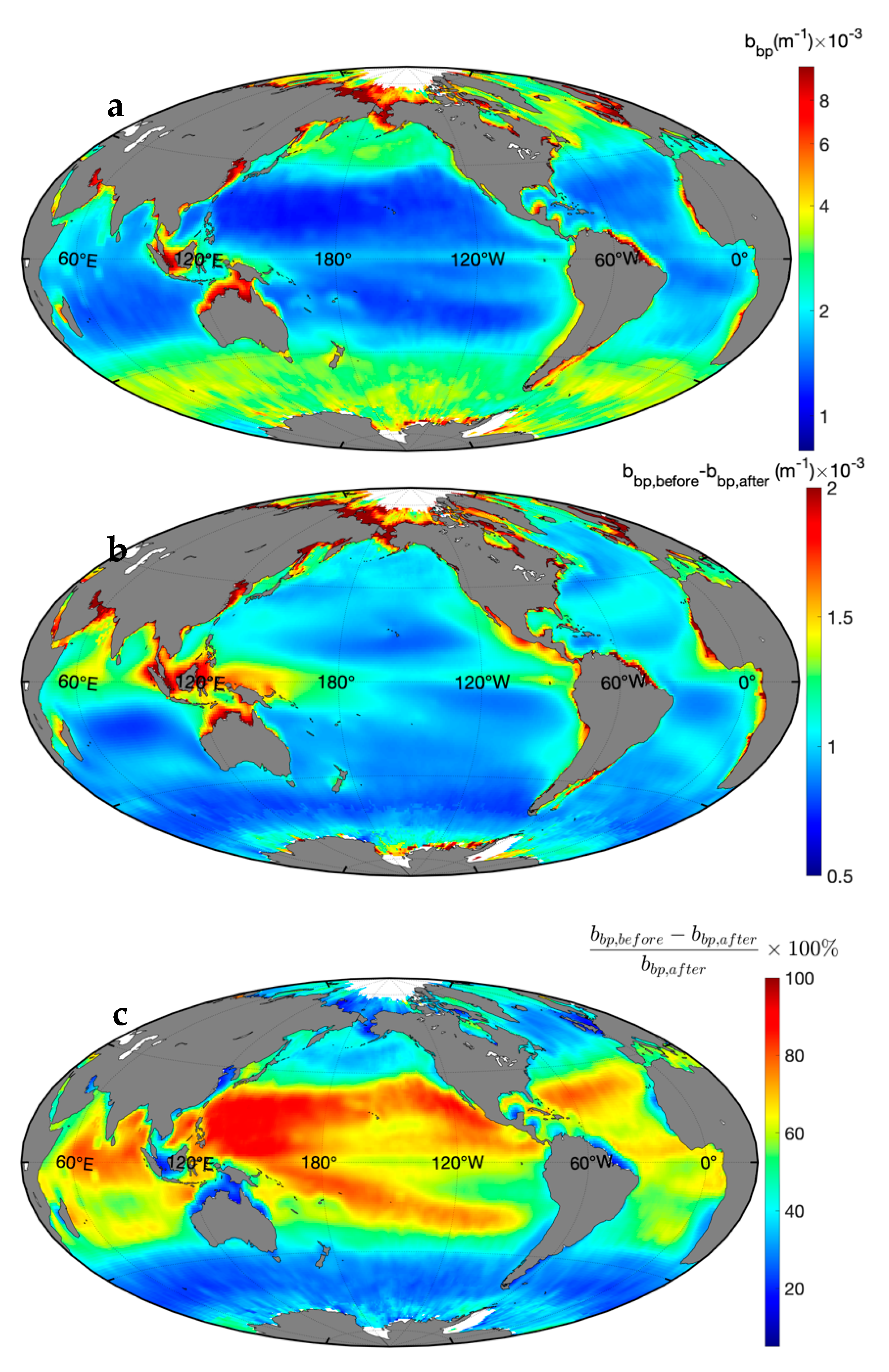
3. Global Ocean Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hunt, W.H.; Winker, D.M.; Vaughan, M.A.; Powell, K.A.; Lucker, P.L.; Weimer, C. CALIPSO Lidar Description and Performance Assessment. J. Atmos. Ocean. Technol. 2009, 26, 1214–1228. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Winker, D.M.; Pelon, J.; Coakley, J.A.; Ackerman, S.A.; Charlson, R.J.; Colarco, P.R.; Flamant, P.; Fu, Q.; Hoff, R.M.; Kittaka, C.; et al. The CALIPSO Mission: A Global 3D View of Aerosols and Clouds. Bull. Am. Meteorol. Soc. 2010, 91, 1211–1229. [Google Scholar] [CrossRef]
- Powell, K.A.; Hostetler, C.A.; Vaughan, M.A.; Lee, K.-P.; Trepte, C.R.; Rogers, R.R.; Winker, D.M.; Liu, Z.; Kuehn, R.E.; Hunt, W.H.; et al. CALIPSO Lidar Calibration Algorithms. Part I: Nighttime 532-Nm Parallel Channel and 532-Nm Perpendicular Channel. J. Atmos. Ocean. Technol. 2009, 26, 2015–2033. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Hu, Y.; Hostetler, C.A.; Dall’Olmo, G.; Rodier, S.D.; Hair, J.W.; Trepte, C.R. Space-Based Lidar Measurements of Global Ocean Carbon Stocks. Geophys. Res. Lett. 2013, 40, 4355–4360. [Google Scholar] [CrossRef]
- Lu, X.; Hu, Y. Estimation of Particulate Organic Carbon in the Ocean from Space-Based Polarization Lidar Measurements. In Proceedings of the SPIE Asia-Pacific Remote Sensing, Beijing, China, 10 December 2014; Volume 9261, pp. 92610Z-1–92610Z-8. [Google Scholar]
- Lacour, L.; Larouche, R.; Babin, M. In Situ Evaluation of Spaceborne CALIOP Lidar Measurements of the Upper-Ocean Particle Backscattering Coefficient. Opt. Express 2020, 28, 26989–26999. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Hu, Y.; Pelon, J.; Trepte, C.; Liu, K.; Rodier, S.; Zeng, S.; Lucker, P.; Verhappen, R.; Wilson, J.; et al. Retrieval of Ocean Subsurface Particulate Backscattering Coefficient from Space-Borne CALIOP Lidar Measurements. Opt. Express 2016, 24, 29001–29008. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Gaube, P.; Della Penna, A.; O’Malley, R.T.; Burt, W.J.; Hu, Y.; Bontempi, P.S.; Steinberg, D.K.; Boss, E.S.; Siegel, D.A.; et al. Global Satellite-Observed Daily Vertical Migrations of Ocean Animals. Nature 2019, 576, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Bisson, K.M.; Boss, E.; Werdell, P.J.; Ibrahim, A.; Behrenfeld, M.J. Particulate Backscattering in the Global Ocean: A Comparison of Independent Assessments. Geophys. Res. Lett. 2021, 48, e2020GL090909. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Hu, Y.; O’Malley, R.T.; Boss, E.S.; Hostetler, C.A.; Siegel, D.A.; Sarmiento, J.L.; Schulien, J.; Hair, J.W.; Lu, X.; et al. Annual Boom-Bust Cycles of Polar Phytoplankton Biomass Revealed by Space-Based Lidar. Nat. Geosci. 2017, 10, 118–122. [Google Scholar] [CrossRef]
- Dionisi, D.; Brando, V.E.; Volpe, G.; Colella, S.; Santoleri, R. Seasonal Distributions of Ocean Particulate Optical Properties from Spaceborne Lidar Measurements in Mediterranean and Black Sea. Remote Sens. Environ. 2020, 247, 111889. [Google Scholar] [CrossRef]
- Lu, X.; Hu, Y.; Trepte, C.; Zeng, S.; Churnside, J.H. Ocean Subsurface Studies with the CALIPSO Spaceborne Lidar. J. Geophys. Res. Ocean. 2014, 119, 4305–4317. [Google Scholar] [CrossRef]
- Churnside, J.; McCarty, B.; Lu, X. Subsurface Ocean Signals from an Orbiting Polarization Lidar. Remote Sens. 2013, 5, 3457–3475. [Google Scholar] [CrossRef] [Green Version]
- Hostetler, C.A.; Behrenfeld, M.J.; Hu, Y.; Hair, J.W.; Schulien, J.A. Spaceborne Lidar in the Study of Marine Systems. Annu. Rev. Mar. Sci. 2018, 10, 121–147. [Google Scholar] [CrossRef] [Green Version]
- Jamet, C.; Ibrahim, A.; Ahmad, Z.; Angelini, F.; Babin, M.; Behrenfeld, M.J.; Boss, E.; Cairns, B.; Churnside, J.; Chowdhary, J.; et al. Going Beyond Standard Ocean Color Observations: Lidar and Polarimetry. Front. Mar. Sci. 2019, 6, 251. [Google Scholar] [CrossRef]
- Churnside, J.H.; Shaw, J.A. Lidar Remote Sensing of the Aquatic Environment: Invited. Appl. Opt. 2020, 59, C92–C99. [Google Scholar] [CrossRef]
- Chris, A.H.; Liu, Z.; Reagan, J.; Vaughan, M.; Winker, D.; Osborn, M.; Hunt, W.; Powell, K.; Trepte, C. CALIOP Algorithm Theoretical Basis Document Calibration and Level 1 Data Products. Pc-Sci-201 Release 1.0, 2006. Available online: https://www-calipso.larc.nasa.gov/resources/pdfs/PC-SCI-201v1.0.pdf (accessed on 13 July 2021).
- Lu, X.; Hu, Y.; Yang, Y.; Neumann, T.A.; Omar, A.; Baize, R.; Vaughan, M.; Rodier, S.; Getzewich, B.; Trepte, C.; et al. New Ocean Subsurface Optical Properties from Space Lidars: CALIOP/CALIPSO and ATLAS/ICESat-2. Earth Space Sci. 2021. [Google Scholar] [CrossRef]
- Pitts, M.C.; Poole, L.R.; Gonzalez, R. Polar Stratospheric Cloud Climatology Based on CALIPSO Spaceborne Lidar Measurements from 2006 to 2017. Atmos. Chem. Phys. 2018, 18, 10881–10913. [Google Scholar] [CrossRef] [Green Version]
- Vaughan, M.; Pitts, M.; Trepte, C.; Winker, D.; Detweiler, P.; Garnier, A.; Getzewich, B.; Hunt, W.; Lambeth, J.; Lee, K.-P.; et al. Cloud—Aerosol LIDAR Infrared Pathfinder Satellite Observations (CALIPSO) Data Management System Data Products Catalog. Document No: PC-SCI-503, 2020. Available online: https://www-calipso.larc.nasa.gov/products/CALIPSO_DPC_Rev4x92.pdf (accessed on 13 July 2021).
- Kar, J.; Vaughan, M.A.; Lee, K.-P.; Tackett, J.L.; Avery, M.A.; Garnier, A.; Getzewich, B.J.; Hunt, W.H.; Josset, D.; Liu, Z.; et al. CALIPSO Lidar Calibration at 532 Nm: Version 4 Nighttime Algorithm. Atmos. Meas. Tech. 2018, 11, 1459–1479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Getzewich, B.J.; Vaughan, M.A.; Hunt, W.H.; Avery, M.A.; Powell, K.A.; Tackett, J.L.; Winker, D.M.; Kar, J.; Lee, K.-P.; Toth, T.D. CALIPSO Lidar Calibration at 532 Nm: Version 4 Daytime Algorithm. Atmos. Meas. Tech. 2018, 11, 6309–6326. [Google Scholar] [CrossRef] [Green Version]
- Siddaway, J.M.; Petelina, S.V. Transport and Evolution of the 2009 Australian Black Saturday Bushfire Smoke in the Lower Stratosphere Observed by OSIRIS on Odin. J. Geophys. Res. Atmos. 2011, 116, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Khaykin, S.; Legras, B.; Bucci, S.; Sellitto, P.; Isaksen, L.; Tencé, F.; Bekki, S.; Bourassa, A.; Rieger, L.; Zawada, D.; et al. The 2019/20 Australian Wildfires Generated a Persistent Smoke-Charged Vortex Rising up to 35 km Altitude. Commun. Earth Environ. 2020, 1, 22. [Google Scholar] [CrossRef]
- Peterson, D.A.; Campbell, J.R.; Hyer, E.J.; Fromm, M.D.; Kablick, G.P.; Cossuth, J.H.; DeLand, M.T. Wildfire-Driven Thunderstorms Cause a Volcano-like Stratospheric Injection of Smoke. NPJ Clim. Atmos. Sci. 2018, 1, 30. [Google Scholar] [CrossRef] [Green Version]
- Christian, K.; Yorks, J.; Das, S. Differences in the Evolution of Pyrocumulonimbus and Volcanic Stratospheric Plumes as Observed by CATS and CALIOP Space-Based Lidars. Atmosphere 2020, 11, 1035. [Google Scholar] [CrossRef]
- Hu, Y.; Stamnes, K.; Vaughan, M.; Pelon, J.; Weimer, C.; Wu, D.; Cisewski, M.; Sun, W.; Yang, P.; Lin, B.; et al. Sea Surface Wind Speed Estimation from Space-Based Lidar Measurements. Atmos. Chem. Phys. 2008, 8, 3593–3601. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Hu, Y.; Liu, Z.; Zeng, S.; Trepte, C. CALIOP Receiver Transient Response Study. In Proceedings of the SPIE 8873, Polarization Science and Remote Sensing VI, San Diego, CA, USA, 27 September 2013; Volume 8873, pp. 887316-1–887316-9. [Google Scholar] [CrossRef]
- Lu, X.; Hu, Y.; Trepte, C.; Liu, Z. A Super-Resolution Laser Altimetry Concept. IEEE Geosci. Remote Sens. Lett. 2014, 11, 298–302. [Google Scholar] [CrossRef]
- Sullivan, J.M.; Twardowski, M.S. Angular Shape of the Oceanic Particulate Volume Scattering Function in the Backward Direction. Appl. Opt. 2009, 48, 6811–6819. [Google Scholar] [CrossRef]
- Stramski, D.; Reynolds, R.A.; Kahru, M.; Mitchell, B.G. Estimation of Particulate Organic Carbon in the Ocean from Satellite Remote Sensing. Science 1999, 285, 239–242. [Google Scholar] [CrossRef] [PubMed]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-Based Ocean Productivity and Phytoplankton Physiology from Space. Glob. Biogeochem. Cycles 2005, 19, 1–14. [Google Scholar] [CrossRef]
- Lu, X.; Hu, Y.; Yang, Y.; Bontempi, P.; Omar, A.; Baize, R. Antarctic Spring Ice-Edge Blooms Observed from Space by ICESat-2. Remote Sens. Environ. 2020, 245, 111827. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Hu, Y.; Omar, A.; Baize, R.; Vaughan, M.; Rodier, S.; Kar, J.; Getzewich, B.; Lucker, P.; Trepte, C.; et al. Global Ocean Studies from CALIOP/CALIPSO by Removing Polarization Crosstalk Effects. Remote Sens. 2021, 13, 2769. https://doi.org/10.3390/rs13142769
Lu X, Hu Y, Omar A, Baize R, Vaughan M, Rodier S, Kar J, Getzewich B, Lucker P, Trepte C, et al. Global Ocean Studies from CALIOP/CALIPSO by Removing Polarization Crosstalk Effects. Remote Sensing. 2021; 13(14):2769. https://doi.org/10.3390/rs13142769
Chicago/Turabian StyleLu, Xiaomei, Yongxiang Hu, Ali Omar, Rosemary Baize, Mark Vaughan, Sharon Rodier, Jayanta Kar, Brian Getzewich, Patricia Lucker, Charles Trepte, and et al. 2021. "Global Ocean Studies from CALIOP/CALIPSO by Removing Polarization Crosstalk Effects" Remote Sensing 13, no. 14: 2769. https://doi.org/10.3390/rs13142769
APA StyleLu, X., Hu, Y., Omar, A., Baize, R., Vaughan, M., Rodier, S., Kar, J., Getzewich, B., Lucker, P., Trepte, C., Hostetler, C., & Winker, D. (2021). Global Ocean Studies from CALIOP/CALIPSO by Removing Polarization Crosstalk Effects. Remote Sensing, 13(14), 2769. https://doi.org/10.3390/rs13142769