A Sparse Denoising-Based Super-Resolution Method for Scanning Radar Imaging
Abstract
:1. Introduction
- We point out that the azimuth echo of a scanning radar can be regarded as a convolution of the antenna pattern and target scattering distribution, so the azimuth resolution of scanning radar can be improved via deconvolution methods.
- To improve on the shortcomings of traditional SSM, we propose the SDBSM method to improve the azimuth resolution of a scanning radar. The proposed SDBSM uses the sparsity constraint of the target to denoise, and it realizes the scanning radar super-resolution imaging through the cross-iteration of denoising and deconvolution.
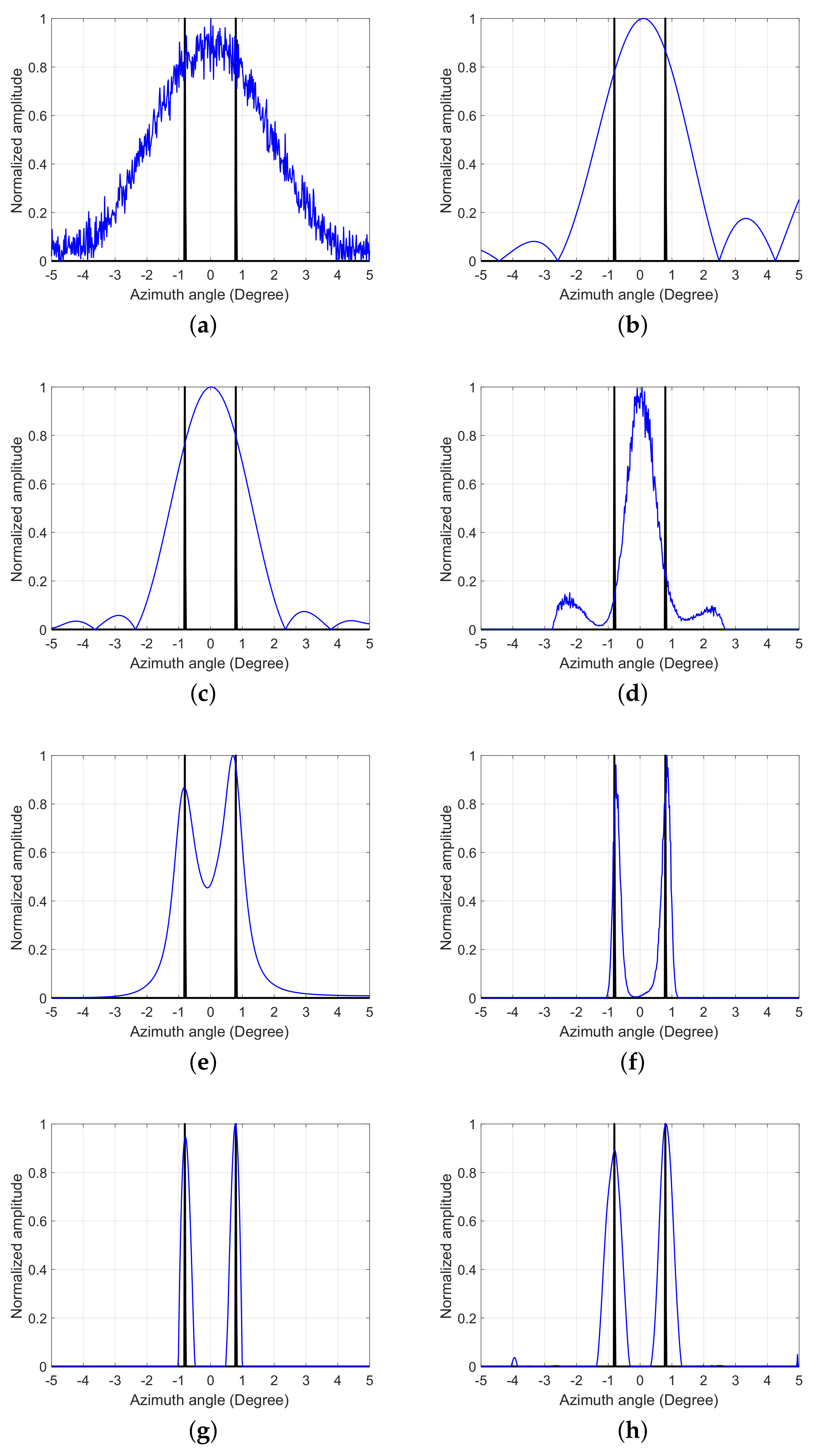
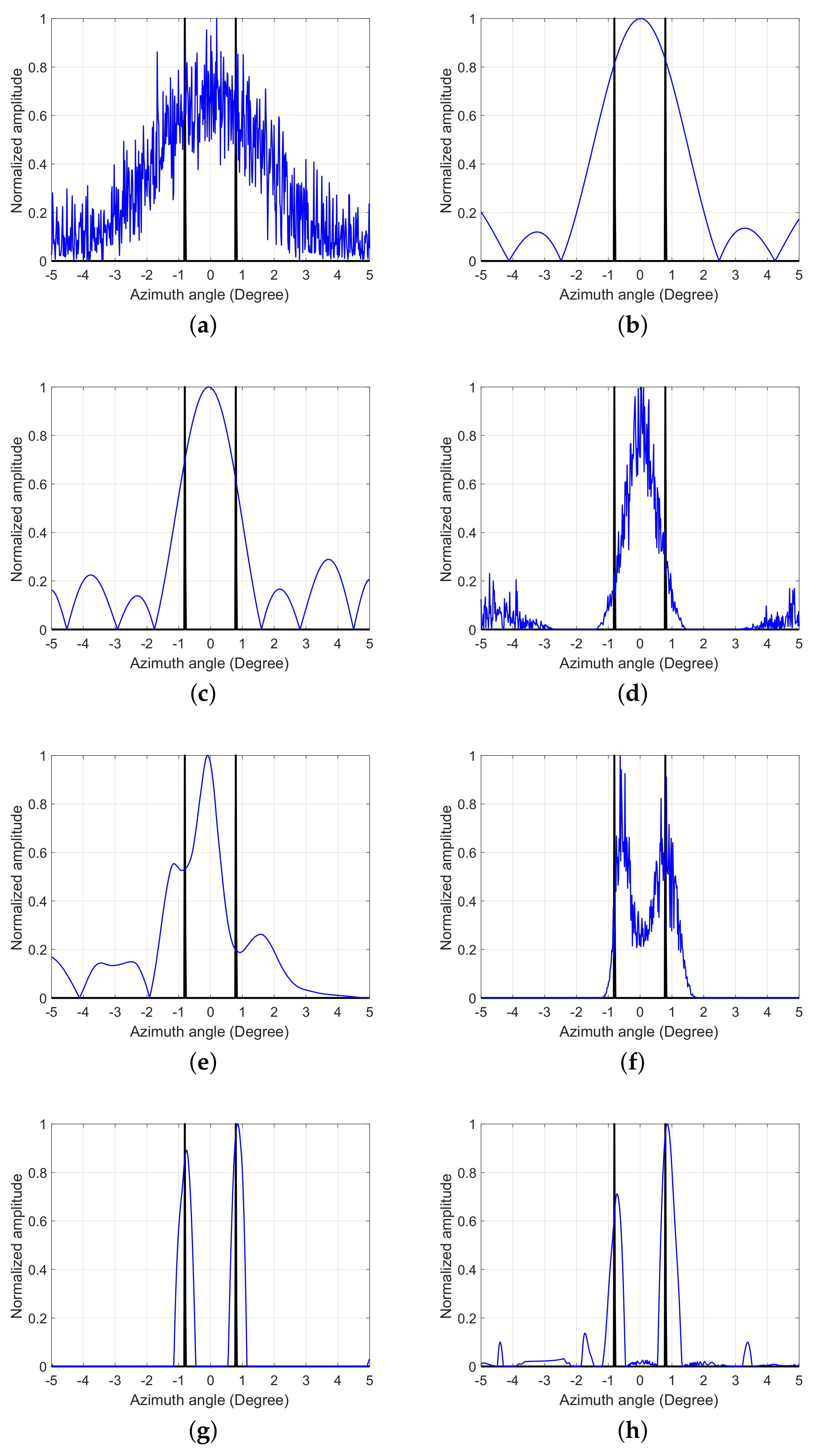
- We compare SDBSM with traditional TSVDM, FTVM, MLE, IAA, MAPE and SSM using simulations and real data. This demonstrates that SDBSM can effectively preserve the shape of a main target while resolving the adjacent targets, which is helpful for identifying the main target.
2. Super-Resolution Imaging Using Traditional SSM
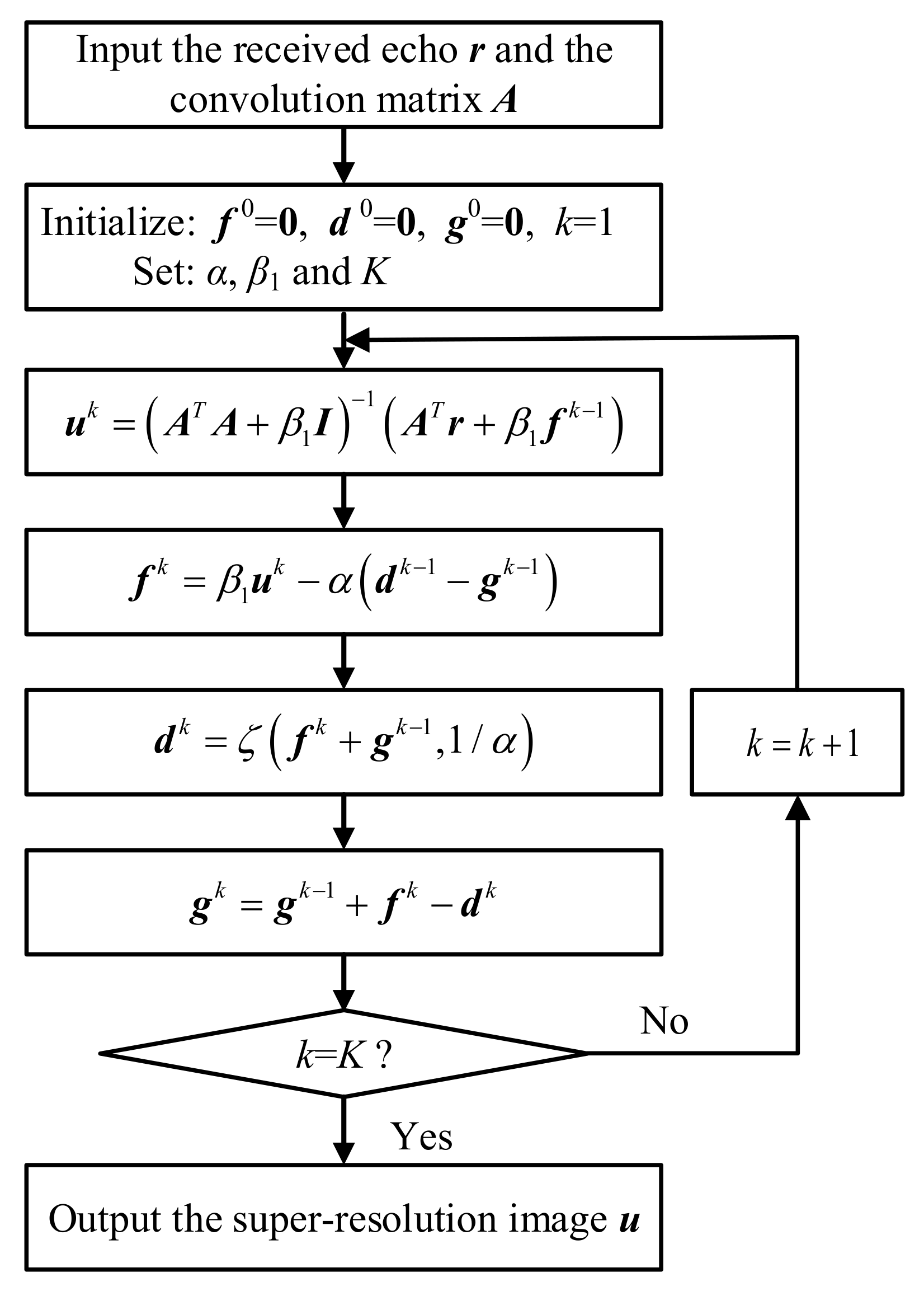
3. Super-Resolution Imaging Using the Proposed SDBSM
3.1. Deduction of the Method
3.2. Analysis of the Computational Complexity
4. Experimental Verification of the Proposed SDBSM
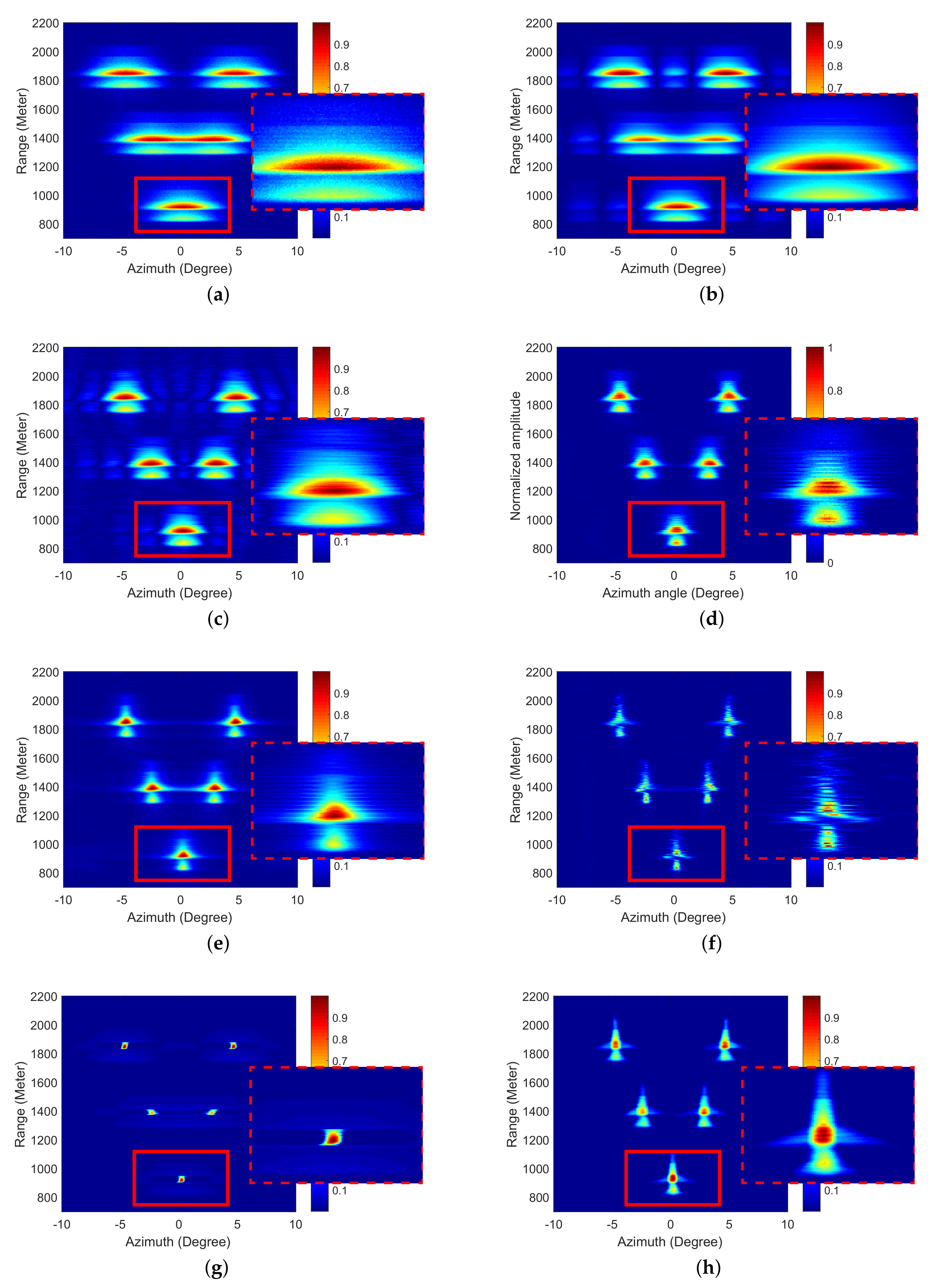
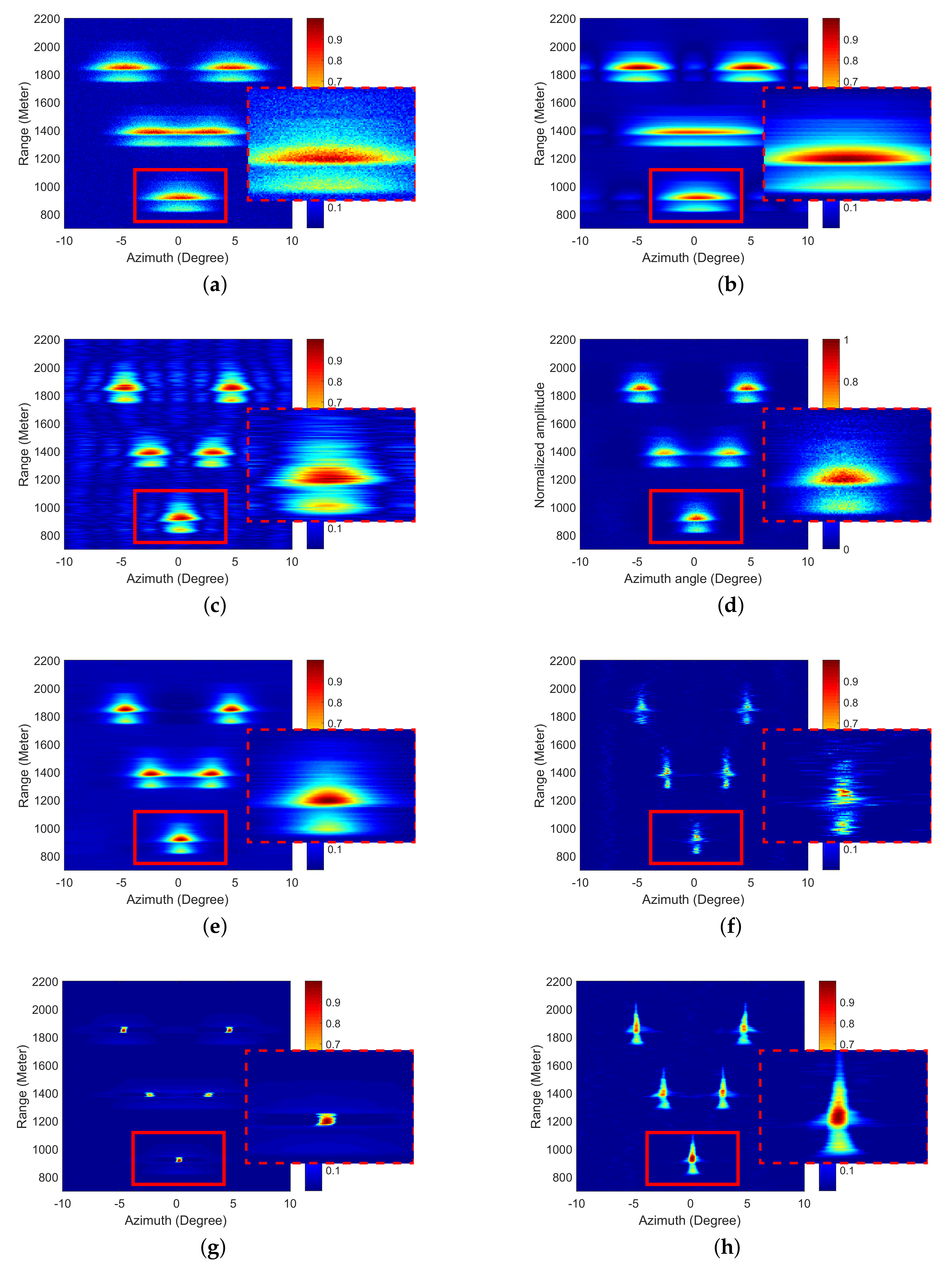
4.1. A Simulation of Strong-Point Targets
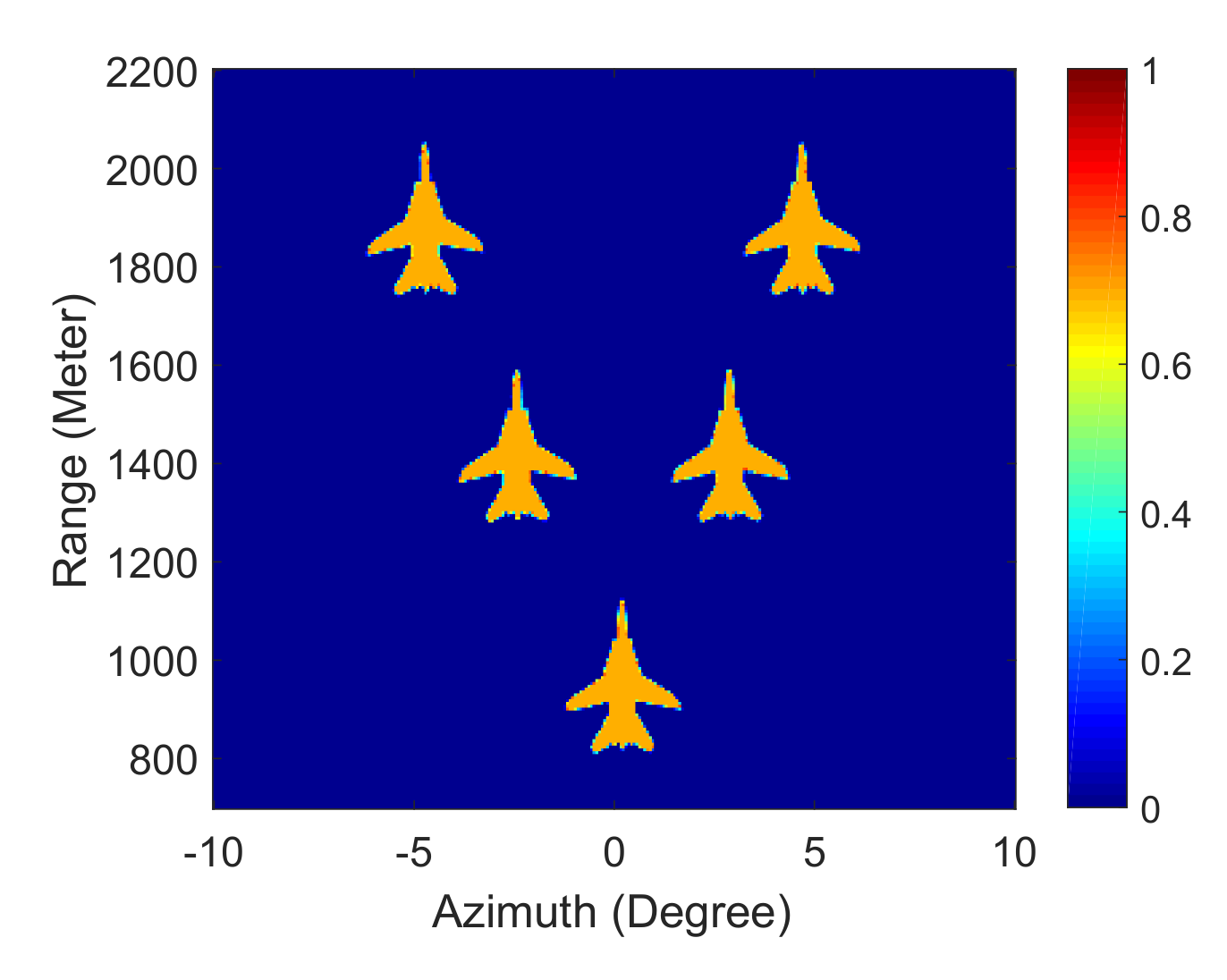
4.2. Simulations of Area Targets
4.3. Real Data Verification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Pseudocode of the Proposed SDBSM
References
- Zhang, Y.; Luo, J.; Li, J.; Mao, D.; Zhang, Y.; Huang, Y.; Yang, J. Fast inverse-scattering reconstruction for airborne high-squint radar imagery based on doppler centroid compensation. IEEE Trans. Geosci. Remote Sens. 2021. [Google Scholar] [CrossRef]
- North, K.W.; Oue, M.; Kollias, P.; Giangrande, S.E.; Collis, S.M.; Potvin, C.K. Vertical air motion retrievals in deep convective clouds using the ARM scanning radar network in oklahoma during MC3E. Atmos. Meas. Tech. 2017, 10, 2785–2806. [Google Scholar] [CrossRef] [Green Version]
- Albright, K.S. Environmental scanning: Radar for success. Inf. Manag. J. 2004, 38, 38–45. [Google Scholar]
- Zhang, Q.; Zhang, Y.; Huang, Y.; Zhang, Y.; Pei, J.; Yi, Q.; Li, W.; Yang, J. TV-sparse super-resolution method for radar forward-looking imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6534–6549. [Google Scholar] [CrossRef]
- Soldovieri, F.; Gennarelli, G.; Catapano, I.; Liao, D.; Dogaru, T.; Soldovieri, F.; Gennarelli, G.; Catapano, I.; Liao, D.; Dogaru, T. Forward-looking radar imaging: A comparison of two data processing strategies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 562–571. [Google Scholar] [CrossRef]
- Biondi, F. Recovery of partially corrupted SAR images by super-resolution based on spectrum extrapolation. IEEE Geosci. Remote Sens. Lett. 2016, 14, 139–143. [Google Scholar] [CrossRef]
- Rehacek, J.; Paúr, M.; Stoklasa, B.; Sánchez-Soto, L.L. Optimal measurements for resolution beyond the Rayleigh limit. Opt. Lett. 2017, 42, 231–234. [Google Scholar] [CrossRef]
- Davis, E.J.; Bridges, M.A. The Rayleigh limit of charge revisited: Light scattering from exploding droplets. J. Aerosol Sci. 1994, 25, 1179–1199. [Google Scholar] [CrossRef]
- Dropkin, H.; Ly, C. Superresolution for scanning antenna. In Proceedings of the 1997 IEEE National Radar Conference, Syracuse, NY, USA, 13–15 May 1997; pp. 306–308. [Google Scholar]
- Li, Y.; Liu, J.; Jiang, X.; Huang, X. Angular superresol for signal model in coherent scanning radars. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3103–3116. [Google Scholar] [CrossRef]
- Sadjadi, F. Radar beam sharpening using an optimum FIR filter. Circuits Syst. Signal Process. 2000, 19, 121–129. [Google Scholar] [CrossRef]
- Hansen, P.C. Truncated singular value decomposition solutions to discrete ill-posed problems with ill-determined numerical rank. Siam J. Sci. Stat. Comput. 1990, 11, 503–518. [Google Scholar] [CrossRef]
- Gao, P.; Rong, J.; Pu, H.; Liu, T.; Zhang, W.; Zhang, X.; Lu, H. Sparse view cone beam x-ray luminescence tomography based on truncated singular value decomposition. Opt. Express 2018, 26, 23233–23250. [Google Scholar] [CrossRef]
- Doğu, S.; Akıncı, M.N.; Çayören, M.; Akduman, I. Truncated singular value decomposition for through-the-wall microwave imaging application. IET Microw. Antennas Propag. 2019, 14, 260–267. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Wang, Z. On robust Capon beamforming and diagonal loading. IEEE Trans. Signal Process. 2003, 51, 1702–1715. [Google Scholar]
- Zhang, H.; López-Dekker, P. Persistent scatterer densification through the application of capon-and apes-based sar reprocessing algorithms. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7521–7533. [Google Scholar] [CrossRef]
- Cheney, M. The linear sampling method and the MUSIC algorithm. Inverse Probl. 2001, 17, 591. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Zhang, Y.; Zheng, G.; Feng, C.; Tang, J. Improved DOA estimation algorithm for co-prime linear arrays using root-MUSIC algorithm. Electron. Lett. 2017, 53, 1277–1279. [Google Scholar] [CrossRef]
- Guili, Z.; Youming, L.I.; Mingchen, Y.U.; Wang, X. Impulsive noise mitigation based on iteration adaptive approach in underwater acoustic communication. Telecommun. Sci. 2017, 33, 66. [Google Scholar]
- Glentis, G.O.; Jakobsson, A. Efficient implementation of iterative adaptive approach spectral estimation techniques. IEEE Trans. Signal Process. 2011, 59, 4154–4167. [Google Scholar] [CrossRef]
- Zhang, Y.; Mao, D.; Zhang, Q.; Zhang, Y.; Huang, Y.; Yang, J. Airborne forward-looking radar super-resolution imaging using iterative adaptive approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2044–2054. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Li, W.; Huang, Y.; Yang, J. Super-Resolution Surface Mapping for Scanning Radar: Inverse Filtering Based on the Fast Iterative Adaptive Approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 127–144. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhao, X.L.; Ma, T.H. Remote sensing images destriping using unidirectional hybrid total variation and nonconvex low-rank regularization. J. Comput. Appl. Math. 2020, 363, 124–144. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.-L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef] [Green Version]
- Thanh, D.N.H.; Thanh, L.T.; Hien, N.N.; Prasath, S. Adaptive total variation L1 regularization for salt and pepper image denoising. Optik 2020, 208, 163677. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. Airborne radar super-resolution imaging based on fast total variation method. Remote Sens. 2021, 13, 549. [Google Scholar] [CrossRef]
- Peng, J.; Li, L.; Tang, Y.Y. Maximum likelihood estimation-based joint sparse representation for the classification of hyperspectral remote sensing images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1790–1802. [Google Scholar] [CrossRef]
- Li, K.; Peng, S.; Zhang, T.; Malik, J. Multimodal image synthesis with conditional implicit maximum likelihood estimation. Int. J. Comput. Vis. 2020, 128, 2607–2628. [Google Scholar] [CrossRef]
- Shao, J.; Liao, W.-C.; Liang, R.; Barnard, K. Resolution enhancement for fiber bundle imaging using maximum a posteriori estimation. Opt. Lett. 2018, 43, 1906–1909. [Google Scholar] [CrossRef]
- Anandhi, D.; Valli, S. An algorithm for multi-sensor image fusion using maximum a posteriori and nonsubsampled contourlet transform. Comput. Electr. Eng. 2018, 65, 139–152. [Google Scholar] [CrossRef]
- Tan, K.; Li, W.; Zhang, Q.; Huang, Y.; Wu, J.; Yang, J. Penalized maximum likelihood angular super-resolution method for scanning radar forward-looking imaging. Sensors 2018, 18, 912. [Google Scholar] [CrossRef] [Green Version]
- Hunziker, J.; Laloy, E.; Linde, N. Bayesian full-waveform tomography with application to crosshole ground penetrating radar data. Geophys. J. Int. 2019, 218, 913–931. [Google Scholar] [CrossRef]
- Wu, Q.; Lai, Z.; Amin, M.G. Through-the-wall radar imaging based on Bayesian compressive sensing exploiting multipath and target structure. IEEE Trans. Comput. Imaging 2021, 7, 422–435. [Google Scholar] [CrossRef]
- Shao, Z.; Wang, L.; Wang, Z.; Deng, J. Remote sensing image super-resolution using sparse representation and coupled sparse autoencoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2019, 12, 2663–2674. [Google Scholar] [CrossRef]
- Poon, C.; Peyré, G. Multidimensional sparse super-resolution. SIAM J. Math. Anal. 2019, 51, 1–44. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, Y.; Huang, Y.; Zhang, Y. Azimuth superresolution of forward-looking radar imaging which relies on linearized Bregman. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2032–2043. [Google Scholar] [CrossRef]
- Zhang, Y.; Jakobsson, A.; Zhang, Y.; Huang, Y.; Yang, J. Wideband sparse reconstruction for scanning radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6055–6068. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1-regularized problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Raju, C.; Reddy, T.S. MST radar signal processing using iterative adaptive approach. Geosci. Lett. 2018, 5, 20. [Google Scholar] [CrossRef]
- Ke, L.; Marcellin, M.W. Near-lossless image compression: Minimum-entropy, constrained-error dpcm. Image Process. IEEE Trans. 1998, 7, 225–228. [Google Scholar]
- Cai, J.; Gu, S.; Zhang, L. Learning a deep single image contrast enhancer from multi-exposure images. IEEE Trans. Image Process. 2018, 27, 2049–2062. [Google Scholar] [CrossRef] [PubMed]

| Methods | BSR | |
|---|---|---|
| High SNR | Low SNR | |
| IAA | 4.06 | None |
| MAPE | 13.3 | 6.66 |
| SSM | 12.0 | 9.6 |
| SDBSM | 8.27 | 5.33 |
| Methods | Entropy | |
|---|---|---|
| High SNR | Low SNR | |
| Echo | 5.45 | 5.49 |
| TSVDM | 5.61 | 5.74 |
| TVM | 5.43 | 6.01 |
| MLE | 3.34 | 3.65 |
| IAA | 4.03 | 4.74 |
| MAPE | 1.98 | 2.87 |
| SSM | 2.72 | 2.78 |
| SDBSM | 1.53 | 2.53 |
| Parameter | Value |
|---|---|
| Beam width of the antenna | 4 |
| Carrier frequency | 30.75 GHz |
| Band width of the transmitted signal | 200 MHz |
| Antenna scanning speed | 60/s |
| Scanning region | ±30 |
| PRF | 500 Hz |
| Methods | Echo | TSVDM | FTVM | MLE | IAA | MAPE | SSM | SDBSM |
|---|---|---|---|---|---|---|---|---|
| Entropy | 4.84 | 4.65 | 4.65 | 4.71 | 4.75 | 4.54 | 4.51 | 4.34 |
| Contrast | 5.89 | 6.01 | 7.69 | 7.46 | 9.21 | 9.38 | 10.95 | 12.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, Y.; Zhang, Y.; Huang, Y.; Yang, J. A Sparse Denoising-Based Super-Resolution Method for Scanning Radar Imaging. Remote Sens. 2021, 13, 2768. https://doi.org/10.3390/rs13142768
Zhang Q, Zhang Y, Zhang Y, Huang Y, Yang J. A Sparse Denoising-Based Super-Resolution Method for Scanning Radar Imaging. Remote Sensing. 2021; 13(14):2768. https://doi.org/10.3390/rs13142768
Chicago/Turabian StyleZhang, Qiping, Yin Zhang, Yongchao Zhang, Yulin Huang, and Jianyu Yang. 2021. "A Sparse Denoising-Based Super-Resolution Method for Scanning Radar Imaging" Remote Sensing 13, no. 14: 2768. https://doi.org/10.3390/rs13142768
APA StyleZhang, Q., Zhang, Y., Zhang, Y., Huang, Y., & Yang, J. (2021). A Sparse Denoising-Based Super-Resolution Method for Scanning Radar Imaging. Remote Sensing, 13(14), 2768. https://doi.org/10.3390/rs13142768







