Passive MIMO Radar Detection with Unknown Colored Gaussian Noise
Abstract
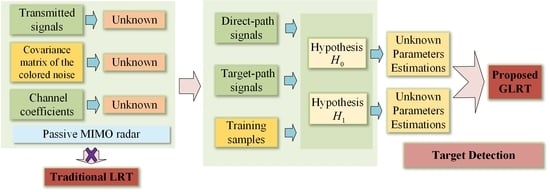
:1. Introduction
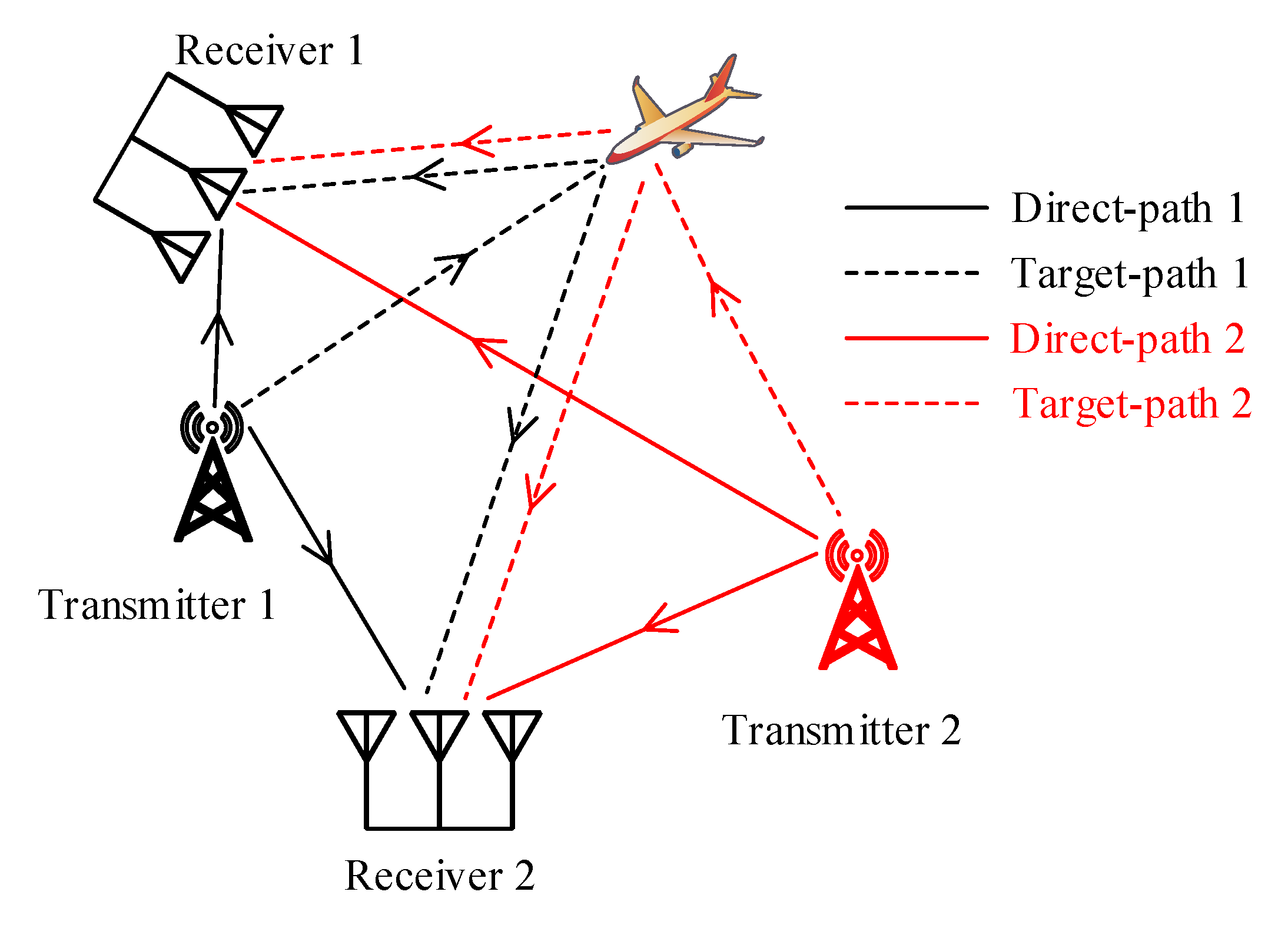
2. Signal Model and Assumption
3. GLRT for Passive MIMO Radar
3.1. Probability Distribution of Received Signal
3.2. GLRT Derivation
3.3. Performance Analysis and Discussion
4. Simulation
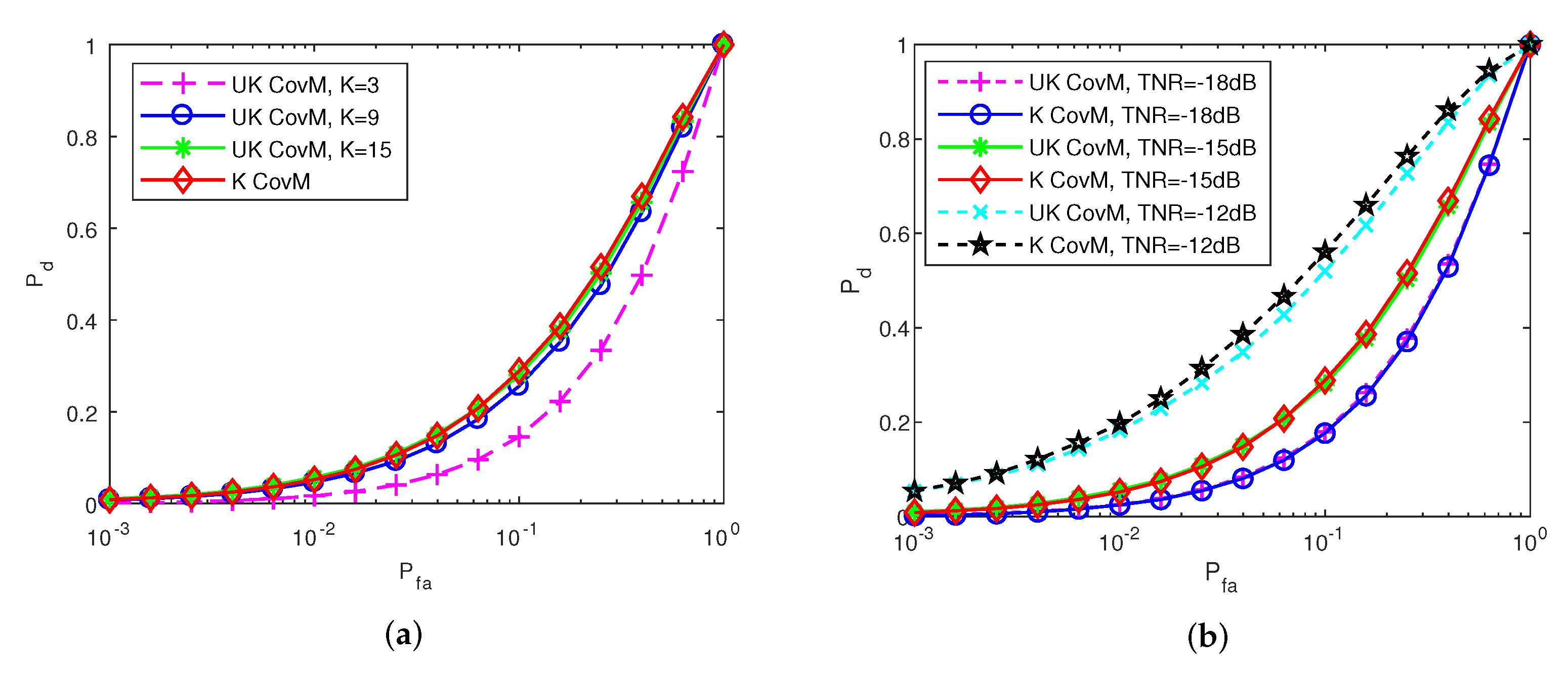
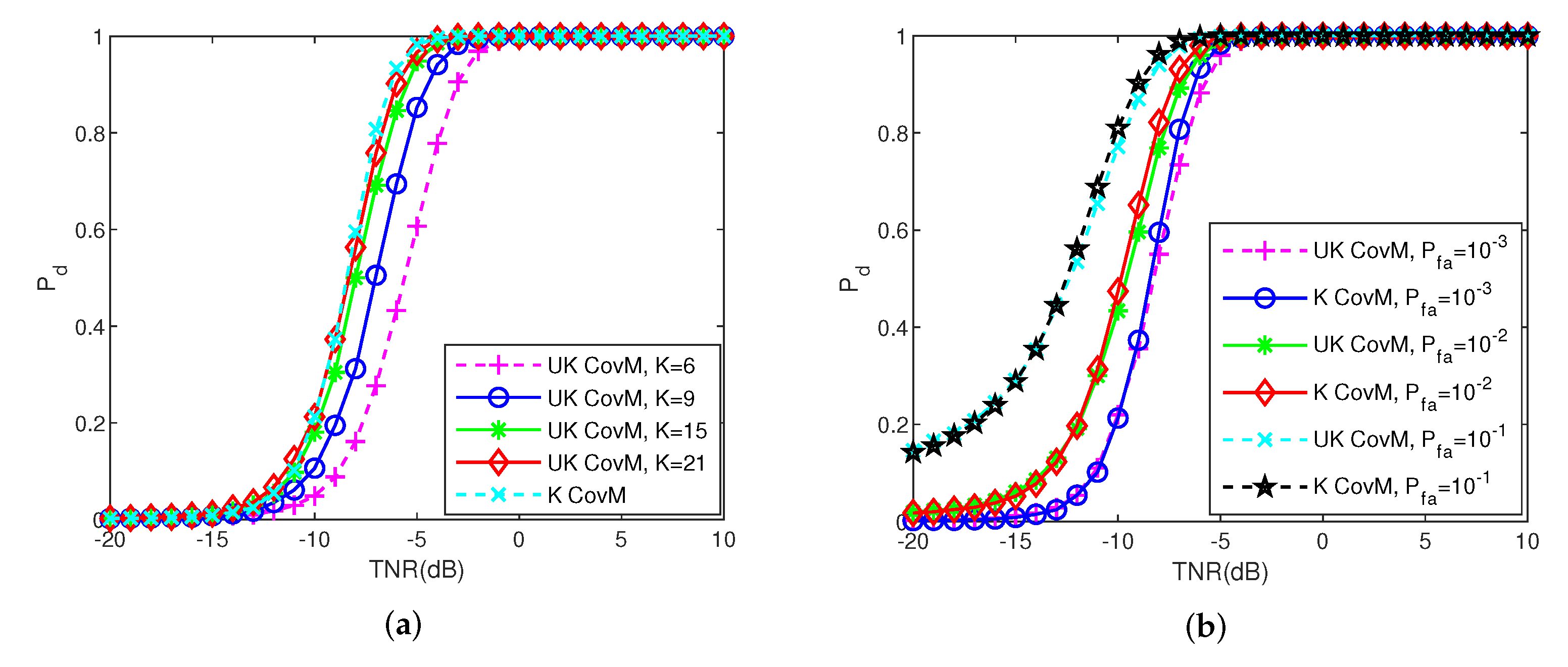
4.1. Variation of Pd with Pfa
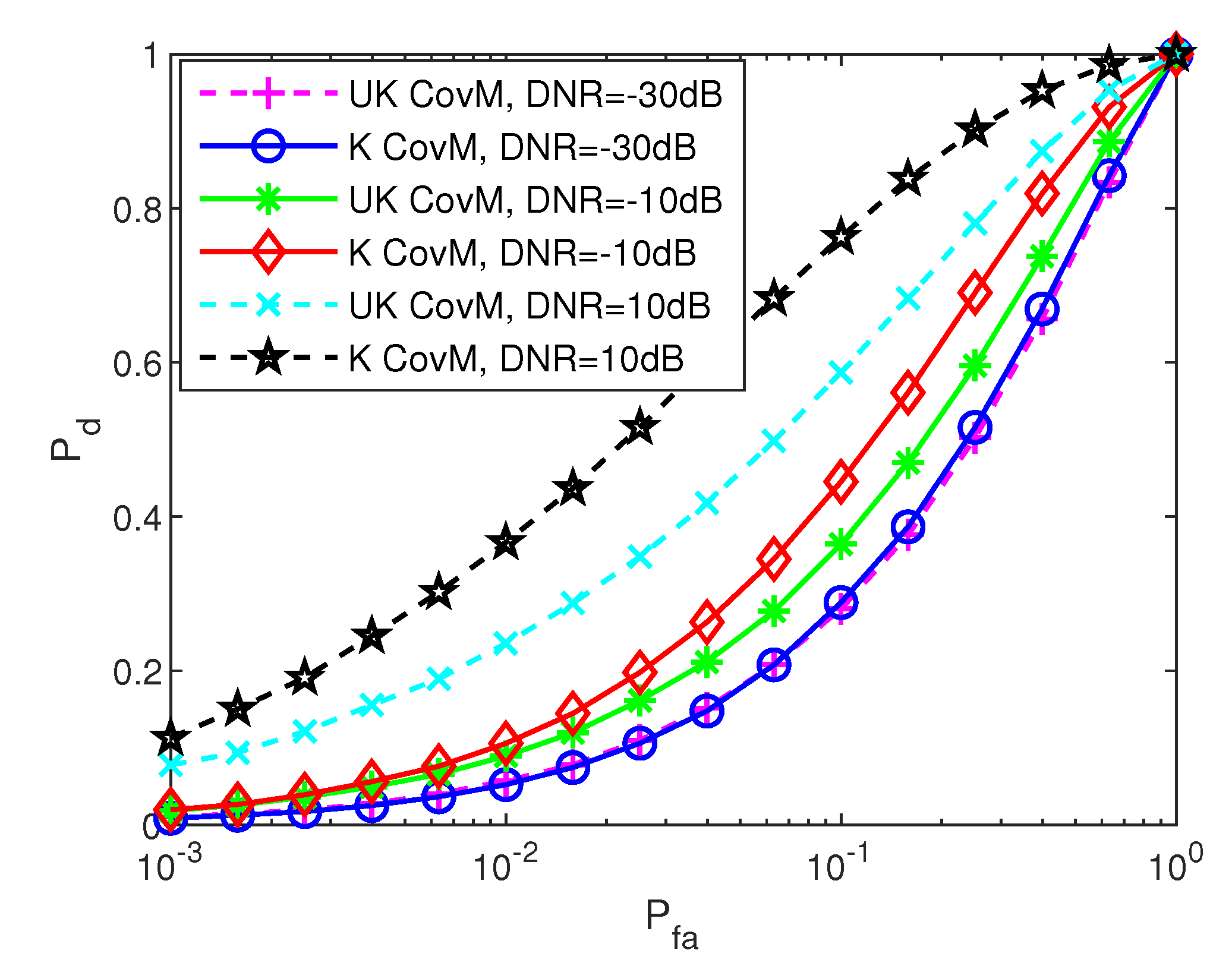
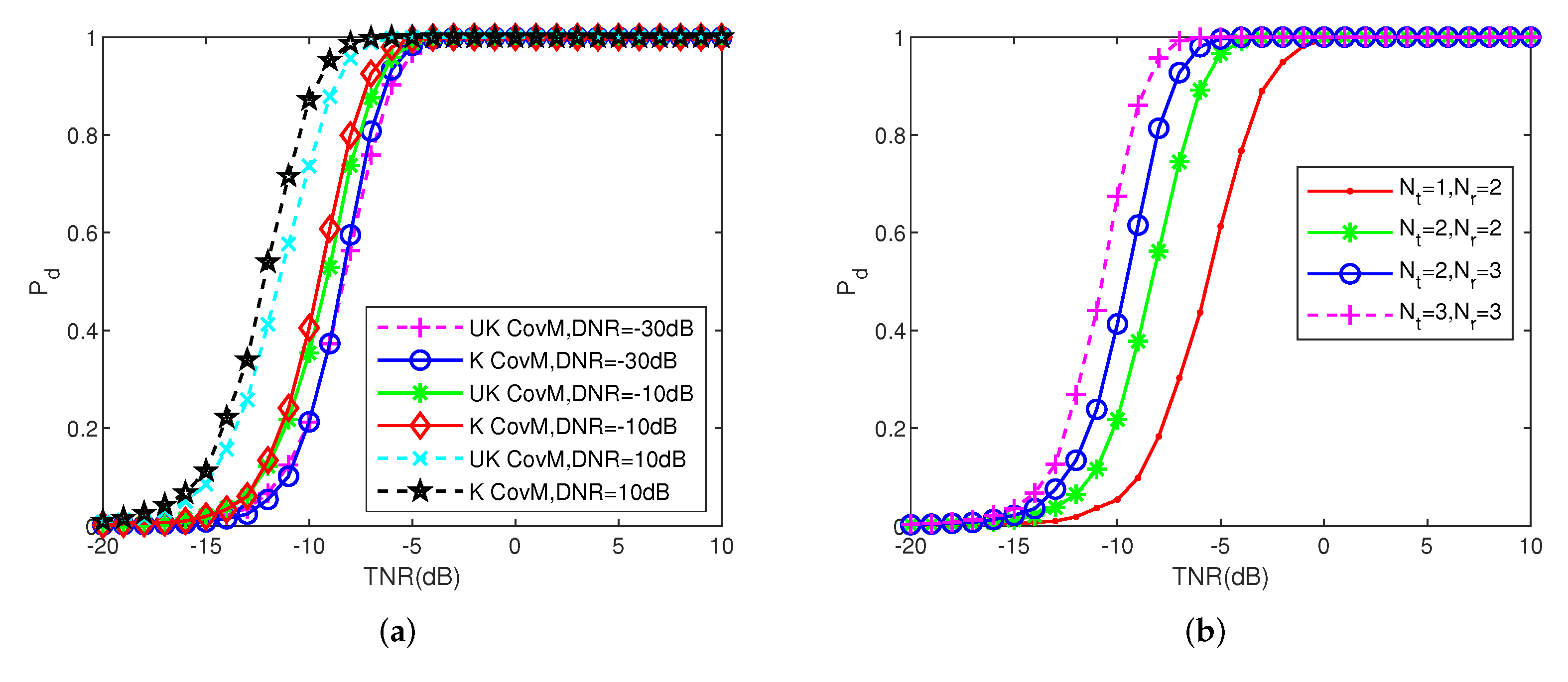
4.2. Variation of Pd with TNR
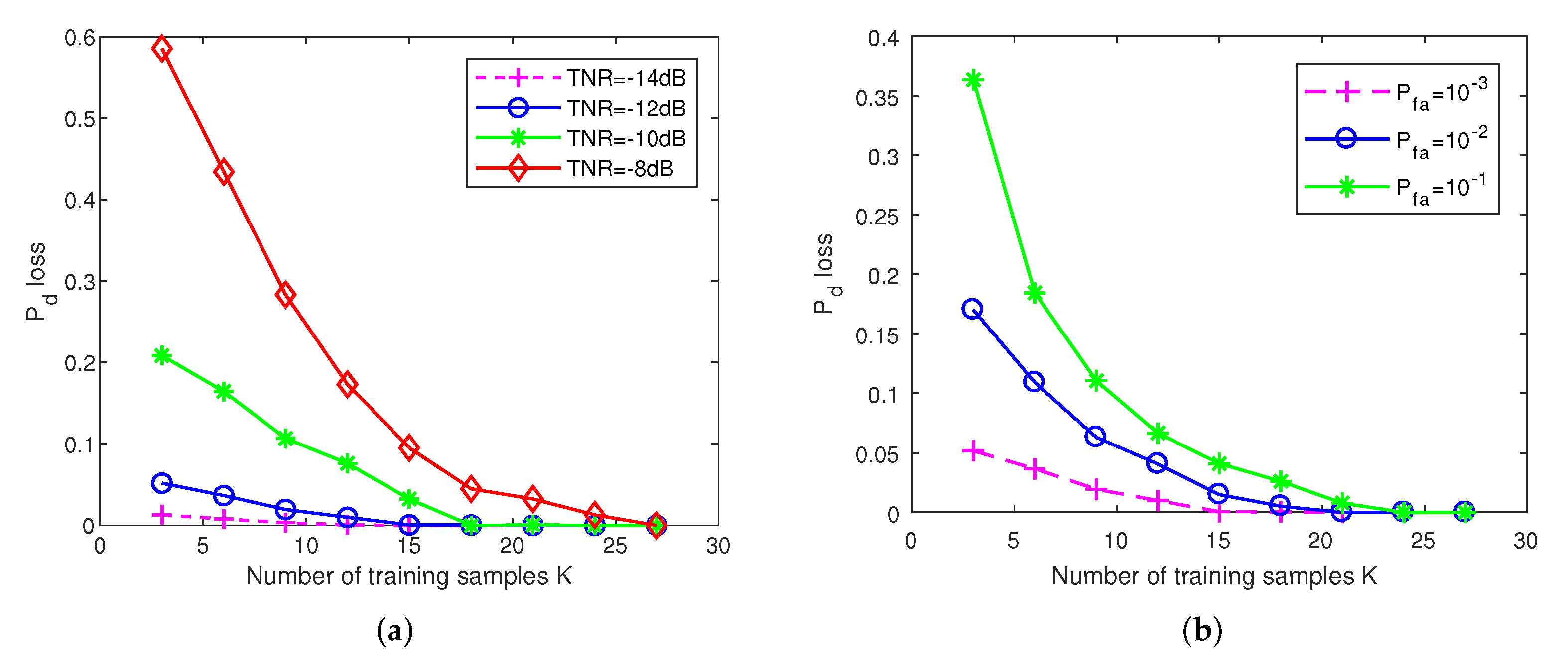
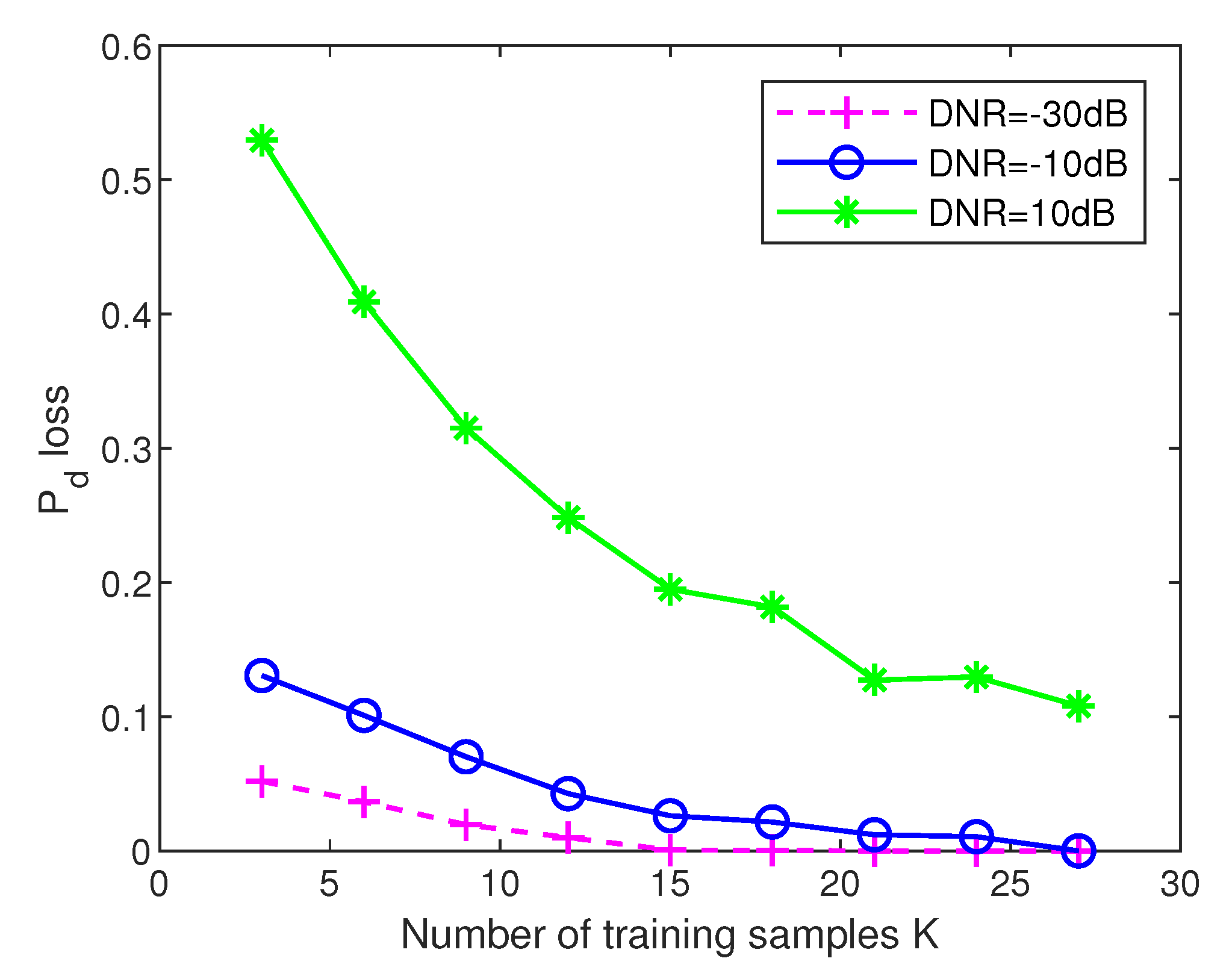
4.3. Pd Loss
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Maximum Likelihood Estimate
References
- Liu, J.; Li, H.; Himed, B. On the performance of the cross-correlation detector for passive radar applications. Signal Process. 2015, 113, 32–37. [Google Scholar] [CrossRef]
- Cui, G.; Liu, J.; Li, H.; Himed, B. Signal detection with noisy reference for passive sensing. Signal Process. 2015, 108, 389–399. [Google Scholar] [CrossRef]
- Subedi, S.; Zhang, Y.D.; Amin, M.G.; Himed, B. Group sparsity based multi-target tracking in passive multi-static radar systems using Doppler-only measurements. IEEE Trans. Signal Process. 2016, 64, 3619–3634. [Google Scholar] [CrossRef]
- Prateek, G.; Hurtado, M.; Nehorai, A. Target detection using weather radars and electromagnetic vector sensors. Signal Process. 2017, 137, 387–397. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Himed, B. Multistatic detection for passive radar with direct-path interference. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 915–925. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Amin, M.G.; Himed, B. Structure-aware sparse reconstruction and applications to passive multistatic radar. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 68–78. [Google Scholar] [CrossRef]
- He, Q.; Blum, R.S. The significant gains from optimally processed multiple signals of opportunity and multiple receive stations in passive radar. IEEE Signal Process. Lett. 2014, 21, 180–184. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Liu, J.; Zhang, Z.J.; Liu, H.; Zhou, S. Linear fusion for target detection in passive multistatic radar. Signal Process. 2017, 130, 175–182. [Google Scholar] [CrossRef]
- Chalise, B.K.; Himed, B. GLRT detector in single frequency multi-static passive radar systems. Signal Process. 2018, 142, 504–512. [Google Scholar] [CrossRef]
- Fazlollahpoor, M.; Derakhtian, M.; Khorshidi, S. Rao Detector for Passive MIMO Radar With Direct-Path Interference. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2999–3009. [Google Scholar] [CrossRef]
- Li, Y.; He, Q.; Blum, R.S. Limited-Complexity Receiver Design for Passive/Active MIMO Radar Detection. IEEE Trans. Signal Process. 2019, 67, 3258–3271. [Google Scholar] [CrossRef]
- Horstmann, S.; Ramírez, D.; Schreier, P.J. Two-Channel Passive Detection of Cyclostationary Signals. IEEE Trans. Signal Process. 2020, 68, 2340–2355. [Google Scholar] [CrossRef]
- Santamaria, I.; Scharf, L.L.; Via, J.; Wang, H.; Wang, Y. Passive detection of correlated subspace signals in two MIMO channels. IEEE Trans. Signal Process. 2017, 65, 5266–5280. [Google Scholar] [CrossRef]
- Santamaria, I.; Via, J.; Scharf, L.L.; Wang, Y. A GLRT approach for detecting correlated signals in white noise in two MIMO channels. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; IEEE: Hoboken, NJ, USA, 2017; pp. 1395–1399. [Google Scholar]
- Santamaria, I.; Scharf, L.L.; Cochran, D.; Vía, J. Passive detection of rank-one signals with a multiantenna reference channel. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; IEEE: Hoboken, NJ, USA, 2016; pp. 140–144. [Google Scholar]
- Howard, S.D.; Sirianunpiboon, S. Passive radar detection using multiple transmitters. In Proceedings of the 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; IEEE: Hoboken, NJ, USA, 2013; pp. 945–948. [Google Scholar]
- Karthik, A.K.; Blum, R.S. Improved Detection Performance for Passive Radars Exploiting Known Communication Signal Form. IEEE Signal Process. Lett. 2018, 25, 1625–1629. [Google Scholar] [CrossRef]
- Liu, Y.; Blum, R.S.; Liao, G.; Zhu, S. Passive MIMO radar detection exploiting known format of the communication signal observed in colored noise with unknown covariance matrix. Signal Process. 2020, 174, 107611. [Google Scholar] [CrossRef]
- Liu, Y.; Liao, G.; Xu, J.; Yang, Z.; Yin, Y. Improving detection performance of passive MIMO radar by exploiting the preamble information of communications signal. IEEE Syst. J. 2020, 1–12. [Google Scholar] [CrossRef]
- Colone, F.; O’hagan, D.; Lombardo, P.; Baker, C. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 698–722. [Google Scholar] [CrossRef]
- Zaimbashi, A.; Derakhtian, M.; Sheikhi, A. GLRT-based CFAR detection in passive bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 134–159. [Google Scholar] [CrossRef]
- Masjedi, M.; Moddares-Hashemi, M.; Sadri, S. Theoretical approach for target detection and interference cancellation in passive radars. IET Radar Sonar Navigat. 2013, 7, 205–216. [Google Scholar] [CrossRef]
- Hack, D.E.; Patton, L.K.; Himed, B.; Saville, M.A. Detection in passive MIMO radar networks. IEEE Trans. Signal Process. 2014, 62, 2999–3012. [Google Scholar] [CrossRef]
- Hack, D.E.; Patton, L.K.; Himed, B.; Saville, M.A. Centralized passive MIMO radar detection without direct-path reference signals. IEEE Trans. Signal Process. 2014, 62, 3013–3023. [Google Scholar]
- Wang, Y.; Scharf, L.L.; Santamaría, I.; Wang, H. Canonical correlations for target detection in a passive radar network. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; IEEE: Hoboken, NJ, USA, 2016; pp. 1159–1163. [Google Scholar]
- Daun, M.; Nickel, U.; Koch, W. Tracking in multistatic passive radar systems using DAB/DVB-T illumination. Signal Process. 2012, 92, 1365–1386. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Zhong, L. Mismatched filter for analogue TV-based passive bistatic radar. IET Radar Sonar Navigat. 2011, 5, 573–581. [Google Scholar] [CrossRef]
- Sun, H.; Tan, D.K.; Lu, Y.; Lesturgie, M. Applications of passive surveillance radar system using cell phone base station illuminators. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 10–18. [Google Scholar] [CrossRef]
- Kelly, E.J. An adaptive detection algorithm. IEEE Trans. Aerosp. Electron. Syst. 1986, 2, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Cui, G.; Yi, W.; Kong, L.; Yang, J. Adaptive detection and estimation for an unknown occurring interval signal in correlated Gaussian noise. Signal Process. 2015, 108, 440–450. [Google Scholar] [CrossRef]
- He, Q.; Lehmann, N.H.; Blum, R.S.; Haimovich, A.M. MIMO radar moving target detection in homogeneous clutter. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1290–1301. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Liu, J.; Himed, B. Moving target detection in distributed MIMO radar on moving platforms. IEEE J. Sel. Top. Signal Process. 2015, 9, 1524–1535. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.; Liu, J.; Xie, W.; Chen, H.; Gu, W. Adaptive detection without training data in colocated MIMO radar. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2469–2479. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, S.; Liu, W.; Zheng, J.; Liu, H.; Li, J. Tunable Adaptive Detection in Colocated MIMO Radar. IEEE Trans. Signal Process. 2017, 66, 1080–1092. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Himed, B. A sparsity based GLRT for moving target detection in distributed MIMO radar on moving platforms. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; IEEE: Hoboken, NJ, USA, 2015; pp. 90–94. [Google Scholar]
- Dogandzic, A.; Nehorai, A. Generalized multivariate analysis of variance-A unified framework for Signal Processing in correlated noise. IEEE Signal Process. Mag. 2003, 20, 39–54. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Monticciolo, P.; Kelly, E.; Porakis, J. A noncoherent adaptive detection technique. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 115–124. [Google Scholar] [CrossRef]
- Tang, B.; Liu, J.; Huang, Z.; Wang, G.; Fan, F. Adaptive Target Detection in Gaussian Clutter Edges. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1662–1673. [Google Scholar] [CrossRef]
- Steven, M.K. Fundamentals of Statistical Signal Processing; PTR Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Wang, F.; Li, H.; Zhang, X.; Himed, B. Signal Parameter Estimation for Passive Bistatic Radar With Waveform Correlation Exploitation. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1135–1150. [Google Scholar] [CrossRef]
- Wang, F.; Wang, P.; Zhang, X.; Li, H.; Himed, B. An Overview of Parametric Modeling and Methods for Radar Target Detection With Limited Data. IEEE Access 2021, 9, 60459–60469. [Google Scholar] [CrossRef]
- Palmer, J.E.; Searle, S.J. Evaluation of adaptive filter algorithms for clutter cancellation in passive bistatic radar. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; IEEE: Hoboken, NJ, USA, 2012; pp. 0493–0498. [Google Scholar]
- Scharf, L.L.; Demeure, C. Statistical Signal Processing: Detection, Estimation, and Time Series Analysis; Addison-Wesley: Reading, MA, USA, 1991; Volume 63. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing. Detection Theory, Volume II; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Muirhead, R.J. Aspects of Multivariate Statistical Theory; John Wiley & Sons: Hoboken, NJ, USA, 1982; Volume 197. [Google Scholar]
- Harville, D.A. Matrix Algebra from a Statistician’s Perspective; Springer: Berlin/Heidelberg, Germany, 1997; Volume 1. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Tang, B.; Tang, J.; Peng, Y. MIMO radar waveform design in colored noise based on information theory. IEEE Trans. Signal Process. 2010, 58, 4684–4697. [Google Scholar] [CrossRef]
- Tang, B.; Li, J. Spectrally Constrained MIMO Radar Waveform Design Based on Mutual Information. IEEE Trans. Signal Process. 2019, 67, 115–127. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liao, G.; Li, H.; Zhu, S.; Li, Y.; Yin, Y. Passive MIMO Radar Detection with Unknown Colored Gaussian Noise. Remote Sens. 2021, 13, 2708. https://doi.org/10.3390/rs13142708
Liu Y, Liao G, Li H, Zhu S, Li Y, Yin Y. Passive MIMO Radar Detection with Unknown Colored Gaussian Noise. Remote Sensing. 2021; 13(14):2708. https://doi.org/10.3390/rs13142708
Chicago/Turabian StyleLiu, Yongjun, Guisheng Liao, Haichuan Li, Shengqi Zhu, Yachao Li, and Yingzeng Yin. 2021. "Passive MIMO Radar Detection with Unknown Colored Gaussian Noise" Remote Sensing 13, no. 14: 2708. https://doi.org/10.3390/rs13142708
APA StyleLiu, Y., Liao, G., Li, H., Zhu, S., Li, Y., & Yin, Y. (2021). Passive MIMO Radar Detection with Unknown Colored Gaussian Noise. Remote Sensing, 13(14), 2708. https://doi.org/10.3390/rs13142708