A New HASM-Based Downscaling Method for High-Resolution Precipitation Estimates
Abstract
:1. Introduction
2. Study Area and Data
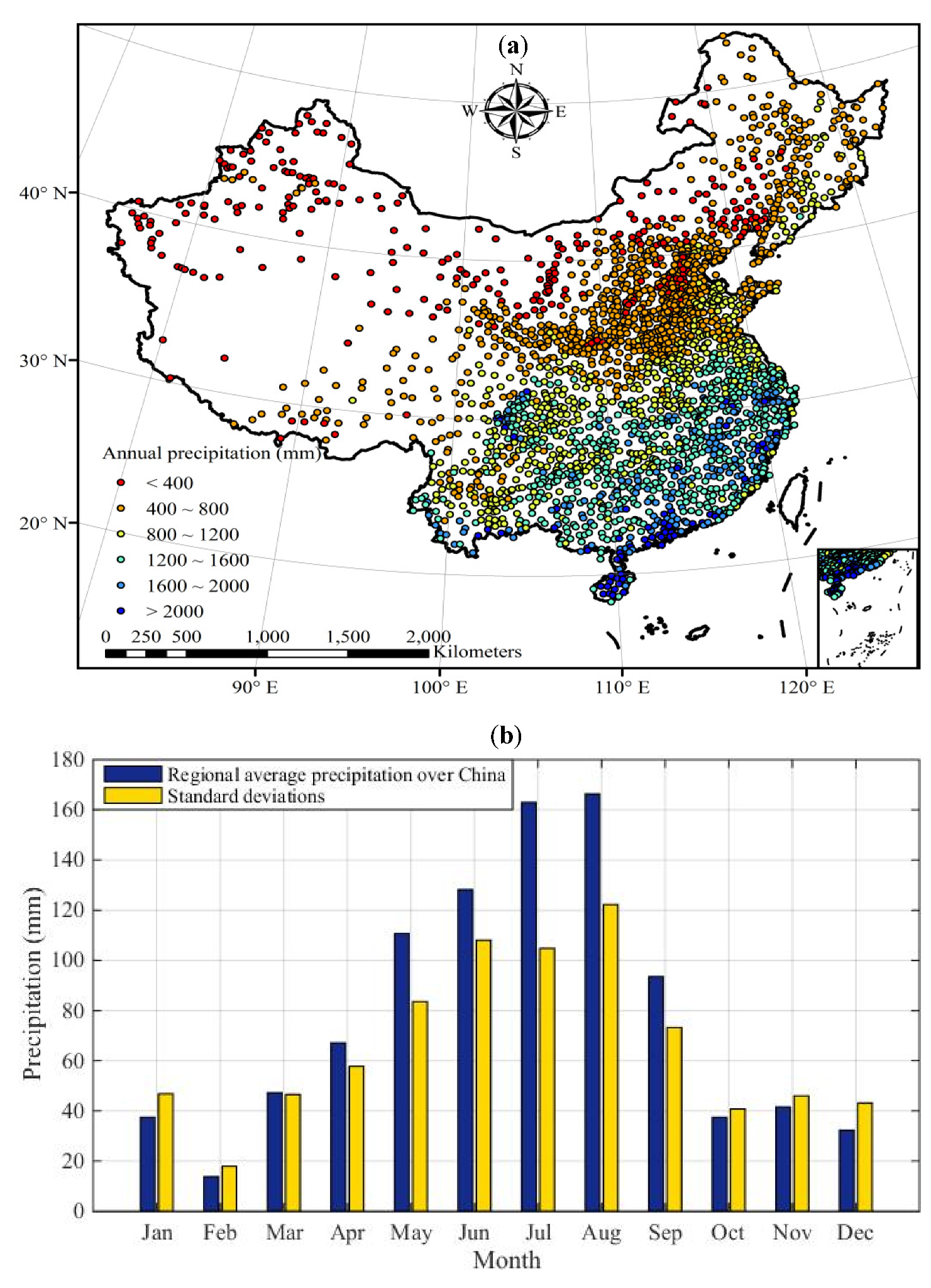
2.1. Study Area
2.2. Station Observations and Satellite Precipitation Products
3. Methods
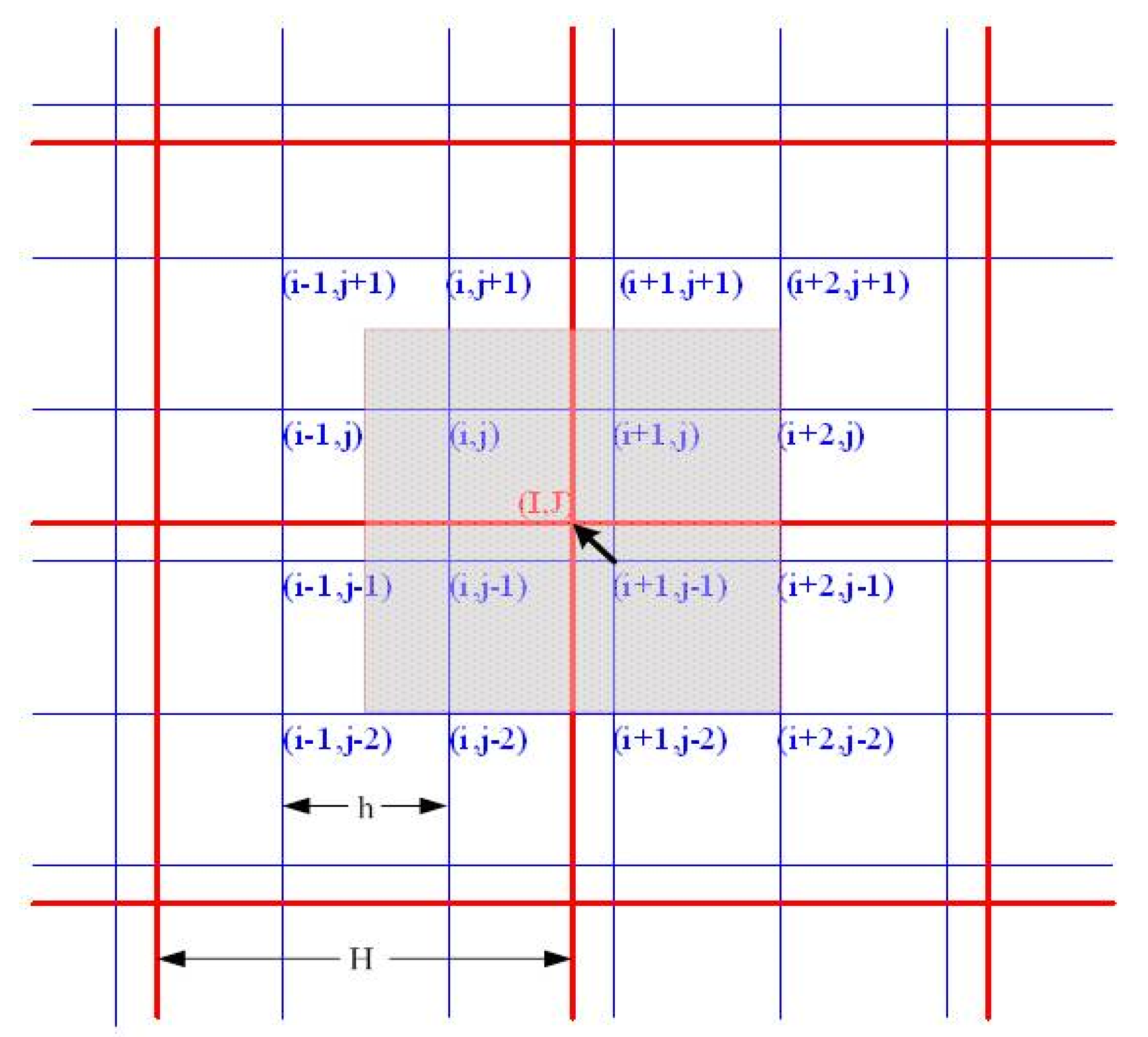
3.1. The HASM-Based Downscaling Method
| set ; ; ; |
| if the fine simulated grid cell (i,j) is located in the coarse grid (I,J), then |
| ; |
| ; |
| end |
3.2. Calibration and Validation
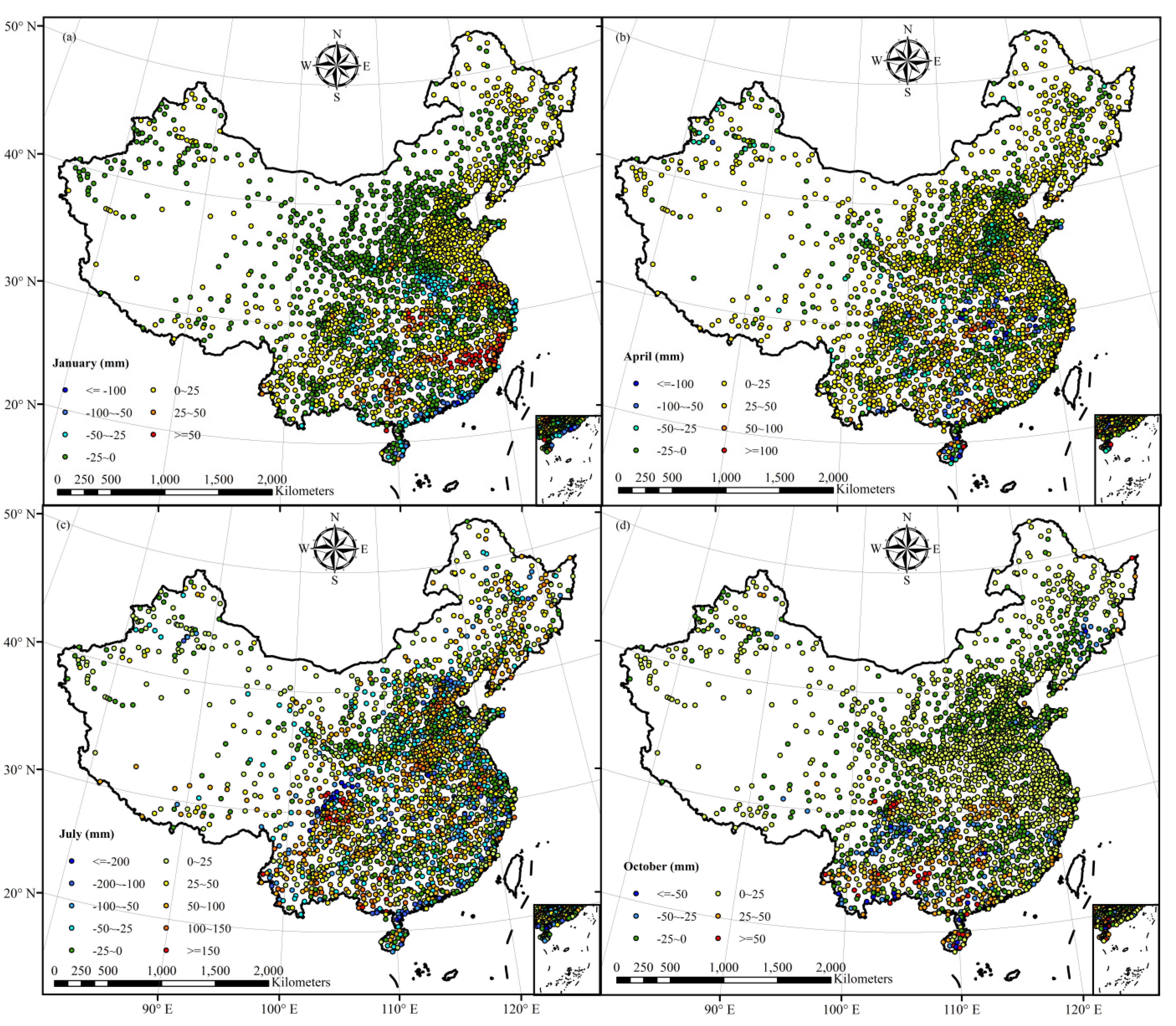
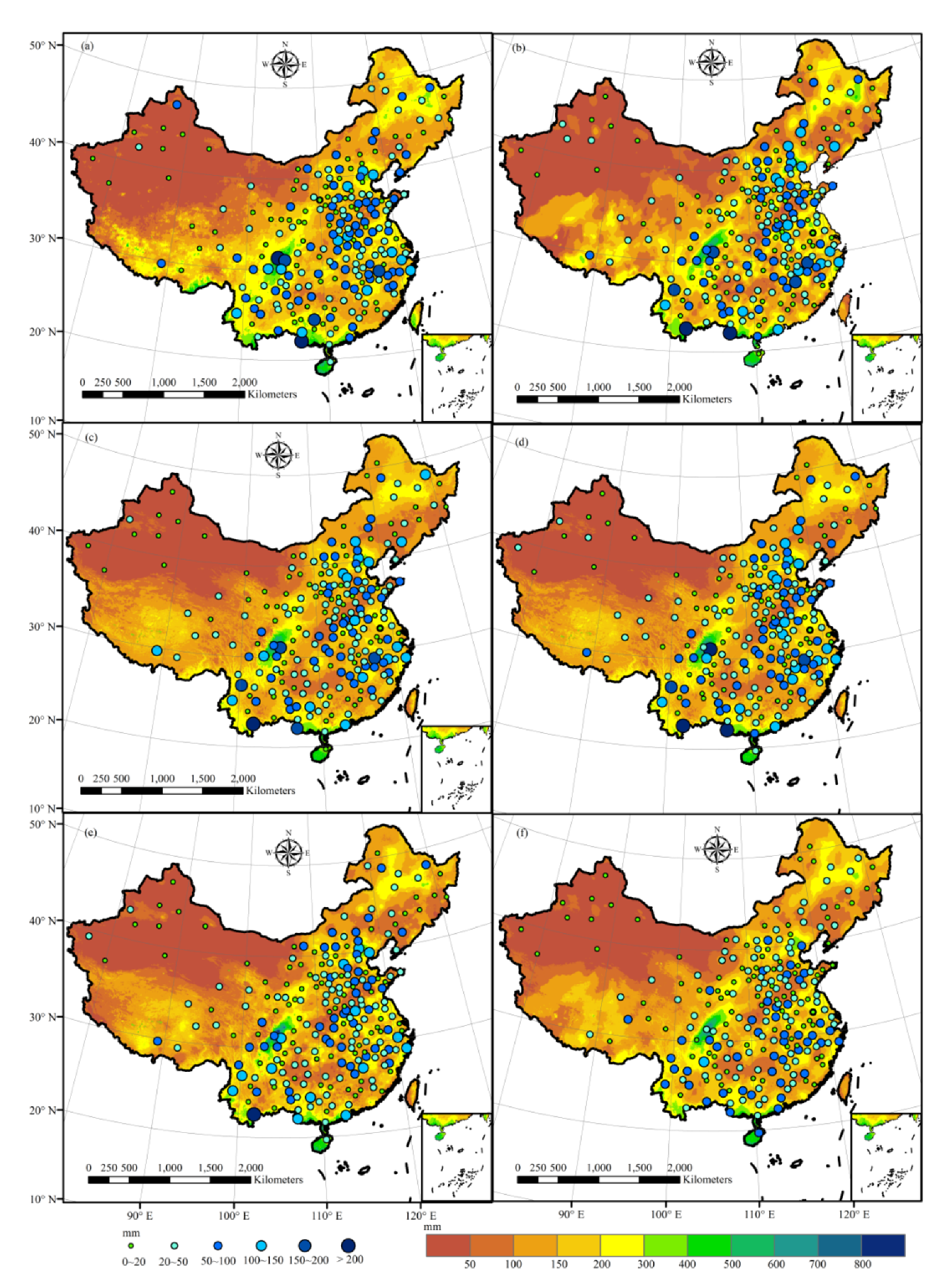
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donohoe, A. Atmospheric science: Energy and precipitation. Nat. Geosci. 2016, 9, 861. [Google Scholar] [CrossRef]
- Tuel, A.; Eltahir, E.A.B. Seasonal precipitation forecast over Morocco. Water Resour. Res. 2018, 54, 9118–9130. [Google Scholar] [CrossRef]
- Casellas, E.; Bech, J.; Veciana, R.; Pineda, N.; Rigo, T.; Miro, J.R.; Sairouni, A. Surface precipitation phase discrimination in complex terrain. J. Hydrol. 2021, 592, 125780. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The global precipitation measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale comparative evaluation of the GPM IMERG v5 and TRMM 3B42 v7 precipitation products from 2015 to 2017 over a climate transition area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Clark, M.P.; Papalexiou, S.M.; Ma, Z.; Hong, Y. Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets. Remote Sens. Environ. 2020, 240, 111697. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Tokay, A. A novel approach to identify sources of errors in IMERG for GPM ground validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Mohammed, S.A.; Hamouda, M.A.; Mohamed, M.M. Impact of topography and rainfall intensity on the accuracy of IMERG precipitation estimates in an arid region. Remote Sens. 2020, 13, 13. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline interpolation techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Yue, T.; Chen, C.; Zhao, M.; Fan, Z. An improved statistical downscaling scheme of tropical rainfall measuring mission precipitation in the Heihe River basin, China. Int. J. Climatol. 2018, 38, 3309–3322. [Google Scholar] [CrossRef]
- Chaudhuri, C.; Robertson, C. CliGAN: A structurally sensitive convolutional neural network model for statistical downscaling of precipitation from multi-model ensembles. Water 2020, 12, 3353. [Google Scholar] [CrossRef]
- Lu, X.Y.; Tang, G.Q.; Wang, X.Q.; Liu, Y.; Wei, M.; Zhang, Y.X. The development of a two-step merging and downscaling method for satellite precipitation products. Remote Sens. 2020, 12, 398. [Google Scholar] [CrossRef] [Green Version]
- Sachindra, D.A.; Perera, B.J. Statistical downscaling of general circulation model outputs to precipitation accounting for non-stationarities in predictor-predictand relationships. PLoS ONE 2016, 11, e0168701. [Google Scholar]
- Xu, M.; Liu, Q.; Sha, D.; Yu, M.; Duffy, D.Q.; Putman, W.M.; Carroll, M.; Lee, T.; Yang, C. PreciPatch: A dictionary-based precipitation downscaling method. Remote Sens. 2020, 12, 1030. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A comparison of different regression algorithms for downscaling monthly satellite-based precipitation over North China. Remote Sens. 2016, 8, 835. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, C.; Srivastava, R. A novel approach for statistical downscaling of future precipitation over the Indo-Gangetic Basin. J. Hydrol. 2017, 547, 21–38. [Google Scholar] [CrossRef]
- Shamir, E.; Halper, E.; Modrick, T.; Georgakakos, K.P.; Chang, H.-I.; Lahmers, T.M.; Castro, C. Statistical and dynamical downscaling impact on projected hydrologic assessment in arid environment: A case study from Bill Williams River basin and Alamo Lake, Arizona. J. Hydrol. 2019, 2, 100019. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Ahmed, K.; Rashid, M.M.; Shahid, S.; Perera, B.J.C. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A spatial downscaling algorithm for satellite-based precipitation over the Tibetan Plateau based on NDVI, DEM, and land surface temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef] [Green Version]
- Seyoum, W.; Kwon, D.; Milewski, A. Downscaling GRACE TWSA data into high-resolution groundwater level anomaly using machine learning-based models in a glacial aquifer System. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef] [Green Version]
- Baez-Villanueva, O.M.; Zambrano-Bigiarini, M.; Beck, H.E.; McNamara, I.; Ribbe, L.; Nauditt, A.; Birkel, C.; Verbist, K.; Giraldo-Osorio, J.D.; Xuan Thinh, N. RF-MEP: A novel random forest method for merging gridded precipitation products and ground-based measurements. Remote Sens. Environ. 2020, 239, 111606. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J. Deep learning in environmental remote sensing: Achievements and challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, Z.; Montzka, C.; Chai, L.; Liu, S.; Ge, Y.; Liu, J.; Lu, Z.; He, X.; Zheng, J. Inter-comparison of several soil moisture downscaling methods over the Qinghai-Tibet Plateau, China. J. Hydrol. 2021, 592, 125616. [Google Scholar] [CrossRef]
- Stott, J.P. Review of Surface Modeling. In Proceedings of the Surface Modeling by Computer, a Conference Jointly Sponsored by the Royal Institution of Chartered Surveyors and the Institition of Civil Engineers, London, UK, 6 October 1976; pp. 1–8. [Google Scholar]
- Yue, T.X. Surface Modeling: High Accuracy and High Speed Methods; CRC Press: New York, NY, USA, 2011. [Google Scholar]
- Hestenes, M.R.; Stiefel, E.F. Methods of conjugate gradients for solving linear systems. J. Res. Nat. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Thompson, J.F.; Thames, F.C.; Mastin, C.W. Automatic numerical generation of body-fitted curvilinear coordinate system for field containing any number of arbitrary two-dimensional bodies. J. Comput. Phys. 1974, 15, 299–319. [Google Scholar] [CrossRef]
- Chen, C.F.; Yue, T.X. A method of DEM construction and related error analysis. Comput. Geosci. 2010, 36, 717–725. [Google Scholar] [CrossRef]
- Chen, C.F.; Yue, T.X.; Dai, H.; Tian, M.Y. The smoothness of HASM. Int. J. Geogr. Inf. Sci. 2013, 27, 1651–1667. [Google Scholar] [CrossRef]
- Shi, W.J.; Yue, T.X.; Du, Z.P.; Wang, Z.; Li, X.W. Surface modeling of soil antibiotics. Sci. Total Environ. 2016, 543, 609–619. [Google Scholar] [CrossRef]
- Shi, W.; Liu, J.; Du, Z.; Song, Y.; Chen, C.; Yue, T. Surface modelling of soil pH. Geoderma 2009, 150, 113–119. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.X. A modification of HASM for interpolating precipitation in China. Theor. Appl. Climatol. 2013, 116, 273–285. [Google Scholar] [CrossRef]
- Zhao, N.; Lu, N.; Chen, C.F.; Li, H.; Yue, T.X.; Zhang, L.L.; Liu, Y. Mapping temperature using a Bayesian statistical method and a high accuracy surface modelling method in the Beijing-Tianjin-Hebei region, China. Meteorol. Appl. 2017, 24, 571–579. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Yue, T.X.; Zhou, X.; Zhao, M.W.; Liu, Y.; Du, Z.P.; Zhang, L.L. Statistical downscaling of precipitation using local regression and high accuracy surface modeling method. Theor. Appl. Climatol. 2016, 129, 281–292. [Google Scholar] [CrossRef]
- Yue, T.X.; Zhao, N.; Fan, Z.M.; Li, J.; Chen, C.F.; Lu, Y.M.; Wang, C.L.; Gao, J.; Xu, B.; Jiao, Y.M.; et al. Methods for simulating climate scenarios with improved spatiotemporal specificity and less uncertainty. Glob. Planet. Chang. 2019, 181, 102973. [Google Scholar] [CrossRef]
- Wang, X.L.; Wen, Q.H.; Wu, Y. Penalized maximal t test for detecting undocumented mean change in climate data series. J. Appl. Meteorol. Climatol. 2007, 46, 916–931. [Google Scholar] [CrossRef]
- Huffman, G.J.; Kirschbaum, D.B.; Adler, R.F.; Braun, S.; Garrett, K.; Jones, E.; McNally, A.; Skofronick-Jackson, G.; Stocker, E.; Wu, H.; et al. NASA’s remotely sensed precipitation: A reservoir for applications users. Bull. Am. Meteorol. Soc. 2017, 98, 1169–1184. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Tan, J. Integrated multi-satellitE retrievals for GPM (IMERG) technical documentation. NASA GSFC Code 2019, 612, 1–25. [Google Scholar]
- Somasundaram, D. Differential Geometry; Alpha Science International Ltd.: Harrow, UK, 2005. [Google Scholar]
- Henderson, D.W. Differential Geometry; Prentice-Hall Inc.: London, UK, 1998. [Google Scholar]
- Liseikin, V.D. A Computational Differential Geometry Approach to Grid Generation; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Toponogov, V.A. Differential Geometry of Curves and Surfaces; Birkhaeuser Boston: New York, NY, USA, 2006. [Google Scholar]
- Golub, H.H.; O’Leary, D.P. Some history of the conjugate gradient and Lanczos algorithms: 1948–1976. SIAM Rev. 1989, 31, 50–102. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. Efficient and reliable iterative methods for linear systems. J. Comput. Appl. Math. 2002, 149, 251–265. [Google Scholar] [CrossRef] [Green Version]
- Paige, C.C.; Saunders, M.A. LSQR: An algorithm for sparse linear euqations and sparse least squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Ford, W. Krylov subspace methods. Numer. Linear Algebr. 2015, 491–532. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Derin, Y. Evaluation of multiple satellite-based precipitation products over complex topography. J. Hydrometeorol. 2014, 15, 1498–1516. [Google Scholar]
- Zhang, T.; Li, B.; Yuan, Y.; Gao, X.; Sun, Q.; Xu, L.; Jiang, Y. Spatial downscaling of TRMM precipitation data considering the impacts of macro-geographical factors and local elevation in the Three-River Headwaters region. Remote Sens. Environ. 2018, 215, 109–127. [Google Scholar] [CrossRef]
- Hunink, J.E.; Immerzeel, W.W.; Droogers, P. A high-resolution precipitation 2-step mapping procedure (HiP2P): Development and application to a tropical mountainous area. Remote Sens. Environ. 2014, 140, 179–188. [Google Scholar] [CrossRef]
- Manz, B.; Buytaert, W.; Zulkafli, Z.; Lavado, W.; Willems, B.; Robles, L.A.; Rodríguez-Sánchez, J.P. High-resolution satellite-gauge merged precipitation climatologies of the Tropical Andes. J. Geophys. Res. Atmos. 2016, 121, 1190–1207. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhang, W.; Nie, N. Spatial downscaling of TRMM precipitation data using an optimal subset regression model with NDVI and terrain factors in the Yarlung Zangbo River basin, China. Adv. Meteorol. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Elnashar, A.; Zeng, H.; Wu, B.; Zhang, N.; Tian, F.; Zhang, M.; Zhu, W.; Yan, N.; Chen, Z.; Sun, Z.; et al. Downscaling TRMM monthly precipitation using Google Earth Engine and Google Cloud computing. Remote Sens. 2020, 12, 3860. [Google Scholar] [CrossRef]
- Stauffer, R.; Mayr, G.J.; Messner, J.W.; Umlauf, N.; Zeileis, A. Spatio-temporal precpitation climatology over complex terrain using a censored additive regression model. Int. J. Climatol. 2016, 37, 3264–3275. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, Q.J.; He, H.; Wu, Z.Y.; Lu, G.H. A method to extend temporal coverage of high quality precipitation datasets by calibrating reanalysis estimates. J. Hydrol. 2020, 581, 124355. [Google Scholar] [CrossRef]
- Dezfuli, A.K.; Ichoku, C.M.; Huffman, G.J.; Mohr, K.I.; Selker, J.S.; van de Giesen, N.; Hochreutener, R.; Annor, F.O. Validation of IMERG precipitation in Africa. J. Hydrometeorol. 2017, 18, 2817–2825. [Google Scholar] [CrossRef]
- Wang, S.M.; Wang, D.K.; Huang, C. Evaluating the applicability of GPM satellite precipitation data in Heihe River Basin. J. Nat. Res. 2018, 33, 1847–1860. [Google Scholar]





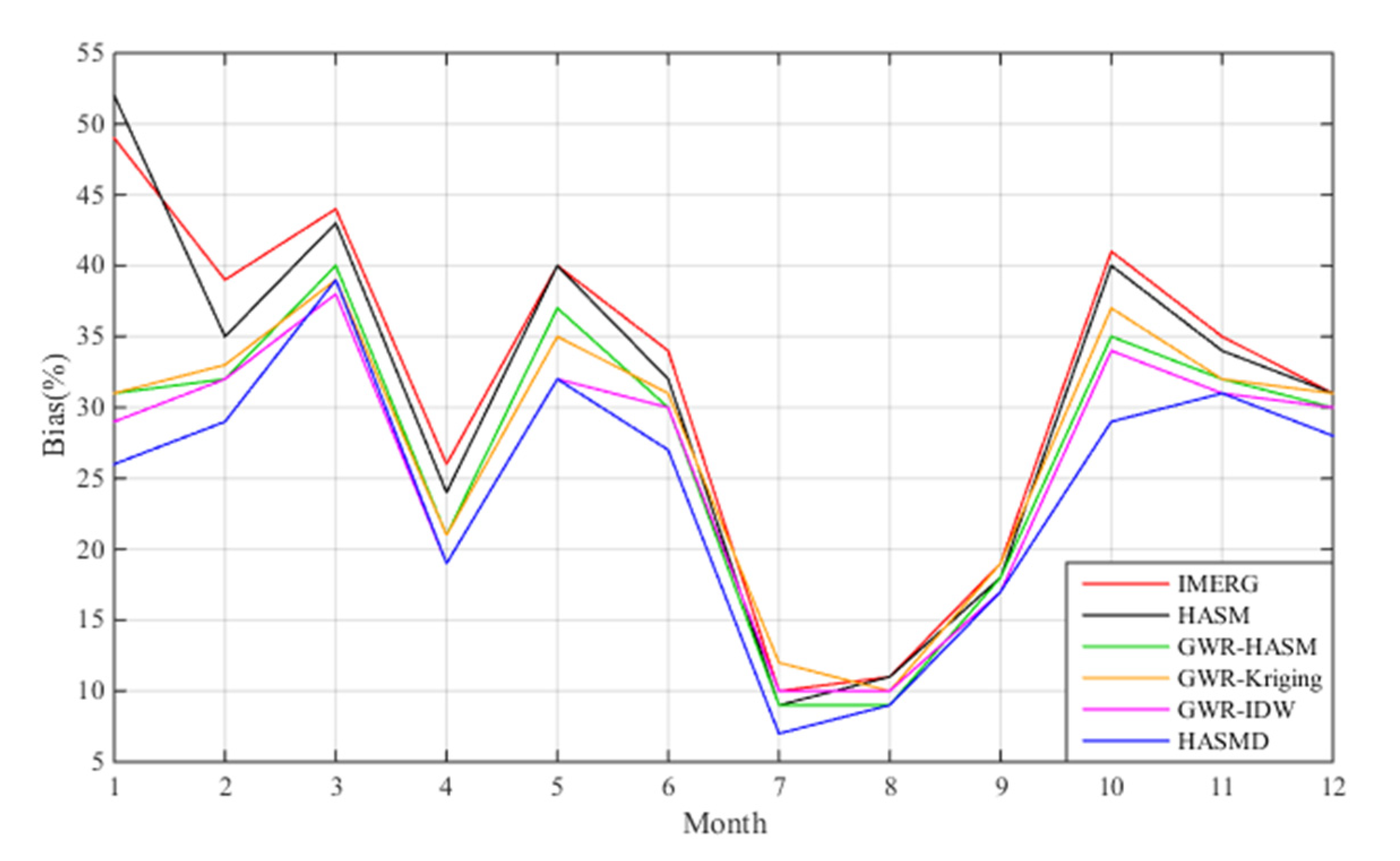
| Months | January | April | July | October | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Errors | Bias (%) | RMSE (mm) | R2 | Bias (%) | RMSE (mm) | R2 | Bias (%) | RMSE (mm) | R2 | Bias (%) | RMSE (mm) | R2 |
| IMERG | 49 | 18.01 | 0.87 | 26 | 30.17 | 0.78 | 10 | 56.81 | 0.66 | 41 | 18.64 | 0.82 |
| HASM | 52 | 11.71 | 0.94 | 24 | 29.86 | 0.78 | 9 | 56.89 | 0.62 | 40 | 18.72 | 0.83 |
| GWR-HASM | 31 | 11.53 | 0.94 | 21 | 27.59 | 0.82 | 9 | 48.84 | 0.73 | 35 | 16.45 | 0.83 |
| GWR-Kriging | 31 | 11.65 | 0.94 | 21 | 27.54 | 0.82 | 12 | 57.22 | 0.63 | 37 | 18.02 | 0.82 |
| GWR-IDW | 29 | 11.04 | 0.95 | 19 | 26.01 | 0.83 | 10 | 49.94 | 0.72 | 34 | 16.46 | 0.85 |
| HASMD | 26 | 9.53 | 0.96 | 19 | 25.01 | 0.88 | 7 | 47.03 | 0.75 | 29 | 14.04 | 0.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, N.; Jiao, Y. A New HASM-Based Downscaling Method for High-Resolution Precipitation Estimates. Remote Sens. 2021, 13, 2693. https://doi.org/10.3390/rs13142693
Zhao N, Jiao Y. A New HASM-Based Downscaling Method for High-Resolution Precipitation Estimates. Remote Sensing. 2021; 13(14):2693. https://doi.org/10.3390/rs13142693
Chicago/Turabian StyleZhao, Na, and Yimeng Jiao. 2021. "A New HASM-Based Downscaling Method for High-Resolution Precipitation Estimates" Remote Sensing 13, no. 14: 2693. https://doi.org/10.3390/rs13142693
APA StyleZhao, N., & Jiao, Y. (2021). A New HASM-Based Downscaling Method for High-Resolution Precipitation Estimates. Remote Sensing, 13(14), 2693. https://doi.org/10.3390/rs13142693







