Direction-of-Arrival Estimation over Sea Surface from Radar Scattering Based on Convolutional Neural Network
Abstract
:1. Introduction
2. Sea Surface Scattering Datasets Generated by AIEM
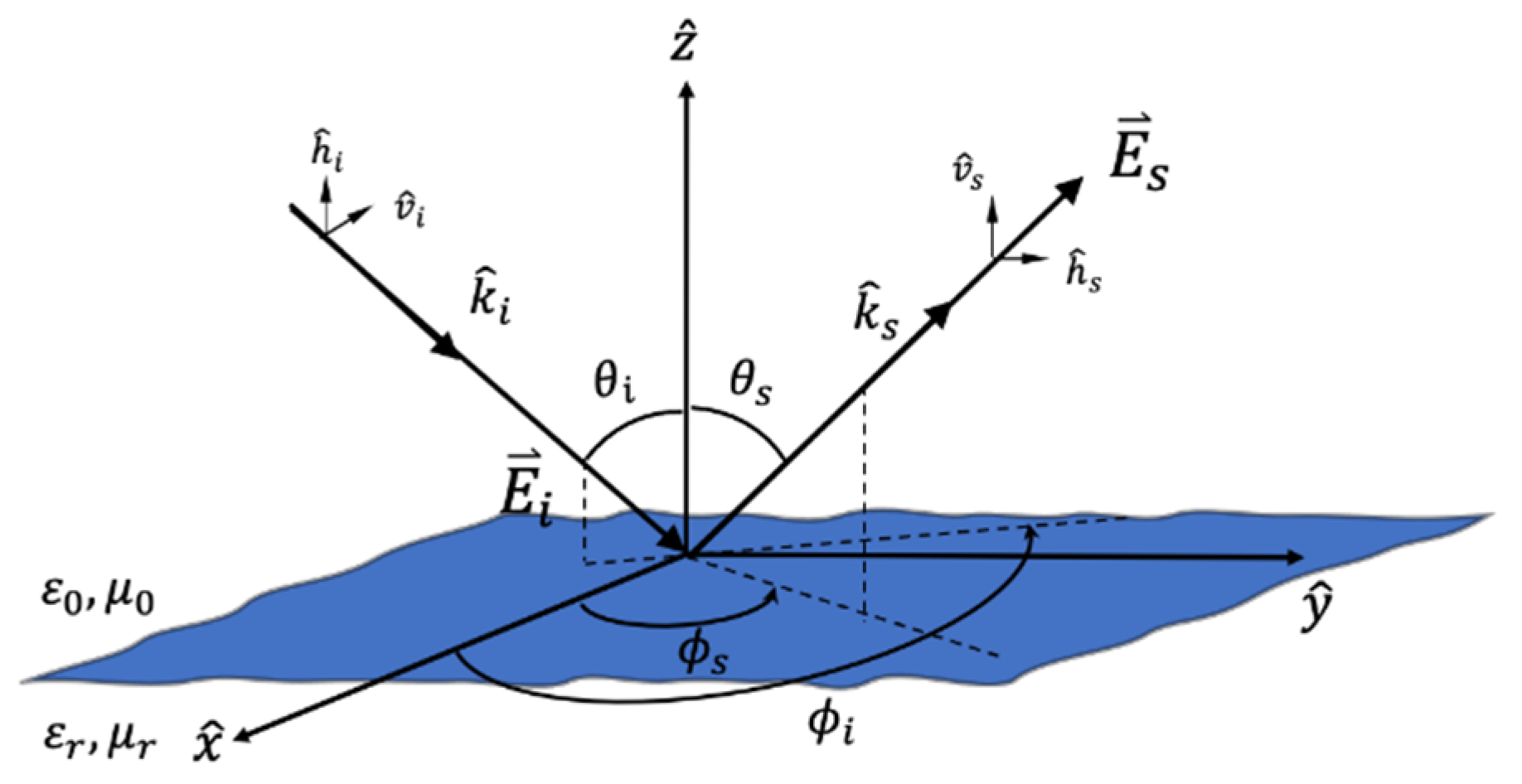
2.1. Bistatic Scattering Model
2.2. Sensitivity of Received Signals to Incidence Location
3. Direction-of-Arrival Estimation
3.1. Problem Formulation
3.2. Data Input-Output and Preprocessing
| Algorithm 1 Generation of Training Data by the AIEM Model |
| For = to step |
| For = to step |
| For = to step |
| \\Define a matrix input |
| input = [] |
| \\Define a vector output |
| output = [] |
| For = to step |
| For = to step |
| [, , , ] = AIEM (, , , , ) |
| \\, , , are generated by function AIEM |
| input = [input; , , , , , ] |
| End |
| End |
| Save generated input |
| output = [, ] |
| Save generated output |
| End |
| End |
| End |
3.3. CNN Configurations for DOA Estimation
4. Results
4.1. Comparison of CNN Configurations
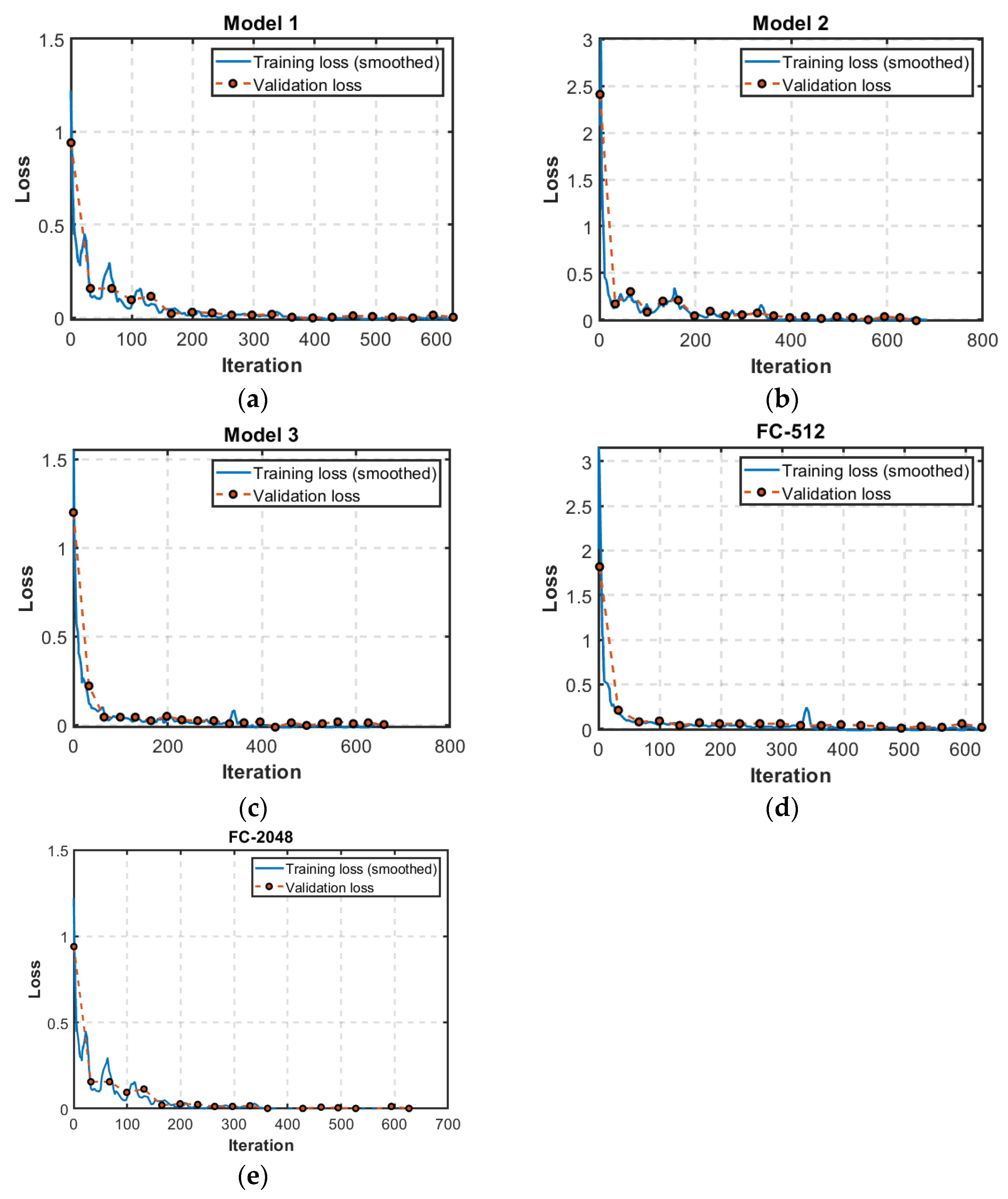
4.1.1. Training
4.1.2. Testing
4.2. DOA Estimation Based on CNN
4.2.1. Model Training
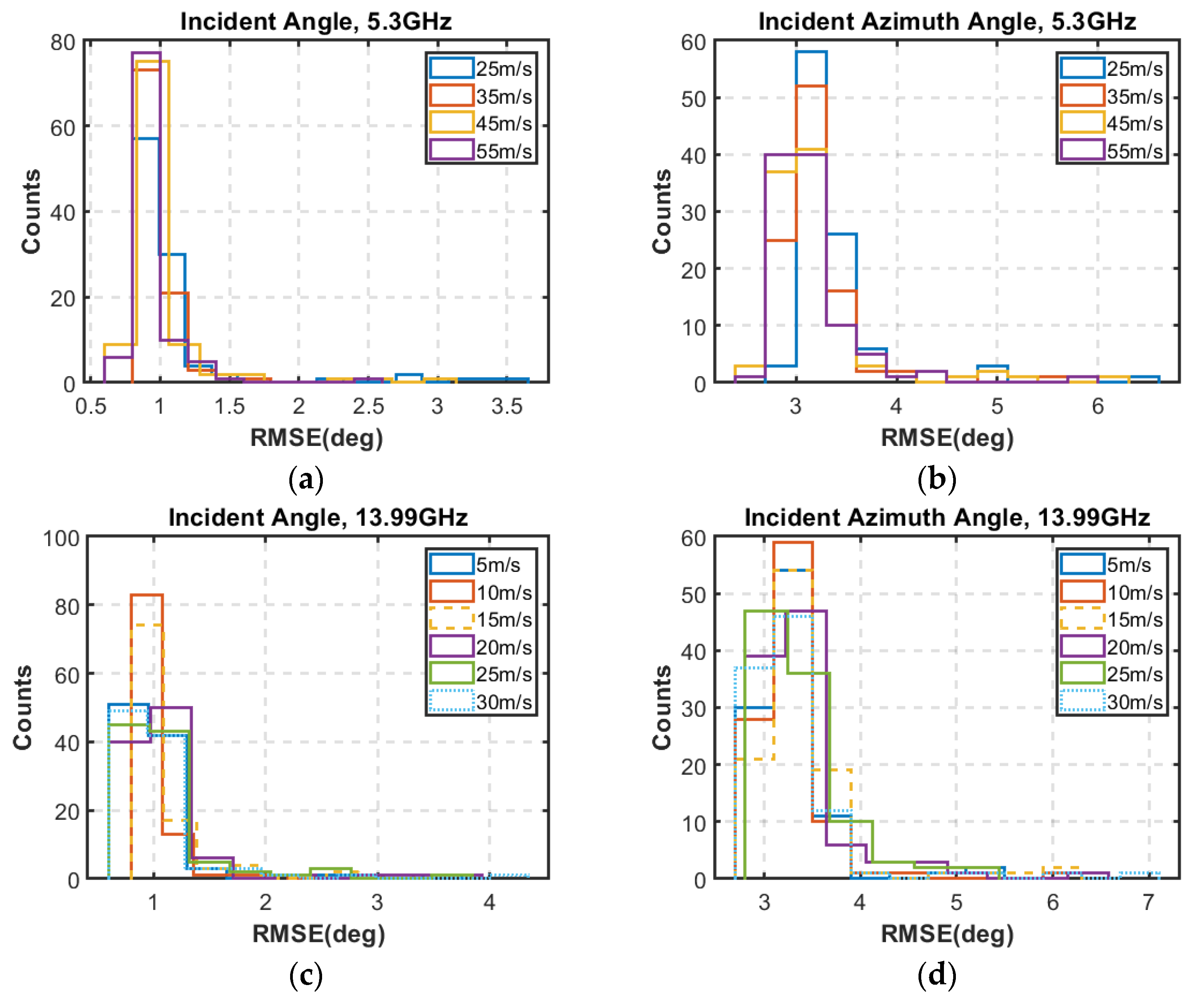
4.2.2. DOA Estimation Result
4.2.3. Validation
5. Discussion
5.1. Results Interpretation
5.2. Comparison with Other Algorithms
5.3. Limitation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bartlett, M.S. Smoothing Periodograms from Time-Series with Continuous Spectra. Nature 1948, 161, 686–687. [Google Scholar] [CrossRef]
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. In Proceedings of the IEEE; IEEE: New York, NY, USA, 1969; pp. 1408–1418. [Google Scholar]
- Lacoss, R.T. Data Adaptive Spectral Analysis Methods. Geophysics 1971, 36, 661–675. [Google Scholar] [CrossRef]
- Schmidt, R.O. A Signal Subspace Approach to Multiple Emitter Location and Spectral Estimation. Ph.D. Thesis, Stanford University, Ann Arbor, MI, USA, 1982. [Google Scholar]
- Kumaresan, R.; Tufts, D.W. Estimating the Angles of Arrival of Multiple Plane Waves. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 134–139. [Google Scholar]
- Reddi, S.S. Multiple Source Location-A Digital Approach. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 95–105. [Google Scholar] [CrossRef]
- Barabell, A. Improving the Resolution Performance of Eigenstructure-based Direction-Finding Algorithms. In Proceedings of the ICASSP ’83-IEEE International Conference on Acoustics, Speech, and Signal Processing, Boston, MA, USA, 14–16 April 1983; pp. 336–339. [Google Scholar]
- DeGroat, R.D.; Dowling, E.M.; Linebarger, D.A. The Constrained MUSIC Problem. IEEE Trans. Signal Process. 1993, 41, 1445–1449. [Google Scholar] [CrossRef]
- Jha, S.; Durrani, T. Direction of Arrival Estimation Using Artificial Neural Networks. IEEE Trans. Syst. Man Cybern. Syst. 1991, 21, 1192–1201. [Google Scholar] [CrossRef]
- Southall, H.L.; Simmers, J.A.; Donnell, T.H.O. Direction Finding in Phased Arrays with a Neural Network Beamformer. IEEE Trans. Antennas Propag. 1995, 43, 1369–1374. [Google Scholar] [CrossRef]
- Rawat, A.; Yadav, R.N.; Shrivastava, S.C. Neural Network Applications in Smart Antenna Arrays: A Review. Int. J. Electron. Commun. 2012, 66, 903–912. [Google Scholar] [CrossRef]
- Terabayashi, K.; Natsuaki, R.; Hirose, A. Ultrawideband Direction-of-Arrival Estimation Using Complex-Valued Spatiotemporal Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1727–1732. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, C.; Yu, P.S. Direction-of-Arrival Estimation Based on Deep Neural Networks With Robustness to Array Imperfections. IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- Zooghby, A.H.E.; Christodoulou, C.G.; Georgiopoulos, M.A. Neural Network-based Smart Antenna for Multiple Source Tracking. IEEE Trans. Antennas Propag. 2000, 48, 768–776. [Google Scholar] [CrossRef]
- Valaee, S.; Champagne, B.; Kabal, P. Parametric Localization of Distributed Sources. IEEE Trans. Signal Process. 1995, 43, 2144–2153. [Google Scholar] [CrossRef]
- Lee, Y.U.; Lee, S.R.; Kim, H.M.; Song, I. Estimation of Direction of Arrival for Angle-Perturbed Sources. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 1997, E80A, 109–117. [Google Scholar]
- Astely, D.; Ottersten, B. The Effects of Local Scattering on Direction of Arrival Estimation with MUSIC. IEEE Trans. Signal Process. 1999, 47, 3220–3234. [Google Scholar] [CrossRef] [Green Version]
- Stoica, P.; Sharman, K.C. Maximum Likelihood Methods for Direction-of-Arrival Estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1132–1143. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, Maximum Likelihood and Cramer-Rao Bound. In Proceedings of the ICASSP ’88-International Conference on Acoustics, Speech, and Signal Processing, New York, NY, USA, 11–14 April 1988; Volume 4, pp. 2296–2299. [Google Scholar]
- Stoica, P.; Nehorai, A. Performance Study of Conditional and Unconditional Direction-of-Arrival Estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Tsakalides, P.; Nikias, C.L. Maximum Likelihood Localization of Sources in Noise Modeled as a Stable Process. IEEE Trans. Signal Process. 1995, 43, 2700–2713. [Google Scholar] [CrossRef]
- Ottersten, B.; Viberg, M.; Stoica, P.; Nehorai, A. Exact and Large Sample Maximum Likelihood Techniques for Parameter Estimation and Detection in Array Processing. In Radar Array Processing; Springer: Berlin/Heidelberg, Germany, 1993; pp. 99–151. [Google Scholar]
- Shan, T.J.; Wax, M.; Kailath, T. On Spatial Smoothing for Direction-of-Arrival Estimation of Coherent Signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Cai, B.; Li, Y.M.; Wang, H.Y. Forward/Backward Spatial Reconstruction Method for Directions of Arrival Estimation of Uncorrelated and Coherent Signals. IET Microw. Antennas Propag. 2012, 6, 1498–1505. [Google Scholar] [CrossRef]
- Dudczyk, J.; Kawalec, A. Adaptive Forming of the Beam Pattern of Microstrip Antenna with the Use of an Artificial Neural Network. Int. J. Antennas Propag. 2012, 2012. [Google Scholar] [CrossRef]
- Gierull, C.H. Ground Moving Target Parameter Estimation for Two-Channel SAR. IEEE Proc.-Radar Sonar Navig. 2006, 153, 224–233. [Google Scholar] [CrossRef]
- Gierull, C.H. Azimuth Positioning of Moving Targets in Two-Channel SAR by Direction-of-Arrival Estimation. Electron. Lett. 2004, 40, 1380–1381. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a Randomly Rough Dielectric Surface. IEEE Trans. Geosci. Remote. Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of Rough Surfaces Calculated by the Integral Equation Method with Comparison to Three-Dimensional Moment Method Simulations. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Chen, K.S. Radar Scattering and Imaging of Rough Surfaces: Modeling and Applications with MATLAB@; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Chen, K.S.; Fung, A.K.; Weissman, D.A. A Backscattering Model for Ocean Surface. IEEE Trans. Geosci. Remote. Sens. 1992, 30, 811–817. [Google Scholar] [CrossRef]
- Xu, F.; Li, X.; Wang, P.; Yang, J.; Pichel, W.G.; Jin, Y. A Backscattering Model of Rainfall Over Rough Sea Surface for Synthetic Aperture Radar. IEEE Trans. Geosci. Remote. Sens. 2015, 53, 3042–3054. [Google Scholar] [CrossRef]
- Xie, D.F.; Chen, K.S.; Zeng, J.F. The frequency selective effect of radar backscattering from multiscale sea surface. Remote. Sens. 2019, 11, 160. [Google Scholar] [CrossRef] [Green Version]
- Xie, D.F.; Chen, K.S.; Yang, X.F. Effects of Wind Wave Spectra on Radar Backscatter from Sea Surface at Different Microwave Bands: A Numerical Study. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 6325–6334. [Google Scholar] [CrossRef]
- Fung, A.K.; Chen, K.S. Microwave Scattering and Emission Models for Users; Artech House: Boston, MA, USA, 2010. [Google Scholar]
- Ulaby, F. Microwave Radar and Radiometric Remote Sensing; The University of Michigan Press: Chicago, IL, USA; Ann Arbor, MI, USA, 2014. [Google Scholar]
- Fung, A.K. Backscattering from Multiscale Rough Surfaces with Application to Wind Scatterometry; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Migliaccio, M.; Huang, L.; Buono, A. SAR Speckle Dependence on Ocean Surface Wind Field. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 5447–5455. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Liang, S.; Srikant, R. Why Deep Neural Networks for Function Approximation? In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017.
- Stoffelen, A.; Verspeek, J.A.; Vogelzang, J.; Verhoef, A. The CMOD7 Geophysical Model Function for ASCAT and ERS Wind Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Li, X.M.; Lehner, S. Algorithm for Sea Surface Wind Retrieval From TerraSAR-X and TanDEM-X Data. IEEE Trans. Geosci. Remote. Sens. 2014, 52, 2928–2939. [Google Scholar] [CrossRef] [Green Version]
- Royal Netherlands Meteorological Institute. NSCAT-4 Geophysical Model Function. Available online: http://knmi.nl/scatterometer/nscat_gmf (accessed on 1 May 2016).
- Schroeder, L.; Schaffner, P.; Mitchell, J.; Jones, W. AAFE RADSCAT 13.9-GHz Measurements and Analysis: Wind-Speed Signature of the Ocean. IEEE J. Ocean. Eng. 1985, 10, 346–357. [Google Scholar] [CrossRef]
- Pastorino, M.; Randazzo, A. A Smart Antenna System for Direction of Arrival Estimation Based on a Support Vector Regression. IEEE Trans. Antennas Propag. 2005, 53, 2161–2168. [Google Scholar] [CrossRef]
- Wen, C.; Shi, G.M.; Xie, X.M. Estimation of directions of arrival of multiple distributed sources for nested array. Signal Process. 2017, 130, 315–322. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, G.J.; Teng, Y.L. Simplified Estimation of 2D DOA for Coherently Distributed Sources. Wirel. Pers. Commun. 2012, 62, 907–922. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, W.Q.; Meng, H.P.; So, H.C.; Zhang, H.B. Efficient Beamspace-Based Algorithm for Two-Dimensional DOA Estimation of Incoherently Distributed Sources in Massive MIMO Systems. IEEE Trans. Veh. Technol. 2018, 67, 11776–11789. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, K.S.; Shang, G.F. Surface Parameters Retrieval from Fully Bistatic Radar Scattering Data. Remote. Sens. 2019, 11, 596. [Google Scholar] [CrossRef] [Green Version]
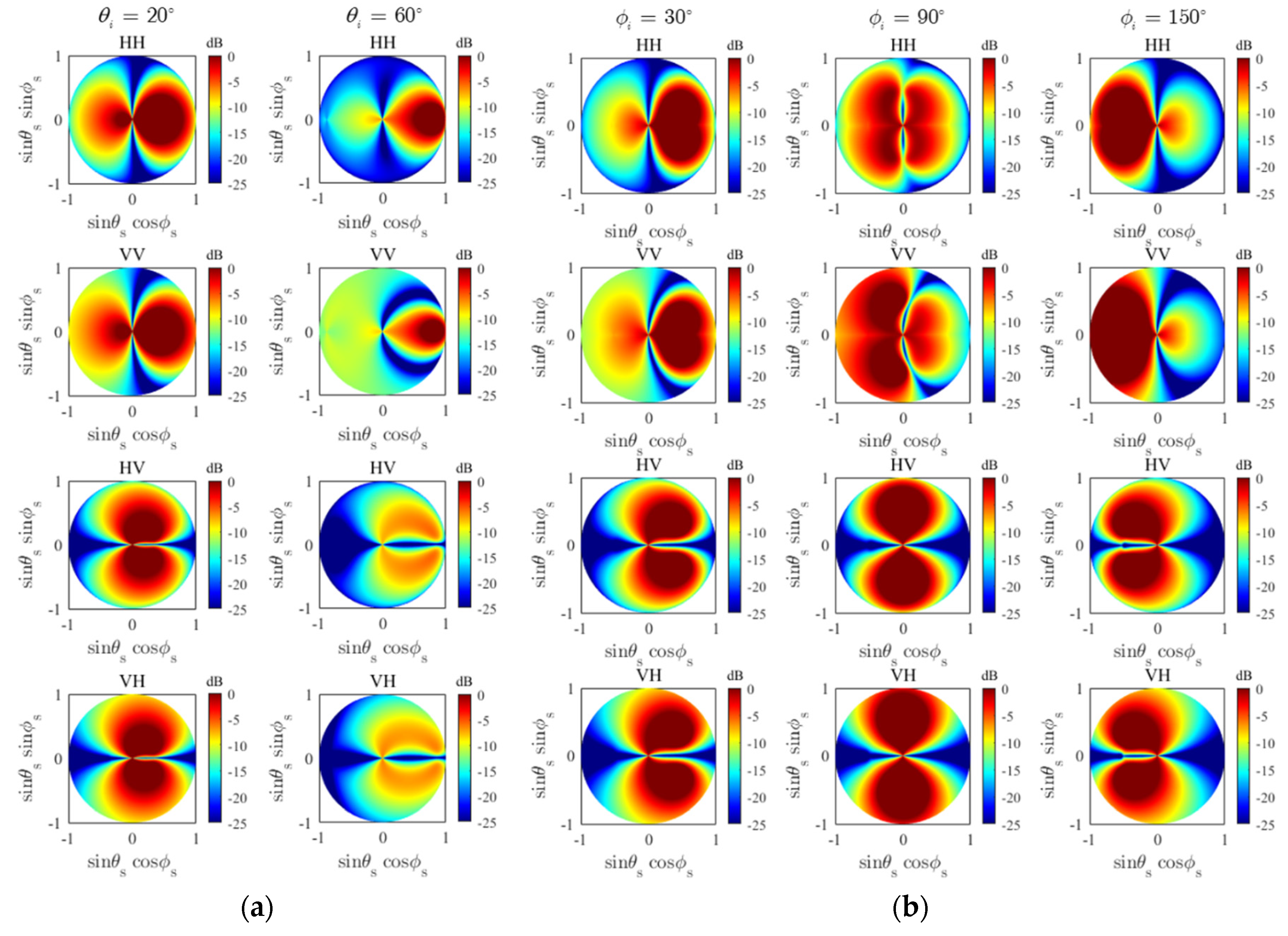
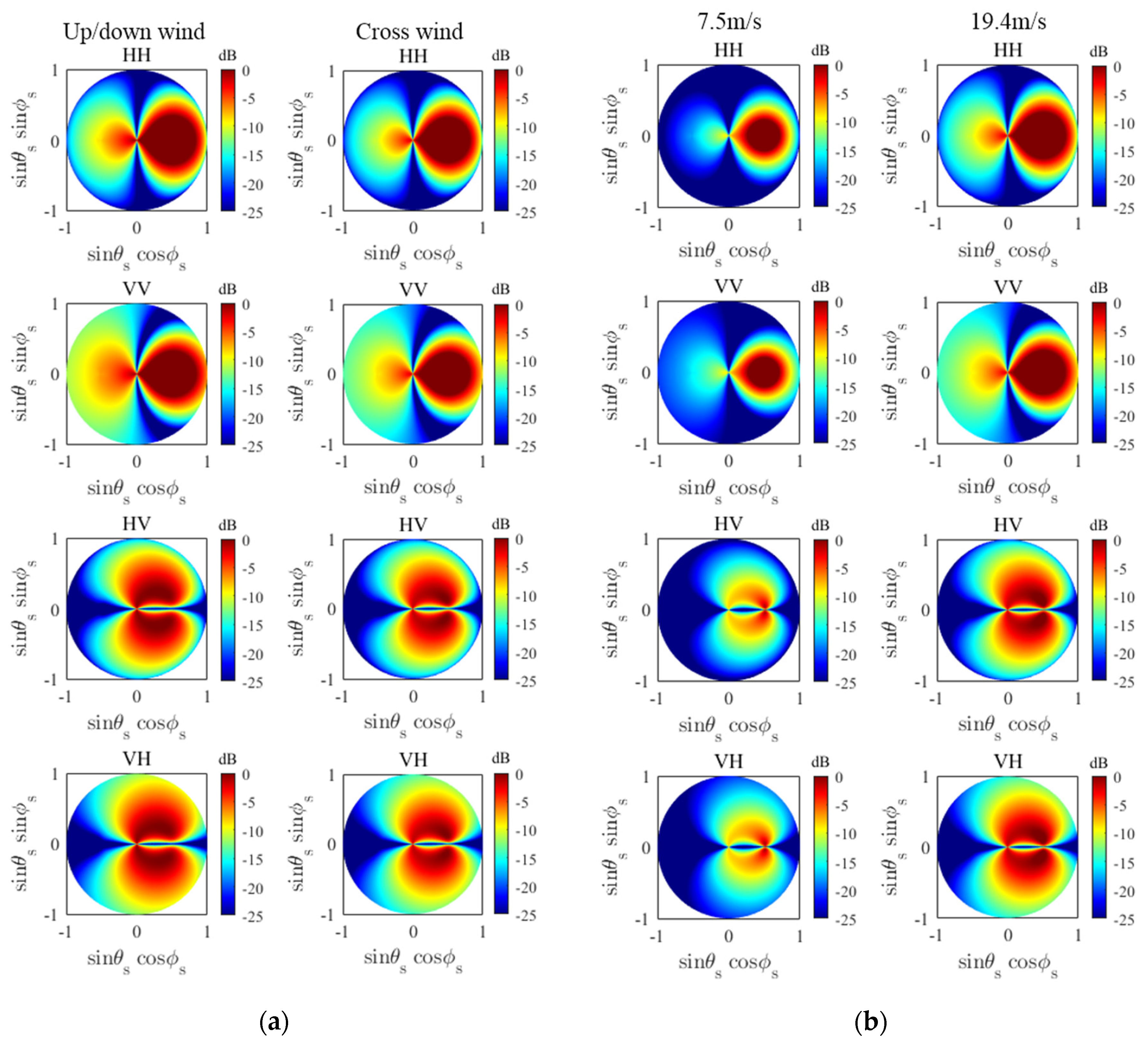


| Parameters | Description | Range | Step Size |
|---|---|---|---|
| Incident angle | |||
| Incident azimuth angle | |||
| Scattering angle | |||
| Scattering azimuth angle | |||
| Wind direction | |||
| Frequency | 5.3 GHz/9.4 GHz/13.9 GHz/13.99 GHz/14.6 GHz | ||
| Wind speed | 25 m/s–55 m/s (5.3 GHz) 5 m/s–30 m/s (13.99 GHz) 5.5 m/s–19.4 m/s (9.4 GHz, 13.9 GHz,14.6 Hz) | 10 m/s (5.3 GHz) 5 m/s (13.99 GHz) |
| Model 1 | Model 2 | Model 3 | FC-512 | FC-2048 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Layer Type | Size | Layer Type | Size | Layer Type | Size | Layer Type | Size | Layer Type | Size |
| Input | 1221 × 6 × 1 | Input | 1221 × 6 × 1 | Input | 1221 × 6 × 1 | Input | 1221 × 6 × 1 | Input | 1221 × 6 × 1 |
| Conv | 1 × 2 × 32, 2 | Conv | 1 × 2 × 32, 2 | Conv | 1 × 2 × 16, 2 | Conv | 1 × 2 × 32, 2 | Conv | 1 × 2 × 32, 2 |
| Conv | 1 × 3 × 32 | Conv | 1 × 3 × 32 | Conv | 1 × 3 × 16 | Conv | 1 × 3 × 32 | Conv | 1 × 3 × 32 |
| Conv | 5 × 1 × 64 | Conv | 5 × 1 × 64 | Conv | 5 × 1 × 32 | Conv | 5 × 1 × 64 | Conv | 5 × 1 × 64 |
| Conv | 5 × 1 × 64 | Conv | 5 × 1 × 64 | Conv | 5 × 1 × 32 | Conv | 5 × 1 × 64 | Conv | 5 × 1 × 64 |
| Avg-p | 6 × 1, 2 | Avg-p | 6 × 1, 2 | Avg-p | 6 × 1, 2 | Avg-p | 6 × 1, 2 | Avg-p | 6 × 1, 2 |
| Conv | 7 × 1 × 128 | Conv | 7 × 1 × 128 | Conv | 7 × 1 × 64 | Conv | 7 × 1 × 128 | Conv | 7 × 1 × 128 |
| Conv | 7 × 1 × 128 | Conv | 7 × 1 × 128 | Conv | 7 × 1 × 64 | Conv | 7 × 1 × 128 | Conv | 7 × 1 × 128 |
| Avg-p | 8 × 1, 2 | Avg-p | 8 × 1, 2 | Avg-p | 8 × 1, 2 | Avg-p | 8 × 1, 2 | Avg-p | 8 × 1, 2 |
| Conv | 9 × 1 × 256 | Conv | 9 × 1 × 256 | Conv | 9 × 1 × 128 | Conv | 9 × 1 × 256 | Conv | 9 × 1 × 256 |
| Conv | 9 × 1 × 256 | Conv | 9 × 1 × 256 | Conv | 9 × 1 × 128 | Conv | 9 × 1 × 256 | Conv | 9 × 1 × 256 |
| Avg-p | 10 × 1, 2 | Avg-p | 10 × 1, 2 | Avg-p | 10 × 1, 2 | Avg-p | 10 × 1, 2 | Avg-p | 10 × 1, 2 |
| FC | 1024 | Conv | 11 × 1 × 512 | Conv | 11 × 1 × 256 | Conv | 11 × 1 × 512 | Conv | 11 × 1 × 512 |
| Regrs | 2 | Conv | 11 × 1 × 512 | Conv | 11 × 1 × 256 | Conv | 11 × 1 × 512 | Conv | 11 × 1 × 512 |
| Avg-p | 12 × 1, 2 | Avg-p | 12 × 1, 2 | Avg-p | 12 × 1, 2 | Avg-p | 12 × 1, 2 | ||
| FC | 1024 | FC | 1024 | FC | 512 | FC | 2048 | ||
| Regrs | 2 | Regrs | 2 | Regrs | 2 | Regrs | 2 | ||
| Model 1 | Model 2 | Model 3 | FC-512 | FC-2048 | |
|---|---|---|---|---|---|
| Time Consuming (sec) | 315 | 425 | 175 | 389 | 621 |
| RMSE of Incident Azimuth Angle | 3.89 | 3.31 | 4.39 | 4.55 | 3.13 |
| RMSE of Incident Angle | 1.04 | 1.05 | 1.14 | 1.11 | 1.01 |
| 5.3 GHz | 25 m/s | ||
| 35 m/s | |||
| 45 m/s | |||
| 55 m/s | |||
| 13.99 GHz | 5 m/s | ||
| 10 m/s | |||
| 15 m/s | |||
| 20 m/s | |||
| 25 m/s | |||
| 30 m/s |
| 9.4 GHz | 5.5 m/s | ||
| 7.5 m/s | |||
| 12 m/s | |||
| 15 m/s | |||
| 19.4 m/s | |||
| 13.9 GHz | 5.5 m/s | ||
| 7.5 m/s | |||
| 12 m/s | |||
| 15 m/s | |||
| 19.4 m/s | |||
| 14.6 GHz | 5.5 m/s | ||
| 7.5 m/s | |||
| 12 m/s | |||
| 15 m/s | |||
| 19.4 m/s |
| Algorithms | |||
|---|---|---|---|
| 1-D DOA estimation | SVM [45] | 1–1.5 | --- |
| Annihilating filter with structured low rank approximation technique [46] | 0.8–3 | ||
| DNN [47] | 0.2–0.4 | ||
| 2-D DOA estimation | ESPRIT-based method [48] | 0.4–0.6 | 3–4 |
| Beamspace transformation [49] | 0.7 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Yang, Y.; Chen, K.-S. Direction-of-Arrival Estimation over Sea Surface from Radar Scattering Based on Convolutional Neural Network. Remote Sens. 2021, 13, 2681. https://doi.org/10.3390/rs13142681
Zhao X, Yang Y, Chen K-S. Direction-of-Arrival Estimation over Sea Surface from Radar Scattering Based on Convolutional Neural Network. Remote Sensing. 2021; 13(14):2681. https://doi.org/10.3390/rs13142681
Chicago/Turabian StyleZhao, Xiuyi, Ying Yang, and Kun-Shan Chen. 2021. "Direction-of-Arrival Estimation over Sea Surface from Radar Scattering Based on Convolutional Neural Network" Remote Sensing 13, no. 14: 2681. https://doi.org/10.3390/rs13142681
APA StyleZhao, X., Yang, Y., & Chen, K.-S. (2021). Direction-of-Arrival Estimation over Sea Surface from Radar Scattering Based on Convolutional Neural Network. Remote Sensing, 13(14), 2681. https://doi.org/10.3390/rs13142681








