Sparse Label Assignment for Oriented Object Detection in Aerial Images
Abstract
:1. Introduction
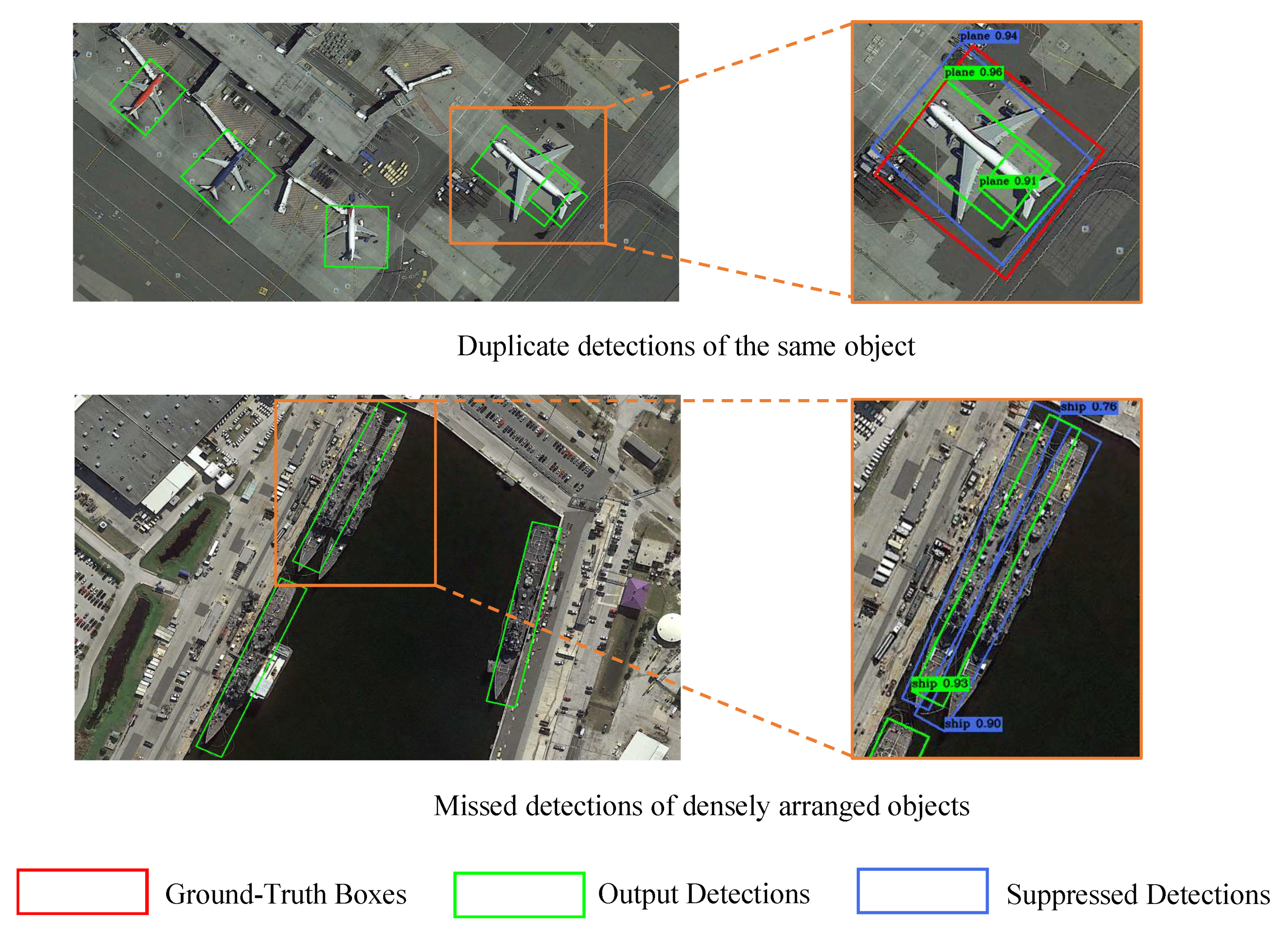
- We suggest that the dense label assignment strategy causes serious false duplicate detections and missed detections in aerial images, which degrades the detection performance;
- A novel sparse label assignment (SLA) strategy is proposed to achieve training sample selection based on their posterior IoU distribution. The posterior non-maximum suppression and representative sampling are used for the selection of positives and negatives, respectively, to improve detection performance;
- The position-sensitive feature pyramid network (PS-FPN) is adopted to extract feature maps for better localization performance. Besides, a novel distance rotated IoU (D-RIoU) loss is proposed to solve the misalignment between training loss and localization accuracy.
2. Related Work
2.1. Generic Object Detection
2.2. Object Detection in Aerial Images
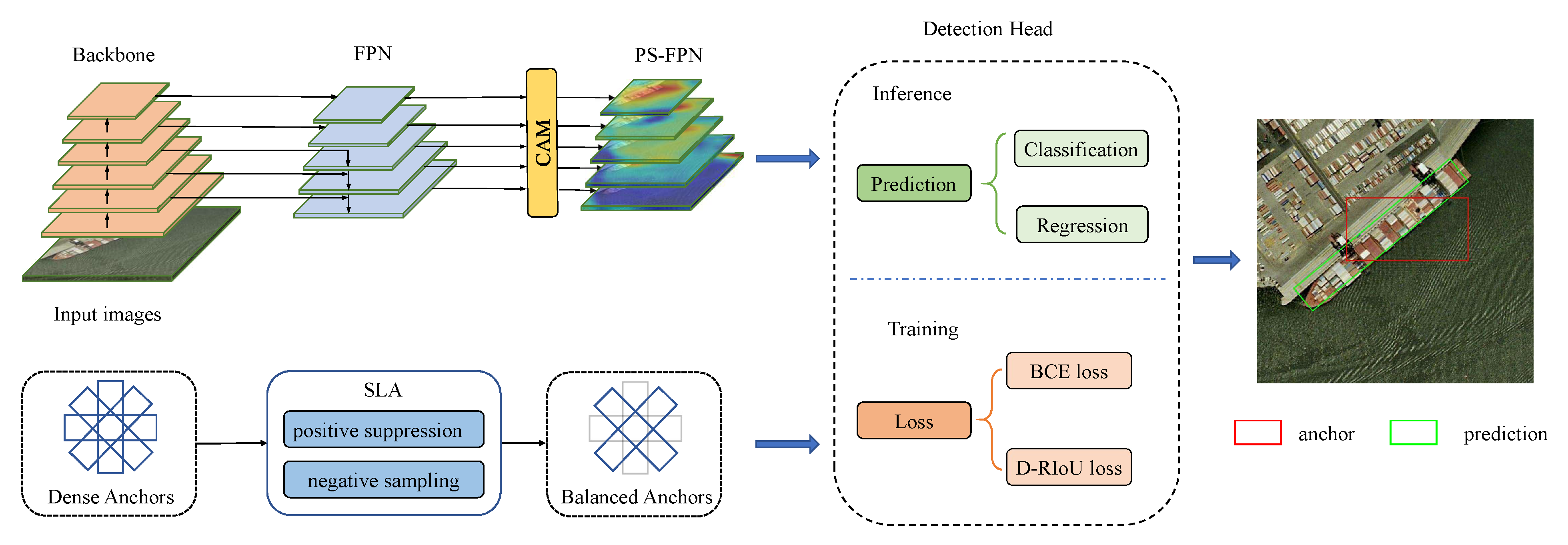
3. The Proposed Method
3.1. Sparse Label Assignment for Efficient Training Sample Selection
| Algorithm 1. Posterior non-maximum suppression. |
| Input: is a matrix of initially selected positive anchors. is a matrix of detection boxes corresponding to . is a matrix of GT boxes assigned to the corresponding anchors in . calculates the IoU between rotated boxes. is the NMS threshold. t denotes the training process, and . dynamically schedules the NMS threshold according to the training process. |
| Output: is a matrix of final selected positive samples. while do for do if then ; end if end for end while return |
- Firstly, the number of negatives is much larger than that of positives, and the implementation of NMS on them requires huge memory and is very time-consuming;
- Secondly, the detector does not perform regression supervision on negative samples, so the IoU between the GT boxes and the predictions of negatives is meaningless.
| Algorithm 2. Representative sampling for negative samples. |
| Input:: is a matrix of initially selected positive anchors. is a matrix of GT boxes assigned to the corresponding anchors in . calculates the IoU between rotated boxes. is the number of positive samples obtained through P-NMS. and are the thresholds for defining negative and background samples, respectively. and are the constant coefficients of sampling strategy, respectively. is a sampling function that randomly selects t elements from the set . |
| Output:: is a matrix of final selected negative samples. for do end for for do end for return |
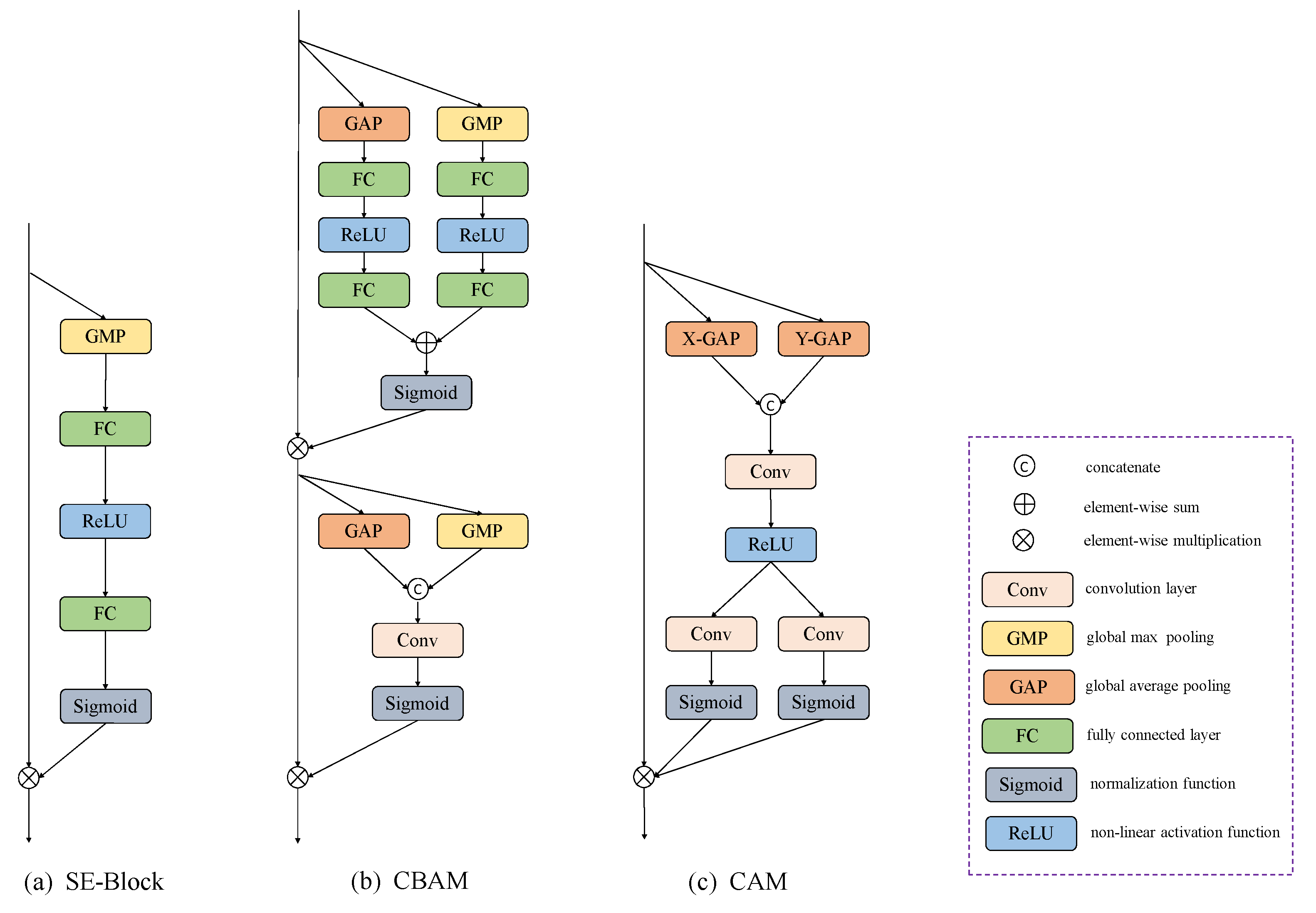
3.2. Position-Sensitive Feature Pyramid Network
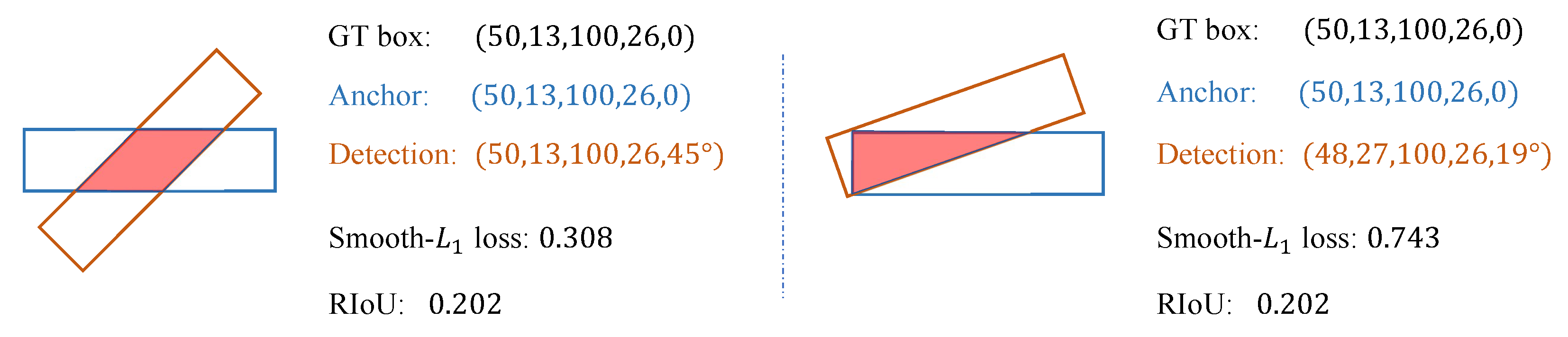
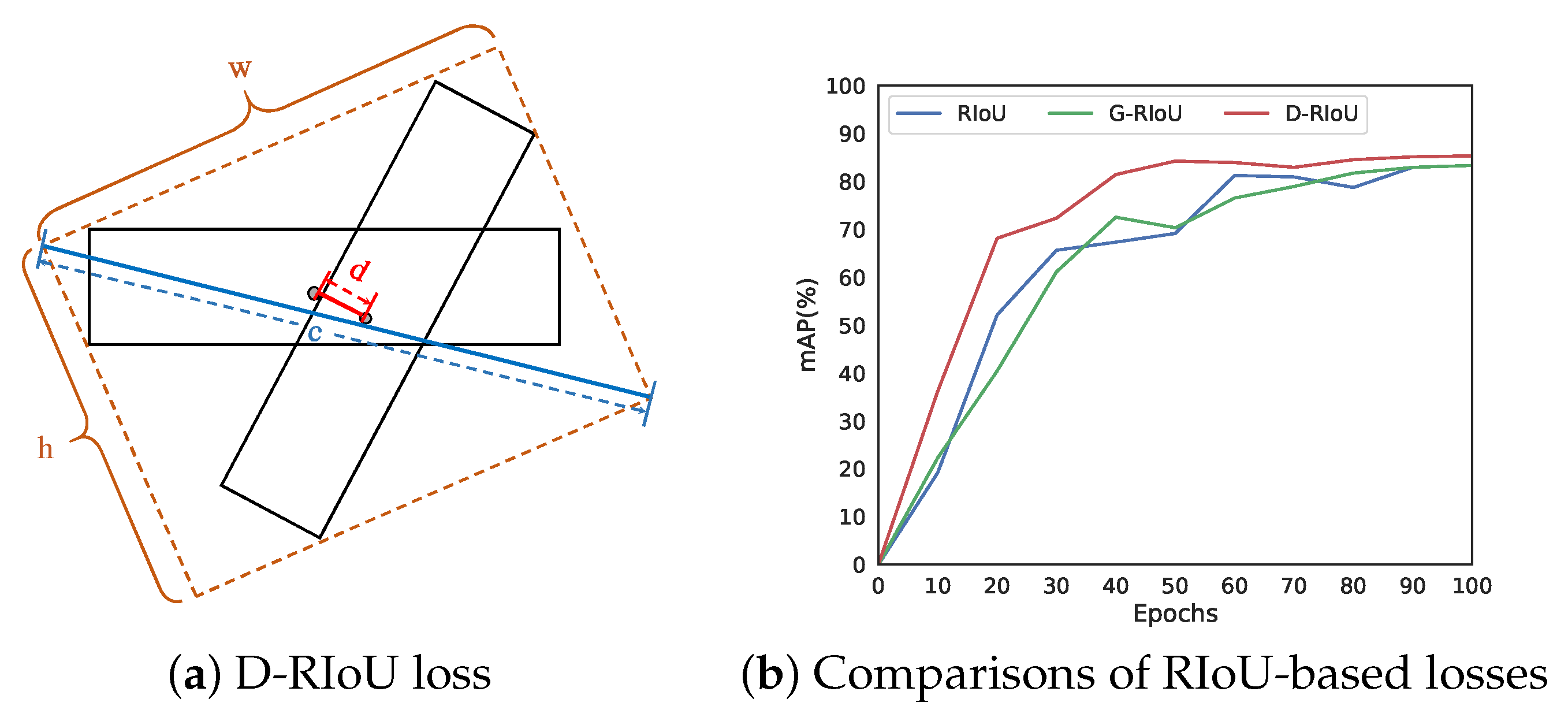
3.3. Distance Rotated IoU Loss for Bounding Box Regression
4. Experiments
4.1. Datasets and Implementation Details
4.1.1. HRSC2016
4.1.2. UCAS-AOD
4.1.3. DOTA
4.2. Ablation Study
4.2.1. Evaluation of the Proposed Modules
4.2.2. Evaluation of Sparse Label Assignment
4.2.3. Evaluation of Position-Sensitive Feature Pyramid Network
4.2.4. Evaluation of Distance Rotated IoU
4.3. Main Results
4.3.1. Results on HRSC2016
4.3.2. Results on UCAS-AOD
4.3.3. Results on DOTA
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. arXiv 2016, arXiv:1605.06409. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar]
- Chen, C.; Zhong, J.; Tan, Y. Multiple-oriented and small object detection with convolutional neural networks for aerial image. Remote Sens. 2019, 11, 2176. [Google Scholar] [CrossRef] [Green Version]
- Qian, X.; Lin, S.; Cheng, G.; Yao, X.; Ren, H.; Wang, W. Object Detection in Remote Sensing Images Based on Improved Bounding Box Regression and Multi-Level Features Fusion. Remote Sens. 2020, 12, 143. [Google Scholar] [CrossRef] [Green Version]
- Zhong, B.; Ao, K. Single-Stage Rotation-Decoupled Detector for Oriented Object. Remote Sens. 2020, 12, 3262. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Ye, Y.; Lau, R.Y.; Zhang, X.; Huang, X. Road detection and centerline extraction via deep recurrent convolutional neural network U-Net. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7209–7220. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, G.; Zhu, P.; Zhang, T.; Li, C.; Jiao, L. GRS-Det: An Anchor-Free Rotation Ship Detector Based on Gaussian-Mask in Remote Sensing Images. IEEE Trans. Geosci. Remot. Sens. 2020, 59, 3518–3531. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, W.; Zhu, S.; Yu, W. Toward arbitrary-oriented ship detection with rotated region proposal and discrimination networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1745–1749. [Google Scholar] [CrossRef]
- Deng, Z.; Sun, H.; Zhou, S.; Zhao, J.; Lei, L.; Zou, H. Multi-scale object detection in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2018, 145, 3–22. [Google Scholar] [CrossRef]
- Li, L.; Zhou, Z.; Wang, B.; Miao, L.; Zong, H. A Novel CNN-Based Method for Accurate Ship Detection in HR Optical Remote Sensing Images via Rotated Bounding Box. IEEE Trans. Geosci. Remote Sens. 2020, 59, 686–699. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Jiang, B.; Luo, R.; Mao, J.; Xiao, T.; Jiang, Y. Acquisition of localization confidence for accurate object detection. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 784–799. [Google Scholar]
- He, Y.; Zhu, C.; Wang, J.; Savvides, M.; Zhang, X. Bounding box regression with uncertainty for accurate object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–19 June 2019; pp. 2888–2897. [Google Scholar]
- Choi, J.; Chun, D.; Kim, H.; Lee, H.J. Gaussian yolov3: An accurate and fast object detector using localization uncertainty for autonomous driving. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 502–511. [Google Scholar]
- Ming, Q.; Zhou, Z.; Miao, L.; Zhang, H.; Li, L. Dynamic Anchor Learning for Arbitrary-Oriented Object Detection. In Proceedings of the AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 2–9 February 2021. [Google Scholar]
- Liu, Z.; Yuan, L.; Weng, L.; Yang, Y. A high resolution optical satellite image dataset for ship recognition and some new baselines. In Proceedings of the International Conference on Pattern Recognition Applications and Methods, Porto, Portugal, 24–26 February 2017; Volume 2, pp. 324–331. [Google Scholar]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Li, B.; Liu, Y.; Wang, X. Gradient harmonized single-stage detector. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8577–8584. [Google Scholar]
- Pang, J.; Chen, K.; Shi, J.; Feng, H.; Ouyang, W.; Lin, D. Libra r-cnn: Towards balanced learning for object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 821–830. [Google Scholar]
- Yang, X.; Sun, H.; Fu, K.; Yang, J.; Sun, X.; Yan, M.; Guo, Z. Automatic ship detection in remote sensing images from google earth of complex scenes based on multiscale rotation dense feature pyramid networks. Remote Sens. 2018, 10, 132. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Diao, W.; Sun, X.; Yan, M.; Gao, X. Towards automated ship detection and category recognition from high-resolution aerial images. Remote Sens. 2019, 11, 1901. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Lu, S.; Zhang, W. CAD-Net: A context-aware detection network for objects in remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10015–10024. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Sun, X.; Diao, W.; Fu, K. FMSSD: Feature-merged single-shot detection for multiscale objects in large-scale remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3377–3390. [Google Scholar] [CrossRef]
- Ming, Q.; Miao, L.; Zhou, Z.; Dong, Y. CFC-Net: A Critical Feature Capturing Network for Arbitrary-Oriented Object Detection in Remote Sensing Images. arXiv 2021, arXiv:2101.06849. [Google Scholar]
- Fu, K.; Chang, Z.; Zhang, Y.; Xu, G.; Zhang, K.; Sun, X. Rotation-aware and multi-scale convolutional neural network for object detection in remote sensing images. ISPRS J. Photogramm. Remote Sens. 2020, 161, 294–308. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J. Arbitrary-Oriented Object Detection with Circular Smooth Label. arXiv 2020, arXiv:2003.05597. [Google Scholar]
- Yang, X.; Hou, L.; Zhou, Y.; Wang, W.; Yan, J. Dense Label Encoding for Boundary Discontinuity Free Rotation Detection. arXiv 2020, arXiv:2011.09670. [Google Scholar]
- Qian, W.; Yang, X.; Peng, S.; Guo, Y.; Yan, J. Learning modulated loss for rotated object detection. arXiv 2019, arXiv:1911.08299. [Google Scholar]
- Ming, Q.; Zhou, Z.; Miao, L.; Yang, X.; Dong, Y. Optimization for Oriented Object Detection via Representation Invariance Loss. arXiv 2021, arXiv:2103.11636. [Google Scholar]
- Yang, X.; Yan, J.; Ming, Q.; Wang, W.; Zhang, X.; Tian, Q. Rethinking Rotated Object Detection with Gaussian Wasserstein Distance Loss. arXiv 2021, arXiv:2101.11952. [Google Scholar]
- Zhu, Y.; Du, J.; Wu, X. Adaptive period embedding for representing oriented objects in aerial images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7247–7257. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wan, F.; Liu, C.; Ji, R.; Ye, Q. Freeanchor: Learning to match anchors for visual object detection. arXiv 2019, arXiv:1909.02466. pp. 147–155. [Google Scholar]
- Zhang, S.; Chi, C.; Yao, Y.; Lei, Z.; Li, S.Z. Bridging the gap between anchor-based and anchor-free detection via adaptive training sample selection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9759–9768. [Google Scholar]
- Cao, Y.; Chen, K.; Loy, C.C.; Lin, D. Prime sample attention in object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11583–11591. [Google Scholar]
- Xiao, Z.; Wang, K.; Wan, Q.; Tan, X.; Xu, C.; Xia, F. A2S-Det: Efficiency Anchor Matching in Aerial Image Oriented Object Detection. Remote Sens. 2021, 13, 73. [Google Scholar] [CrossRef]
- Ke, W.; Zhang, T.; Huang, Z.; Ye, Q.; Liu, J.; Huang, D. Multiple anchor learning for visual object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 10206–10215. [Google Scholar]
- Zhang, X.; Wan, F.; Liu, C.; Ji, X.; Ye, Q. Learning to match anchors for visual object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate attention for efficient mobile network design. arXiv 2021, arXiv:2103.02907. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized intersection over union: A metric and a loss for bounding box regression. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 658–666. [Google Scholar]
- Zheng, Z.; Wang, P.; Liu, W.; Li, J.; Ye, R.; Ren, D. Distance-IoU loss: Faster and better learning for bounding box regression. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 12993–13000. [Google Scholar]
- Zhu, H.; Chen, X.; Dai, W.; Fu, K.; Ye, Q.; Jiao, J. Orientation robust object detection in aerial images using deep convolutional neural network. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3735–3739. [Google Scholar]
- Ma, J.; Shao, W.; Ye, H.; Wang, L.; Wang, H.; Zheng, Y.; Xue, X. Arbitrary-oriented scene text detection via rotation proposals. IEEE Trans. Multimed. 2018, 20, 3111–3122. [Google Scholar] [CrossRef] [Green Version]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.S.; Lu, Q. Learning RoI transformer for oriented object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2849–2858. [Google Scholar]
- Xu, Y.; Fu, M.; Wang, Q.; Wang, Y.; Chen, K.; Xia, G.S.; Bai, X. Gliding vertex on the horizontal bounding box for multi-oriented object detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 1452–1459. [Google Scholar] [CrossRef] [Green Version]
- Song, Q.; Yang, F.; Yang, L.; Liu, C.; Hu, M.; Xia, L. Learning Point-guided Localization for Detection in Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 14, 1084–1094. [Google Scholar] [CrossRef]
- Liao, M.; Zhu, Z.; Shi, B.; Xia, G.s.; Bai, X. Rotation-sensitive regression for oriented scene text detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5909–5918. [Google Scholar]
- Yi, J.; Wu, P.; Liu, B.; Huang, Q.; Qu, H.; Metaxas, D. Oriented object detection in aerial images with box boundary-aware vectors. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 2150–2159. [Google Scholar]
- Yang, X.; Liu, Q.; Yan, J.; Li, A.; Zhang, Z.; Yu, G. R3det: Refined Single-Stage Detector with Feature Refinement for Rotating Object. arXiv 2019, arXiv:1908.05612. [Google Scholar]
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Sun, X.; Fu, K. Scrdet: Towards more robust detection for small, cluttered and rotated objects. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 8232–8241. [Google Scholar]
- Wei, H.; Zhang, Y.; Chang, Z.; Li, H.; Wang, H.; Sun, X. Oriented objects as pairs of middle lines. ISPRS J. Photogramm. Remote Sens. 2020, 169, 268–279. [Google Scholar] [CrossRef]
- Pan, X.; Ren, Y.; Sheng, K.; Dong, W.; Yuan, H.; Guo, X.; Ma, C.; Xu, C. Dynamic Refinement Network for Oriented and Densely Packed Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11207–11216. [Google Scholar]



| Different Variants | ||||
|---|---|---|---|---|
| with SLA | × | ✔ | ✔ | ✔ |
| with PS-FPN | × | × | ✔ | ✔ |
| with D-RIoU loss | × | × | × | ✔ |
| 85.34 | 86.08 | 86.73 | 87.14 | |
| 48.11 | 55.60 | 58.88 | 62.92 | |
| ID | Balanced Sampling | Sampling Ratio | P-NMS | NMS Threshold | AP | AP |
|---|---|---|---|---|---|---|
| 0 | - | - | - | - | 85.34 | 48.11 |
| 1 | pos/neg | 1:1 | - | - | 83.70 | 50.82 |
| 2 | - | 0.7 | 82.75 | 47.26 | ||
| 3 | - | 0.8 | 83.91 | 50.74 | ||
| 4 | - | 0.9 | 83.58 | 50.96 | ||
| 5 | ✔ | adaptive | 84.09 | 51.28 | ||
| 6 | pos/hard/neg | 1:1:10 | - | - | 84.27 | 52.44 |
| 7 | - | 0.7 | 84.03 | 51.84 | ||
| 8 | - | 0.8 | 84.47 | 52.73 | ||
| 9 | - | 0.9 | 84.58 | 52.15 | ||
| 10 | ✔ | adaptive | 85.60 | 54.07 | ||
| 11 | pos/hard/neg | 1:2:100 | - | - | 86.05 | 52.26 |
| 12 | - | 0.7 | 85.09 | 51.20 | ||
| 13 | - | 0.8 | 85.72 | 54.50 | ||
| 14 | - | 0.9 | 85.21 | 53.19 | ||
| 15 | ✔ | adaptive | 86.08 | 55.60 |
| Backbone | PS-FPN | Param. Share | Reduction | mAP |
|---|---|---|---|---|
| ResNet-50 | - | - | - | 86.08 |
| ResNet-50 | ✔ | ✔ | 32 | 86.41 |
| ResNet-50 | × | 16 | 86.13 | |
| ResNet-50 | × | 24 | 86.01 | |
| ResNet-50 | × | 32 | 86.73 |
| Losses | Smooth-L | RIoU (Linear) | RIoU (log) | G-RIoU | D-RIoU |
|---|---|---|---|---|---|
| AP | 86.39 | 86.11 | 86.85 | 86.21 | 87.92 |
| AP | 54.88 | 55.21 | 57.64 | 51.24 | 59.15 |
| Methods | Backbone | Size | mAP |
|---|---|---|---|
| Two-stage: | |||
| RRPN [49] | ResNet101 | 800 × 800 | 79.08 |
| RPN [13] | VGG16 | — | 79.60 |
| RoI Trans. [50] | ResNet101 | 512 × 800 | 86.20 |
| Gliding Vertex [51] | ResNet101 | 512 × 800 | 88.20 |
| OPLD [52] | ResNet50 | 1024 × 1333 | 88.44 |
| DCL [32] | ResNet101 | 800 × 800 | 89.46 |
| Single-stage: | |||
| RetinaNet [16] | ResNet50 | 416 × 416 | 80.81 |
| RRD [53] | VGG16 | 384 × 384 | 84.30 |
| RSDet [33] | ResNet50 | 800 × 800 | 86.50 |
| BBAVector [54] | ResNet101 | 608 × 608 | 88.60 |
| DAL [20] | ResNet101 | 416 × 416 | 88.95 |
| R3Det [55] | ResNet101 | 800 × 800 | 89.26 |
| SLA (Ours) | ResNet50 | 384 × 384 | 87.14 |
| SLA (Ours) | ResNet101 | 768 × 768 | 89.51 |
| Methods | RetinaNet [16] | ATSS [38] | RIDet-O [34] | DAL [20] | SLA(Ours) |
|---|---|---|---|---|---|
| 83.49 | 86.67 | 88.35 | 89.42 | 89.51 | |
| 49.11 | 59.10 | 54.94 | 66.56 | 68.12 |
| Methods | Car | Airplane | mAP |
|---|---|---|---|
| YOLOv3 [6] | 74.63 | 89.52 | 82.08 |
| RetinaNet [16] | 84.64 | 90.51 | 87.57 |
| FR-O [22] | 86.87 | 89.86 | 88.36 |
| RoI Transformer [50] | 87.99 | 89.90 | 88.95 |
| RIDet-Q [34] | 88.50 | 89.96 | 89.23 |
| SLA(ours) | 88.57 | 90.30 | 89.44 |
| Methods | Backbone | PL | BD | BR | GTF | SV | LV | SH | TC | BC | ST | SBF | RA | HA | SP | HC | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Two-stage: | |||||||||||||||||
| RRPN [49] | R-101 | 88.52 | 71.20 | 31.66 | 59.30 | 51.85 | 56.19 | 57.25 | 90.81 | 72.84 | 67.38 | 56.69 | 52.84 | 53.08 | 51.94 | 53.58 | 61.01 |
| RoI Trans. [50] | R-101 | 88.64 | 78.52 | 43.44 | 75.92 | 68.81 | 73.68 | 83.59 | 90.74 | 77.27 | 81.46 | 58.39 | 53.54 | 62.83 | 58.93 | 47.67 | 69.56 |
| CAD-Net [27] | R-101 | 87.80 | 82.40 | 49.40 | 73.50 | 71.10 | 63.50 | 76.70 | 90.90 | 79.20 | 73.30 | 48.40 | 60.90 | 62.00 | 67.00 | 62.20 | 69.90 |
| SCRDet [56] | R-101 | 89.98 | 80.65 | 52.09 | 68.36 | 68.36 | 60.32 | 72.41 | 90.85 | 87.94 | 86.86 | 65.02 | 66.68 | 66.25 | 68.24 | 65.21 | 72.61 |
| Gliding Vertex [51] | R-101 | 89.64 | 85.00 | 52.26 | 77.34 | 73.01 | 73.14 | 86.82 | 90.74 | 79.02 | 86.81 | 59.55 | 70.91 | 72.94 | 70.86 | 57.32 | 75.02 |
| CSL [31] | R-152 | 90.25 | 85.53 | 54.64 | 75.31 | 70.44 | 73.51 | 77.62 | 90.84 | 86.15 | 86.69 | 69.60 | 68.04 | 73.83 | 71.10 | 68.93 | 76.17 |
| Single-stage: | |||||||||||||||||
| A-Det [40] | R-101 | 89.59 | 77.89 | 46.37 | 56.47 | 75.86 | 74.83 | 86.07 | 90.58 | 81.09 | 83.71 | 50.21 | 60.94 | 65.29 | 69.77 | 50.93 | 70.64 |
| O-DNet [57] | H-104 | 89.31 | 82.14 | 47.33 | 61.21 | 71.32 | 74.03 | 78.62 | 90.76 | 82.23 | 81.36 | 60.93 | 60.17 | 58.21 | 66.98 | 61.03 | 71.04 |
| DAL [20] | R-101 | 88.61 | 79.69 | 46.27 | 70.37 | 65.89 | 76.10 | 78.53 | 90.84 | 79.98 | 78.41 | 58.71 | 62.02 | 69.23 | 71.32 | 60.65 | 71.78 |
| RSDet [33] | R-101 | 89.80 | 82.90 | 48.60 | 65.20 | 69.50 | 70.10 | 70.20 | 90.50 | 85.60 | 83.40 | 62.50 | 63.90 | 65.60 | 67.20 | 68.00 | 72.20 |
| DRN [58] | H-104 | 89.71 | 82.34 | 47.22 | 64.10 | 76.22 | 74.43 | 85.84 | 90.57 | 86.18 | 84.89 | 57.65 | 61.93 | 69.30 | 69.63 | 58.48 | 73.23 |
| BBAVector [54] | R-101 | 88.35 | 79.96 | 50.69 | 62.18 | 78.43 | 78.98 | 87.94 | 90.85 | 83.58 | 84.35 | 54.13 | 60.24 | 65.22 | 64.28 | 55.70 | 72.32 |
| CFC-Net [29] | R-50 | 89.08 | 80.41 | 52.41 | 70.02 | 76.28 | 78.11 | 87.21 | 90.89 | 84.47 | 85.64 | 60.51 | 61.52 | 67.82 | 68.02 | 50.09 | 73.50 |
| RDet [55] | R-152 | 89.49 | 81.17 | 50.53 | 66.10 | 70.92 | 78.66 | 78.21 | 90.81 | 85.26 | 84.23 | 61.81 | 63.77 | 68.16 | 69.83 | 67.17 | 73.74 |
| SLA (Ours) | R-50 | 85.23 | 83.78 | 48.89 | 71.65 | 76.43 | 76.80 | 86.83 | 90.62 | 88.17 | 86.88 | 49.67 | 66.13 | 75.34 | 72.11 | 64.88 | 74.89 |
| SLA (Ours) | R-50 | 88.33 | 84.67 | 48.78 | 73.34 | 77.47 | 77.82 | 86.53 | 90.72 | 86.98 | 86.43 | 58.86 | 68.27 | 74.10 | 73.09 | 69.30 | 76.36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, Q.; Miao, L.; Zhou, Z.; Song, J.; Yang, X. Sparse Label Assignment for Oriented Object Detection in Aerial Images. Remote Sens. 2021, 13, 2664. https://doi.org/10.3390/rs13142664
Ming Q, Miao L, Zhou Z, Song J, Yang X. Sparse Label Assignment for Oriented Object Detection in Aerial Images. Remote Sensing. 2021; 13(14):2664. https://doi.org/10.3390/rs13142664
Chicago/Turabian StyleMing, Qi, Lingjuan Miao, Zhiqiang Zhou, Junjie Song, and Xue Yang. 2021. "Sparse Label Assignment for Oriented Object Detection in Aerial Images" Remote Sensing 13, no. 14: 2664. https://doi.org/10.3390/rs13142664
APA StyleMing, Q., Miao, L., Zhou, Z., Song, J., & Yang, X. (2021). Sparse Label Assignment for Oriented Object Detection in Aerial Images. Remote Sensing, 13(14), 2664. https://doi.org/10.3390/rs13142664






