IGS-CMAES: A Two-Stage Optimization for Ground Deformation and DEM Error Estimation in Time Series InSAR Data
Abstract
:1. Introduction
2. Materials and Methods
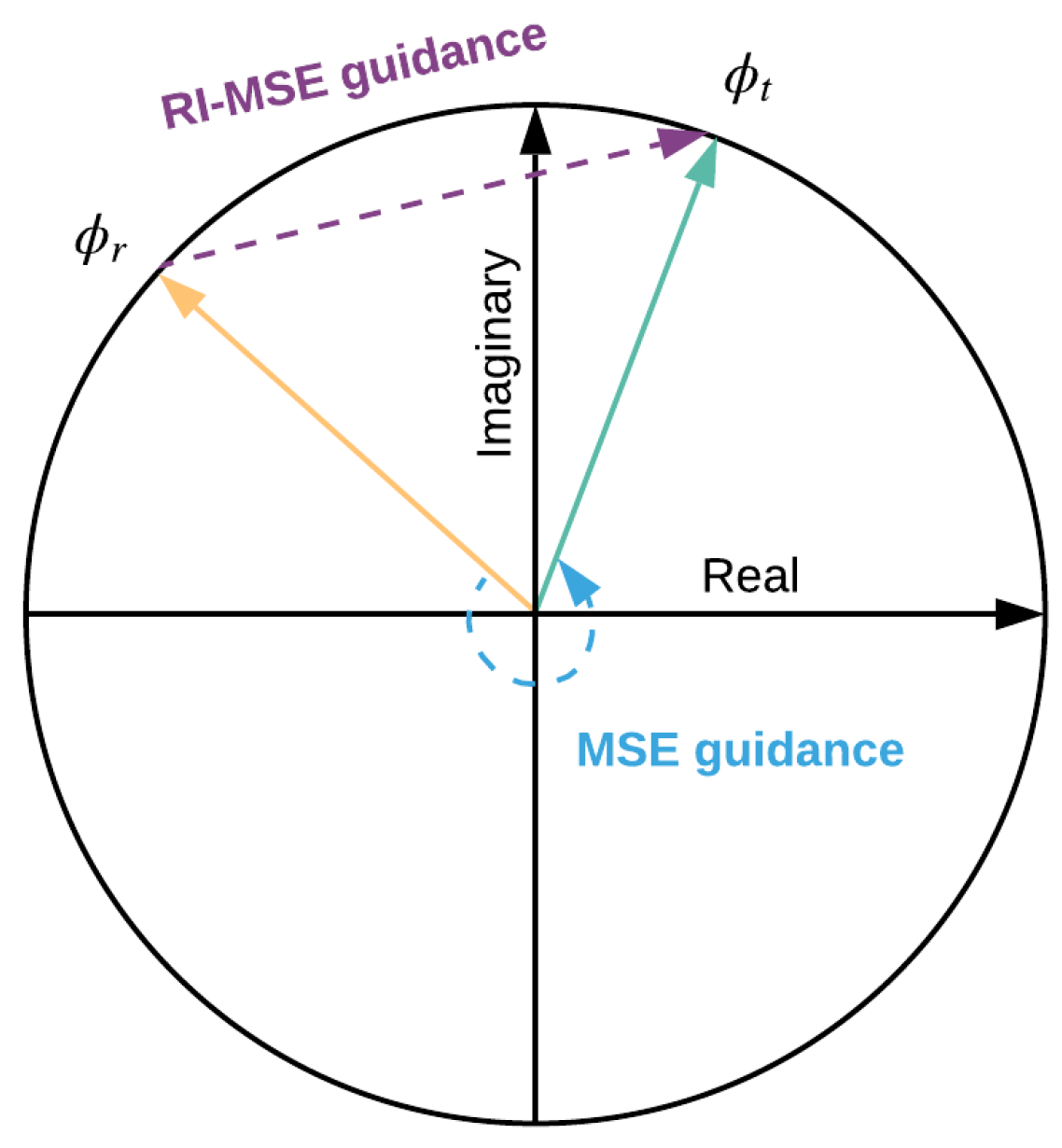
2.1. Mathematical Modelling for InSAR Phase
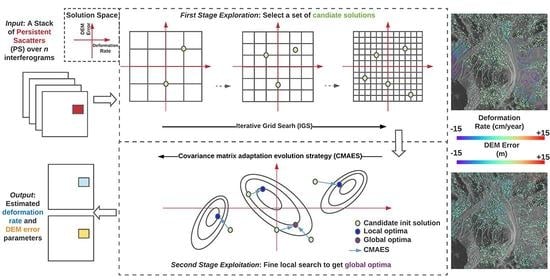
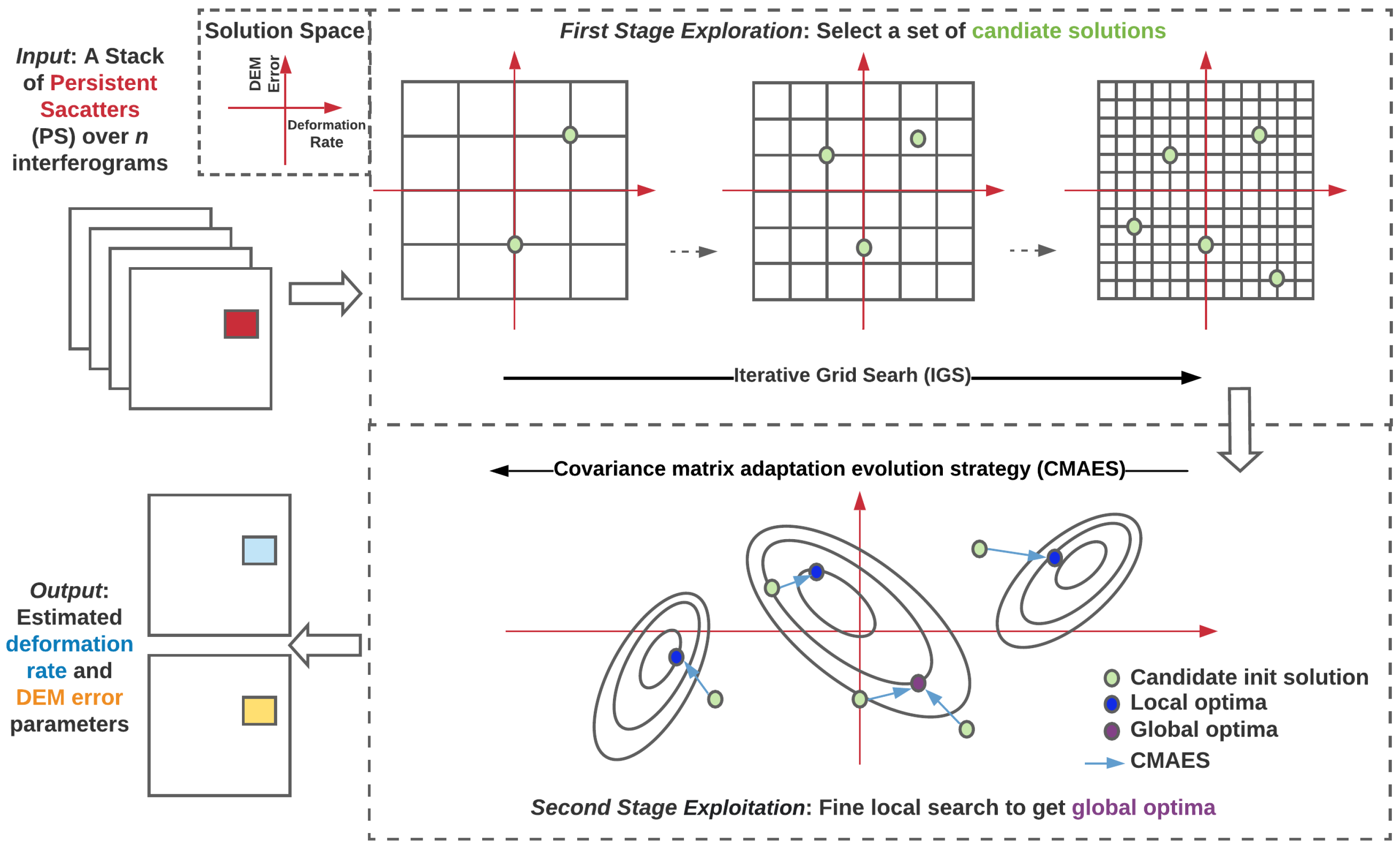
2.2. Proposed Method
2.2.1. Definition of Optimization Problem
2.2.2. CMAES
2.2.3. Iterative Grid Search (IGS)
2.2.4. IGS-CMAES
| Algorithm 1: IGS-CMAES for deformation rate and DEM error estimation. |
 |
3. Results
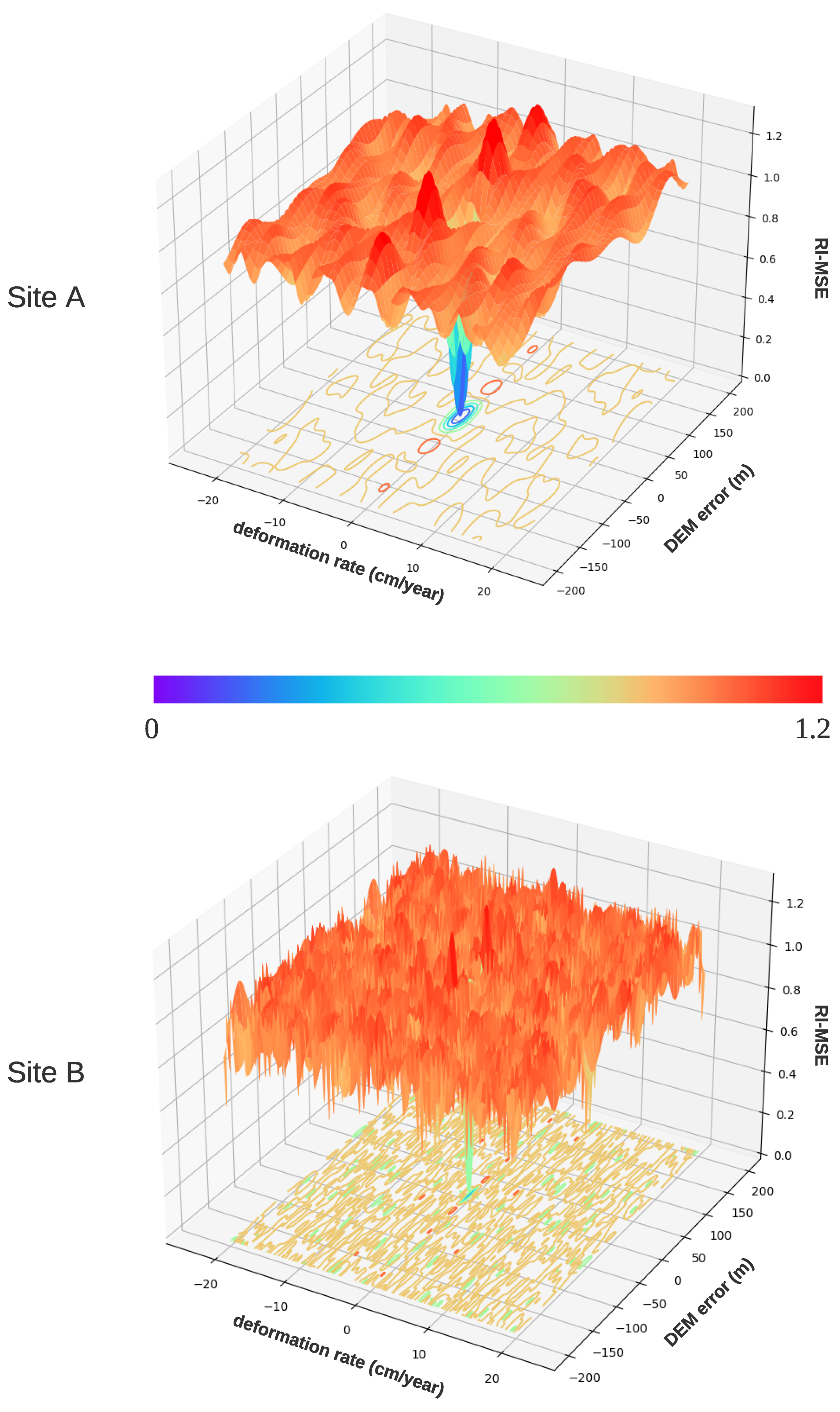
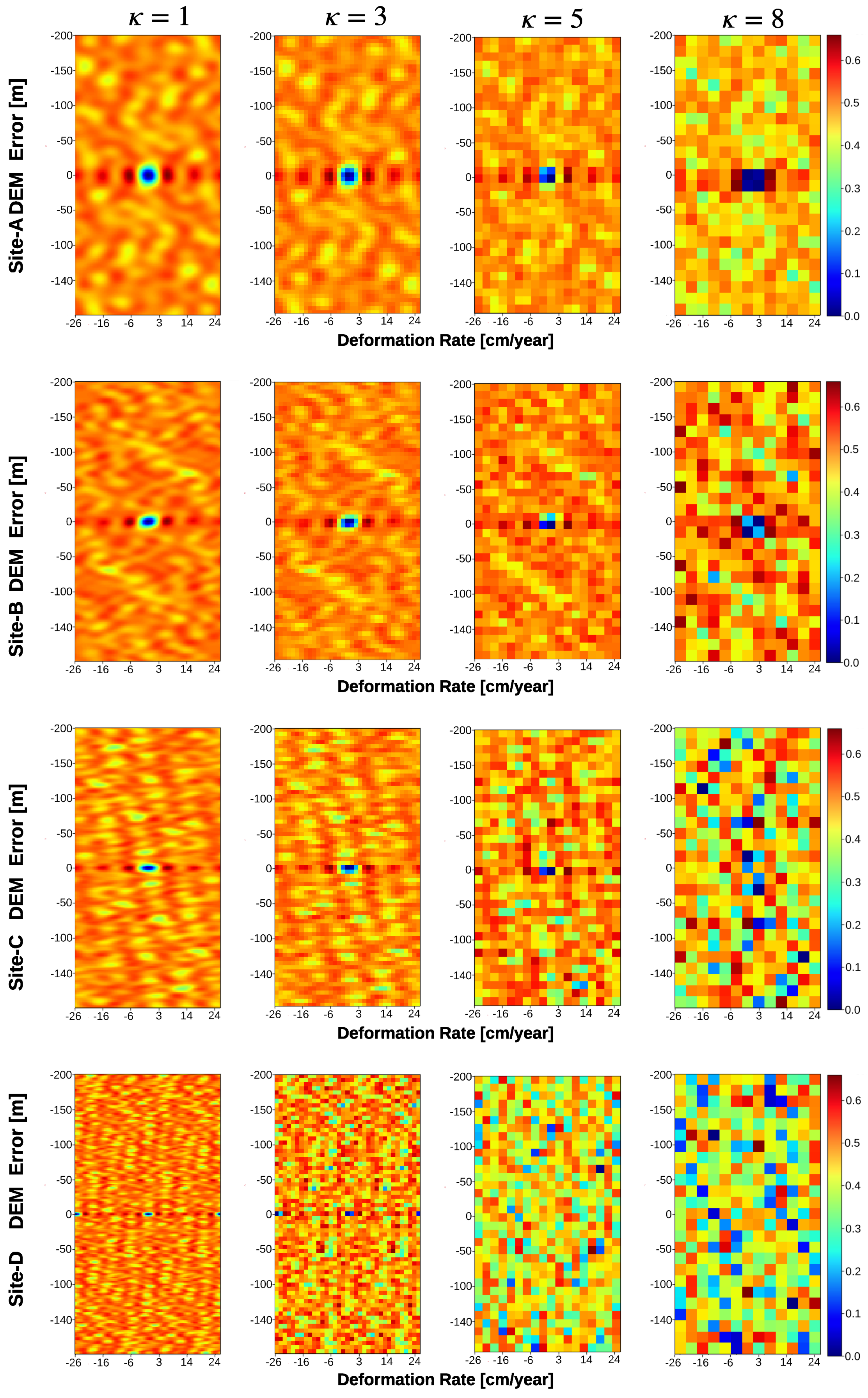
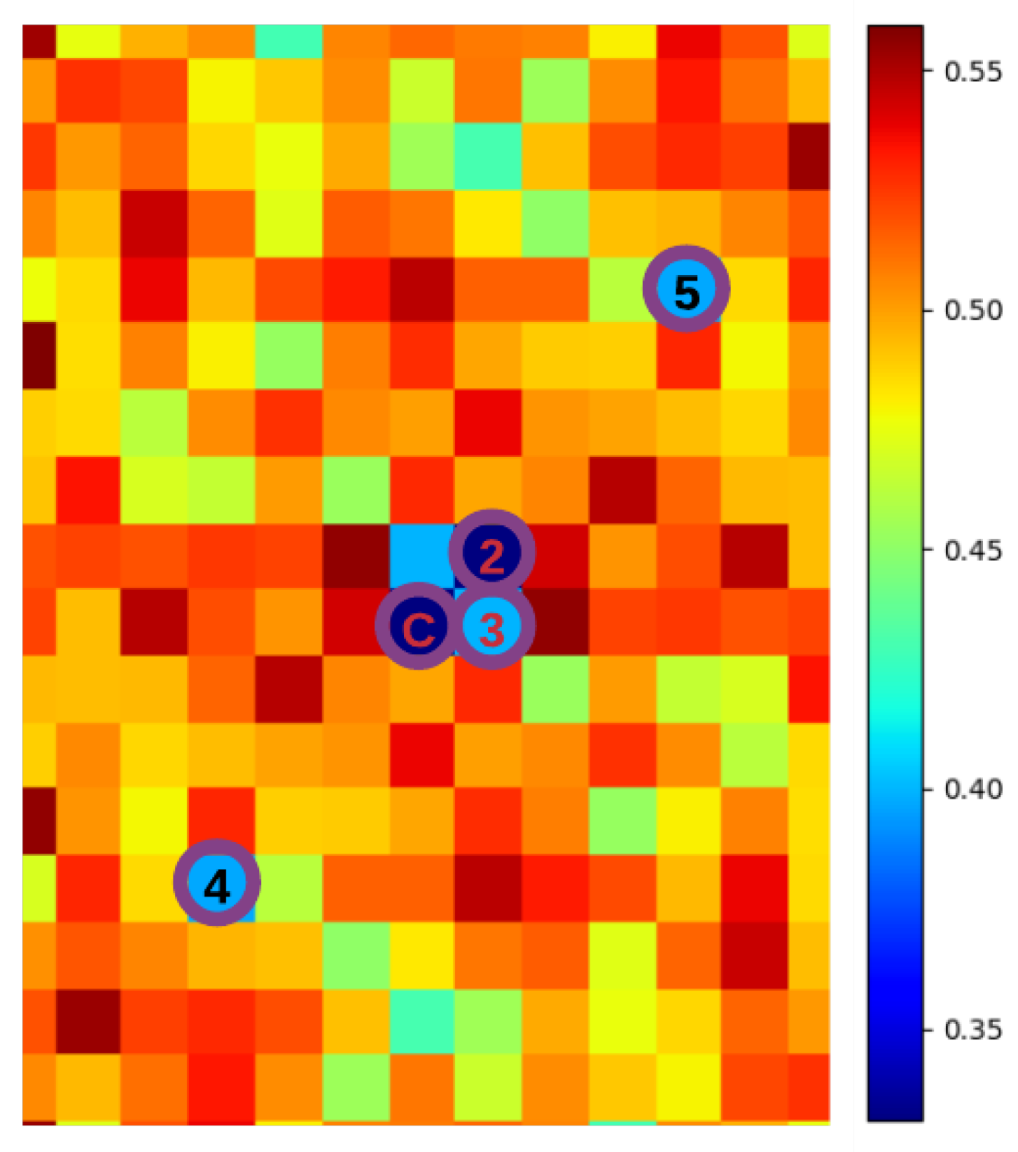
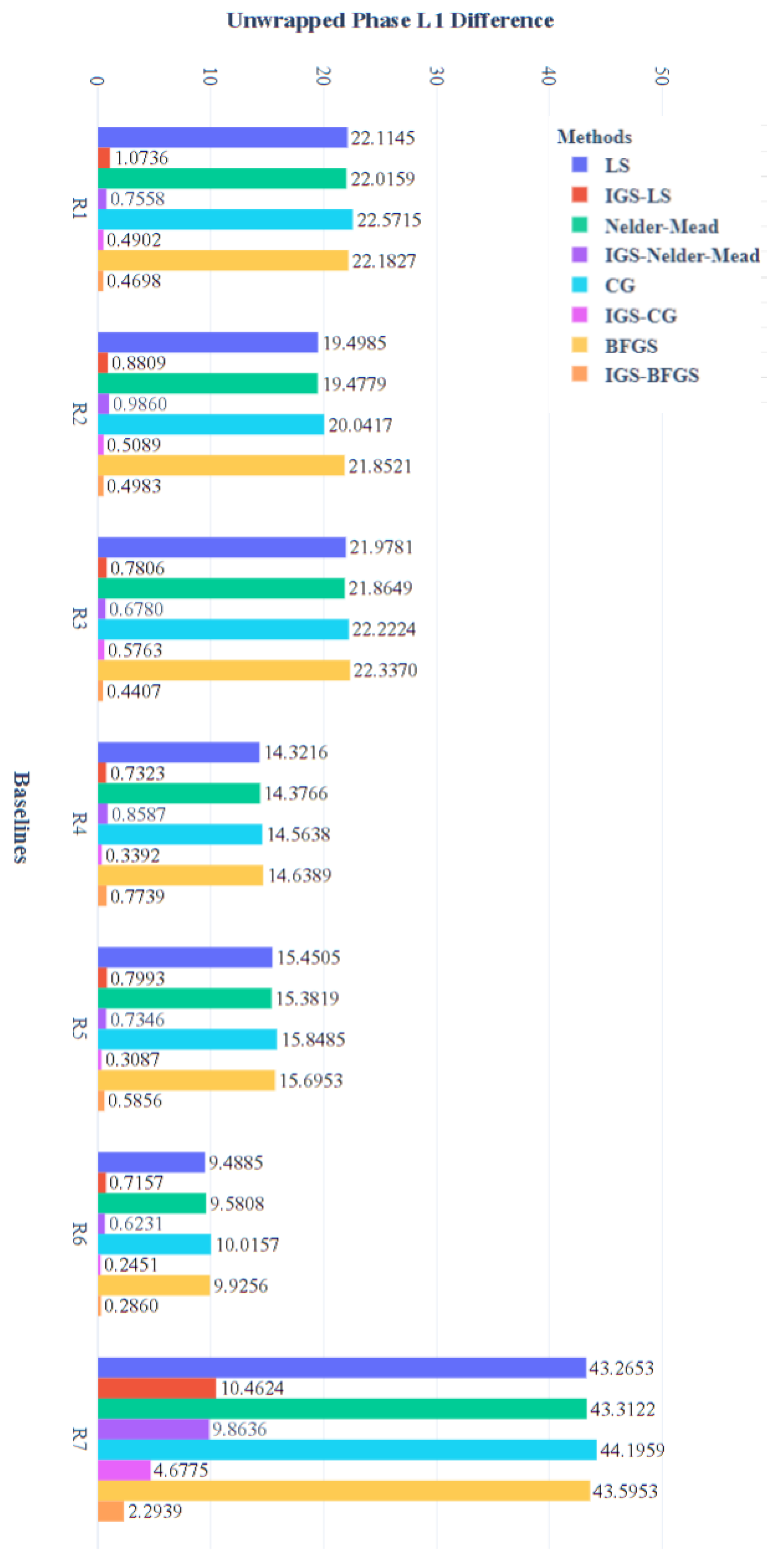
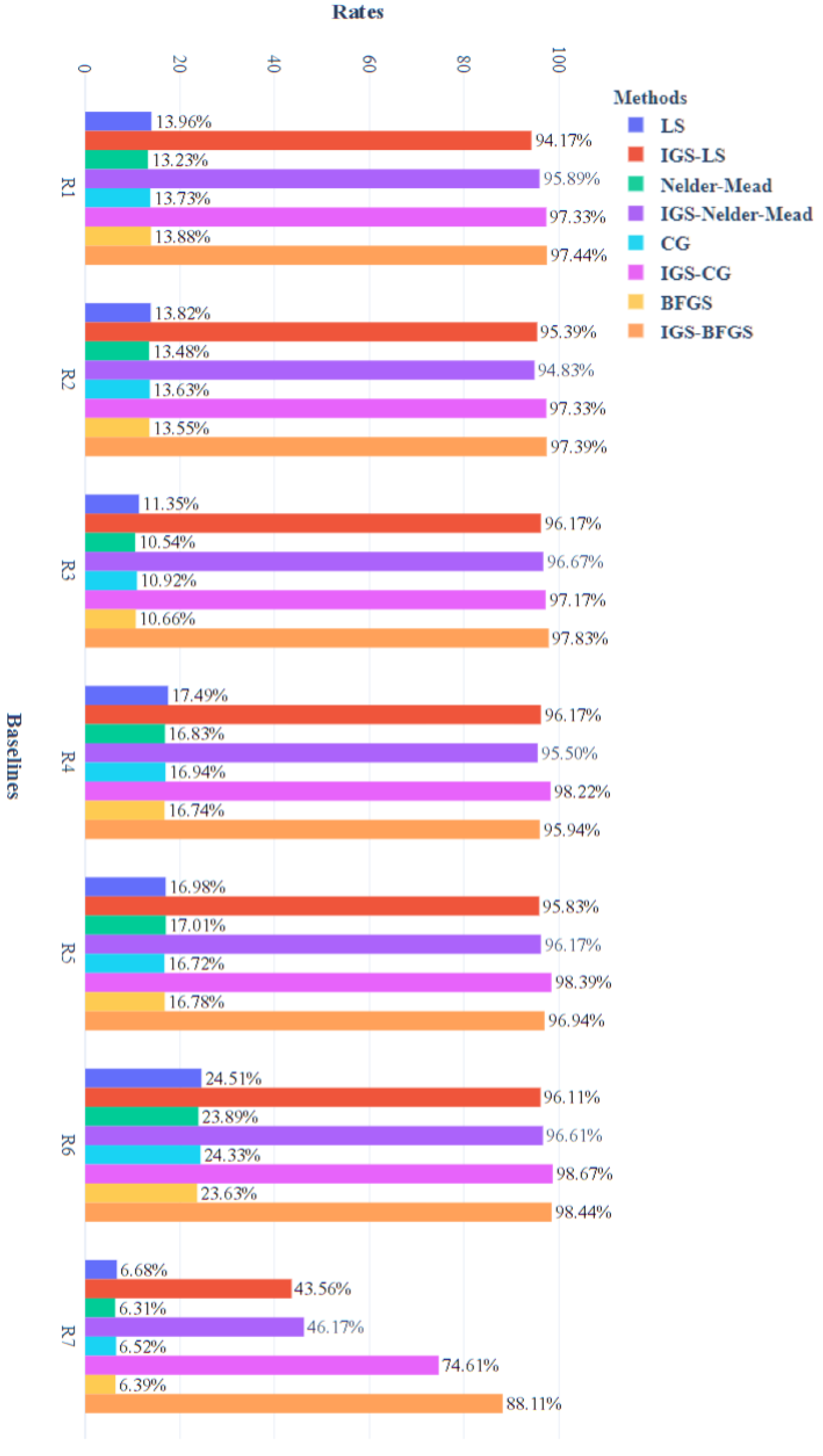
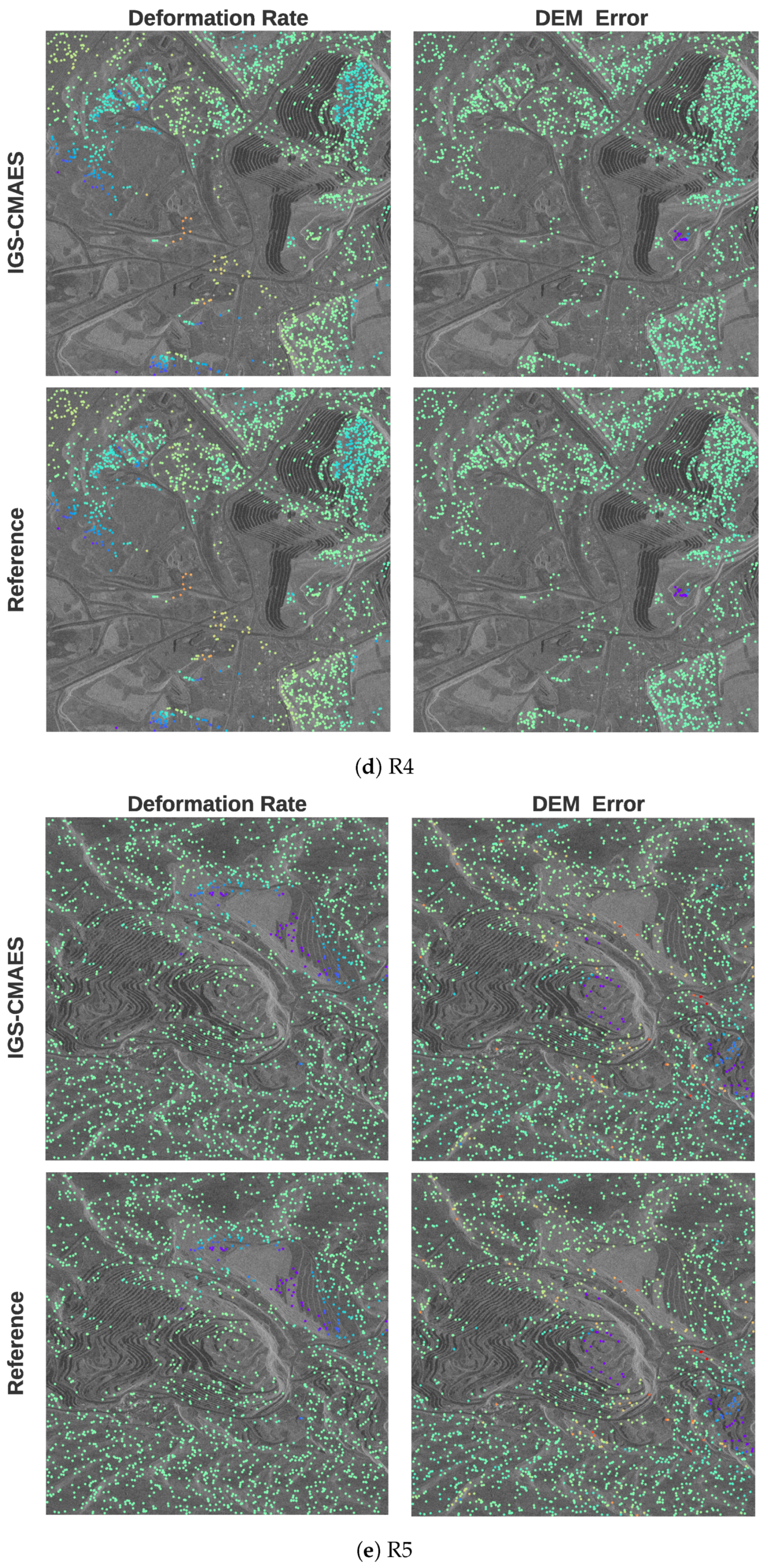
3.1. Experimental Setup
3.1.1. Simulation Data
3.1.2. Real-World Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Sousa, J.J.; Hooper, A.J.; Hanssen, R.F.; Bastos, L.C.; Ruiz, A.M. Persistent Scatterer InSAR: A comparison of methodologies based on a model of temporal deformation vs. spatial correlation selection criteria. Remote Sens. Environ. 2011, 115, 2652–2663. [Google Scholar] [CrossRef]
- Usai, S. The use of man-made features for long time scale insar. In Proceedings of the IGARSS’97. 1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997; Volume 4, pp. 1542–1544. [Google Scholar]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Reza, T.; Zimmer, A.; Blasco, J.M.D.; Ghuman, P.; Aasawat, T.K.; Ripeanu, M. Accelerating persistent scatterer pixel selection for InSAR processing. IEEE Trans. Parallel Distrib. Syst. 2017, 29, 16–30. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Ding, X.; Lu, Z. Modeling PSInSAR time series without phase unwrapping. IEEE Trans. Geosci. Remote Sens. 2010, 49, 547–556. [Google Scholar] [CrossRef]
- Hu, F.; Wu, J. Improvement of the multi-temporal InSAR method using reliable arc solutions. Int. J. Remote Sens. 2018, 39, 3363–3385. [Google Scholar] [CrossRef]
- Bekaert, D.; Walters, R.; Wright, T.; Hooper, A.; Parker, D. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Duan, W.; Zhang, H.; Wang, C. Deformation Estimation for Time Series InSAR Using Simulated Annealing Algorithm. Sensors 2019, 19, 115. [Google Scholar] [CrossRef] [Green Version]
- Anantrasirichai, N.; Biggs, J.; Kelevitz, K.; Sadeghi, Z.; Wright, T.; Thompson, J.; Achim, A.M.; Bull, D. Detecting Ground Deformation in the Built Environment using Sparse Satellite InSAR data with a Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2940–2950. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No. 03CH37477), Toulouse, France, 21–25 July 2003; Volume 7, pp. 4362–4364. [Google Scholar]
- Bert, M.K. Radar Interferometry: Persistent Scatterers Technique; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F. A new method for identification and analysis of persistent scatterers in series of SAR images. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 2, p. II-449. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F.; Trillo, F.; Vecchioli, F. Persistent scatterer pair interferometry: Approach and application to COSMO-SkyMed SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2869–2879. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Lauknes, T.R.; Zebker, H.A.; Larsen, Y. InSAR deformation time series using an L_{1}-norm small-baseline approach. IEEE Trans. Geosci. Remote Sens. 2010, 49, 536–546. [Google Scholar] [CrossRef] [Green Version]
- Fattahi, H.; Amelung, F. DEM error correction in InSAR time series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4249–4259. [Google Scholar] [CrossRef]
- Peltier, A.; Bianchi, M.; Kaminski, E.; Komorowski, J.C.; Rucci, A.; Staudacher, T. PSInSAR as a new tool to monitor pre-eruptive volcano ground deformation: Validation using GPS measurements on Piton de la Fournaise. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Patrascu, C.; Popescu, A.A.; Datcu, M. SBAS and PS measurement fusion for enhancing displacement measurements. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3947–3950. [Google Scholar]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer InSAR for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. 2007, 112, 19. [Google Scholar]
- Sica, F.; Cozzolino, D.; Zhu, X.X.; Verdoliva, L.; Poggi, G. InSAR-BM3D: A Nonlocal Filter for SAR Interferometric Phase Restoration. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3456–3467. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Zimmer, A.; Mukherjee, S.; Kottayil, N.K.; Ghuman, P.; Cheng, I. DeepInSAR—A deep learning framework for SAR interferometric phase restoration and coherence estimation. Remote Sens. 2020, 12, 2340. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tupin, F.; Reigber, A.; Jäger, M. NL-SAR: A unified nonlocal framework for resolution-preserving (Pol)(In) SAR denoising. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2021–2038. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for Interferometric Synthetic Aperture Radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Costantini, M.; Minati, F.; Trillo, F.; Vecchioli, F. Enhanced PSP SAR interferometry for analysis of weak scatterers and high definition monitoring of deformations over structures and natural terrains. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 876–879. [Google Scholar]
- Sousa, J.J.; Ruiz, A.M.; Hanssen, R.F.; Bastos, L.; Gil, A.J.; Galindo-Zaldívar, J.; de Galdeano, C.S. PS-InSAR processing methodologies in the detection of field surface deformation—Study of the Granada basin (Central Betic Cordilleras, southern Spain). J. Geodyn. 2010, 49, 181–189. [Google Scholar] [CrossRef]
- Kampes, B.; Usai, S. Doris: The delft object-oriented radar interferometric software. In Proceedings of the 2nd International Symposium on Operationalization of Remote Sensing, Enschede, The Netherlands, 16–20 August 1999; Citeseer: Princeton, NJ, USA, 1999; pp. 16–20. [Google Scholar]
- Chen, Y.; Bruzzone, L.; Jiang, L.; Sun, Q. ARU-Net: Reduction of Atmospheric Phase Screen in SAR Interferometry Using Attention-Based Deep Residual U-Net. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5780–5793. [Google Scholar] [CrossRef]
- Pu, L.; Zhang, X.; Zhou, Z.; Shi, J.; Wei, S.; Zhou, Y. A Phase Filtering Method with Scale Recurrent Networks for InSAR. Remote Sens. 2020, 12, 3453. [Google Scholar] [CrossRef]
- Mukherjee, S.; Zimmer, A.; Sun, X.; Ghuman, P.; Cheng, I. An unsupervised generative neural approach for InSAR phase filtering and coherence estimation. IEEE Geosci. Remote Sens. Lett. 2020. [Google Scholar] [CrossRef]
- Schlögl, M.; Widhalm, B.; Avian, M. Comprehensive time-series analysis of bridge deformation using differential satellite radar interferometry based on Sentinel-1. ISPRS J. Photogramm. Remote Sens. 2021, 172, 132–146. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Azadnejad, S.; Maghsoudi, Y.; Perissin, D. Evaluation of polarimetric capabilities of dual polarized Sentinel-1 and TerraSAR-X data to improve the PSInSAR algorithm using amplitude dispersion index optimization. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101950. [Google Scholar] [CrossRef]
- Liu, H.L.; Gu, F.; Zhang, Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. Evol. Comput. 2013, 18, 450–455. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.; Li, K.; Kwong, S.; Zhang, Q.; Zhang, J. Learning to decompose: A paradigm for decomposition-based multiobjective optimization. IEEE Trans. Evol. Comput. 2018, 23, 376–390. [Google Scholar] [CrossRef] [Green Version]
- Holden, D.; Donegan, S.; Pon, A. Brumadinho Dam InSAR study: Analysis of TerraSAR-X, COSMO-SkyMed and Sentinel-1 images preceding the collapse. In Proceedings of the 2020 International Symposium on Slope Stability in Open Pit Mining and Civil Engineering, Perth, Australia, 12–14 May 2020; Australian Centre for Geomechanics: Crawley, Australia, 2020; pp. 293–306. [Google Scholar]
- Kottayil, N.K.; Zimmer, A.; Mukherjee, S.; Sun, X.; Ghuman, P.; Cheng, I. Accurate Pixel-Based Noise Estimation for InSAR Interferograms. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Loshchilov, I. CMA-ES with restarts for solving CEC 2013 benchmark problems. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 369–376. [Google Scholar]
- Hansen, N. Benchmarking a BI-population CMA-ES on the BBOB-2009 function testbed. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers, Montreal, QC, Canada, 8–12 July 2009; ACM: New York, NY, USA, 2009; pp. 2389–2396. [Google Scholar]
- Hansen, N. The CMA Evolution Strategy: A Comparing Review. In Towards a New Evolutionary Computation; Lozano, J.A., Larranaga, P., Inza, I., Bengoetxea, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 192. [Google Scholar]
- Loshchilov, I.; Schoenauer, M.; Sebag, M. Alternative restart strategies for CMA-ES. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Taormina, Italy, 1–5 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 296–305. [Google Scholar]
- Salimans, T.; Ho, J.; Chen, X.; Sidor, S.; Sutskever, I. Evolution strategies as a scalable alternative to reinforcement learning. arXiv 2017, arXiv:1703.03864. [Google Scholar]
- Hansen, N.; Kern, S. Evaluating the CMA evolution strategy on multimodal test functions. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Birmingham, UK, 18–22 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 282–291. [Google Scholar]
- Hansen, N. Tutorial: Covariance Matrix Adaptation (CMA) Evolution Strategy; Institute of Computational Science, ETH Zurich: Zurich, Switzerland, 2006. [Google Scholar]
- Pitz, W.; Miller, D. The TerraSAR-X satellite. IEEE Trans. Geosci. Remote Sens. 2010, 48, 615–622. [Google Scholar] [CrossRef]
- Cusson, D.; Trischuk, K.; Hébert, D.; Hewus, G.; Gara, M.; Ghuman, P. Satellite-Based InSAR Monitoring of Highway Bridges: Validation Case Study on the North Channel Bridge in Ontario, Canada. Transp. Res. Rec. 2018, 2672, 76–86. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the Nelder-Mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Sequential quadratic programming. Numer. Optim. 2006, 35, 529–562. [Google Scholar]
- Li, D.H.; Fukushima, M. A modified BFGS method and its global convergence in nonconvex minimization. J. Comput. Appl. Math. 2001, 129, 15–35. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Gubian, S.; Suomela, B.; Hoeng, J. Generalized Simulated Annealing for Global Optimization: The GenSA Package. R J. 2013, 5, 13. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Definition | Value |
|---|---|---|
| S | Number of candidate solutions at each iteration | 30 |
| Initial step size | 0.01 | |
| Number of selected top ranked solutions | 7 | |
| Threshold value to terminate the optimization | ||
| c | Learning rate for updating evolution path | 0.5 |
| Learning rate for updating covariance matrix | 0.5 | |
| Learning rate for updating step size | 0.5 |
| Baseline | Categories | LS | IGS- LS | Nelder- Mead | IGS- Nelder- Mead | CG | IGS- CG | BFGS | IGS- BFGS |
|---|---|---|---|---|---|---|---|---|---|
| R1 | -RMSE (cm/year) | 12.2382 | 2.9481 | 12.4695 | 2.0734 | 12.5197 | 1.3484 | 12.4414 | 1.2893 |
| -RMSE (m) | 107.0381 | 0.0011 | 105.6981 | 0.0001 | 107.6607 | 0.0000 | 106.5213 | 0.0000 | |
| R2 | -RMSE (cm/year) | 13.2260 | 2.3247 | 13.3805 | 2.5936 | 13.6642 | 1.3439 | 13.6011 | 1.3143 |
| -RMSE (m) | 107.2283 | 0.0016 | 106.3737 | 0.0002 | 107.4976 | 0.0000 | 107.5918 | 0.0000 | |
| R3 | -RMSE (cm/year) | 13.0308 | 1.9413 | 13.1002 | 1.6877 | 13.3366 | 1.4307 | 13.2444 | 1.0897 |
| -RMSE (m) | 107.8291 | 0.0016 | 106.5126 | 0.0002 | 108.3554 | 0.0000 | 108.7696 | 0.0000 | |
| R4 | -RMSE (cm) | 12.7119 | 1.9372 | 13.1455 | 2.2679 | 13.1560 | 0.8951 | 13.2614 | 2.0387 |
| -RMSE (m) | 107.5101 | 0.0032 | 106.5326 | 0.0002 | 108.2290 | 0.0000 | 108.4366 | 0.0000 | |
| R5 | -RMSE (cm/year) | 12.6042 | 2.1055 | 12.6375 | 1.9330 | 12.8295 | 0.8136 | 12.8457 | 1.5362 |
| -RMSE (m) | 106.7188 | 0.0022 | 105.9384 | 0.0002 | 109.1707 | 0.0000 | 107.6000 | 0.0000 | |
| R6 | -RMSE (cm/year) | 12.4571 | 1.9549 | 12.5720 | 1.7121 | 12.5872 | 0.6817 | 12.6906 | 0.7807 |
| -RMSE (m) | 105.3393 | 0.0062 | 106.0447 | 0.0003 | 108.2960 | 0.0000 | 109.1020 | 0.0000 | |
| R7 | -RMSE (cm/year) | 12.5991 | 14.9993 | 12.6070 | 14.1472 | 12.7588 | 6.7126 | 12.6561 | 3.2887 |
| -RMSE (m) | 106.6014 | 0.0006 | 106.0582 | 0.0001 | 108.0011 | 0.0000 | 12.6561 | 0.0000 |
| Baseline | Categorie | IGS-CMAES | Grid-Search | Dual-SA |
|---|---|---|---|---|
| R1 | -RMSE | 0.0284 | 0.0967 | 0.6336 |
| -RMSE | 0.0000 | 0.5611 | 31.7574 | |
| L1-UWPD | 0.0424 | 0.1191 | 1.3113 | |
| ACC | 99.94% | 100% | 96.88% | |
| NFev | 2725.03 | 20800 | 4109.38 | |
| R2 | -RMSE | 0.1137 | 0.0967 | 0.1792 |
| -RMSE | 0.0000 | 0.5610 | 6.7533 | |
| L1-UWPD | 0.0424 | 0.1051 | 0.1279 | |
| ACC | 99.94% | 100% | 99.35% | |
| NFev | 2585.18 | 20800 | 4103.06 | |
| R3 | -RMSE | 0.1991 | 0.0967 | 0.4899 |
| -RMSE | 0.0000 | 0.5613 | 15.5361 | |
| L1-UWPD | 0.0791 | 0.1180 | 0.7239 | |
| ACC | 99.61% | 100% | 96.33% | |
| NFev | 2687.90 | 20800 | 4112.38 | |
| R4 | -RMSE | 0.2276 | 0.0967 | 0.0588 |
| -RMSE | 0.0000 | 0.5617 | 7.5336 | |
| L1-UWPD | 0.0848 | 0.0806 | 0.0534 | |
| ACC | 99.56% | 100% | 99.69% | |
| NFev | 2500.69 | 20800 | 4089.58 | |
| R5 | -RMSE | 0.2844 | 0.0967 | 0.1556 |
| -RMSE | 0.0000 | 0.5617 | 5.8893 | |
| L1-UWPD | 0.1065 | 0.0864 | 0.0853 | |
| ACC | 99.44% | 100% | 99.52% | |
| NFev | 2520.12 | 20800 | 4093.36 | |
| R6 | -RMSE | 0.0000 | 0.0967 | 0.0000 |
| -RMSE | 0.0000 | 0.5617 | 0.0000 | |
| L1-UWPD | 0.0000 | 0.0591 | 0.0000 | |
| ACC | 100% | 100% | 100.00% | |
| NFev | 2381.48 | 20,800 | 4070.47 | |
| R7 | -RMSE | 1.6145 | 7.763333 | 13.902 |
| -RMSE | 0.0000 | 0.5609 | 104.1441 | |
| L1-UWPD | 1.1259 | 5.5327 | 27.8864 | |
| ACC | 94.88% | 70% | 39.03% | |
| NFev | 3576.92 | 20800 | 4121.54 |
| Baseline | NFev | RI-MSE Proposed (Rad) | RI-MSE Reference (Rad) | WPR IGS-CMAES (Rad) | WPR Reference (Rad) | -RMSE (cm) | -RMSE (m) |
|---|---|---|---|---|---|---|---|
| R1 | 4023.67 | 0.305124 | 0.307999 | 0.431716 | 0.435595 | 0.114381 | 0.061021 |
| R2 | 3960.59 | 0.306338 | 0.307771 | 0.438660 | 0.439584 | 0.080547 | 0.053405 |
| R3 | 3872.19 | 0.238092 | 0.242657 | 0.371183 | 0.374736 | 0.109501 | 0.052438 |
| R4 | 3510.90 | 0.120080 | 0.119850 | 0.238335 | 0.238453 | 0.034719 | 0.048583 |
| R5 | 3563.92 | 0.120687 | 0.122859 | 0.249803 | 0.250186 | 0.059676 | 0.122966 |
| R6 | 3496.90 | 0.161789 | 0.161793 | 0.321250 | 0.321475 | 0.025550 | 0.102940 |
| R7 | 3817.64 | 0.191073 | 0.210659 | 0.326159 | 0.352141 | 0.190598 | 0.061347 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Zimmer, A.; Mukherjee, S.; Ghuman, P.; Cheng, I. IGS-CMAES: A Two-Stage Optimization for Ground Deformation and DEM Error Estimation in Time Series InSAR Data. Remote Sens. 2021, 13, 2615. https://doi.org/10.3390/rs13132615
Sun X, Zimmer A, Mukherjee S, Ghuman P, Cheng I. IGS-CMAES: A Two-Stage Optimization for Ground Deformation and DEM Error Estimation in Time Series InSAR Data. Remote Sensing. 2021; 13(13):2615. https://doi.org/10.3390/rs13132615
Chicago/Turabian StyleSun, Xinyao, Aaron Zimmer, Subhayan Mukherjee, Parwant Ghuman, and Irene Cheng. 2021. "IGS-CMAES: A Two-Stage Optimization for Ground Deformation and DEM Error Estimation in Time Series InSAR Data" Remote Sensing 13, no. 13: 2615. https://doi.org/10.3390/rs13132615
APA StyleSun, X., Zimmer, A., Mukherjee, S., Ghuman, P., & Cheng, I. (2021). IGS-CMAES: A Two-Stage Optimization for Ground Deformation and DEM Error Estimation in Time Series InSAR Data. Remote Sensing, 13(13), 2615. https://doi.org/10.3390/rs13132615