Petri-Net Based Multi-Objective Optimization in Multi-UAV Aided Large-Scale Wireless Power and Information Transfer Networks

Abstract

Power consumption in wireless sensor networks is high, and the lifetime of a battery has become a bottleneck, restricting network performance. Wireless power transfer with a ground mobile charger is vulnerable to interference from the terrain and other factors, and hence it is difficult to deploy in practice. Accordingly, a novel paradigm is adopted where a multi-UAV (unmanned aerial vehicle) with batteries can transfer power and information to SDs (sensor devices) in a large-scale sensor network. However, there are discrete events, continuous process, time delay, and decisions in such a complicated system. From the perspective of a hybrid system, a hybrid colored cyber Petri net system is proposed here to depict and analyze this problem. Furthermore, the energy utilization rate and information collection time delay are conflict with each other; therefore, UAV-aided wireless power and information transfer is formulated as a multi-objective optimization problem. For this reason, the MAC-NSGA II (multiple ant colony-nondominated sorting genetic algorithm II) is proposed in this work. Firstly, the optimal trajectory of multiple UAVs was obtained, and on this basis, the above two objectives were optimized simultaneously. Large-scale simulation results show that the proposed algorithm is superior to NSGA II and MOEA/D in terms of energy efficiency and information collection delay.

1. Introduction

Wireless sensor networks collect and exchange data via the interconnection between heterogeneous devices, and such networks are widely applied in intelligent logistics, smart cities, disasters, and so on [1,2]. The third and fourth generations of mobile communication technology (3G and 4G) are excellent infrastructures for supporting Internet of Things (IoT) due to the wide coverage, low deployment cost, and high security. However, it is difficult to achieve the high data rate, low latency, and low power consumption for physical communication. Fortunately, the Internet of Everything has been made possible by the advent of 5G technology, which provides connected devices with gigabit data rates and low-latency communications. The 5G-enabled WSN has consequently attracted a lot of attention from the industry and academia [3,4,5,6,7].

In fact, wireless sensor networks connect a large number of devices that consume huge amounts of power, making the lifetime of the battery a bottleneck for network performance. Energy harvesting (EH) and wireless power transfer (WPT) can be regarded as promising technologies that are able to extend a battery’s lifetime. The former absorbs energy from wind and solar but is less sustainable. Typical technologies for wireless power transfer include inductively coupled charging and electromagnetic magnetic resonance coupling, both of which can transfer power to distances ranging from centimeters to meters but not over longer distances. The wireless power transfer supported by radio frequency technology belongs to far field charging, which can transfer energy several kilometers away. Therefore, radio frequency wireless power transfer (RF-WPT) has aroused great interest in the research community and industry. Static charger is the main implementation of RF-WPT, while the disadvantage of this is that it will cause a waste of energy, and it is difficult to satisfy the various energy requirements [8,9,10]. One way to fix it is to employ a ground mobile charger to replenish the sensor devices (SDs). However, the drawbacks are also obvious. The path planning and communication quality of ground mobile chargers are susceptible to the terrain, and therefore it is difficult to replenish energy efficiently and to do so in a timely way [11,12,13,14,15,16,17].

Compared with mobile charging vehicles on the ground, UAVs have advantages of rapid deployment and high communication quality, which are particularly suitable for deployment in rural and harsh environment regions. Not only does the UAV power the SDs, but it also enables air-to-ground communication via an onboard wireless transceiver, allowing data to be collected from a wider area at a faster rate. Consequently, it is feasible to use the UAVs equipped with RF-WPT to improve the performance of wireless network [18,19,20]. Specifically, a UAV is assigned a preset the trajectory to visit SDs distributed across the target area. When hovering over a SD, the downlink provides wireless charging to the SD, while the uplink provides data transmission services.

The mobility of the UAV enables easy access to SDs; however, limited capacity makes it difficult for a single UAV to perform charging and communication tasks in a large-scale network, and hence it is necessary to deploy multiple UAVs at the same time. In addition, the generated status information needs to be delivered to the destination as quickly as possible for online data analysis and decision making, and outdated information may lead to false control or even major disasters. Therefore, on the one hand, information collection delay needs to be limited to a short period. On the other hand, the energy efficiency of UAVs should be improved as much as possible, that is to say, to replenish more energy for SDs. They are two conflicting objectives that need to be considered jointly.

Based on the above analysis, this paper constructs a multi-objective optimization for multi-UAV aided power and information transmission in order to maximize the energy utilization of the UAVs and minimize the time delay of information collection. The UAV’s energy efficiency is defined as the ratio of the energy received by SDs to the energy consumption of the UAV, which is most affected by the flight trajectory and is independent of the hover time. Therefore, the trajectory of each UAV can be assigned first, so as to minimize the cost of the UAV’s flight. Moreover, this is a typical multiple traveling salesman problem, which is NP-complete and difficult to be solved by traditional optimization methods. For this reason, the MAC-NSGA II (multiple ant colony-nondominated sorting genetic algorithm II) is proposed here to minimize the total trajectory of the UAVs, while minimizing their maximum trajectory to balance the flight load. On this basis, the Pareto optimal solution set of energy efficiency and information collection delay is obtained by NSGA II.

The multi-UAV aided wireless power and information transfer is a hybrid dynamic system, where the power transfer is continuous, and the information collection can be regarded as a discrete event due to its instantaneous completion. As a powerful visual mathematical tool, Petri net has the ability to represent concurrent and synchronous behavior. Moreover, the dynamic process triggered by the transition is not affected by the system parameters and network topology. Consequently, the wireless power and information transfer can be modeled and analyzed by Petri net [21,22].

The main contributions of the article are concentrated in the following three aspects:

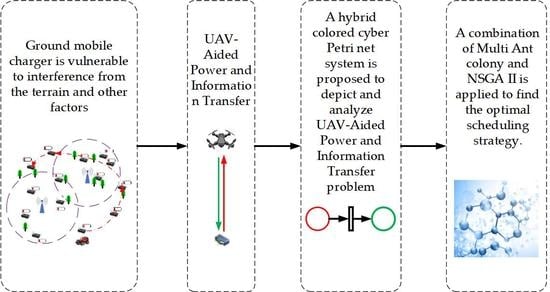
• The HCCPNS (hybrid colored cyber Petri net system) is proposed for the first time to model the multi-UAV aided wireless power and information transfer system. The place represents the status of the UAV or SD, where the continuous part is the energy, and the discrete part is information. The variation of a marking or a token corresponds to the continuous transition and the discrete transition, respectively. To the best of our knowledge, this is the first time that Petri net is employed to express the energy flow, control flow, and information flow simultaneously.
• The multi-UAV aided wireless power and information transfer is constructed as a multi-objective optimization problem. On the one hand, we hoped that the UAV can replenish more energy for SDs, thus improving energy efficiency. Since the wireless charging power is constant, this inevitably results in a longer hovering time. On the other hand, when an SD sends out the request for information transmission, it expects a UAV to arrive at the corresponding position to receive data as soon as possible, that is, the time delay of information collection should be minimal. It is not difficult to see that the two targets are in conflict and a trade-off needs to be found.
• Under the premise of one-to-one service, the strategy of trajectory assignment and hover of multiple UAVs is designed. The MAC-NSGA II is proposed in order to optimize the energy utilization and average delay of information simultaneously based on the optimal trajectory of multiple UAVs. Numerical simulation results demonstrate that the proposed algorithm has excellent performance, especially for large scale networks.

The rest of the paper is organized as follows. Section 2 reviews the work related to wireless power transfer and Petri nets. The specification of multi-UAV wireless power and information transfer based on HCCPNS is proposed, and the multi-objective optimization problem is formulated in Section 3. Section 4 presents the MSC-NSGA II. Section 5 demonstrates and analyzes the simulation results. Section 6 summarizes the paper and looks into the future research.

2. Related Work

In recent years, as a major paradigm of wireless power transfer, ground mobile charging has been widely studied. Mo et al. proposed a novel multiple mobile chargers coordination framework for a wireless rechargeable sensor network, where the scheduling, the moving time, and the charging time of the mobile chargers were jointly considered [11]. In order to maximize the overall task utility concerning sensor selection and task cooperation for wireless rechargeable sensor networks, Wu et al. proposed a novel energy allocation scheme with a specific theoretical analysis of the submodularity and gap property for the surrogate [12]. In a large-scale rechargeable wireless sensor network, Sha et al. assigned the sensor nodes into groups according to their remaining lifetime and balanced the energy consumption among several mobile wireless chargers (MWCs) to maximize the utilization rate of the MWCs and reduce the charging delay [13]. Lan et al. employed a mobile sink to charge the sensor nodes and gather data simultaneously so as to maximize the data gathering performance, and they proposed a distributed speed control and routing algorithm to reduce the computing load of the mobile sink [14]. To maintain a perpetual network operation, Lyu et al. divided the network into multiple cells and used a mobile device to charge several sensor nodes simultaneously; the mobile device periodically traversed each cell to charge and collect data with the objective of maximizing the amount of data by the unit energy of the mobile device [15]. To enhance the network utility, Zhao et al. optimized the charging vehicle route, the data rate, and the charging time together, and they presented multiple period iterative algorithms [16]. Considering that the energy consumption rate of nodes is dynamically changed, Yang et al. proposed a real-time global charging scheme in wireless rechargeable sensor networks based on the actor–critic reinforcement learning algorithm [17]. Although existing studies have made many achievements from the perspectives of charging time, data transmission delay, network utility, etc., more work is still needed, as the mobility and communication performance of mobile charging vehicles are affected by terrain and other factors, while UAV assisted charging is rarely limited.

Xu et al. employed a UAV-mounted mobile energy transmitter to deliver wireless energy to a set of energy receivers (ERs) at known locations on the ground. They optimally exploited the mobility of UAV via trajectory design to maximize the amount of transferred power to all ERs during a finite charging period [23]. Du et al. considered a UAV-enabled mobile edge computing (MEC) system, where a UAV powered IoT devices (IDs) by utilizing wireless power transfer and collected the data of them. The objective was to minimize the total energy consumption of the UAV by jointly optimizing the SD association, computing resources allocation, UAV hovering time, wireless powering duration, and the services sequence of the SDs [24]. Hu et al. took into account a simplified UAV-enabled wireless power transfer network with a linear topology, in which multiple ground nodes were deployed in a straight line. The objective was to maximize the minimum received energy among all ground nodes by optimizing the UAV’s one-dimensional trajectory, subject to the maximum UAV flying speed constraint [25]. According to the authors in [26], the UAV in their work employed RF wireless power transfer to charge the users in the downlink and to collect the information from the users in the uplink. Subject to the maximum speed constraint and the users’ energy neutrality constraints, the uplink common throughput among all ground users was maximized. Beak et al. jointly optimized the UAV hovering location and duration to maximize the minimum energy of sensors after data transmission and energy harvesting under data collection and UAV energy consumption constraints, and a near-optimal UAV route was determined by adjusting the initial feasible UAV route iteratively [27]. Su et al. proposed a novel multiple-stage dynamic matching to model the charging relationship between energy-constrained devices (ECDs) and UAVs. They maximized the total amount of charging energy by a multiple-period charging process [28]. Wu et al. studied the UAV’s trajectory optimization from the viewpoint of UAV’s energy utilization efficiency. For this purpose, they presented a polynomial-time randomized approximation scheme (PARS) to obtain the minimal number of hovering locations [29]. Subsequently, to achieve balanced energy consumption among UAVs, they maximized the energy utilization efficiency of UAVs, and they minimized the communication delay by optimizing the trajectory jointly with constraints of the energy capacity and the area of the target region [30]. Taking into account the power consumption of the UAV, the charging process from a base station to the UAV and the conversion loss of the energy harvester, Yan et al. designed two different charging schemes to maximize the sum-energy received by all sensors for a one-dimensional and a two-dimensional wireless power transfer system [31]. Hu et al. formulated an optimization problem to enhance the UAV’s sensing performance and power allocation as well as its placement, minimizing the time of transmitting data according to different communication requirements [32]. Hu et al. formulated an optimization problem to minimize the average Age of Information of the data collected from all ground sensor nodes. They used Karush–Kuhn–Tucker (KKT) conditions to find the optimal energy transfer and the data collection time allocation; through this, a UAV’s trajectory planning was obtained by dynamic programming and an ant colony heuristic algorithm [33]. Considering the UAV’s hovering inaccuracy on received power at ground deployed sensor nodes, Suman et al. proposed a hovering inaccuracy-aware optimal charging system design algorithm to find the optimal transmit power, hovering altitude, and antenna exponent [34]. Yuan et al. took into account the realistic nonlinear energy harvesting model for the first time in order to maximize the minimum harvested energy among ground devices under the constraint of a UAV’s maximum flight speed limit [35]. Caillouet et al. made a trade-off between the altitude of a drone and its charging coverage to ensure good harvesting capabilities for industrial scenarios [36]. For the studies in [37,38,39], the UAV was used to collect data from sensors, and routing protocols were studied to reduce the data loss as well as energy consumption. Although the above work involves energy consumption, UAV flight trajectory, computational performance, and other aspects, most of them use a single UAV as the energy output source, which actually limits the improvement of UAV performance. In this paper, several UAVs are used to serve SDs, and factors such as the number of UAVs, flight trajectory and communication delay are jointly considered to be applicable to large-scale wireless power and information transfer networks.

Petri net has unique advantages in the modeling and analysis of a cyber-physical system (CPS) and also automated manufacturing systems. Casalino et al. addressed the problem of scheduling robotic activities in human–robot collaborative contexts based on time Petri nets [40]. Aiming at a kind of CPS containing discrete events, continuous processes, stochastic phenomena, time delay, and decision, Cao et al. proposed the modeling methods of a CPS based on the modified hybrid stochastic timed Petri net with three-tier architecture, and they introduced a decision place to strengthen the decision-making ability of a CPS [41]. Yang et al. modeled the deadlock problem in large-scale automated manufacturing systems based on Petri nets and developed an innovative distributed approach [42]. To address the collision issue of automated guided vehicles, Luo et al. proposed an approach to the design of a maximally permissive controller to prevent vehicles from any collision using labeled Petri nets [43]. In addition, they focused on using developed timed Petri nets to model variable traffic light control systems to analyze the performance of urban traffic networks [44]. In our previous work, a generalized synchronizing colored cyber Petri net was proposed to establish the fixed chargers’ deployment, and later a hybrid cyber Petri net was applied to model and analyze the master–slave charging behavior [45,46]. In this paper, a hybrid colored cyber Petri net system is to be proposed to characterize the energy flow, information flow, and control flow relationship in UAVs’ aided wireless power and information transmission.

3. System Model and Problem Formulation

In this section, the model of wireless power and information transfer is firstly introduced. Then, based on the classical Petri net, a hybrid colored cyber Petri net system is proposed, and the dynamic behavior of the system is described from the mathematical and graphical perspectives. Finally, the multi-UAV aided wireless power and information transfer is formulated as a multi-objective optimization problem. The schematic diagram of multi-UAV aided wireless power and information transfer is illustrated in Figure 1.

3.1. UAV-Aided Wireless Power and Information Transfer Model

As shown in Figure 1, we consider a multi-UAV aided wireless power and information transfer network, where an $M$ number of UAVs replenish energy and collect the information for an $N$ number of SDs within given area. The UAVs are indexed by the set $ℳ=\left\{1,2,\cdots \cdots ,M\right\}$, and the SDs are indexed by the set $\mathcal{N}=\left\{1,2,\cdots \cdots ,N\right\}$. In a three-dimensional Cartesian coordinate system, the coordinate of the $i$th UAV can be expressed as $\left(x_i,y_i,H\right)$, and the coordinate of the $j$-th SD is represented as $\left({\mathbb{w}}_j,0\right)$. The UAV cruises at an economic speed $V_e$ for energy saving. Let $\mathbb{q}\left(t\right)=\left[x_i\left(t\right),y_i\left(t\right)\right]$ denote the coordinate projected by the $i$-th UAV on the plane $\beta$, then the flight distance of the UAV can be given. The main parameters are summarized in

Table 1. Main notations.

Notation	Description
$M$	number of UAVs
$N$	number of SDs
$P_{mov}$	moving power of the UAV
$P_{hov}$	hovering power of the UAV
$P_{tra}$	transmitting power of the UAV
$E_{j,rec}^i$	received energy of the $j$th SD from the $i$th UAV
$E_{mov}^i$	moving energy of the $i$th UAV
$E_{hov}^i$	hovring energy of the $i$th UAV
$E_{tra}^i$	transmitting energy of the $i$th UAV

.

Assuming that a UAV starts from and returns to the depot, it should immediately fly back to the depot if the energy is carried below a certain threshold. Let the flight period be $T$, then

$$q_i\left(0\right)=q_i\left(T\right)=\left(x_0,y_0\right),i\in ℳ$$

(1)

Assuming that the UAV is flying at a fixed altitude H, H is then the minimum height at which obstacles such as buildings, trees, and streetlights can be avoided. Moreover, there are three modes of power consumption: flight, hovering, and power transmission. The first two are driven by propulsion power and shown as follows,

$$P_{pro}\left(V\right)=P_0\left(1+\frac{3V^2}{U_{tip}{}^2}\right)+P_i{\left(\sqrt{1+\frac{V^4}{4v_0{}^4}}-\frac{V^2}{2v_0{}^2}\right)}^{\frac{1}{2}}+\frac{1}{2}{d}_0\rho sA{V}^3$$

(2)

where $P_0$ and $P_i$ are two constants representing the blade profile power and induced power in hovering status, respectively; $U_{tip}$ denotes the tip speed of the rotor; $v_0$ is known as the mean rotor induced velocity in hover; $d_0$ and $s$ are fuselage drag ratio and rotor solidity, respectively; and $\rho$ and $A$ denote the air density and rotor disc area [28]. During the flight of the UAV, if the additional losses caused by acceleration and deceleration are ignored, the moving power is

$$P_{mov}=P_{pro}\left(V=V_e\right)$$

(3)

and the hovering power is

$$P_{hov}=P_{pro}\left(V=0\right)=P_0+P_i$$

(4)

The channel power gain at time $t$ between the $i$-th UAV and $j$-th SD is

$$h_{i,j}\left(t\right)=\frac{{\beta }_0}{\parallel q_i\left(t\right)-w_j\parallel {}^2+H^2}$$

(5)

where ${\beta }_0$ is the channel power gain at a reference distance 1 m, and $\parallel ·\parallel$ is the Euclidean norm. The receiving power of SD at time $t\in T$ is

$$P_{rec}={\eta }^{\prime }{P}_{tra}{h}_{i,j}\left(t\right)$$

(6)

where $P_{tra}$ is the transmitting power of UAV, and $0\le {\eta }^{\prime }\le 1$ is the energy efficiency of RF-WPT.

The UAV’s energy utilization rate is denoted as $\varphi$, which is the ratio of the total energy received by the SDs to the total energy consumed by the UAV. Since the UAV energy consumption consists of flight, hovering, and power transmission, then the UAV energy utilization rate is

$$\varphi =\frac{{{\displaystyle \sum }}_{j=1}^N{E}_{j,rec}^i}{E_{mov}^i+E_{hov}^i+E_{tra}^i}$$

(7)

Since the amount of data perceived by a SD is not large, it can be considered that the moment a UAV arrives directly above a SD is the moment the UAV receives the information. Compared with the charging time, this process is considered to be instantaneous, and hence the time of wireless information transfer is ignored. In Equation (8), $t_k^i$ denotes the charging time of the $i$-th UAV for the $k$-th SD. Once the trajectory of the UAV is determined, the time delay of information transfer in SD $I_j$ can be expressed as

$$\Delta {\tau }_j={\displaystyle \sum }_{k=1}^{j-1}{t}_k^i+\frac{d_{j-1,j}}{V_{eco}}$$

(8)

Moreover, the average time delay can be given as

$$\overline{\Delta \tau }=\frac{1}{N}{\displaystyle \sum }_{j=1}^N\Delta {\tau }_j$$

(9)

The objective of this paper is to maximize the UAVs’ energy utilization rate while minimizing the average time delay of information transfer. The numerator in $\varphi$ is related to hovering time, and the denominator involves both flight time and hovering time. Shorter flight time and longer hovering time can increase $\varphi$; however, the average time delay is positively correlated with hovering time. Therefore, maximizing the energy utilization rate and minimizing the average time delay are in conflict with each other, which is a multi-objective optimization problem.

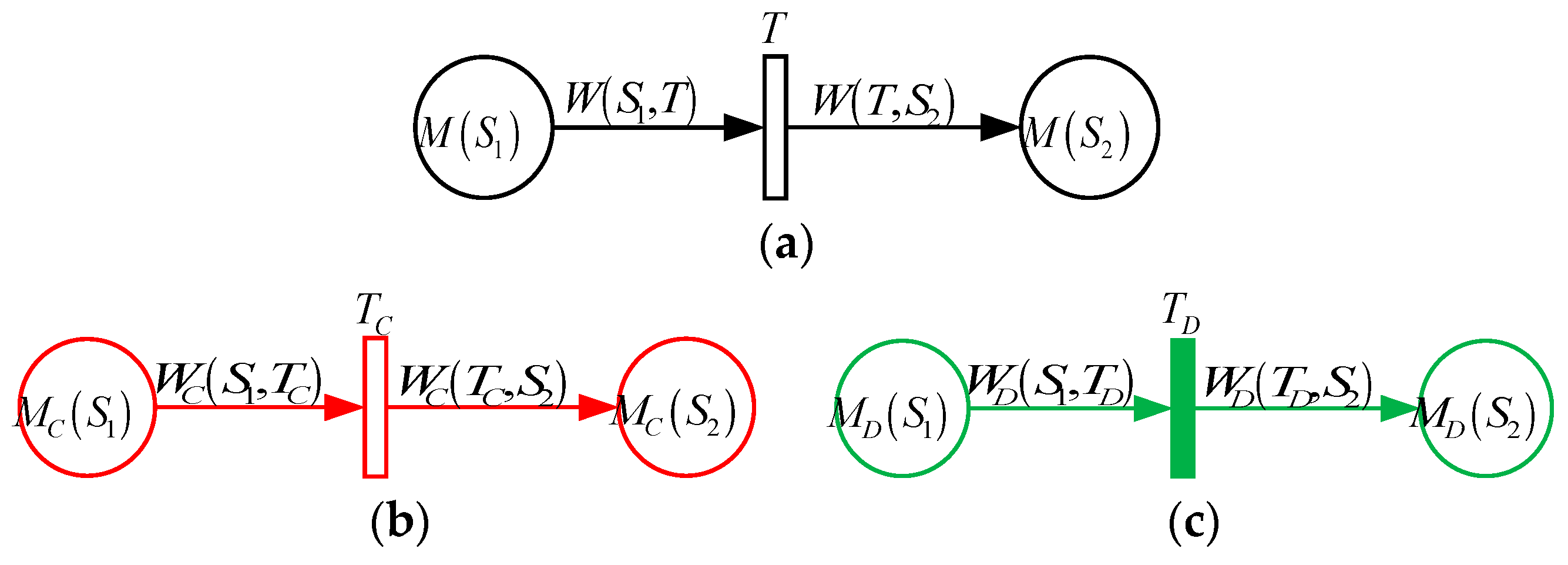
3.2. The Specification of Petri Net

Petri nets are usually applied to characterize asynchronous and concurrent behaviors, which depict the logical relationship between events and deduce the state activities of the system with an algebraic matrix based on network theory. The classical Petri net consists of place, transition, token, and incidence matrix. On this basis, we extended it to be suitable for describing wireless power transmission. For more details, please refer to our previous work [41,42]. Furthermore, in order to character the state and behavior of multi-UAV aided wireless power and information transfer, we propose a hybrid colored cyber Petri net system, and the definition is as follows.

Definition 1.

A 11-tuple${\displaystyle \sum }=\left(S,T;F,C,W,M;Rd,Wr,Inhibit,Permit,K\right)$is said to be a hybrid colored cyber Petri net system (HCCPNS), if it satisfied the following conditions:

(1) 

$N=\left(S,T;F\right)$is a directed net, which is named the basic net of${\displaystyle \sum }$;

(2) 

C is the vector of colors with red and green,$C=\left\{c_1,c_2\right\}$;

(3) 

The place, transition, and weight function of directed arc all contain two colors; the red one represents the continuous part and the green one represents the discrete part, i.e.,$M\left(S\right)=\left[M_C\left(S\right),M_D\left(S\right)\right]$,$T=\left[T_C,T_D\right]$,$W=\left[W_C,W_D\right]$;

(4) 

$F\subseteq S\times T\cup T\times S$,$Rd\subseteq S\times T$,$Wr\subseteq T\times S$and$F\cap Rd\cap Wr=\Phi$;$F$,$Rd$,$Wr$,$Inhibit$and$Permit$is the flow, read, write, inhibitor, and permission relationship;

(5) 

$K=\left\{k_L,k_H\right\}$is the lower and upper capacity function of$N$, and$k_L:S\to ℝ;k_H:S\to ℝ$,where$ℝ$is a set of real numbers;

(6) 

$W:F\to ℝ\cup Exp\left(S,\tau \right)$is the weight function, where$Exp\left(S,\tau \right)$is the set of functional expressions for$\tau$;

(7) 

$M:F\to ℝ$is the marking, and$M_0$is the initial marking.

Definition 2.

The condition that transition$t$will be fired:

$$\begin{gathered} \forall s\in {}_{}{}^{•}t:\left(M\left(s\right)-W_M\left(s,t\right)\right)\in \left[k_L\left(s\right),k_H\left(s\right)\right]\wedge \\ \forall s\in t^{•}:\left(M\left(s\right)+W_M\left(t,s\right)\right)\in \left[k_L\left(s\right),k_H\left(s\right)\right] \\ \wedge \forall s\in t_W^{•}:W\left(t,s\right)\in \left[k_L\left(s\right),k_H\left(s\right)\right] \end{gathered}$$

(10)

If transition t is fired, it can be recorded as$M[t>$.

Definition 3.

Result of transition firing. After transition t is fired, the original marking$M$will be changed to$M^{\prime }$, then

$$M{\left(s\right)}^{\prime }=\{\begin{array}{c}M\left(s\right)-W\left(s,t\right)\\ M\left(s\right)+W\left(t,s\right)\\ M\left(s\right)-W\left(s,t\right)+W\left(t,s\right)\\ W\left(t,s\right)\\ M\left(s\right)\end{array}\begin{array}{c}s\in {}_{}{}^{•}t-t^{•}\\ s\in t^{•}-{}_{}{}^{•}t\\ s\in {}_{}{}^{•}t\cap t^{•}\\ s\in t_W^{•}\\ s\notin \left({}_{}{}^{•}t\cap t^{•}\cup t_W^{•}\right)\end{array}$$

(11)

The dynamic equation of HCCPNS is:

$$M\left(t_n\right)=\left[\begin{array}{c}{M}_C\left(t_n\right)\\ M_D\left(t_n\right)\end{array}\right]+\left[\begin{array}{c}{A}_C·\left[{{\displaystyle \int }}_{t_0}^{t_n}( )\right]d\tau \\ A_D\end{array}\right]$$

(12)

where$A_C$and$A_D$are the incidence matrix of the continuous and discrete part, respectively.

A simple HCCPNS model is shown in Figure 2. Figure 2a is the folded specification, and Figure 2b is the unfolded specification as well as Figure 2c. They represent the continuous parts and the discrete part denoted in red and green, respectively, i.e., $M\left(S_1\right)=\left[M_C\left(S_1\right),M_D\left(S_1\right)\right]$, $M\left(S_2\right)=\left[M_C\left(S_2\right),M_D\left(S_2\right)\right]$, $T=\left[T_C,T_D\right]$, $W\left(S_1,T\right)=\left[W_C\left(S_1,T_C\right),W_D\left(S_1,T_D\right)\right]$, $W\left(T,S_2\right)=\left[W_C\left(T_C,S_2\right),W_D\left(T_D,S_2\right)\right]$.

In fact, multi-UAV aided wireless power and information transfer is a dynamic system in which the location of the UAV changes over time. It is necessary to monitor the UAV’s energy status in real time and pay attention to the event of arrival or departure from the hovering point. Therefore, this is a hybrid system with continuous and discrete variables, and it is appropriate for HCCPNS to describe its formal specification.

Figure 3 shows a representative part of the HCCPNS model for a multi-UAV aided wireless power and information transfer system. Directed arcs with solid black dots and hollow circles at the end of the arrows are the permit arc and the inhibit arc, respectively. The arrow of the read arc and the write arc are both in the middle of directed arc. The explanation of the main places, transitions, and arcs are given in

Table 2. Description of representative places and transitions.

Name	Function
$U_j^i$	Place when the $i$-th UAV hovers directly over the $j$-th SD
$I_j$	Place of the $j$-th SD
$T{\left(i\right)}_{j+1}^j$	Transition that the $i$-th UAV flies from the $j$-th to ($j+1$)th SD
$T{h}_j^i$	Transition that the $i$-th UAV hovers directly over the $j$-th SD
$T{d}_j^i$	Transition that the $i$-th UAV collects information from the $j$-th SD
$T_{se{n}_j}$	Transition that the $j$-th SD consumes energy
$Teme\left(i\right)$	Transition that the $i$-th UAV returns to the depot emergently

and

Table 3. Description of representative arcs.

Arc	Weight
$W_C\left(U_j^i,T{\left(i\right)}_C{}_{j+1}^j\right)$	$M_C\left(U_j^i\_t_j^{+}\right)$
$W_D\left(U_j^i,T{\left(i\right)}_D{}_{j+1}^j\right)$	$M_D\left(U_j^i\_t_j^{+}\right)$
$writ{e}_D\left(T{\left(i\right)}_D{}_{j+1}^j,U_{j+1}^i\right)$	$M_D\left(U_j^i\_t_j^{+}\right)$
$writ{e}_C\left(T{\left(i\right)}_C{}_{j+1}^j,U_{j+1}^i\right)$	$M_C\left(U_j^i\_t_j^{+}\right)$-$P_{mov}\times t_{j,j+1}$
$W\left(U_j^i,T{h}_j^i\right)$	$P_{hov}$
$W\left(U_j^i,T{c}_j^i\right)$	$P_{tra}$
$W\left(T{c}_j^i,I_j\right)$	$P_{rec}$
$W\left(I_j,T_{se{n}_j}\right)$	$P_{sen}^j$
$W\left(I_j,T{d}_j^i\right)$	1
$write\left(T{d}_j^i,U_j^i\right)$	1
$inhibit\left(I_j,T{c}_j^i\right)$,$permit\left(I_j,T{\left(i\right)}_{j+1}^j\right)$,	$M_C\left(I_j\right)=k_H\left(I_j\right)$
$inhibit\left(U_j^i,T{c}_j^i\right)$,$inhibit\left(U_j^i,T{h}_j^i\right)$, $inhibit\left(U_j^i,T{\left(i\right)}_{j+1}^j\right)$	$M_C\left(U_j^i\right)=k_L\left(U_j^i\right)$
$permit\left(U_j^i,Teme\left(i\right)\right)$	$M_C\left(U_j^i\right)=k_L\left(U_j^i\right)$

.

When the $i$-th UAV arrives right above the $j$-th SD, discrete transition $T{d}_j^i$ fires immediately, that is, the information sensed by the SD is collected. At this point, continuous transition $T{c}_j^i$ and $T{h}_j^i$ are also enabled. Furthermore, $T{c}_j^i$ is inhibited by $inhibit\left(I_j,T{c}_j^i\right)$ when the charging threshold is reached. In the meanwhile, $permit\left(I_j,T{\left(i\right)}_{j+1}^j\right)$ enables the transition $T{\left(i\right)}_{j+1}^j$ and disables $T{h}_j^i$. If the UAV is in the emergency, $inhibit\left(U_j^i,T{c}_j^i\right)$, $inhibit\left(U_j^i,T{h}_j^i\right)$, and $inhibit\left(U_j^i,T{\left(i\right)}_{j+1}^j\right)$ are all fired, meaning that the UAV can no longer serve for the SD. Instead, it should return to the depot immediately with the firing of $permit\left(U_j^i,Teme\left(i\right)\right)$. The time a UAV arrives at and leaves the $j$-th SD is denoted as $t_j^{-}$ and $t_j^{+}$; the hovering time is denoted as $t_j^i$. If the model in Figure 3 is unfolded, the flow of continuous energy and discrete information, as well as the control strategy of arc weight function, can be more clearly demonstrated. For example, $U_j^i$ is the place when the $i$-th UAV hovers directly over the $j$-th SD, then $M\left(U_j^i\right)=\left[M_C\left(U_j^i\right),M_D\left(U_j^i\right)\right]$, where $M_C\left(U_j^i\right)$ and $M_D\left(U_j^i\right)$ denote the UAV’s energy and carrying information. $T{\left(i\right)}_{j+1}^j=\left[T{\left(i\right)}_C{}_{j+1}^j,T{\left(i\right)}_D{}_{j+1}^j\right]$, $T{\left(i\right)}_C{}_{j+1}^j$ and $T{\left(i\right)}_D{}_{j+1}^j$ are used to transmit energy and information, respectively. As for the weight function of arc, i.e., $W\left(U_j^i,T{\left(i\right)}_{j+1}^j\right)=\left[W_C\left(U_j^i,T{\left(i\right)}_C{}_{j+1}^j\right),W_D\left(U_j^i,T{\left(i\right)}_D{}_{j+1}^j\right)\right]$, it indicates that the marking of place $U_j^i$ is 0 after transition $T{\left(i\right)}_{j+1}^j$ is finished, and the corresponding energy and information is written to place $U_{j+1}^i$ according to $write\left(T{\left(i\right)}_{j+1}^j,U_{j+1}^i\right)=\left[writ{e}_C\left(T{\left(i\right)}_C{}_{j+1}^j,U_{j+1}^i\right),writ{e}_D\left(T{\left(i\right)}_D{}_{j+1}^j,U_{j+1}^i\right)\right]$. In addition, some transitions such as $T{h}_j^i$ and $T_{se{n}_j}$ only represent the flow of continuous energy, and hence the discrete component is 0.

Based on the above analysis, the HCCPNS specification of energy utilization is given as follows.

$$\mathsf{\Phi }=\frac{{{\displaystyle \sum }}_{i=1}^M{{\displaystyle \sum }}_{j=1}^N\left[W\left(T{c}_j^i,I_j\right)·t_j^i\right]}{{{\displaystyle \sum }}_{i=1}^M\left\{\left(P_{mov}^i·t_{j,j+1}\right)+\left[W\left(U_j^i,T{h}_j^i\right)+W\left(U_j^i,T{c}_j^i\right)\right]·t_j^i\right\}}$$

(13)

Thus, the multi-objective optimization problem can be formulated:

$$P1:arg\underset{\Phi ,\overline{\Delta \tau }}{min}F=\left\{{\Phi }^{-1},\overline{\Delta \tau }\right\}$$

(14)

$$\mathrm{s}.\mathrm{t}.\frac{k_H\left(I_j\right)\times \delta -M_C\left(I_j\_t_j^{-}\right)}{P_{rec}^j-P_{sen}^j}\le t_j^i\le \frac{k_H\left(I_j\right)-M_C\left(I_j\_t_j^{-}\right)}{P_{rec}^j-P_{sen}^j}$$

(15)

$$M_C\left(U_j^i\right)\ge k_L\left(U_j^i\right)$$

(16)

where Equation (15) gives the upper and lower bounds of the hovering time; $0.5<\delta \le 1$ is the charging threshold; and Equation (16) indicates that a UAV’s energy should not fall below the lower bound, otherwise it will fly back to the depot.

As can be seen from the above, HCCPNS depicts multi-UAV aided wireless power and information transfer from both visual graphics and mathematical formulas. On the one hand, the original abstract model can be visualized. On the other hand, the dynamic equation not only reveals the result of logical evolution, but it also captures the changes of system state. These properties provide an observable interface for the evaluation of the optimization method and the theoretical and practical basis for further improvement of the control effect.

4. Multiple Ant Colony-Nondominated Sorting Genetic Algorithm II

Multi-UAV aided wireless power and information transfer is a multi-objective optimization problem, and there are two difficulties: firstly, how to allocate a large number of SDs to different UAVs in an optimal order, and secondly, how to determine the hovering time of the UAV so that the SDs can receive a certain amount of energy and ensure that the time delay of information collection is as short as possible.

We notice that in problem $P1$, the energy efficiency of UAV and the average time delay of information transfer are optimized simultaneously. Moreover, the moving time and hovering time are independent, while the former only depends on the trajectory. Therefore, the first step is to minimize the moving time of several UAVs. Substantially, this is a multi-traveling salesman problem, which can be reduced to a traveling salesman problem. Obviously, it is an NP-complete (nondeterministic polynomial-complete) problem, which is difficult to solve by classical optimization methods. It can be known from literature [47] that ant colony algorithm simulates the foraging behavior of ants in nature and is a heuristic algorithm to find the optimal path. Compared with the heuristic algorithms such as particle swarm optimization algorithm and simulated annealing algorithm, ant colony algorithm is more suitable to solve the path planning problem. Professor Deb proposed NSGA II (nondominated sorting genetic algorithm II) in literature [48], where the fast nondominated sorting with elite strategy and the crowded distance principle are employed to strengthen the diversity and uniformity of a noninferior solution set, improving the defects of the NSGA algorithm, such as slow searching speed and easy to fall into the local optimal. For this reason, the MAC-NSGA II (multi-ant colony-nondominated sorting genetic algorithm II) is proposed. In trajectory planning, the total flight trajectory of multiple UAVs is minimized. Moreover, the longest path among them is minimized by using the min–max framework to balance the flight load. On this basis, the Pareto sets of the hovering time and energy utilization of the UAVs are obtained. Therefore, MAC-NSGA II refers to a combination of a multiple ant colony algorithm and NSGA II. The state transition and pheromone update strategies in the algorithm are explained below, and NSGA II will not be detailed. The algorithm pseudocode is given in Algorithm 1.

4.1. Ant State Transition Strategy

Ant colony algorithm is an iterative technique with random search that is inspired by real ant colony foraging behavior. As ants search for food, they release chemicals called pheromones along the way. Over time, pheromone concentration varies with the accumulation of passing ants and the volatilization of the pheromone itself.

Algorithm 1 Pseudo-code of the multiple ant colony-nondominated sorting genetic algorithm II

Input: Number of UAVs and SDs, Location of the depot and SDs, Residual energy and power consumption of SDs

Output: Optimal trajectory of UAVs, the set of hovering

1: Initialize all parameters and pheromone trails; 2: $iter\leftarrow 0$;

3: while $iter\le ite{r}_{max}$ do

4: for each UAV 5:  for each SD 6:   generate initial solution with pheromone concentration and distances between SDs; 7:  end for 8:  construct solution following (20); 9: update the pheromone following (21) and according to the residual pheromone and the length of path;

10: end for

11: end while

12: Obtain the optimal flying trajectory; 13: Taking the hovering time above every SD as independent variable, initialize the population $P_t$; 14: Combine parent and offspring population $R_t=P_t\cup Q_t$; 15: all nondominated of $R_t$: $F=fast-non-dominated-sort\left(R_t\right)$; 16: $P_{t+1}=\varnothing$ and $i=1$; 17: while $\left|P_{t+1}\right|+\left|F_i\right|\le N$ do 18: calculate crowding-distance in $F_i$; 19: $P_{t+1}=P_{t+1}\cup F_i$; 20: $i=i+1$; 21: $Sort\left(F_i,{\prec }_n\right)$; 22: Choose the first $\left(N-P_{t+1}\right)$ element of $F_i$,$P_{t+1}=P_{t+1}\cup F_i\left[1:\left(N-P_{t+1}\right)\right]$; 23: Use selection, crossover and mutation to create a new population $Q_{t+1}=make-new-pop\left(P_{t+1}\right)$; 24: $t=t+1$; 25: end while 26: The pareto set of hovering time.

In this way, the ants find the shorter route to the food by selecting the path with high pheromone concentration, thus forming a pheromone-based positive feedback and autocatalysis mechanism between individual ants and colonies. In this paper, the ants and cities are regarded as UAVs and SDs, respectively. At the initial moment, the ants visit different nodes from the depot for path selection, and the following factors should be taken into consideration when selecting the next node:

• The greater the pheromone concentration from one location to the next, the more likely the ant is to choose that path.
• The shorter the distance between the current position and the next position the ant traverses, the greater the probability that the ant chooses the path.

Based on the above factors, the state transition formula is given as follows:

$$p_{ij}^k\left(t\right)=\{\begin{array}{cc}\frac{{\left[{\sigma }_{ij}\left(t\right)\right]}^{\alpha }·{\left[{\eta }_{ij}\left(t\right)\right]}^{\beta }}{{{\displaystyle \sum }}_{s\in allowed}{\left[{\sigma }_{is}\left(t\right)\right]}^{\alpha }·{\left[{\eta }_{is}\left(t\right)\right]}^{\beta }},& j\in allowed\\ 0& others\end{array}$$

(17)

where ${\sigma }_{ij}\left(t\right)$ is the pheromone concentration between two positions in $t$-th iteration; ${\eta }_{ij}\left(t\right)$ is a reciprocal of distance; $\alpha$ is weight coefficient as well as $\beta$; and $allowed$ is an alternative city set for ants.

4.2. Pheromone Update Strategies

In order to avoid too much residual pheromones submerging the heuristic information, the residual pheromones on the path should be updated after each ant completes the traversal of all nodes in each round. Therefore, the pheromone updating strategy concentration is as follows:

$${\sigma }_{ij}\left(t+1\right)=\left(1-\rho \right)·{\sigma }_{ij}\left(t\right)+{\displaystyle \sum }_{k=1}^m\Delta {\sigma }_{ij}^k\left(t\right)$$

(18)

where $\rho$ is pheromone volatility coefficient, and ${{\displaystyle \sum }}_{k=1}^m\Delta {\sigma }_{ij}^k\left(t\right)$ represents the pheromone content added in $t$-th round. The current pheromone concentration is not only related to the previous round of pheromone concentration, but also the following factors should be considered:

(1)

Pheromones $\lambda$ that are positively correlated with the superiority of feasible solutions are uniformly added to all subpath.

(2)

If the length of the subpath is less than the mean of all the subpaths, $\lambda$ is reduced to $\left(0.7~0.95\right)\lambda$. On the contrary, $\lambda$ is reduced to $\left(0.1~0.5\right)\lambda$.

(3)

The pheromone of the shortest subpath and the longest subpath is reduced to$0.1\lambda$, so that they can be recombined to form a better feasible solution.

5. Simulation and Numeric Results

5.1. Simulation Setup and Environment Parameters

This section demonstrates the performance of the proposed algorithm through large-scale numerical simulation. Unless otherwise stated, the values are set as follows (

Table 4. Simulation parameters.

Parameter	Value	Parameter	Value
$N$	$\left\{100,200,\cdots ,1000\right\}$	$h_0$	$\left(200,200\right)$
$\mathrm{A}({\mathrm{m}}^2$)	0.503	$v_0$	4.03
$U_{tip}\left(\mathrm{m}/\mathrm{s}\right)$	120	$d_0$	0.6
$s$	0.05	$\rho \left(\mathrm{kg}/{\mathrm{m}}^3\right)$	1.225
$H\left(\mathrm{m}\right)$	20	$P_{hov}\left(\mathrm{W}\right)$	13.7
$V_e\left(\mathrm{m}/\mathrm{s}\right)$	10	$P_{mov}\left(\mathrm{W}\right)$	30
${\eta }^{\prime }$	90%	$P_{tra}\left(\mathrm{W}\right)$	3
$M\left({\mathrm{m}}^2\right)$	$400\times 400$	${\rho }_0\left(\mathrm{dB}\right)$	−60

).

UAVs are allocated to serve for$N$ SDs, which are randomly and evenly distributed over a $400\times 400 {\mathrm{m}}^2$ area. To simplify the analysis, the acceleration and deceleration process of the UAV is ignored when it leaves and arrives at the hovering point. The depot’s coordinate is $h_0=\left(200 \mathrm{m},200 \mathrm{m}\right)$, and the cruising speed of a UAV is $V_e=10 \mathrm{m}/\mathrm{s}$. Moreover, when the UAV takes off from the depot, it flies at a fixed altitude $H=20 \mathrm{m}$ with a constant speed. The main simulation parameters are given in Table 4. Since more than two objectives can be optimized at the same time, NSGAIII and MOEA/D were selected for a comparison algorithm. Each scenario was run 50 times independently, and the average value was statistically analyzed.

In addition, we used the three criteria described below.

(1)

UAV’s trajectory. This indicator reflects the influence of the number of UAVs on the trajectory length.

(2)

UAV’s energy efficiency. It represents the proportion of the energy received by SDs in the total energy consumption of UAVs, which is affected by different network sizes and the number of UAVs.

(3)

Average time delay of information collection. This index reflects the timeliness of gathering information perceived by SDs.

5.2. Performance

This section compares the change trend of flight path between MAC-NSGA II, NSGAIII, and MOEA/D when the number of SDs increases from 100 to 1000. As shown in Figure 4, when the number of UAVs is 6, the longest trajectory of MAC-NSGA II is the shortest among the three algorithms, and the difference is not obvious as the network size is small. However, the longest path of the other two algorithms can be as high as 1.5 times of the proposed algorithm with the increase of network size. In terms of average growth rate, the proposed algorithm recorded about 40%, and the other two algorithms are also significantly higher, which are 47% and 48% respectively. The reason for this phenomenon is that the other two algorithms have no practical strategy to adjust the path structure, while the min–max framework is introduced into the proposed algorithm to further reduce the longest trajectory of UAVs and balance the flight load between UAVs.

Figure 5 and Figure 6 also reveal the results of the longest trajectory and average trajectory at different network scales when the number of UAVs is 6, 9, 12, and 15. It is not difficult to see that the performance of the 15 UAVs in the large-scale network outperforms the other three conditions in both the longest trajectory and the average trajectory. The reason is that in a small-scale network, a handful of UAVs can realize power and information transmission. In this case, increasing UAVs can reduce the number of SDs traversed by each UAV, yet its flight trajectory cannot be significantly reduced, which is actually a wasteful strategy. Nevertheless, in a large-scale network, as the number of SDs grows exponentially, the original UAVs can only complete their missions by expanding their flight range and increasing the number of SDs serving them, which is more time-consuming and more burdensome. If the scale of UAVs is expanded, the flight load of each UAV can be reduced and the energy efficiency can be improved.

Figure 7 shows the worst value and median value of the Pareto optimal solution for the average delay of the longest trajectory information collection of six UAVs under different network scales. The maximum delay of MACO-NSGA II decreases by 27.7% and 43.4% compared with NSGAIII and MOEA/D, respectively, while the median value decreases by 25.3% and 43%, respectively. The reason is that although the other two algorithms can optimize more than two targets at the same time, they do not have a separate path optimization framework. In addition, it can be found that with the increase of network size, the average time delay of the three algorithms is significantly reduced. This is because when the distribution area remains unchanged, the increase in the number of SDs means that the distribution density becomes larger, thus shortening the distance of the hovering point of a UAV.

Table 5. The energy efficiency of UAV with longest trajectory.

Number of SDs	Number of UAVs	MAC-NSGA II				NSGAIII		MOEA/D
		Optimal	Worst	Average	Median	Optimal	Median	Optimal	Median
200	6	2.13%	1.08%	1.64%	1.69%	2.02%	1.59%	1.93%	1.54%
	9	2.15%	1.13%	1.69%	1.72%	2.06%	1.62%	1.97%	1.57%
	12	2.16%	1.17%	1.75%	1.82%	2.09%	1.72%	1.97%	1.69%
	15	2.21%	1.32%	1.84%	1.88%	2.12%	1.79%	2.00%	1.70%
400	6	1.90%	0.66%	1.32%	1.33%	1.80%	1.27%	1.73%	1.25%
	9	1.92%	0.69%	1.33%	1.35%	1.83%	1.30%	1.75%	1.27%
	12	2.00%	0.80%	1.42%	1.39%	1.92%	1.34%	1.82%	1.30%
	15	2.09%	0.98%	1.58%	1.61%	1.97%	1.51%	1.84%	1.47%
600	6	1.58%	0.39%	0.93%	0.90%	1.49%	0.84%	1.43%	0.79%
	9	1.72%	0.51%	1.09%	1.03%	1.61%	0.97%	1.55%	0.92%
	12	1.74%	0.51%	1.17%	1.19%	1.67%	1.12%	1.57%	1.07%
	15	1.88%	0.64%	1.28%	1.30%	1.77%	1.22%	1.71%	1.14%
800	6	1.48%	0.33%	0.83%	0.84%	1.39%	0.80%	1.35%	0.73%
	9	1.51%	0.35%	0.86%	0.87%	1.44%	0.77%	1.37%	0.75%
	12	1.70%	0.47%	1.03%	1.00%	1.62%	0.94%	1.57%	0.89%
	15	1.77%	0.53%	1.12%	1.13%	1.67%	1.07%	1.63%	1.04%
1000	6	1.20%	0.22%	0.62%	0.58%	1.13%	0.54%	1.09%	0.51%
	9	1.49%	0.34%	0.86%	0.83%	1.42%	0.79%	1.35%	0.74%
	12	1.54%	0.36%	0.90%	0.87%	1.47%	0.82%	1.39%	0.78%
	15	1.60%	0.40%	0.95%	0.95%	1.51%	0.89%	1.46%	0.84%

demonstrates the optimal value, worst value, mean value and median value of the energy efficiency of the longest trajectory under 20 scenarios. Due to space limitation, only the optimal and median values of the two comparison algorithms are given. In terms of optimal value, NSGAII and MOEA/D increased by 5.28% and 10.12%, respectively, when compared with MACO-NSGA II, while they increased by 6.18% and 11.02% respectively on the median value. Moreover, with the same number of UAVs, the energy efficiency of the three algorithms decreased significantly as the network size increased. The reason is that compared with the more received energy by SDs, the flight energy consumption of the UAV increases more, which is the denominator of Equation (13). However, more UAVs can improve energy efficiency with the same network size, which is consistent with the phenomenon in Figure 5 and Figure 6. Especially in a large distribution, the improvement is more obvious.

6. Conclusions

In this paper, the HCCPNS was proposed for the first time and applied for the modelling and analysis of a multi-UAV aided wireless power and information transfer system. The established specification intuitively described the relationship between the energy flow, control flow, and information flow of the system, and the state equation demonstrates the dynamic characteristics of continuous and discrete quantities. In order to optimize energy utilization rate and the time delay of information collection simultaneously, a multi-objective optimization was formulated. Furthermore, the set of SDs should be updated periodically in real-time system. The proposed MAC-NSGA II was employed to assign the number of UAVs, the flying trajectory, and the hovering time, which called for a combination of a multiple ant colony algorithm and nondominated sorting genetic algorithm II. Firstly, the flight trajectory of multiple UAVs was minimized, and the flight load between UAVs was balanced by using the min–max framework. On this basis, the Pareto frontier was obtained, and the trade-off point between the two targets was found. A large number of simulation results show that the proposed algorithm is superior to the comparison algorithm in energy efficiency and information collection delay.

Some interesting open questions related to this work merit further investigation. Firstly, if the urgency of SDs’ energy supplement is also taken into account, we should look at how to further optimize the UAVs’ moving trajectory. Secondly, it is also worth investigating how to cooperate with multiple UAVs, such as partner charging or emergency rescue, so as to achieve better network utility.