Mapping Water Infiltration Rate Using Ground and UAV Hyperspectral Data: A Case Study of Alento, Italy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.1.1. The UAV Campaign Study Site: Alento, Italy
2.1.2. Mediterranean Sites for Generating the FSSL
- I.
- Alento, Italy (21 samples): The area described above.
- II.
- Kibbutz Sde Yoav, Israel (30 samples): Kibbutz Sde Yoav is an agricultural settlement located in southcentral Israel, between the cities of Ashkelon, Kiryat Gat, and Kiryat Malakhi. The soil type in the study area is alluvial [41] (Fluvisol according to the WRB-FAO general classes). According to an updated version of the Köppen climate classification [39], the climate is hot-semiarid (Bsh). The center of the study site is located at 31°38′35″N, 34°40′15″E.
- III.
- Afeka, Tel Aviv, Israel (18 samples): Afeka is a residential neighborhood located in north Tel Aviv. The soil type in the study area is brown-red sandy soil [42] (Ferralsol according to the WRB-FAO reference soil groups), and the climate is hot-summer Mediterranean (Csa). The samples at this study site were collected around the coordinates 32°7′9.16″N, 34°48′14.84″E.
- IV.
- Central Macedonia, Greece (45 samples from three different fields): Three different agricultural fields were selected in this region. The climate is hot-summer Mediterranean (Csa) [39]. According to the WRB-FAO reference soil groups, the soil type in the first field (40°37′32.03″N, 21°34′1.23″E) is classified as Fluvisol. The second (40°39′55.31″N, 21°36′20.49″E) and third (40°40′11.46″N, 21°37′56.67″E) field soils are classified as Cambisol [43].
2.2. Field and Laboratory Data Acquisition
- I.
- The whole dataset: samples collected from all sites (114 samples).
- II.
- The “sandy” dataset: samples from Afeka (Tel Aviv), Israel and from the three fields in Central Macedonia, Greece (58 samples).
- III.
- The “clayey” dataset: samples from Sde Yoav, Israel and Alento, Italy (46 samples).
2.3. The UAV Data Acquisition
2.4. Data Analysis
2.5. Spectral Similarity Analysis
2.6. Spatial Analysis
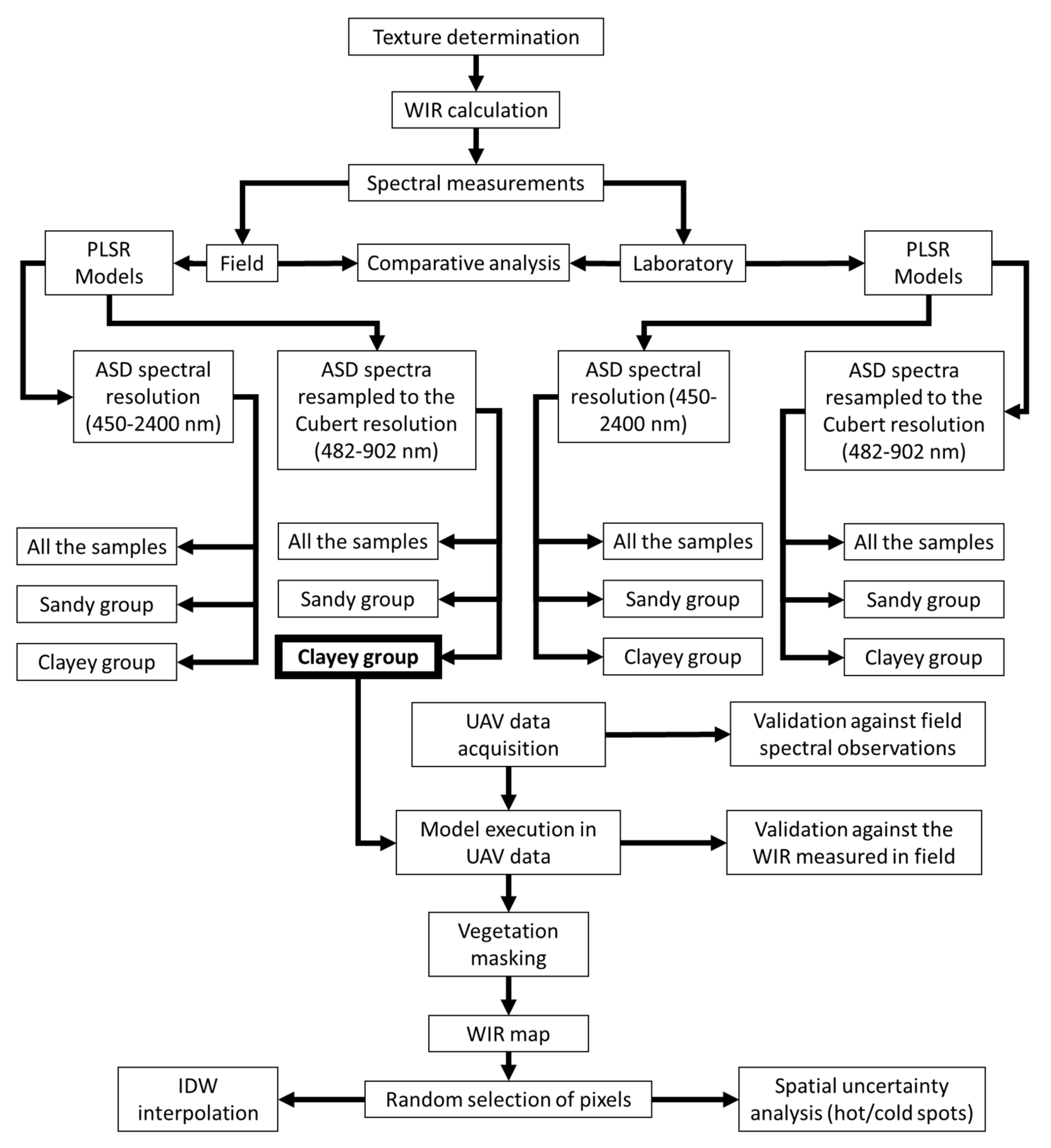
2.7. Flowchart
3. Results
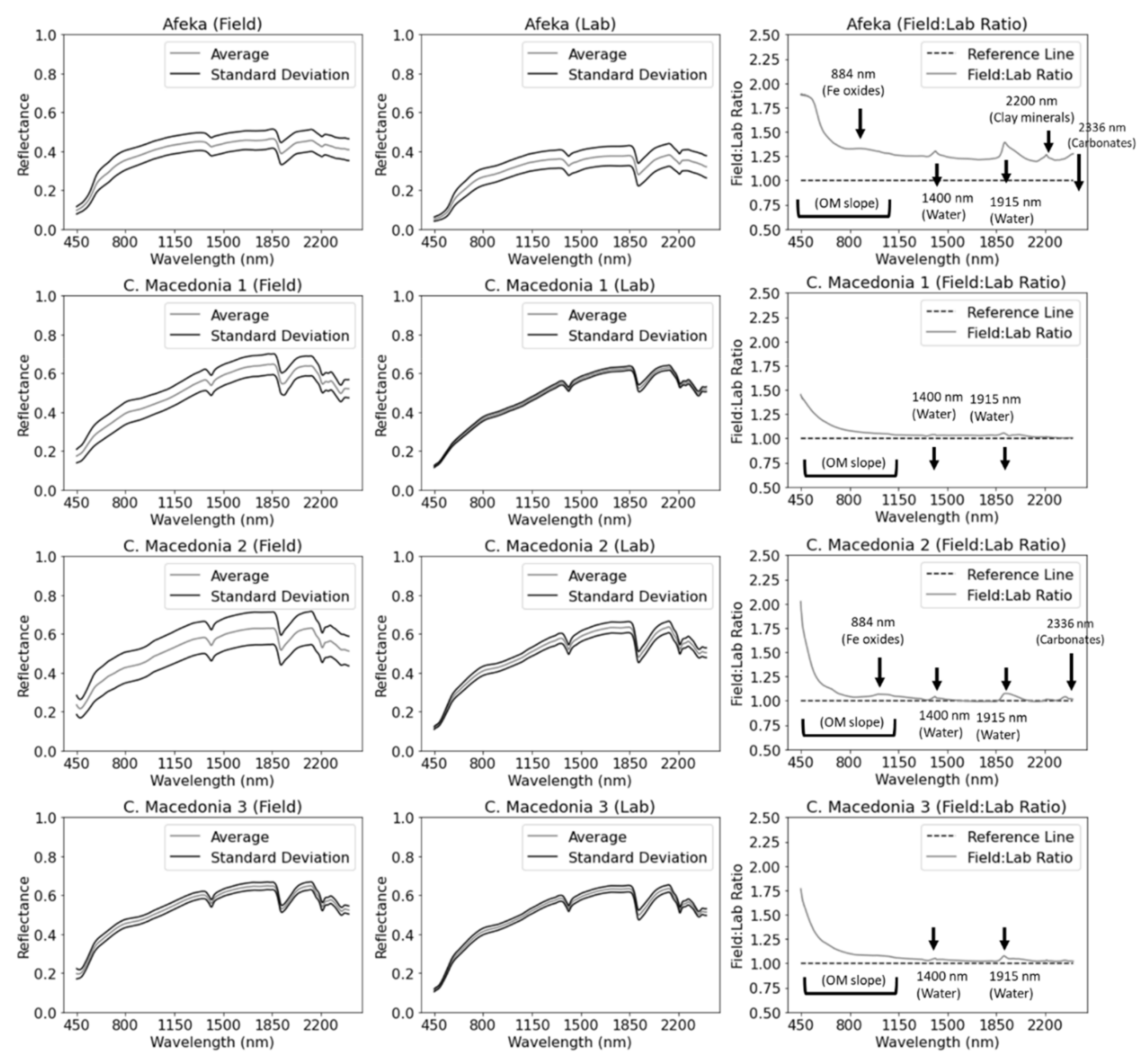
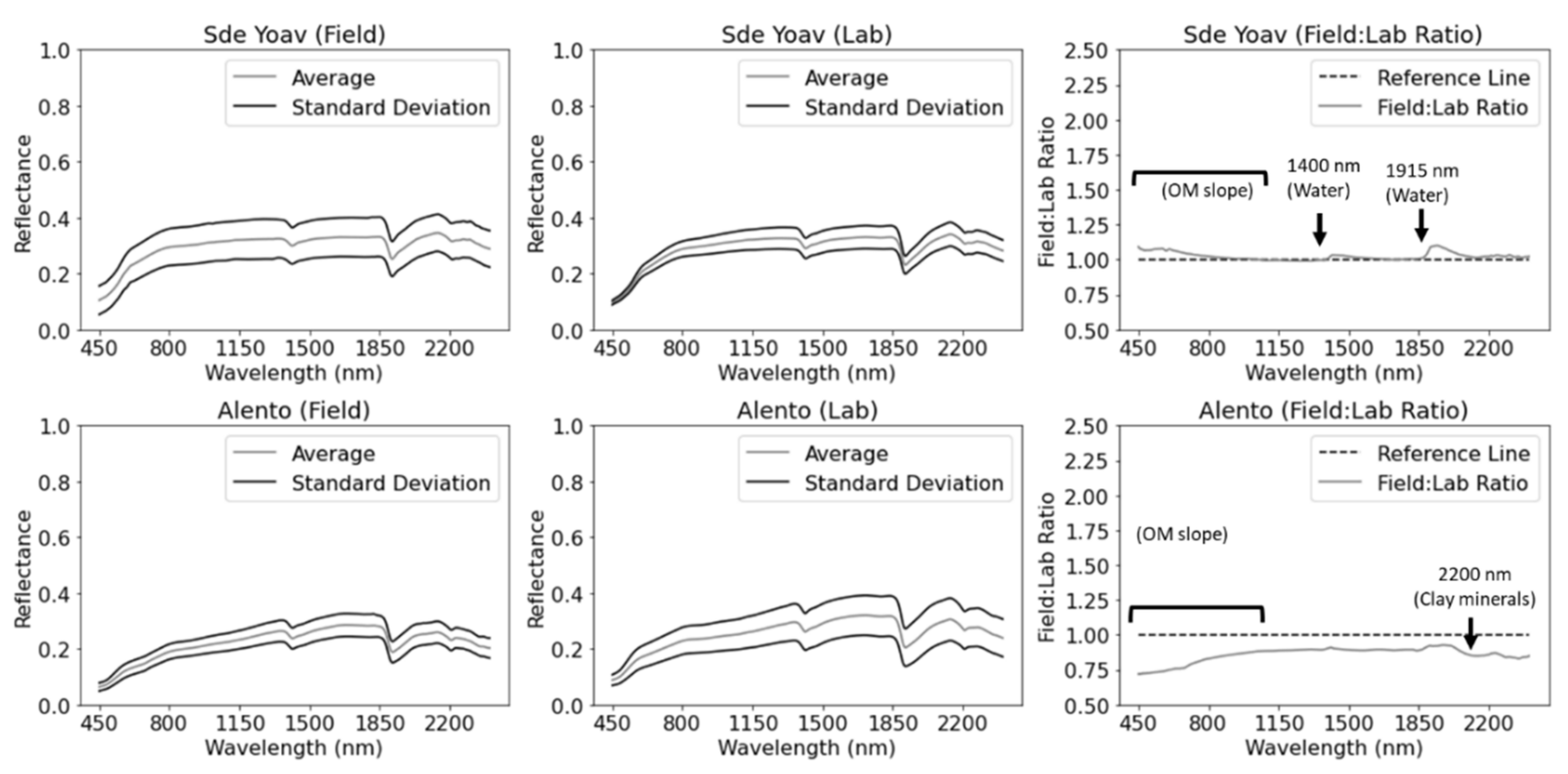
3.1. Spectral Characteristics Per Field
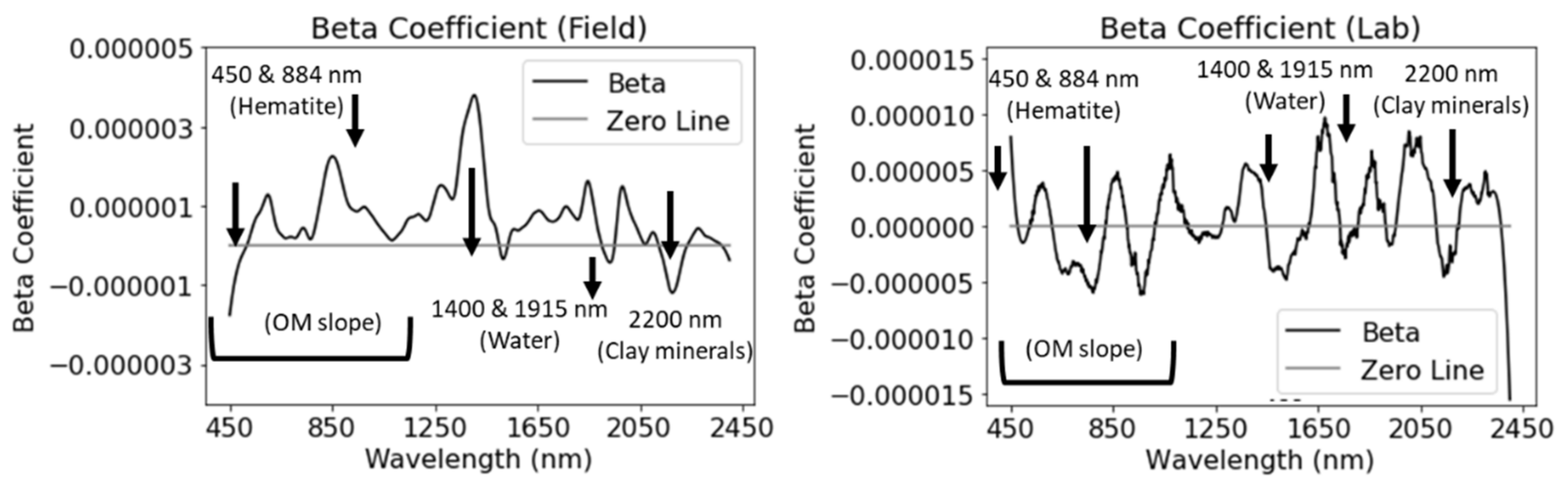
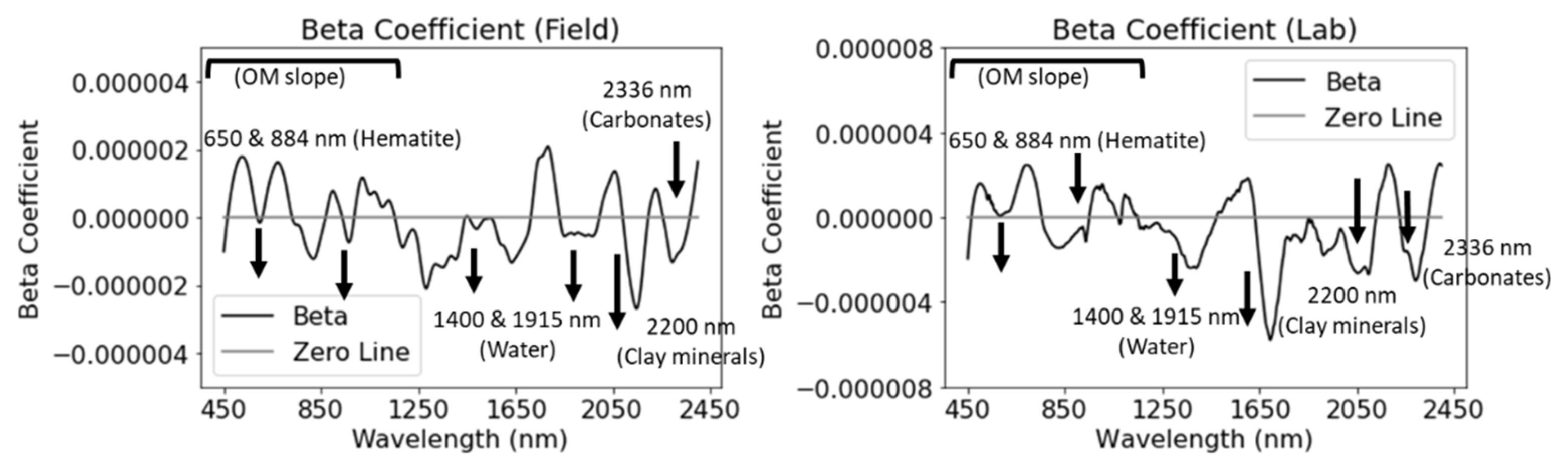
3.2. Spectral-Based Modeling and Interpretation
3.2.1. The Whole Dataset in the ASD Spectral Configuration
3.2.2. The Whole Dataset in the Cubert Spectral Configuration
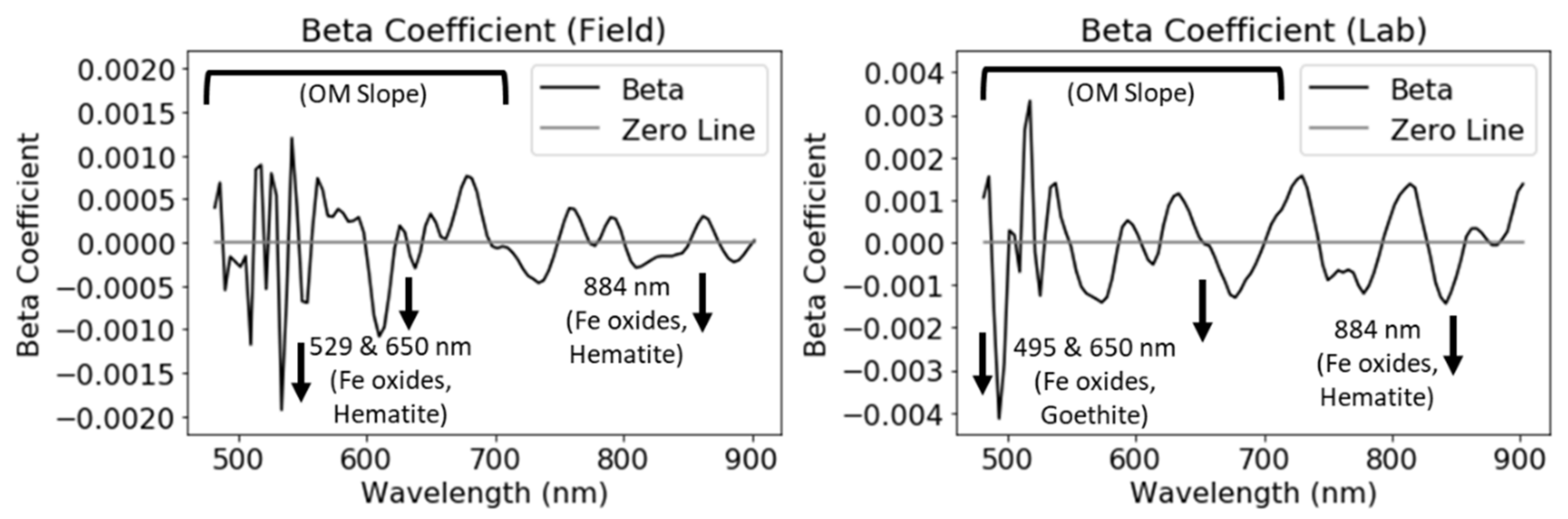
3.2.3. Sandy Dataset in the ASD Spectral Configuration
3.2.4. Sandy Dataset in the Cubert Spectral Configuration
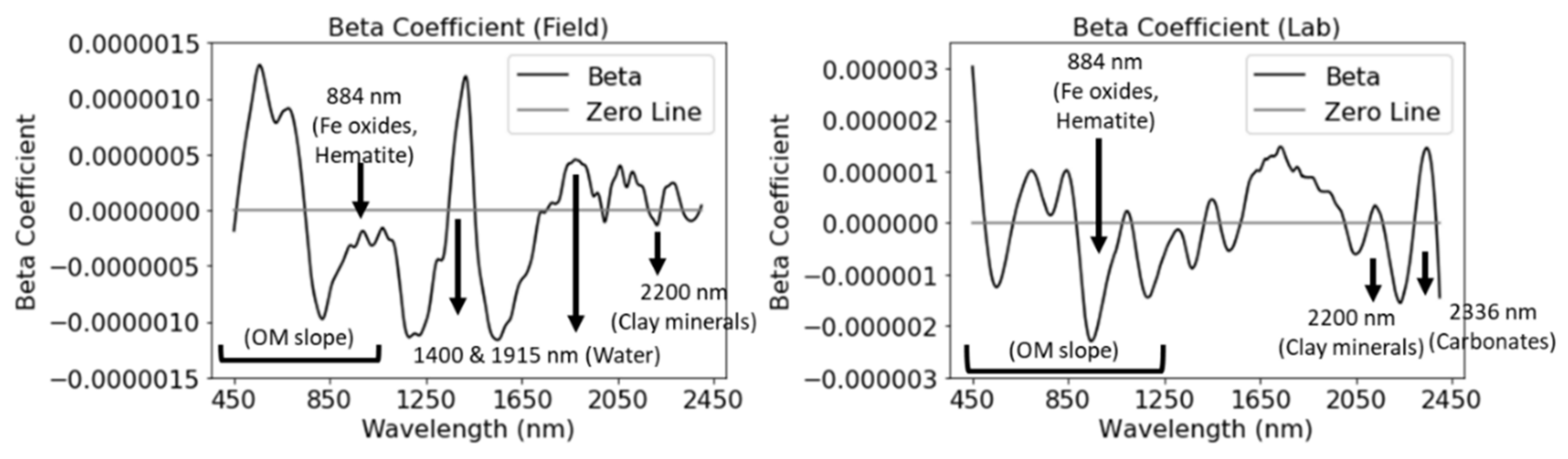
3.2.5. Clayey Dataset in the ASD Spectral Configuration
3.2.6. Clayey Dataset in the Cubert Spectral Configuration
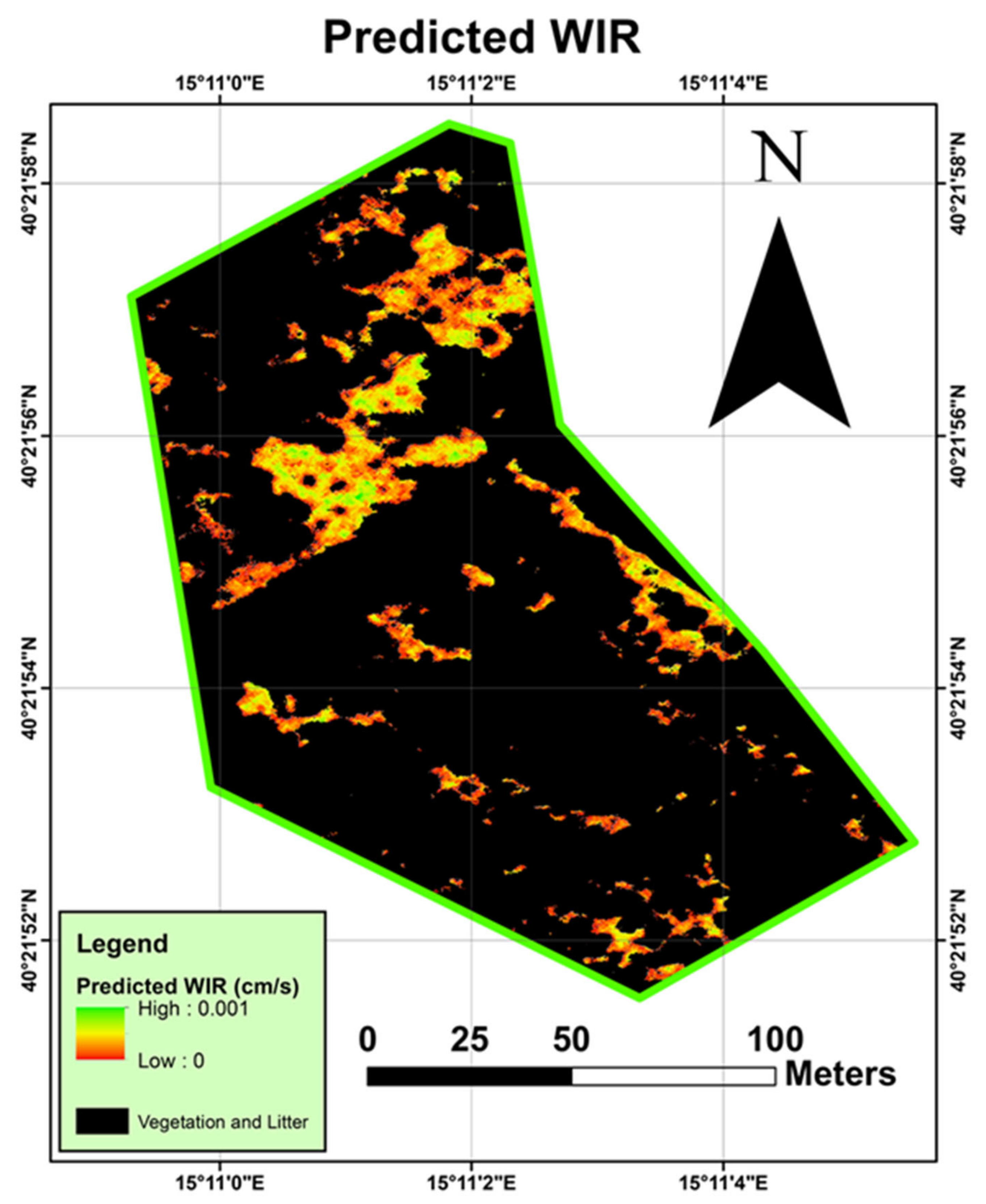
3.3. Execution of the Field-Based Model with the Cubert UHD-185 Data
3.3.1. Validation of the UAV Reflectance Calibration and WIR Predictions
3.3.2. Spatial and Uncertainty Analyses
4. Discussion
4.1. Influence of Sampling Procedures on the Soil Surface
4.2. The Potential of Soil Surface Reflectance and the SoilPRO Assembly
4.3. Spectral Range and Resolution
4.4. Vegetation Cover
4.5. Future Studies and Remarks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franzluebbers, A.J. Water infiltration and soil structure related to organic matter and its stratification with depth. Soil Tillage Res. 2002, 66, 197–205. [Google Scholar] [CrossRef]
- Basche, A.D.; DeLonge, M.S. Comparing infiltration rates in soils managed with conventional and alternative farming methods: A meta-analysis. PLoS ONE 2019, 14, e0215702. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, B.P.; Wilding, L.P.; Woodruff, C.M. Soil and topographic controls on runoff generation from stepped landforms in the Edwards Plateau of Central Texas. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef] [Green Version]
- Rietkerk, M.; van de Koppel, J. Alternate stable states and threshold effects in semi-arid grazing systems. Oikos 1997, 79, 69–76. [Google Scholar] [CrossRef] [Green Version]
- Thurow, T.L.; Blackburn, W.H.; Taylor, C.A., Jr. Hydrologic characteristics of vegetation types as affected by livestock grazing systems, Edwards Plateau, Texas. J. Range Manag. 1986, 39, 505–509. [Google Scholar] [CrossRef]
- Thurow, T.L.; Blackburn, W.H.; Taylor, C.A., Jr. Infiltration and interrill erosion responses to selected livestock grazing strategies, Edwards Plateau, Texas. J. Range Manag. 1988, 41, 296–302. [Google Scholar] [CrossRef]
- Van de Koppel, J.; Rietkerk, M.; Weissing, F.J. Catastrophic vegetation shifts and soil degradation in terrestrial grazing systems. Trends Ecol. Evol. 1997, 12, 352–356. [Google Scholar] [CrossRef] [Green Version]
- Van de Koppel, J.; Rietkerk, M.; van Langevelde, F.; Kumar, L.; Klausmeier, C.A.; Fryxell, J.M.; Hearne, J.W.; van Andel, J.; de Ridder, N.; Skidmore, A.; et al. Spatial heterogeneity and irreversible vegetation change in semiarid grazing systems. Am. Nat. 2002, 159, 209–218. [Google Scholar] [CrossRef]
- Walker, B.H.; Ludwig, D.; Holling, C.S.; Peterman, R.M. Stability of semi-arid savanna grazing systems. J. Ecol. 1981, 69, 473–498. [Google Scholar] [CrossRef]
- Moody, J.A.; Kinner, D.A.; Úbeda, X. Linking hydraulic properties of fire-affected soils to infiltration and water repellency. J. Hydrol. 2009, 379, 291–303. [Google Scholar] [CrossRef]
- Lado, M.; Paz, A.; Ben-Hur, M. Organic matter and aggregate size interactions in infiltration, seal formation, and soil loss. Soil Sci. Soc. Am. J. 2004, 68, 935–942. [Google Scholar] [CrossRef]
- Stern, R.; Benhur, M.; Shainberg, I. Clay mineralogy effect on rain infiltration, seal formation and soil losses. Soil Sci. 1991, 152, 455–462. [Google Scholar] [CrossRef]
- Ben-Hur, M.; Letey, J. Effect of polysaccharides, clay dispersion, and impact energy on water infiltration. Soil Sci. Soc. Am. J. 1989, 53, 233–238. [Google Scholar] [CrossRef]
- Agassi, M.; Morin, J.; Shainberg, I. Effect of raindrop impact energy and water salinity on infiltration rates of sodic soils. Soil Sci. Soc. Am. J. 1985, 49, 186–190. [Google Scholar] [CrossRef]
- Agassi, M.; Bloem, D.; Ben-Hur, M. Effect of drop energy and soil and water chemistry on infiltration and erosion. Water Resour. Res. 1994, 30, 1187–1193. [Google Scholar] [CrossRef]
- Bertrand, A.R.; Sor, K. The effects of rainfall intensity on soil structure and migration of colloidal materials in soils. Soil Sci. Soc. Am. J. 1962, 26, 297–300. [Google Scholar] [CrossRef]
- Levy, G.J.; van der Watt, H.v.H. Effects of clay mineralogy and soil sodicity on soil infiltration rate. S. Afr. J. Plant. Soil 1988, 5, 92–96. [Google Scholar] [CrossRef]
- Bullard, J.E.; Ockelford, A.; Strong, C.; Aubault, H. Effects of cyanobacterial soil crusts on surface roughness and splash erosion. J. Geophys. Res. Biogeosci. 2018, 123, 3697–3712. [Google Scholar] [CrossRef]
- Six, J.; Elliott, E.T.; Paustian, K. Soil structure and soil organic matter II. A normalized stability index and the effect of mineralogy. Soil Sci. Soc. Am. J. 2000, 64, 1042–1049. [Google Scholar] [CrossRef]
- Nadler, A.; Levy, G.J.; Keren, R.; Eisenberg, H. Sodic calcareous soil reclamation as affected by water chemical composition and flow rate. Soil Sci. Soc. Am. J. 1996, 60, 252–257. [Google Scholar] [CrossRef]
- Nimmo, J.R. Aggregation: Physical Aspects. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2013; ISBN 978-0-12-409548-9. [Google Scholar]
- Angers, D.A.; Caron, J. Plant-induced changes in soil structure: Processes and feedbacks. Biogeochemistry 1998, 42, 55–72. [Google Scholar] [CrossRef]
- Vaezi, A.R.; Ahmadi, M.; Cerdà, A. Contribution of raindrop impact to the change of soil physical properties and water erosion under semi-arid rainfalls. Sci. Total Environ. 2017, 583, 382–392. [Google Scholar] [CrossRef]
- Morin, J.; Goldberg, D.; Seginer, I. A rainfall simulator with a rotating disk. Trans. ASAE 1967, 10, 74–77. [Google Scholar] [CrossRef]
- Decagon Devices, Inc. Minidisk Infiltrometer; User’s Manual; Decagon Devices, Inc: Pullman, WA, USA, 2005. [Google Scholar]
- Ben-Dor, E. Quantitative remote sensing of soil properties. Adv. Agron. 2002, 75, 173–243. [Google Scholar]
- Viscarra Rossel, R.A.; Behrens, T.; Ben-Dor, E.; Brown, D.J.; Demattê, J.A.M.; Shepherd, K.D.; Shi, Z.; Stenberg, B.; Stevens, A.; Adamchuk, V.; et al. A global spectral library to characterize the world’s soil. Earth Sci. Rev. 2016, 155, 198–230. [Google Scholar] [CrossRef] [Green Version]
- Tóth, G.; Jones, A.; Montanarella, L. The LUCAS topsoil database and derived information on the regional variability of cropland topsoil properties in the European Union. Environ. Monit. Assess. 2013, 185, 7409–7425. [Google Scholar] [CrossRef]
- Tziolas, N.; Tsakiridis, N.; Ben-Dor, E.; Theocharis, J.; Zalidis, G. A memory-based learning approach utilizing combined spectral sources and geographical proximity for improved VIS-NIR-SWIR soil properties estimation. Geoderma 2019, 340, 11–24. [Google Scholar] [CrossRef]
- Ogen, Y.; Zaluda, J.; Francos, N.; Goldshleger, N.; Ben-Dor, E. Cluster-based spectral models for a robust assessment of soil properties. Geoderma 2019, 340, 175–184. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Goldshleger, N.; Braun, O.; Kindel, B.; Goetz, A.F.H.; Bonfil, D.; Margalit, N.; Binaymini, Y.; Karnieli, A.; Agassi, M. Monitoring infiltration rates in semiarid soils using airborne hyperspectral technology. Int. J. Remote Sens. 2004, 25, 2607–2624. [Google Scholar] [CrossRef]
- Goldshleger, N.; Ben-Dor, E.; Chudnovsky, A.; Agassi, M. Soil reflectance as a generic tool for assessing infiltration rate induced by structural crust for heterogeneous soils. Eur. J. Soil Sci. 2009, 60, 1038–1051. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Granot, A.; Notesco, G. A simple apparatus to measure soil spectral information in the field under stable conditions. Geoderma 2017, 306, 73–80. [Google Scholar] [CrossRef]
- Romano, N.; Nasta, P.; Bogena, H.; De Vita, P.; Stellato, L.; Vereecken, H. Monitoring hydrological processes for land and water resources management in a Mediterranean ecosystem: The Alento River Catchment Observatory. Vadose Zone J. 2018, 17, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and an application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Su, Z.; Zeng, Y.; Romano, N.; Manfreda, S.; Francés, F.; Ben Dor, E.; Szabó, B.; Vico, G.; Nasta, P.; Zhuang, R.; et al. An integrative information aqueduct to close the gaps between satellite observation of water cycle and local sustainable management of water resources. Water 2020, 12, 1495. [Google Scholar] [CrossRef]
- Paruta, A.; Ciraolo, G.; Capodici, F.; Manfreda, S.; Sasso, S.F.D.; Zhuang, R.; Romano, N.; Nasta, P.; Ben-Dor, E.; Francos, N.; et al. A geostatistical approach to map near-surface soil moisture through hyperspatial resolution thermal inertia. IEEE Trans. Geosci. Remote Sens. 2020, 1–18. [Google Scholar] [CrossRef]
- Rubel, F.; Kottek, M. Observed and projected climate shifts 1901-2100 depicted by world maps of the Köppen-Geiger climate classification. Meteorol. Z. 2010, 135–141. [Google Scholar] [CrossRef] [Green Version]
- Costantini, E.A.C.; Dazzi, C. The Soils of Italy; Springer Science & Business Media: Berlin, Germany, 2013; ISBN 978-94-007-5642-7. [Google Scholar]
- Ravikovitch, S. The Soils of Israel: Formation, Nature and Properties; Hakibbutz Hameuchad Publication House: Bnei Brak, Israel, 1992. [Google Scholar]
- Ravikovitch, S. Manual and Map of Soils of Israel; The Magnes Press, The Hebrew University: Jerusalem, Israel, 1969. [Google Scholar]
- Soil Map of Greece—ESDAC—European Commission. Available online: https://esdac.jrc.ec.europa.eu/content/soil-map-greece-0 (accessed on 27 October 2019).
- Ben Dor, E.; Ong, C.; Lau, I.C. Reflectance measurements of soils in the laboratory: Standards and protocols. Geoderma 2015, 245–246, 112–124. [Google Scholar] [CrossRef]
- Thien, S.J. A flow diagram for teaching texture-by-feel analysis. J. Agronom. Educ. 1979, 8, 54–55. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Schamberger, T.; Schuberth, F.; Henseler, J.; Dijkstra, T.K. Robust partial least squares path modeling. Behaviormetrika 2020, 47, 307–334. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, T.K.; Henseler, J. Consistent and asymptotically normal PLS estimators for linear structural equations. Comput. Stat. Data Anal. 2015, 81, 10–23. [Google Scholar] [CrossRef] [Green Version]
- Hair, J.F.; Hult, G.T.M.; Ringle, C.M.; Sarstedt, M.; Thiele, K.O. Mirror, mirror on the wall: A comparative evaluation of composite-based structural equation modeling methods. J. Acad. Market. Sci. 2017, 45, 616–632. [Google Scholar] [CrossRef]
- Takane, Y.; Hwang, H. Comparisons among several consistent estimators of structural equation models. Behaviormetrika 2018, 45, 157–188. [Google Scholar] [CrossRef]
- Zhao, D.; Arshad, M.; Wang, J.; Triantafilis, J. Soil exchangeable cations estimation using Vis-NIR spectroscopy in different depths: Effects of multiple calibration models and spiking. Comput. Electron. Agric. 2021, 182, 105990. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Kindel, B.; Goetz, A.F.H. Quality assessment of several methods to recover surface reflectance using synthetic imaging spectroscopy data. Remote Sens. Environ. 2004, 90, 389–404. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Tsuchida, S.; Oguma, H. Applicability of green-red vegetation index for remote sensing of vegetation phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef] [Green Version]
- IDW—Help. ArcGIS for Desktop. Available online: http://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/idw.htm (accessed on 27 January 2019).
- George, D.; Mallery, P. IBM SPSS Statistics 23 Step by Step: A Simple Guide and Reference, 14th ed.; Routledge: New York, NY, USA, 2016; ISBN 978-0-13-432025-0. [Google Scholar]
- Rawls, W.J.; Pachepsky, Y.A.; Ritchie, J.C.; Sobecki, T.M.; Bloodworth, H. Effect of soil organic carbon on soil water retention. Geoderma 2003, 116, 61–76. [Google Scholar] [CrossRef]
- Olness, A.; Archer, D. Effect of organic carbon on available water in soil. Soil Sci. 2005, 170, 90–101. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J. Soil water characteristic estimates by texture and organic matter for hydrologic solutions. Soil Sci. Soc. Am. J. 2006, 70, 1569–1578. [Google Scholar] [CrossRef] [Green Version]
- Inda, A.V.; Fink, J.R.; dos Santos, T.F. Pedogenic iron oxides in soils of the Acre State, Brazil. Ciênc. Rural 2018, 48. [Google Scholar] [CrossRef]
- Ogen, Y.; Faigenbaum-Golovin, S.; Granot, A.; Shkolnisky, Y.; Goldshleger, N.; Ben-Dor, E. Removing moisture effect on soil reflectance properties: A case study of clay content prediction. Pedosphere 2019, 29, 421–431. [Google Scholar] [CrossRef]
- Santos, F.; Abney, R.; Barnes, M.; Bogie, N.; Ghezzehei, T.A.; Jin, L.; Moreland, K.; Sulman, B.N.; Berhe, A.A. Chapter 9—The Role of the Physical Properties of Soil in Determining Biogeochemical Responses to Soil Warming. In Ecosystem Consequences of Soil Warming; Mohan, J.E., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 209–244. ISBN 978-0-12-813493-1. [Google Scholar]
- Pingping, H.; Xue, S.; Li, P.; Zhanbin, L. Effect of vegetation cover types on soil infiltration under simulating rainfall. Nat. Environ. Pollut. Technol. 2013, 12, 193–198. [Google Scholar]





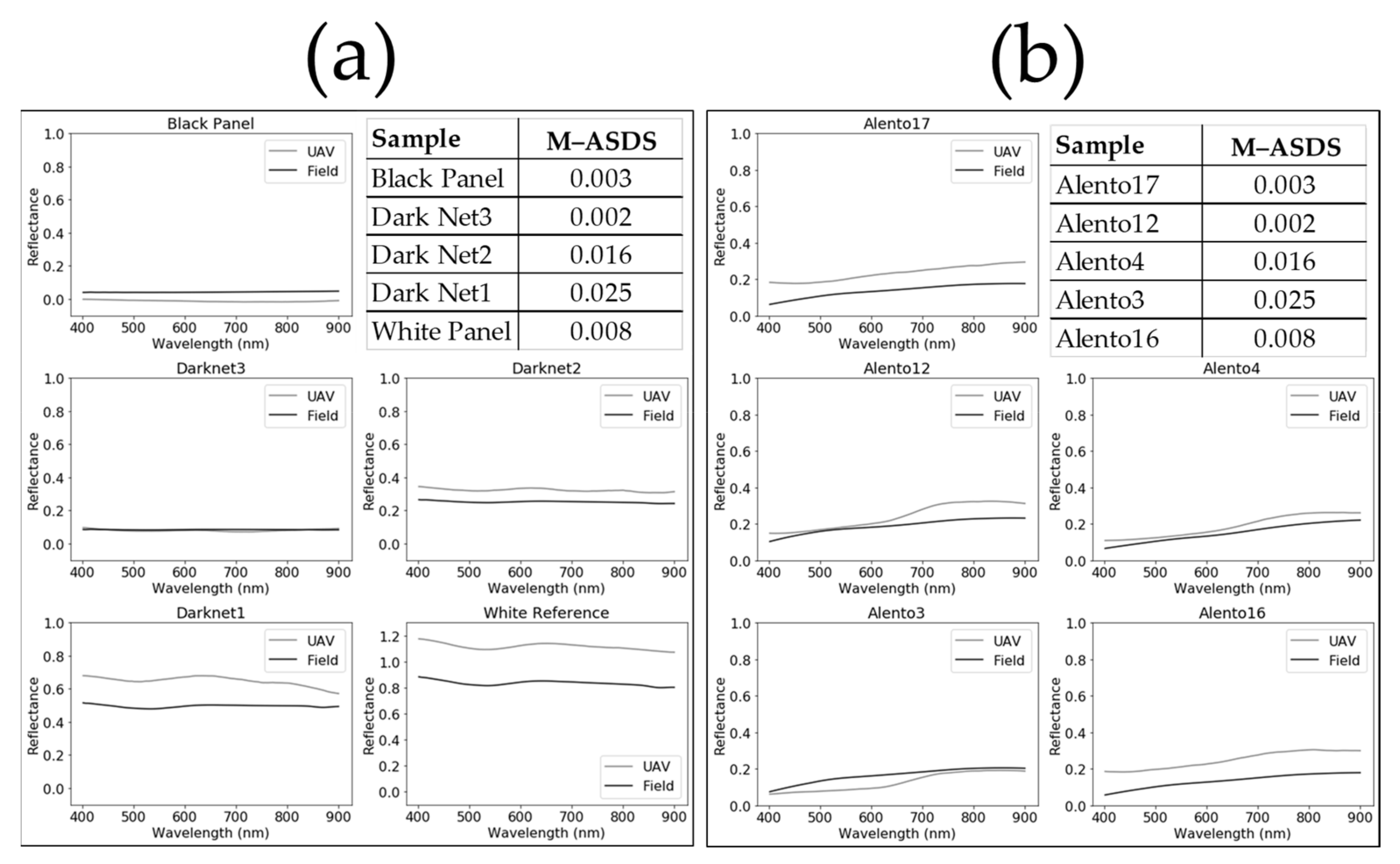

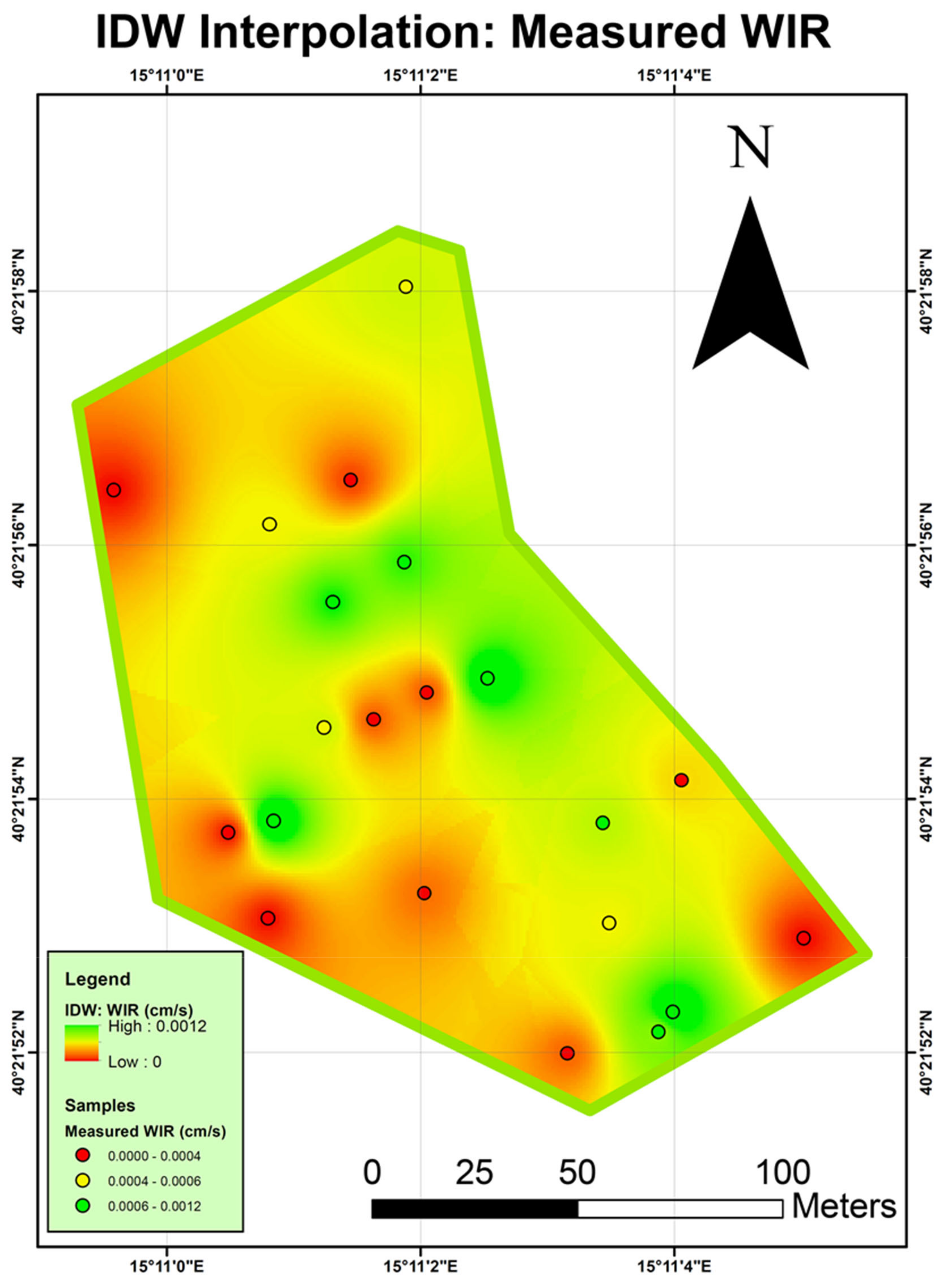
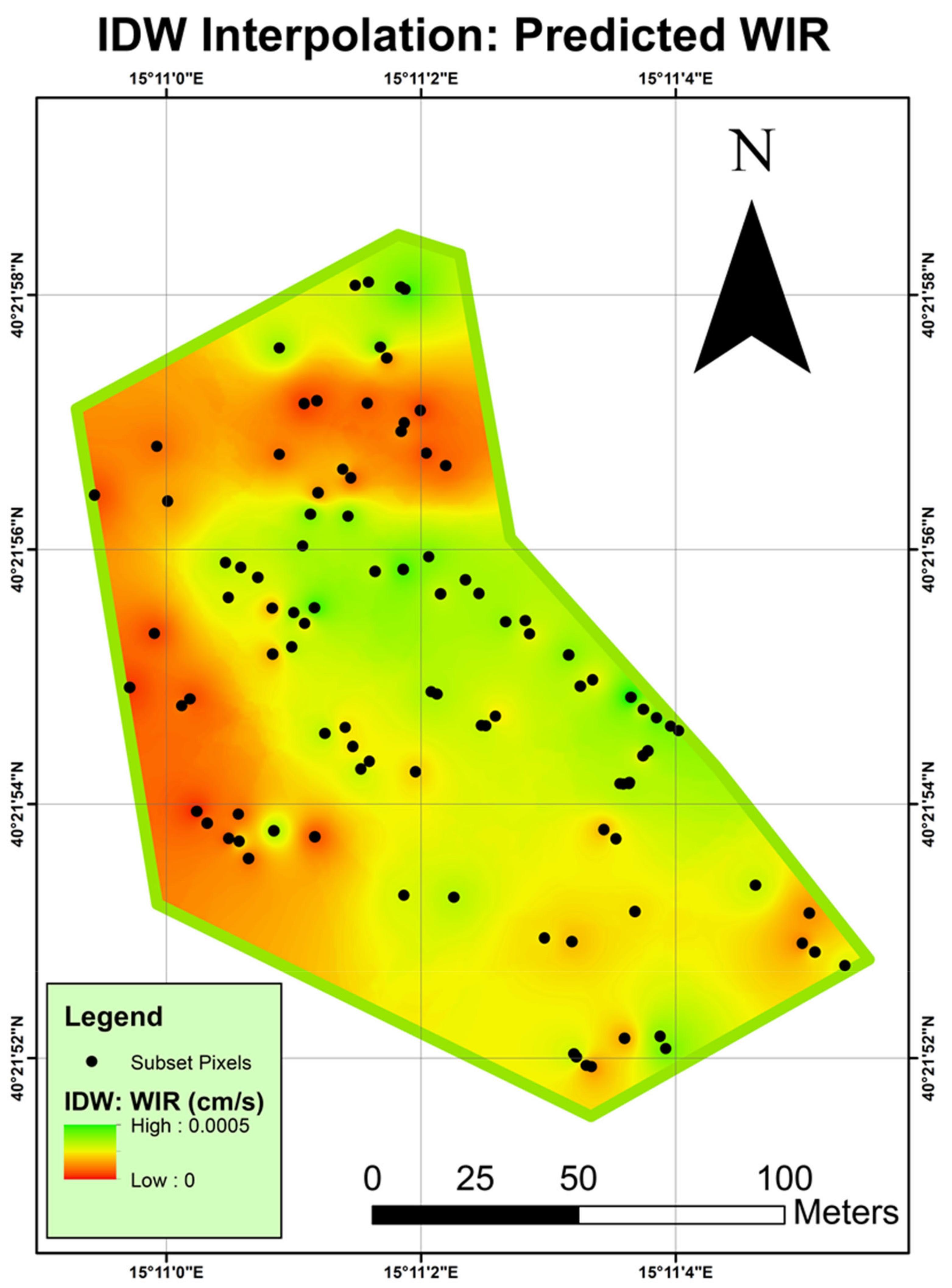
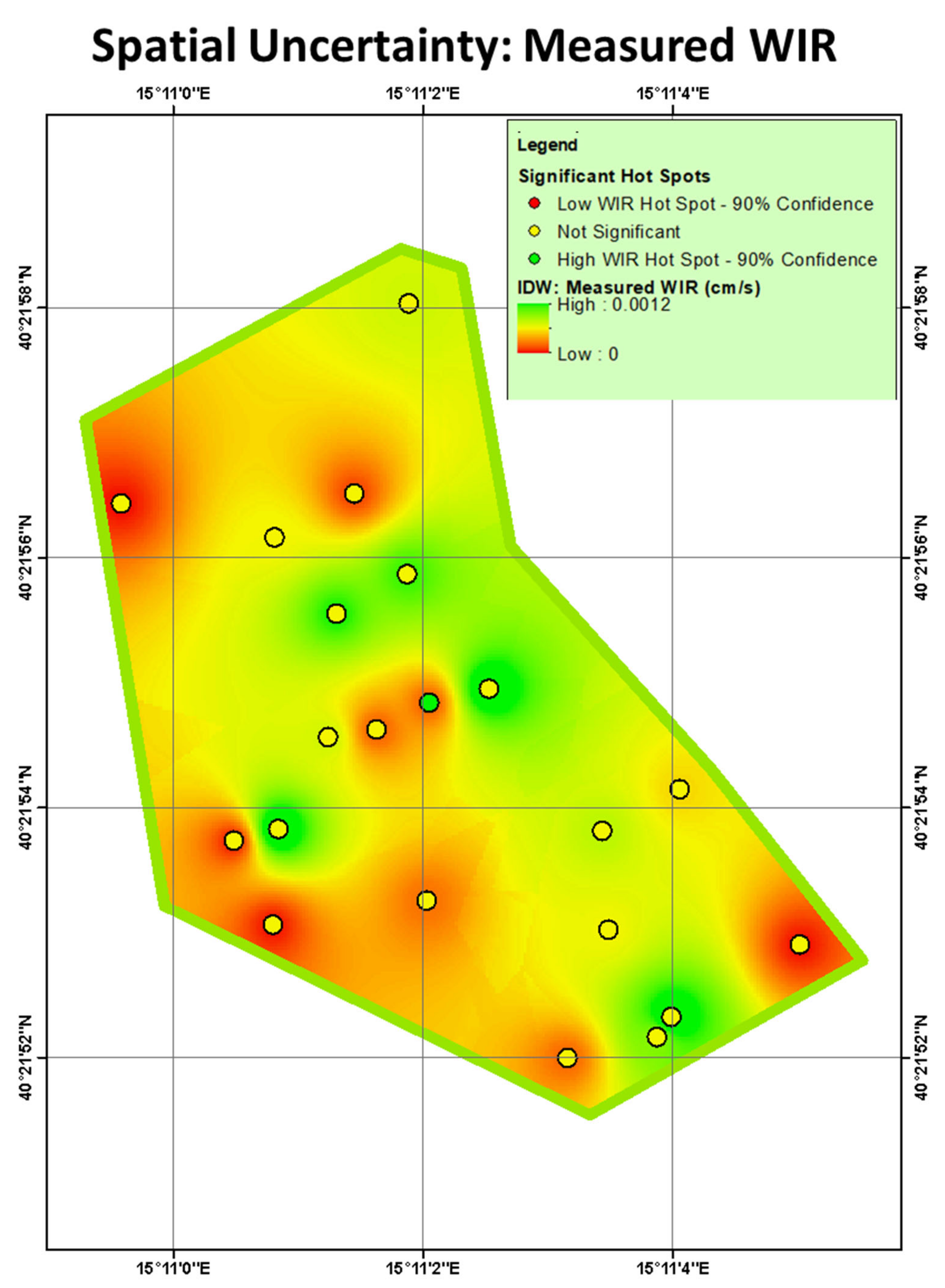

| Field | Country | No. of Samples | Classification | Texture Group |
|---|---|---|---|---|
| Sde Yoav | Israel | 30 | Clay Loam | Clayey (heavy) |
| Afeka | Israel | 18 | Sandy Clay Loam | Clayey (heavy) |
| Alento | Italy | 21 | Loam | Clayey (heavy) |
| C. Macedonia 1 | Greece | 16 | Sand | Sandy (light) |
| C. Macedonia 2 | Greece | 15 | Sandy Loam | Sandy (light) |
| C. Macedonia 3 | Greece | 14 | Sandy Loam | Sandy (light) |
| Group | Parameter | Value (cm/s) |
|---|---|---|
| Whole dataset | Mean | 0.00134 |
| Standard deviation | 0.00076 | |
| Interquartile range | 0.00075–0.00183 | |
| Skewness | 0.44 | |
| Kurtosis | −0.3 | |
| WIR range | 0.00007–0.00355 | |
| Sandy dataset | Mean | 0.001533 |
| Standard deviation | 0.00078 | |
| Interquartile range | 0.00091–0.00204 | |
| Skewness | 0.4 | |
| Kurtosis | 0.49 | |
| WIR range | 0.00008–0.00355 | |
| Clayey dataset | Mean | 0.00111 |
| Standard deviation | 0.00065 | |
| Interquartile range | 0.000570.00155 | |
| SkewnessKurtosis | 0.25 | |
| Kurtosis | 0.83 | |
| WIR range | 0.00007–0.00249 |
| Group | Field | Parameter | Value (cm/s) |
|---|---|---|---|
| Sandy dataset | Afeka | Mean | 0.0013 |
| Standard deviation | 0.00061 | ||
| Interquartile range | 0.00085–0.00171 | ||
| Skewness | 0.03557 | ||
| Kurtosis | −0.82087 | ||
| WIR range | 0.00021–0.0025 | ||
| C. Macedonia 1 | Mean | 0.00202 | |
| Standard deviation | 0.00079 | ||
| Interquartile range | 0.00139–0.00254 | ||
| Skewness | −0.41873 | ||
| Kurtosis | −0.91797 | ||
| WIR range | 0.00064–0.00324 | ||
| C. Macedonia 2 | Mean | 0.00178 | |
| Standard deviation | 0.00085 | ||
| Interquartile range | 0.00109–0.00235 | ||
| Skewness | 0.21709 | ||
| Kurtosis | −0.66361 | ||
| WIR range | 0.00043–0.00355 | ||
| C. Macedonia 3 | Mean | 0.00108 | |
| Standard deviation | 0.00046 | ||
| Interquartile range | 0.00077–0.00134 | ||
| Skewness | −0.22813 | ||
| Kurtosis | −0.33763 | ||
| WIR range | 0.00008–0.00182 | ||
| Clayey dataset | Sde Yoav | Mean | 0.00143 |
| Standard deviation | 0.00057 | ||
| Interquartile range | 0.00109–0.00179 | ||
| Skewness | −0.06322 | ||
| Kurtosis | −0.65508 | ||
| WIR range | 0.00023–0.00249 | ||
| Alento | Mean | 0.00056 | |
| Standard deviation | 0.00037 | ||
| Interquartile range | 0.00016–0.00088 | ||
| Skewness | 0.26864 | ||
| Kurtosis | −1.15855 | ||
| WIR range | 0.00007–0.00119 |
| Group | Parameter | Field | Laboratory |
|---|---|---|---|
| Whole dataset | RPIQ (Cal) | 10.83 | 5.26 |
| R2 (Cal) | 0.98 | 0.92 | |
| RMSE (Cal) | 0.0001 | 0.0002 | |
| No. of samples (Cal) | 83 | 83 | |
| RPIQ (Val) | 2.26 | 1.87 | |
| R2 (Val) | 0.70 | 0.57 | |
| RMSE (Val) | 0.0004 | 0.0004 | |
| No. of samples (Val) | 21 | 21 | |
| p-Value (Val) | 0.0000 | 0.0001 | |
| No. of components | 9 | 9 | |
| Spectral preprocessing | 1st derivative | ||
| Sandy dataset | RPIQ (Cal) | 4.24 | 1.8 |
| R2 (Cal) | 0.90 | 0.48 | |
| RMSE (Cal) | 0.0002 | 0.22 | |
| No. of samples (Cal) | 46 | 46 | |
| RPIQ (Val) | 3.19 | 1.84 | |
| R2 (Val) | 0.82 | 0.22 | |
| RMSE (Val) | 0.0004 | 0.0007 | |
| No. of samples (Val) | 12 | 12 | |
| p-Value (Val) | 0.0001 | 0.123 | |
| No. of components | 5 | 5 | |
| Spectral preprocessing | Absorbance and 1st derivative | ||
| Clayey dataset | RPIQ (Cal) | 17.66 | 4.96 |
| R2 (Cal) | 0.99 | 0.89 | |
| RMSE (Cal) | 5.86 | 0.0002 | |
| No. of samples (Cal) | 37 | 37 | |
| RPIQ (Val) | 3.14 | 2.85 | |
| R2 (Val) | 0.81 | 0.7 | |
| RMSE (Val) | 0.0003 | 0.0004 | |
| No. of samples (Val) | 9 | 9 | |
| p-Value (Val) | 0.0004 | 0.0025 | |
| No. of components | 6 | 6 | |
| Spectral preprocessing | 1st derivative | ||
| Group | Parameter | Field | Laboratory |
|---|---|---|---|
| Whole dataset | RPIQ (Cal) | 2.26 | 2.05 |
| R2 (Cal) | 0.52 | 0.41 | |
| RMSE (Cal) | 0.0005 | 0.0006 | |
| No. of samples (Cal) | 83 | 83 | |
| RPIQ (Val) | 1.06 | 1.02 | |
| R2 (Val) | 0.36 | 0.30 | |
| RMSE (Val) | 0.0007 | 0.0007 | |
| No. of samples (Val) | 21 | 21 | |
| p-Value (Val) | 0.0038 | 0.0106 | |
| No. of components | 10 | 10 | |
| Spectral preprocessing | Absorbance and 1st derivative | ||
| Sandy dataset | RPIQ (Cal) | 2.36 | 2.59 |
| R2 (Cal) | 0.63 | 0.55 | |
| RMSE (Cal) | 0.0005 | 0.0005 | |
| No. of samples (Cal) | 46 | 46 | |
| RPIQ (Val) | 2.7 | 1.66 | |
| R2 (Val) | 0.83 | 0.45 | |
| RMSE (Val) | 0.0003 | 0.0005 | |
| No. of samples (Val) | 12 | 12 | |
| p-Value (Val) | 0.0000 | 0.0169 | |
| No. of components | 11 | 11 | |
| Spectral preprocessing | Absorbance and 1st derivative | ||
| Clayey dataset | RPIQ (Cal) | 2.26 | 2.05 |
| R2 (Cal) | 0.66 | 0.47 | |
| RMSE (Cal) | 0.0004 | 0.0005 | |
| No. of samples (Cal) | 37 | 37 | |
| RPIQ (Val) | 3.67 | 2.18 | |
| R2 (Val) | 0.86 | 0.49 | |
| RMSE (Val) | 0.0003 | 0.0005 | |
| No. of samples (Val) | 9 | 9 | |
| p-Value (Val) | 0.0001 | 0.0048 | |
| No. of components | 6 | 6 | |
| Spectral preprocessing | 1st derivative | ||
| Parameter | Value |
|---|---|
| RPIQ (Val) | 2.61 |
| R2 (Val) | 0.76 |
| RMSE (Val) | 0.0002 |
| No. of samples (Val) | 5 |
| p-Value (Val) | 0.052 |
| Spectral range | 482–902 nm |
| WIR range (cm/s) | 0.00007–0.00014 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Francos, N.; Romano, N.; Nasta, P.; Zeng, Y.; Szabó, B.; Manfreda, S.; Ciraolo, G.; Mészáros, J.; Zhuang, R.; Su, B.; et al. Mapping Water Infiltration Rate Using Ground and UAV Hyperspectral Data: A Case Study of Alento, Italy. Remote Sens. 2021, 13, 2606. https://doi.org/10.3390/rs13132606
Francos N, Romano N, Nasta P, Zeng Y, Szabó B, Manfreda S, Ciraolo G, Mészáros J, Zhuang R, Su B, et al. Mapping Water Infiltration Rate Using Ground and UAV Hyperspectral Data: A Case Study of Alento, Italy. Remote Sensing. 2021; 13(13):2606. https://doi.org/10.3390/rs13132606
Chicago/Turabian StyleFrancos, Nicolas, Nunzio Romano, Paolo Nasta, Yijian Zeng, Brigitta Szabó, Salvatore Manfreda, Giuseppe Ciraolo, János Mészáros, Ruodan Zhuang, Bob Su, and et al. 2021. "Mapping Water Infiltration Rate Using Ground and UAV Hyperspectral Data: A Case Study of Alento, Italy" Remote Sensing 13, no. 13: 2606. https://doi.org/10.3390/rs13132606
APA StyleFrancos, N., Romano, N., Nasta, P., Zeng, Y., Szabó, B., Manfreda, S., Ciraolo, G., Mészáros, J., Zhuang, R., Su, B., & Ben-Dor, E. (2021). Mapping Water Infiltration Rate Using Ground and UAV Hyperspectral Data: A Case Study of Alento, Italy. Remote Sensing, 13(13), 2606. https://doi.org/10.3390/rs13132606














