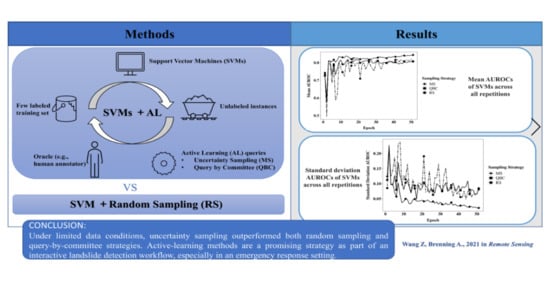
Active-Learning Approaches for Landslide Mapping Using Support Vector Machines
Abstract
:1. Introduction
2. Materials and Methods
2.1. Active-Learning and Traditional Learning Strategies Used
2.1.1. Uncertainty Sampling
- (1)
- Least Confidence
- (2)
- Margin Sampling (MS)
- (3)
- Entropy measure
2.1.2. Query by Committee
2.1.3. Random Sampling as a Baseline
2.2. Landslide Classification Model
2.3. Repetition and Performance Estimation
2.4. Study Area and Data
3. Results
3.1. Model Performance
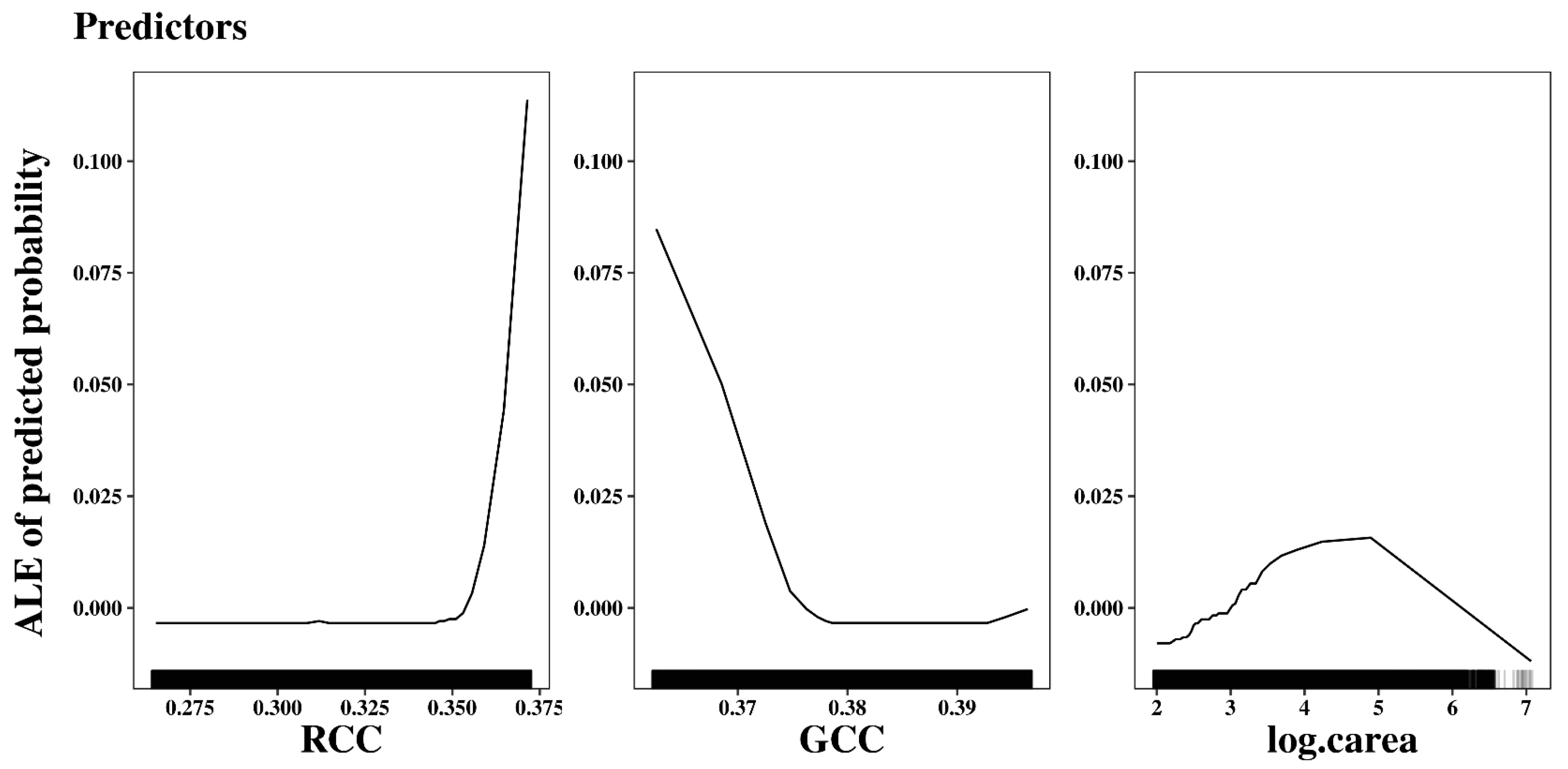
3.2. Model Interpretation
4. Discussion
4.1. Potential of SVM with AL
4.2. Limitations of SVM with AL
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Highland, L.M.; Bobrowsky, P. The Landslide Handbook—A Guide to Understanding Landslides; Kidd, M., Ed.; U.S. Geological Survey Circular 1325: Reston, VA, USA, 2008; p. 129. ISBN 978-141-132-226-4.
- Formetta, G.; Rago, V.; Capparelli, G.; Rigon, R.; Muto, F.; Versace, P. Integrated physically based system for modeling landslide susceptibility. Procedia Earth Planet. Sci. 2014, 9, 74–82. [Google Scholar] [CrossRef] [Green Version]
- Aimaiti, Y.; Liu, W.; Yamazaki, F.; Maruyama, Y. Earthquake-induced landslide mapping for the 2018 Hokkaido eastern Iburi earthquake using PALSAR-2 data. Remote Sens. 2019, 11, 2351. [Google Scholar] [CrossRef] [Green Version]
- Regmi, N.R.; Walter, J.I. Detailed mapping of shallow landslides in eastern Oklahoma and western Arkansas and potential triggering by Oklahoma earthquakes. Geomorphology 2020, 366, 106806. [Google Scholar] [CrossRef]
- Fan, X.; Yang, F.; Subramanian, S.S.; Xu, Q.; Feng, Z.; Mavrouli, O.; Peng, M.; Ouyang, C.; Jansen, J.D.; Huang, R. Prediction of a multi-hazard chain by an integrated numerical simulation approach: The Baige landslide, Jinsha River, China. Landslides 2020, 17, 147–164. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Shi, W.Z.; Zhang, X.K.; Benediktsson, J.A. Landslide inventory mapping from bitemporal high-resolution remote sensing images using change detection and multiscale segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1520–1532. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Saeidi, V.; Ahmadi, K.; Halin, A.A.; Shabani, F. Landslide susceptibility mapping: Machine and ensemble learning based on remote sensing big data. Remote Sens. 2020, 12, 1737. [Google Scholar] [CrossRef]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.C.; Moayedi, H.; Phong, T.V.; Ly, H.B.; Le, T.T.; Trinh, P.T.; et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. Catena 2020, 188, 104451. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Kerle, N.; Poesen, J.; Hervás, J. Object-oriented identification of forested landslides with derivatives of single pulse LiDAR data. Geomorphology 2012, 173, 30–42. [Google Scholar] [CrossRef]
- Petschko, H.; Bell, R.; Glade, T. Effectiveness of visually analyzing LiDAR DTM derivatives for earth and debris slide inventory mapping for statistical susceptibility modeling. Landslides 2016, 13, 857–872. [Google Scholar] [CrossRef]
- Knevels, R.; Petschko, H.; Leopold, P.; Brenning, A. Geographic object-based image analysis for automated landslide detection using open source GIS software. ISPRS Int. J. Geo-Inf. 2019, 8, 551. [Google Scholar] [CrossRef] [Green Version]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Bin Ahmad, B.; Panahi, M.; Hong, H.Y.; et al. Landslide detection and susceptibility mapping by AIRSAR data using support vector machine and index of entropy models in Cameron highlands, Malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef] [Green Version]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Huang, S.J.; Jin, R.; Zhou, Z.H. Active learning by querying informative and representative examples. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1936–1949. [Google Scholar] [CrossRef] [Green Version]
- Bachman, P.; Sordoni, A.; Trischler, A. Learning algorithms for active learning. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 301–310. [Google Scholar]
- Demir, B.; Bovolo, F.; Bruzzone, L. Detection of land-cover transitions in multitemporal remote sensing images with active-learning-based compound classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1930–1941. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Copa, L.; Kanevski, M.; Munoz-Mari, J. A Survey of Active Learning Algorithms for Supervised Remote Sensing Image Classification. IEEE J. Sel. Top. Signal Process. 2011, 5, 606–617. [Google Scholar] [CrossRef]
- Lin, J.Z.; Zhao, L.; Li, S.Y.; Ward, R.; Wang, Z.J. Active-learning-incorporated deep transfer learning for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4048–4062. [Google Scholar] [CrossRef]
- Stumpf, A.; Lachiche, N.; Malet, J.P.; Kerle, N.; Puissant, A. Active learning in the spatial domain for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2492–2507. [Google Scholar] [CrossRef]
- Shao, X.Y.; Ma, S.Y.; Xu, C.; Zhang, P.F.; Wen, B.Y.; Tian, Y.Y.; Zhou, Q.; Cui, Y.L. Planet image-based inventorying and machine learning-based susceptibility mapping for the landslides triggered by the 2018 Mw6.6 Tomakomai, Japan earthquake. Remote Sens. 2019, 11, 978. [Google Scholar] [CrossRef] [Green Version]
- Peng, L.; Niu, R.Q.; Huang, B.; Wu, X.L.; Zhao, Y.N.; Ye, R.Q. Landslide susceptibility mapping based on rough set theory and support vector machines: A case of the three gorges area, China. Geomorphology 2014, 204, 287–301. [Google Scholar] [CrossRef]
- Muenchow, J.; Brenning, A.; Richter, M. Geomorphic process rates of landslides along a humidity gradient in the tropical Andes. Geomorphology 2012, 139, 271–284. [Google Scholar] [CrossRef]
- Settles, B. Active Learning Literature Survey; Computer Sciences Technical Report 1648; University of Wisconsin: Madison, WI, USA, 2010. [Google Scholar]
- Angluin, D. Queries and concept learning. Mach. Learn. 1988, 2, 319–342. [Google Scholar] [CrossRef] [Green Version]
- Cohn, D.; Atlas, L.; Ladner, R. Improving generalization with active learning. Mach. Learn. 1994, 15, 201–221. [Google Scholar] [CrossRef] [Green Version]
- Mackay, D.J.C. Information-based objective functions for active data selection. Neural Comput. 1992, 4, 590–604. [Google Scholar] [CrossRef]
- Tong, S. Active Learning: Theory and Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, August 2001. [Google Scholar]
- Baum, E.B.; Lang, K. Query learning can work poorly when a human oracle is used. In Proceedings of the International Joint Conference on Neural Networks, Baltimore, MD, USA, 7–11 June 1992; p. 8. [Google Scholar]
- Lewis, D.D.; Gale, W.A. A sequential algorithm for training text classifiers. In Proceedings of the 17th Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 1 July 1994; pp. 3–12. [Google Scholar]
- Culotta, A.; McCallum, A. Reducing labeling effort for structured prediction tasks. In Proceedings of the 20th National Conference on Artificial Intelligence, Pittsburgh, PA, USA, 9–13 July 2005; pp. 746–751. [Google Scholar]
- Scheffer, T.; Decomain, C.; Wrobel, S. Active hidden markov models for information extraction. In Proceedings of the International Symposium on Intelligent Data Analysis, Cascais, Portugal, 13–15 September 2001; pp. 309–318. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Seung, H.S.; Opper, M.; Sompolinsky, H. Query by committee. In Proceedings of the 5th Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 287–294. [Google Scholar]
- McCallum, A.K.; Nigam, K. Employing EM in pool-based active learning for text classification. In Proceedings of the 15th International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998; pp. 350–358. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. Available online: http://www.jstor.org/stable/2236703 (accessed on 23 April 2021). [CrossRef]
- Dagan, I.; Engelson, S.P. Committee-based sampling for training probabilistic classifiers. In Proceedings of the 12th International Conference on Machine Learning, Tahoe, CA, USA, 9–12 July 1995; pp. 150–157. [Google Scholar]
- Stańczyk, U.; Zielosko, B.; Jain, L.C. Advances in Feature Selection for Data and Pattern Recognition; Springer: Cham, Switzerland, 2018; p. 328. ISBN 978-3-319-67587-9. [Google Scholar]
- Ramirez-Loaiza, M.E.; Sharma, M.; Kumar, G.; Bilgic, M. Active learning: An empirical study of common baselines. Data Min. Knowl. Discov. 2017, 31, 287–313. [Google Scholar] [CrossRef]
- Xu, H.L.; Li, L.Y.; Guo, P.S. Semi-supervised active learning algorithm for SVMs based on QBC and tri-training. J. Ambient Intell. Humaniz. Comput. 2020, 1–14. [Google Scholar] [CrossRef]
- Vapnik, V. The support vector method of function estimation. In Nonlinear Modeling; Suykens, J.A.K., Vandewalle, J., Eds.; Springer: Boston, MA, USA, 1998; pp. 55–85. [Google Scholar]
- Pawluszek, K.; Borkowski, A.; Tarolli, P. Sensitivity analysis of automatic landslide mapping: Numerical experiments towards the best solution. Landslides 2018, 15, 1851–1865. [Google Scholar] [CrossRef] [Green Version]
- Dou, J.; Paudel, U.; Oguchi, T.; Uchiyama, S.; Hayakavva, Y.S. Shallow and Deep-Seated Landslide Differentiation Using Support Vector Machines: A Case Study of the Chuetsu Area, Japan. Terr. Atmos. Ocean. Sci. 2015, 26, 227–239. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Tham, L.G.; Dai, F.C. Landslide susceptibility mapping based on support vector machine: A case study on natural slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Moguerza, J.M.; Munoz, A. Support vector machines with applications. Stat. Sci. 2006, 21, 322–336. [Google Scholar] [CrossRef] [Green Version]
- Ruß, G.; Brenning, A. Data mining in precision agriculture: Management of spatial information. In Proceedings of the International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, Dortmund, Germany, 28 June–2 July 2010; pp. 350–359. [Google Scholar]
- Begueria, S. Validation and evaluation of predictive models in hazard assessment and risk management. Nat. Hazards 2006, 37, 315–329. [Google Scholar] [CrossRef] [Green Version]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398, ISBN 978-0-470-58247-3. [Google Scholar]
- Molnar, C. Interpretable Machine Learning. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 14 June 2021).
- Ruß, G.; Brenning, A. Spatial variable importance assessment for yield prediction in precision agriculture. In Proceedings of the International Symposium on Intelligent Data Analysis, Tucson, AZ, USA, 19–21 May 2010; pp. 184–195. [Google Scholar]
- Apley, D.W.; Zhu, J.Y. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Version 3.6.3; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 30 June 2021).
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Weingessel, A. e1071: Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. R Package Version 1.7-3. 2019. Available online: https://CRAN.R-project.org/package=e1071 (accessed on 30 June 2021).
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. ROCR: Visualizing classifier performance in R. Bioinformatics 2009, 21, 3940–3941. [Google Scholar] [CrossRef]
- Molnar, C.; Casalicchio, G.; Bischl, B. Iml: An R package for interpretable machine learning. J. Open Source Softw. 2018, 3, 786. [Google Scholar] [CrossRef] [Green Version]
- Brenning, A.; Bangs, D.; Becker, M. RSAGA: SAGA Geoprocessing and Terrain Analysis. R package Version 1.3.0. 2018. Available online: https://CRAN.R-project.org/package=RSAGA (accessed on 30 June 2021).
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef] [Green Version]
- Beck, E.; Makeschin, F.; Haubrich, F.; Richter, M.; Bendix, J.; Valerezo, C. The Ecosystem (Reserva Biológica San Francisco). In Gradients in a Tropical Mountain Ecosystem of Ecuador. Ecological Studies (Analysis and Synthesis), 198; Beck, E., Bendix, J., Kottke, I., Makeschin, F., Mosandl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Bussmann, R.W. The vegetation of Reserva Biológica San Francisco, Zamora–Chinchipe, southern Ecuador: A phytosociological synthesis. Lyonia 2003, 3, 145–254. [Google Scholar]
- Emck, P. A Climatology of South Ecuador. with Special Focus on the Major Andean Ridge as Atlantic-Pacific Climate Divide. Ph.D. Thesis, University of Erlangen, Nuremberg, Germany, 2007. [Google Scholar]
- Beck, E.; Bendix, J.; Kottke, I.; Makeschin, F.; Mosandl, R. Gradients in a Tropical Mountain Ecosystem of Ecuador; Springer: Berlin/Heidelberg, Germany, 2008; Volume 198, p. 525. ISBN 978-3-540-73525-0. [Google Scholar]
- Peters, T.; Diertl, K.H.; Gawlik, J.; Rankl, M.; Richter, M. Vascular plant diversity in natural and anthropogenic ecosystems in the Andes of southern Ecuador. Mt. Res. Dev. 2010, 30, 344–352. [Google Scholar] [CrossRef]
- Brenning, A.; Schwinn, M.; Ruiz-Paez, A.P.; Muenchow, J. Landslide susceptibility near highways is increased by 1 order of magnitude in the Andes of southern Ecuador, Loja province. Nat. Hazards Earth Syst. Sci. 2015, 15, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Mwaniki, M.; Möller, M.; Schellmann, G. Landslide inventory using knowledge based multi-sources classification time series mapping: A case study of central region of Kenya. GI_Forum 2015, 2015, 209–219. [Google Scholar] [CrossRef] [Green Version]
- Fernández, T.; Jiménez, J.; Fernández, P.; El Hamdouni, R.; Cardenal, F.; Delgado, J.; Irigaray, C.; Chacón, J. Automatic detection of landslide features with remote sensing techniques in the Betic Cordilleras (Granada, southern Spain). Int. Soc. Photogramme 2008, 37, 351–356. [Google Scholar]
- Gillespie, A.R.; Kahle, A.B.; Walker, R.E. Color enhancement of highly correlated images. 2. Channel ratio and chromaticity transformation techniques. Remote Sens. Environ. 1987, 22, 343–365. [Google Scholar] [CrossRef]
- Larrinaga, A.R.; Brotons, L. Greenness indices from a low-cost UAV imagery as tools for monitoring post-fire forest recovery. Drones 2019, 3, 6. [Google Scholar] [CrossRef] [Green Version]
- Sonnentag, O.; Hufkens, K.; Teshera-Sterne, C.; Young, A.M.; Friedl, M.; Braswell, B.H.; Milliman, T.; O’Keefe, J.; Richardson, A.D. Digital repeat photography for phenological research in forest ecosystems. Agric. For. Meteorol. 2012, 152, 159–177. [Google Scholar] [CrossRef]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Wainer, J.; Cawley, G. Empirical evaluation of resampling procedures for optimising SVM hyperparameters. J. Mach. Learn. Res. 2017, 18, 475–509. [Google Scholar] [CrossRef]








| RCC | GCC | Slope | Plancurv | Profcurv | Log.carea | Cslope | |
|---|---|---|---|---|---|---|---|
| RCC | 100 | −36 | −11 | 9 | 8 | −16 | −17 |
| GCC | −36 | 100 | 14 | −18 | −18 | 34 | 28 |
| Slope | −11 | 14 | 100 | 3 | 3 | −3 | 75 |
| plancurv | 9 | −18 | 1 | 100 | 52 | −68 | −17 |
| profcurv | 8 | −18 | 3 | 52 | 100 | −58 | −23 |
| log.carea | −16 | 34 | −3 | −68 | −58 | 100 | 22 |
| cslope | −17 | 28 | 75 | −17 | −23 | 22 | 100 |
| Sampling Strategy | Non-Landslide | Landslide |
|---|---|---|
| Margin sampling | 1013 | 447 |
| Query by committee | 1280 | 180 |
| Random sampling | 1415 | 45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Brenning, A. Active-Learning Approaches for Landslide Mapping Using Support Vector Machines. Remote Sens. 2021, 13, 2588. https://doi.org/10.3390/rs13132588
Wang Z, Brenning A. Active-Learning Approaches for Landslide Mapping Using Support Vector Machines. Remote Sensing. 2021; 13(13):2588. https://doi.org/10.3390/rs13132588
Chicago/Turabian StyleWang, Zhihao, and Alexander Brenning. 2021. "Active-Learning Approaches for Landslide Mapping Using Support Vector Machines" Remote Sensing 13, no. 13: 2588. https://doi.org/10.3390/rs13132588
APA StyleWang, Z., & Brenning, A. (2021). Active-Learning Approaches for Landslide Mapping Using Support Vector Machines. Remote Sensing, 13(13), 2588. https://doi.org/10.3390/rs13132588