Application of 3D Laser Image Scanning Technology and Cellular Automata Model in the Prediction of the Dynamic Process of Rill Erosion
Abstract
:1. Introduction
2. Experimental Procedure and Theoretical Foundation
2.1. Experimental Procedure
2.2. Description of the CA Model
2.2.1. Model Structure
2.2.2. Model Parameter Calibration
2.2.3. Specification of the Transition Function
- Infiltration Rule
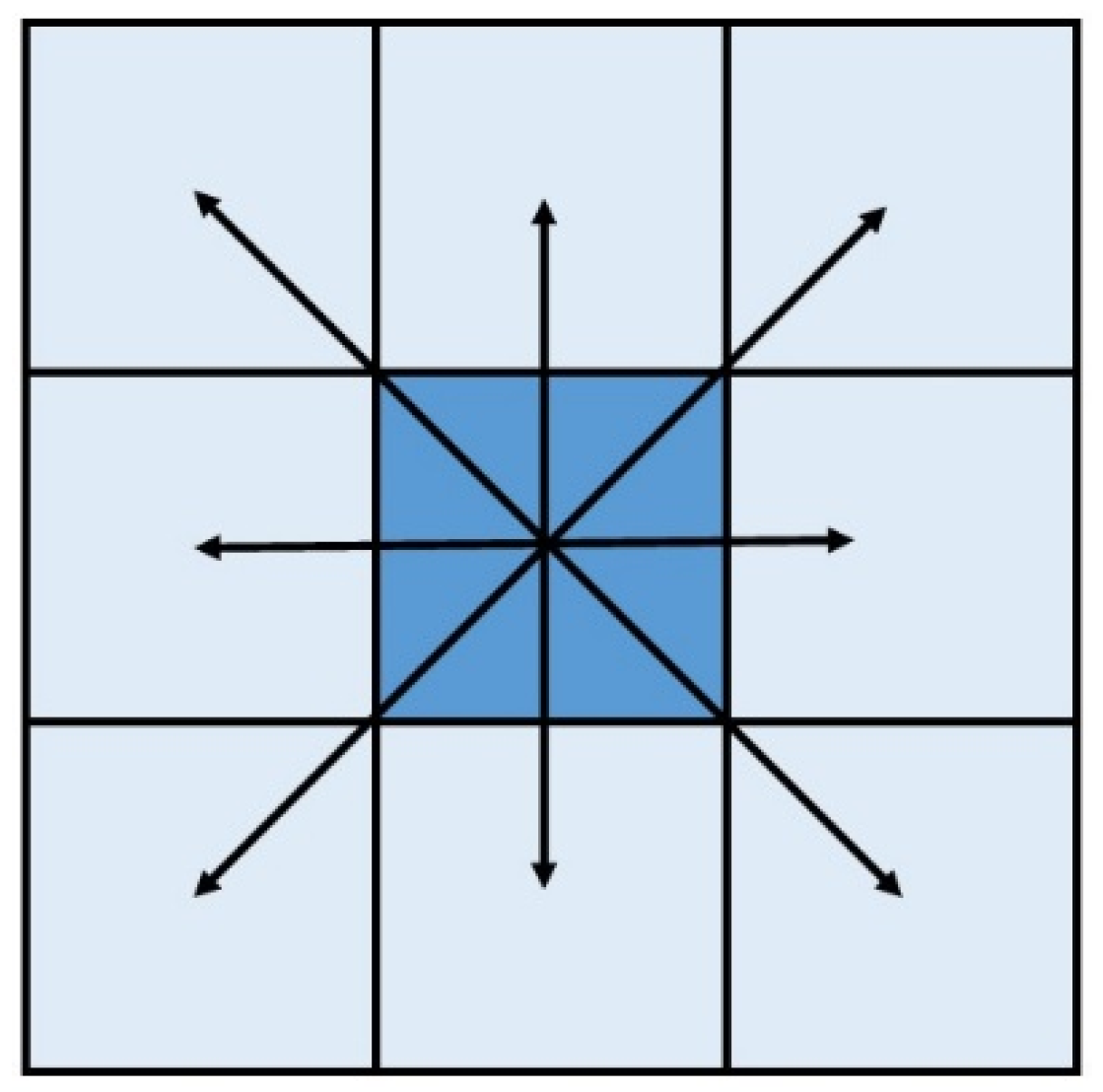
- Rules of Flow and Sediment Transport Direction
- Water Allocation Rules
- Calculation Rules of Flow Rate
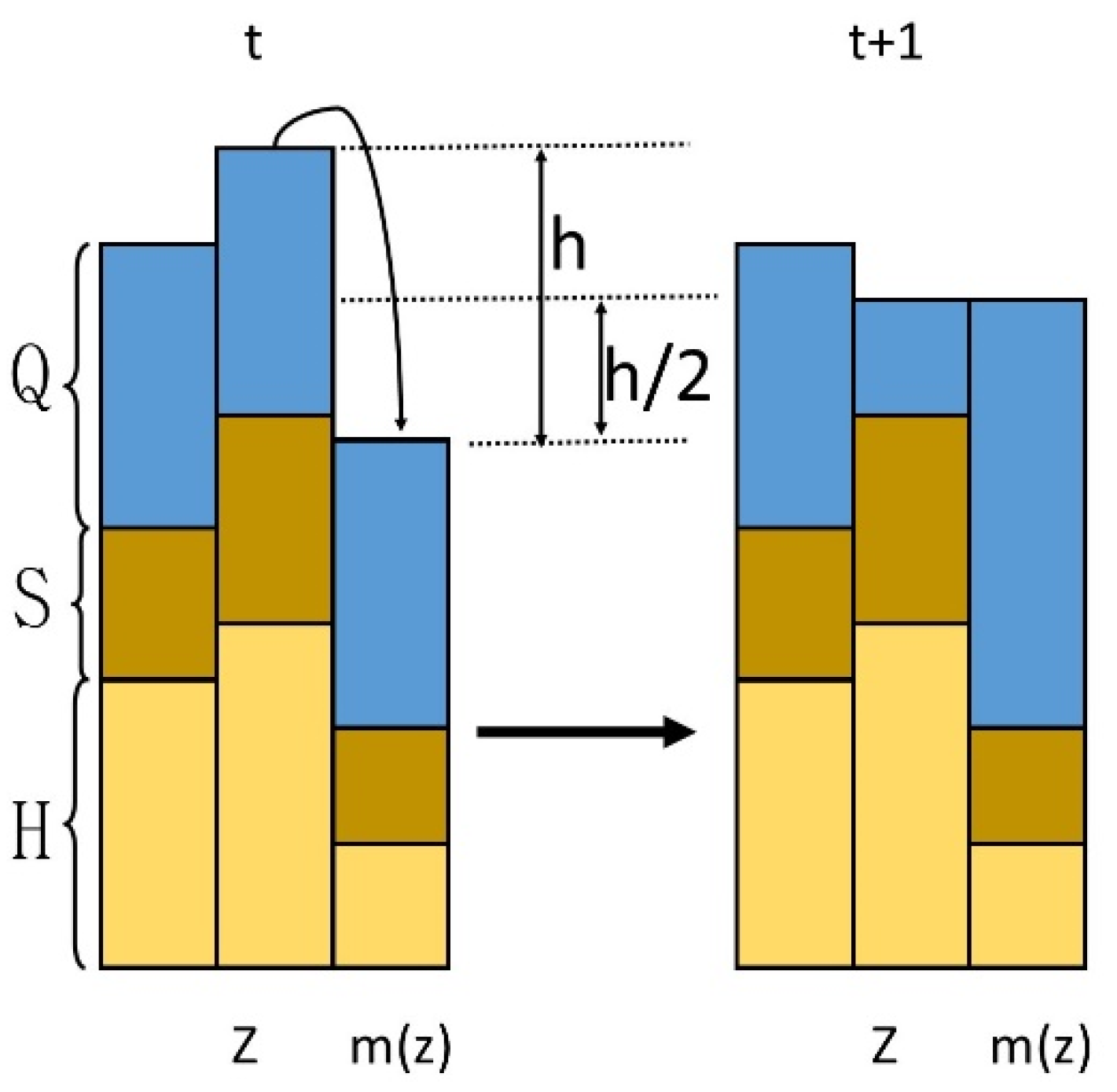
- Rules of Erosion Transport and Deposition
3. Results
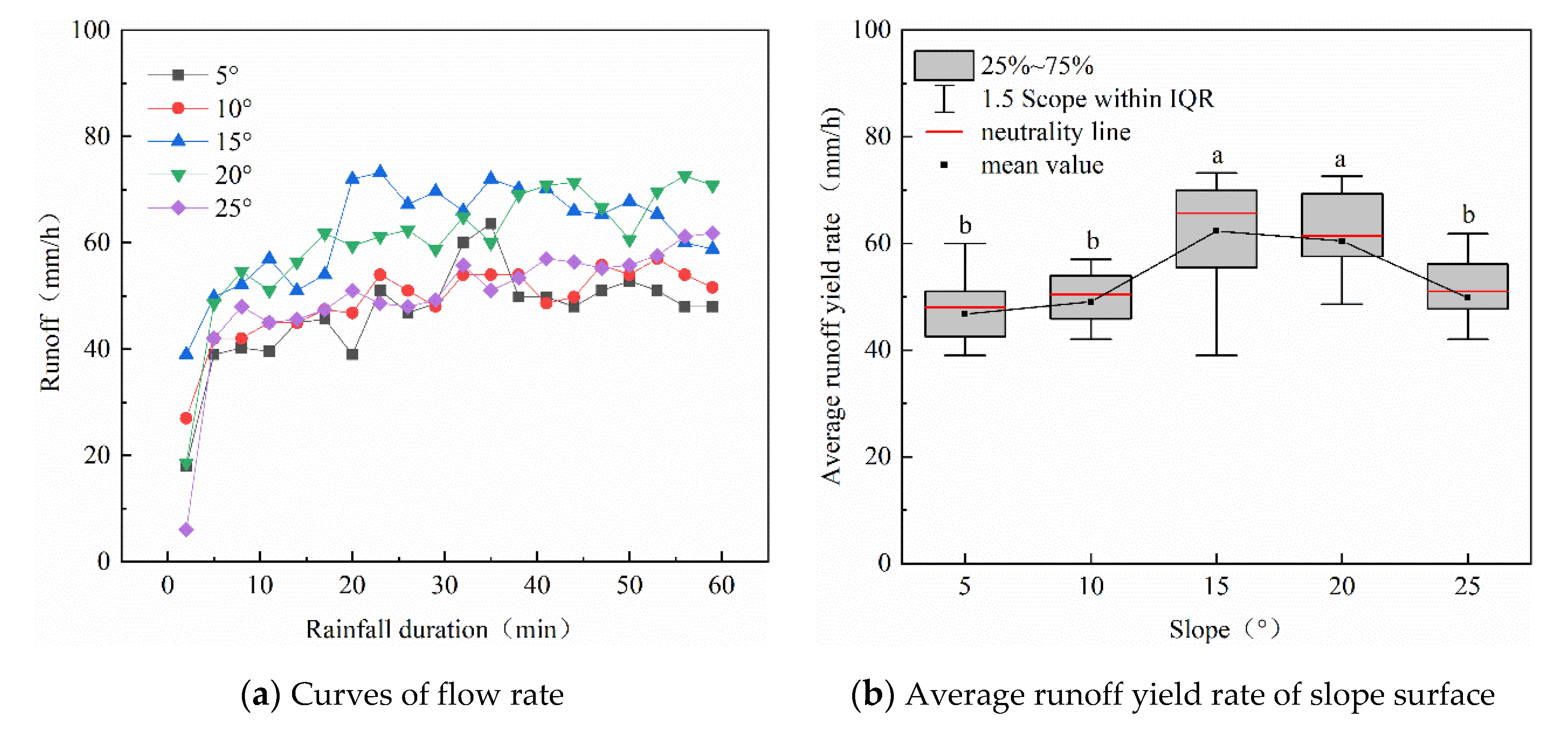
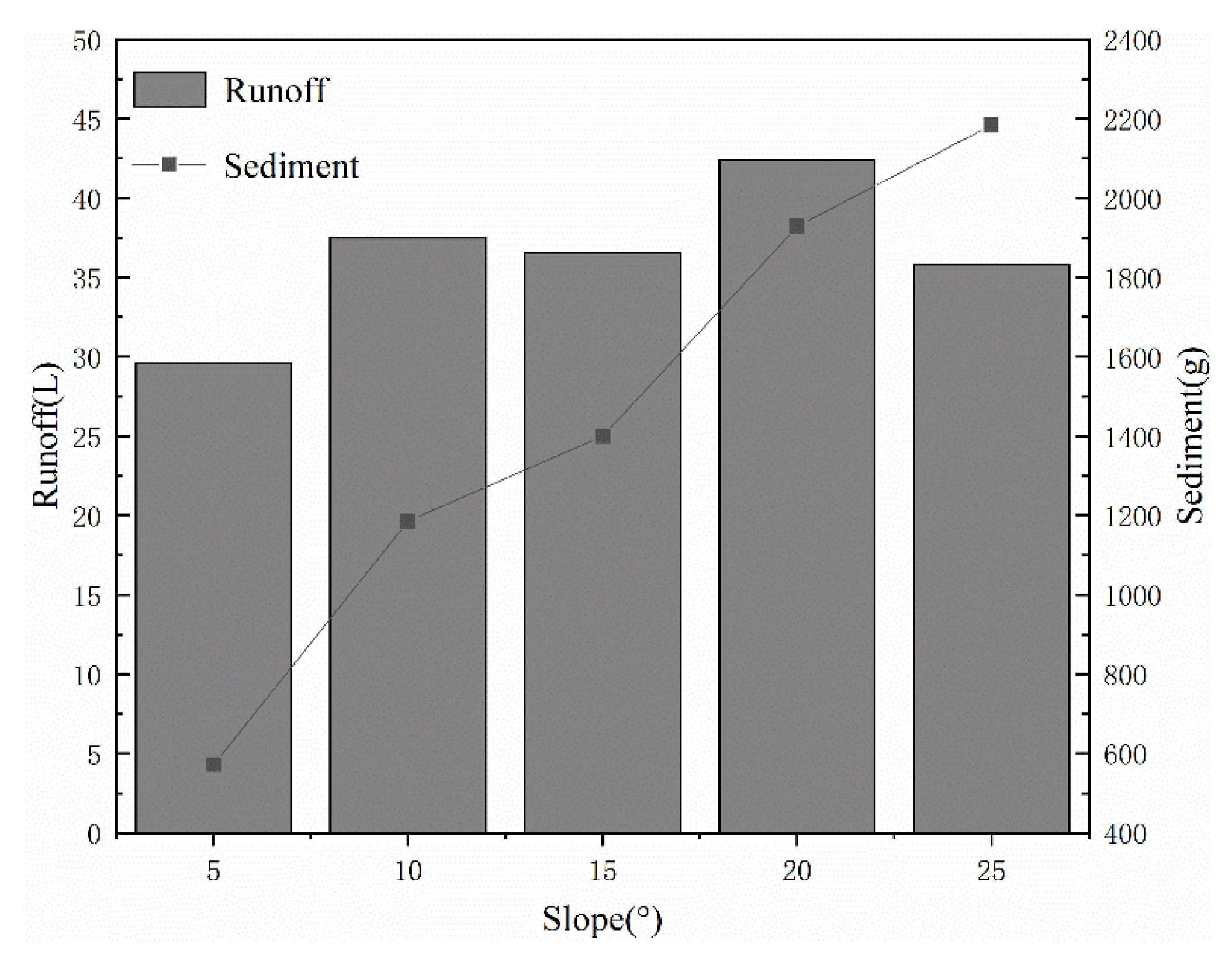
3.1. The Influence of Slope on the Yield Rate
3.2. The Influence of Slope on Sediment Yield
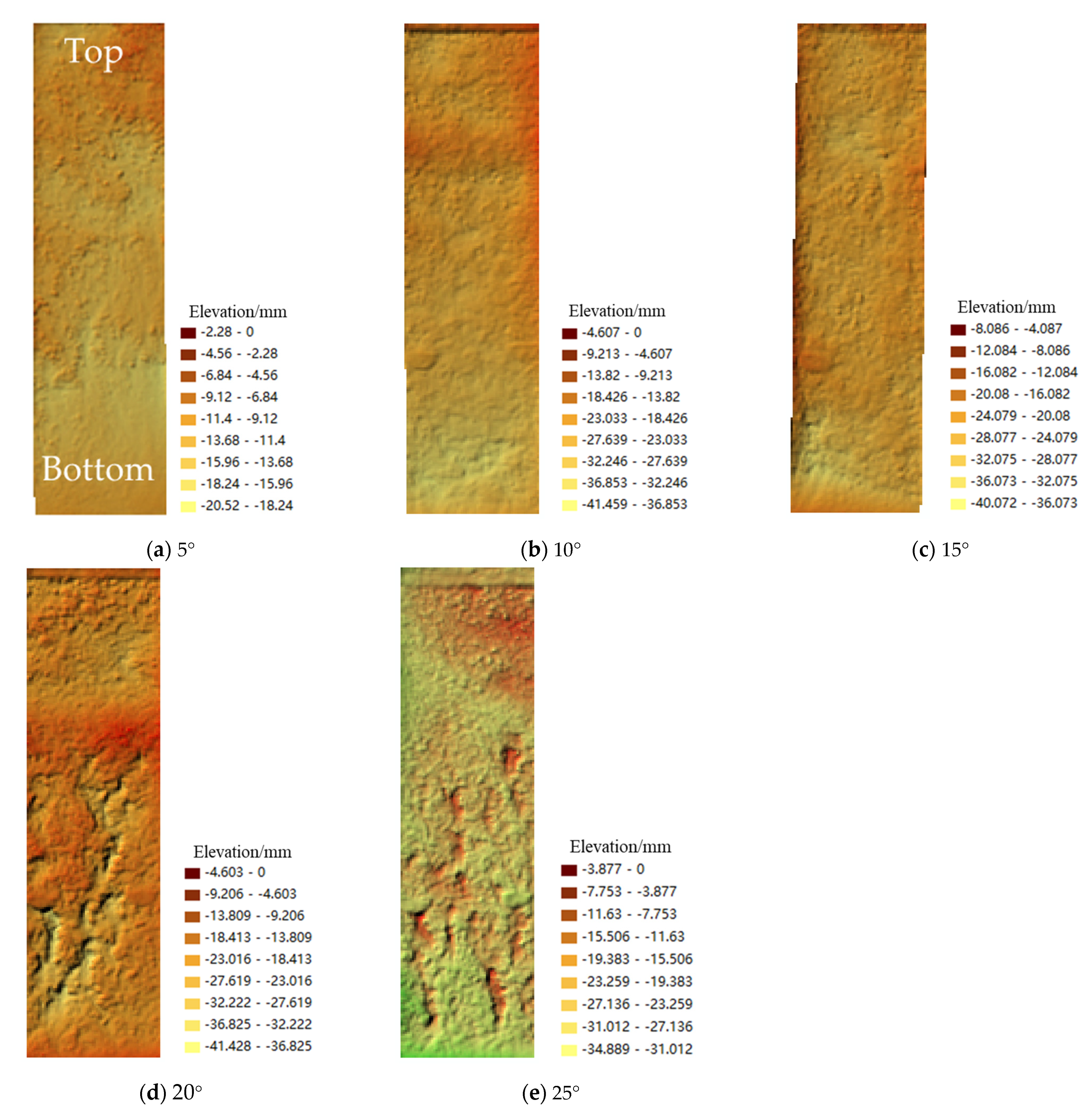
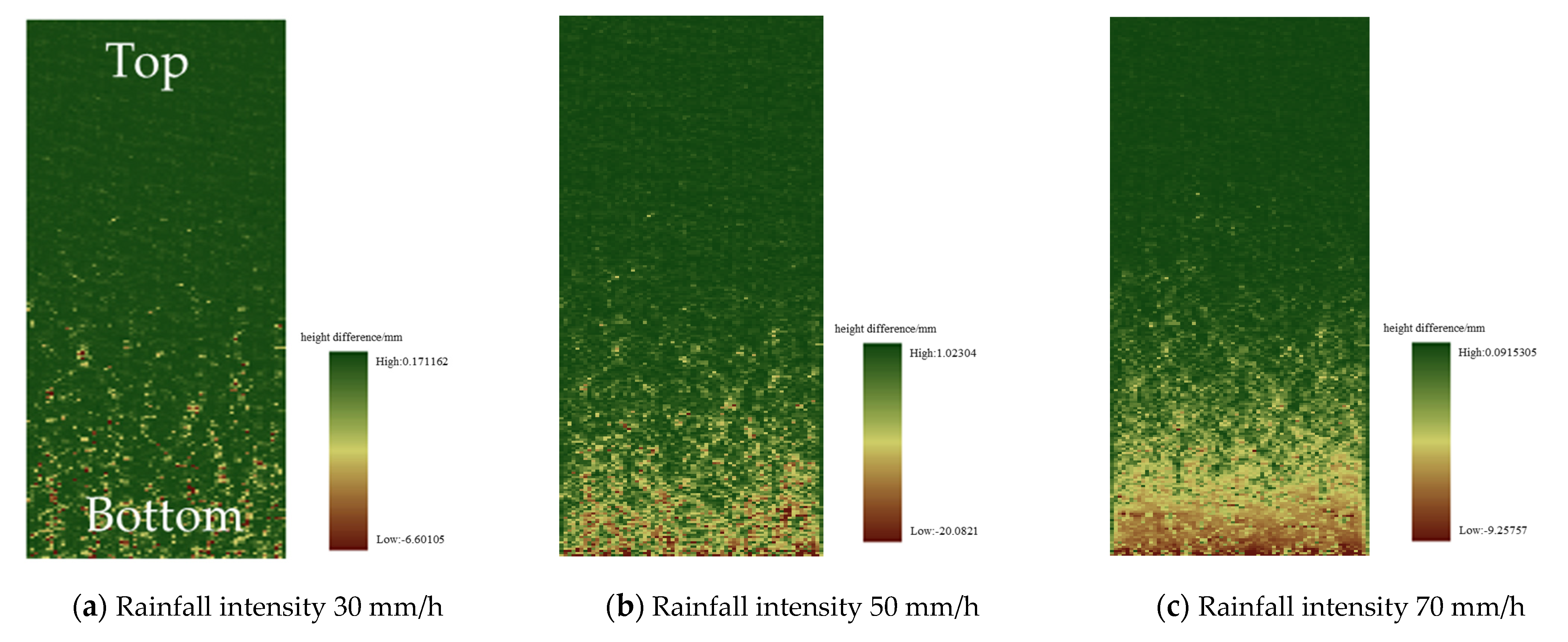
3.3. Erosion Patterns of Bare Black Soil Slopes under Different Gradients
3.4. Confluence Path Development Process
4. Discussion
4.1. Effect of Slope on Runoff Erosion
4.2. Validation of the Model in Black Soil Area
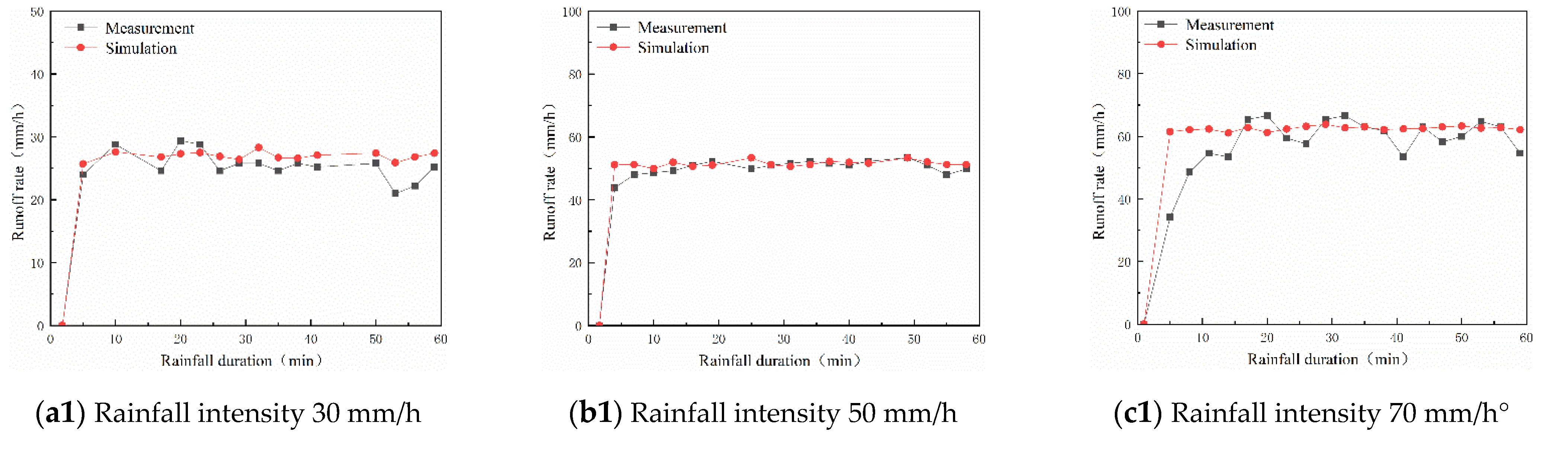
4.3. Validation of Model Production Process
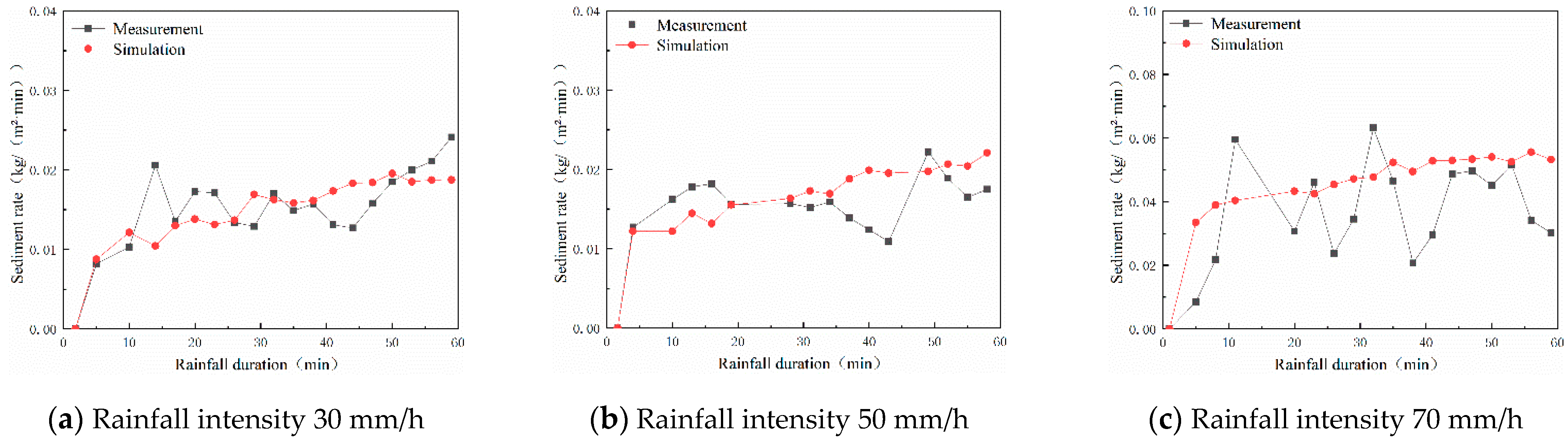
4.4. Verification of Sediment Production Process of the Model
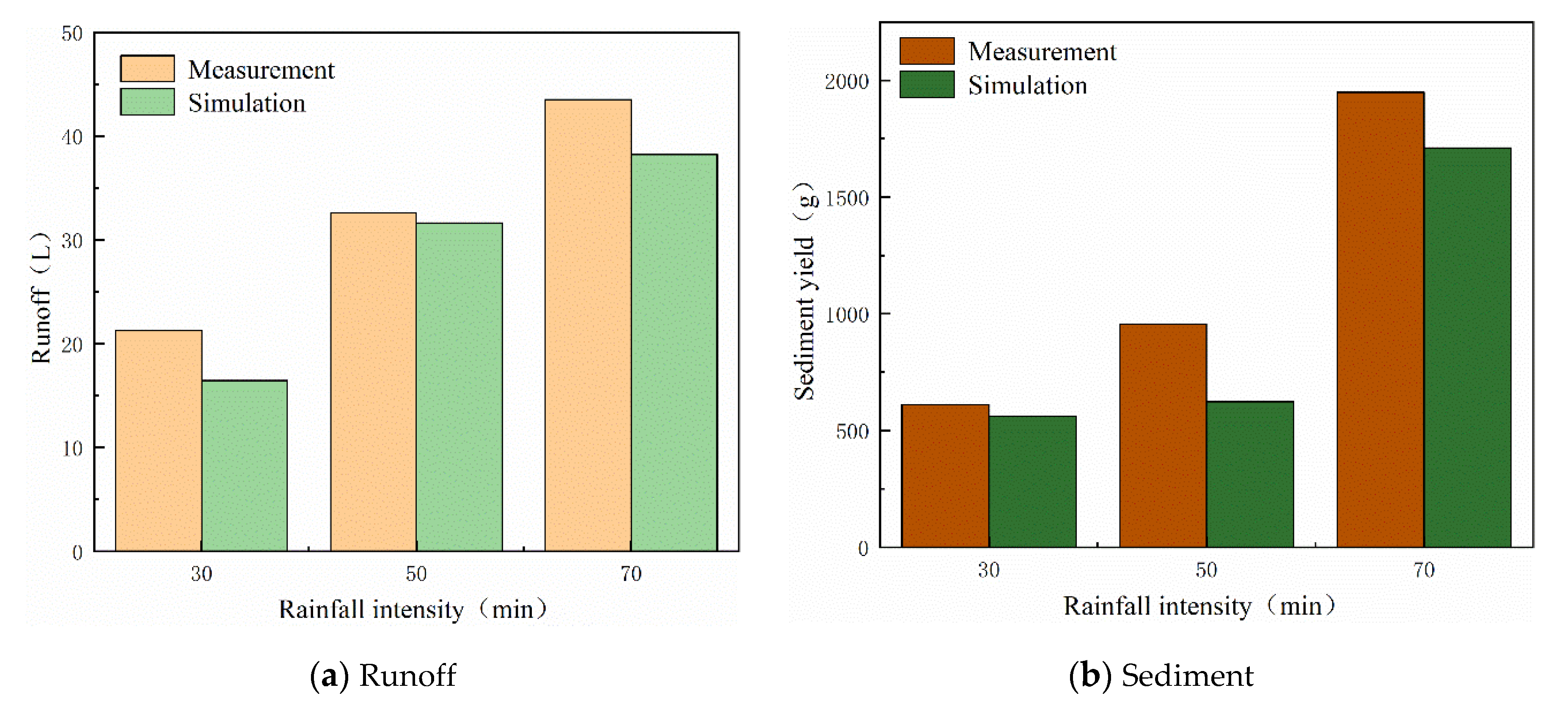
4.5. Verification of Total Yield and Sediment Yield of the Model
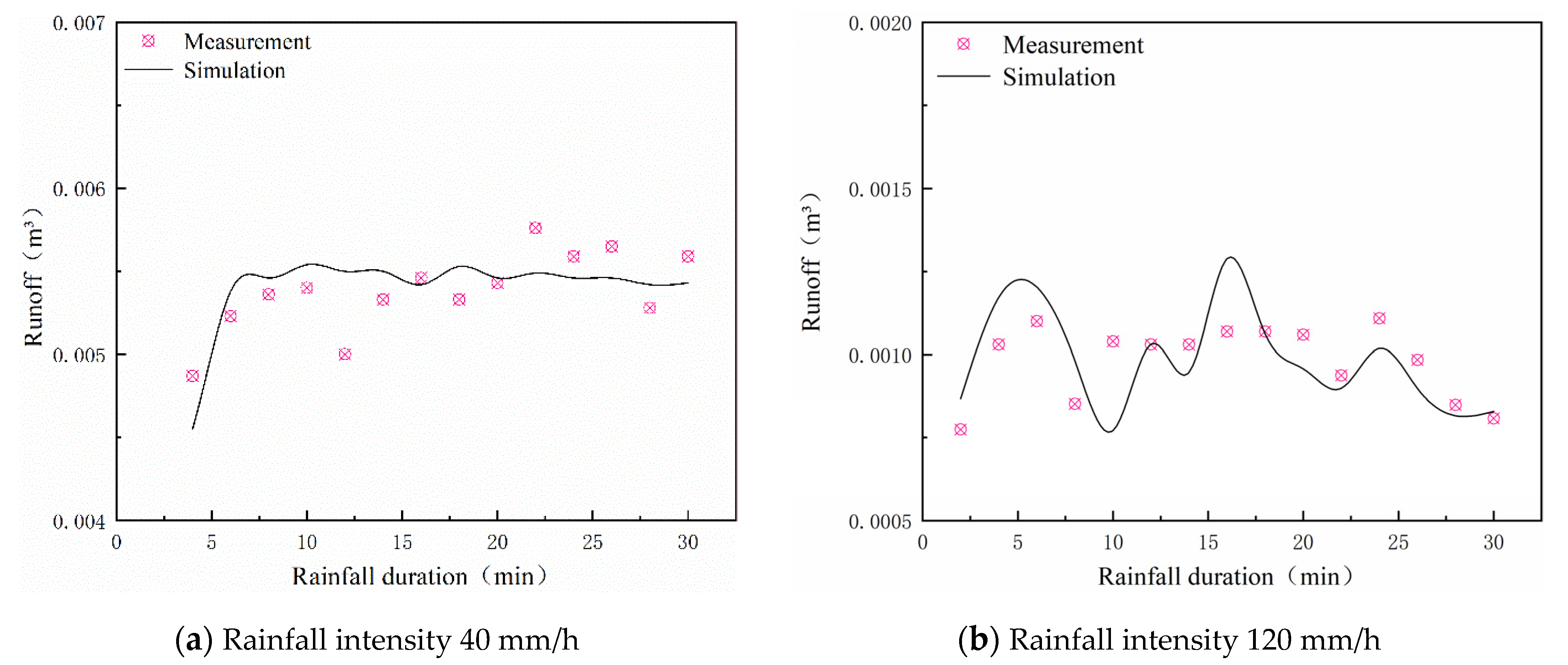
4.6. Validation on Runoff Model in Loess Area
4.7. Analysis of Slope Erosion Morphology Development Process
4.8. Limitations and Future Work Prospects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, X.M.; Zhang, X.P.; Deng, W.; Fang, H.J. Black soil degradation by rainfall erosion in Jilin, China. Land Degrad. Dev. 2003, 14, 409–420. [Google Scholar] [CrossRef]
- Yin, L.; Zhang, B.; Pan, X.; Shi, D. Current status and comprehensive control strategies of soil erosion for hilly region in the Southern China. Sci. Soil Water Conserv. 2008, 6, 22–27. [Google Scholar]
- Welch, R.; Jordan, T.R.; Thomas, A.W. A photogrammetric technique for measuring soil-erosion. J. Soil Water Conserv. 1984, 39, 191–194. [Google Scholar]
- Dymond, J.R.; Hicks, D.L. Steepland erosion measured from historical aerial photographs. J. Soil Water Conserv. 1986, 41, 252–255. [Google Scholar]
- Gessesse, G.D.; Fuchs, H.; Mansberger, R.; Klik, A.; Rieke-Zapp, D.H. Assessment of Erosion, Deposition and Rill Development on Irregular Soil Surfaces Using Close Range Digital Photogrammetry. Photogramm. Rec. 2010, 25, 299–318. [Google Scholar] [CrossRef]
- Cook, K.L. An evaluation of the effectiveness of low-cost UAVs and structure from motion for geomorphic change detection. Geomorphology 2017, 278, 195–208. [Google Scholar] [CrossRef]
- Vinci, A.; Todisco, F.; Brigante, R.; Mannocchi, F.; Radicioni, F. A smartphone camera for the structure from motion reconstruction for measuring soil surface variations and soil loss due to erosion. Hydrol. Res. 2017, 48, 673–685. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river. Earth Surf. Process. Landf. 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Eitel, J.U.H.; Williams, C.J.; Vierling, L.A.; Al-Hamdan, O.Z.; Pierson, F.B. Suitability of terrestrial laser scanning for studying surface roughness effects on concentrated flow erosion processes in rangelands. Catena 2011, 87, 398–407. [Google Scholar] [CrossRef]
- Bremer, M.; Sass, O. Combining airborne and terrestrial laser scanning for quantifying erosion and deposition by a debris flow event. Geomorphology 2012, 138, 49–60. [Google Scholar] [CrossRef]
- Smith, R. The application of cellular automata to the erosion of landforms. Earth Surf. Process. Landf. 1991, 16, 273–281. [Google Scholar] [CrossRef]
- Murray, A.B.; Paola, C. A cellular-model of braided rivers. Nature 1994, 371, 54–57. [Google Scholar] [CrossRef]
- Pilotti, M.; Menduni, G. Application of lattice gas techniques to the study of sediment erosion and transport caused by laminar sheetflow. Earth Surf. Process. Landf. 1997, 22, 885–893. [Google Scholar] [CrossRef]
- D’Ambrosio, D.; Di Gregorio, S.; Gabriele, S.; Gaudio, R. A cellular automats model for soil erosion by water. Phys. Chem. Earth Part B-Hydrol. Ocean. Atmos. 2001, 26, 33–39. [Google Scholar] [CrossRef]
- Wei, L. LANDSAP: A coupled surface and subsurface cellular automata model for landform simulation. Comput. Geosci. 2001, 27, 363–367. [Google Scholar] [CrossRef]
- Bursik, M.; Martinez-Hackert, B.; Delgado, H.; Gonzalez-Huesca, A. A smoothed-particle hydrodynamic automaton of landform degradation by overland flow. Geomorphology 2003, 53, 25–44. [Google Scholar] [CrossRef]
- Valette, G.; Prevost, S.; Lucas, L.; Leonard, J. SoDA project: A simulation of soil surface degradation by rainfall. Comput. Graph. UK 2006, 30, 494–506. [Google Scholar] [CrossRef]
- Rinaldi, P.R.; Dalponte, D.D.; Venere, M.J.; Clausse, A. Cellular automata algorithm for simulation of surface flows in large plains. Simul. Model. Pract. Theory 2007, 15, 315–327. [Google Scholar] [CrossRef]
- Yuan, L.F.; Chang, C.P.; Zhang, Q.F. Soil Erosion and Sediment Yield Model in a Small Watershed Based on Cellular Automata. Bull. Soil Water Conserv. 2008, 28, 85–89. (In Chinese) [Google Scholar]
- Narteau, C.; Zhang, D.; Rozier, O.; Claudin, P. Setting the length and time scales of a cellular automaton dune model from the analysis of superimposed bed forms. J. Geophys. Res. Earth Surf. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Yuan, L.F.; Wu, S.F.; Liu, X.F.; Zhang, Q.F.; Huo, Y.Y. Study on loess hill slope rill erosion model based on cellular automata. J. Soil Sci. 2012, 49, 1043–1049. (In Chinese) [Google Scholar]
- Wu, S.; Liu, Z.; Huo, Y.; Meng, Q. Development process and simulation of gully erosion on loess slope. J. Soil Sci. 2015, 052, 48–56. (In Chinese) [Google Scholar] [CrossRef]
- Sun, L.Q.; Wu, S.F.; Zhang, B.B.; Lei, Q. Development of rill erosion and its simulation with cellular automata-rill model in Chinese Loess Plateau. Arch. Agron. Soil Sci. 2020, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.X.; Xin, Y.; Xie, Y.; Wang, W.T. Effects of slope and rainfall intensity on runoff and soil erosion from furrow diking under simulated rainfall. Catena 2019, 177, 92–100. [Google Scholar] [CrossRef]
- de Almeida, W.S.; Seitz, S.; de Oliveira, L.F.C.; de Carvalho, D.F. Duration and intensity of rainfall events with the same erosivity change sediment yield and runoff rates. Int. Soil Water Conserv. Res. 2021, 9, 69–75. [Google Scholar] [CrossRef]
- Horton, R.E. An Approach Toward a Physical Interpretation of Infiltration-Capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Fairfield, J.; Leymarie, P. Drainage networks from grid digital elevation models. Water Resour. Res. 1991, 27, 709–717. [Google Scholar] [CrossRef]
- Alberts, E.E.; Nearing, M.A.; Weltz, M.A.; Risse, L.M.; Simanton, J.R. Soil Component; USDA-Water Erosion Prediction Project: Hillslope Profile and Watershed Model Documentation; NSERL Report No.10S; USDA-ARS Nation Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1995. [Google Scholar]
- Zhang, K.L.; Zhang, Z.M. Experimental study of fine gully erosion and its sand production characteristics on steep loess slopes. Nat. Sci. Prog. 2000, 12, 82–85. (In Chinese) [Google Scholar]
- Zhao, L.S.; Zhang, Q.F.; Song, X.Y.; Wu, F.Q. Characterization of surface potholes in loess slope cultivated land based on DEM under micro-scale. J. Soil Sci. 2012, 49, 179–183. (In Chinese) [Google Scholar]
- Hu, Y.; Fister, W.; He, Y.; Kuhn, N.J. Assessment of crusting effects on interrill erosion by laser scanning. PeerJ 2020, 8, e8487. [Google Scholar] [CrossRef]





| Depth/cm | Percentage of Particle Content/% | Soil Type | ||
|---|---|---|---|---|
| 2.0~0.02 mm | 0.02~0.002 mm | <0.002 mm | ||
| 0~20 | 39.06 | 54.44 | 6.50 | Powdered loam |
| 20~40 | 34.48 | 58.70 | 6.82 | Powdered loam |
| 40~80 | 33.39 | 59.37 | 7.24 | Powdered loam |
| Parameter | Different Working Conditions | The Data Source | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| Rainfall intensity (mm/h) | 30 | 50 | 70 | Test set |
| Initial infiltration rate (mm/min) | 0.150 | 0.150 | 0.150 | Test set |
| Steady infiltration rate (mm/min) | 0.072 | 0.072 | 0.072 | Test set |
| Decreasing parameters | 0.04 | 0.04 | 0.04 | |
| Cellular side length (mm) | 5 | 5 | 5 | |
| Roughness | 0.5 | 0.5 | 0.5 | DEM data |
| Slope (°) | 18 | 18 | 18 | Test set |
| Empirical coefficient | −31.47 | −31.47 | −31.47 | The literature [30] |
| Empirical coefficient | 38.61 | 38.61 | 38.61 | The literature [30] |
| Empirical coefficient | 0.845 | 0.845 | 0.845 | The literature [30] |
| Empirical coefficient | 0.412 | 0.412 | 0.412 | The literature [30] |
| Soil density (g/mm3) | 0.0013 | 0.0013 | 0.0013 | |
| Water density (g/cm3) | 1 | 1 | 1 | |
| Erosion coefficient Kr (kg/(N·s)) | 0.05 | 0.05 | 0.05 | Test set |
| Critical shear stress (Pa) | 4.010 | 4.642 | 4.625 | Test set |
| Gravitational acceleration (m/s2) | 9.8 | 9.8 | 9.8 | |
| Rainfall Intensity (mm/h) | Rainfall Duration (min) | The Longest Ditch Long (cm) | The Biggest Groove Depth (mm) | The Mean Width of the Longest Ditch (mm) | Erosion Plane Density | The Intensity of Erosion (kg/m³) |
|---|---|---|---|---|---|---|
| 30 | 60 | 15.3 | 1.9 | 6.5 | 0.0804 | 0.933 |
| 50 | 60 | 17.1 | 2.9 | 10.4 | 0.1148 | 1.076 |
| 70 | 60 | -- | -- | -- | 0.3028 | 2.851 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Li, Q.; Chen, J.; Han, Y. Application of 3D Laser Image Scanning Technology and Cellular Automata Model in the Prediction of the Dynamic Process of Rill Erosion. Remote Sens. 2021, 13, 2586. https://doi.org/10.3390/rs13132586
Li S, Li Q, Chen J, Han Y. Application of 3D Laser Image Scanning Technology and Cellular Automata Model in the Prediction of the Dynamic Process of Rill Erosion. Remote Sensing. 2021; 13(13):2586. https://doi.org/10.3390/rs13132586
Chicago/Turabian StyleLi, Song, Qiqi Li, Jian Chen, and Yu Han. 2021. "Application of 3D Laser Image Scanning Technology and Cellular Automata Model in the Prediction of the Dynamic Process of Rill Erosion" Remote Sensing 13, no. 13: 2586. https://doi.org/10.3390/rs13132586
APA StyleLi, S., Li, Q., Chen, J., & Han, Y. (2021). Application of 3D Laser Image Scanning Technology and Cellular Automata Model in the Prediction of the Dynamic Process of Rill Erosion. Remote Sensing, 13(13), 2586. https://doi.org/10.3390/rs13132586







