A New Model of Quasigeoid for the Baltic Sea Area
Abstract
:1. Introduction
2. Materials and Methods
Zero Degree
3. Data
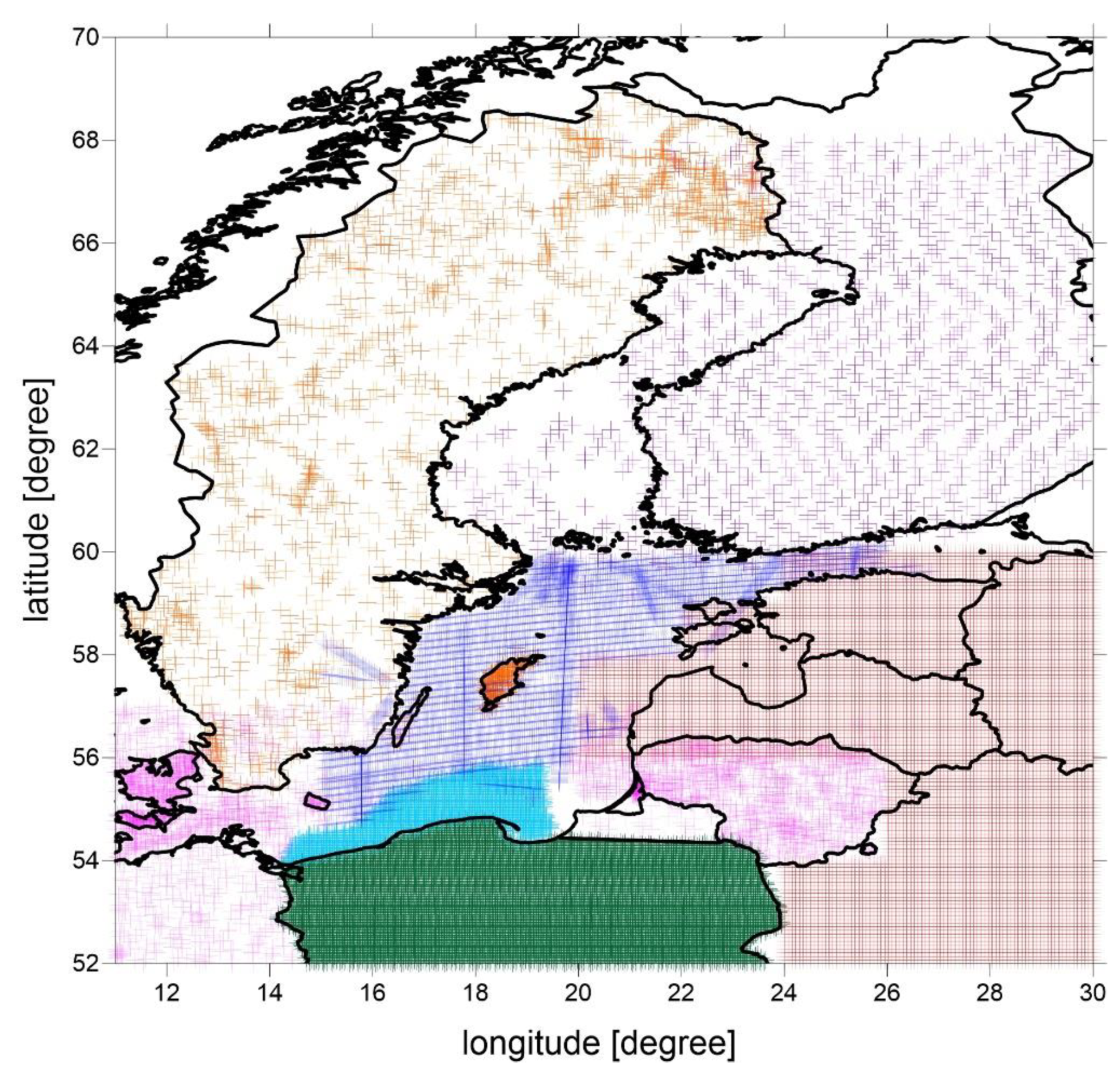
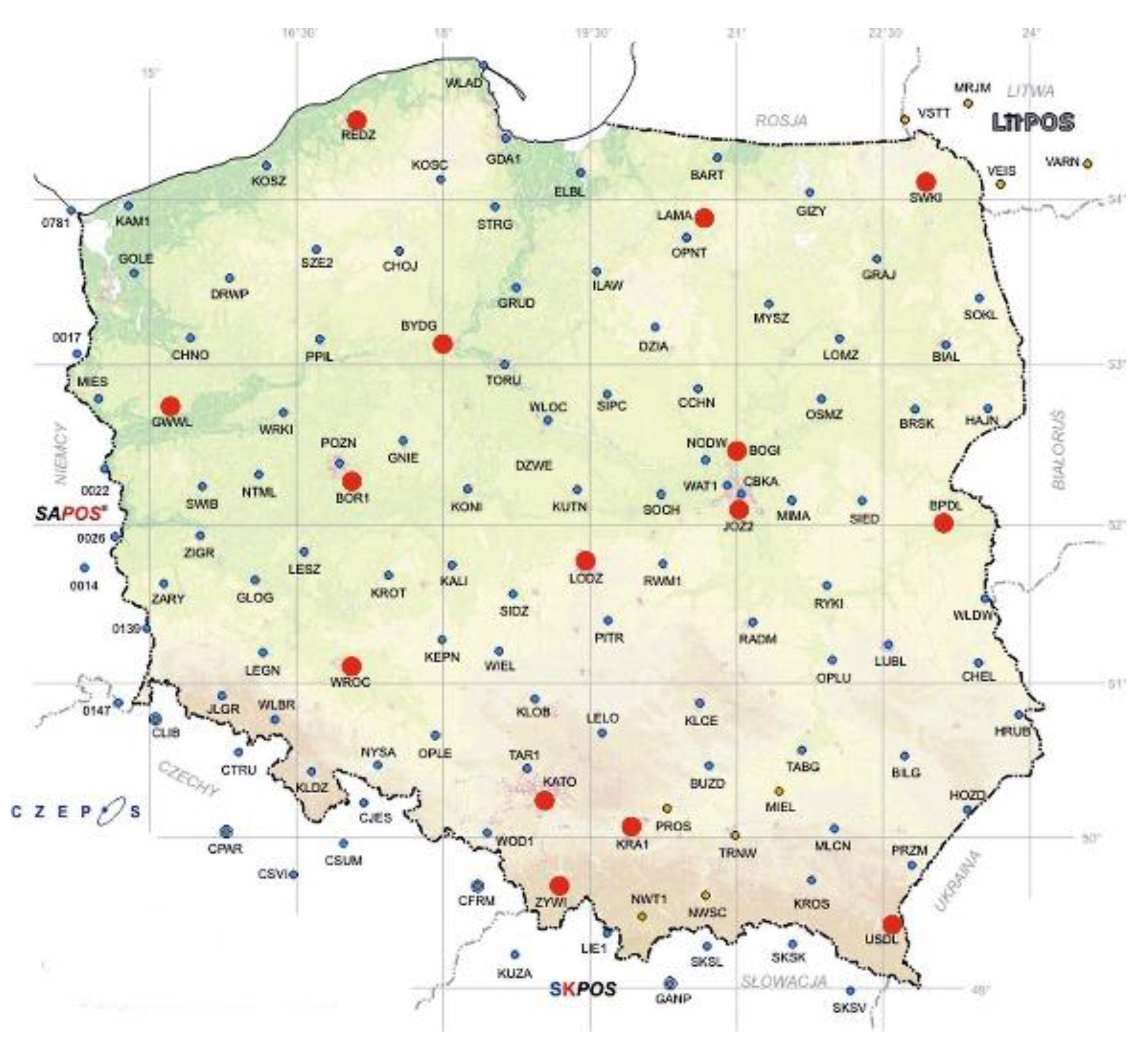
3.1. Gravity Data
Combined Data Set
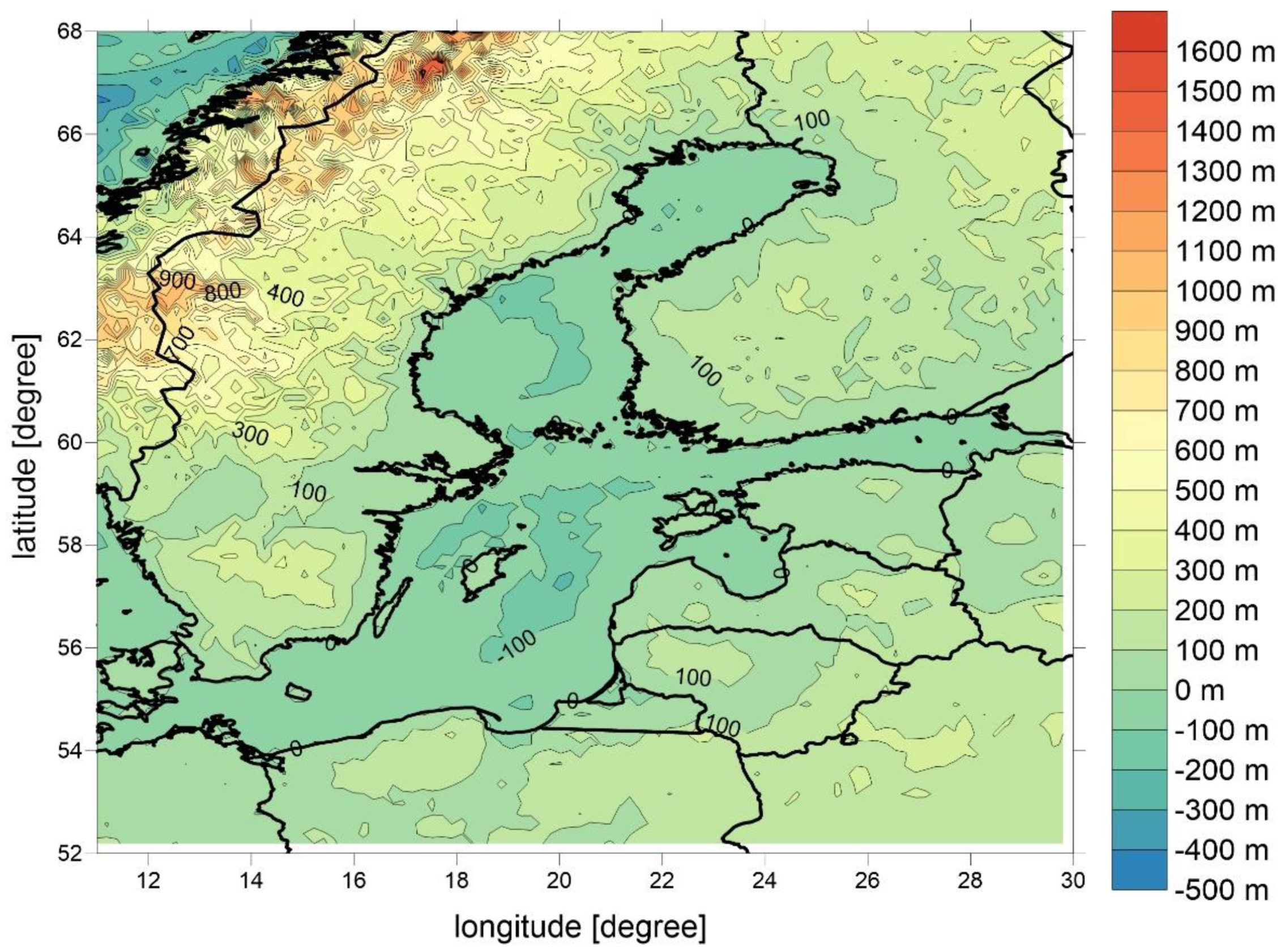
3.2. DTM Data
3.3. Global Geopotential Models
3.4. GNSS and Leveling Data
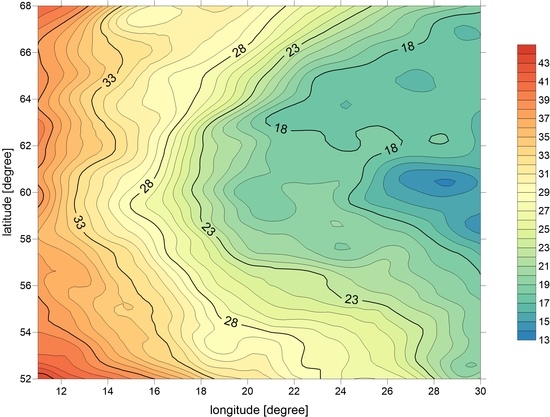
4. Quasigeoid Computation
4.1. N and Δg from Geopotential Models
4.2. Gravity Data Gridding
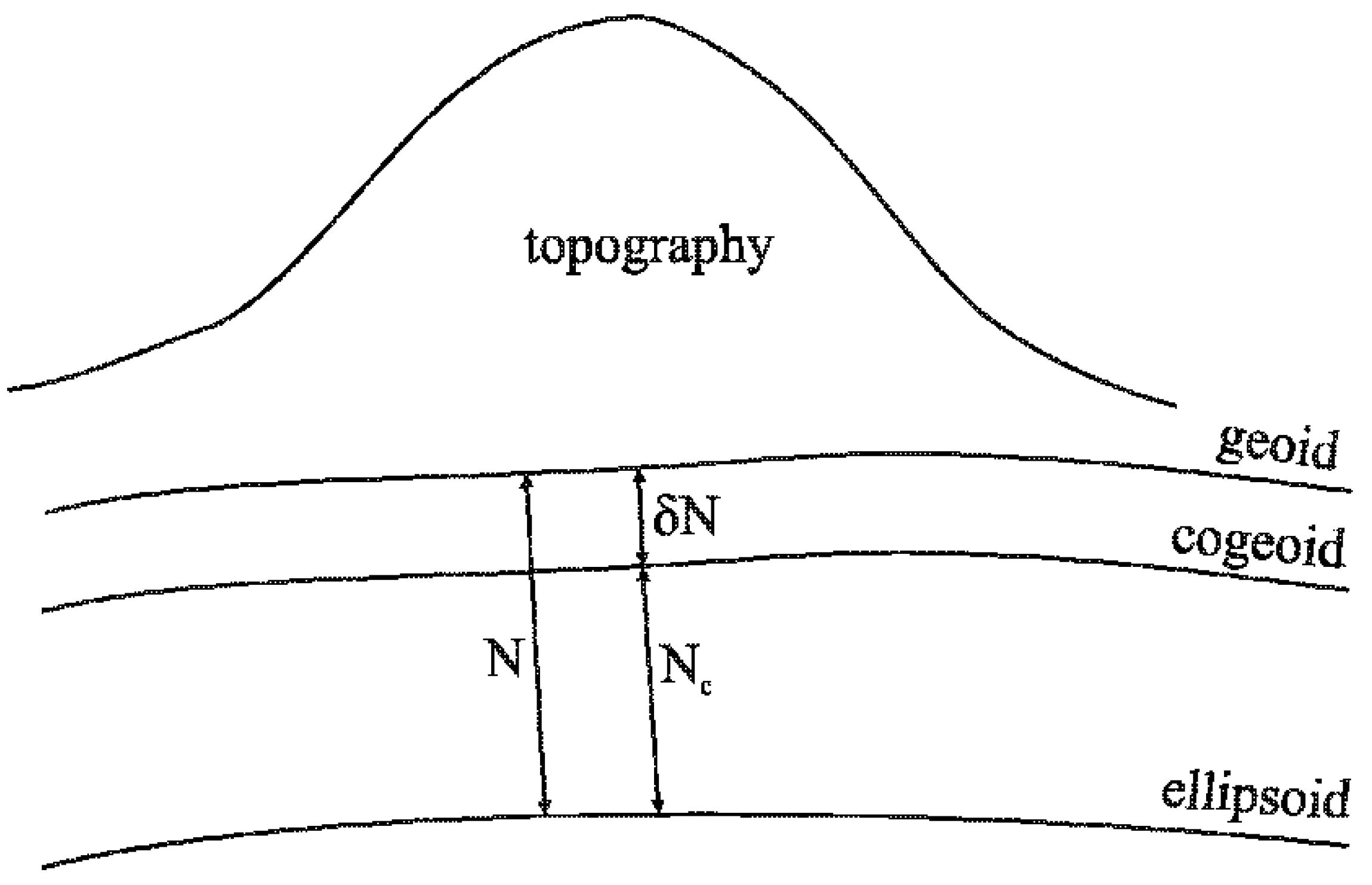
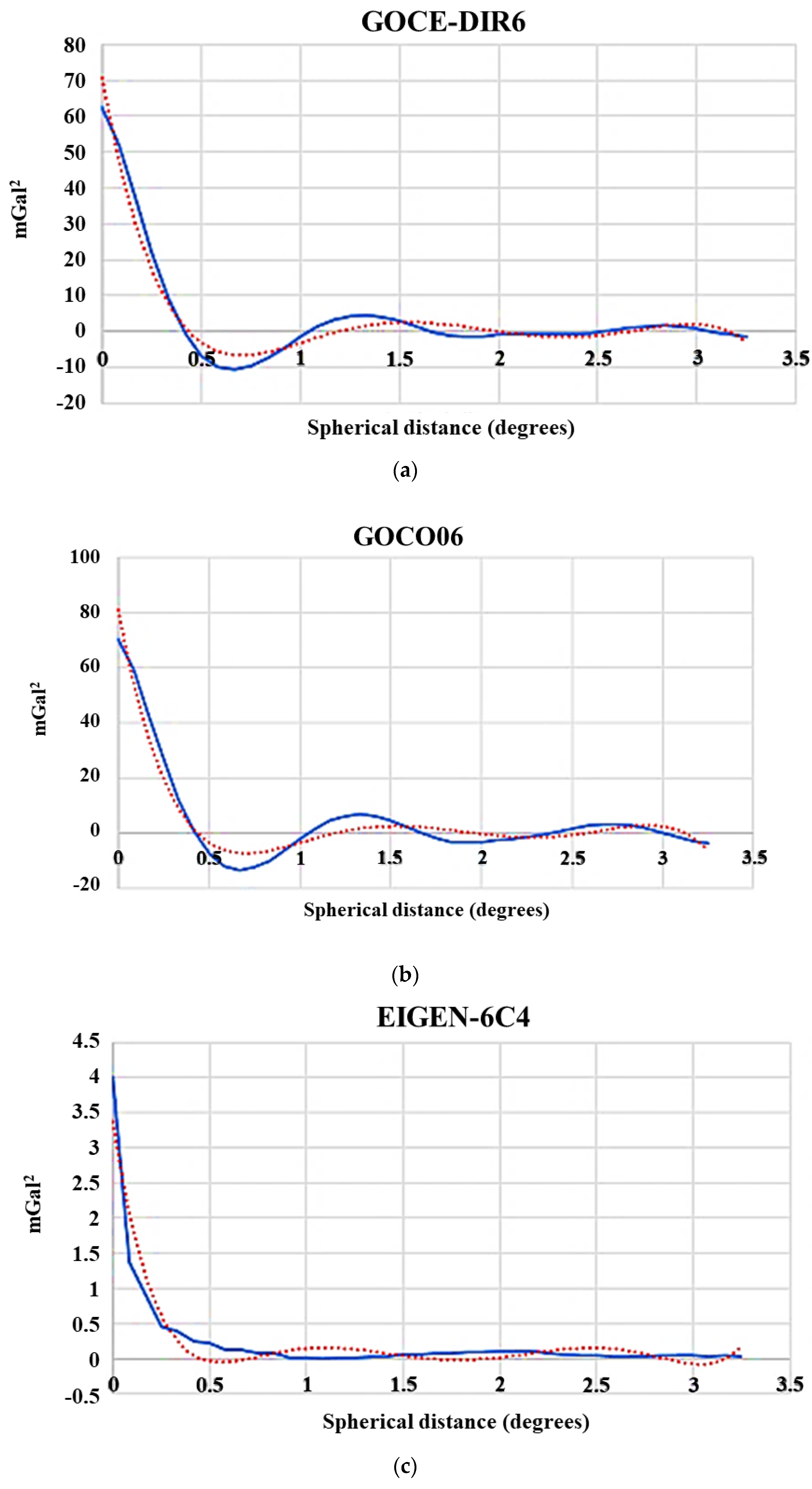
4.3. Calculation of Residual Geoid
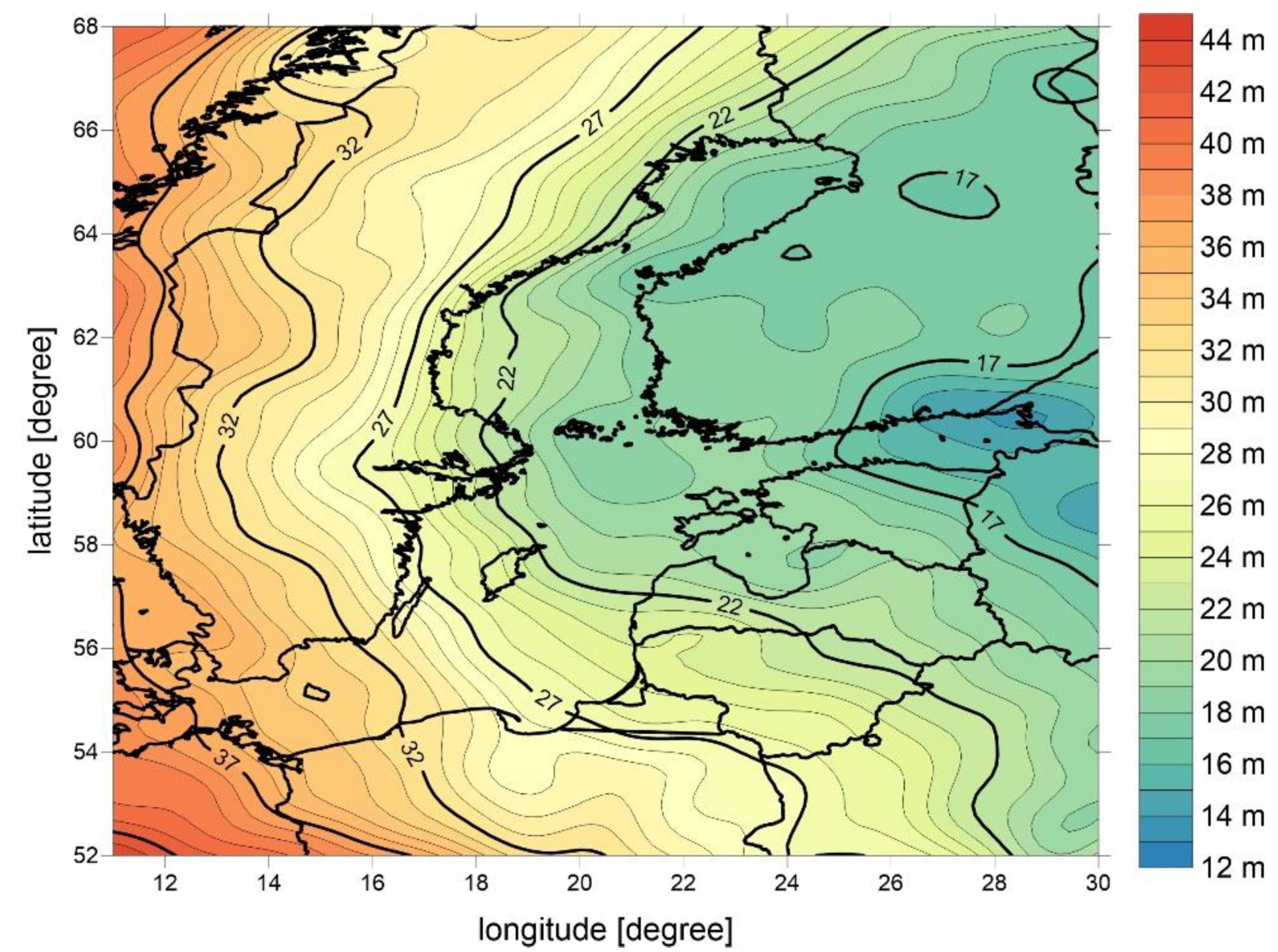
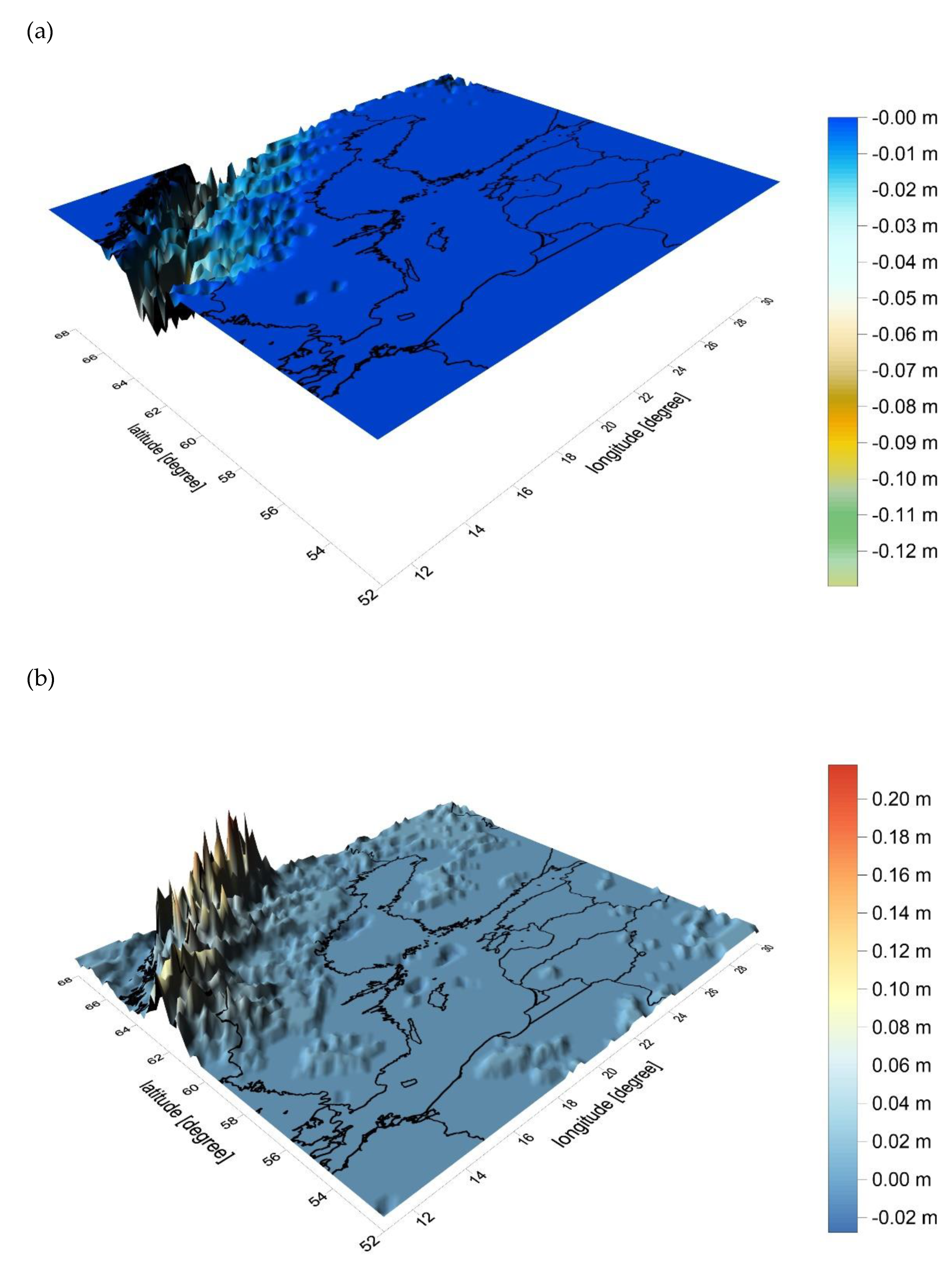
4.4. Qusigeoid Validation
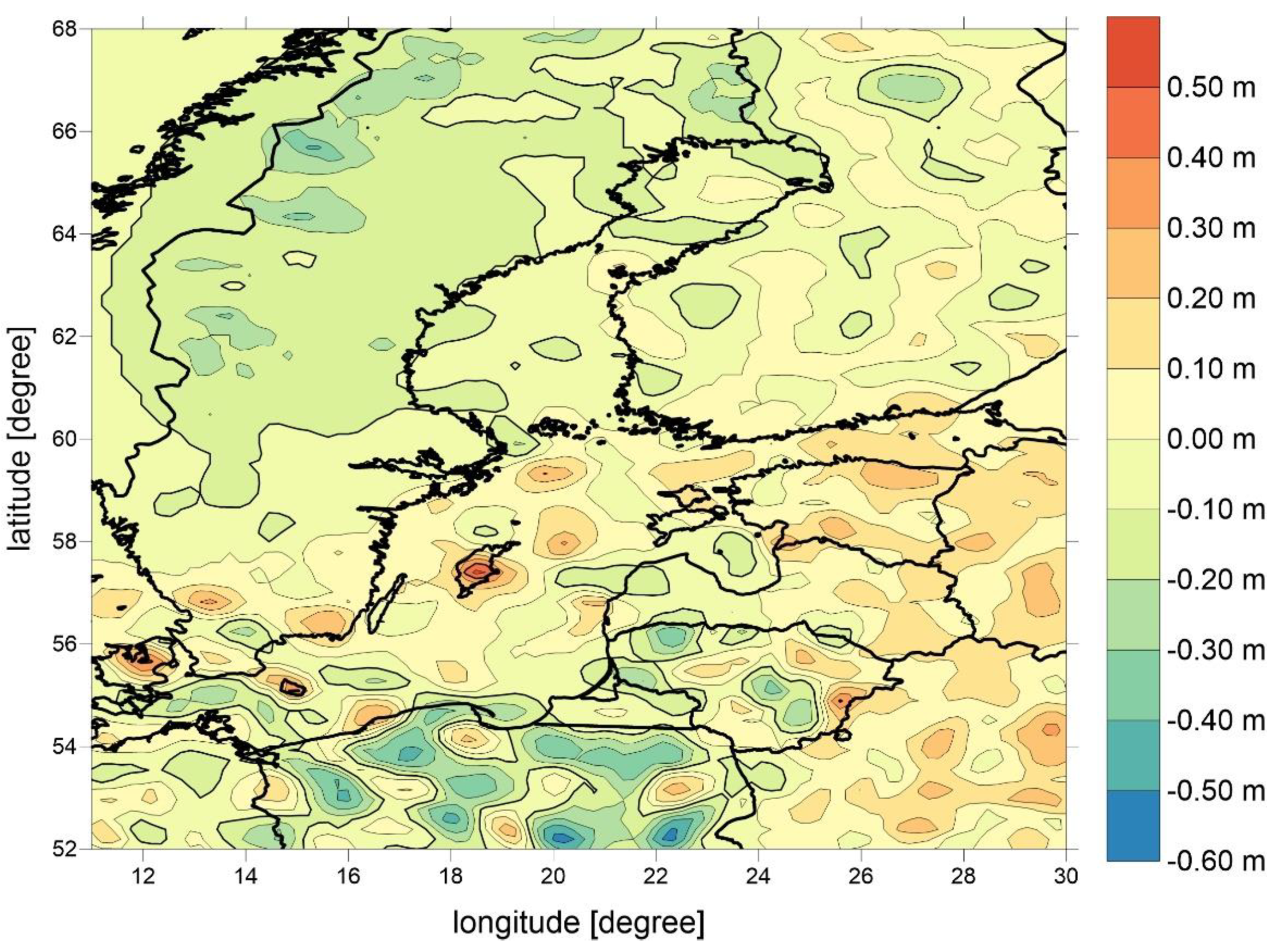
5. Calculation of Quasigeoid Anomalies at Selected Tide Gauge Stations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gruber, T.; Ågren, J.; Angermann, D.; Ellmann, A.; Engfeldt, A.; Gisinger, C.; Jaworski, L.; Marila, S.; Nastula, J.; Nilfouroushan, F.; et al. Geodetic SAR for Height System Unification and Sea Level Research—Observation Concept and Preliminary Results in the Baltic Sea. Remote. Sens. 2020, 12, 3747. [Google Scholar] [CrossRef]
- Torge, W. Geodesy, 3rd ed.; de Gruyter: New York, NY, USA, 2001. [Google Scholar]
- Sánchez, L.; Ågren, J.; Huang, J.; Wang, Y.M.; Mäkinetn, J.; Pail, R.; Barzaghi, R.; Vergos, G.S.; Ahlgren, K.; Liu, Q. Strategy for the realisation of the International Height Reference System (IHRS). J. Geod. 2021, 95, 33. [Google Scholar] [CrossRef]
- Tenzer, R.; Vaníček, P.; Santos, M.; Featherstone, W.E.; Kuhn, M. The rigorous determination of orthometric heights. J. Geod. 2005, 79, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Featherstone, W.E.; Claessens, S.J. Closed-form transformation between geodetic and ellipsoidal coordinates. Stud. Geophys. Geod. 2008, 52, 1. [Google Scholar] [CrossRef] [Green Version]
- Ihde, J.; Augath, W.; Sacher, M. The Vertical Reference System for Europe. In Vertical Reference Systems. International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2002; Volume 4249, pp. 345–350. [Google Scholar]
- Scharroo, R.; Visser, P. Precise orbit determination and gravity field improvement for the ERS satellites. J. Geophys. Res. Space Phys. 1998, 103, 8113–8127. [Google Scholar] [CrossRef]
- Tanni, L. The regional rise of the geoid in Central Europe. Ann. Acad. Sci. Fenn. Ser. A 1949, 3, 20. [Google Scholar]
- Jarmołowski, W. Determination of the Geoid Course in the Southern Baltic Sea Area from Marine and Aviation Gravimetric Observations and Satellite Altimetry (Published in Polish: Wyznaczenie przebiegu geoidy na obszarze południowego Morza Bałtyckiego z morskich i lotniczych obserwacji grawimetrycznych oraz altimetrii satelitarnej). Ph.D. Thesis, University of Warmia and Mazury in Olsztyn, Olsztyn, Poland, 2006. [Google Scholar]
- Kuczynska-Siehien, J.; Lyszkowicz, A.; Sideris, M.G. Evaluation of Altimetry Data in the Baltic Sea Region for Computation of New Quasigeoid Models over Poland. In Proceedings of the International Symposium on Advancing Geodesy in a Changing World, Kobe, Japan, 30 July–4 August 2017; International Association of Geodesy Symposia. Springer: Cham, Switzerland, 2019; Volume 149, pp. 51–60. [Google Scholar] [CrossRef]
- Forsberg, R.S.D. Geoid of the Nordic/Baltic region from surface/airborne gravimetry and GPS draping. In Proceedings of the International Symposium on Gravity, Geoid and Marine Geodesy, Tokyo, Japan, 30 September–5 October 1996; Springer: Berlin/Heidelberg, Germany, 1997; Volume 117, ISBN 3-540-63352-9. [Google Scholar]
- Ågren, J.; Strykowski, G.; Bilker-Koivula, M.; Omang, O.; Märdla, S.; Forsberg, R.; Ellmann, A.; Oja, T.; Liepins, I.; Parseliunas, E.; et al. The NKG2015 Gravimetric Geoid Model for the Nordic-Baltic Region. Available online: http://gghs2016.com/wp-content/uploads/2016/07/GGHS2016_paper_143.pdf (accessed on 20 April 2021).
- Ellmann, A. The Geoid for the Baltic Countries Determined by the Least-Squares Modification of Stokes’ Formula; Geodesy Report No 1061; Royal Institute of Technology, Department of Infrastructure: Stockholm, Sweden, 2004. [Google Scholar]
- Becker, J.J.; Sandwell, D.T.; Smith, W.; Braud, J.; Binder, B.; Depner, J.; Fabre, D.; Factor, J.; Ingalls, S.; Kim, S.-H.; et al. Global Bathymetry and Elevation Data at 30 Arc Seconds Resolution: SRTM30_PLUS. Mar. Geod. 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Visser, P. Gravity field determination with GOCE and GRACE. Adv. Space Res. 1999, 23, 771–776. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; W.H. Freeman and Company: San Francisco, CA, USA; Springer: Berlin/Heidelberg, Germany, 1967; Volume 41, pp. 491–492. [Google Scholar]
- Forsberg, R.; Tscherning, C.C. Topographic effects in gravity field modelling for BVP. Eng. Geol. Infrastruct. Plan. Eur. 2005, 239–272. [Google Scholar]
- Wichiencharoen, C. The Indirect Effects on the Computation of Geoid Undulation. Ohio State University, Department of Geodetic Science and Surveying, Report No. 336. 1982. Available online: http://www.ghbook.ir/index.php?name (accessed on 20 April 2021).
- Rapp, R.R. Methods for the Computations Detailed Geoid; Report No 233; Department of Geodetic Science, The Ohio State University: Columbus, OH, USA, 1975. [Google Scholar]
- Matsuo, K.; Forsberg, R. Gravimetric geoid computation over Colorado based on Remove–Compute–Restore Stokes–Helmert scheme. In Proceedings of the 27th International Union of Geodesy, Montréal, QC, Canada, 8–18 July 2019. [Google Scholar]
- Dahl, O.; Forsberg, R. Different ways to handle topography in practical geoid determination. Phys. Chem. Earth, Part A: Solid Earth Geod. 1999, 24, 41–46. [Google Scholar] [CrossRef]
- Forsberg, R.; Sideris, M.G. Geoid computations by the multi-band spherical FFT approach. Manuscr. Geod. 1993, 18, 82–90. [Google Scholar]
- Królikowski, C. Explanations to the Gravimetric Map of Poland 1:200,000 (Published in Polish: Objaśnienia do mapy grawimetrycznej Polski 1:200 000); Państwowy Instutut Geologiczny: Warszawa, Poland, 1994. [Google Scholar]
- Cisak, M.; Sas, A. Coordinates Transformation of Points from the “Borowa Góra” System to the “1942”. Available online: http://bc.igik.edu.pl/Content/147/PI_108_2004_2.pdf (accessed on 20 April 2021).
- Kryński, J. Precise Quasigeoid Modelling in Poland—Results and Accuracy Estimation (Published in Polish: Precyzyjne modelowanie quasigeoidy na obszarze Polski wyniki i ocena dokładności); Seria Monograficzna nr 13; Instytut Geodezji i Kartografii: Warsaw, Poland, 2007; ISBN 978-83-60024-11-9. [Google Scholar]
- Łyszkowicz, A. About the Problems Related to the Creation of a Uniform Heigh Reference System in the Region of the Baltic Sea (Published in Polish: O problemach związanych z tworzeniem jednolitego wysokościowego układu odniesienia w rejonie morza Bałtyckiego); First Continental Workshop on the Geoid in Europe; Published by Research Institute of Geodesy and Cartograph: Warszawa, Poland, 1992. [Google Scholar]
- Łyszkowicz, A. Description of the Geoid Survey Algorithm in Poland, Gravimetric and Height Data, Gravimetric Database GRAVBASE ver. 1-Altitude Reference System in the Baltic Sea Region (Published in Polish: Opis algorytmu badania geoidy na obszarze Polski, dane grawimetryczne i wysokościowe, grawimetryczna baza danych GRAVBASE ver. 1); Space Research Centre Polish Academy of Sciences: Warszawa, Poland, 1994. [Google Scholar]
- Kostiainen, M.K.J. On the accuracy of the gravity determined from the Bouguer anomaly register for leveling benchmarks. In Proceedings of the Second International Symposium on Problems Related to the Redefinition of North America Vertical Geodetic Networks (NAD Symposium), Ottawa, ON, Canada, 26–30 May 1980; pp. 525–536. [Google Scholar]
- Ekman, M. Impacts of geodynamic phenomena on systems for height and gravity. J. Geod. 1989, 63, 281–296. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.V.; Keller, K.; Møller, M.; Gidskehaug, A.; Solheim, D. Airborne Gravity and Geoid Surveys in the Arctic and Baltic Seas. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics, and Navigation (KIS - 2001), Banff, AB, Canada, 5–8 June 2001; pp. 586–592. [Google Scholar]
- Fairhead, J. West-East European Gravity Project. 1995. Available online: https://www.earthdoc.org/content/papers/10.3997/2214-4609.201410155 (accessed on 20 April 2021).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Space Phys. 2012, 117, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Rülke, A.; Liebsch, G.; Sacher, M.; Schäfer, U.; Schirmer, U.; Ihde, J. Unification of European height system realizations. J. Geod. Sci. 2013, 2, 343–354. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Global Sea Floor Topography from Satellite Altimetry and Ship Depth Soundings. Science 1997, 277, 1956–1962. [Google Scholar] [CrossRef] [Green Version]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef] [Green Version]
- Heck, B. An evaluation of some systematic error sources affecting terrestrial gravity anomalies. J. Geod. 1990, 64, 88–108. [Google Scholar] [CrossRef]
- Gatti, A.; Reguzzoni, M.; Venuti, G. The height datum problem and the role of satellite gravity models. J. Geod. 2012, 87, 15–22. [Google Scholar] [CrossRef]
- Bruinsma, S.L.; Förste, C.; Abrikosov, O.; Lemoine, J.-M.; Marty, J.-C.; Mulet, S.; Rio, M.-H.; Bonvalot, S. ESA’s satellite-only gravity field model via the direct approach based on all GOCE data. Geophys. Res. Lett. 2014, 41, 7508–7514. [Google Scholar] [CrossRef] [Green Version]
- Shako, R.; Förste, C.; Abrikosov, O.; Bruinsma, S.L.; Marty, J.-C.; Lemoine, J.-M.; Flechtner, F.; Neumayer, H.; Dahle, C. EIGEN-6C: A High-Resolution Global Gravity Combination Model Including GOCE Data. In Observation of the System Earth from Space—CHAMP, GRACE, GOCE and Future Missions; Advanced Technologies in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2013; pp. 155–161. [Google Scholar]
- Förste, C.; Bruinsma, S.L.; Abrikosov, O.; Lemoine, J.-M.; Schaller, T.; Götze, H.J. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Postdam and GRGS Toulouse. In Proceedings of the 5th GOCE User Workshop, Paris, France, 22–28 November 2014. [Google Scholar]
- Kvas, A.; Brockmann, J.M.; Schubert, T.; Krauss, S.; Gruber, T.; Meyer, U.; Pail, R. A satellite-only global gravity field model. Earth Syst. Sci. Data 2020, 13, 99–118. [Google Scholar] [CrossRef]
- Bosy, J.; Graszka, W.; Oruba, A. ASG-EUPOS and the basic geodetic network in Poland (Published in Polish: ASG-EUPOS i podstawowa osnowa geodezyjna w Polsce). Biuletyn Wojskowej Akademii Technicznej 2010, 59, 7–15. [Google Scholar]
- Wyrzykowski, T. Monograph of the National 1st Class Precision Leveling Networks (Published in Polish: Monografia krajowych sieci niwelacji precyzyjnej I klasy); Published by Institute of Geodesy: Warszawa, Poland, 1988. [Google Scholar]
- Forsberg, R.; Tscherning, C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modeling Programs. Contract Report for JUPEM 2008. Available online: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:An+overview+manual+for+the+GRAVSOFT+Geodetic+Gravity+Field+Modelling+Programs#0 (accessed on 28 April 2021).
- Available online: http://icgem.gfz-potsdam.de/home (accessed on 28 April 2021).
- Van Hees, G.S. Stokes formula using Fast Fourier Techniques. In Determination of the Geoid; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 1991; Volume 106, pp. 405–408. [Google Scholar]
- Kadaj, R. Transformations between the height reference frames: Kronsztadt’60, PL-KRON86-NH, PL-EVRF2007-NH. Czasopismo Inżynierii Lądowej, Środowiska i Architektury 2018, 65, 5–24. [Google Scholar] [CrossRef]
- Kadaj, R.; Świętoń, T. Transpol v. 2.06; 2013; p. 45. Available online: https://docer.pl/doc/x1sxnvn (accessed on 26 May 2021).
- Gruber, T.; Oikonomidou, X.; Tum, D.A.; Dlr, C.G. BALTIC + Geodetic SAR for Baltic Height System Unification and Baltic Sea Level Research; Algorithm Theoretical Basis Document; SAR-HSU-AT-0013. Remote Sens. 2020, 12, 3747. [Google Scholar] [CrossRef]



| Data | n | Mean | Std dev | Min | Max |
|---|---|---|---|---|---|
| Combined data set | 150,842 | −7.0 | 16.7 | −102.6 | 212.5 |
| Model | Mean | Std dev. | Min | Max |
|---|---|---|---|---|
| GOCO06s | −0.3 | 9.6 | −114.2 | 182.8 |
| GOCE-DIR6 | −0.4 | 9.2 | −117.1 | 186.4 |
| EIGEN-6C4 | −0.4 | 2.5 | −141.2 | 174.7 |
| Model | Co mGal2 | x km |
|---|---|---|
| GOCO06s | 70.4 | 18.2 |
| GOCE-DIR6 | 62.6 | 18.0 |
| EIGEN-6C4 | 4.0 | 9.4 |
| Model | Mean | Std dev | Min | Max |
|---|---|---|---|---|
| GOCE-DIR6 | 0.35 | 0.04 | 0.27 | 0.40 |
| GOCO06s | 0.36 | 0.04 | 0.27 | 0.40 |
| EIGEN-6C4 | 0.34 | 0.04 | 0.24 | 0.40 |
| Model | Mean | Std dev | Min | Max |
|---|---|---|---|---|
| GOCE-DIR6 | 0.18 | 0.04 | 0.10 | 0.25 |
| GOCO06s | 0.18 | 0.04 | 0.09 | 0.26 |
| EIGEN-6C4 | 0.17 | 0.04 | 0.09 | 0.25 |
| Mean | Std dev | Min | Max | |
|---|---|---|---|---|
| GOCE-GOCO | 0.01 | 0.02 | −0.20 | 0.15 |
| GOCE-EIGEN | 0.00 | 0.05 | −0.51 | 0.49 |
| GOCO-EIGEN | 0.00 | 0.05 | −051 | 0.52 |
| No | Name | ϕ | λ | GOCO | GOCE | EIGEN | Mean | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ˚ | ‘ | “ | ˚ | ‘ | “ | ||||||
| 1 | Władysławowo | 54 | 47 | 48.324 | 18 | 25 | 7.493 | 28.824 | 28.830 | 28.838 | 28.831 |
| 2 | Rozewie | 54 | 49 | 46.1 | 18 | 20 | 7.9 | 28.968 | 28.966 | 28.993 | 28.976 |
| 3 | Łeba | 54 | 45 | 13.3 | 17 | 32 | 5.6 | 30.712 | 30.714 | 30.726 | 30.717 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyszkowicz, A.; Nastula, J.; Zielinski, J.B.; Birylo, M. A New Model of Quasigeoid for the Baltic Sea Area. Remote Sens. 2021, 13, 2580. https://doi.org/10.3390/rs13132580
Lyszkowicz A, Nastula J, Zielinski JB, Birylo M. A New Model of Quasigeoid for the Baltic Sea Area. Remote Sensing. 2021; 13(13):2580. https://doi.org/10.3390/rs13132580
Chicago/Turabian StyleLyszkowicz, Adam, Jolanta Nastula, Janusz B. Zielinski, and Monika Birylo. 2021. "A New Model of Quasigeoid for the Baltic Sea Area" Remote Sensing 13, no. 13: 2580. https://doi.org/10.3390/rs13132580
APA StyleLyszkowicz, A., Nastula, J., Zielinski, J. B., & Birylo, M. (2021). A New Model of Quasigeoid for the Baltic Sea Area. Remote Sensing, 13(13), 2580. https://doi.org/10.3390/rs13132580