Woody Above-Ground Biomass Estimation on Abandoned Agriculture Land Using Sentinel-1 and Sentinel-2 Data
Abstract
:1. Introduction
2. Materials and Methods
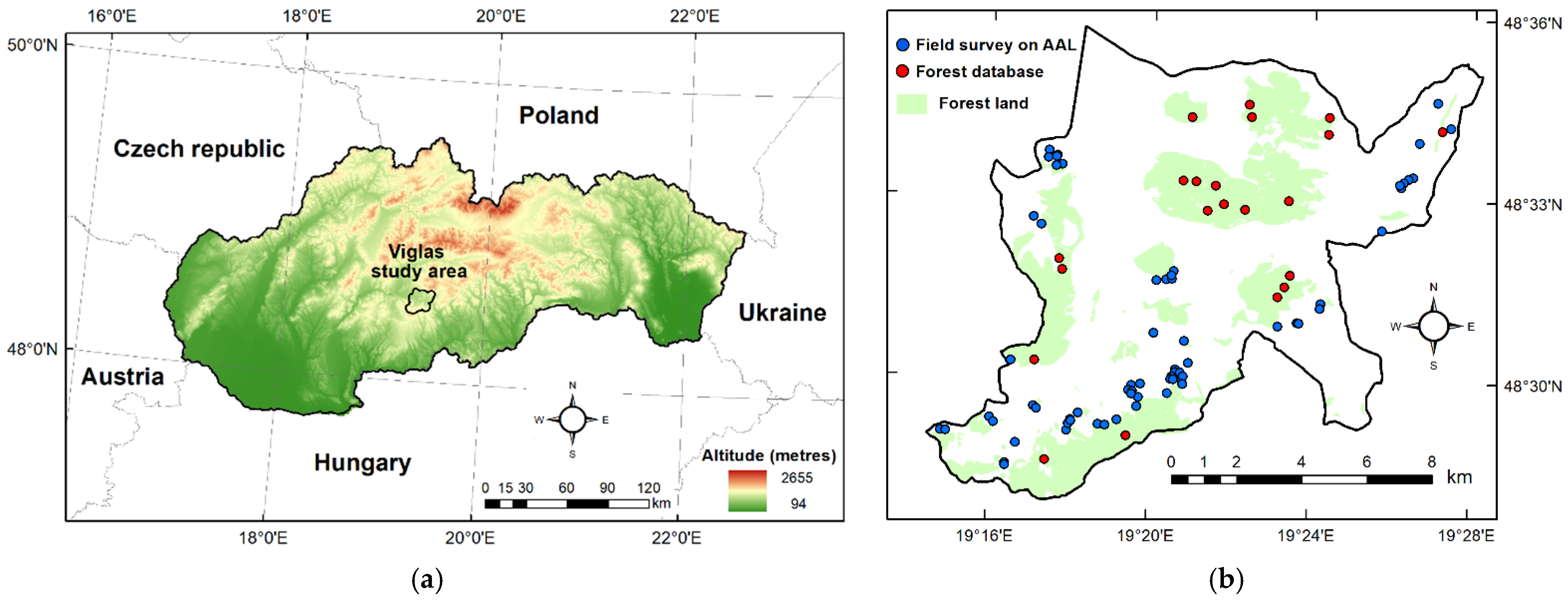
2.1. Study Area
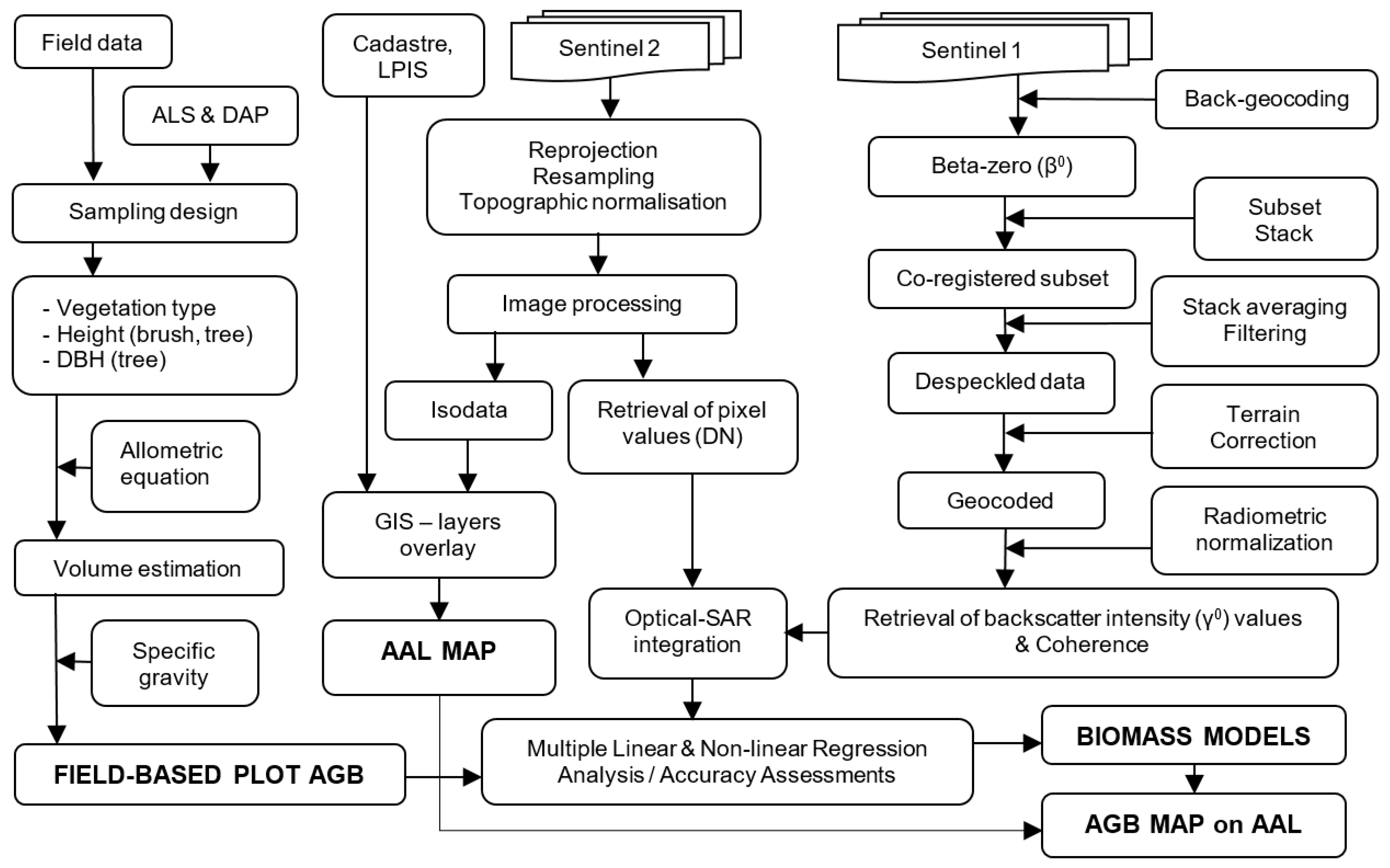
2.2. Concept of Biomass Estimation on Abandoned Agricultural Land
2.3. AAL Identification
2.4. Field Survey
2.4.1. Shrub Biomass Estimation
2.4.2. Tree Biomass Estimation
- Mature tree volume was determined according to Czech–Slovak volume tables [25]. This empirical material includes 18,087 sample trees from areas across Slovakia and Czechia. The model predictors are tree height and diameter at breast height (DBH) for selected tree species. The volume tables contain volume equations for 11 economically important tree species and 4 volume units (stem, over 7 cm thick, over 3 cm thick, whole tree) with or without bark. We used the volume of the whole tree with the bark (m3). This unit represents the volume without the stump.
- Stump volume was calculated according to [26] using the following formulas, for broadleaf and coniferous trees, respectively:where Vp is the stump volume (m3 with the bark), d1.3 is the breast diameter (cm), and hp is the stump height (m), and a default value of 0.3 m was used in the calculations.
- The biomass models for young trees up to 10 m were taken from [27]. The models calculate the dry above-ground biomass of individual trees based on tree height and thickness at the base of the trunk for 11 tree species.
2.4.3. Shrub-Tree Ground Plots Extension
- The homogeneous areas around the plots were derived using aerial images (Figure 3b) and a normalised digital surface model (nDSM) layer (Figure 3c). Around each plot, an area with homogeneous vegetation cover was designed by a human operator with experience in GIS and remote sensing. The size of the identified homogeneous areas varied from 0.05 to 0.52 hectare, with a mean of 0.16 hectare (see Table 1).
- Measured and calculated data on AGB per hectare of each plot were stored in the database and joined to the field plot vector layer created in step 1. The result was a spatially georeferenced vector layer with attributes of the AGB and the woody species composition, which enabled the next step to be performed: the extraction of the plot’s statistical characteristics from the satellite data using zonal statistics.
2.5. Satellite Data
2.6. Statistical Models for AGB Estimation
2.7. Validation of AGB Estimation
3. Results
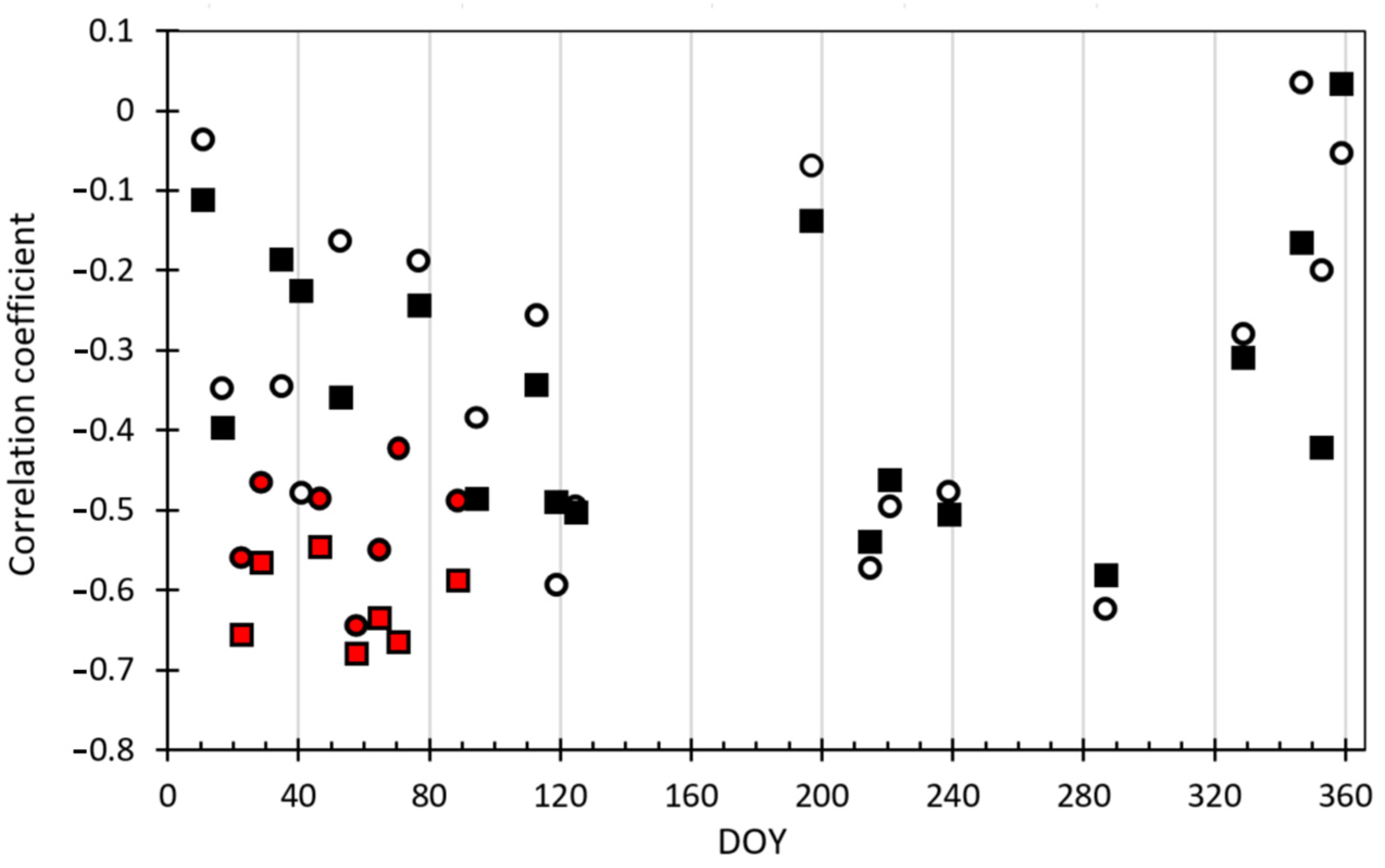
3.1. Predictor Variable Pre-Selection
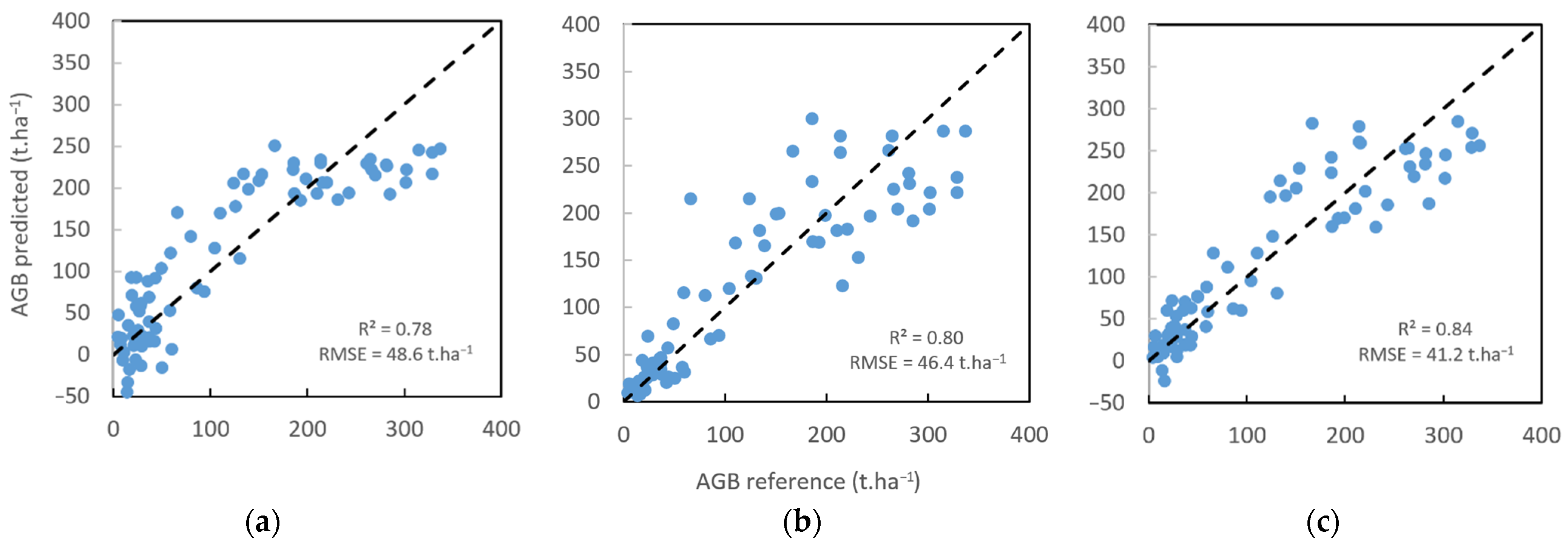
3.2. Performance of AGB Predictive Models
3.3. AGB Estimation on AAL in the Study Area
4. Discussion
4.1. Remarks on the Proposed Approach of AGB Identification and Enumeration on AAL
4.2. Procedures for Improving AGB Estimation
4.3. Economic and Environmental Aspects of Agricultural Land Overgrowth
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- FAO, UN. Global Forest Resources Assessment 2015, 2nd ed.; FAO UN: Rome, Italy, 2016; p. 3. [Google Scholar]
- FAO, UN. Global Forest Resources Assessment 2010, 1st ed.; FAO UN: Rome, Italy, 2010; p. 18. [Google Scholar]
- Kuemmerle, T.; Hostert, P.; Radeloff, V.C.; van der Linden, S.; Perzanowski, K.; Kruhlov, I. Cross-border Comparison of Post-socialist Farmland Abandonment in the Carpathians. Ecosystems 2008, 11, 614–628. [Google Scholar] [CrossRef]
- Griffiths, P.; Müller, D.; Kuemmerle, T.; Hostert, P. Agricultural land change in the Carpathian ecoregion after the breakdown of socialism and expansion of the European Union. Environ. Res. Lett. 2013, 8, 045024. [Google Scholar] [CrossRef]
- Zaušková, Ľ.; Midriak, R. Abandonment of Agricultural Land. Životné Prostr. 2016, 50, 45–51. [Google Scholar]
- Alcantara, C.; Kuemmerle, T.; Baumann, M.; Bragina, E.V.; Griffiths, P.; Hostert, P.; Knorn, J.; Müller, D.; Prishchepov, A.V.; Schierhorn, F.; et al. Mapping the extent of abandoned farmland in Central and Eastern Europe using MODIS time series satellite data. Environ. Res. Lett. 2013, 8, 035035. [Google Scholar] [CrossRef]
- Griffiths, P.; van der Linden, S.; Kuemmerle, T.; Hostert, P. A Pixel-Based Landsat Compositing Algorithm for Large Area Land Cover Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2088–2101. [Google Scholar] [CrossRef]
- Kozak, J.; Ziółkowska, E.; Vogt, P.; Dobosz, M.; Kaim, D.; Kolecka, N.; Ostafin, K. Forest-Cover Increase Does Not Trigger Forest-Fragmentation Decrease: Case Study from the Polish Carpathians. Sustainability 2018, 10, 1472. [Google Scholar] [CrossRef] [Green Version]
- Kolecka, N. Height of Successional Vegetation Indicates Moment of Agricultural Land Abandonment. Remote Sens. 2018, 10, 1568. [Google Scholar] [CrossRef] [Green Version]
- Sačkov, I.; Barka, I.; Bucha, T. Mapping Aboveground Woody Biomass on Abandoned Agricultural Land Based on Airborne Laser Scanning Data. Remote Sens. 2020, 12, 4189. [Google Scholar] [CrossRef]
- Goga, T.; Feranec, J.; Bucha, T.; Rusnák, M.; Sačkov, I.; Barka, I.; Kopecká, M.; Papčo, J.; Oťaheľ, J.; Szatmári, D.; et al. A Review of the Application of Remote Sensing Data for Abandoned Agricultural Land Identification with Focus on Central and Eastern Europe. Remote Sens. 2019, 11, 2759. [Google Scholar] [CrossRef] [Green Version]
- Kuemmerle, T.; Olofsson, P.; Chaskovskyy, O.; Baumann, M.; Ostapowicz, K.; Woodcock, C.E.; Houghton, R.A.; Hostert, P.; Keeton, W.S.; Radeloff, V.C. Post-Soviet farmland abandonment, forest recovery, and carbon sequestration in western Ukraine. Glob. Chang. Biol. 2010, 17, 1335–1349. [Google Scholar] [CrossRef]
- Zurqani, H.A.; Post, C.J.; Mikhailova, E.A.; Allen, J.S. Mapping Urbanization Trends in a Forested Landscape Using Google Earth Engine. Remote Sens. Earth Syst. Sci. 2019, 2, 173–182. [Google Scholar] [CrossRef]
- Imhoff, M. Radar backscatter and biomass saturation: Ramifications for global biomass inventory. IEEE Trans. Geosci. Remote Sens. 1995, 33, 511–518. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.; Fransson, J.; Holmgren, J.; Le Toan, T. L- and P-band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Quegan, S.; Carreiras, J.; Persson, H.J.; Fransson, J.E.; Hoscilo, A.; Ziółkowski, D.; Stereńczak, K.; Lohberger, S.; Stängel, M.; et al. Forest biomass retrieval approaches from earth observation in different biomes. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 53–68. [Google Scholar] [CrossRef]
- Huang, X.; Ziniti, B.; Torbick, N.; Ducey, M.J. Assessment of Forest above Ground Biomass Estimation Using Multi-Temporal C-band Sentinel-1 and Polarimetric L-band PALSAR-2 Data. Remote Sens. 2018, 10, 1424. [Google Scholar] [CrossRef] [Green Version]
- Monteith, C.A.R.; Ulander, L.M.H. Temporal survey of P- and L-band polarimetric backscatter in boreal forests. IEEE J. Sel. Top. Appl. Earth. Obs. Remote Sens. 2018, 11, 3564–3576. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Mura, M.; Zolli, C.; Maselli, F.; Chiesi, M.; Bottai, L.; Chirici, G. The potential of multifrequency SAR images for estimating forest biomass in Mediterranean areas. Remote Sens. Environ. 2017, 200, 63–73. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef] [Green Version]
- Hawryło, P.; Wężyk, P. Predicting Growing Stock Volume of Scots Pine Stands Using Sentinel-2 Satellite Imagery and Airborne Image-Derived Point Clouds. Forests 2018, 9, 274. [Google Scholar] [CrossRef] [Green Version]
- Antropov, O.; Rauste, Y.; Häme, T.; Praks, J. Polarimetric ALOS PALSAR Time Series in Mapping Biomass of Boreal Forests. Remote Sens. 2017, 9, 999. [Google Scholar] [CrossRef] [Green Version]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Elzein, T.M.; Blarquez, O.; Gauthier, O.; Carcaillet, C. Allometric equations for biomass assessment of subalpine dwarf shrubs. Alp Bot. 2011, 121, 129–134. [Google Scholar] [CrossRef]
- Petráš, R.; Pajtík, J. Sústava česko-slovenských objemových tabuliek drevín. Lesnícky Časopis 1991, 37, 49–56. (In Slovak) [Google Scholar]
- Šmelko, Š. Nové metodické postupy na kvantifikáciu mŕtveho dreva a jeho zložiek v lesných ekosystémoch. Lesnícky Časopis 2010, 56, 155–175. (In Slovak) [Google Scholar]
- Pajtík, J.; Konôpka, B.; Šebeň, V. Mathematical Biomass Models for Young Individuals of Forest Tree Species in the Region of the Western Carpathians; National Forest Centre: Zvolen, Slovakia, 2018; pp. 22–68. ISBN 978-80-8093-241-1. [Google Scholar]
- Požgaj, A.; Chovanec, D.; Kurjatko, S.; Babjak, M. Štruktúra a Vlastnosti Dreva; Priroda: Bratislava, Slovakia, 2003; 463p. (In Slovak) [Google Scholar]
- Marklund, L.G. Biomass Functions for Norway Spruce (Picea abies (L.) Karst.) in Sweden; Report No.43; Department of Forest Survey, Swedish University of Agricultural Sciences: Umea, Sweden, 1987. [Google Scholar]
- Efron, B.; Tibshirani, R. Bootstrap Methods for Standard Errors, Confidence Intervals, and Other Measures of Statistical Accuracy. Stat. Sci. 1986, 1, 54–75. [Google Scholar] [CrossRef]
- Mestre-Quereda, A.; Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Jacob, A.W.; Engdahl, M.E. Time-Series of Sentinel-1 Interferometric Coherence and Backscatter for Crop-Type Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4070–4084. [Google Scholar] [CrossRef]
- National Forest Centre, Slovakia. Forest GIS. Available online: http://gis.nlcsk.org/lgis/ (accessed on 20 March 2020).
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Ambagau’, Y.; Palm, C. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Zhao, W.; Deledalle, C.-A.; Denis, L.; Maitre, H.; Nicolas, J.-M.; Tupin, F. Ratio-Based Multitemporal SAR Images Denoising: RABASAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3552–3565. [Google Scholar] [CrossRef] [Green Version]
- Laurin, G.V.; Balling, J.; Corona, P.; Mattioli, W.; Papale, D.; Puletti, N.; Rizzo, M.; Truckenbrodt, J.; Urban, M. Above-ground biomass prediction by Sentinel-1 multitemporal data in central Italy with integration of ALOS2 and Sentinel-2 data. J. Appl. Remote Sens. 2018, 12, 016008. [Google Scholar] [CrossRef]
- Kumar, S.; Pandey, U.; Kushwaha, S.P.; Chatterjee, R.S.; Bijker, W. Aboveground biomass estimation of tropical forest from Envisat advanced synthetic aperture radar data using modeling approach. J. Appl. Remote Sens. 2012, 6, 063588. [Google Scholar] [CrossRef]
- Koskinen, J.; Palliainen, J.; Hyyppa, J.; Engdahl, M.; Hallikainen, M. The seasonal behavior of interferometric coherence in boreal forest. IEEE Trans. Geosci. Remote Sens. 2001, 39, 820–829. [Google Scholar] [CrossRef]
- Ranson, K.; Sun, G. Effects of environmental conditions on boreal forest classification and biomass estimates with SAR. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1242–1252. [Google Scholar] [CrossRef]
- Santoro, M.; Fransson, J.E.S.; Eriksson, L.E.B.; Magnusson, M.; Ulander, L.M.H.; Olsson, H. Signatures of ALOS PALSAR L-Band Backscatter in Swedish Forest. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4001–4019. [Google Scholar] [CrossRef] [Green Version]
- Ackermann, N. Growing Stock Volume Estimation in Temperate Forested Areas Using a Fusion Approach with SAR Satellites Imagery; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoscilo, A.; Lewandowska, A.; Ziólkowski, D.; Stereńczak, K.; Lisańczuk, M.; Schmullius, C.; Pathe, C. Forest Aboveground Biomass Estimation Using a Combination of Sentinel-1 and Sentinel-2 Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S.; Das, A.K.; Mohan, S. Developing synergy regression models with space-borne ALOS PALSAR and Landsat TM sensors for retrieving tropical forest biomass. J. Earth Syst. Sci. 2016, 125, 725–735. [Google Scholar] [CrossRef] [Green Version]
- Mauya, E.W.; Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Malimbwi, R.E.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rain forests of Tanzania. Carbon Balance Manag. 2015, 10, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Schlund, M.; Davidson, M.W.J. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef] [Green Version]
- Šebeň, V. Národná inventarizácia a monitoring lesov Slovenskej republiky 2015–2016. Lesnícke Štúdie 2017, 65, 43. (In Slovak) [Google Scholar]


| AGB | |||||
|---|---|---|---|---|---|
| Number of Plot | Mean Size (ha) | Mean (t·ha−1) | Min–Max (t·ha−1) | Percentiles 25–75% (t·ha−1) | |
| All plots | 77 | 1.36 | 117.5 | 4.4–336.6 | 26–210 |
| Shrub-tree plots on AAL | 56 | 0.16 | 76.9 | 4.4–336.6 | 22–99 |
| Tree plots on FL | 21 | 4.58 | 225.5 | 110.3–328.9 | 166–281 |
| Vegetation Formation | Model | n | R2 | RMSE (%) | p-Value |
|---|---|---|---|---|---|
| Shrubs (blackthorn) | mAGB = 1.2417 × h1.45361 | 20 | 0.81 | 23.9 | <0.001 |
| Sensor/Product | Bands/Predictors | Remark |
|---|---|---|
| Sentinel-1/Level-1 SLC | VV, VH | 60 images from ascending pass (track 175) and 60 images from descending pass (track 51): 1 September 2017 to 30 September 2018 |
| Sentinel-1/stack average | γ°VH γ°VV | Whole sample for ascending and descending pass: 1 September 2017 to 30 September 2018 |
| Stratum 1: Leaf-on period, 1 September to 13 October 2017 and 21 April to 30 September 2018 | ||
| Stratum 2: Leaf-off period with snow cover, 6 December 2017 to 22 March 2018 | ||
| Stratum 3: Leaf-off period without snow cover, 17 October to 30 November 2017 and 30 March to 17 April 2018 | ||
| Sentinel-1/coherence | CohVH CohVV | 26 coherence image pairs in 6-day steps based on a combination of S1A and S1B acquisitions |
| Sentinel-2/S2A | B4, B5, B8, B11 | 4 images: Leaf-off season with snow, 28 January 2017; leaf-off season without snow, 29 March 2017; top of vegetation season, 22 June 2016; end of vegetation season, 30 September 2018 |
| S1 γ°VH | r | S1 γ°VV | r |
|---|---|---|---|
| leaf-off (des, s3) | 0.79 +++ | leaf-off (des, s3) | 0.77 +++ |
| leaf-off (asc_des, s3) | 0.77 +++ | leaf-off (asc_des, s3) | 0.77 +++ |
| leaf-off-snow (des, s2) | 0.76 +++ | leaf-off-snow (des, s2) | 0.75 +++ |
| leaf-off-snow (asc_des, s2) | 0.72 +++ | leaf-off-snow (asc_dec, s2) | 0.73 +++ |
| leaf-off (asc, s3) | 0.64 +++ | leaf-on (des, s1) | 0.66 +++ |
| leaf-on (des, s1) | 0.57 +++ | leaf-on (asc, s1) | 0.60 +++ |
| leaf-off-snow (asc, s2) | 0.57 +++ | leaf-off (asc, s3) | 0.60 +++ |
| leaf-on (asc, s1) | 0.56 +++ | leaf-off-snow (asc, s2) | 0.54 +++ |
| whole sample | 0.57 +++ | 0.66 +++ |
| 28 January 2017 | 29 March 2017 | 22 June 2016 | 30 September 2018 | ||||
|---|---|---|---|---|---|---|---|
| Band | r | Band | r | Band | r | Band | r |
| B5 | −0.65 *** | B4 | −0.65 *** | B5 | −0.85 *** | B4 | −0.74 *** |
| B4 | −0.64 *** | B11 | −0.65 *** | B4 | −0.76 *** | B5 | −0.63 *** |
| B8 | −0.57 *** | B5 | −0.62 *** | B11 | −0.47 *** | B11 | −0.56 *** |
| B11 | 0.07° | B8 | −0.49 *** | B8 | 0.01° | B8 | 0.44 +++ |
| Model | B522vi | γ°VH_leaf-off | γ°VV_leaf-off | CohVH_avg | CohVV_avg | CohVH_avg × B522vi | γ°VV_leaf-off/B522vi |
|---|---|---|---|---|---|---|---|
| MR1 | ** | n.s. | +++ | ** | n.s. | n.a. | n.a. |
| MPW | *** | +++ | n.s. | n.s. | (*) | n.a. | n.a. |
| MR2 | *** | n.s. | n.s. | *** | n.s. | +++ | +++ |
| Model | Reference AGB (t·ha−1) | N | RMSE (t·ha−1) | RMSE% | BIAS (t·ha−1) (MAD) | SE (t·ha−1) | CV |
|---|---|---|---|---|---|---|---|
| MR1 | 0–100 | 42 | 40.0 | 121.2 | 8.2 | 39.2 | 4.8 |
| 100–200 | 15 | 53.2 | 34.9 | 43.0 | 31.2 | 0.7 | |
| 200–350 | 20 | 61.1 | 22.8 | −49.4 | 36.0 | 0.7 | |
| Overall | 77 | 48.6 | 41.4 | 0 (42.4) | 48.6 | - | |
| MPW | 0–100 | 42 | 29.3 | 88.8 | 7.7 | 28.3 | 3.7 |
| 100–200 | 15 | 55.1 | 36.2 | 37.5 | 40.4 | 1.1 | |
| 200–350 | 20 | 64.9 | 24.2 | −44.3 | 47.4 | 1.1 | |
| Overall | 77 | 46.4 | 39.5 | 0 (32.9) | 46.4 | - | |
| MR2 | 0–100 | 42 | 23.7 | 70.5 | 5.1 | 22.7 | 4.5 |
| 100–200 | 15 | 56.4 | 37.0 | 31.6 | 46.7 | 1.5 | |
| 200–350 | 20 | 55.0 | 20.5 | −34.3 | 42.9 | 1.3 | |
| Overall | 77 | 41.2 | 35.1 | 0.3 (32.3) | 41.2 | - |
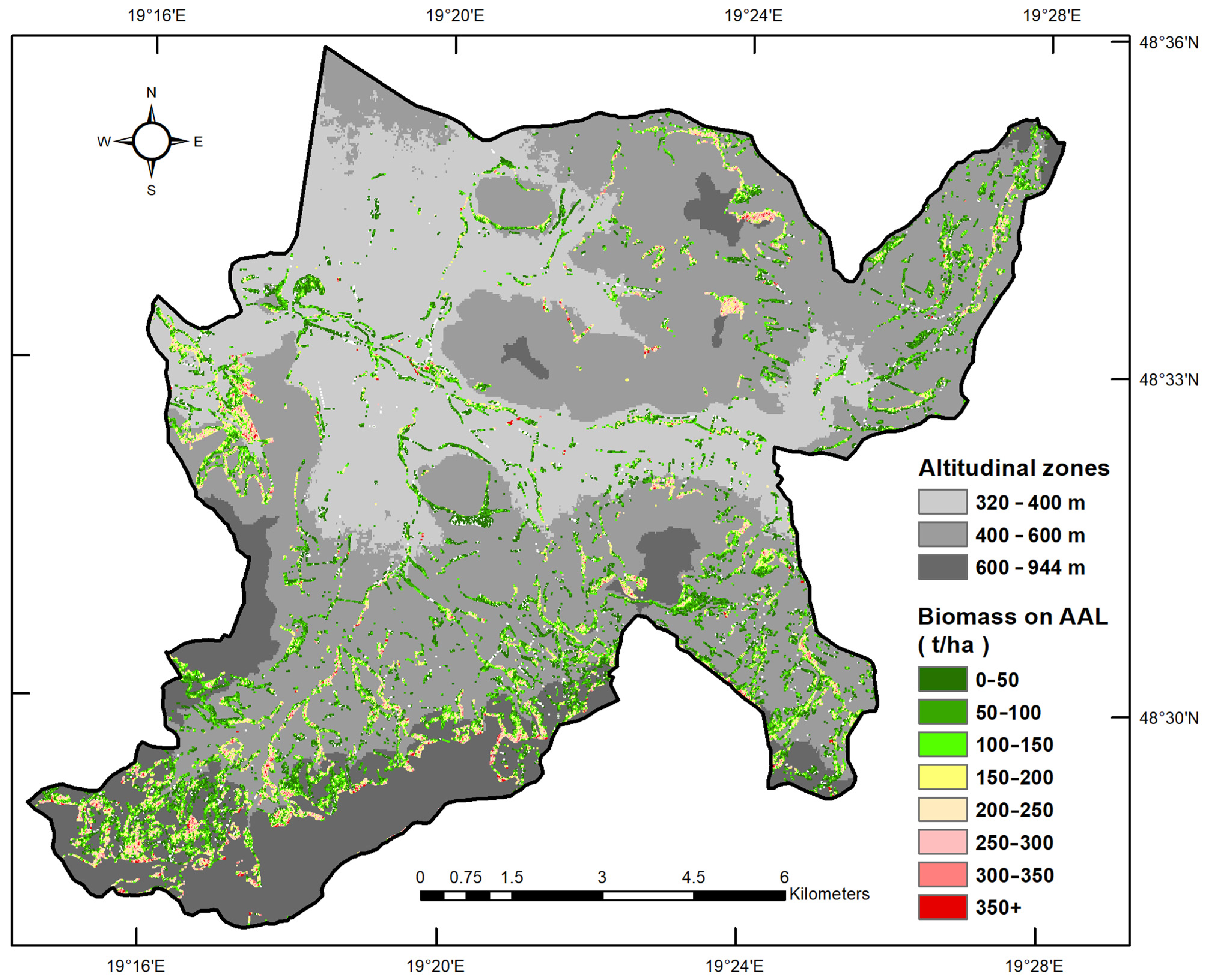
| Class | Area | AGB | ||
|---|---|---|---|---|
| t·ha−1 | ha | % | Tonne (t) | % |
| <0 | 47 | 5 | 0 | 0 |
| 0–50 | 194 | 20 | 4858 | 4 |
| 50–100 | 221 | 22 | 16,590 | 14 |
| 100–150 | 183 | 18 | 22,913 | 19 |
| 150–200 | 145 | 15 | 25,410 | 21 |
| 200–250 | 104 | 10 | 23,352 | 19 |
| 250–300 | 60 | 6 | 16,401 | 13 |
| 300–350 | 26 | 3 | 8479 | 7 |
| 350+ | 12 | 1 | 4343 | 3 |
| 992 | 100 | 122,346 | 100 | |
| 320–400 m | 400–600 m | 600–944 m | Overall | |
|---|---|---|---|---|
| Total area of agricultural land (ha) | 2894 | 4587 | 996 | 8477 |
| Area of abandoned agricultural land (ha) | 162 | 554 | 276 | 992 |
| Share of AAL from AL (%) | 5.6 | 12.1 | 27.7 | 11.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bucha, T.; Papčo, J.; Sačkov, I.; Pajtík, J.; Sedliak, M.; Barka, I.; Feranec, J. Woody Above-Ground Biomass Estimation on Abandoned Agriculture Land Using Sentinel-1 and Sentinel-2 Data. Remote Sens. 2021, 13, 2488. https://doi.org/10.3390/rs13132488
Bucha T, Papčo J, Sačkov I, Pajtík J, Sedliak M, Barka I, Feranec J. Woody Above-Ground Biomass Estimation on Abandoned Agriculture Land Using Sentinel-1 and Sentinel-2 Data. Remote Sensing. 2021; 13(13):2488. https://doi.org/10.3390/rs13132488
Chicago/Turabian StyleBucha, Tomáš, Juraj Papčo, Ivan Sačkov, Jozef Pajtík, Maroš Sedliak, Ivan Barka, and Ján Feranec. 2021. "Woody Above-Ground Biomass Estimation on Abandoned Agriculture Land Using Sentinel-1 and Sentinel-2 Data" Remote Sensing 13, no. 13: 2488. https://doi.org/10.3390/rs13132488
APA StyleBucha, T., Papčo, J., Sačkov, I., Pajtík, J., Sedliak, M., Barka, I., & Feranec, J. (2021). Woody Above-Ground Biomass Estimation on Abandoned Agriculture Land Using Sentinel-1 and Sentinel-2 Data. Remote Sensing, 13(13), 2488. https://doi.org/10.3390/rs13132488










