A Method for Quantifying the Impacts of Human Activities on Net Primary Production of Grasslands in Northwest China
Abstract
:1. Introduction
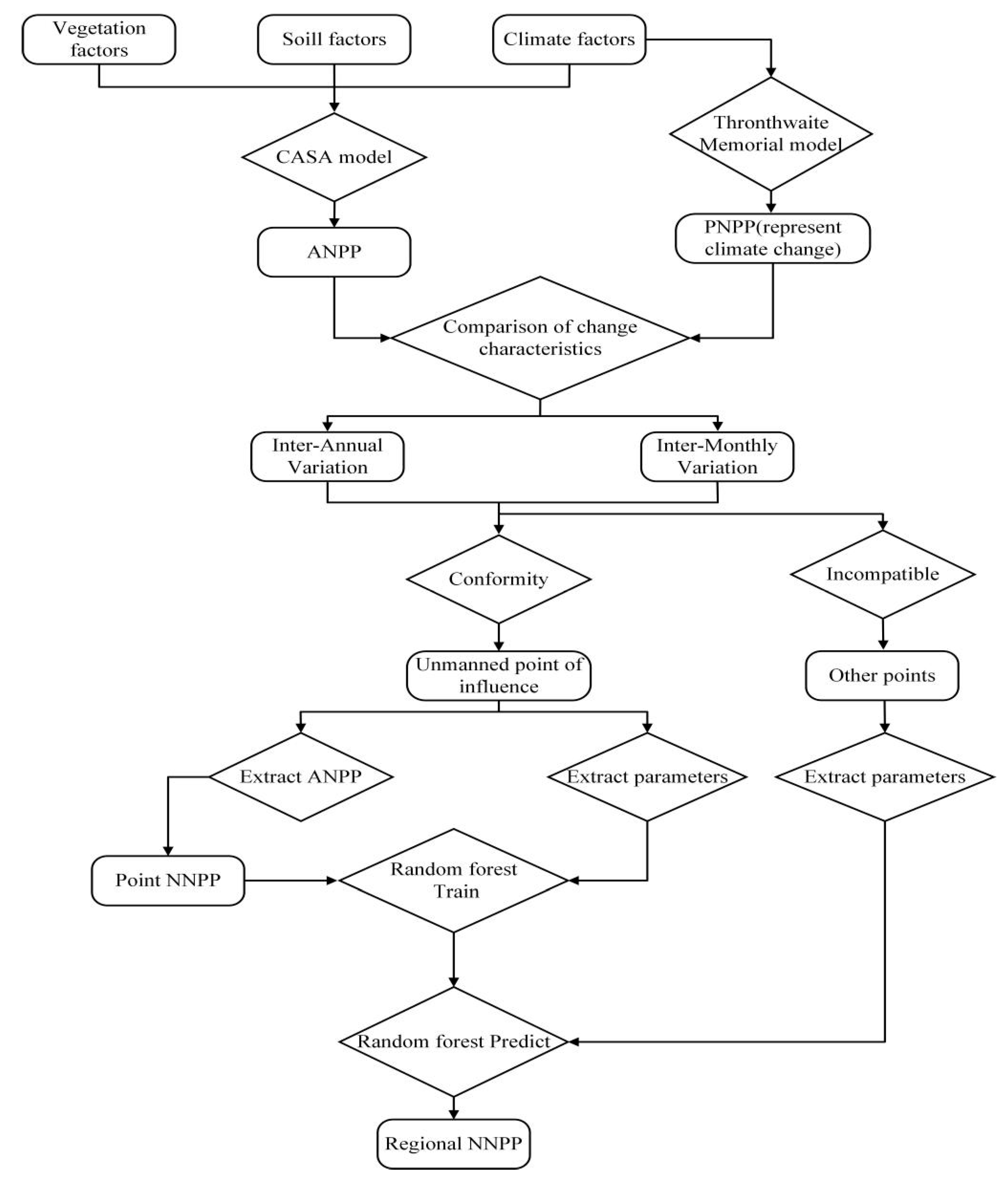
2. Materials and Methods
2.1. Study Area
2.2. Data and Processing
2.3. Methods
2.3.1. Calculation of ANPP
2.3.2. Calculation of NNPP
- (1)
- Identify the grid without human influence
- (2)
- Upscaling the NPP to regional scale
2.4. Calculation of HNPP
2.5. Changing Trend
3. Results
3.1. ANPP Estimation and Spatial and Temporal Distribution
3.2. NNPP and PNPP
3.2.1. Non-Human Affected Grids
3.2.2. Spatial and Temporal Distribution
3.3. HNPP_N and HNPP_P
3.4. The Relative Roles of Human Activities and Climate Change in Grassland Change
4. Discussion
4.1. NNPP and PNPP
4.2. HNPP_N Is More Consistent with the Actual Situation Than HNPP_T
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Zhang, Z.; Tong, L.; Khalifa, M.; Wang, Q.; Gang, C.; Wang, Z.; Li, J.; Sun, Z. Assessing the effects of climate variation and human activities on grassland degradation and restoration across the globe. Ecol. Indic. 2019, 106, 105504. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Z.; Li, J.; Gang, C.; Zhang, Y.; Zhang, Y.; Odeh, I.; Qi, J. Comparative assessment of grassland degradation dynamics in response to climate variation and human activities in China, Mongolia, Pakistan and Uzbekistan from 2000 to 2013. J. Arid Environ. 2016, 135, 164–172. [Google Scholar] [CrossRef]
- Ying, Z.; Zhang, C.-B.; Wang, Z.-Q.; Yang, Y.; Zhang, Y.-Z.; Li, J.-L.; An, R. Quantitative assessment of relative roles of climate change and human activities on grassland net primary productivity in the Three-River Source Region, China. Acta Prataculturae Sin. 2017, 26, 1–14. [Google Scholar]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gang, C.; Zhou, W.; Chen, Y.; Wang, Z.; Sun, Z.; Li, J.; Qi, J.; Odeh, I. Quantitative assessment of the contributions of climate change and human activities on global grassland degradation. Environ. Earth Sci. 2014, 72, 4273–4282. [Google Scholar] [CrossRef]
- Saikku, L.; Mattila, T.; Akujaervi, A.; Liski, J. Bioenergy, Human appropriation of net primary production in Finland during 1990–2010. Biomass Bioenergy 2015, 83, 559–567. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, W.; Yu, X.; Song, Q.; Yang, J.; Wu, J.; Zhang, H. Variation of net primary production and its correlation with climate change and anthropogenic activities over the Tibetan Plateau. Remote Sens. 2018, 10, 1352. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Shen, Y.; Jia, W.; Jiao, L. Quantitative assessment of the relative roles of climate change and human activities in desertification processes on the Qinghai-Tibet Plateau based on net primary productivity. Catena 2016, 147, 789–796. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Mu, S.; Zhou, S.; Chen, Y.; Li, J.; Ju, W.; Odeh, I.J.G.; Change, P. Assessing the impact of restoration-induced land conversion and management alternatives on net primary productivity in Inner Mongolian grassland, China. Glob. Planet. Chang. 2013, 108, 29–41. [Google Scholar] [CrossRef]
- Chen, T.; Bao, A.; Jiapaer, G.; Guo, H.; Zheng, G.; Jiang, L.; Chang, C.; Tuerhanjiang, L. Disentangling the relative impacts of climate change and human activities on arid and semiarid grasslands in Central Asia during 1982–2015. Sci. Total Environ. 2019, 653, 1311–1325. [Google Scholar] [CrossRef] [PubMed]
- Lieth, H.J. Resources, Modeling the Primary Productivity of the World. In Primary Productivity of the Biosphere; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Thornthwaite, C. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Wu, X.; Fang, H.; Zhao, Y.; Smoak, J.M.; Li, W.; Shi, W.; Sheng, Y.; Zhao, L.; Ding, Y. A conceptual model of the controlling factors of soil organic carbon and nitrogen densities in a permafrost-affected region on the eastern Qinghai-Tibetan Plateau. J. Geophys. Res. Biogeosci. 2017, 122, 1705–1717. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, X.; Li, J.; Hua, T. Roles of climate changes and human interventions in land degradation: A case study by net primary productivity analysis in China’s Shiyanghe Basin. Environ. Earth Sci. 2011, 64, 2183–2193. [Google Scholar] [CrossRef]
- Ni, J. Carbon storage in grasslands of China. J. Arid Environ. 2002, 50, 205–218. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, L.; Xiao, J.; Williams, C.A.; Vitkovskaya, I.; Bao, A. Spatiotemporal transition of institutional and socioeconomic impacts on vegetation productivity in Central Asia over last three decades. Sci. Total Environ. 2019, 658, 922–935. [Google Scholar] [CrossRef]
- Chen, T.; Tang, G.; Yuan, Y.; Guo, H.; Xu, Z.; Jiang, G.; Chen, X. Unraveling the relative impacts of climate change and human activities on grassland productivity in Central Asia over last three decades. Sci. Total Environ. 2020, 743, 140649. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Wang, Z.; Yang, Y.; Li, J. Impact of human activities and climate change on the grassland dynamics under different regime policies in the Mongolian Plateau. Sci. Total Environ. 2020, 698, 134304. [Google Scholar] [CrossRef]
- Wang, P.; Xie, D.; Zhou, Y.; Youhao, E.; Zhu, Q. Estimation of net primary productivity using a process-based model in Gansu Province, Northwest China. Environ. Earth Sci. 2014, 71, 647–658. [Google Scholar] [CrossRef]
- Xia, J.; Ma, M.; Liang, T.; Wu, C.; Yang, Y.; Zhang, L.; Zhang, Y.; Yuan, W. Estimates of grassland biomass and turnover time on the Tibetan Plateau. Environ. Res. Lett. 2018, 13, 014020. [Google Scholar] [CrossRef]
- Zhu, W.-Q.; Pan, Y.-Z.; Zhang, J.-S. Estimation of net primary productivity of Chinese terrestrial vegetation based on remote sensing. Chin. J. Plant Ecol. 2007, 31, 413. [Google Scholar]
- Yu, D.; Shi, P.; Shao, H.; Zhu, W.; Pan, Y. Modelling net primary productivity of terrestrial ecosystems in East Asia based on an improved CASA ecosystem model. Int. J. Remote Sens. 2009, 30, 4851–4866. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; Hao, H.; Yu, D.; Hu, H. Simulation of maximum light use efficiency for some typical vegetation types in China. Chin. Sci. Bull. 2006, 51, 457–463, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Glob. Chang. Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; He, J. Variations in vegetation net primary production in the Qinghai-Xizang Plateau, China, from 1982 to 1999. Clim. Chang. 2006, 74, 253–267. [Google Scholar] [CrossRef]
- Box, E. Quantitative Evaluation of Global Primary Productivity Models Generated by Computers. In Primary Productivity of the Biosphere; Springer: Berlin/Heidelberg, Germany, 1975. [Google Scholar]
- Fang, K.N.; Jian-Bina, W.U.; Zhu, J.P.; Bang-Changa, S.J.S.; Forum, I. A review of technologies on random forests. Stat. Inf. Forum 2011, 26, 32–38. [Google Scholar]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random Forest classification of Mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Yu, B.; Chen, F.; Chen, H. NPP estimation using random forest and impact feature variable importance analysis. Spat. Sci. 2017, 64, 1–20. [Google Scholar] [CrossRef]
- Silveira, E.M.O.; Silva, S.H.G.; Acerbi-Junior, F.W.; Carvalho, M.C.; Carvalho, L.M.T.; Scolforo, J.R.S.; Wulder, M.A. Object-based random forest modelling of aboveground forest biomass outperforms a pixel-based approach in a heterogeneous and mountain tropical environment. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 175–188. [Google Scholar] [CrossRef]
- Piao, S.; Friedlingstein, P.; Ciais, P.; Viovy, N.; Demarty, J. Growing season extension and its impact on terrestrial carbon cycle in the Northern Hemisphere over the past 2 decades. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Fan, J.-W.; Shao, Q.-Q.; Liu, J.-Y.; Wang, J.-B.; Harris, W.; Chen, Z.-Q.; Zhong, H.-P.; Xu, X.-L.; Liu, R.-G. Assessment of effects of climate change and grazing activity on grassland yield in the Three Rivers Headwaters Region of Qinghai–Tibet Plateau, China. Environ. Monit. Assess. 2009, 170, 571–584. [Google Scholar] [CrossRef]
- Zhou, W.; Gang, C.; Zhou, L.; Chen, Y.; Odeh, I. Dynamic of grassland vegetation degradation and its quantitative assessment in the northwest China. Acta Oecol. 2014, 55, 86–96. [Google Scholar] [CrossRef]
- Piao, S.; Mohammat, A.; Fang, J.; Cai, Q.; Feng, J. NDVI-based increase in growth of temperate grasslands and its responses to climate changes in China. Glob. Environ. Chang. 2006, 16, 340–348. [Google Scholar] [CrossRef]
- Ying, L.I.; Hao, R. Ecology, grazing resource management and grassland degradation in Northern China. J. Resour. Ecol. 2011, 2, 286–288. [Google Scholar]

















| Grassland Status | Area (%) | Scenarios | SlopeN | SlopeH | Definition of Driving Factors of Grassland Dynamic |
|---|---|---|---|---|---|
| Grassland Restoration (SlopeA > 0) | 35.67 | 1 | >0 | >0 | Both of two factors dominated grassland restoration |
| 39.01 | 2 | >0 | <0 | Climate-dominated grassland restoration | |
| 9.64 | 3 | <0 | >0 | Human activities-dominated grassland restoration | |
| Grassland Degradation (SlopeA < 0) | 5.02 | 4 | <0 | <0 | Both of two factors dominated grassland degradation |
| 3.96 | 5 | <0 | >0 | Climate-dominated grassland degradation | |
| 6.70 | 6 | >0 | <0 | Human activities-dominated grassland degradation |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Dou, T.; Wang, Y.; Zhu, T.; Yin, H.; Zhou, M.; Liu, L.; Wu, X. A Method for Quantifying the Impacts of Human Activities on Net Primary Production of Grasslands in Northwest China. Remote Sens. 2021, 13, 2479. https://doi.org/10.3390/rs13132479
Li C, Dou T, Wang Y, Zhu T, Yin H, Zhou M, Liu L, Wu X. A Method for Quantifying the Impacts of Human Activities on Net Primary Production of Grasslands in Northwest China. Remote Sensing. 2021; 13(13):2479. https://doi.org/10.3390/rs13132479
Chicago/Turabian StyleLi, Chuanhua, Tianbao Dou, Yutao Wang, Tongbin Zhu, Huanhuan Yin, Min Zhou, Lihui Liu, and Xiaodong Wu. 2021. "A Method for Quantifying the Impacts of Human Activities on Net Primary Production of Grasslands in Northwest China" Remote Sensing 13, no. 13: 2479. https://doi.org/10.3390/rs13132479
APA StyleLi, C., Dou, T., Wang, Y., Zhu, T., Yin, H., Zhou, M., Liu, L., & Wu, X. (2021). A Method for Quantifying the Impacts of Human Activities on Net Primary Production of Grasslands in Northwest China. Remote Sensing, 13(13), 2479. https://doi.org/10.3390/rs13132479








