Estimation of the Monthly Dynamics of Surface Water in Wetlands from Satellite and Secondary Hydro-Climatological Data
Abstract
1. Introduction
2. Study Area
3. Methodology and Data
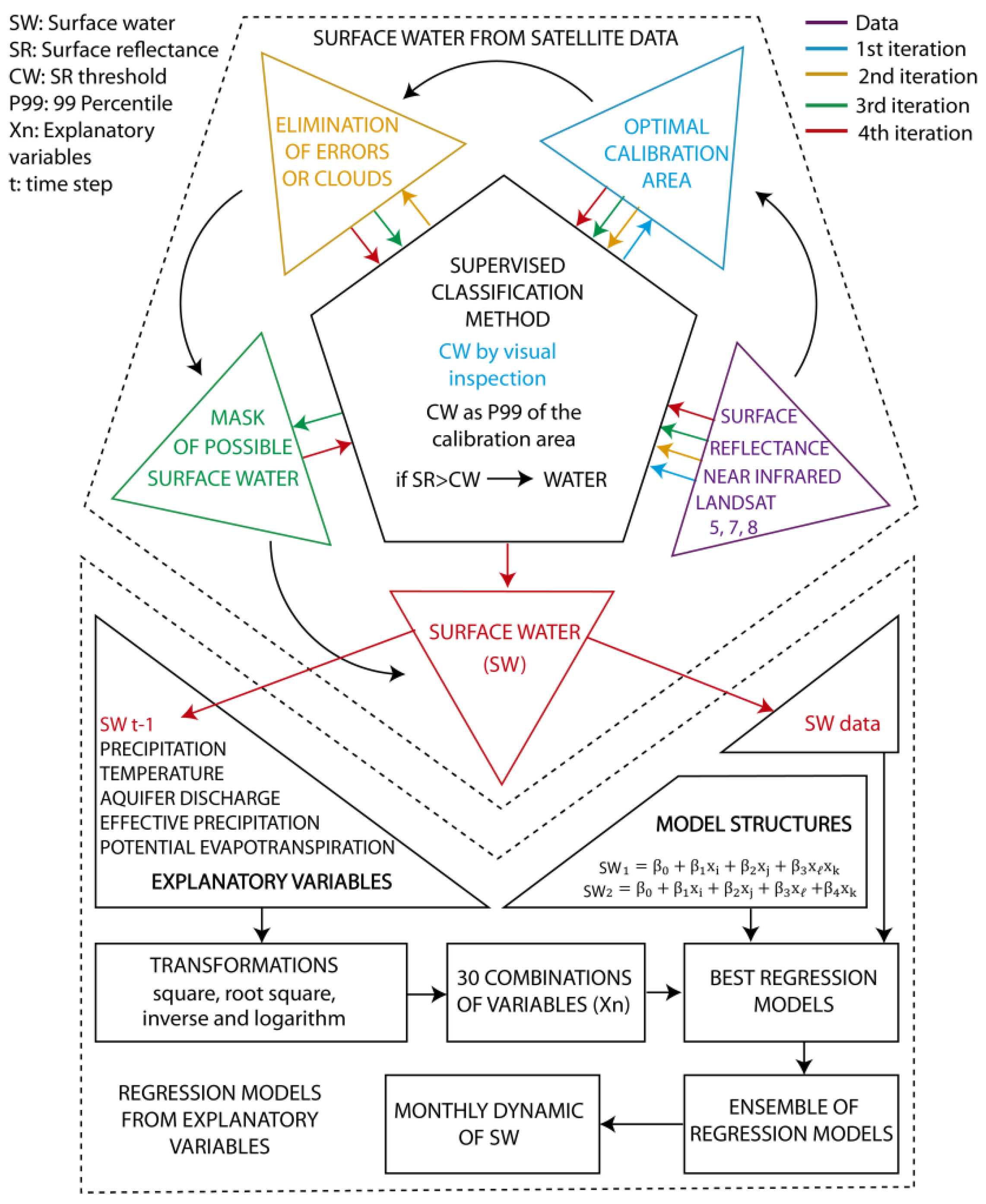
3.1. Identification of the Surface Water from Satellite Data
- (a)
- Selection of the calibration area
- (b)
- Elimination of images with errors or clouds
- (c)
- Creation of a mask of possible surface water
- (d)
- Surface water mapping by applying a temporally variable threshold
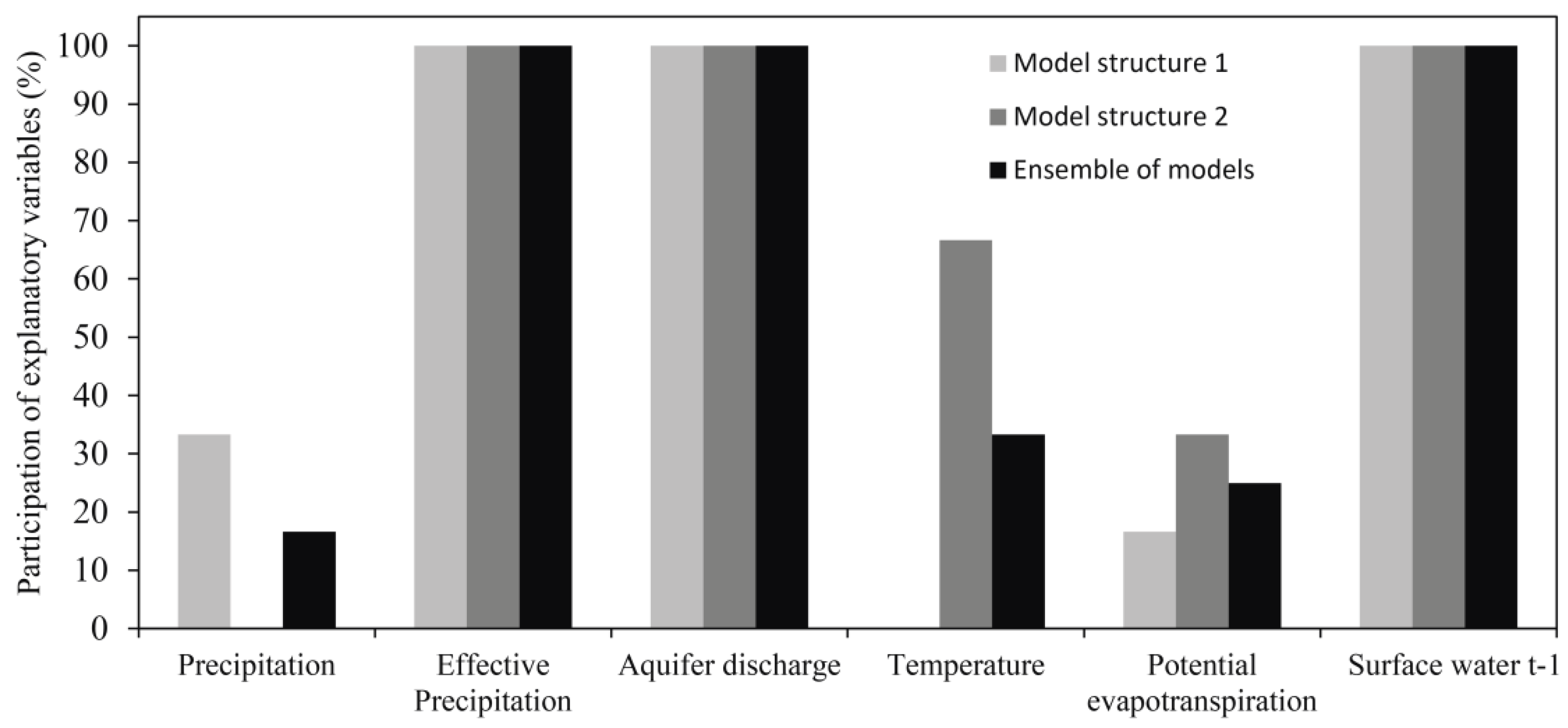
3.2. Regression Models from Explanatory Variables
- (a)
- Main climatic variables: precipitation and temperature.
- (b)
- Those derived from the main climatic variables: potential evapotranspiration and effective precipitation.
- (c)
- Hydrological variables: aquifer discharge and surface water in the previous month.
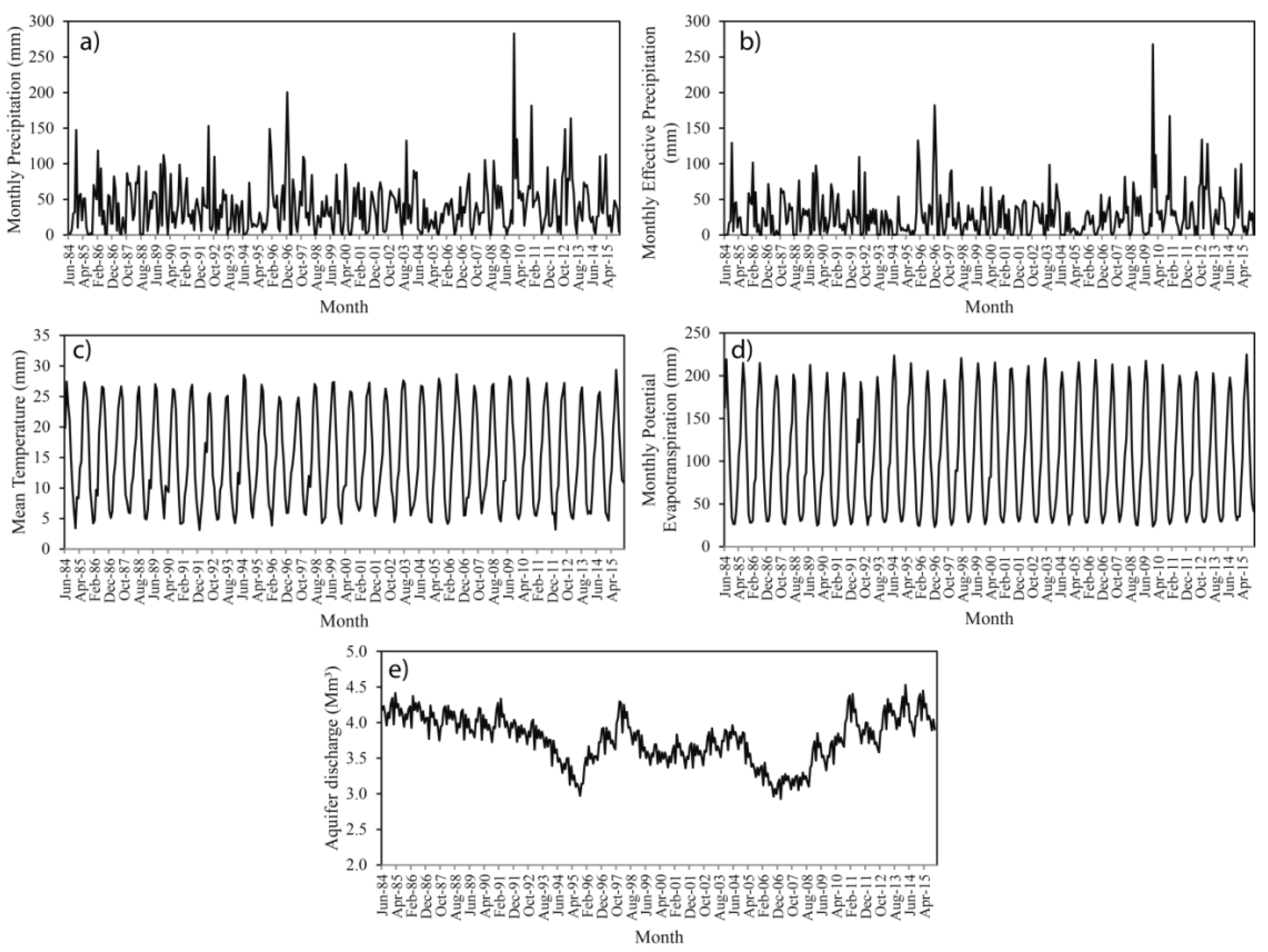
3.3. Data
4. Results
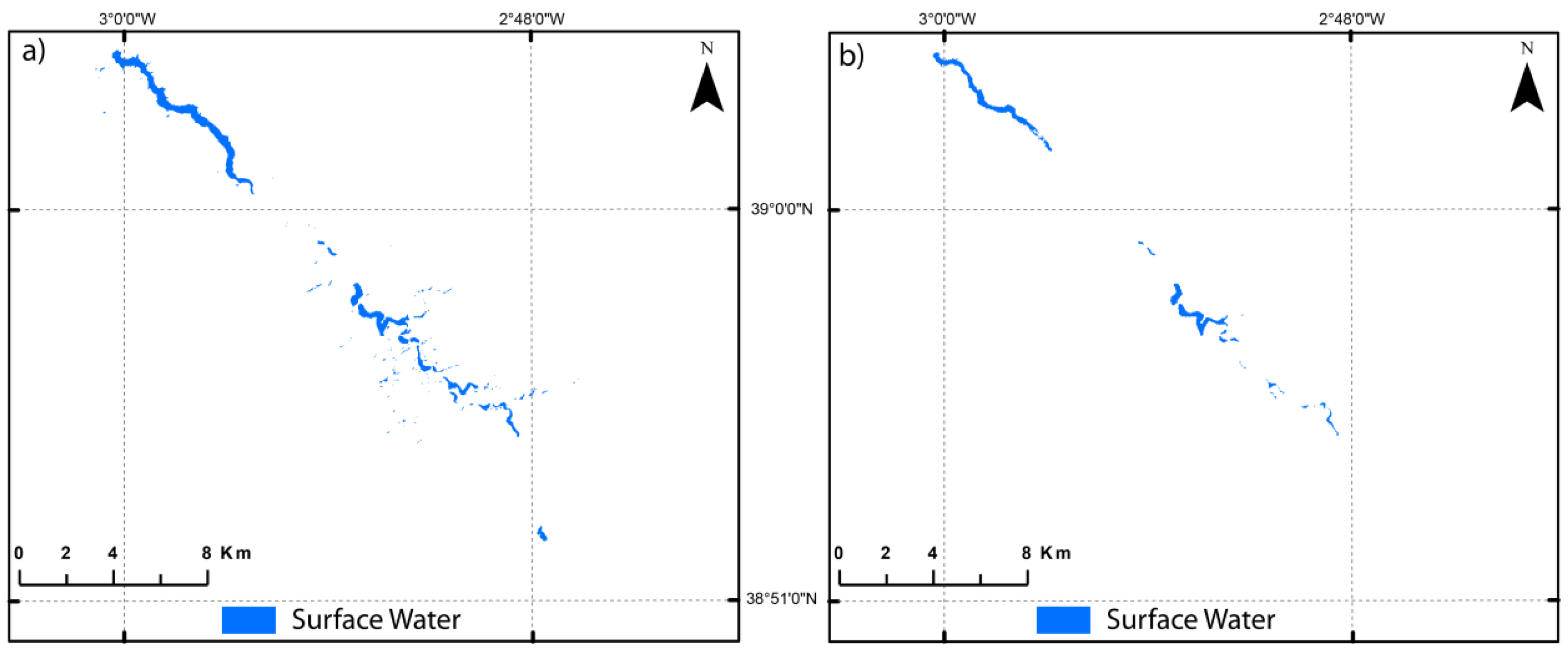
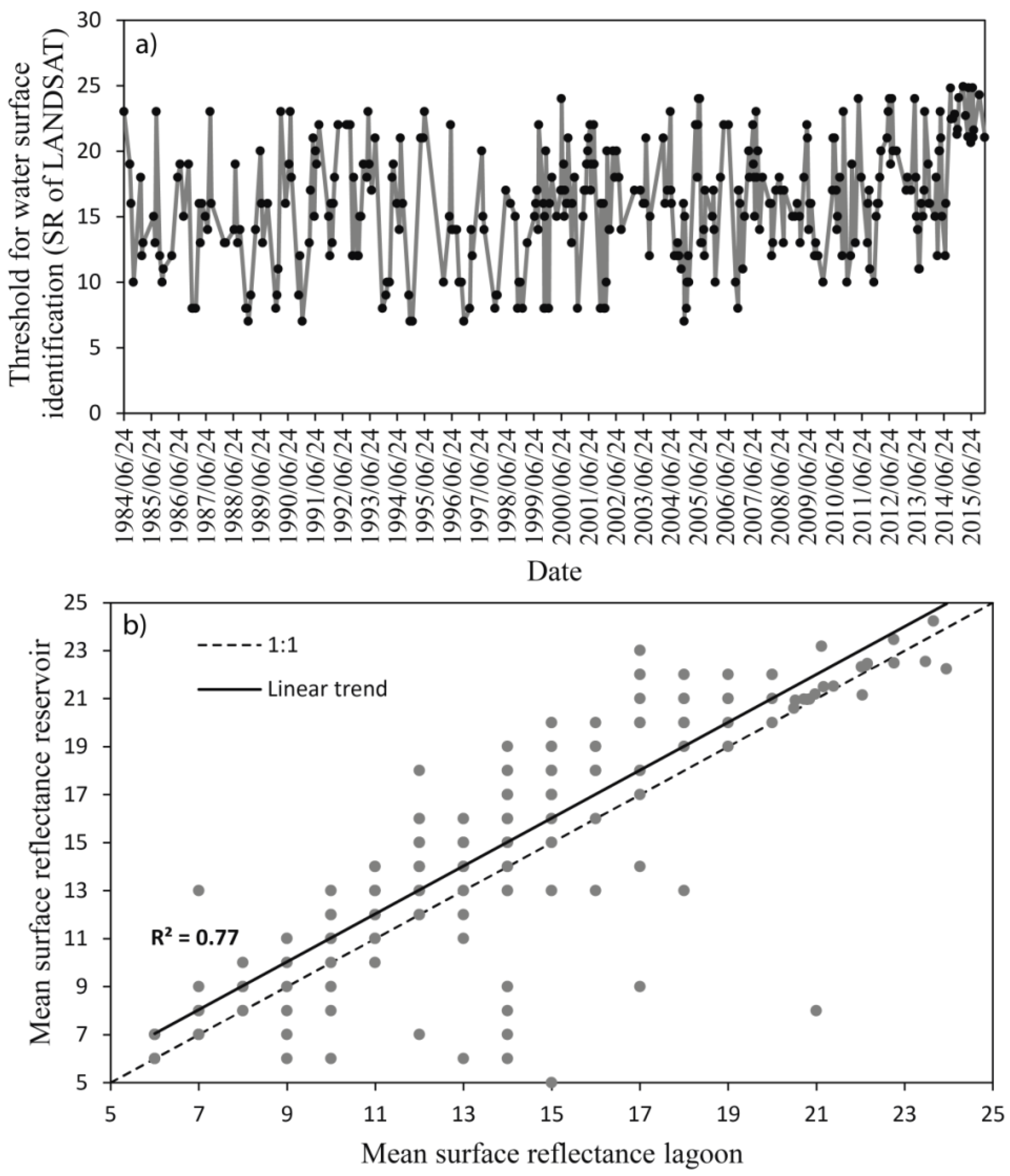
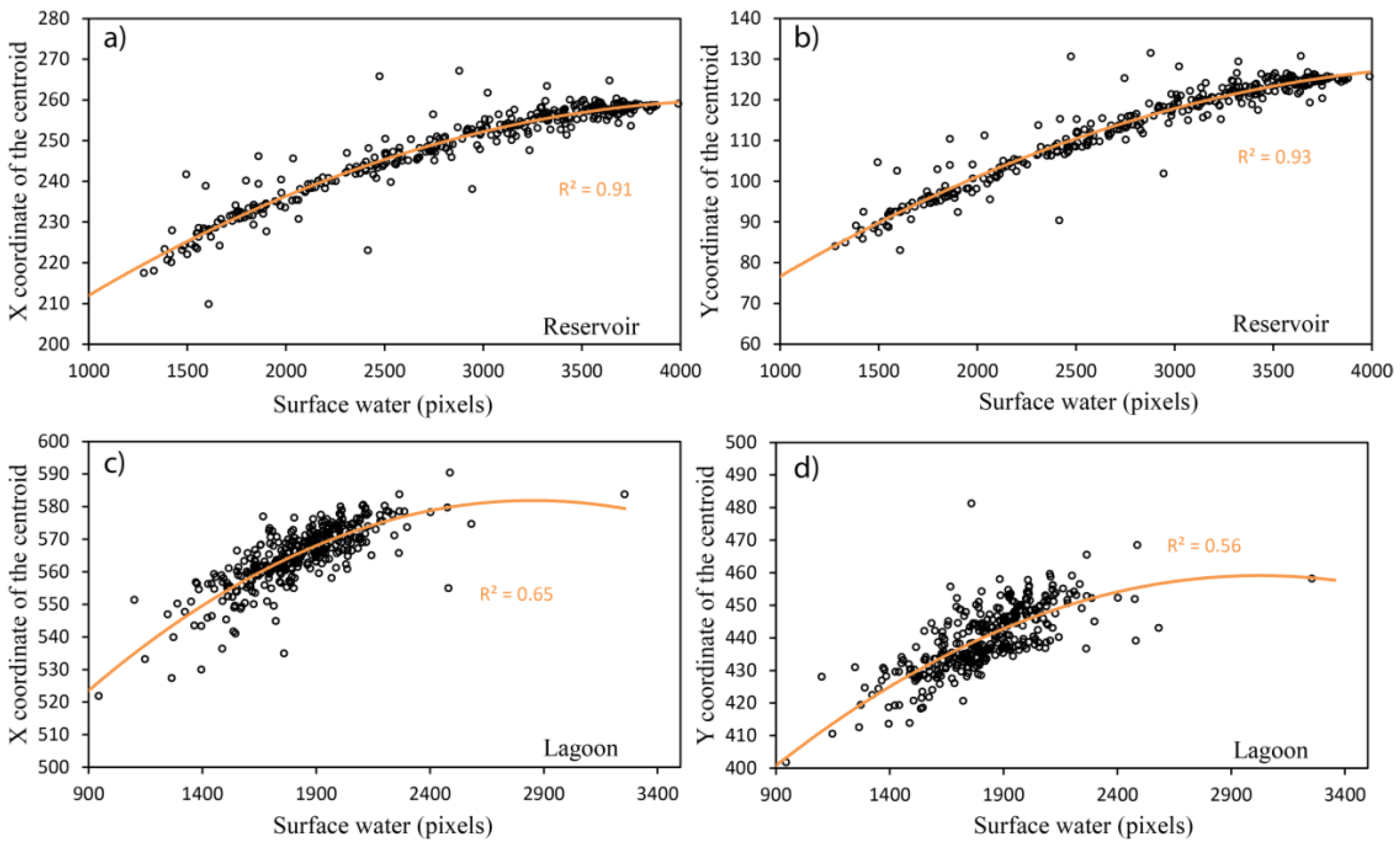
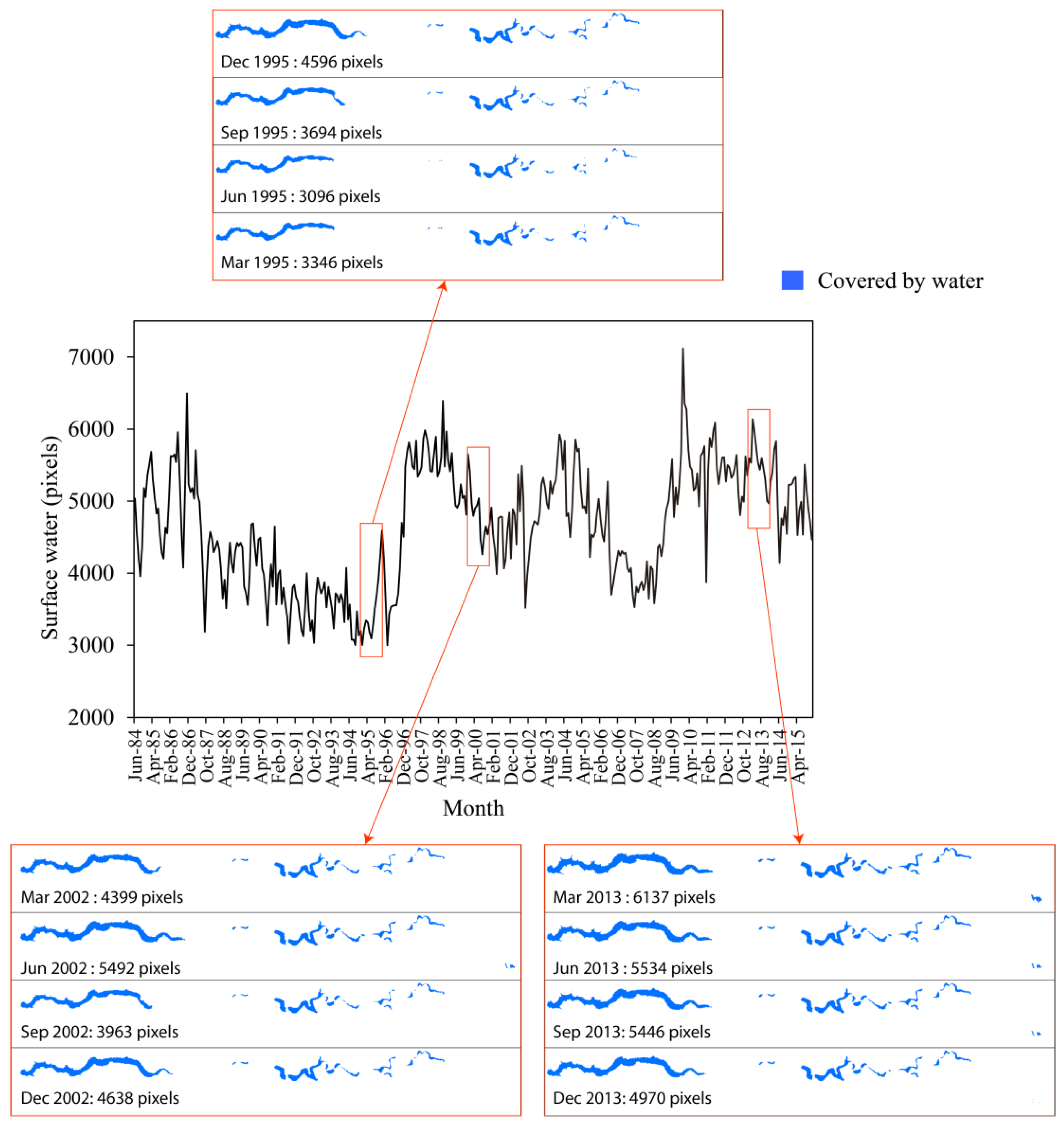
4.1. Surface Water from Satellite Data
- -
- The number of pixels covered by clouds was less than 15,000 in the study domain (total of 895,275 pixels).
- -
- The reflectance threshold for water identification was smaller than 25 (considering surface reflectance from 0 to 255).
- -
- The number of pixels covered by water increased from 3000 to 7000.
4.2. Surface Water from Regression Models
5. Discussion
Limitations and Future Research
- (a)
- This study was focused on estimating the monthly dynamic, but in some applications daily information can be necessary. The proposed regression approach cannot be used for daily completion. It uses the surface water of the previous time step and there are no consecutive days with data for the case study. For daily dynamic characterisation other approaches should be explored.
- (b)
- The proposed approach to complete surface water by using hydro-climatological variables requires a good correlation between these variables and the surface water. However, in other cases studies this correlation may not exist or the information of secondary variables may not be available (especially for the aquifer discharge which requires the calibration of a groundwater model).
- (c)
- The studied area highlights a strong conflict between groundwater-dependent ecosystems such as wetlands, and groundwater pumping to supply demands (mainly irrigation). This problem might be exacerbated in the future due to the impact of climate change. In this area a reduction in precipitation from 1.0 to 2.7% and an increase in temperature from 14.1 to 14.5% are expected for the period 2016–2045 with respect the period 1974–2015 considering the RCP8.5 emission scenario [15]. These changes will also have an impact on the surface water of the wetland. The proposed methodology is useful to propagate the impact on the explanatory hydro-climatological variables to the surface water through the proposed regression ensemble. This approach could be explored in future research.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Dong, J.; Xiao, X.; Xiao, T.; Yang, Z.; Zhao, G.; Zou, Z.; Qin, Y. Open Surface Water Mapping Algorithms: A Comparison of Water-Related Spectral Indices and Sensors. Water 2017, 9, 256. [Google Scholar] [CrossRef]
- Colditz, R.R.; Souza, C.T.; Vazquez, B.; Wickel, A.J.; Ressl, R. Analysis of optimal thresholds for identification of open water using MODIS-derived spectral indices for two coastal wetland systems in Mexico. Int. J. Appl. Earth Obs. Geoinf. 2018, 70, 13–24. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Pulido-Velazquez, D. Spatiotemporal estimation of snow depth using point data from snow stakes, digital terrain models, and satellite data. Hydrol. Process. 2017, 31, 1966–1982. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Collados-Lara, A.-J.; Pulido-Velazquez, D. Estimation of the spatiotemporal dynamics of snow covered area by using cellular automata models. J. Hydrol. 2017, 550, 230–238. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Rabe, A.; Peters, M.; Hostert, P. Mapping pan-European land cover using Landsat spectral-temporal metrics and the European LUCAS survey. Remote Sens. Environ. 2019, 221, 583–595. [Google Scholar] [CrossRef]
- He, B.-J.; Zhao, Z.-Q.; Shen, L.-D.; Wang, H.-B.; Li, L.-G. An approach to examining performances of cool/hot sources in mitigating/enhancing land surface temperature under different temperature backgrounds based on landsat 8 image. Sustain. Cities Soc. 2019, 44, 416–427. [Google Scholar] [CrossRef]
- Matthews, G.V.T. The Ramsar Convention on Wetlands: Its History and Development; Ramsar Convention Bureau: Gland, Switzerland, 1993; ISBN 2940073007. [Google Scholar]
- He, B.-J.; Zhu, J.; Zhao, D.-X.; Gou, Z.-H.; Qi, J.-D.; Wang, J. Co-benefits approach: Opportunities for implementing sponge city and urban heat island mitigation. Land Use Policy 2019, 86, 147–157. [Google Scholar] [CrossRef]
- De La Hera, A.; Gimena, E.C.; Cortés, À.G. Evaluating ecosystem services and drivers of change in Spanish groundwater-related wetlands included in the Ramsar Convention. AIMS Environ. Sci. 2017, 4, 232–250. [Google Scholar] [CrossRef]
- Anand, V.; Oinam, B. Future land use land cover prediction with special emphasis on urbanization and wetlands. Remote Sens. Lett. 2020, 11, 225–234. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Jahanishakib, F. Vulnerability assessment of wetland landscape ecosystem services using driver-pressure-state-impact-response (DPSIR) model. Ecol. Indic. 2017, 82, 293–303. [Google Scholar] [CrossRef]
- Baena-Ruiz, L.; Pulido-Velazquez, D.; Collados-Lara, A.-J.; Renau-Pruñonosa, A.; Morell, I. Global Assessment of Seawater Intrusion Problems (Status and Vulnerability). Water Resour. Manag. 2018, 32, 2681–2700. [Google Scholar] [CrossRef]
- Renau-Pruñonosa, A.; Morell, I.; Pulido-Velazquez, D. A Methodology to Analyse and Assess Pumping Management Strategies in Coastal Aquifers to Avoid Degradation Due to Seawater Intrusion Problems. Water Resour. Manag. 2016, 30, 4823–4837. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Pulido-Velazquez, D.; Pardo-Igúzquiza, E. An Integrated Statistical Method to Generate Potential Future Climate Scenarios to Analyse Droughts. Water 2018, 10, 1224. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Collados-Lara, A.-J.; Alcalá, F.J. Assessing impacts of future potential climate change scenarios on aquifer recharge in continental Spain. J. Hydrol. 2018, 567, 803–819. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Renau-Pruñonosa, A.; Llopis-Albert, C.; Morell, I.; Collados-Lara, A.-J.; Senent-Aparicio, J.; Baena-Ruiz, L. Integrated assessment of future potential global change scenarios and their hydrological impacts in coastal aquifers—A new tool to analyse management alternatives in the Plana Oropesa-Torreblanca aquifer. Hydrol. Earth Syst. Sci. 2018, 22, 3053–3074. [Google Scholar] [CrossRef]
- Escriva-Bou, A.; Pulido-Velazquez, M.; Pulido-Velazquez, D. Economic Value of Climate Change Adaptation Strategies for Water Management in Spain’s Jucar Basin. J. Water Resour. Plan. Manag. 2017, 143, 04017005. [Google Scholar] [CrossRef]
- Baena-Ruiz, L.; Pulido-Velazquez, D.; Collados-Lara, A.-J.; Renau-Pruñonosa, A.; Morell, I.; Senent-Aparicio, J.; Llopis-Albert, C. Summarizing the impacts of future potential global change scenarios on seawater intrusion at the aquifer scale. Environ. Earth Sci. 2020, 79, 1–13. [Google Scholar] [CrossRef]
- Vuolo, F.; Żółtak, M.; Pipitone, C.; Zappa, L.; Wenng, H.; Immitzer, M.; Weiss, M.; Baret, F.; Atzberger, C. Data Service Platform for Sentinel-2 Surface Reflectance and Value-Added Products: System Use and Examples. Remote Sens. 2016, 8, 938. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Zhan, X.; Sohlberg, R.; Townshend, J.; DiMiceli, C.; Carroll, M.; Eastman, J.; Hansen, M.; DeFries, R. Detection of land cover changes using MODIS 250 m data. Remote Sens. Environ. 2002, 83, 336–350. [Google Scholar] [CrossRef]
- Xiao, F.; Cheng, W.; Zhu, L.; Feng, Q.; Du, Y. Downscaling MODIS-derived water maps with high-precision topographic data in a shallow lake. Int. J. Remote Sens. 2018, 39, 7846–7860. [Google Scholar] [CrossRef]
- Che, X.; Yang, Y.; Feng, M.; Xiao, T.; Huang, S.; Xiang, Y.; Chen, Z. Mapping Extent Dynamics of Small Lakes Using Downscaling MODIS Surface Reflectance. Remote Sens. 2017, 9, 82. [Google Scholar] [CrossRef]
- Rokni, K.; Ahmad, A.; Selamat, A.; Hazini, S. Water Feature Extraction and Change Detection Using Multitemporal Landsat Imagery. Remote Sens. 2014, 6, 4173–4189. [Google Scholar] [CrossRef]
- Girona-Mata, M.; Miles, E.S.; Ragettli, S.; Pellicciotti, F. High-Resolution Snowline Delineation From Landsat Imagery to Infer Snow Cover Controls in a Himalayan Catchment. Water Resour. Res. 2019, 55, 6754–6772. [Google Scholar] [CrossRef]
- Alam, A.; Bhat, M.S.; Maheen, M. Using Landsat satellite data for assessing the land use and land cover change in Kashmir valley. GeoJournal 2020, 85, 1529–1543. [Google Scholar] [CrossRef]
- Jolly, I.D.; McEwan, K.L.; Holland, K.L. A review of groundwater-surface water interactions in arid/semi-arid wetlands and the consequences of salinity for wetland ecology. Ecohydrology 2008, 1, 43–58. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Pulido-Velazquez, D.; Jiménez-Sánchez, J. Precipitation fields in an alpine Mediterranean catchment: Inversion of precipitation gradient with elevation or undercatch of snowfall? Int. J. Clim. 2018, 38, 3565–3578. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Pulido-Velazquez, D.; Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Senent-Aparicio, J.; Baena-Ruiz, L. A Preliminary Assessment of the “Undercatching” and the Precipitation Pattern in an Alpine Basin. Water 2020, 12, 1061. [Google Scholar] [CrossRef]
- Collados-Lara, A.-J.; Pulido-Velazquez, D.; Pardo-Igúzquiza, E.; Alonso-González, E. Estimation of the spatiotemporal dynamic of snow water equivalent at mountain range scale under data scarcity. Sci. Total Environ. 2020, 741, 140485. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Sánchez, J.; Senent-Aparicio, J.; Segura-Méndez, F.; Pulido-Velazquez, D.; Srinivasan, R. Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustainability 2019, 11, 2872. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J.; Pulido-Velazquez, M. A general methodology to simulate groundwater flow of unconfined aquifers with a reduced computational cost. J. Hydrol. 2007, 338, 42–56. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; López-Ballesteros, A.; Pérez-Sánchez, J.; Segura-Méndez, F.J.; Pulido-Velazquez, D. Using Multiple Monthly Water Balance Models to Evaluate Gridded Precipitation Products over Peninsular Spain. Remote Sens. 2018, 10, 922. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Sáez, P.J.; Bueno-Crespo, A.; Pérez-Sánchez, J.; Pulido-Velázquez, D. Coupling machine-learning techniques with SWAT model for instantaneous peak flow prediction. Biosyst. Eng. 2019, 177, 67–77. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Garrote, L.; Andreu, J.; Martin-Carrasco, F.-J.; Iglesias, A. A methodology to diagnose the effect of climate change and to identify adaptive strategies to reduce its impacts in conjunctive-use systems at basin scale. J. Hydrol. 2011, 405, 110–122. [Google Scholar] [CrossRef]
- Santos, F.; Peña, A.; Nogales, B.; Soria-Soria, E.; del Cura, M.; Ángeles, G.; González-Martín, J.A.; Antón, J. Bacterial diversity in dry modern freshwater stromatolites from Ruidera Pools Natural Park, Spain. Syst. Appl. Microbiol. 2010, 33, 209–221. [Google Scholar] [CrossRef] [PubMed]
- Foster, J.S.; Green, S.J. Microbial Diversity in Modern Stromatolites; Springer Science and Business Media LLC: Berlin, Germany, 2011; pp. 383–405. [Google Scholar]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J. A two-step explicit solution of the Boussinesq equation for efficient simulation of unconfined aquifers in conjunctive-use models. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J.; Pulido-Velazquez, M. An efficient conceptual model to simulate surface water body-aquifer interaction in conjunctive use management models. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Pulido-Velazquez, D. Using MODFLOW code to approach transient hydraulic head with a sharp-interface solution. Hydrol. Process. 2015, 29, 2052–2064. [Google Scholar] [CrossRef]
- McCormack, T.; Naughton, O.; Johnston, P.M.; Gill, L. Quantifying the influence of surface water–groundwater interaction on nutrient flux in a lowland karst catchment. Hydrol. Earth Syst. Sci. 2016, 20, 2119–2133. [Google Scholar] [CrossRef]
- Hardy, A.; Oakes, G.; Ettritch, G. Tropical Wetland (TropWet) Mapping Tool: The Automatic Detection of Open and Vegetated Waterbodies in Google Earth Engine for Tropical Wetlands. Remote Sens. 2020, 12, 1182. [Google Scholar] [CrossRef]
- Herrera, S.; Gutiérrez, J.M.; Ancell, R.; Pons, M.R.; Frías, M.D.; Fernández, J. Development and analysis of a 50-year high-resolution daily gridded precipitation dataset over Spain (Spain02). Int. J. Clim. 2010, 32, 74–85. [Google Scholar] [CrossRef]
- Herrera, S.; Fernández, J.; Gutiérrez, J.M. Update of the Spain02 gridded observational dataset for EURO-CORDEX evaluation: Assessing the effect of the interpolation methodology. Int. J. Clim. 2016, 36, 900–908. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Khandelwal, A.; Karpatne, A.; Marlier, M.E.; Kim, J.; Lettenmaier, D.P.; Kumar, V. An approach for global monitoring of surface water extent variations in reservoirs using MODIS data. Remote Sens. Environ. 2017, 202, 113–128. [Google Scholar] [CrossRef]
- Di Vittorio, C.A.; Georgakakos, A.P. Land cover classification and wetland inundation mapping using MODIS. Remote Sens. Environ. 2018, 204, 1–17. [Google Scholar] [CrossRef]
- Huang, W.; DeVries, B.; Huang, C.; Lang, M.W.; Jones, J.W.; Creed, I.F.; Carroll, M.L. Automated Extraction of Surface Water Extent from Sentinel-1 Data. Remote Sens. 2018, 10, 797. [Google Scholar] [CrossRef]
- Luo, Y.; Doxaran, D.; Vanhellemont, Q. Retrieval and Validation of Water Turbidity at Metre-Scale Using Pléiades Satellite Data: A Case Study in the Gironde Estuary. Remote Sens. 2020, 12, 946. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]




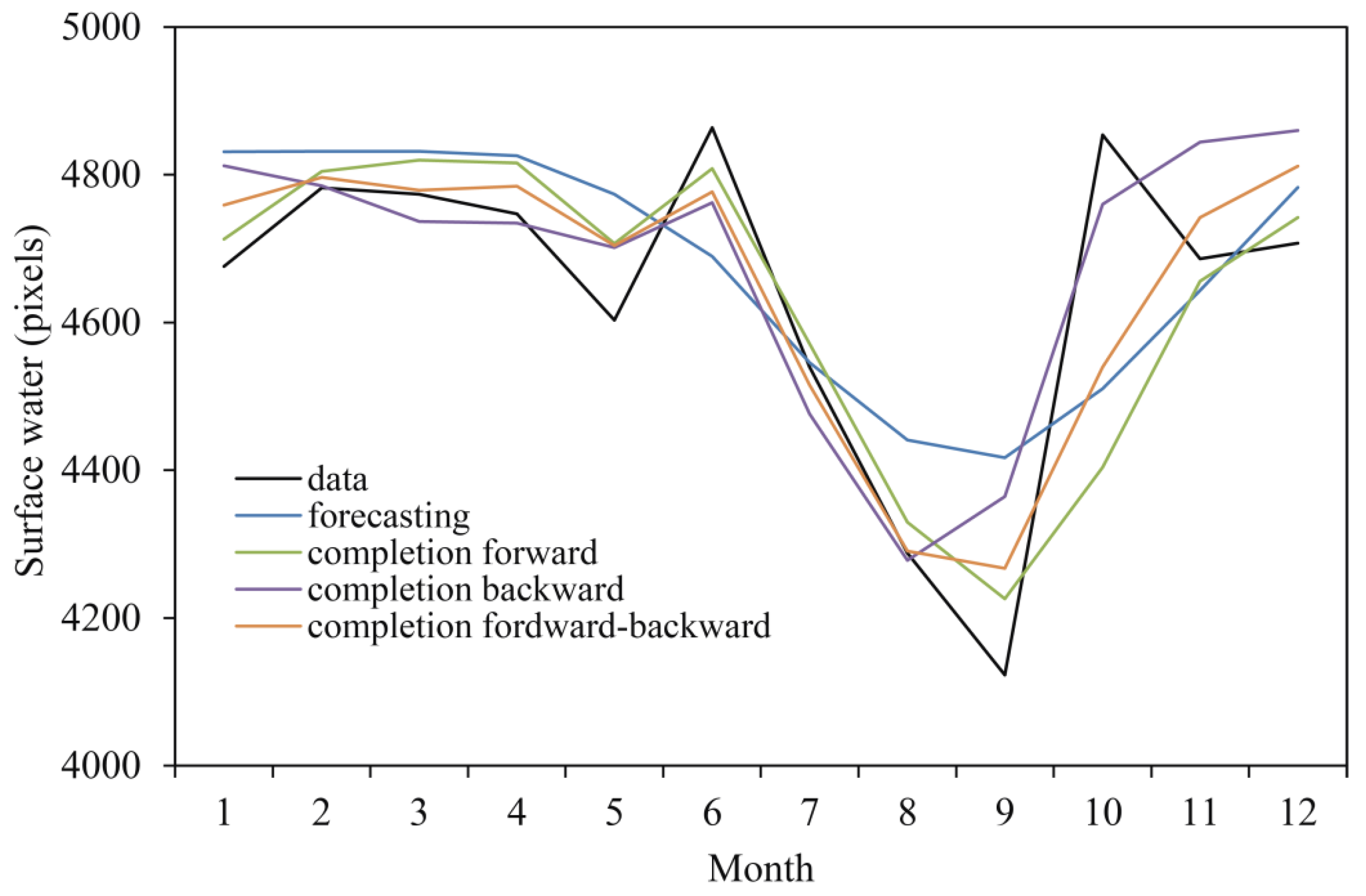
| Model | xi | xj | xl | xk | R² Calibration | RMSE (Pixels) Forecasting | RMSE (Pixels) Completion Forward | RMSE (Pixels) Completion Backward | RMSE (Pixels) Completion Forward–Backward |
|---|---|---|---|---|---|---|---|---|---|
| 1.1 | (D) | (W) | (PE) | LOG(D) | 0.709 | 777.374 | 497.764 | 589.183 | 476.856 |
| 1.2 | (W) | LOG(D) | 1/(P) | (PE)2 | 0.707 | 777.878 | 501.515 | 586.689 | 477.398 |
| 1.3 | (D) | (W) | (PE) | SQRT(D) | 0.709 | 778.372 | 498.137 | 588.780 | 476.825 |
| 1.4 | (W) | (PE) | LOG(W) | 1/(D) | 0.709 | 778.419 | 498.782 | 588.137 | 476.714 |
| 1.5 | (D) | (W) | 1/(P) | (PE)2 | 0.707 | 778.557 | 501.822 | 587.120 | 477.638 |
| 1.6 | (W) | 1/(D) | 1/(PE) | (PE)2 | 0.709 | 778.733 | 498.290 | 587.081 | 476.276 |
| 2.1 | (W) | (PE) | 1/(D) | 1/(T) | 0.709 | 778.41 | 497.683 | 586.064 | 475.621 |
| 2.2 | (W) | (PE) | LOG(D) | 1/(T) | 0.709 | 779.114 | 497.983 | 586.479 | 475.854 |
| 2.3 | (W) | (PE) | 1/(D) | 1/(E) | 0.709 | 779.45 | 497.351 | 587.411 | 476.175 |
| 2.4 | (W) | (PE) | 1/(T) | SQRT(D) | 0.709 | 779.497 | 498.125 | 586.684 | 475.965 |
| 2.5 | (D) | (W) | (PE) | 1/(T) | 0.709 | 779.849 | 498.280 | 586.919 | 476.094 |
| 2.6 | (W) | (PE) | LOG(D) | 1/(E) | 0.709 | 780.244 | 497.652 | 587.810 | 476.400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collados-Lara, A.-J.; Pardo-Igúzquiza, E.; Pulido-Velazquez, D.; Baena-Ruiz, L. Estimation of the Monthly Dynamics of Surface Water in Wetlands from Satellite and Secondary Hydro-Climatological Data. Remote Sens. 2021, 13, 2380. https://doi.org/10.3390/rs13122380
Collados-Lara A-J, Pardo-Igúzquiza E, Pulido-Velazquez D, Baena-Ruiz L. Estimation of the Monthly Dynamics of Surface Water in Wetlands from Satellite and Secondary Hydro-Climatological Data. Remote Sensing. 2021; 13(12):2380. https://doi.org/10.3390/rs13122380
Chicago/Turabian StyleCollados-Lara, Antonio-Juan, Eulogio Pardo-Igúzquiza, David Pulido-Velazquez, and Leticia Baena-Ruiz. 2021. "Estimation of the Monthly Dynamics of Surface Water in Wetlands from Satellite and Secondary Hydro-Climatological Data" Remote Sensing 13, no. 12: 2380. https://doi.org/10.3390/rs13122380
APA StyleCollados-Lara, A.-J., Pardo-Igúzquiza, E., Pulido-Velazquez, D., & Baena-Ruiz, L. (2021). Estimation of the Monthly Dynamics of Surface Water in Wetlands from Satellite and Secondary Hydro-Climatological Data. Remote Sensing, 13(12), 2380. https://doi.org/10.3390/rs13122380








