Multi-Task Collaboration Deep Learning Framework for Infrared Precipitation Estimation
Abstract
1. Introduction
- We proposed a multi-task collaboration framework named MTCF, i.e., a novel combination mode of the classification and estimation model, which alleviates the error accumulation and retains the ability to improve the data balance;
- We propose a multi-task consistency constraint mechanism. Through this mechanism, the information abundance and the prediction accuracy of the classification branch are largely improved;
- We propose a cross-branch interactive module, i.e., CBIM, which realizes the soft feature transformation between branches via the soft spatial attention mechanism. The consistency constraint mechanism and CBIM together make up a positive information feedback loop to produce more accurate estimation results;
- We model and analyze the correlation between infrared bands of different wavelengths of Himawari-8 under different precipitation intensities to improve the applicability of the model on other data.
2. Data
2.1. Himawari 8
2.2. GPM
2.3. Data Processing
2.4. Data Statistics
3. Methods
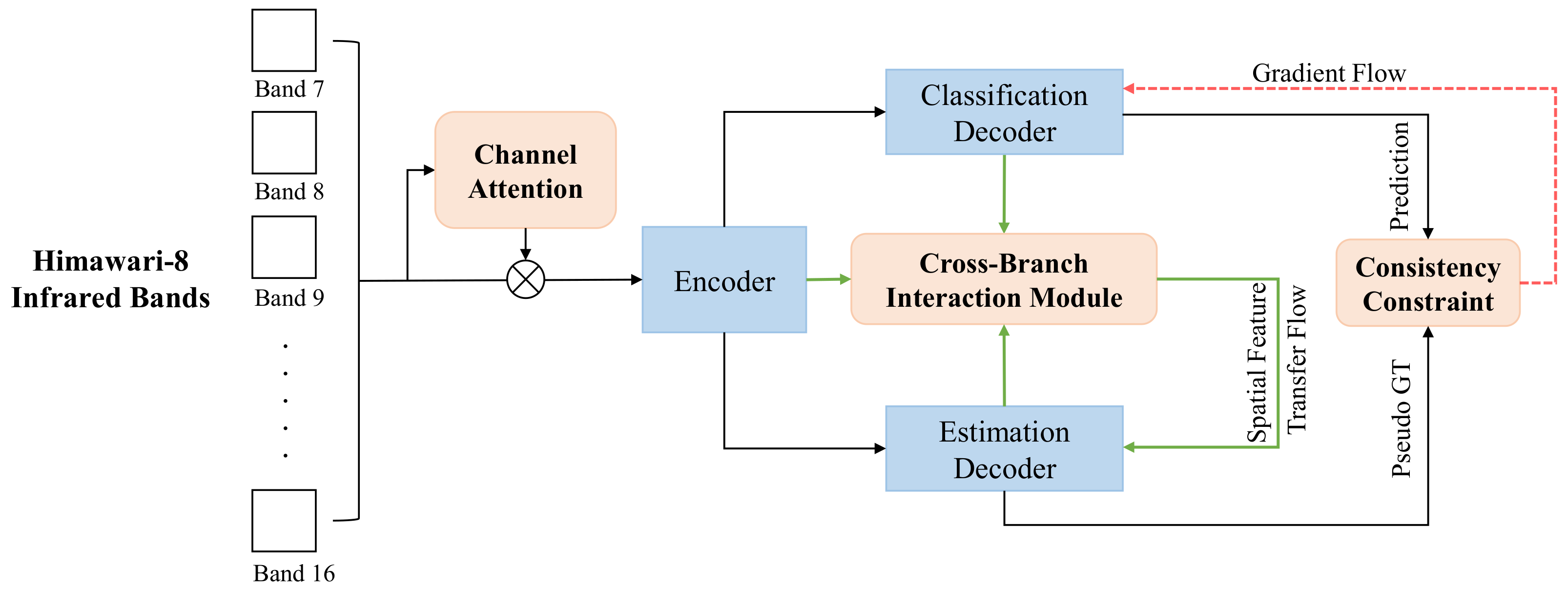
3.1. Overview
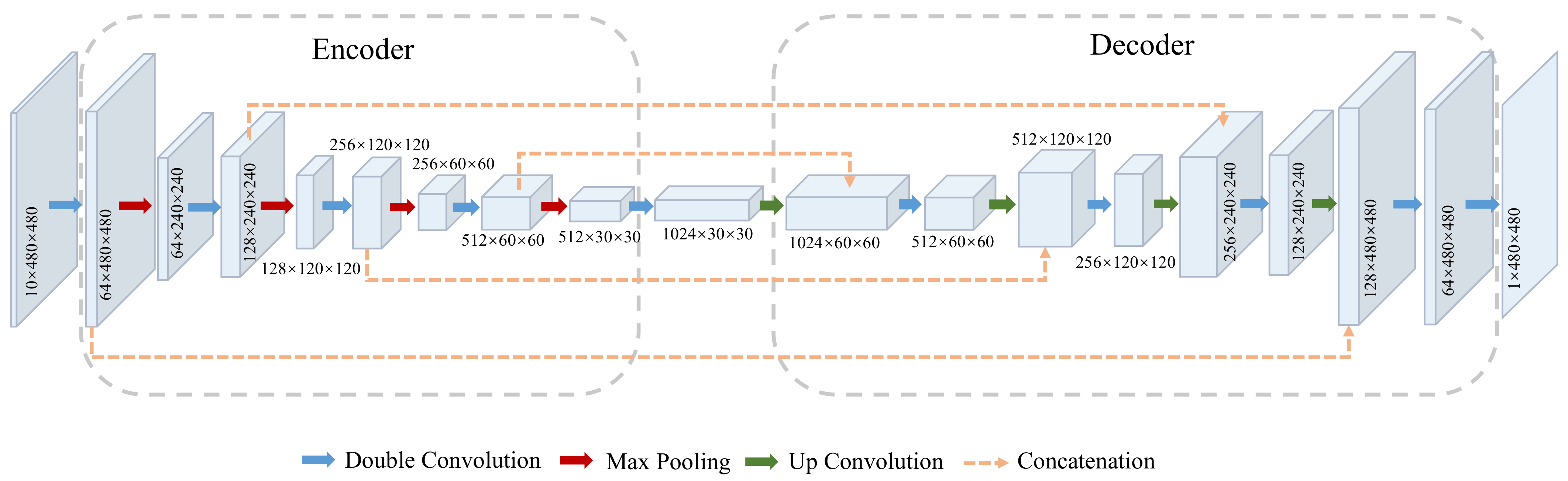
3.2. Baseline Network
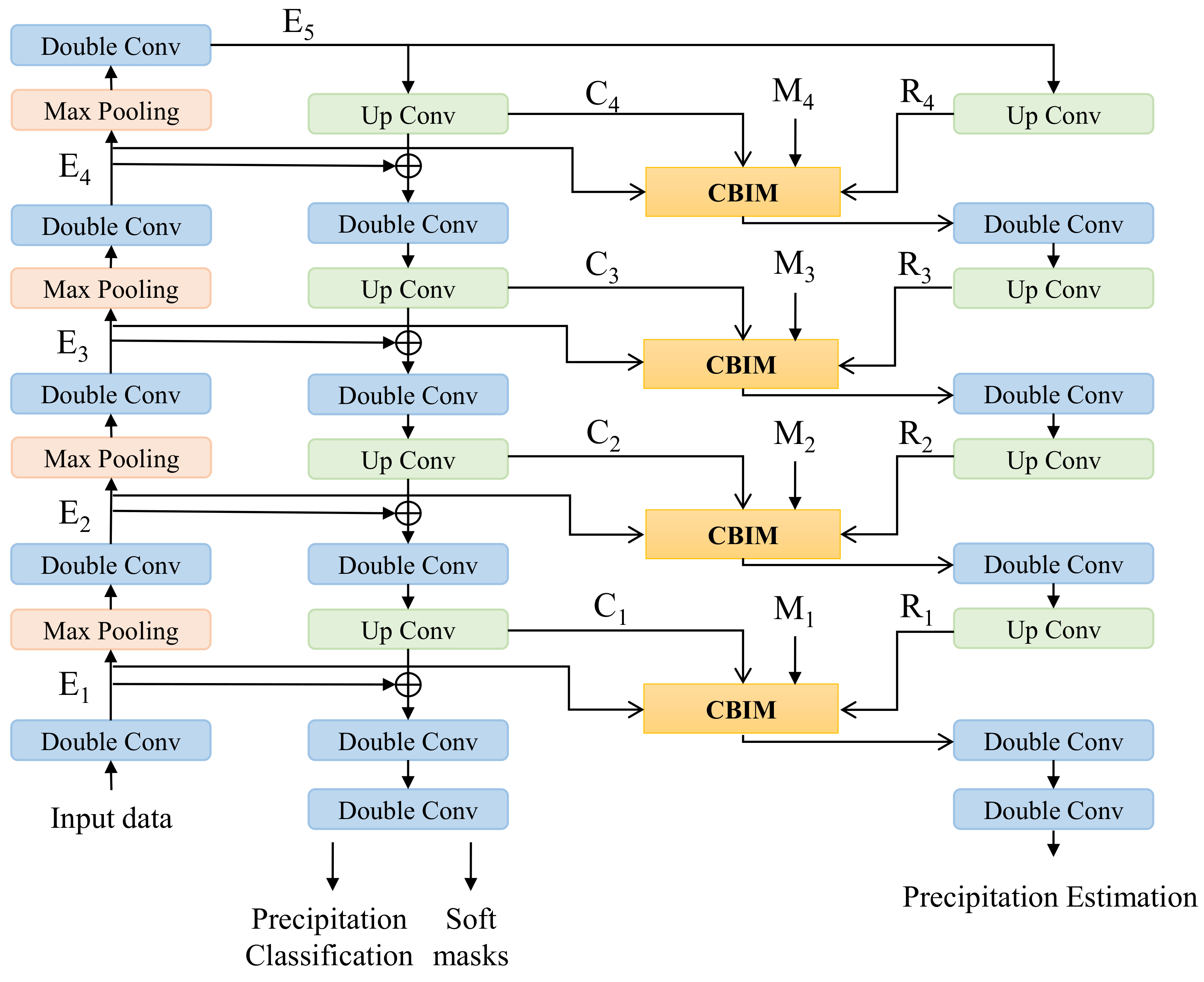
3.3. Multi-Branch Network with Consistency Constraint
3.4. Cross-Branch Interaction with Soft Attention
3.5. Implementation Details
4. Results
4.1. Evaluation Metrics
4.1.1. Precipitation Classification
4.1.2. Precipitation Estimation
4.2. Quantitative Results
4.3. Visualization Results
4.4. Ablation Study
4.4.1. The Effectiveness of Multi-Task Collaboration
4.4.2. The Impact of the Classification Threshold
4.5. The Analysis of Band Correlation
5. Discussion
- The performance of the single U-Net classification model is worse than that of the single U-Net estimation model. We suspect that this is caused by the fact that the information abundance obtained by the classification model is much lower than that obtained by the estimation model, which makes the cognitive ability of the classification model significantly weaker than that obtained by the estimation model. The two-stage framework, in which the above two models are connected in series through masks to alleviate the data imbalance problem, will result in the accumulation of classification errors and limit the accuracy improvement of the model to a certain extent. This is also the main reason why the accuracy of the two-stage framework is lower than our multi-task collaboration framework.
- The consistency constraint and the CBIM can effectively improve the accuracy of the model under different precipitation intensities. Figure 8 shows that MTCF can predict the precipitation spatial distribution and small-scale precipitation in more detail, and also has a superior performance in typhoon precipitation prediction. The reason is that the consistency constraint enhances the information abundance of the classification model through the gradient back-propagation and improves the cognitive ability of the classification model. The CBIM changes the spatial attention of the estimation model to the precipitation data by transmitting the classification predictions and spatial features, so as to enhance the estimation capacity of the model for high-intensity precipitation. The combination of the above two forms a positive information feedback loop of “estimation-classification-estimation”, which makes the accuracy of both the classification model and estimation model significantly improved.
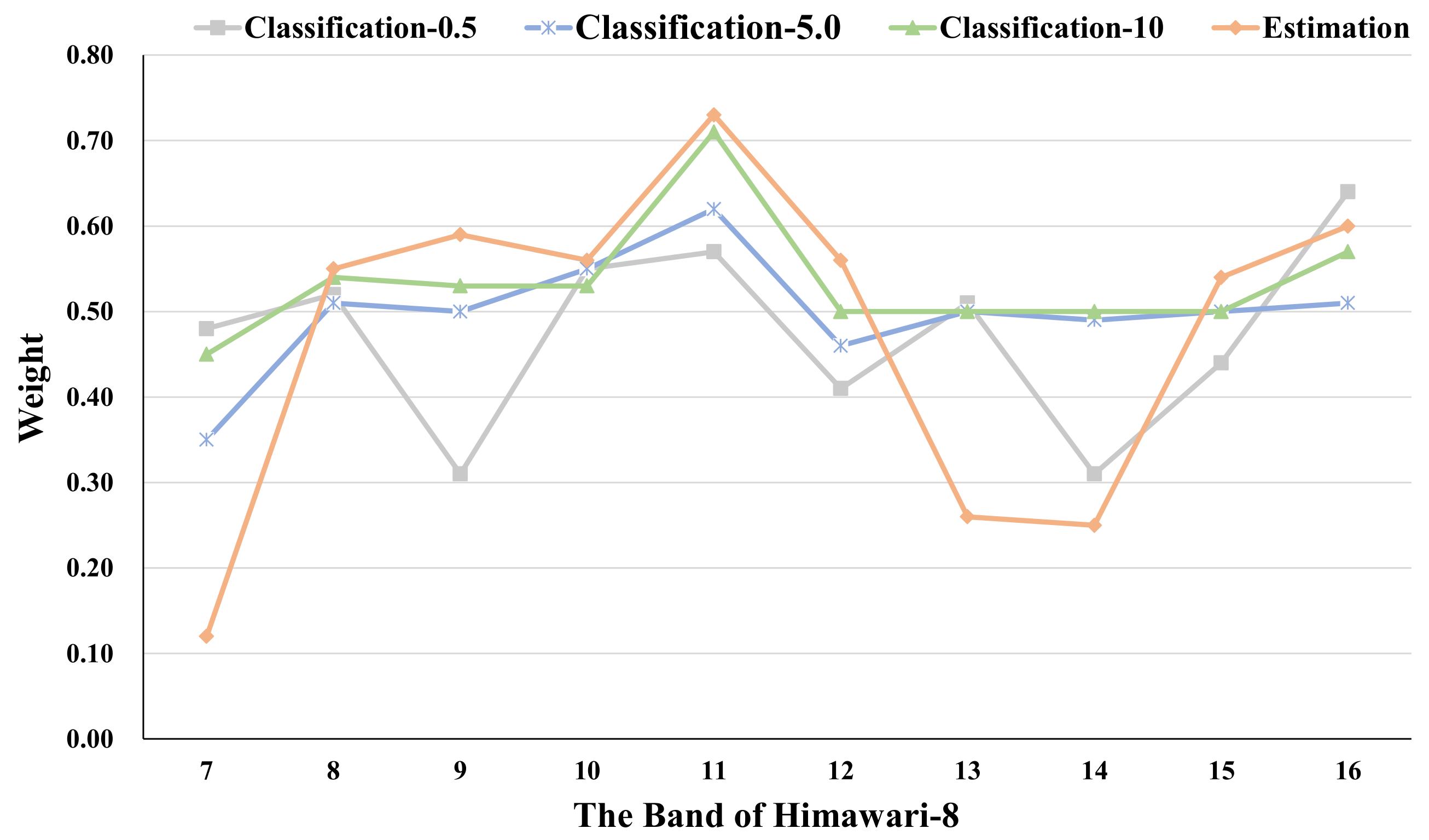
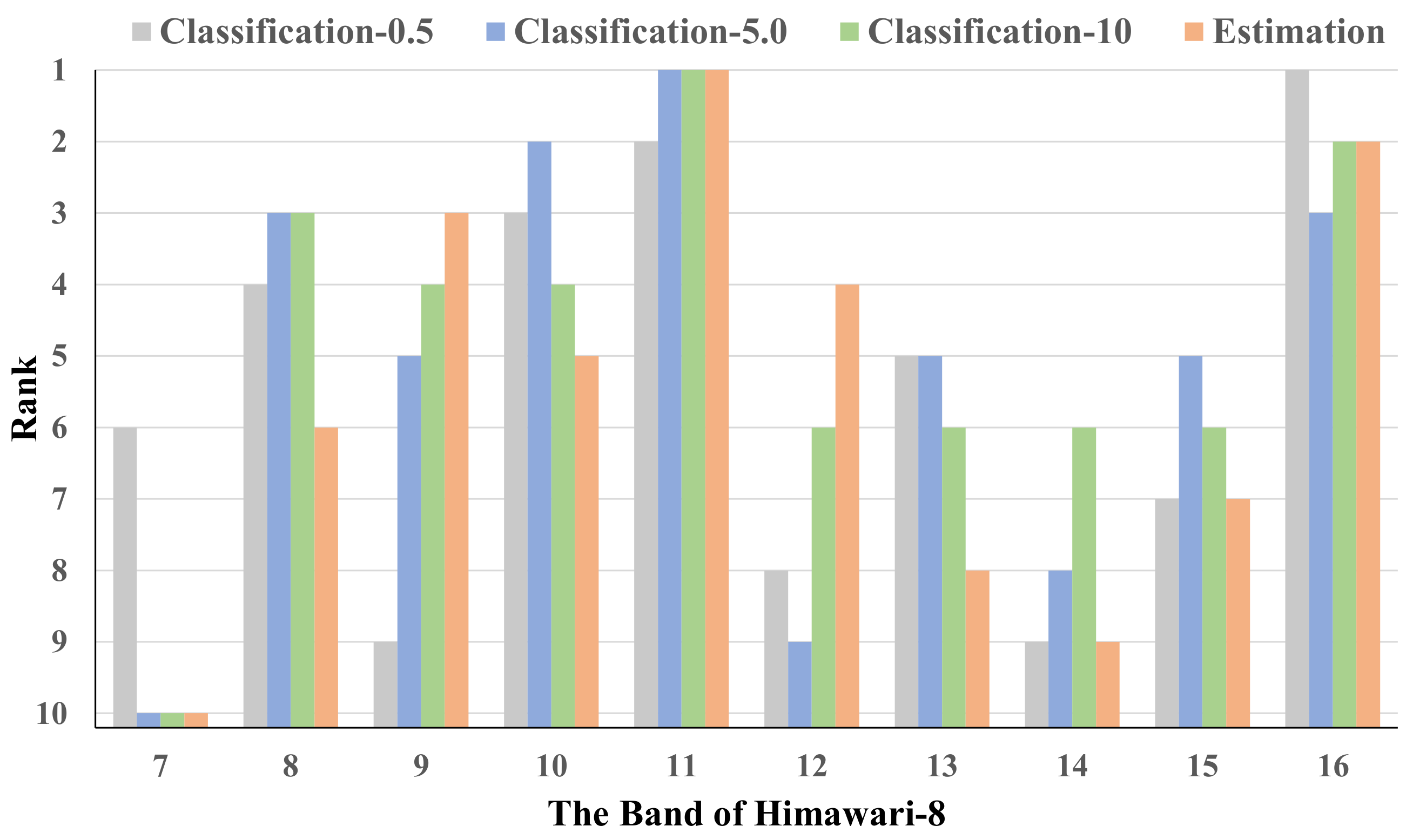
- By introducing the channel attention module, the model has a small and relatively insignificant performance improvement. However, more importantly, we can observe the importance of the input bands in the model by this. From the comparison, we observe that the band-11 (8.59 μm) and the band-16 (13.28 μm) are related to the precipitation intensity, and these two bands can monitor cloud phase and cloud top height, respectively, which has been verified in some works [23,45,46,47,48]. In addition, the changes of the weights of band-8, band-9, and band-10 under different precipitation intensities indicate that the correlation between the low-intensity precipitation and water vapor density in the middle troposphere is great, meanwhile, the high-intensity precipitation has a great correlation with water vapor density in the higher troposphere.
- Although the multi-task collaboration framework can effectively improve the accuracy under each precipitation intensity, the estimation accuracy of high-intensity precipitation, which has attracted great attention in production and life, flood control and disaster prevention, and other applications, is still not ideal. We suspect that the complex patterns of high-intensity precipitation and the scarcity of samples increase the difficulty of the model training. In addition, the errors in GPM are also a potential cause.
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
- Himawari-8: Data can be obtained from JAXA Himawari Monitor system and are available at ftp.ptree.java.jp accessed on 15 October 2020 after applying for an account.
- GPM IMERG data: Data can be obtained from NASA EarthData webpage and are available at https://disc.gsfc.nasa.gov/datasets/GPM_3IMERGHH_06/summary?keywords=GPM accessed on 3 December 2019.
Acknowledgments
Conflicts of Interest
References
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Akbari Asanjan, A.; Yang, T.; Gao, X.; Hsu, K.; Sorooshian, S. Short-range quantitative precipitation forecasting using Deep Learning approaches. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 11–15 December 2017; Volume 2017, p. H32B-02. [Google Scholar]
- Nguyen, P.; Sellars, S.; Thorstensen, A.; Tao, Y.; Ashouri, H.; Braithwaite, D.; Hsu, K.; Sorooshian, S. Satellites track precipitation of super typhoon Haiyan. Eos Trans. Am. Geophys. Union 2014, 95, 133–135. [Google Scholar] [CrossRef]
- Scofield, R.A.; Kuligowski, R.J. Status and outlook of operational satellite precipitation algorithms for extreme-precipitation events. Weather Forecast. 2003, 18, 1037–1051. [Google Scholar] [CrossRef]
- Arnaud, P.; Bouvier, C.; Cisneros, L.; Dominguez, R. Influence of rainfall spatial variability on flood prediction. J. Hydrol. 2002, 260, 216–230. [Google Scholar] [CrossRef]
- Foresti, L.; Reyniers, M.; Seed, A.; Delobbe, L. Development and verification of a real-time stochastic precipitation nowcasting system for urban hydrology in Belgium. Hydrol. Earth Syst. Sci. 2016, 20, 505. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Van Dijk, A.I.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Gehne, M.; Hamill, T.M.; Kiladis, G.N.; Trenberth, K.E. Comparison of global precipitation estimates across a range of temporal and spatial scales. J. Clim. 2016, 29, 7773–7795. [Google Scholar] [CrossRef]
- Folino, G.; Guarascio, M.; Chiaravalloti, F.; Gabriele, S. A Deep Learning based architecture for rainfall estimation integrating heterogeneous data sources. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R.J. Evaluation of the high-resolution CMORPH satellite rainfall product using dense rain gauge observations and radar-based estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Westrick, K.J.; Mass, C.F.; Colle, B.A. The limitations of the WSR-88D radar network for quantitative precipitation measurement over the coastal western United States. Bull. Am. Meteorol. Soc. 1999, 80, 2289–2298. [Google Scholar] [CrossRef]
- Chang, N.B.; Hong, Y. Multiscale Hydrologic Remote Sensing: Perspectives and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Ajami, N.K.; Hornberger, G.M.; Sunding, D.L. Sustainable water resource management under hydrological uncertainty. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hong, Y.; Tang, G.; Ma, Y.; Huang, Q.; Han, Z.; Zeng, Z.; Yang, Y.; Wang, C.; Guo, X. Remote Sensing Precipitation: Sensors, Retrievals, Validations, and Applications; Observation and Measurement; Li, X., Vereecken, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–23. [Google Scholar]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Hsu, K.l.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) Version 2015, 4, 26. [Google Scholar]
- Bellerby, T.; Todd, M.; Kniveton, D.; Kidd, C. Rainfall estimation from a combination of TRMM precipitation radar and GOES multispectral satellite imagery through the use of an artificial neural network. J. Appl. Meteorol. 2000, 39, 2115–2128. [Google Scholar] [CrossRef]
- Ba, M.B.; Gruber, A. GOES multispectral rainfall algorithm (GMSRA). J. Appl. Meteorol. 2001, 40, 1500–1514. [Google Scholar] [CrossRef]
- Behrangi, A.; Hsu, K.L.; Imam, B.; Sorooshian, S.; Huffman, G.J.; Kuligowski, R.J. PERSIANN-MSA: A precipitation estimation method from satellite-based multispectral analysis. J. Hydrometeorol. 2009, 10, 1414–1429. [Google Scholar] [CrossRef]
- Ramirez, S.; Lizarazo, I. Detecting and tracking mesoscale precipitating objects using machine learning algorithms. Int. J. Remote Sens. 2017, 38, 5045–5068. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Tao, Y.; Gao, X.; Ihler, A.; Hsu, K.; Sorooshian, S. Deep neural networks for precipitation estimation from remotely sensed information. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 1349–1355. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A.; Bottou, L. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. Persiann-cnn: Precipitation estimation from remotely sensed information using artificial neural networks—Convolutional neural networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Tao, Y.; Hsu, K.; Ihler, A.; Gao, X.; Sorooshian, S. A two-stage deep neural network framework for precipitation estimation from bispectral satellite information. J. Hydrometeorol. 2018, 19, 393–408. [Google Scholar] [CrossRef]
- Moraux, A.; Dewitte, S.; Cornelis, B.; Munteanu, A. Deep learning for precipitation estimation from satellite and rain gauges measurements. Remote Sens. 2019, 11, 2463. [Google Scholar] [CrossRef]
- Hayatbini, N.; Kong, B.; Hsu, K.L.; Nguyen, P.; Sorooshian, S.; Stephens, G.; Fowlkes, C.; Nemani, R.; Ganguly, S. Conditional Generative Adversarial Networks (cGANs) for Near Real-Time Precipitation Estimation from Multispectral GOES-16 Satellite Imageries—PERSIANN-cGAN. Remote Sens. 2019, 11, 2193. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.; Tang, G.; Yang, Y.; Hong, Y. Infrared precipitation estimation using convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8612–8625. [Google Scholar] [CrossRef]
- Miller, S.D.; Schmit, T.L.; Seaman, C.J.; Lindsey, D.T.; Gunshor, M.M.; Kohrs, R.A.; Sumida, Y.; Hillger, D. A sight for sore eyes: The return of true color to geostationary satellites. Bull. Am. Meteorol. Soc. 2016, 97, 1803–1816. [Google Scholar] [CrossRef]
- Thies, B.; Nauß, T.; Bendix, J. Discriminating raining from non-raining clouds at mid-latitudes using meteosat second generation daytime data. Atmos. Chem. Phys. 2008, 8, 2341–2349. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2013, 95, 701–722. [Google Scholar] [CrossRef]
- Huffman, G.; Bolvin, D.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.; Sorooshian, S.; Tan, J.; Xie, P. Algorithm Theoretical Basis Document (ATBD) Version 4.5: NASA Global Precipitation Measurement (GPM) Integrated Multi-SatellitE Retrievals for GPM (IMERG); NASA: Greenbelt, MD, USA, 2015.
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [PubMed]
- Lebedev, V.; Ivashkin, V.; Rudenko, I.; Ganshin, A.; Molchanov, A.; Ovcharenko, S.; Grokhovetskiy, R.; Bushmarinov, I.; Solomentsev, D. Precipitation nowcasting with satellite imagery. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2680–2688. [Google Scholar]
- Lou, A.; Chandran, E.; Prabhat, M.; Biard, J.; Kunkel, K.; Wehner, M.F.; Kashinath, K. Deep Learning Semantic Segmentation for Climate Change Precipitation Analysis. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2019; Volume 2019, p. GC43D-1350. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Lecture Notes in Computer Science, Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 8–12 June 2015; pp. 3431–3440. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 8026–8037. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Arkin, P.A.; Meisner, B.N. The relationship between large-scale convective rainfall and cold cloud over the western hemisphere during 1982–1984. Mon. Weather Rev. 1987, 115, 51–74. [Google Scholar] [CrossRef]
- Adler, R.F.; Negri, A.J. A satellite infrared technique to estimate tropical convective and stratiform rainfall. J. Appl. Meteorol. 1988, 27, 30–51. [Google Scholar] [CrossRef]
- Cotton, W.R.; Anthes, R.A. Storm and Cloud Dynamics; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Xu, L.; Sorooshian, S.; Gao, X.; Gupta, H.V. A cloud-patch technique for identification and removal of no-rain clouds from satellite infrared imagery. J. Appl. Meteorol. 1999, 38, 1170–1181. [Google Scholar] [CrossRef]
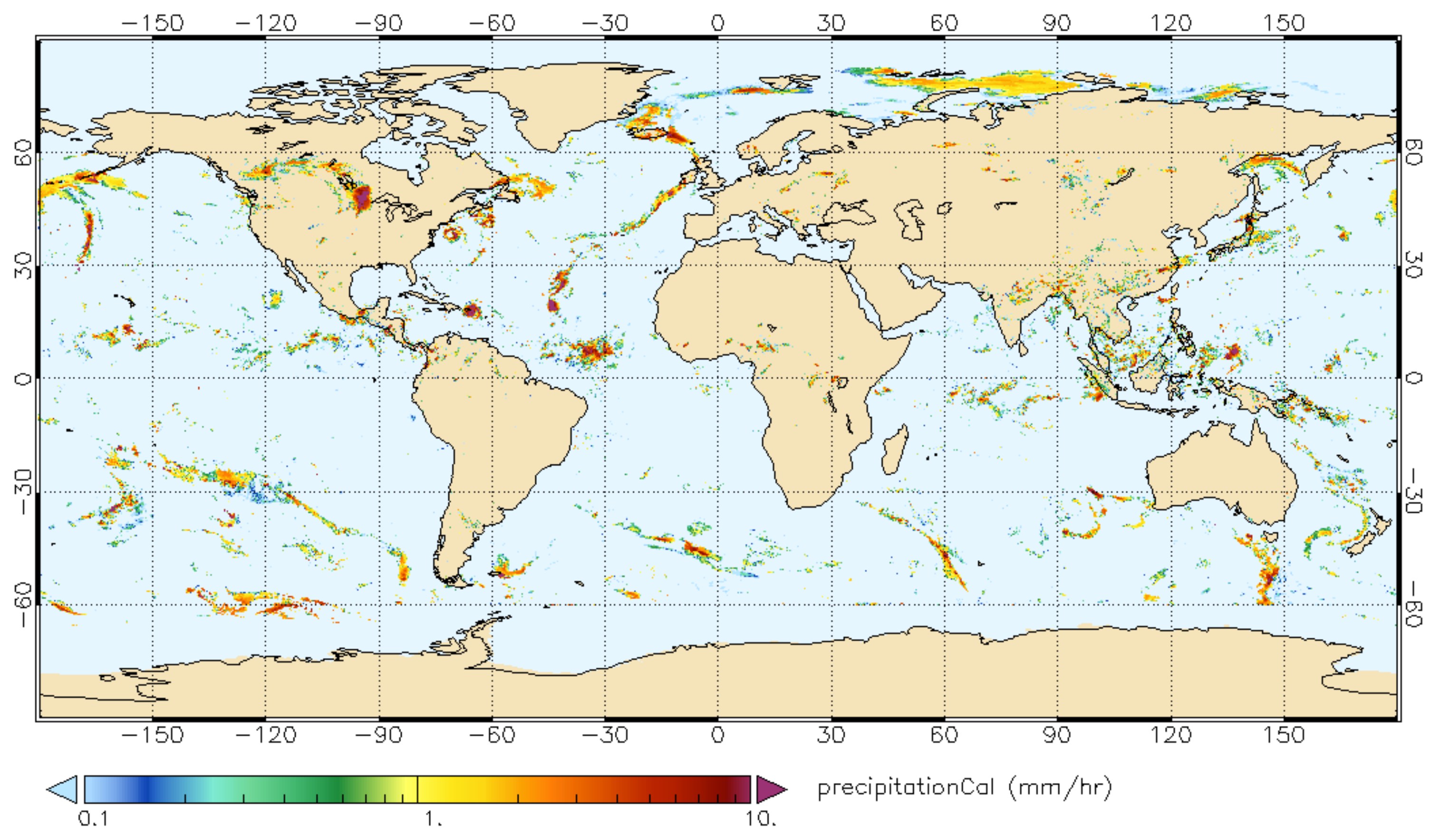




| Channel | NO. | Abbrev. | Bands (μm) | Detection |
|---|---|---|---|---|
| Visible | 1 | V1 | 0.47063 | Vegetation, aerosol, color image (blue) |
| 2 | V2 | 0.51000 | Vegetation, aerosol, color image (green) | |
| 3 | VS | 0.63914 | Vegetation, low clouds and fog, color image (red) | |
| Near Infrared | 4 | N1 | 0.85670 | Vegetation, aerosol |
| 5 | N2 | 1.6101 | Cloud phase | |
| 6 | N3 | 2.2568 | Cloud condensation nuclei radius | |
| Infrared | 7 | I4 | 3.8853 | Low clouds and fog, spontaneous fire |
| 8 | WV | 6.2429 | Upper troposphere water vapor density | |
| 9 | W2 | 6.9410 | Middle to upper troposphere water vapor density | |
| 10 | W3 | 7.3467 | Middle troposphere water vapor density | |
| 11 | MI | 8.5926 | Cloud phase, Sulfur dioxide | |
| 12 | O3 | 9.6372 | Ozone | |
| 13 | IR | 10.4073 | Cloud image, cloud top information | |
| 14 | L2 | 11.2395 | Cloud image, sea surface temperature | |
| 15 | I2 | 12.3806 | Cloud image, sea surface temperature | |
| 16 | CO | 13.2807 | Cloud top height |
| Precipitation Intensity (mm/h) | Proportion (%) | Precipitation Level |
|---|---|---|
| <0.5 | 90.47 | No/Hardly noticeable |
| 0.5–2 | 5.58 | Light |
| 2.0–5.0 | 2.46 | Light to moderate |
| 5.0–10 | 0.93 | Moderate |
| >10 | 0.56 | Heavy |
| Ground Truth | |||
|---|---|---|---|
| 1 | 0 | ||
| Prediction | 1 | Hits (TP) | False Alarm (FP) |
| 0 | Miss (FN) | Ignored (TN) | |
| Metrics | Threshold (mm/h) | Others | Baseline | Ours | |||
|---|---|---|---|---|---|---|---|
| PERSIANN-CNN [28] | Two-stage [30] | U-Net [41] | U-Net +CA | U-Net +CA+CC | U-Net+CA +CC+CBIM | ||
| Precision | 0.5 | 0.6722 | 0.73 | 0.7325 | 0.7286 | 0.738 | 0.7439 |
| 2 | 0.6723 | 0.7085 | 0.7148 | 0.7185 | 0.7298 | 0.7335 | |
| 5 | 0.6382 | 0.6832 | 0.6743 | 0.6799 | 0.6964 | 0.6995 | |
| 10 | 0.6114 | 0.6669 | 0.6408 | 0.646 | 0.6708 | 0.6907 | |
| Recall | 0.5 | 0.6268 | 0.7078 | 0.6742 | 0.6858 | 0.6979 | 0.7247 |
| 2 | 0.5302 | 0.6367 | 0.6237 | 0.6305 | 0.6486 | 0.6756 | |
| 5 | 0.4148 | 0.5484 | 0.5479 | 0.5529 | 0.5776 | 0.6175 | |
| 10 | 0.3366 | 0.4717 | 0.4758 | 0.4826 | 0.4974 | 0.5096 | |
| F1 | 0.5 | 0.6497 | 0.7187 | 0.7022 | 0.7066 | 0.7174 | 0.7342 |
| 2 | 0.5928 | 0.6707 | 0.6661 | 0.6713 | 0.6869 | 0.7034 | |
| 5 | 0.5054 | 0.6085 | 0.6046 | 0.6098 | 0.6315 | 0.6559 | |
| 10 | 0.4342 | 0.5526 | 0.5461 | 0.5524 | 0.5712 | 0.5865 | |
| Model | RMSE | Correlation | Ratio Bias |
|---|---|---|---|
| PERSIANN-CCS [23] | 1.7388 | 0.4853 | 0.8321 |
| PERSIANN-CNN [28] | 1.3584 | 0.6019 | 0.8274 |
| Two-stage [30] | 1.2321 | 0.6674 | 0.8531 |
| U-Net [41] | 1.2366 | 0.6648 | 0.8289 |
| U-Net+CA | 1.2228 | 0.6705 | 0.8413 |
| U-Net+CA+CC | 1.1829 | 0.6880 | 0.8527 |
| U-Net+CA+CC+CBIM | 1.1592 | 0.6966 | 1.0959 |
| Model | Single U-Net | MTCF | ||
|---|---|---|---|---|
| Classification | Estimation | Classification | Estimation | |
| Precision | 0.5263 | 0.6743 | 0.7055 | 0.6995 |
| Recall | 0.5405 | 0.5479 | 0.6169 | 0.6175 |
| F1 | 0.5331 | 0.6046 | 0.6582 | 0.6559 |
| Threshold (mm/h) | 0.01 | 0.5 | 2 | 5 | 10 | |
|---|---|---|---|---|---|---|
| Precision | 0.5 | 0.749 | 0.7329 | 0.7516 | 0.7439 | 0.7411 |
| 2 | 0.7414 | 0.7258 | 0.7285 | 0.7335 | 0.7138 | |
| 5 | 0.6891 | 0.6853 | 0.6793 | 0.6995 | 0.668 | |
| 10 | 0.6483 | 0.6521 | 0.649 | 0.6907 | 0.6448 | |
| Recall | 0.5 | 0.7149 | 0.7692 | 0.702 | 0.7247 | 0.6998 |
| 2 | 0.6331 | 0.6598 | 0.6922 | 0.6756 | 0.6651 | |
| 5 | 0.5688 | 0.5693 | 0.5994 | 0.6175 | 0.6001 | |
| 10 | 0.5071 | 0.4964 | 0.5004 | 0.5096 | 0.534 | |
| F1 | 0.5 | 0.7316 | 0.7506 | 0.726 | 0.7342 | 0.7143 |
| 2 | 0.6814 | 0.6912 | 0.7099 | 0.7034 | 0.6855 | |
| 5 | 0.6232 | 0.6219 | 0.6369 | 0.6559 | 0.63 | |
| 10 | 0.5691 | 0.5637 | 0.5773 | 0.5865 | 0.5821 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Sun, P.; Zhang, F.; Du, Z.; Liu, R. Multi-Task Collaboration Deep Learning Framework for Infrared Precipitation Estimation. Remote Sens. 2021, 13, 2310. https://doi.org/10.3390/rs13122310
Yang X, Sun P, Zhang F, Du Z, Liu R. Multi-Task Collaboration Deep Learning Framework for Infrared Precipitation Estimation. Remote Sensing. 2021; 13(12):2310. https://doi.org/10.3390/rs13122310
Chicago/Turabian StyleYang, Xuying, Peng Sun, Feng Zhang, Zhenhong Du, and Renyi Liu. 2021. "Multi-Task Collaboration Deep Learning Framework for Infrared Precipitation Estimation" Remote Sensing 13, no. 12: 2310. https://doi.org/10.3390/rs13122310
APA StyleYang, X., Sun, P., Zhang, F., Du, Z., & Liu, R. (2021). Multi-Task Collaboration Deep Learning Framework for Infrared Precipitation Estimation. Remote Sensing, 13(12), 2310. https://doi.org/10.3390/rs13122310






