Abstract
Remotely sensing data have advantages in filling spatiotemporal gaps of in situ observation networks, showing potential application for monitoring floods in data-sparse regions. By using the water level retrievals of Jason-2/3 altimetry satellites, this study estimates discharge at a 10-day timescale for the virtual station (VS) 012 and 077 across the midstream Yangtze River Basin during 2009–2016 based on the developed Manning formula. Moreover, we calibrate a hybrid model combined with Gravity Recovery and Climate Experiment (GRACE) data, by coupling the GR6J hydrological model with a machine learning model to simulate discharge. To physically capture the flood processes, the random forest (RF) model is employed to downscale the 10-day discharge into a daily scale. The results show that: (1) discharge estimates from the developed Manning formula show good accuracy for the VS012 and VS077 based on the improved Multi-subwaveform Multi-weight Threshold Retracker; (2) the combination of the GR6J and the LSTM models substantially improves the performance of the discharge estimates solely from either the GR6J or LSTM models; (3) RF-downscaled daily discharge demonstrates a general consistency with in situ data, where NSE/KGE between them are as high as 0.69/0.83. Our approach, based on multi-source remotely sensing data and machine learning techniques, may benefit flood monitoring in poorly gauged areas.
1. Introduction
A flood is the sudden rise of water volume caused by heavy rain, rapid melting of ice/snow and storm surges [1]. As one of the most destructive weather-related hazards, flood has caused huge adverse impacts on infrastructures and the ecosystem [2,3]. Under climate warming and anthropogenic activities, frequency and intensity of floods have substantially intensified in the recent decades, suggesting a pressing need to better monitor flood processes for sustainable development. Gauge stations can provide accurate measurements of river discharge at point scale, facilitating both flood warning and water resources monitoring, which contribute to a better understanding of the water cycle process [4,5]. However, the distribution of hydrological stations is sparse, and the number of observation stations worldwide has decreased continuously due to considerable financial and material costs [6,7]. Considering the unique advantages that covering inaccessible regions and ones not affected by extreme hydrological events, the remote sensing technologies provide a preferable tool to evaluate river discharge, particularly in poorly gauged areas [8]. In this context, multiple remote sensing platforms have been used to return adequate streamflow observations.
This study classified methods to generate discharge data using remote sensing data into two main categories. The first category exploits statistical relation between discharge and some indices sensitive to discharge regardless of the hydraulic features of rivers. This kind of method was initially developed by Brakenridge et al. [9], who calculated the ratio of Advanced Microwave Scanning Radiometer (AMSR-E) band values between a stable pixel located outside the river for calibration (C) and a pixel within the river for measurement (M). Subsequently, the empirical regression between C/M ratio series and observed discharge series can be used to derive discharge data. The advantages of microwave data that are not impacted by weather and cloud layer enabled many scientists to evaluate discharge based on microwave sensors [10,11,12]. Alternatively, as one of the most widely used optical satellite data, the near infrared (NIR) band of Moderate Resolution Imaging Spectroradiometer (MODIS) sensors can identify the grid cells within and outside the river by distinctive reflectance values, and their ratio was also exploited to estimate discharge in medium-sized catchments (area < 10,000 km2) [13,14]. Landsat data were also utilized to generate discharge because of fine resolution (30 m) and long duration (~50 years up to present) [15]. Considering the long visit period of 16 days of Landsat series satellites, the two Sentinel-2 satellites launched in 2015 and 2017 have managed to provide high-quality optical images with spatial resolution ranging from 10 to 60 m and a cycle period between 3 and 5 days [16,17].
Elsewhere, the second type of method relies on the correlation between river discharge and retrievals of hydraulic parameters, including water level, water surface width, as well as water surface area [18,19]. Many previous studies validated the discharge estimation potential of MODIS images as they can effectively detect changes in water surface width and inundation extent [20,21]. Water extent from spaceborne optical and microwave sensors were also used to derive river discharge globally [22]. Even though designed for measuring sea level, radar altimetry satellites additionally provide adequate water level information for inland rivers, wetlands and lakes, which is the most important variable to estimate discharge. Launched in 1992, the TOPEX/POSEIDON satellite has demonstrated the ability to monitor water levels in the Ganga-Brahmaputra Basin [23]. Subsequently Santos da Silva et al. [24] used ERS-2 data to estimate water level time series over rivers of very different widths (from < 100 m to several kilometers). As the successor of the ERS-2 mission, the water level observations from the ENVISAT satellite over the Amazon Basin were validated by Frappart et al. [25]. Getirana et al. [26] further accessed the discharge from ENVISAT water level retrievals over the Amazon Basin by using the Multi-objective Complex Evolution optimization algorithm. During the 11-year travel between 2002 and 2012, the ENVISAT satellite supported estimating discharge experiments using radar altimetry data all around the Earth [27,28]. Moreover, Jason series satellites that have observed the Earth surface since 2001 provide a strong tool to estimate continuous discharge at a short revisit period of 10 days. Tourian et al. [29] accessed Jason-1 samplings and produced accurate water levels for the Congo, Mississippi, and Danube Rivers, with an average correlation of 0.7 and a Nash–Sutcliffe efficiency coefficient of 0.5. Sichangi et al. [30], furthermore, used Jason-1 data as well as other remote sensing products to estimate continental river basin discharges globally. Jason-2 and Jason-3 also presented good discharge estimation performance with a state-of-the-art Poseidon-3 altimeter [31,32]. In recent years, the retrieved water levels from newly-launched Sentinel-3 (i.e., Sentinel-3A and Sentinel-3B) altimetry satellites were validated by comparing with in situ measurements [33,34], and the assessment of their discharge estimating potential was also conducted by Zakharova et al. [35]. The upcoming (~2022) Surface Water and Ocean Topography (SWOT) satellite is expected to produce high-resolution surface water knowledge, including water level and slope, which will provide a great innovation for estimating discharge [36,37]. Alternatively, the Gravity Recovery and Climate Experiment (GRACE) satellite and its following mission (i.e., GRACE Follow-On) have provided monthly global terrestrial water storage anomalies (TWSA) since 2002. Dinh and Fllipe [38] found that water volume change evaluated from GRACE TWSA was highly correlated to river discharge with correlations ranging from 0.77 to 0.88 over the Amazon River Basin. Chen et al. [39] and Xie et al. [40] also declared that TWSA data from GRACE satellites were essential to estimate discharge at a monthly and seasonal time scale, by comparing with simulations and in situ measurements. Based on the fact that the above-mentioned studies merely focused on single data sources, the combination of Jason-2/3 altimetry satellites and the GRACE mission in this study will greatly improve the discharge estimation.
However, as simple and practical estimating discharge from space is, the discontinuous observations and coarse-resolution of remote sensing data challenge their application in flood monitoring. Hence, combining remote sensing data with hydrological models is fundamental to produce continuous discharge data for poorly gauged catchments. Michailovsky et al. [41] assimilated radar altimetry data to a routing model and improved its performance. Hulsman et al. [42] used altimetry observations and GRACE data to select parameter sets of a hydrological model in a data-scarce catchment of Zambia. Assimilation of future pre-SWOT data clearly corrected hydrological models on a global and continental scale, by reducing discharge errors from ~30% to ~24% [43]. The remote sensing-enabled hydrological simulation has been conducted across many basins [44,45]. Furthermore, revolutionary advances in machine learning methods have demonstrated great potential in streamflow prediction. For example, Cheng et al. [46] established three machine learning models involving Artificial Neural Network (ANN), Support Vector Regression, and Long Short-Term Memory (LSTM) to predict discharge fluctuation in North China, and satisfactory accuracy was obtained. Gauch et al. [47] applied the multi-timescale LSTM model to 516 basins over the continental United States and achieved a significantly better runoff simulation performance than the US National Water Model. Machine learning models have been used to discharge modeling with remarkable success [48]. Several studies developed the so-called hybrid modeling approach by coupling physical-models with machine learning techniques to improve the modeling performance [49,50]. The so-called hybrid models exploit the predictive ability of physical models, then harvest available data to correct modeling bias [51]. Alternatively, the flood generation is a complex interacting phenomena, which is inherently characterized by peak discharge, flood volume and hydrograph shape, particularly in natural hazard risk assessment and water resources management [52]. The daily streamflow extremes, having a high correlation with peak discharge, represent a key readily available measure of extreme storms and are frequently used to assess flood hazard risk. However, most of the existing studies only derive the ten-day streamflow, which cannot be used for representing a flood event.
Although a few studies have estimated discharge using either remotely sensing data or a hybrid model across many basins, some shortcomings still exist, including: (1) their joint application has not been systematically validated; (2) the temporal resolution is too coarse for water management and water risk assessment. Therefore, the objectives of this study are to: (1) estimate river discharge using water level retrievals from satellite altimetry based on the improved Multi-subwaveform Multi-weight Threshold Retracker and the developed Manning formula; (2) develop a hybrid hydrological model using satellite-based discharge and other remotely sensing datasets (e.g., GRACE TWSA, rainfall) by coupling a GR6J model with a LSTM model; (3) statistically downscale the hydrological simulations into a daily scale using the Random Forest method.
2. Methods and Data
2.1. Study Area
The Yangtze River Basin controls a drainage area of about 1,800,000 km2. High-mountain regions dominate the upper reach of the Yangtze River Basin and the very high-altitude results in the problem that the antenna needs to be very large in order to distinguish individual radar waveforms reflected by the water surface. In addition, the lower reach of the Yangtze River Basin characterized by a developed shipping and port industry [53] is likely to affect the reflection of echoes with high uncertainty [54]. Free from the impact of extremely high-altitude and intense human activities, this study focused on the middle reach of the Yangtze River Basin located between Zhicheng and Huangshigang (ZHY) because the river here is generally wider than 1000 m, and so it is feasible to extract water surface signals from radar waves (see Figure 1). Moreover, the ZHY is located downstream from the Three Gorges Dam with a total storage capacity of 39.3 km3, facing high flood risk in the context of increasing precipitation extremes. The flood intensity has changed from decadal to inter-decadal cycles due to the rapid expansion of urban populations, high shrinkage of river and lake systems, and fast construction of water facilities [55]. In addition, changes in flood frequency show an overall increasing trend in the ZHY over the past 50 years [56]). Hydrological simulation using remote sensing technologies is of great significance for the reduction of financial and life losses in flood disasters, particularly in the data-limited region [57]. This study divided the ZHY into three sub-basins, consisting of the poorly gauged Hanjiang River Basin (sub-basin 1), the Dongting Lake Basin (sub-basin 3) with sparse stations, and the remaining area within the ZHY (sub-basin 2). Moreover, two ground tracks of Jason-2/3 satellites were selected to derive the water level at the virtual station (VS) 012 and the VS077 along the Yangtze River. The hydrological records at the Zhicheng station near the VS012 and the Huangshigang station near the VS077 were used for comparison (see Figure 1).
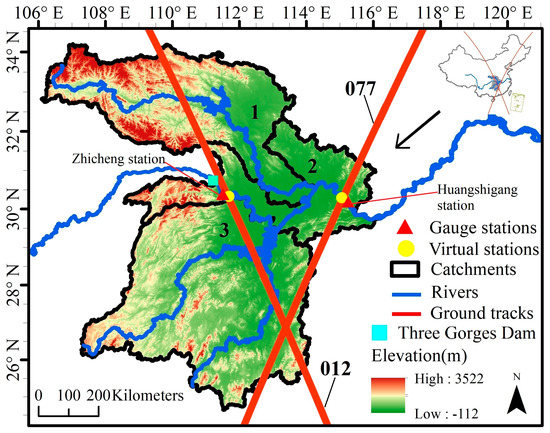
Figure 1.
Location of the Zhicheng–Huangshigang reach of the Yangtze River (ZHY) Basin and the ground track 012 and 077 of Jason-2/3 satellites.
2.2. Methods
The overall implementation details of our experiments are demonstrated in Figure 2. We aim to apply a satellite-derived water level to estimate river discharge and further calibrate the GR6J hydrological model to produce continuous discharge; then, improve the modeling results using the Long Short-Term Memory model combined with GRACE TWSA before downscaling the results into a daily time scale based on the random forest method. Different from the conventional offline downloading method, Google Earth Engine (GEE) was used to extract regional precipitation, potential evaporation, and air temperature in the ZHY from GPM and ERA-interim datasets. GEE is a freely available cloud computing platform for scientific analysis and visualization of geospatial datasets. Specifically, the open-source QGIS software is used for spatial analysis and map preparation and the GEE Code Editor requires the JavaScript Application Programming Interface (API) to communicate with the data catalogue. The powerful cloud servers and petabytes, and publicly available remote sensing archived datasets of GEE, enable a planetary-scale environmental data analysis, greatly reducing the computation cost of academic users [58].
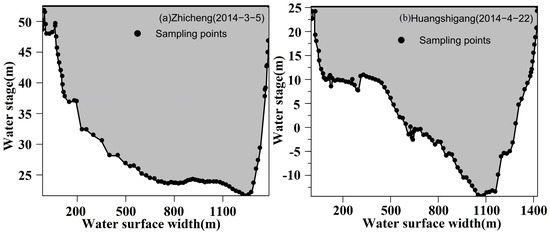
Figure 2.
River cross-section at (a) the Zhicheng station (left panel) measured on 5 March 2014 and (b) the Huangshigang station (right panel) measured on 22 April 2014.
2.2.1. Improved Multi-Subwaveform Multi-Weight Threshold Retracker
To avoid land contaminations as much as possible, this study exploited the high-resolution cloud-free Landsat-8 images of the VS012 and VS077 between November and April to exclude footprints outside the river bank, which is called footprint selection in Figure 3. Moreover, the raw waveform selection was conducted using the pulse peakiness (PP) index proposed by Strawbridge and Laxon [59] to select the waveforms that show dominant peaks and consistent peak locations. The PP index is defined as follows:
where denotes the maximum power of the waveform, and represents the return power of the sampling gate; is the number of sampling gates (104 for Jason-2/3). The waveforms with a PP index lower than 1.2 are discarded due to the difficulty of extracting water surface height information from them [60].
Figure 3.
Work chain considered in this study.
Yuan et al. [60] proposed the Multi-subwaveform Multi-weight Threshold Retracker (MSMWTR) method to improve the quality of satellite altimetry data. The MSMWTR method first identifies subwave forms, then derives a retracking gate using the threshold algorithm for each one [61] and obtains the subwaveform retracked ranges for water level extraction. The major novelty of the MSMWTR method is calculating the weight for each subwaveform as Equation (2); hence, the abnormal outliers can be removed by inspecting the relative weight of each subwaveform artificially.
where is the number of subwaveforms; represents the return power at the sampling gate of the subwaveform.
Although the MSMWTR method performed well in the middle reach of the Yangtze River [60], the approach relied heavily on manual intervention to remove the outlies. Hence, this study can improve the original MSMWTR method as follows:
- (1)
- Set an empirical threshold (0.5) after repeated experiments.
- (2)
- Implement the MSMWTR algorithm and exclude the subwaveform retracked ranges whose weight is lower than the threshold for each cycle.
- (3)
- Recalculate the weight for each subwaveform and perform steps (2–3) iteratively until no sampling points are excluded under the designated threshold.
- (4)
- Apply the Concentrated Probability Density Function (CPDF) method to detect outliers in each cycle and consider the median of remaining samples as the final range [62].
The improved MSMWTR method relies less on manual intervention and has the potential to be used in poorly gauged regions, as any prior knowledge about the river is not required. After resolving the satellite altimetry range, water level retrievals can be calculated as follows:
where represents the derived water level (m, asl), means the altitude of the satellite, and is the retracked range., , , , and are the corrections of dry tropospheric, wet tropospheric, ionospheric, solid Earth tide, and polar tide, respectively. denotes the EGM96 geoid. All correction items, the altitude of the satellite, and the EGM96 geoid are included in the SGDRs product of Jason-2 and Jason-3 satellites.
2.2.2. Developed Manning Formula
The Manning formula can be expressed as follows:
where is the discharge (m3/s) and represents the Manning roughness factor; A denotes the cross-section area of the flow (m2), R is the hydraulic radius (m) and S denotes the slope of the energy gradient of the river channel. The Manning formula considers the hydraulic geometry of the river and estimates river discharge simply and feasibly. Figure 2 presents the measured cross-sections of the Zhicheng station (near the VS012) and the Huangshigang station (near the VS077). We assume that the cross-sections between the two locations keep a similar width-to-depth radio and approximately belong to the trapezoidal shape, and the bed level in the ZHY is known. Moreover, based on the fact that an accurate estimation of discharge can be achieved without inputting the Manning roughness factor and the difficulty of measuring the changing slope of the energy gradient along the river channel [18], the slope and roughness coefficient in the Manning formula were considered as constants. Hence, the developed Manning formula by Huang et al. [63] for trapezoidal cross-section was applied as follows:
where represents the influence of water surface slope and the roughness coefficient, is the elevation of the river bottom, and denotes the water level retrievals from satellite radar altimetry. Parameters and are calibrated using the least square method combined with a few in situ discharges from between 2008 and 2010.
The trained Manning formula was employed to estimate discharge using water levels from satellite altimetry. It is noted that the developed Equation (5) is only feasible for poorly gauged areas with prior information in bed level and cross-sections of the river but not for ungauged sites.
2.2.3. Hybrid Model
The GR6J hydrological model is a lumped, conceptual, and parsimonious model with six parameters to identify, which is simple and feasible that only requires precipitation, air temperature and potential evapotranspiration as inputs, and has been widely used due to the comparable performance to other more complex models over various catchments worldwide [64,65].
The LSTM model is capable of overcoming the weakness of the traditional recurrent neural network (e.g., vanishing and exploding gradients) to learn long-term dependencies. As a special kind of recurrent neural network structure, the LSTM model is one of the most popular neural network models in nonlinear time series analyses because it can store and relate previous information in a sequence, enabling it to predict time series in near real-time. LSTM has been widely used in hydrological simulation and prediction, extreme flood monitoring, and precise water resource management [66,67].
Combining hydrological simulation with machine learning technologies has been validated effective to improve the accuracy of stream flow simulations [68]. The discharge modeling based on the hybrid model was carried out from 2009 to 2016 due to the data gap and the decomposition of the GRACE mission. As illustrated in Figure 2, the rainfall-runoff model GR6J [69] was firstly applied for regional stream flow modeling for the whole of ZHY. The input variables were: the satellite-based discharge at the VS012 that flows into the sub-basin 2 using the developed Manning formula, IMERG Final precipitation, air temperature and potential evaporation from ERA5. The discharge estimates based on the developed Manning formula at the VS077 was used to calibrate the GR6J model. The datasets from 2009 to 2012 (~%50 of samples) were used for training the GR6J hydrological model and those from 2013 to 2016 (~%50 of samples) were used for testing the model’s performance. Subsequently, the Long Short-Term Memory model (LSTM) method was employed to improve the discharge modeling accuracy of the GR6J hydrological model. The inputs of the LSTM model compromise GRACE TWSA for the sub-basin 1 and sub-basin 3 representing the water volume flowing into the mainstream of the Yangtze River, GR6J-modeled discharge at the VS077, and remote sensing meteorological forcing data (i.e., GPM precipitation, ERA air temperature, and ERA potential evapotranspiration) for the whole of the ZHY. Satellite-based discharge at the VS077 was still used to train the LSTM model for direct comparison with the simulations not coupled with the LSTM model. Similarly, the datasets between 2009 and 2013 were spilt as training (2009 to 2012, ~%50 of samples) and testing (2013 to 2016, ~%50 of samples) periods, respectively. In addition, we designed another experiment solely using the LSTM model to evaluate the performance improvement of the hybrid model compared with the GR6J and LSTM model, respectively. We note that the datasets and experiment setting of the single LSTM model were the same as the GR6J hydrological model. Moreover, for the single GR6J and LSTM model, as well as the hybrid model, the flow discharge data at the Huangshigang gauge station (near the VS077) were used for comparison.
2.2.4. Random Forest Model
The 10-day discharge time series from the hybrid model is generally too infrequent for flood simulation. Therefore, this study applied the random forest (RF) model to downscale simulated discharge data into the daily scale based on the strong statistical correlation between river height from spaceborne radar altimeters and the difference between daytime and nighttime land surface temperatures [70]. Random forest (RF) regression is an ensemble learning method based on classification and regression trees (CART). Each tree computes bootstrap samples chosen randomly from the predictor dataset at each node so the RF model can produce reasonable predictions by averaging the results of CARTs [71,72]. As the RF models do not require specific distributional assumptions of the original dataset and have an easy implementation, they have been widely used in the statistical downscaling field [73]. This study established the RF model between simulated discharge and three predictors, including the maximum skin temperature (i.e., at 14 p.m.), the minimum skin temperature (i.e., at 4 a.m.), together with the difference between them (see Figure 3).
2.2.5. Performance Metrics
Discharge estimation performance metrics were accessed by the correlation coefficient (CC), Nash–Sutcliffe efficiency coefficient (NSE) [74], the Kling–Gupta efficiency (KGE) [75], the normalized root mean square error (NRMSE), and the relative bias (BIAS):
where and are the simulated and observed discharge, respectively. Similarly, / and / represent the mean value and the standard deviation of /, respectively. is the number of discharge simulations.
The NRMSE and BIAS were used to quantify the relative deviations of the estimates from the observations considering the distance between the VS and hydrological stations. The CC ranging from to 1, NSE ranging from to 1 and KGE changes between 0 and 1 were applied for evaluation of the model performance. The closer CC, NSE and KGE were to 1, the better the models perform.
2.3. Data
2.3.1. Jason-2/3 Missions
As the successor of Jason-1, Jason-2 was launched in 2008 with the Poseidon-3 radar altimeter on board. The sensor geophysical data records (SGDRs) of the Jason-2 satellite from the CNES Archiving, Validation and Interpretation of Satellite Oceanographic (AVISO+) team, including ranges, waveforms, geo-physical, and atmospheric corrections during 2008–2016 were obtained to retrieve water level at a high sampling rate of 20 Hz. The waveforms from the SGDRs were retracked using the improved MSMWTR algorithm proposed in this study [60] (refer to Section 2.2.1 for details) to improve the accuracy of water level retrievals at the VS012 and VS077 (see Figure 1). Jason-3 inherited the orbit of Jason-2 after its launch in 2016, with Jason-2 being shifted into an interleaved orbit and continuing functioning until 2019; this, increased the spatial coverage of the Jason altimetry series to some degree, with Poseidon-3B being the main instrument [76]. The water level retrievals of water level at the VS012 and VS077 between 2016 and 2019 were obtained from Jason-3 SGDRs data, and their waveforms were retracked using the improved MSMWTR algorithm for higher accuracy. The revisit period of the Jason-2/3 satellites is 10 days; hence, the sub-monthly knowledge of water level can be derived.
2.3.2. ITSG-Grace 2018 Product
This study used daily GRACE TWSA to improve hydrological simulations (see Figure 3). Solved by Graz University of Technology, the ITSG-Grace2018 gravity field product provides unrestricted daily GRACE solutions processed from GRACE-measured Level-1B data. As the GRACE data coverage within one day is not sufficient to resolve the global gravity field, the daily ITSG-Grace2018 solution was stabilized using an autoregressive model of order three in order to recover sub-monthly gravity variations, which was derived by fitting coefficients to the de-aliasing error estimates contained in the ESA’s Earth system model and the de-trended residuals of land surface discharge model [77]. For each day of the observation period, a set of spherical harmonic coefficients for degrees ranging from 2 to 40 were estimated. The adjustment delivered daily solutions, even if there were no GRACE data available for a specific day. The daily solution shares the same signal definition as the official monthly GRACE products. They contain the full hydrological, cryospheric and GIA signal. The atmosphere and ocean signals are relative to AOD1B RL06 [78,79]. The daily TWSA data were resampled with 10-day intervals to be consistent with Jason-2/3 data.
2.3.3. Forcing Data for the Hydrologic Model
The daily remote sensing precipitation dataset used for hydrological simulation is from the Global Precipitation Measurement (GPM) mission, which is an international network of satellites that provide next-generation global observations of rain and snow. The Core Observatory satellite of the GPM, launched in February 2014, carried out the Dual-frequency Precipitation Radar and GPM Microwave Imager instruments to generate a global precipitation dataset. The Integrated Multi-Satellite Retrievals (IMERG) algorithm was employed to merge microwave-calibrated infrared satellite estimates, satellite microwave precipitation estimates, and in situ precipitation data with fine accuracy and consistency all over the globe [80]. The GPM IMERG Final version 06 product was applied with a 3-month latency. Moreover, the daily precipitation dataset from the GPM mission was with a high spatial resolution of 0.1° × 0.1°, which showed good applicability and high accuracy in the Yangtze River Basin [81]. Alternatively, daily potential evaporation (mm) and air temperature (K) from ERA-interim reanalysis datasets were used in this study for hydrological modeling, which contains physical data for atmospheric and surface analyses since 1979 based on the European Centre for Medium-Range Weather Forecasts’ Integrated Forecast System Release Cy31r2 [82]. The daily precipitation, potential evaporation, and air temperature data were resampled with 10-day intervals, with radar altimetry observations. We also calculated the maximum and the minimum air temperature of the day from hourly ERA-interim product to downscale 10-day period discharge into a daily timescale using the random forest method [70].
2.3.4. In Situ Measurement
We collected in situ observations of water level and river discharge at the Zhicheng station (near the VS012, see Figure 1) and the Huangshigang station (near the VS077, see Figure 1). The in situ data follow a strict quality control policy. The measurements were used mainly to validate water level retrievals from Jason-2/3 data and corresponding discharge estimations. In addition, a 3-year discharge time series was applied to fit hydrodynamic parameters in the developed Manning formula (refer to Section 2.2.2 for details).
3. Results
3.1. Discharge Estimation Based on Satellite Altimetry Data
Figure 4 presents satellite-derived water level time series at the VS012 and the VS077, and water level measurements at the Zhicheng station (near the VS012) and the Huangshigang station (near the VS077) were used for comparison. The results show that water level retrievals of Jason-2/3 satellites are generally consistent with observed series, particularly in the wet season between May and October as the waveforms are less noisy with obvious dominant peaks and consistent peak locations [60]. Contrarily, the obvious underestimation during the dry season between November and April suggests more noise and various peak locations among waveforms. We furthermore established the developed Manning formula using the satellite-based water level and a few in situ observed discharges between 2008 and 2010; simulated discharge between 2011 and 2019 were used for testing. Figure 5 shows the calibration and validation results of the developed Manning formula and relative performance metrics are summarized in Table 1.
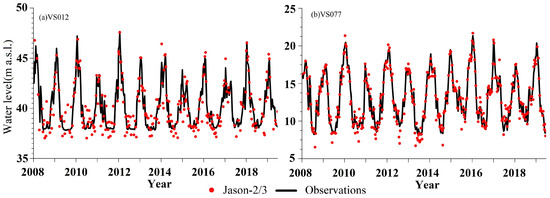
Figure 4.
Water level retrievals (m a.s.l.) of satellite radar altimetry at (a) VS012 and (b) VS 077 between 2008 and 2019.
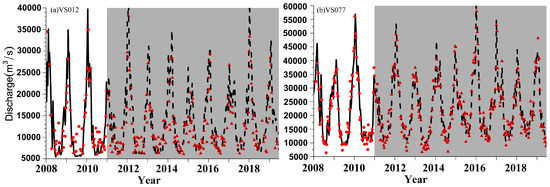
Figure 5.
Simulated discharge from satellite radar altimetry at (a) VS012 and (b) VS077 between 2008 and 2019. Note: The white background area is the calibration results of the developed Manning formula and the grey shaded area represents the validation results. The black solid and dashed lines represent the observed discharge during the calibration and validation periods, respectively; the red circle and triangle mean the simulated results during the calibration and validation periods, respectively.

Table 1.
Comparison between simulated discharge from satellite radar altimetry at VS012 and VS 077 between 2008 and 2019.
At the VS012, the trained model overestimates discharge during the dry season with a CC of 0.88 between 2008 and 2010, and the NSE and KGE reaches 0.74 and 0.83, respectively (see Table 1). The poorer model performance during the test period is because of the underestimation of streamflow peaks during the wet season (CC/NSE/KGE = 0.75/0.66/0.70). However, the developed Manning formula presents better performance at the VS077 with CC, NSE and KGE as high as 0.97, 0.93 and 0.96 during the calibration period. The trained model illustrates continuous satisfactory performance during the test period according to Table 1, although some underestimation during the dry season still occurs because of the water level bias. Figure 6 presents the scatter plot between the satellite-estimated discharge and the in situ measurements during the whole period during 2009–2019. The results indicate that the fitted linear regression line at the VS012 is with a slope of 0.88 and the corresponding correlation coefficient of 0.91, and a stronger linear relationship (CC = 0.96) between estimates of discharge and observations is discovered at the VS077, consistent with the calibration and validation results for the VS012 and VS077.
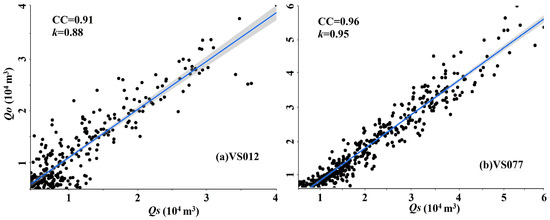
Figure 6.
Scatter plots between simulated discharge from the Manning formula and observed discharge during 2008–2019. Note: The blue line is the fitted linear regression line and the blue shaded area denotes its 95% confidence interval. k is the slope of the linear regression line.
3.2. Hydrological Simulation Using a Hybrid Model
Figure 7 presents discharge estimates from the GR6J, LSTM and hybrid models as well as observations for the ZHY from 2009 to 2016. The comparison indicates that the LSTM model outperforms the GR6J model, especially during the dry season. In addition, discharge data from the hybrid model are generally in better agreement with in situ data than that solely from either the GR6J or LSTM model, which is consistent with the scatter plot and Tayler diagram between simulations and observations in Figure 8. A stronger correlation was discovered between in situ discharge and hybrid model results (CC = 0.96) than the GR6J results (CC = 0.92) and LSTM data (CC = 0.92). Table 2 summarizes the performance metrics of the GR6J, LSTM and hybrid models during the high flows period (May to October) and low flows period (November to April) together with the period 2009–2016, which show the comprehensive improvements of discharge simulations after coupling with the LSTM model. The CC, KGE and NSE of the hybrid model increases by 3.4/3.4%, 1.1/2.1 % and 8.4/3.4% more than the GR6J/LSTM model, respectively, during the period 2009–2016. A noticeable decrease in NRMSE of 14.3/25.0% and BIAS of 13.3/23.5% was detected by comparing with the GR6J/LSTM model, respectively between 2009 and 2016. In addition, the hybrid model also outperforms the GR6J and LSTM model during the high flows and low flows period.
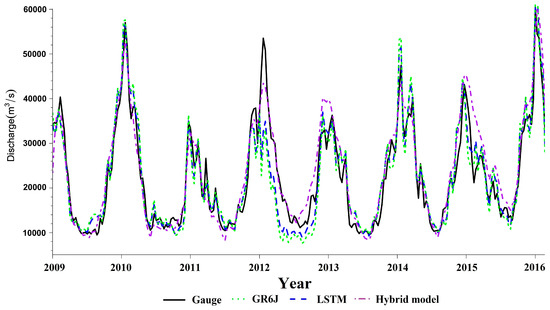
Figure 7.
Estimated flow discharges by the GR6J model, LSTM model, and hybrid model at the VS077, and the observed flow discharges at the Huangshigang station between 2009 and 2016.
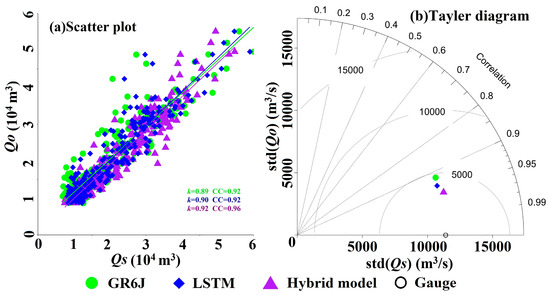
Figure 8.
(a) Scatter plots and (b) Tayler diagram between estimated flow discharges by the GR6J, LSTM and hybrid models at the VS077, and observed flow discharges at the Huangshigang station during 2009–2016. Note: The green, blue, and purple lines in subfigure (a) indicate the fitted linear regression lines between estimated flow discharges by the GR6J, LSTM, and hybrid models, and observed flow discharges.

Table 2.
Comparison between estimated flow discharges by the GR6J, LSTM and hybrid models at the VS077, and observed discharges at the Huangshigang station during 2009–2016.
3.3. Downscaling of Modeling Results at a Daily Timescale
Figure 9a demonstrates the comparison between downscaled discharge simulated by the hybrid model at the VS077 and in situ data at the Huangshigang station from 2009 to 2016. The daily streamflow is generally consistent with in situ results although some underestimations during the flood peaks exist. The KGE and NSE between downscaling results and in situ data are as high as 0.83 and 0.69, with NRMSE and BIAS of 0.15 and 21%, respectively. In addition, the scatter plots between discharge simulations and observations in Figure 9b indicate a strong linear relationship (CC = 0.87) between them.
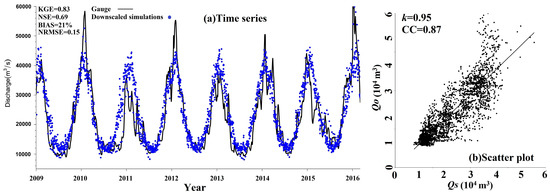
Figure 9.
(a) Time series and (b) scatter plot between downscaled discharges from the hybrid model at the VS077 and observed discharges at the Huangshigang station during 2009–2016. Note: The discharge data was normalized and divided by the maximum discharge for intuitive comparison. The black line in subfigure (b) indicates the fitted linear regression line. k is the slope of the linear regression line.
4. Discussion
A few previous studies have simulated discharge using either remote sensing data or hydrological models in the Yangtze River Basin. Xu et al. [83] used very high-resolution QuickBird-2 data to establish a width-discharge curve and estimate flow discharge in the Yangtze River with high accuracy. However, the method heavily relies on the spatial resolution and data quality of satellite images. Based on the accurate water level retrievals of satellite altimetry data over the Yangtze River [84], Sichangi et al. [85] initially combined satellite altimetry-derived water level and MODIS-derived river width to estimate flow discharge at the Datong gauge station in the Yangtze River between 2003 and 2008. However, the accuracy of discharge estimations is relatively lower (NSE = ~0.5) than this study, with NSE ranging from 0.66 to 0.93. Chen et al. [86] also successfully estimated total basin discharge solely based on remote sensing data, including TRMM precipitation, GRACE TWSA, and MODIS images of the Yangtze River Basin during 2003–2012. Although achieving a reasonable accuracy with correlation coefficient of 0.89 and RMSE of ~5900 m3/s, the monthly discharge estimations are too infrequent to support flood simulation. Alternatively, the discharge prediction ability of hydrological models has been comprehensively validated across many sub-basins of the Yangtze River Basin [87,88]. However, these works mainly applied observed discharge to calibrate the models; hence, experiments in some poorly gauged regions (e.g., upper reach of the Yangtze River Basin) are rarely carried out previously. In addition, Xu et al. [89] applied the LSTM model to model river flow in the upper reach of the Yangtze River and achieved better performance compared with several hydrological models. Liu et al. [90] tested several deep learning neural networks, including the LSTM and the Empirical Mode Decomposition model in the ZHY and achieved good forecasting accuracy in terms of NSE and RMSE because of the powerful capacity in learning non-linear and complex processes of machine learning technologies. Nevertheless, the hydrological models and machine learning methods are mostly employed for comparison rather than combination.
Even though our developed approach successfully generated daily outlet discharge for the ZHY between 2009 and 2016 using remote sensing data and the hybrid model, some limitations still exist as follows: (1) Satellite radar altimetry observations are difficult to extract the water height signals of the rivers located on high-mountain regions due to the very high-altitude and complicated topography, which challenge the applications of our algorithm in such kind of basins. Huang et al. [63] developed a combined waveform retracker to retrieve water levels in the upstream Brahmaputra River Basin with high mountains, while the method showed poor performance in the Yangtze River due to intense human activities. Moreover, the coarse spatial resolution of GRACE TWSA restricts the discharge estimation ability of our approach in medium-sized basins [91]. Advanced post-processing methods, including mass concentration blocks and constrained forward modeling, can enable the small-scale hydrological applications such as: flood and drought monitoring, groundwater depletion detection, and mass balance of Greenland and Antarctica [92]. It is still interesting to establish the skill of the adopted algorithm in smaller rivers that has higher confidence in discharge measurements, which will be further investigated and fully evaluated in the near future after solving the above-mentioned problems. (2) Multistep post-processing dynamics of our developed approach generated uncertainty in data, parameters, and structures of the developed Manning formula, GR6J model, and machine learning methods. Quantifying uncertainty contribution of each model and dataset is fundamental for our better understanding of hydrological forecasting mechanism, which will be further investigated and fully evaluated in the near future using uncertainty analysis tools such as analysis of variance [93]. (3) Due to the relatively short operation life of the Jason-2/3 satellite from 2009 up to present day, and the GRACE mission between April 2002 and June 2017, the length of the discharge series in this study is limited. Combining multi-source satellite data, including Envisat, TOPEX/Poseidon, and SARAL missions may be beneficial to overcome this shortage. Moreover, the SWOT satellite that is expected to launch in late 2021 will produce high-resolution surface water knowledge, including water level and slope, providing a great innovation for estimating discharge [36]. In addition, the in-orbit GRACE Follow-On satellite has provided accurate monthly TWSA data around the world since June 2018. The reconstruction of the historical satellite data and accumulation of the future satellite data will greatly extend our study time span [94].
5. Conclusions
This study estimated discharge using the water level retrievals from satellite radar altimetry based on the developed Manning formula at the VS012 and VS077 across the Yangtze River between 2008 and 2019, and further used the satellite-based discharge to calibrate the GR6J model. Subsequently, the LSTM method was employed to improve the hydrological modeling results combined with GRACE TWSA. Finally, the 10-day discharge time series at the outlet of the ZHY was statistically downscaled into a daily scale using the RF approach. The main conclusions of this study are summarized as follows:
- (1)
- The developed Manning formula shows an effective discharge estimation ability at the VS012 and the VS077. The fitted linear regression line between discharge estimates and in situ observations at the VS012 is with a slope of 0.88 and CC of 0.91 between them. A stronger linear relationship between estimated and observed flow discharges was discovered at the VS077 (k/CC = 0.95/0.96).
- (2)
- The hybrid model clearly shows the improvements of discharge estimation in comparison with either the sole GR6J or LSTM models. The CC, KGE and NSE of the hybrid model increased by 3.4/3.4%, 1.1/2.1% and 8.4/3.4% more than the GR6J/LSTM models, respectively. In addition, a noticeable decrease in NRMSE of 14.3/25.0% and BIAS of 13.3/23.5% was detected by comparing with the GR6J/LSTM models, respectively.
- (3)
- The RF-downscaled daily flow discharge is generally consistent with in situ results, although some underestimations during the flood peaks exist. The KGE and NSE between downscaled results and in situ data are as high as 0.83 and 0.69 with NRMSE and BIAS of 0.15 and 21%, respectively. A strong correlation (CC = 0.87) exists between them.
Author Contributions
Conceptualization, J.X. and S.G.; methodology, J.Y.; software, J.X.; validation, J.X., J.Y. and S.G.; writing—review and editing, J.X.; supervision, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, (U20A20317, 52009091), the Natural Science Foundation of Hubei Province (2020CFB239) and the “111 Project” Fund of China (B18037).
Acknowledgments
The authors wish to express their gratitude to all the authors of the numerous technical reports used for this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barredo, J.I. Major flood disasters in Europe: 1950–2005. Nat. Hazards 2007, 42, 125–148. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Wetherald, R.T.; Dunne, K.A.; Delworth, T. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Zhou, S.; Sullivan, S.C.; Wang, R.; Zhang, Y.; Guo, S. Large increase in global storm runoff extremes driven by climate and anthropogenic changes. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef]
- Shao, Z.; Fu, H.; Li, D.; Altan, O.; Cheng, T. Remote sensing monitoring of multi-scale watersheds impermeability for urban hydrological evaluation. Remote Sens. Environ. 2019, 232, 111338. [Google Scholar] [CrossRef]
- Puttock, A.; Graham, H.A.; Cunliffe, A.M.; Elliott, M.; Brazier, R.E. Eurasian beaver activity increases water storage, attenuates flow and mitigates diffuse pollution from intensively-managed grasslands. Sci. Total Environ. 2017, 576, 430–443. [Google Scholar] [CrossRef]
- Schumann, C.M.; Bloss, C.; Barnes, C.C.; Wideman, G.M.; Carper, R.A.; Akshoomoff, N.; Pierce, K.; Hagler, D.; Schork, N.; Lord, C.; et al. Longitudinal Magnetic Resonance Imaging Study of Cortical Development through Early Childhood in Autism. J. Neurosci. 2010, 30, 4419–4427. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, C.; Yang, S.; Liu, C.; Xiang, H.; Sun, Y.; Yang, Z.; Zhang, Y.; Yu, X.; Shao, N.; et al. Calculating e-flow using UAV and ground monitoring. J. Hydrol. 2017, 552, 351–365. [Google Scholar] [CrossRef]
- Lopez, T.; Al Bitar, A.; Biancamaria, S.; Güntner, A.; Jäggi, A. On the Use of Satellite Remote Sensing to Detect Floods and Droughts at Large Scales. Surv. Geophys. 2020, 41, 1–27. [Google Scholar] [CrossRef]
- Brakenridge, G.R.; Nghiem, S.V.; Anderson, E.; Mic, R.-P. Orbital microwave measurement of river discharge and ice status. Water Resour. Res. 2007, 43, W04405. [Google Scholar] [CrossRef]
- Revillaromero, B.; Thielen, J.; Salamon, P.; De Groeve, T.; Brakenridge, G.R. Evaluation of the satellite-based Global Flood Detection System for measuring river discharge: Influence of local factors. Hydrol. Earth Syst. Sci. 2014, 18, 4467–4484. [Google Scholar] [CrossRef]
- Temimi, M.; Lacava, T.; Lakhankar, T.; Tramutoli, V.; Ghedira, H.; Ata, R.; Khanbilvardi, R. A multi-temporal analysis of AMSR-E data for flood and discharge monitoring during the 2008 flood in Iowa. Hydrol. Process 2011, 25, 2623–2634. [Google Scholar] [CrossRef]
- Khan, S.I.; Hong, Y.; Gourley, J.J.; Khattak, M.U.; De Groeve, T. Multi-Sensor Imaging and Space-Ground Cross-Validation for 2010 Flood along Indus River, Pakistan. Remote Sens. 2014, 6, 2393–2407. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Brocca, L.; Lacava, T.; Melone, F.; Moramarco, T.; Faruolo, M.; Pergola, N.; Tramutoli, V. Toward the estimation of river discharge variations using MODIS data in ungauged basins. Remote Sens. Environ. 2013, 136, 47–55. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Amarnath, G.; Brocca, L.; Massari, C.; Moramarco, T. Discharge estimation and forecasting by MODIS and altimetry data in Niger-Benue River. Remote Sens. Environ. 2017, 195, 96–106. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Wang, J.; Hao, X. Extending the ability of near-infrared images to monitor small river discharge on the northeastern Tibetan Plateau. Water Resour. Res. 2019, 55, 8404–8421. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Ayad, M.; Li, J.; Holt, B.; Lee, C. Analysis and Classification of Stormwater and Wastewater Runoff from the Tijuana River Using Remote Sensing Imagery. Front. Environ. Sci. 2020, 8, 599030. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Lawrence, D.S.; Vorosmarty, C.J.; Bolster, C.H.; Congalton, R.G. Evaluating the potential for measuring river discharge from space. J. Hydrol. 2003, 278, 17–38. [Google Scholar] [CrossRef]
- Smith, L.C.; Isacks, B.L.; Bloom, A.L.; Murray, A.B. Estimation of discharge from three braided Rivers using synthetic aperture radar satellite imagery: Potential application to ungauged basins. Water Resour. Res. 1996, 32, 2021–2034. [Google Scholar] [CrossRef]
- Brakenridge, R.; Anderson, E. MODIS-based flood detection, mapping and measurement: The potential for operational hydrological applications. In Transboundary Floods: Reducing Risks Through Flood Management; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–12. [Google Scholar] [CrossRef]
- Smith, L.C.; Pavelsky, T.M. Estimation of river discharge, propagation speed, and hydraulic geometry from space: Lena River, Siberia. Water Resour. Res. 2008, 44, W03427. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Brakenridge, G.R.; Kettner, A.J.; Beck, H.E.; De Groeve, T.; Schellekens, J. River gauging at global scale using optical and passive microwave remote sensing. Water Resour. Res. 2016, 52, 6404–6418. [Google Scholar] [CrossRef]
- Papa, F.; Durand, F.; Rossow, W.B.; Rahman, A.; Bala, S.K. Satellite altimeter-derived monthly discharge of the Ganga-Brahmaputra River and its seasonal to interannual variations from 1993 to 2008. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- da Silva, J.S.; Calmant, S.; Seyler, F.; Filho, O.C.R.; Cochonneau, G.; Mansur, W.J. Water levels in the Amazon basin derived from the ERS 2 and ENVISAT radar altimetry missions. Remote Sens. Environ. 2010, 114, 2160–2181. [Google Scholar] [CrossRef]
- Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Cazenave, A. Preliminary results of ENVISAT RA-2-derived water levels validation over the Amazon basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Boone, A.; Yamazaki, D.; Mognard, N. Automatic parameterization of a flow routing scheme driven by radar altimetry data: Evaluation in the Amazon basin. Water Resour. Res. 2013, 49, 614–629. [Google Scholar] [CrossRef]
- Leon, J.; Calmant, S.; Seyler, F.; Bonnet, M.-P.; Cauhopé, M.; Frappart, F.; Filizola, N.; Fraizy, P. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. J. Hydrol. 2006, 328, 481–496. [Google Scholar] [CrossRef]
- Sulistioadi, Y.B.; Tseng, K.-H.; Shum, C.K.; Hidayat, H.; Sumaryono, M.; Suhardiman, A.; Setiawan, F.; Sunarso, S. Satellite radar altimetry for monitoring small rivers and lakes in Indonesia. Hydrol. Earth Syst. Sci. 2015, 19, 341–359. [Google Scholar] [CrossRef]
- Tourian, M.J.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series by multimission satellite altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef]
- Sichangi, A.W.; Wang, L.; Yang, K.; Chen, D.; Wang, Z.; Li, X.; Zhou, J.; Liu, W.; Kuria, D. Estimating continental river basin discharges using multiple remote sensing data sets. Remote Sens. Environ. 2016, 179, 36–53. [Google Scholar] [CrossRef]
- Paris, A.; De Paiva, R.D.; Da Silva, J.S.; Moreira, D.M.; Calmant, S.; Garambois, P.-A.; Collischonn, W.; Bonnet, M.-P.; Seyler, F. Stage-discharge rating curves based on satellite altimetry and modeled discharge in the Amazon basin. Water Resour. Res. 2016, 52, 3787–3814. [Google Scholar] [CrossRef]
- Kim, D.; Yu, H.; Lee, H.; Beighley, E.; Durand, M.; Alsdorf, D.E.; Hwang, E. Ensemble learning regression for estimating river discharges using satellite altimetry data: Central Congo River as a Test-bed. Remote Sens. Environ. 2019, 221, 741–755. [Google Scholar] [CrossRef]
- Huang, Q.; Li, X.; Han, P.; Long, D.; Zhao, F.; Hou, A. Validation and application of water levels derived from Sentinel-3A for the Brahmaputra River. Sci. China Technol. Sci. 2019, 62, 1760–1772. [Google Scholar] [CrossRef]
- Kittel, C.M.M.; Jiang, L.; Tøttrup, C.; Bauer-Gottwein, P. Sentinel-3 radar altimetry for river monitoring—A catchment-scale evaluation of satellite water surface elevation from Sentinel-3A and Sentinel-3B. Hydrol. Earth Syst. Sci. 2021, 25, 333–357. [Google Scholar] [CrossRef]
- Zakharova, E.; Nielsen, K.; Kamenev, G.; Kouraev, A. River discharge estimation from radar altimetry: Assessment of satellite performance, river scales and methods. J. Hydrol. 2020, 583, 124561. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT mission and its capabilities for land hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Oubanas, H.; Gejadze, I.; Malaterre, P.O.; Mercier, F. River discharge estimation from synthetic SWOT-type observations using variational data assimilation and the full Saint-Venant hydraulic model. J. Hydrol. 2018, 559, 638–647. [Google Scholar] [CrossRef]
- Dinh, T.L.A.; Filipe, A. River discharge estimation based on satellite water extent and topography: An application over the Amazon. J. Hydrometeorol. 2019, 20, 1851–1866. [Google Scholar] [CrossRef]
- Chen, Y.; Fok, H.S.; Ma, Z.; Tenzer, R. Improved remotely sensed total basin discharge and its seasonal error characterization in the Yangtze River Basin. Sensors 2019, 19, 3386. [Google Scholar] [CrossRef]
- Xie, J.; Xu, Y.P.; Gao, C.; Xuan, W.; Bai, Z. Total basin discharge from GRACE and water balance method for the Yarlung Tsangpo River basin, Southwestern China. J. Geophys. Res. Atmos. 2019, 124, 7617–7632. [Google Scholar] [CrossRef]
- Michailovsky, C.I.B.; Milzow, C.; Bauer-Gottwein, P. Assimilation of radar altimetry to a routing model of the Brahmaputra River. Water Resour. Res. 2013, 49, 4807–4816. [Google Scholar] [CrossRef]
- Hulsman, P.; Winsemius, H.C.; Michailovsky, C.I.; Savenije, H.H.G.; Hrachowitz, M. Using altimetry observations combined with GRACE to select parameter sets of a hydrological model in a data-scarce region. Hydrol. Earth Syst. Sci. 2020, 24, 3331–3359. [Google Scholar] [CrossRef]
- Sly, W.-C.; Rodrigo, C.D.; Sylvain, B.; Walter, C. Assimilation of future SWOT-based river elevations, surface extent observations and discharge estimations into uncertain global hydrological models. J. Hydrol. 2020, 590, 125473. [Google Scholar] [CrossRef]
- Brinkerhoff, C.B.; Gleason, C.J.; Feng, D.; Lin, P. Constraining Remote River Discharge Estimation Using Reach-Scale Geomorphology. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Pathak, J.; Wikner, A.; Fussell, R.; Chandra, S.; Hunt, B.R.; Girvan, M.; Ott, E. Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model. Chaos 2018, 28, 041101. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Qiao, X.; Shi, Y.; Wang, D. Machine learning for predicting discharge fluctuation of a karst spring in North China. Acta Geophys. 2021, 69, 257–270. [Google Scholar] [CrossRef]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nearing, G.; Lin, J.; Hochreiter, S. Rainfall–runoff prediction at multiple timescales with a single Long Short-Term Memory network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Karpatne, A.; Watkins, W.; Read, J.; Kumar, V. Physicsguided Neural Networks (PGNN): An application in lake temperature modeling. arXiv 2017, arXiv:1710.11431. [Google Scholar]
- Yin, J.; Guo, S.; Gentine, P.; Sullivan, S.C.; Gu, L.; He, S.; Chen, J.; Liu, P. Does the hook structure constrain future flood intensification under anthropogenic climate warming? Water Resour. Res. 2021, 57, e2020WR028491. [Google Scholar] [CrossRef]
- Mehdi, K.; Joseph, A. Altimetry-derived surface water data assimilation over the Nile Basin. Sci. Total Environ. 2020, 735, 139008. [Google Scholar] [CrossRef]
- Cui, M.; Guo, Q.; Wei, R.; Chen, T. Temporal-spatial dynamics of anthropogenic nitrogen inputs and hotspots in a large river basin. Chemosphere 2021, 269, 129411. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Nielsen, K.; Dinardo, S.; Andersen, O.B.; Bauer-Gottwein, P. Evaluation of Sentinel-3 SRAL SAR altimetry over Chinese rivers. Remote Sens. Environ. 2020, 237, 111546. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, G. Multiscale Variability of Historical Meteorological Droughts and Floods in the Middle Yangtze River Basin, China. Nat. Hazards Rev. 2020, 21, 04020036. [Google Scholar] [CrossRef]
- Wu, S.; Cao, S.; Wang, Z.; Qu, X.; Li, S.; Zhao, W. Spatiotemporal Variations in Agricultural Flooding In Middle and Lower Reaches of Yangtze River From 1970 to 2018. Sustainability 2019, 11, 6613. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J. Assessing Terrestrial Water Storage and Flood Potential Using GRACE Data in the Yangtze River Basin, China. Remote Sens. 2017, 9, 1011. [Google Scholar] [CrossRef]
- Noel, G.; Matt, H.; Mike, D.; Simon, I.; David, T.; Rebecca, M. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Strawbridge, F.; Laxon, S. ERS-1 altimeter fast delivery data quality flagging over land surfaces. Geophys. Res. Lett. 1994, 21, 1995–1998. [Google Scholar] [CrossRef]
- Yuan, C.; Gong, P.; Zhang, H.; Guo, H.; Pan, B. Monitoring water level changes from retracked Jason-2 altimetry data: A case study in the Yangtze River, China. Remote Sens. Lett. 2017, 8, 399–408. [Google Scholar] [CrossRef]
- Hwang, C.; Guo, J.; Deng, X.; Hsu, H.-Y.; Liu, Y. Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry: Improvement, Limitation and the Role of Airborne Gravity Data. J. Geodesy 2006, 80, 204–216. [Google Scholar] [CrossRef]
- Liu, Z.; Yao, Z.; Wang, R. Evaluation and Validation of CryoSat-2-Derived Water Levels Using In Situ Lake Data from China. Remote Sens. 2019, 11, 899. [Google Scholar] [CrossRef]
- Huang, Q.; Long, D.; Du, M.; Zeng, C.; Qiao, G.; Li, X.; Hou, A.; Hong, Y. Discharge estimation in high-mountain regions with improved methods using multisource remote sensing: A case study of the Upper Brahmaputra River. Remote Sens. Environ. 2018, 219, 115–134. [Google Scholar] [CrossRef]
- Nicolle, P.; Pushpalatha, R.; Perrin, C.; Francois, D.; Thiery, D.; Mathevet, T.; Le Lay, M.; Besson, F.; Soubeyroux, J.-M.; Viel, C.; et al. Benchmarking hydrological models for low-flow simulation and forecasting on French catchments. Hydrol. Earth Syst. Sci. 2014, 18, 2829–2857. [Google Scholar] [CrossRef]
- Crochemore, L.; Isberg, K.; Pimentel, R.; Pineda, L.E.; Hasan, A.; Arheimer, B. Lessons learnt from checking the quality of openly accessible river flow data worldwide. Hydrol. Sci. J. 2020, 65, 699–711. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Computation of evapotranspiration with artificial intelligence for precision water resource management. Appl. Sci. 2020, 10, 1621. [Google Scholar] [CrossRef]
- Lv, N.; Liang, X.; Chen, C.; Zhou, Y.; Li, J.; Wei, H.; Wang, H. A long Short-Term memory cyclic model with mutual information for hydrology forecasting: A Case study in the xixian basin. Adv. Water Resour. 2020, 141, 103622. [Google Scholar] [CrossRef]
- Yang, T.; Sun, F.; Gentine, P.; Liu, W.; Wang, H.; Yin, J.; Du, M.; Liu, C. Evaluation and machine learning improvement of global hydrological model-based flood simulations. Environ. Res. Lett. 2019, 14, 114027. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Hung, T.P.; Lucy, M.; Fiona, J.; Ashish, S. Deriving daily water levels from satellite altimetry and land surface temperature for sparsely gauged catchments: A case study for the Mekong River. Remote Sens. Environ. 2018, 212, 31–46. [Google Scholar] [CrossRef]
- Breiman, L. Using iterated bagging to debias regressions. Mach. Learn. 2021, 45, 261–277. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Chen, L.; He, Q.; Liu, K.; Li, J.; Jing, C. Downscaling of GRACE-Derived Groundwater Storage Based on the Random Forest Model. Remote Sens. 2019, 11, 2979. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Brêda, J.P.L.F.; Paiva, R.C.D.; Bravo, J.M.; Passaia, O.A.; Moreira, D.M. Assimilation of Satellite Altimetry Data for Effective River Bathymetry. Water Resour. Res. 2019, 55, 7441–7463. [Google Scholar] [CrossRef]
- Bergmann-Wolf, I.; Forootan, E.; Klemann, V.; Kusche, J.; Dobslaw, H. Updating ESA’s Earth System Model for Gravity Mission Simulation Studies: 3. A Realistically Perturbed Nontidal Atosphere and Ocan Dealiasing Model, (Scientific Technical Report; 14/09), Potsdam: Deutsches Geo Forschungs Zentrum; GFZ: Berlin, Germany, 2015; 62p. [Google Scholar] [CrossRef]
- Gürr, M.; Behzadpur, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Strasser, S.; Zehentner, N. ITSG-Grace2018-monthly, daily and static gravity field solutions from GRACE. GFZ Data Serv. 2018. [Google Scholar] [CrossRef]
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and evaluation of a new GRACE-only gravity field time series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, J.; Watanabe, M.; Sun, C. Estimating river discharge from very high-resolution satellite data: A case study in the Yangtze River, China. Hydrol. Process. 2004, 18, 1927–1939. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, K.; Yang, Y.; Qi, L.; Hayashi, S.; Watanabe, M. Measuring Water Storage Fluctuations in Lake Dongting, China, by Topex/Poseidon Satellite Altimetry. Environ. Monit. Assess. 2006, 115, 23–37. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.P.; Poli, P.; Brugge, R.; Fielding, M.; Fuentes, M.; Kallberg, P.W.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive Version 2.0; ERA Report Series 1; ECMWF: Shinfield Park, UK, 2011; Available online: https://www.ecmwf.int/node/8174 (accessed on 23 January 2021).
- Sichangi, A.W.; Wang, L.; Hu, Z. Estimation of River Discharge Solely from Remote-Sensing Derived Data: An Initial Study Over the Yangtze River. Remote Sens. 2018, 10, 1385. [Google Scholar] [CrossRef]
- Yin, J.; Guo, S.; Gu, L.; Zeng, Z.; Liu, D.; Chen, J.; Shen, Y.; Xu, C. Blending multi-satellite, atmospheric reanalysis and gauge precipitation products to facilitate hydrological modelling. J. Hydrol. 2021, 593, 125878. [Google Scholar] [CrossRef]
- Wen, S.; Su, B.; Wang, Y.; Zhai, J.; Sun, H.; Chen, Z.; Huang, J.; Wang, A.; Jiang, T. Comprehensive evaluation of hydrological models for climate change impact assessment in the Upper Yangtze River Basin, China. Clim. Chang. 2020, 163, 1207–1226. [Google Scholar] [CrossRef]
- Wu, Y.; Luo, G.; Chen, C.; Duan, Z.; Gao, C. Using Integrated Hydrological Models to Assess the Impacts of Climate Change on Discharges and Extreme Flood Events in the Upper Yangtze River Basin. Water 2021, 13, 299. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Zhang, X.; Li, Y.; Zhang, R.; Fu, G. Using long short-term memory networks for river flow prediction. Hydrol. Res. 2020, 51, 1358–1376. [Google Scholar] [CrossRef]
- Liu, D.; Jiang, W.; Mu, L.; Wang, S. Streamflow Prediction Using Deep Learning Neural Network: Case Study of Yangtze River. IEEE Access 2020, 8, 90069–90086. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Zhang, L.; Yuan, F.; Wang, B.; Ren, L.; Zhao, C.; Shi, J.; Liu, Y.; Jiang, S.; Yang, X.; Chen, T.; et al. Quantifying uncertainty sources in extreme flow projections for three watersheds with different climate features in China. Atmos. Res. 2021, 249, 105331. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q. Water Level Reconstruction Based on Satellite Gravimetry in the Yangtze River Basin. ISPRS Int. J. Geo-Inf. 2018, 7, 286. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).