Abstract
Digital agriculture services can greatly assist growers to monitor their fields and optimize their use throughout the growing season. Thus, knowing the exact location of fields and their boundaries is a prerequisite. Unlike property boundaries, which are recorded in local council or title records, field boundaries are not historically recorded. As a result, digital services currently ask their users to manually draw their field, which is time-consuming and creates disincentives. Here, we present a generalized method, hereafter referred to as DECODE (DEtect, COnsolidate, and DElinetate), that automatically extracts accurate field boundary data from satellite imagery using deep learning based on spatial, spectral, and temporal cues. We introduce a new convolutional neural network (FracTAL ResUNet) as well as two uncertainty metrics to characterize the confidence of the field detection and field delineation processes. We finally propose a new methodology to compare and summarize field-based accuracy metrics. To demonstrate the performance and scalability of our method, we extracted fields across the Australian grains zone with a pixel-based accuracy of 0.87 and a field-based accuracy of up to 0.88 depending on the metric. We also trained a model on data from South Africa instead of Australia and found it transferred well to unseen Australian landscapes. We conclude that the accuracy, scalability and transferability of DECODE shows that large-scale field boundary extraction based on deep learning has reached operational maturity. This opens the door to new agricultural services that provide routine, near-real time field-based analytics.
1. Introduction
Fields shape agricultural landscapes. As a result, their size and distribution can inform about agriculture mechanization [1], human development, species richness [2], resource allocation and economic planning [3,4,5]. Beyond their value as ecological and economical indicators, precise knowledge of the field distribution can help stakeholders across the agricultural sector monitor and manage crop production by enabling field-based analytics [6]. Unlike property boundaries, which are recorded in local council or title records, field boundaries are not historically recorded. As a result, digital services currently ask their users to manually draw their field, which is time-consuming and creates disincentives. The objective of this work is to provide hassle-free access to field boundary data for unlocking field-based applications and insights to the Australian land sector. Given the structuring role of fields in agricultural systems, procurement of field boundary data is essential for the development of modern digital agriculture services. Therefore, efficient tools to routinely generate and update field boundaries are relevant for actors across the data value chain so that they can generate value and useful insights.
Satellite, aerial and drone images are prime sources of data used to automatically generate field boundaries. Aside from manual digitization based on photo interpretation, field boundaries can automatically be extracted by four main types of methods. First, edge-based methods rely on filters to emphasize discontinuities in images, that is, where pixel values change rapidly [7,8,9]. Second, contour-based methods generate curves that move within images to find object boundaries by minimizing some energy function [10]. Third, object-based methods cluster pixels together (i.e., fields) based on their color similarity [9]. Finally, because not all edges are of interest, model-based methods are trained to recognize specific image objects to emphasize certain edges and attenuate others. Models range from simple logistic regression [11] to structured random forest [12], or more sophisticated models such as convolutional neural networks [6,13,14,15,16,17]. Convolutional neural networks have proven particularly accurate because they can learn discriminative hierarchical contextual features from the input images. Thus, the focus of this study is on convolutional neural networks.
Several convolutional neural networks have been proposed to extract field boundaries. Their performance has been demonstrated in a range of cropping systems from smallholder [17] to large-scale commercial cropping systems [6], with <1 m data [18] to 3 m [16,17], 10 and 30 m data [6]. Typically, these convolutional neural networks are trained to predict the presence or absence of field boundaries for each image pixel, i.e., they perform semantic segmentation. However, there is evidence that jointly predicting the task of interest (boundaries) with related tasks (such as the field extent or the distance to the closest boundary) improves prediction accuracy [19], a process known as multitasking. In fact, in a previous study, we demonstrated that multitask learning maintained a high accuracy level when transferred across resolutions, sensors, space and time without recalibration [6]. Such high transferability informed clear guidelines to scale up to larger landscapes. This paper capitalizes and expands on these past results to demonstrate nationwide field boundary extraction.
Semantic segmentation models (and edge-based methods) do not necessarily yield closed boundaries, and additional post-processing is required to define regions with closed contours (and achieve instance segmentation). Examples of post-processing methods include globalized boundary probability estimates, growing contours, thresholding or object-based image analysis [6,17,20,21]. In addition, once boundaries are mapped, one still needs ancillary information to define where the fields are. For instance, Yan and Roy [7] and Graesser and Ramankutty [8] sourced that information from cropland and type maps. While end-to-end instance segmentation methods could extract closed field boundaries in one go, they have not been widely tested for field boundary detection. So far, post-processing solves the problem of open boundaries.
In this paper, we introduce a new method based on deep learning field boundary extraction and demonstrate its performance by extracting fields across Australia. Our method is called DECODE in reference to its three processing steps: DEtection, COnsolidation and DElinetation. Detection is achieved with a state-of-the-art deep convolutional neural network that jointly predicts the extent of the fields, their boundaries and the distance to the closest boundary from single-date images. Consolidation is achieved by averaging single-date predictions over the growing season, thereby integrating temporal cues. Finally, delineation of individual fields is done by post-processing the boundary mask using hierarchical watershed segmentation. Our specific contributions are:
- A deep learning network, the FracTAL ResUNet, tailored for the task of semantic segmentation of satellite images. In particular, our architecture is a multitasking encoder–decoder network, with the same backbone structure as in Waldner and Diakogiannis [6]. The main difference is that we changed the residual building blocks with atrous convolutions with the newest FracTAL ResNet building blocks. FracTAL ResNet building blocks have been recently proposed as part of a change detection network that demonstrated state-of-the-art performance [22];
- Two field-level measures of uncertainty to characterize the semantic (assigning labels to pixels) and instance (grouping pixels together) uncertainty;
- A framework to report and compare field-based accuracy metrics.
Put together, these elements provide an accurate, scalable and transferable framework to extract field boundaries from satellite imagery. To demonstrate the performance of DECODE, we extracted 1.7 million fields across Australia using Sentinel-2 images. Two FracTAL ResUNet models were compared: one trained with data of Australia (the target domain), and the other with data of South Africa (the source domain). As this paper will show, both models yielded accurate results in Australia, which is remarkable since no adjustments were applied to the source-to-target case. This is evidence that our approach generalizes well and can be transferred to other regions.
2. Materials and Methods
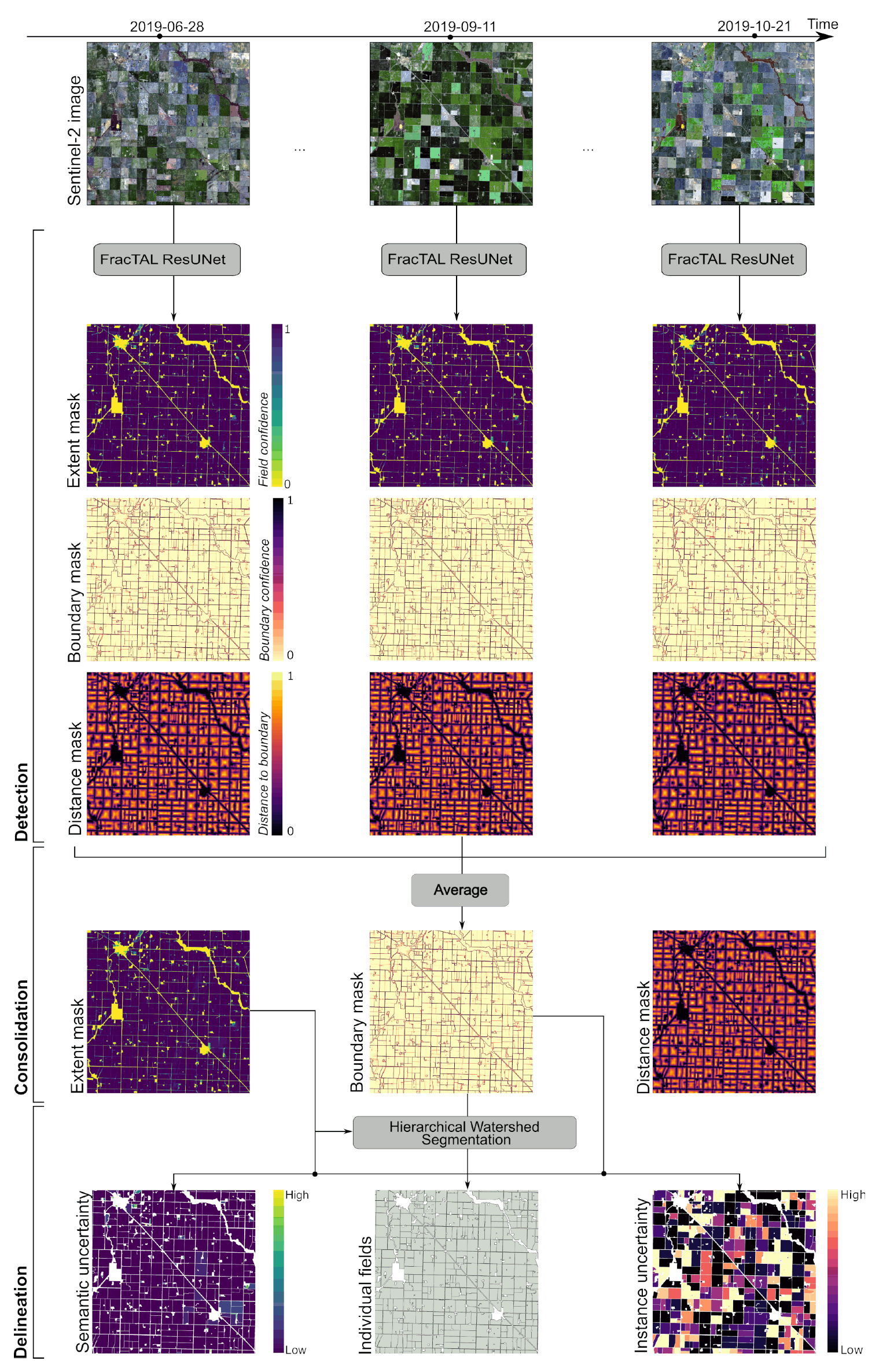
The DECODE method extracts field boundaries from satellite imagery in three sequential steps (Figure 1). The first step (detect) is a semantic segmentation step, where a convolutional neural network, FracTAL ResUNet, assigns multiple labels (field presence, boundary presence and distance to boundary) to image pixels (Section 2.1). The second step (consolidate) averages model predictions obtained for different observation dates so that temporal cues are integrated (Section 2.2). This creates consolidated model predictions from which individual fields can be extracted. The third and final step (delineate) is an instance segmentation step, where image pixels are grouped into individual objects (fields) based on the consolidated network predictions (Section 2.3). During this process, two uncertainty metrics—one that relates to the semantic segmentation step and the other to the instance segmentation step—are computed for each field. Code is available on https://github.com/waldnerf/decode (accessed on 3 May 2021).
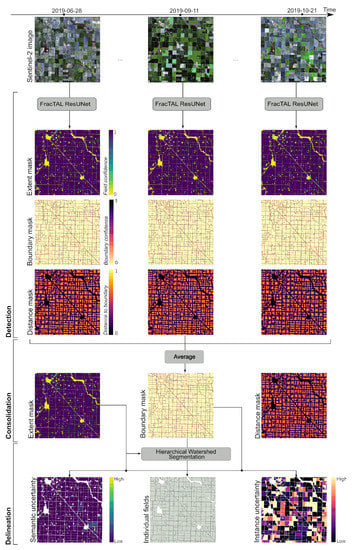
Figure 1.
Field boundary mapping with the DECODE method. Fields are extracted from a stack of single-date satellite images in three sequential steps: (1) semantic segmentation of fields, their boundaries and their distance to the closest boundary with FracTAL ResUNet (detection), single-date model outputs are time averaged (consolidation), and instance segmentation of fields by means of hierarchical watershed segmentation (delineation). Here, Sentinel-2 images (blue, green, red, near-infrared channels) were used as input to the FracTAL ResUNet model.
2.1. Detect: Multi-Task Semantic Segmentation
Semantic segmentation has attracted significant interest in the fields of computer vision and remote sensing, where automatically annotating images is common. In the next paragraphs, we summarize the main contributions leading to this work and we refer to Brodrick et al. [23] for a thorough introduction to convolutional neural networks.
The UNet architecture [24], which introduced the encoder–decoder paradigm, made major breakthroughs in image semantic segmentation. The encoder encodes the input image into feature representations at multiple levels through a series of convolutions, activation functions (such as ReLU activations) and pooling layers. The decoder semantically projects the discriminative features learnt by the encoder onto the pixel space to derive a dense classification through a series of upsampling, concatenation and convolution operations. As networks became increasingly deeper, they became more difficult to train due to vanishing (or exploding) gradients. Residual networks (ResNets) [25] mitigate this problem by introducing skip connections to allow gradient information to pass through layers. As a result, information from the earlier parts of the network flows to the deeper parts, helping maintain signal propagation. Pyramid scene parsing pooling (PSP pooling) [26] was introduced to capture the global context in the image, which helps models classify the pixels based on the global information present in the image. In PSP pooling layers, the feature map is pooled at different scales before passing through a convolution layer. Then, the pooled features are upsampled to make them the same size as the original feature map. Finally, the upsampled maps and the original feature map are concatenated and passed to the decoder. This technique fuses the features at different scales, hence aggregating the overall context. Multitasking, where multiple tasks are simultaneously learned by a model, is another approach to improving generalization. The UNet, residual connections, pyramid scene parsing pooling, and multi-tasking inference were combined in ResUnet-a and showed state-of-the-art performance on very high resolution aerial images [19].
In recent years, attention mechanisms have improved the success of various deep learning models, and continue to be omnipresent in state-of-the-art models. One of those attention mechanisms is self-attention, which quantifies the interdependence within the input elements. Self-attention is a form of “memory” acquired during the training of a network that helps emphasize important features in convolution layers. It was pioneered in the task of neural machine translation [27] where it helped emphasize important words, as well as their relative syntax between different languages, in long sentences. It has been shown consistently to improve performance and it is now a standard in all modern architectures e.g., [28]. Self-attention layers can be combined in multi-head attention layers that jointly learn different representations from different positions. Among the attention modules that have been proposed, the fractal Tanimoto attention layer is memory efficient and scales well with the size of input features. It uses the fractal Tanimoto similarity coefficient as a means of quantifying the similarity between query and key entries. FracTAL ResNet blocks have a small memory footprint and excellent convergence and performance properties that outperform standard ResNet building blocks; see [22] for more details.
In this paper, we introduce FracTAL ResUNet, a convolutional neural network that is largely based on ResUnet-a [19] but where the atrous ResNet blocks are replaced by the more efficient FracTAL ResNet blocks. In the next sections, we describe FracTAL ResUNet in terms of its micro-topology (feature extraction units), macro-topology (backbone) and classification head.
2.1.1. Architecture Micro-Topology
The founding block used for this paper is the FracTAL ResNet unit [22]. It consists of the standard sequence one finds in residual building blocks enhanced by a FracTAL unit (i.e., a channel and spatial self-attention layer). In the FracTAL ResNet, the order of operations is as follows: the input layer () is first subjected to the standard sequence of batch normalization, ReLU activation and 2D convolution operations. This sequence produces an output layer (). The input layer is also subject to the FracTAL unit that produces a self-attention layer (). The input, the output of the residual blocks and the attention layer are fused together with a learnable annealing parameter () initialized at zero when training starts:
Here, ⊙ designates elementwise multiplication. The summation is what one obtains by using a standard residual unit [29]. This residual output is emphasized in an annealing way by the attention layer, . This unit has excellent performance but a small memory footprint, which is critical when dealing with deep architectures and large training data sets.
2.1.2. Architecture Macro-Topology
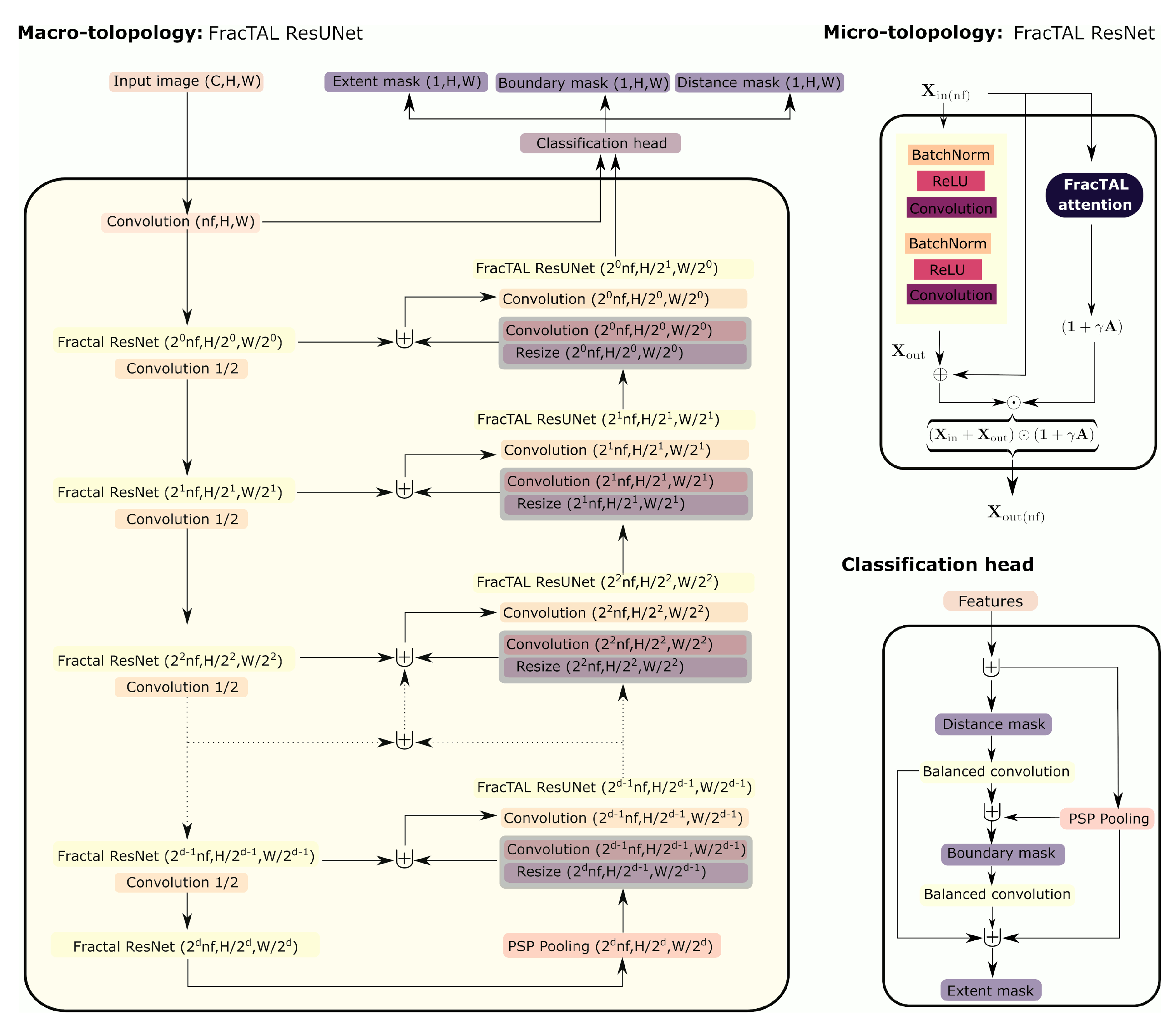
The feature extraction units were inserted in an encoder–decoder scheme similar to the UNet architecture used in Diakogiannis et al. [22] (Figure 2). The input of the encoder is first processed by a normed convolution to bring the number of channels to the desired number of features (without activation). These features are then subjected to a set of FracTAL ResNet units. Between FracTAL ResNet units, the size of the spatial extent is halved and the number of filters doubled. This is achieved with a normed convolution of stride (s = 2; without activation). At the end of the encoder, we apply the pyramid scene parsing pooling operator [30]. This operator provides context information at different scales of the spatial dimensions of the input features (successively, 1, 1/2, 1/4, 1/8) and has been shown to improve performance. In the decoder, features are upscaled using bilinear interpolation followed by a normed convolution. At each level, the upscaled features are first concatenated with the encoder features of the same level. Next, a normed convolution brings these features to a desired size and the output is inserted into the next FracTAL ResNet unit. The final layer of the decoder, as well as the output of the first convolution layer, are the inputs to the classification head.
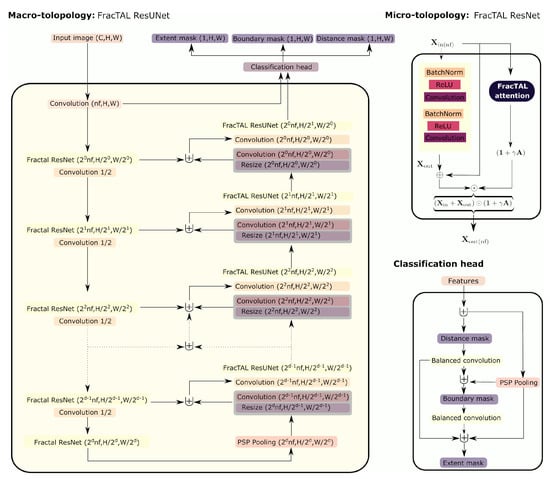
Figure 2.
Components of the FracTAL ResUNet architecture. The network macro-topology shows how feature extraction units (convolution layers, FracTAL ResNet units and PSP pooling layers) are applied to an image input with C channels, and with H and W pixels in y and x dimensions. Here, d corresponds to the depth of the network and corresponds to the initial number of filters. The micro-topology (FracTAL ResNet unit) shows the fusion process between the FracTAL and the sequence of residual blocks. The conditioned multitasking classification head first predicts the distance mask (without PSP Pooling), then uses this information to detect boundaries, and finally, re-uses both estimates to predict the extent mask.
2.1.3. Classification Head
The classification head follows conditioned multitasking [6,19] and is identical to the one presented in Diakogiannis et al. [22]. It first predicts the presence of field boundaries (i.e., the boundary mask). Then, it balances the boundary mask and re-uses it to estimate the distance to the closest field boundary (i.e., distance transform). Here, “balanced” means that the number of output channels (e.g., of the distance mask) was changed to correspond to the number of channels of the input features (usually 32). This scheme weights intermediate prediction layers and feature layers equally, thereby counterbalancing the lesser number of channels in the former. Finally, it re-uses both previous outputs to map the presence or absence of fields (i.e., the extent mask). The number of features in each of these layers was carefully balanced in each of these layers and, for the case of boundaries prediction, a scaled sigmoid activation was introduced, as this sharpens the boundary predictions.
2.1.4. Evolving Loss Strategy
Our training loss was the fractal Tanimoto with complement loss [22]. Assuming that represents one of the predictions of the network (i.e., it is a fuzzy binary vector) and represents the ground truth labels, then the fractal Tanimoto similarity coefficient is defined through:
where:
Here d, represents the depth of the iteration in the fractal definition. The higher the value of d, the finer the similarity between predictions and labels.
This similarity coefficient takes the value 1 when (predictions are perfect) and zero when (no correlation between predictions and ground truth labels). The loss can be defined for minimization problems as the negative of this coefficient:
In this formulation, the loss function admits values in the range . As we optimized three learning tasks jointly, the full loss function was defined as the average of the loss of all tasks:
The training procedure we followed was the evolving loss strategy [22]: starting from fractal depth and an initial learning rate, lr=1.e-3, we increased the depth of the fractal Tanimoto loss each time we reduced the learning rate (Section 2.5.2). This training scheme helps avoid local minima by making the loss landscape steeper towards optimality. It has been shown to improve all statistical metrics; for the case of intersection over union, the improvement was ∼1% performance [22].
2.2. Consolidate: Time Averaging
The outputs of the deep-learning model are three semantic segmentation layers per input image. The consolidate step aims at consolidating single-date predictions while maintaining flexibility (the method still works with a single image). Averaging across observations also significantly increases accuracy, especially when more than four observations are available [6].
2.3. Delineate: Hierarchical Watershed Segmentation
The outputs of the consolidate step are thus three consolidated semantic segmentation layers but individual fields remain to be defined. We achieve instance segmentation by post-processing the boundary mask using hierarchical watershed segmentation.
2.3.1. Hierarchical Watershed Segmentation
Watershed segmentation is one of the most popular image segmentation methods. Consider a grey-scale image as a topographic surface; pixel values correspond to elevation. Valleys appear in dark grays and mountain tops and crest lines appear in light grays. Following the drop of water principle [31], watersheds are defined as groups of pixels from which a drop of water can flow down towards distinct minima.
This intuitive idea has been formalized for defining a watershed of an edge-weighted graph [32]. The graph G is defined as a pair (P, E) where P is a finite set and E is composed of unordered pairs of distinct elements in P [33]. Each element of P is an image pixel, and each element of E is called an edge. The graph G models the image spatial domain: P is the regular 2D grid of pixels and E is the or adjacency relation. Spatial relations have different weights W that the dissimilarity between pixels, so that (G, W) is an edge-weighted graph. A segmentation of P is then defined as a subset of V such that the intersection of any two distinct instances of is empty, and the union of instances of equals V. Thus, one can obtain a sequence of nested segmentations, hence a hierarchy of segmentations.
A hierarchy of watershed segmentations is a nested sequence of coarse to fine instances, which can be shown as a tree of regions [32,34]. Therefore, coarser to finer image instances or objects can be obtained by cutting the hierarchy lower or higher in the tree.
2.3.2. Closing Boundaries with Hierarchical Watershed Segmentation
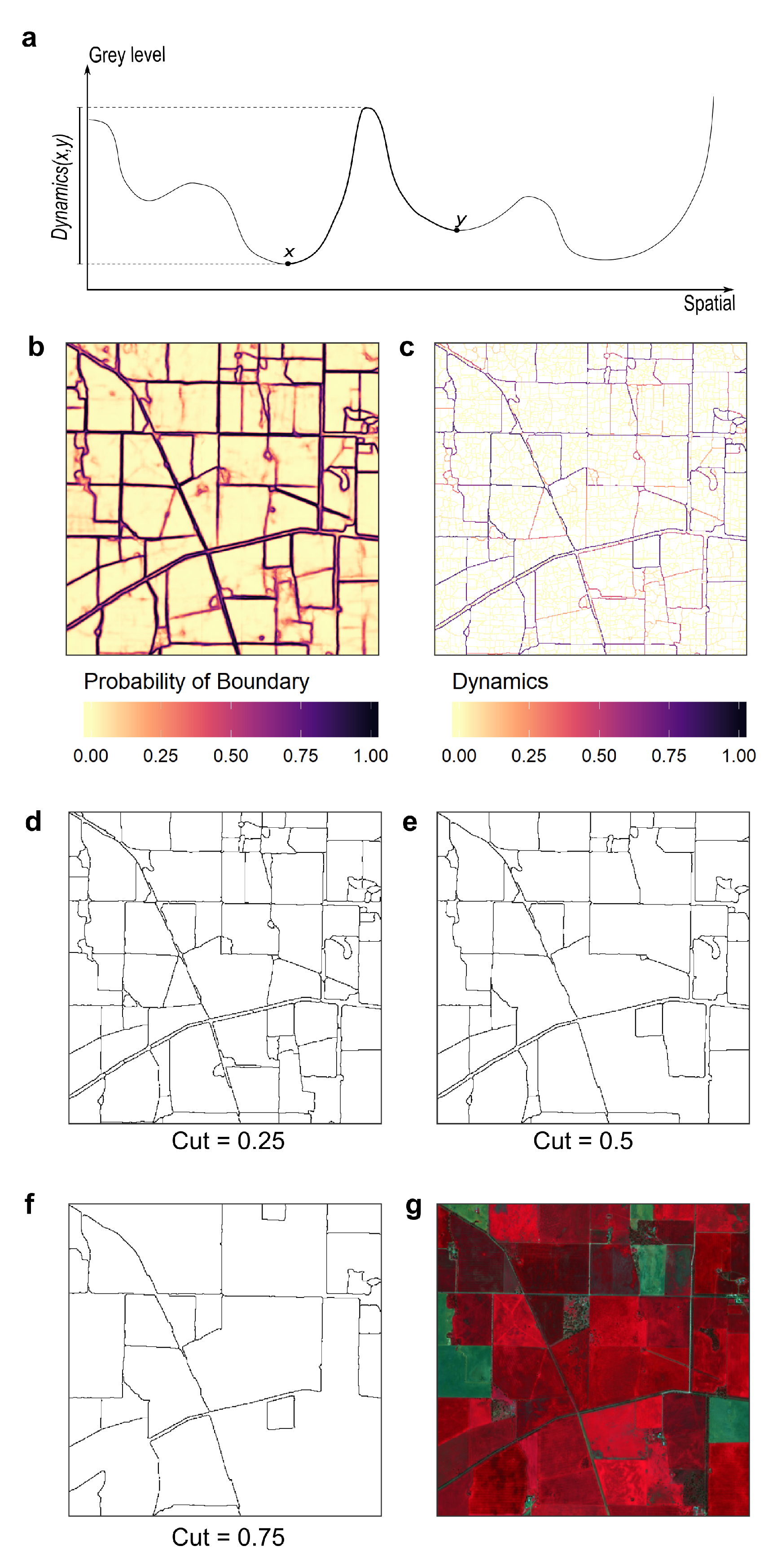
Instance segmentation can be obtained by cutting hierarchical watershed segmentations into k regions at any level of the hierarchy [32]. The resulting segments will have closed boundaries regardless of the threshold use to cut the hierarchy. In this paper, we built a watershed hierarchy based on the boundary mask (Figure 3b,d–f). The weights of the graph edges were measured by their dynamics [35]. The dynamics of a path that links two pixels is the difference in altitude between the points of highest and lowest altitude of the path (Figure 3a). In an image, the dynamics of two pixels is equal to the dynamics of the path with the lowest dynamics (Figure 3c). Once the edge-weighted graph is generated from the boundary mask, instances fields with closed boundaries can be generated by cutting the graph at a specific dynamics ().
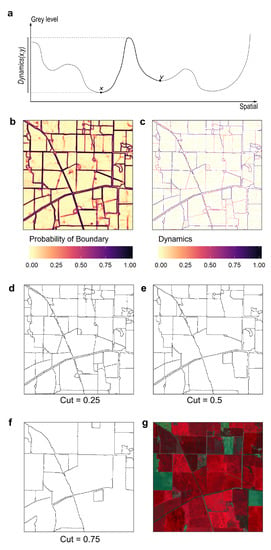
Figure 3.
Defining hierarchical segmentation with the dynamics criterion. (a) Dynamics of two points along a path (the path is illustrative and does not relate to a path on the following figure components), (b) boundary mask as produced by the model, (c) corresponding watershed built with the dynamics criterion, (d–f) cuts of the segmentation hierarchy at different dynamics levels, (g) input model image.
Before constructing the watershed hierarchy, we set another threshold () to binarize the extent mask and define field pixels and non-field pixels. The value of non-field pixels in the boundary mask is then changed to 1, which corresponds to the maximum confidence of having a boundary. This step reduces the occurrence of very small fields. We finally construct the watershed hierarchy and cut it at the desired level. Here, and were defined by trial and error and set to 0.2 and 0.4, respectively.
2.4. Defining Semantic and Instance Uncertainty
Two types of uncertainty can be characterized for each field: the uncertainty related to the identification of the fields (semantic uncertainty) and the uncertainty related to their delineation (instance uncertainty).
We propose to measure semantic uncertainty using the extent mask, which describes the probability of a pixel to belong to a field. Semantic uncertainty is defined as the average normalized difference between the extent probabilities of all pixels in a field and the threshold value:
where ranges between 0 and 1 and values close to 1 indicate a high uncertainty of the detection process.
Fields must have closed boundaries. Confidence in these boundaries relates to the uncertainty of the pixels making up these boundaries. We propose to measure instance uncertainty using the concept of dynamics that was introduced previously. Pixels with high dynamics were identified as boundary pixels with high confidence, and conversely for low dynamics. Therefore, if defines the ensemble of boundary pixels of a specific field, instance uncertainty can be derived from the boundary pixel with the lowest dynamics (i.e., the weakest link between boundary pixels):
where ranges between 0 and 1 and values close to 1 indicate a high uncertainty of the delineation process.
2.5. Experimental Design
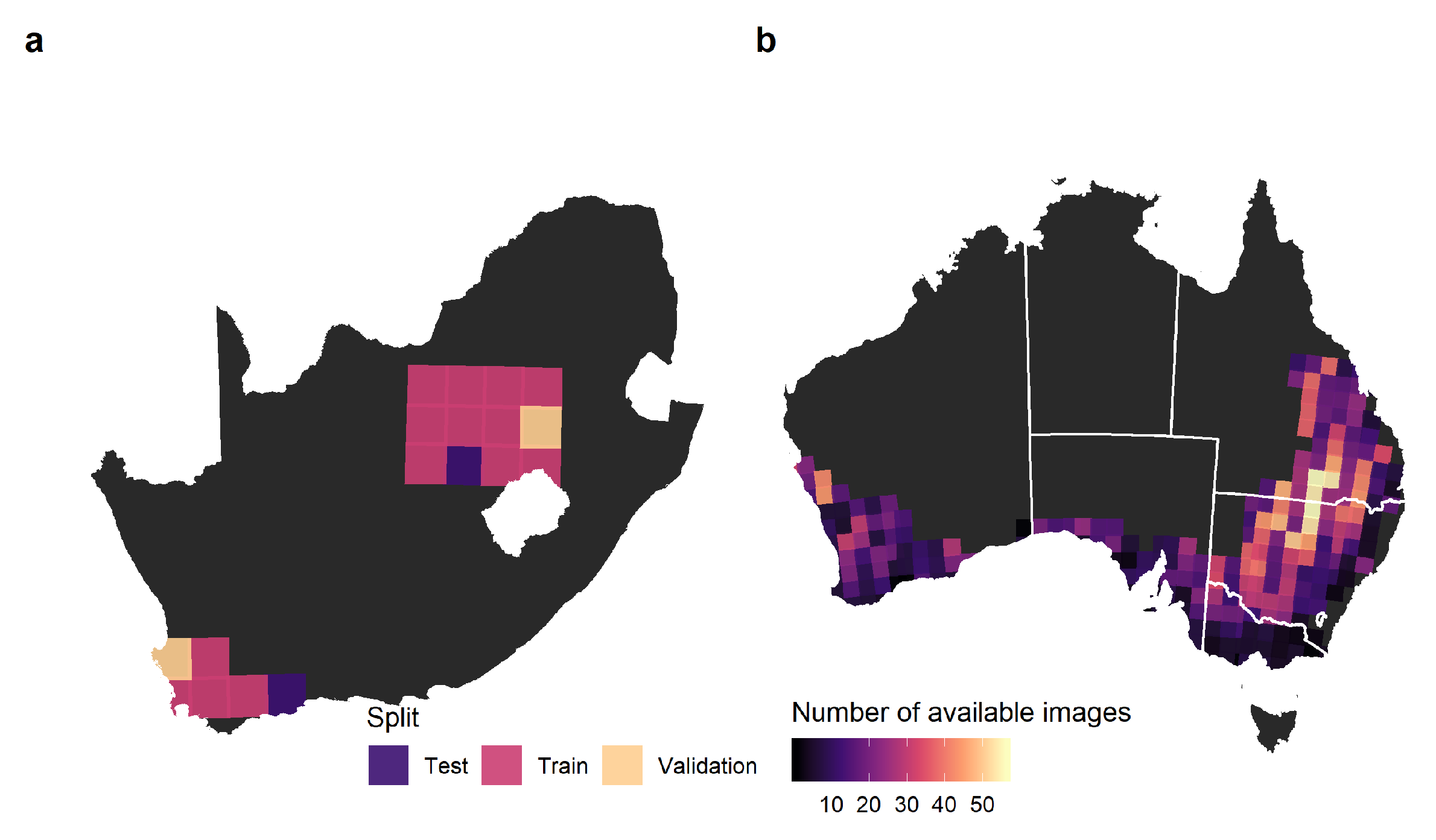
We evaluated the DECODE method by extracting field boundaries across the Australian grains zone (Figure 4) and trained a first FracTAL ResUNet model using data from Australia (the target domain). We also trained a second model using data from South Africa (the source domain) to assess its transferability. We note that the fields in these countries have some similarity in size and shapes. To better understand how transferable models trained on different domains are, we compared the following two cases:
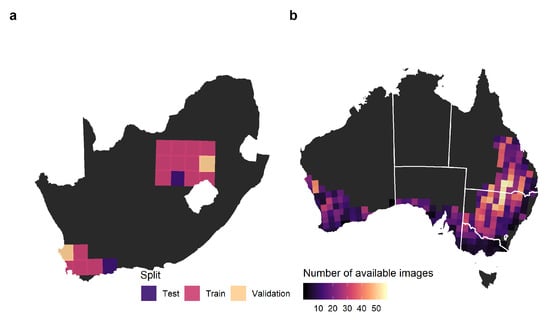
Figure 4.
Study sites. (a) The two study sites in South Africa, the source domain; (b) the number of cloud-free images per tile in the Australia, the target domain.
- Target to target, where a FracTAL ResUNet model was trained and evaluated on data from Australia (the target domain);
- Source to target, where a FracTAL ResUNet model was trained on data from South Africa (the source domain) and evaluated in Australia.
While the source-to-source case (where a FracTAL ResUNet model was trained and evaluated on data from South Africa) was not our primary focus, it provides an interesting benchmark and is thus included in some analyses.
2.5.1. Data and Study Sites
We had two study sites in South Africa: one in the “Maize quadrangle”, which spans across the major maize-producing area; and the other in the Western Free State. These sites cover 18 Sentinel-2 tiles: 14 tiles were used for training, two for validating and two for testing. In practice, the two testing sites were only used to provide informative accuracy measures. Two cloud-free images were available per tile, one early (aiming for February) and the other late in the season (aiming for May; Table A1). They were partitioned into a set of smaller images (hereafter referred to as input images) of a size of 256 × 256 pixels because entire images cannot be process at once due to limited GPU memory. As in Waldner and Diakogiannis [6], we kept the blue, green, red and near-infrared bands.
We sourced boundaries that were created by manually digitizing all fields throughout the country based on 2.5 m resolution, pan-merged SPOT imagery acquired between 2015 and 2017. About 380,000 fields were available for training, 65,000 for validation and 35,000 for testing (Table 1). We rasterized field polygons at 10 m pixel resolution so as to match Sentinel-2’s grid, providing a rich wall-to-wall data set. We finally created the three annotated masks needed by FracTAL ResUNet during training: the extent mask (binary), the boundary mask (binary; a 10 m buffer was applied), and the distance mask (continuous), representing, for every within-field pixel, the distance to the closest boundary. Distances were normalized per field so that the largest distance was always one. As boundaries are updated every three years, discrepancies might exist between them and those seen on Sentinel-2 images. While these discrepancies might be handled during the training phase, their impact is far greater in accuracy assessment. Therefore, accuracy measures for the source-to-source approach remain indicative.

Table 1.
Number of training fields available for training, validation and testing in the source and target domain.
In Australia, we downloaded 5302 cloud-free images across 269 tiles (Figure 4). Partial images due to orbital tracks were discarded if complete images were also available from other orbits. The median number of available images per tile was 14, ranging from a maximum of 56 (55JEH and 55JEK) to a minimum of 1 (50HQH, 50JKM, 51HTC, 52JDL, 53HMB, 53HPA, 54HYC and 55HFU), totaling more than 500 million 10 m pixels.
Field boundaries for training and testing in Australia were generated differently because of their different requirements. On the one hand, training requires a large amount of contiguous data representative of the variety of landscapes and can tolerate some level of noise. On the other hand, testing requires fewer data points but quality control and sampling design are critical. Therefore, field boundaries for training were generated by a two-step process where operators edited objects generated by an image segmentation method while field boundaries for testing were manually digitized. Field boundaries for training were obtained from five tiles (55HEE, 55HDA, 54HXE, 53HNC and 50JPL) for which two cloud-free dates were available. First, we extracted the first five components of these images using principal component analysis and non-cropped areas were masked using the Catchment-scale Land-Use of Australia Map (CLUM) [36]. Next, we extracted field polygons using a meanshift segmentation algorithm [37]. To define the optimal segmentation parameters, Bayesian optimization [38] was used to minimize over- and under-segmentation, which were measured by comparison of the segmentation outputs to 200 randomly drawn fields. The resulting polygons were then reviewed, deleted, added or corrected manually using all of the Sentinel-2 images available as well as Google Earth. Editing reduced the number of polygons by up to 80% depending on the tile, which illustrates the challenge that lies in calibrating object-based methods. As a result, more than 50,000 and 10,000 fields were available for training and validation, respectively. Test data were manually digitized by photo-interpreting Sentinel-2 images (Table 1). To define the sampling locations, Sentinel-2 tiles were split into chips of 2.5 by 2.5 km and their respective crop proportions were computed based on CLUM. Then, we randomly selected one of these chips per tile. Tiles where all chips had less than 10% cropping were ignored. Finally, photo-interpreters labelled 176 well-distributed chips (Figure A1), resulting in 5555 test fields.
2.5.2. Model Training
FracTAL ResUNet models were trained by feeding input images (with the shape 256 pixels × 256 pixels × 4 spectral bands) to the network and comparing their three output masks (extent, boundary and distance) to the reference masks generated as explained in the previous section. In all experiments, our models had the following hyperparameters: 32 initial filters, a depth of 6, a width of 1, and a PSP pooling depth of 4. We also set the depth of the FracTAL attention layer to 5. We initialized the model weights using Xavier initialization [39] and used Adam as the optimizer because it achieves faster convergence than other alternatives [40]. We followed the parameter settings recommended in Kingma and Ba [40]. Training was initiated with the standard Tanimoto loss (). Then, we increased the depth d of the fractal Tanimoto loss each time we reduced the learning rate (when training converges). We chose the following sets of values for the various learning rate () reduction steps: , , , .
Data augmentation artificially inflates the variance of training data, which boosts the ability of convolutional neural networks to generalize. Indeed, convolutional neural networks, and specifically UNets, are not equivariant to spatial transformations such as scaling and rotation [41]. Therefore, during training, we flipped the original images (in the horizontal and vertical reflections) and randomly modified their brightness. This means the network never exactly saw the same data during training. We also performed temporal data augmentation as we used the same labels for multiple image dates.
2.5.3. Large-Scale Instance Segmentation
Instance segmentation was performed per tile to minimize memory usage and allow distributed computing. To combine fields from multiple overlapping tiles into a seamless, continuous data layer, we implemented the following two rules. First, all fields touching the tiles’ bounding box were discarded because they were most likely incomplete. Second, in overlap areas between tiles, we retained the field with the lowest instance uncertainty.
2.5.4. Accuracy Assessment
When characterizing the accuracy of extracted field boundaries, both the geometric and thematic accuracy must be assessed. Thematic accuracy is computed at the pixel level and is expressed by common metrics derived from the error matrix. Here, we report the overall accuracy, the users’ accuracy, the producers’ accuracy [42] and Matthews’ correlation coefficient (MCC; [43]) of the extent mask.
Geometric accuracy is computed at the instance level and can be broken down into four components parts—similarity in shape, label, contour and location, each depicting a specific view of the similarity between reference and extracted fields. We report six geometric accuracy metrics:
- The boundary similarity, which compares the boundary of a reference object coincident with that of a classified object [44]. Boundary similarity calculates the percentage of the target field boundary that coincides with the extracted field boundary:where is the length of the point set intersection between the boundaries of the target and extracted fields, and k is +1 when is less than or equal to , and −1 otherwise.
- The location similarity, which evaluates the similarity between the centroid position of classified and reference objects [44]. Location similarity is evaluated first, by calculating the Euclidiean distance between corresponding the centroids of the target and extracted fields, and then by normalizing it by the diameter of a combined area circle (), i.e., the diameter of a circle whose area corresponds to the sum of the areas of the target and extracted fields:where d is a function that computes the Euclidian distance between the centroids of the reference field () and the corresponding extracted field(s) (), and is the diameter of the combined area circle.
- The oversegmentation rate, which measures incorrect subdivision of larger objects into smaller ones:where is an operator that calculates the area of a field from E or T and ∩ is the intersection operator.
- The undersegmentation rate, which measures incorrect consolidation of small adjacent objects into larger ones [45]:
- The intersection over union, which evaluates the overlap between reference and classified objects;
- The shape similarity, which compares the geometric form of a reference object with that of the corresponding classified object(s) [44]. Shape similarity is based on the normalized perimeter index () and the concept of an equal area circle (), which is a circle with an area equal to the area of an object (here a field). The of an object is in fact the ratio between the perimeter of the equal area circle and the perimeter of the object (). Here, shape similarity compares the geometric form of a target field with that of the corresponding extracted field(s):where k is given the value +1 when is less than or equal to 1.0, and the value –1 otherwise.
All of these metrics were defined to range between 0 and 1; the closer to 1, the more accurate. If an extracted field intersected with more than one field in T, metrics were weighted by the corresponding intersection areas.
As object-based metrics are available for all reference fields, we introduce the concept of the Area Under the Probability of Exceedance Curve (AUPEC) to facilitate comparison between methods and provide a synoptic summary of a method’s performance. Probability of exceedance curve is a common type of chart that gives the probability (vertical axis) that an accuracy level (horizontal axis) will be exceeded. To illustrate this concept, let us consider a probability of exceedance of 50% for an accuracy level of 0.9. This indicates that every second reference field has an accuracy value of at least 0.9. As perfectly extracted fields have an accuracy value of 1, perfect segmentation for the full reference data set should yield a probability of exceedance of 100% for an accuracy of 1 and a probability of exceedance of 100%. It follows that the area under the probability of exceedance curve summarizes the distribution of accuracy of the reference data. An area under the probability of exceedance curve close to 1 indicates that nearly all extracted fields were error-free for the metric considered, and conversely for values close to 0.
3. Results
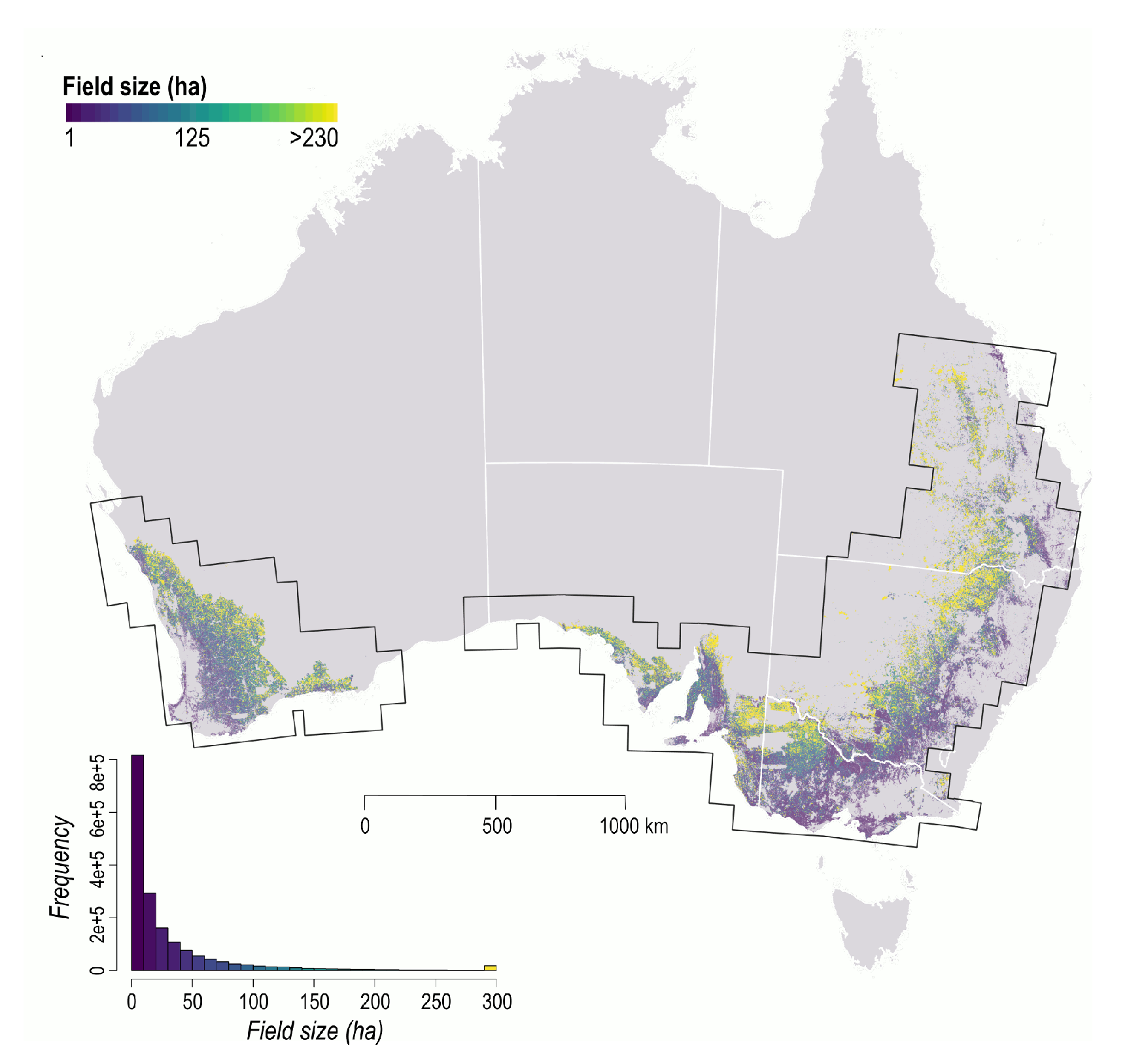
To extract fields in Australia, we trained two FracTAL ResUNet models: one model with data from South Africa (source-to-target) and the other with data from Australia (target-to-target). Training lasted for 72 h per model, using 24 nodes equipped with 4 P100 GPUs and 16 GB of memory each. Optimal training was achieved after 254 epochs for the model trained on data from South Africa (MCC = 0.85) and 161 epochs for the model trained on data from Australia (MCC = 0.87). Inference for Australia ran for 5 days on 16 to 24 nodes, each having 4 P100 GPUs and 128 GB of memory. About 1.7 million fields (>1 ha) were extracted with both methods (Figure 5).
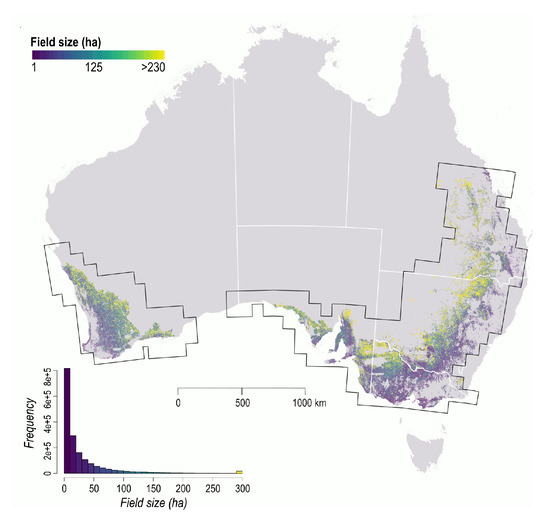
Figure 5.
Field distribution across Australia obtained with the source-to-target approach.
We then assessed the pixel-based accuracy of both models in the target domain (Table 2). Overall, the source-to-target and target-to-target approaches yielded similar accuracy levels (0.87). The target-to-target approach yielded larger producers’ accuracy than the source-to-target approach (0.83 vs. 0.78) but this was achieved at the expense of the field class (0.90 vs. 0.94). Users’ accuracy for both approaches and classes was >0.85.

Table 2.
Pixel-level assessment of the extent mask produced by FracTAL ResUNet. (a) Error matrix for the source-to-target approach and (b) for the target-to-target approach. Both approaches detected fields at the pixel level with similar accuracy.
Visual inspection of the extent, boundary and extent masks confirmed the good performance of the source-to-target approach across a range of cropping regions (Figure 6). The model showed great confidence in detecting fields regardless of the fragmentation levels. Most errors were observed in southern Queensland and central and northern New South Wales, which were stricken by drought during the period of interest. As a result, separability with other natural vegetation classes was reduced. Checker-board artifacts in the semantic segmentation outputs were largely avoided thanks to our specific inference method.

Figure 6.
Semantic segmentation outputs in a range of Australian cropping regions (5 km × 5 km). These outputs were obtained for the source-to-target case, that is, a FracTAL ResUNet trained on South African data and applied across Australia.
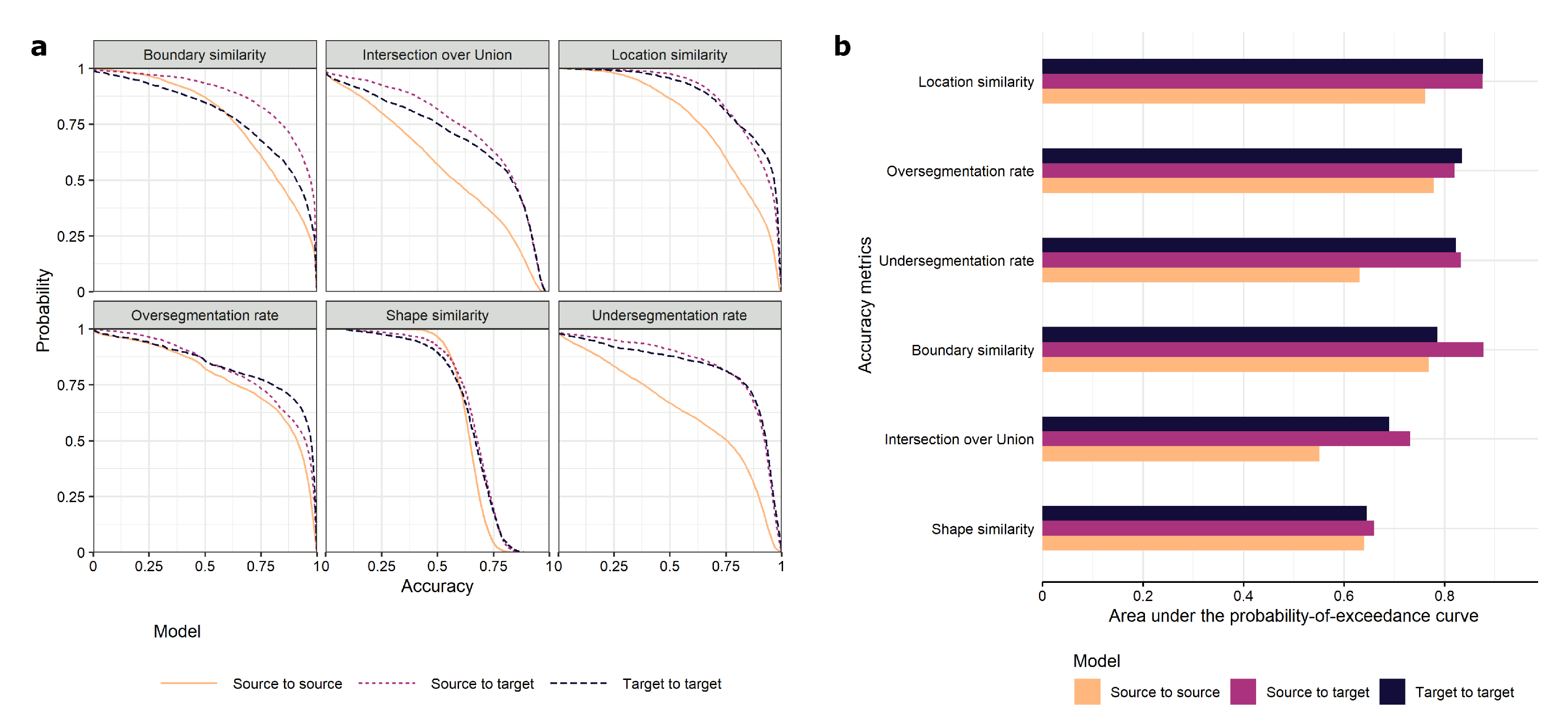
We then evaluated object-based accuracy based on six metrics (boundary similarity, intersection over union, location similarity, oversegmentation rate, shape similarity and undersegmentation rate). We compared the source-to-target and the target-to-target approaches based on the probability of exceedance curves and their associated areas under the curves (Figure 7a). Even though they are not directly comparable, we also included the accuracy metrics for source-to-source results for reference.
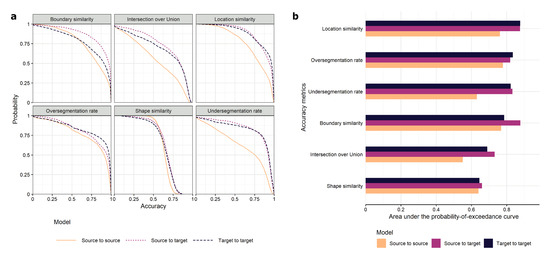
Figure 7.
Object-based accuracy measures. (a) Probability of exceedance curves by metric; (b) area under the probability of exceedance curves by metric. Interpretation of the area under the probability of exceedance curves differs from the interpretation of the metrics themselves as it conveys information about their distribution for the validation set. As perfectly extracted fields have an accuracy value of 1, perfect segmentation for the full reference data set should yield a probability of exceedance of 100% for an accuracy of 1 and a probability of exceedance of 100%.
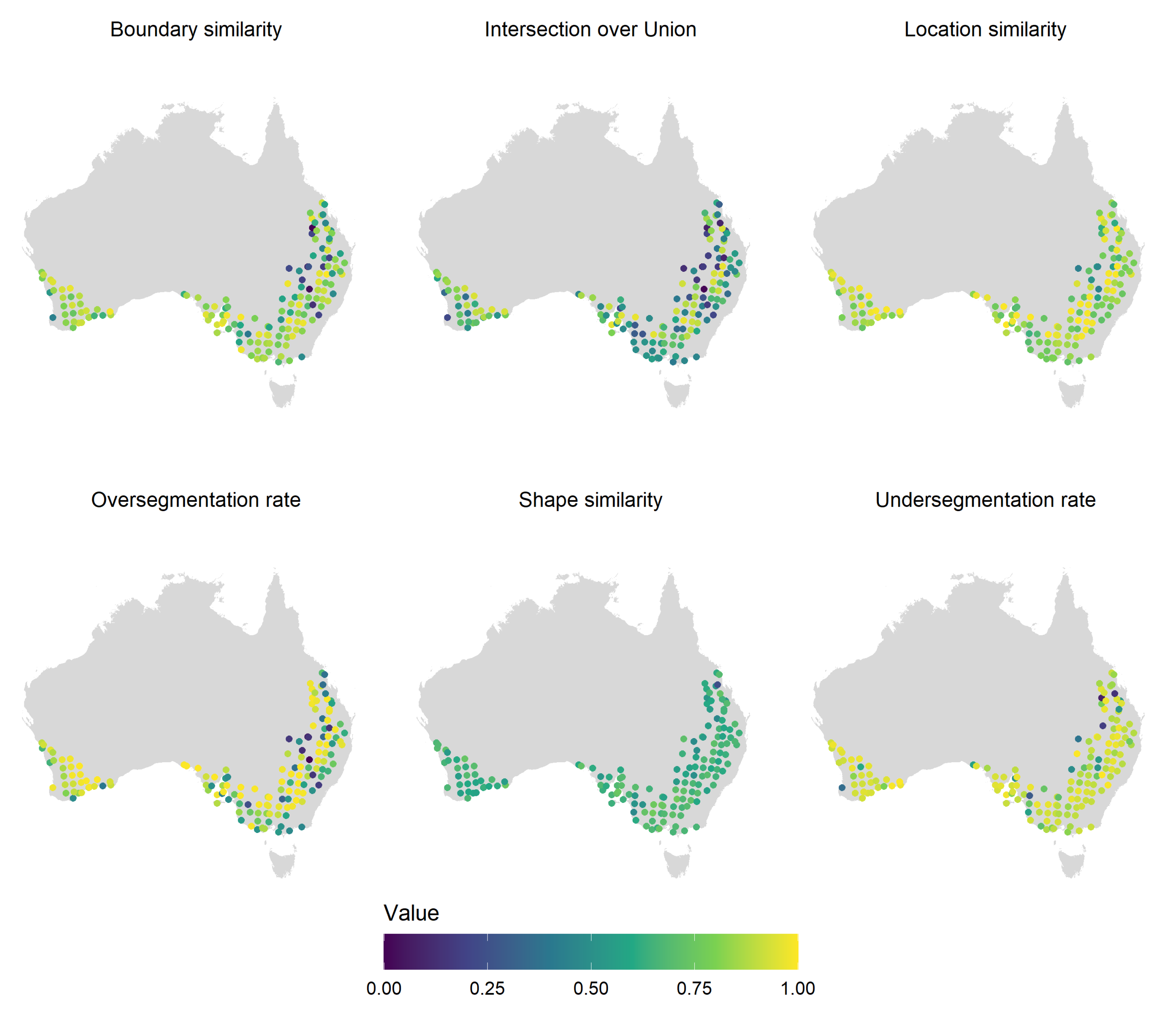
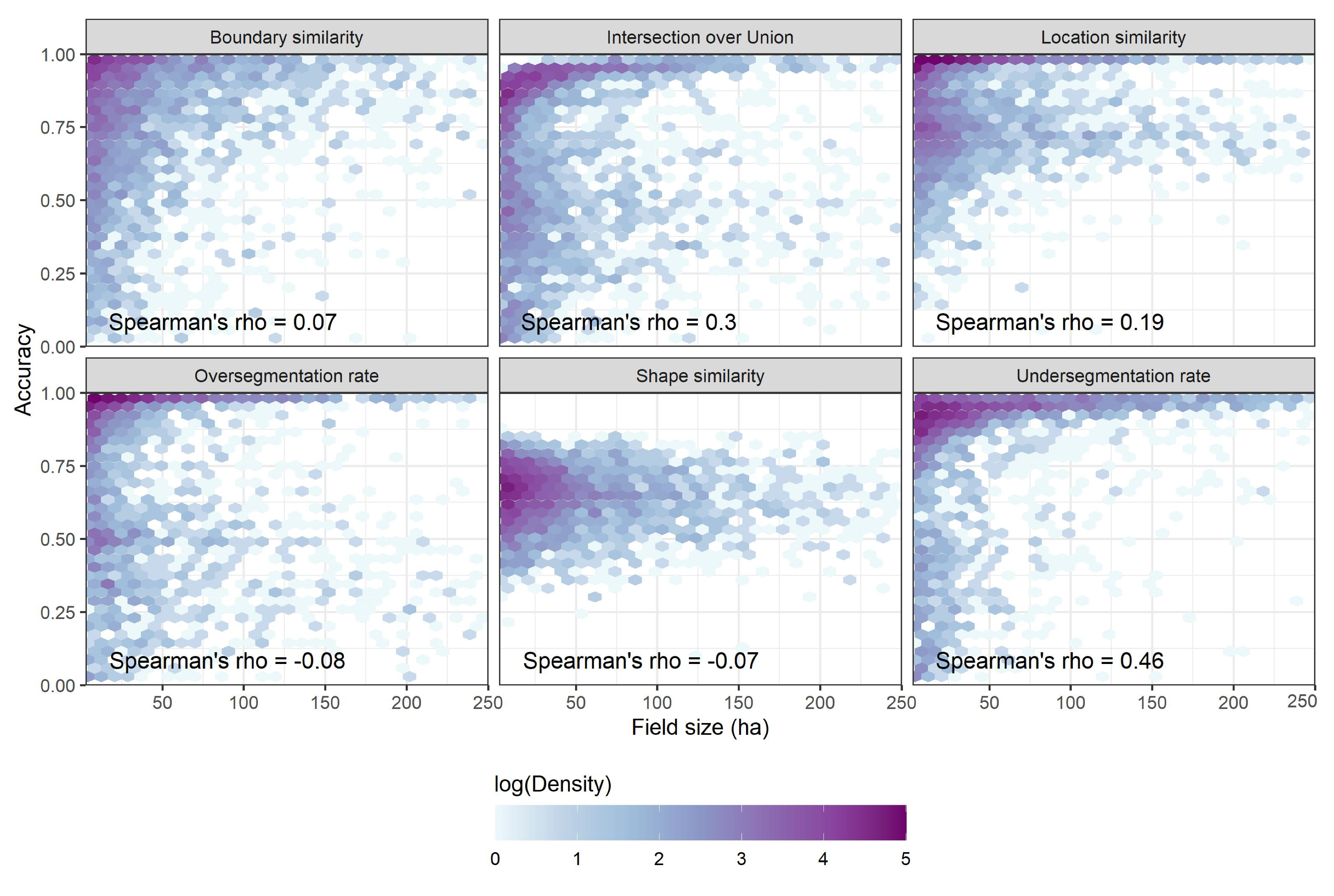
Extracted fields were very similar to reference fields across metrics and approaches. In particular, they had high location similarity and over/undersegmentation rates. For example, 75% of the extracted fields reached an over/undersegmentation rate of at least 0.75. Shape similarity was the poorest metric, with 50% of the fields yielding to a similarity of 0.6. Surprisingly, the source-to-target approach outperformed the target-to-target approach for most metrics (Figure 7b). The largest differences in areas under the probability of exceedance curves were observed for boundary similarity (0.89 vs. 0.79). The larger size of the source training set data might have exposed the model to a larger diversity of cases, leading to improved accuracy. Poor performance in the source-to-source case was likely due to discrepancies between the observation date and the reference. While the shape and undersegmentation errors seemed relatively evenly distributed, oversegmentation and location errors tended to decrease in low rainfall zones (more inland) where pasture fields are less prevalent (Figure 8). The undersegmentation rate and intersection over union increased as field size grew larger. The other accuracy metrics did not indicate any strong relationship with field size (Figure A2).
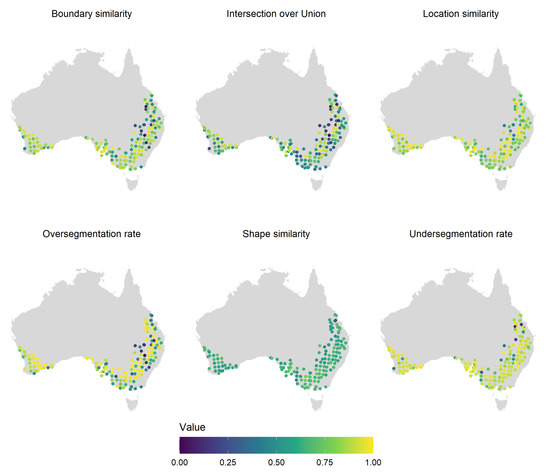
Figure 8.
Distribution of median object-based accuracy metrics. Points indicate the centroids of the validation sites.
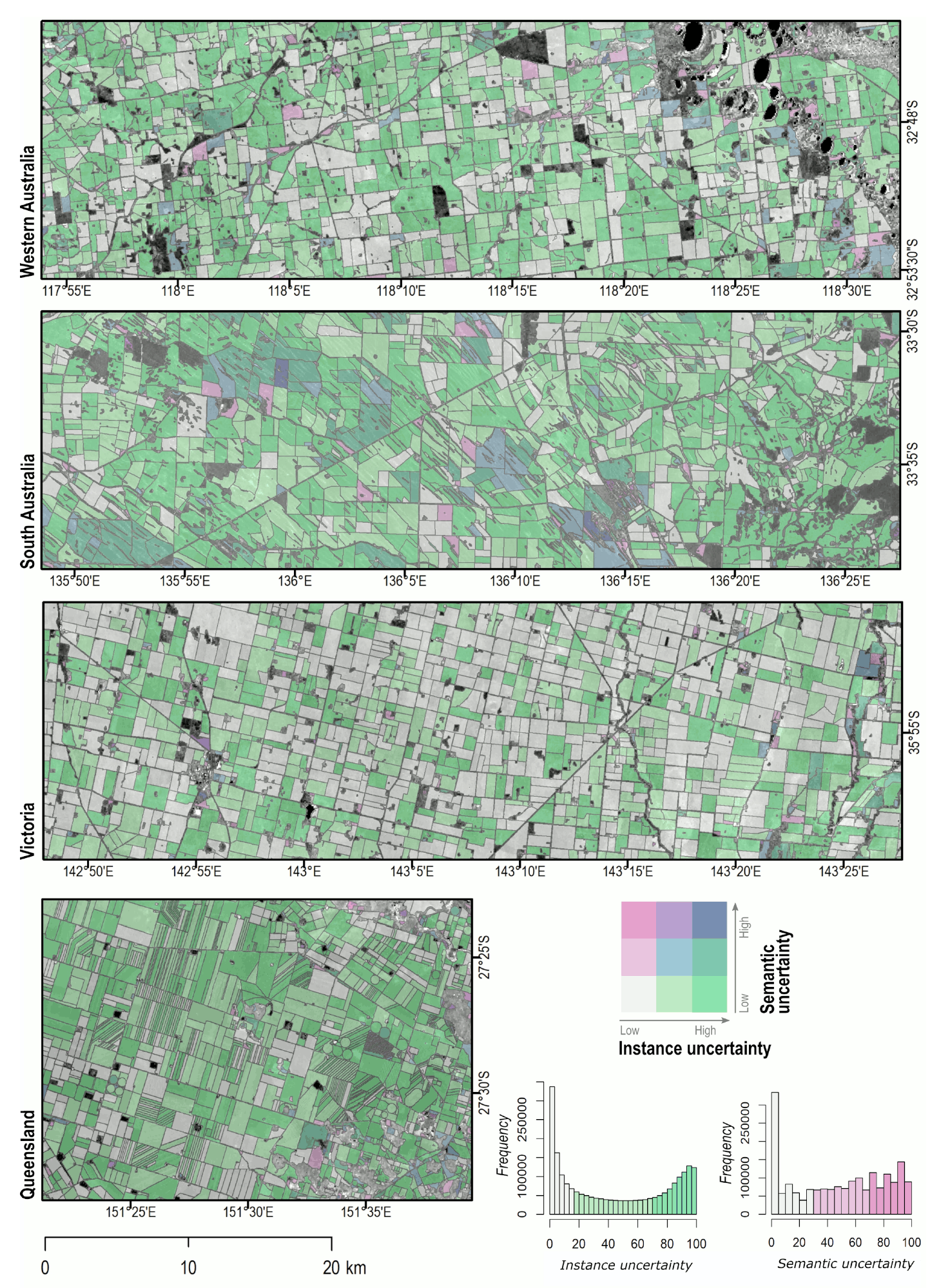
Again, visual assessment confirmed the results of the quantitative accuracy assessment (Figure 9). Our method showed good performance across agricultural landscapes. For instance, it delineated fields with high fidelity and accuracy, even in the more complex landscapes (e.g., South Australia and Queensland). It also successfully retrieved fields with interior boundaries (e.g., lakes, tree lines, buildings) and in areas where crop cover was sparse (New South Wales and Queensland). This suggests that our method still yields good results in the absence of peak season images. Nonetheless, the large number of small fields (<10 ha) suggests that a non-negligible proportion of those is erroneous. Confidence in the extracted fields can also rapidly communicate the uncertainty related to the field extraction process (Figure 10).

Figure 9.
Instance segmentation outputs in a range of Australian cropping regions (5 km × 5 km). These outputs were obtained for the source-to-target case, that is, a FracTAL ResUNet model trained on South African data and applied across Australia.
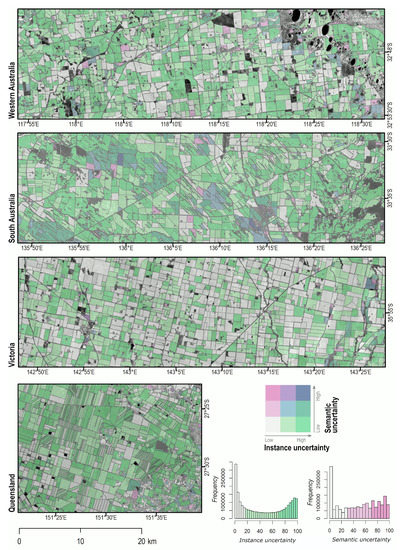
Figure 10.
Semantic and instance uncertainty across a range of cropping regions.
4. Discussion
4.1. Methodological Advancement and Their Relevance
In this paper, we taught machines to delineate field boundaries according to spatial, spectral and temporal properties. To demonstrate the performance of our method, DECODE, we have processed >200 billion Sentinel-2 pixels across the Australian grains zone from which we extracted about 1.7 million fields. As input images are single-date observations, field boundaries can be updated at any time in the season according to users’ needs.
Convolutional neural networks have pushed the boundaries of boundary detection [46]. In this paper, we addressed the problem of satellite-based delineation of field boundaries as multiple semantic segmentation tasks, resulting in excellent performance both at the pixel level and the field level. This is because neural networks learn to discard edges that are not part of field boundaries and to emphasize those that are using spectral and multilevel contextual features that are relevant for multiple correlated tasks. As such, it confirms the results of previous studies that evaluated deep-learning for field boundaries extraction (e.g., Waldner and Diakogiannis [6], Masoud et al. [16], Persello et al. [17]) but our contribution is unprecedented in scale. While our results show clear improvement over previous work, direct and fair comparison may be difficult for two main reasons. First, there are several differences in the experimental setup, such as the imagery data (resolution, spectral bands, multi-sensor, multi-date), the training set (size, proportion), the landscape complexity and fragmentation, or the extent of the area of interest. Second, field boundary extraction, unlike more land-use/land-cover classification tasks, lacks a shared protocol for evaluation. As a result, the variety of metrics reported, regardless of their merit, undermines comparison. This highlights the need for common data sets as well as a shared set of evaluation metrics to allow systematic method benchmarking.
FracTAL ResUNet demonstrated excellent generalization and transfer properties. The greater accuracy level shown by the source-to-target approach over the target-to-target approach clearly evidences its excellent transferability. We believe that three factors help explain this behavior. First, learning from multiple, correlated tasks is pivotal to minimize over-fitting and achieve high generalization. Using this strategy, we showed in an earlier contribution that models could generalize and transfer across space, time and resolution [6]. Second, we included target-domain images and source-domain images when computing the standardization parameters. Third, we performed data augmentation in space and associated labels to multiple images. On top of the usual geometric augmentations (rotations, zooms), labels were associated with two images acquired at different dates, thereby covering a wide range of growing conditions. Pretraining the model and then refining it with target-domain data from the target domain, i.e., transfer learning, is likely to further improve its performance and out-of-domain robustness [47]. Nonetheless, our approach successfully minimized over-fitting, a prevalent problem in deep learning.
Boundaries retrieved by FracTAL ResUNet are also likely to be sharper than those obtained by other models due to the fact that the scaled sigmoid layers used in the multitasking classification head were largely avoided thanks to our specific inference method; see [22] for more details. Other similar approaches could lead to similar effect [48]. Several features could further improve DECODE. First, larger amounts of training data from more diverse locations could be used. Second, models trained in the source domain could be fine-tuned with target-domain data to better accommodate domain differences. Finally, the instance segmentation thresholds ( and ) could be optimized using, for instance, a Pareto frontier approach; see [6]. However, this procedure can result in significant computing costs. Convolutional neural networks set the new standard for field boundaries’ extraction.
4.2. Managing, Communicating and Reducing Uncertainty
In any artificial-intelligence application, uncertainty is the only certainty. Here, we devised two new metrics (semantic and instance uncertainty) to communicate confidence in the extracted field boundaries. These can for instance serve as a visual aid for end users or be propagated down to derivative products. Here, we leveraged instance uncertainty to merge fields extracted from adjacent, overlapping tiles. Semantic and instance uncertainty provide transparency to users of the product.
With its 10 m spatial resolution, Sentinel-2 can be used to map a large range of field sizes. The absence of strong correlations between object-based metrics and field size suggests that much of Australia’s cropping region is above Sentinel-2’s minimum size requirements. However, delineation of fields is only accurate if there is sufficient separation between fields’ interior and their edges. Field boundary delineation thus relies on man-made features such as roads and tree lines. In the absence of such features, adjacent fields with the same crop type and growing patterns may not display sufficient differences to be accurately delineated. For example, we observed that field boundaries were less accurate in areas where pastures are more prevalent in the crop rotation. The increased error rate for small fields can be mitigated by artificially enlarging the input data during inference. As our algorithm was trained with zoom in/out operations, it tolerates similar zoom levels during inference. By zooming in, the ratio of the area occupied by small fields to the total input image size (256 × 256 pixels) will increase, leading to improved detection abilities. While this approach might improve algorithmic performance, it further increases the computational cost of the inference process. Access to very high spatial resolution imagery will also be critical to reduce these scale impediments.
4.3. Perspectives
In demonstrating the fitness of deep-learning algorithms to retrieve individual fields from satellite imagery, our work shows that semantic segmentation combined with multitasking is state-of-the-art, and that this technology has reached operational maturity. Indeed, data sets extracted with this technology are now available for mainland Australia [49] (CSIRO’s ePaddocks™ product) and this is being replicated in Europe [50] (e.g., Sentinel Hub’s ParcelIO). Besides facilitating field-based agricultural services, greater availability of field boundary data will support applications such as crop identification and land-use mapping [51,52,53,54,55] and yield estimation [56,57,58,59], as well as the collection of reference data [60]. Our work also points toward further research directions. Foremost amongst these is the quantification of the model sensitivity to training set size and labelling errors. Evidence-based responses to those questions would for instance help address the lack of adequate labeled images in smallholder cropping systems. Indeed, these systems are not only challenging because of their small field size. They also display large variations in color, texture, and shape, and often have weak boundaries. Other agricultural systems, such as intensively managed dairy systems with sub-field strip grazing or rangeland systems, also provide research challenges. To what extent can a model pretrained in a data-rich contexts extract field boundaries in smallholder farming systems? Marvaniya et al. [61] presented a first attempt to address this problem. A third direction is to benchmark end-to-end object detectors, for which no post-processing is necessary. While there is some evidence that end-to-end object detectors may perform better [62], they often require longer training epochs to converge, and deliver relatively low performance at detecting objects, especially small ones. Finally, models that exploit spatial, spectral and temporal features altogether (i.e., 3D convolutions) are worth exploring. However, they require preprocessed, consistent time series as input. They also have a very large GPU memory footprint, making their effective implementation a challenging task. These additional requirements might reduce their practicality and, therefore, their uptake.
5. Conclusions
We presented DECODE, a method that extracts fields and their boundaries from satellite imagery based on spatial, spectral and temporal information. DECODE is based on a novel convolutional neural network, FracTAL ResUNet, which is applied to the cloud-free Sentinel-2 images that are available across the season. Then, these predictions are time-averaged and individual fields are retrieved from these consolidated predictions by means of hierarchical watershed segmentation. By extracting field boundaries across Australia, we demonstrated that our method is accurate and scalable, and that it not only generalizes well but also transfers well to unseen regions. Indeed, a model trained with images of South Africa and transferred to Australia achieved accuracy levels similar to or larger than a model specifically trained for Australian conditions. This ability to transfer to unseen areas paves the way to wider availability of field boundary data as it alleviates the problem of collecting training labels.
Author Contributions
Conceptualization, F.W. and F.I.D.; methodology, F.W. and F.I.D.; software, F.I.D., M.C.-C. and E.C.-W.; data curation, K.B., C.H., G.M. and A.T.; funding acquisition, F.W. All authors have read and agreed to the published version of the manuscript.
Funding
We received funding from “Grains” and “ePaddocks”, two projects of the Digiscape Future Science Platform supported by the CSIRO.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Available cloud-free images in the source domain.
Table A1.
Available cloud-free images in the source domain.
| Tile | Dates | Split |
|---|---|---|
| T34HBH | 20190327, 20190824 | Train |
| T34HBJ | 20190625, 20190903 | Validation |
| T34HCH | 20190406, 20190908 | Train |
| T34HCJ | 20190506, 20190824 | Train |
| T34HDH | 20190615, 20190809 | Train |
| T34HEH | 20190418, 20190821 | Test |
| T35JLJ | 20190301, 20190425 | Train |
| T35JLK | 20190301, 20190510 | Train |
| T35JLL | 20190301, 20190430 | Train |
| T35JMJ | 20190301, 20190505 | Test |
| T35JMK | 20190331, 20190505 | Train |
| T35JML | 20190326, 20190510 | Train |
| T35JNJ | 20190427, 20190517 | Train |
| T35JNK | 20190226, 20190427 | Train |
| T35JNL | 20190226, 20190427 | Train |
| T35JPJ | 20190226, 20190502 | Train |
| T35JPK | 20190226, 20190417 | Validation |
| T35JPL | 20190226, 20190328 | Train |
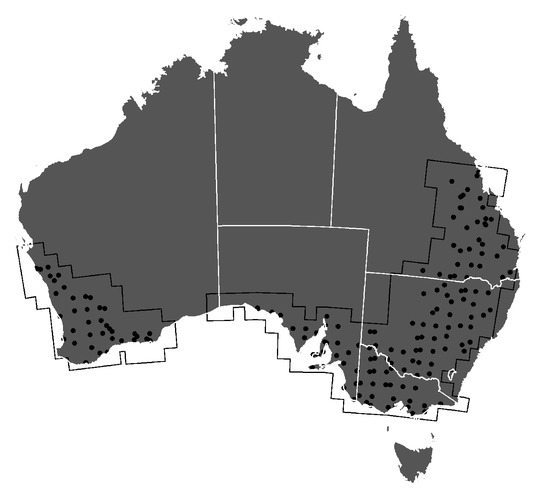
Figure A1.
Distribution of the validation sites in the target domain.
Figure A1.
Distribution of the validation sites in the target domain.
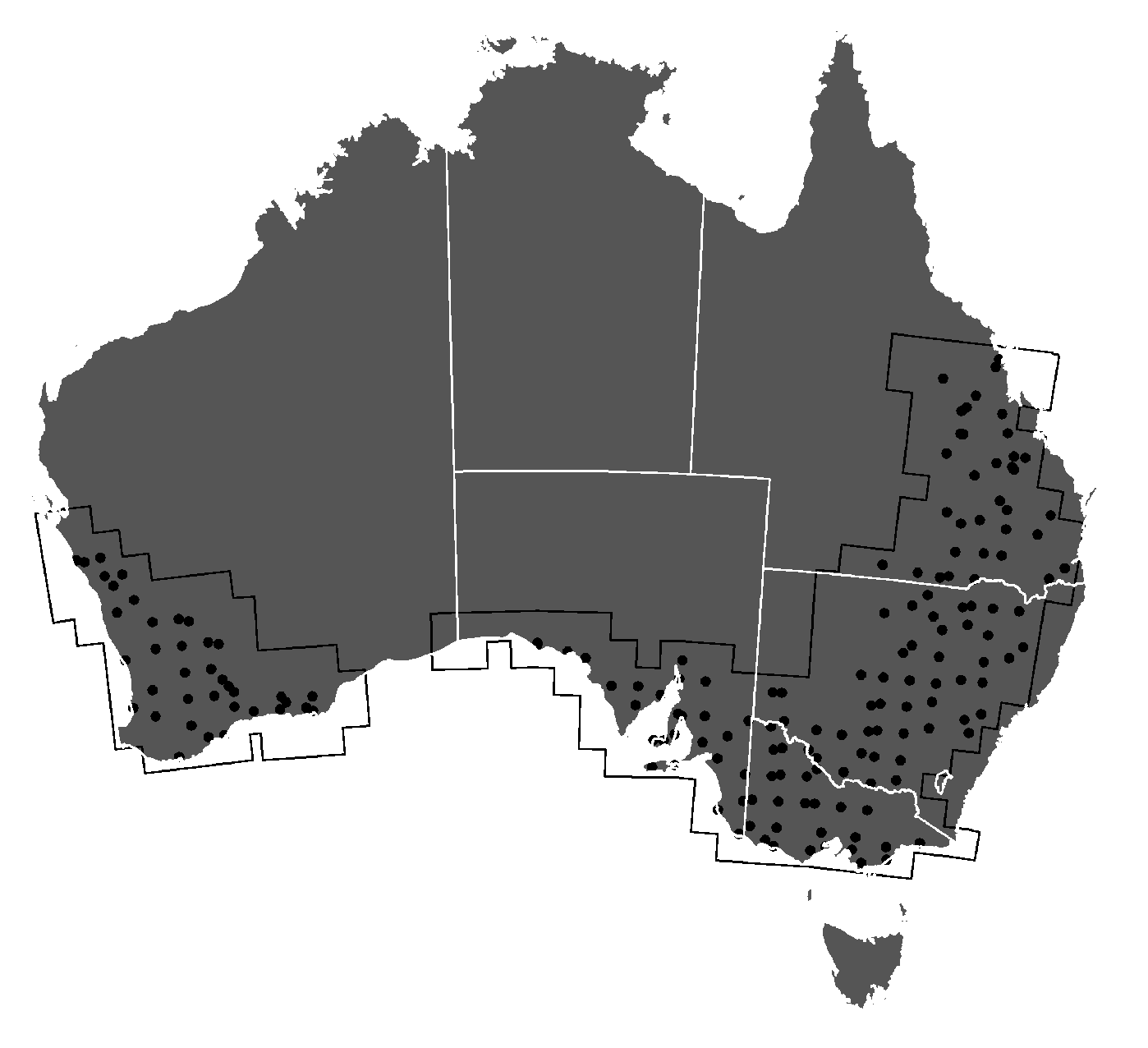
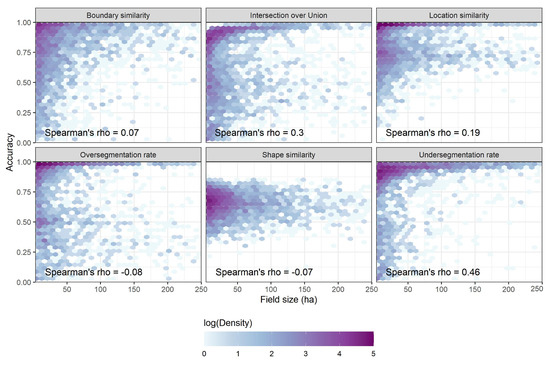
Figure A2.
Object-based accuracy binned scatter plots.
Figure A2.
Object-based accuracy binned scatter plots.
References
- Kuemmerle, T.; Erb, K.; Meyfroidt, P.; Müller, D.; Verburg, P.H.; Estel, S.; Haberl, H.; Hostert, P.; Jepsen, M.R.; Kastner, T.; et al. Challenges and opportunities in mapping land use intensity globally. Curr. Opin. Environ. Sustain. 2013, 5, 484–493. [Google Scholar] [CrossRef]
- Geiger, F.; Bengtsson, J.; Berendse, F.; Weisser, W.W.; Emmerson, M.; Morales, M.B.; Ceryngier, P.; Liira, J.; Tscharntke, T.; Winqvist, C.; et al. Persistent negative effects of pesticides on biodiversity and biological control potential on European farmland. Basic Appl. Ecol. 2010, 11, 97–105. [Google Scholar] [CrossRef]
- Carfagna, E.; Gallego, F.J. Using remote sensing for agricultural statistics. Int. Stat. Rev. 2005, 73, 389–404. [Google Scholar] [CrossRef]
- Rudel, T.K.; Schneider, L.; Uriarte, M.; Turner, B.L.; DeFries, R.; Lawrence, D.; Geoghegan, J.; Hecht, S.; Ickowitz, A.; Lambin, E.F.; et al. Agricultural intensification and changes in cultivated areas, 1970–2005. Proc. Natl. Acad. Sci. USA 2009, 106, 20675–20680. [Google Scholar] [CrossRef] [PubMed]
- Johnson, D.M. A 2010 map estimate of annually tilled cropland within the conterminous United States. Agric. Syst. 2013, 114, 95–105. [Google Scholar] [CrossRef]
- Waldner, F.; Diakogiannis, F.I. Deep learning on edge: Extracting field boundaries from satellite images with a convolutional neural network. Remote Sens. Environ. 2020, 245, 111741. [Google Scholar] [CrossRef]
- Yan, L.; Roy, D. Conterminous United States crop field size quantification from multi-temporal Landsat data. Remote Sens. Environ. 2016, 172, 67–86. [Google Scholar] [CrossRef]
- Graesser, J.; Ramankutty, N. Detection of cropland field parcels from Landsat imagery. Remote Sens. Environ. 2017, 201, 165–180. [Google Scholar] [CrossRef]
- Watkins, B.; van Niekerk, A. A comparison of object-based image analysis approaches for field boundary delineation using multi-temporal Sentinel-2 imagery. Comput. Electron. Agric. 2019, 158, 294–302. [Google Scholar] [CrossRef]
- Wagner, M.P.; Oppelt, N. Extracting Agricultural Fields from Remote Sensing Imagery Using Graph-Based Growing Contours. Remote Sens. 2020, 12, 1205. [Google Scholar] [CrossRef]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef] [PubMed]
- Dollár, P.; Zitnick, C.L. Structured forests for fast edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 1841–1848. [Google Scholar]
- Bertasius, G.; Shi, J.; Torresani, L. DeepEdge: A multi-scale bifurcated deep network for top-down contour detection. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 4380–4389. [Google Scholar]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder–decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Masoud, K.M.; Persello, C.; Tolpekin, V.A. Delineation of Agricultural Field Boundaries from Sentinel-2 Images Using a Novel Super-Resolution Contour Detector Based on Fully Convolutional Networks. Remote Sens. 2020, 12, 59. [Google Scholar] [CrossRef]
- Persello, C.; Tolpekin, V.; Bergado, J.; de By, R. Delineation of agricultural fields in smallholder farms from satellite images using fully convolutional networks and combinatorial grouping. Remote Sens. Environ. 2019, 231, 111253. [Google Scholar] [CrossRef]
- Crommelinck, S.; Bennett, R.; Gerke, M.; Yang, M.Y.; Vosselman, G. Contour detection for UAV-based cadastral mapping. Remote Sens. 2017, 9, 171. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Wagner, M.P.; Oppelt, N. Deep Learning and Adaptive Graph-Based Growing Contours for Agricultural Field Extraction. Remote Sens. 2020, 12, 1990. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P. Looking for change? Roll the Dice and demand Attention. arXiv 2020, arXiv:cs.CV/2009.02062. [Google Scholar]
- Brodrick, P.G.; Davies, A.B.; Asner, G.P. Uncovering ecological patterns with convolutional neural networks. Trends Ecol. Evol. 2019, 34, 734–745. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Identity mappings in deep residual networks. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2016; pp. 630–645. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Zhang, H.; Wu, C.; Zhang, Z.; Zhu, Y.; Lin, H.; Zhang, Z.; Sun, Y.; He, T.; Mueller, J.; Manmatha, R.; et al. ResNeSt: Split-Attention Networks. arXiv 2020, arXiv:2004.08955. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. arXiv 2017, arXiv:1612.01105. [Google Scholar]
- Meyer, F. The dynamics of minima and contours. In Mathematical Morphology and Its Applications to Image and Signal Processing; Springer: Berlin/Heidelberg, Germany, 1996; pp. 329–336. [Google Scholar]
- Cousty, J.; Bertrand, G.; Najman, L.; Couprie, M. Watershed Cuts: Minimum Spanning Forests and the Drop of Water Principle. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 1362–1374. [Google Scholar] [CrossRef]
- Perret, B.; Cousty, J.; Guimaraes, S.J.F.; Maia, D.S. Evaluation of hierarchical watersheds. IEEE Trans. Image Process. 2017, 27, 1676–1688. [Google Scholar] [CrossRef]
- Meyer, F. Minimum spanning forests for morphological segmentation. In Mathematical Morphology and Its Applications to Image Processing; Springer: Berlin/Heidelberg, Germany, 1994; pp. 77–84. [Google Scholar]
- Grimaud, M. New measure of contrast: The dynamics. In Image Algebra and Morphological Image Processing III; International Society for Optics and Photonics: Washington, DC, USA, 1992; Volume 1769, pp. 292–305. [Google Scholar]
- ABARES. The Australian Land Use and Management Classification Version 8; ABARES: Canberra, Australia, 2016.
- Michel, J.; Youssefi, D.; Grizonnet, M. Stable mean-shift algorithm and its application to the segmentation of arbitrarily large remote sensing images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 952–964. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, NIPS’12, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference On Artificial Intelligence And Statistics, JMLR Workshop and Conference Proceedings, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Matthews, B.W. Comparison of the predicted and observed secondary structure of T4 phage lysozyme. Biochim. Biophys. Acta-(Bba)-Protein Struct. 1975, 405, 442–451. [Google Scholar] [CrossRef]
- Lizarazo, I. Accuracy assessment of object-based image classification: Another STEP. Int. J. Remote Sens. 2014, 35, 6135–6156. [Google Scholar] [CrossRef]
- Persello, C.; Bruzzone, L. A novel protocol for accuracy assessment in classification of very high resolution images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1232–1244. [Google Scholar] [CrossRef]
- Kokkinos, I. Pushing the boundaries of boundary detection using deep learning. arXiv 2015, arXiv:1511.07386. [Google Scholar]
- Mathis, A.; Yüksekgönül, M.; Rogers, B.; Bethge, M.; Mathis, M.W. Pretraining boosts out-of-domain robustness for pose estimation. arXiv 2019, arXiv:1909.11229. [Google Scholar]
- Wang, Y.; Zhao, X.; Huang, K. Deep crisp boundaries. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3892–3900. [Google Scholar]
- ePaddocks ™Australian Paddock Boundaries. Available online: https://acds.csiro.au/epaddock-australian-paddock-boundaries (accessed on 31 May 2021).
- ParcelIO: Automatic Parcel Boundary Detection and Delineation. Available online: http://parcelio.sentinel-hub.com/ (accessed on 31 May 2021).
- Pringle, M.J.; Schmidt, M.; Tindall, D.R. Multi-decade, multi-sensor time-series modelling—Based on geostatistical concepts—To predict broad groups of crops. Remote Sens. Environ. 2018, 216, 183–200. [Google Scholar] [CrossRef]
- Waldner, F.; Chen, Y.; Lawes, R.; Hochman, Z. Needle in a haystack: Mapping rare and infrequent crops using satellite imagery and data balancing methods. Remote Sens. Environ. 2019, 233, 111375. [Google Scholar] [CrossRef]
- Defourny, P.; Bontemps, S.; Bellemans, N.; Cara, C.; Dedieu, G.; Guzzonato, E.; Hagolle, O.; Inglada, J.; Nicola, L.; Rabaute, T.; et al. Near real-time agriculture monitoring at national scale at parcel resolution: Performance assessment of the Sen2-Agri automated system in various cropping systems around the world. Remote Sens. Environ. 2019, 221, 551–568. [Google Scholar] [CrossRef]
- Wang, S.; Azzari, G.; Lobell, D.B. Crop type mapping without field-level labels: Random forest transfer and unsupervised clustering techniques. Remote Sens. Environ. 2019, 222, 303–317. [Google Scholar] [CrossRef]
- Zhao, L.; Waldner, F.; Scarth, P.; Mack, B.; Hochman, Z. Combining Fractional Cover Images with One-Class Classifiers Enables Near Real-Time Monitoring of Fallows in the Northern Grains Region of Australia. Remote Sens. 2020, 12, 1337. [Google Scholar] [CrossRef]
- Azzari, G.; Jain, M.; Lobell, D.B. Towards fine resolution global maps of crop yields: Testing multiple methods and satellites in three countries. Remote Sens. Environ. 2017, 202, 129–141. [Google Scholar] [CrossRef]
- Donohue, R.J.; Lawes, R.A.; Mata, G.; Gobbett, D.; Ouzman, J. Towards a national, remote-sensing-based model for predicting field-scale crop yield. Field Crop. Res. 2018, 227, 79–90. [Google Scholar] [CrossRef]
- Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. ISPRS J. Photogramm. Remote Sens. 2020, 160, 124–135. [Google Scholar] [CrossRef]
- Chen, Y.; McVicar, T.R.; Donohue, R.J.; Garg, N.; Waldner, F.; Ota, N.; Li, L.; Lawes, R. To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction. Remote Sens. 2020, 12, 1653. [Google Scholar] [CrossRef]
- Waldner, F.; Schucknecht, A.; Lesiv, M.; Gallego, J.; See, L.; Pérez-Hoyos, A.; d’Andrimont, R.; De Maet, T.; Bayas, J.C.L.; Fritz, S.; et al. Conflation of expert and crowd reference data to validate global binary thematic maps. Remote Sens. Environ. 2019, 221, 235–246. [Google Scholar] [CrossRef]
- Marvaniya, S.; Devi, U.; Hazra, J.; Mujumdar, S.; Gupta, N. Small, Sparse, but Substantial: Techniques for Segmenting Small Agricultural Fields Using Sparse Ground Data. arXiv 2020, arXiv:2005.01947. [Google Scholar]
- Ruiz-Santaquiteria, J.; Bueno, G.; Deniz, O.; Vallez, N.; Cristobal, G. Semantic versus instance segmentation in microscopic algae detection. Eng. Appl. Artif. Intell. 2020, 87, 103271. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).