Linear-Based Incremental Co-Registration of MLS and Photogrammetric Point Clouds
Abstract
1. Introduction
- An end-to-end automatic cross-source point-cloud registration method;
- A method to extract the same linear features from cross-source point clouds to reduce noise and simplify the scene, thereby guaranteeing the similarity measures of features;
- An incremental registration strategy that can simplify the complex registration process and restore both the scale and 3D alignment.
2. Literature Review
3. Methodology
3.1. Problem Formulation and Overview of Methods
3.2. Extract a Simplified Point Cloud by Eliminating Noise from the Cross-Source Point Cloud
3.3. D Registration and Scale Recovery Based on Line-Group Matching
3.4. Incremental Height Offset and Overall Optimization
4. Experiments
4.1. Data Sets and Evaluation Metric Descriptions
4.2. Experiment Results
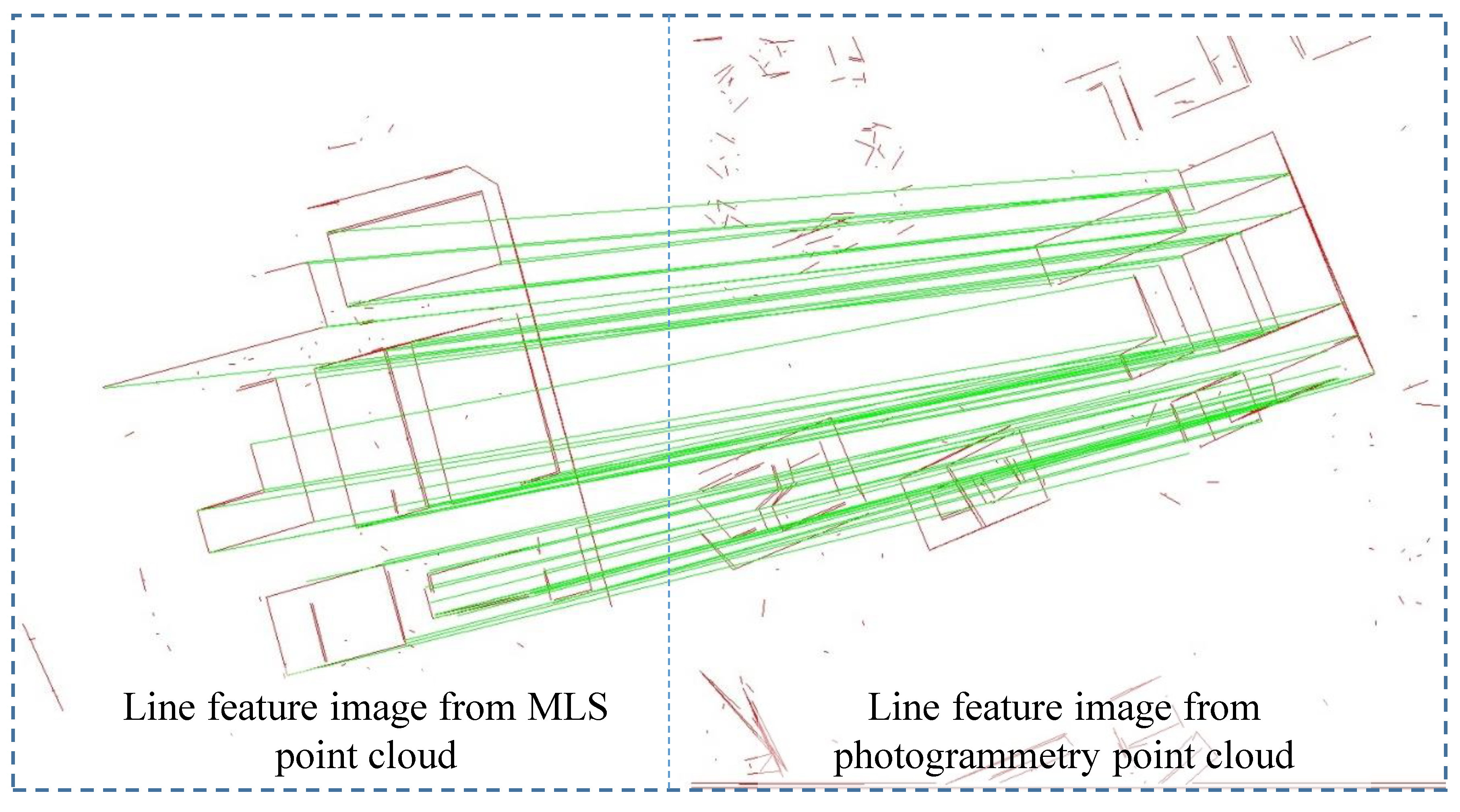
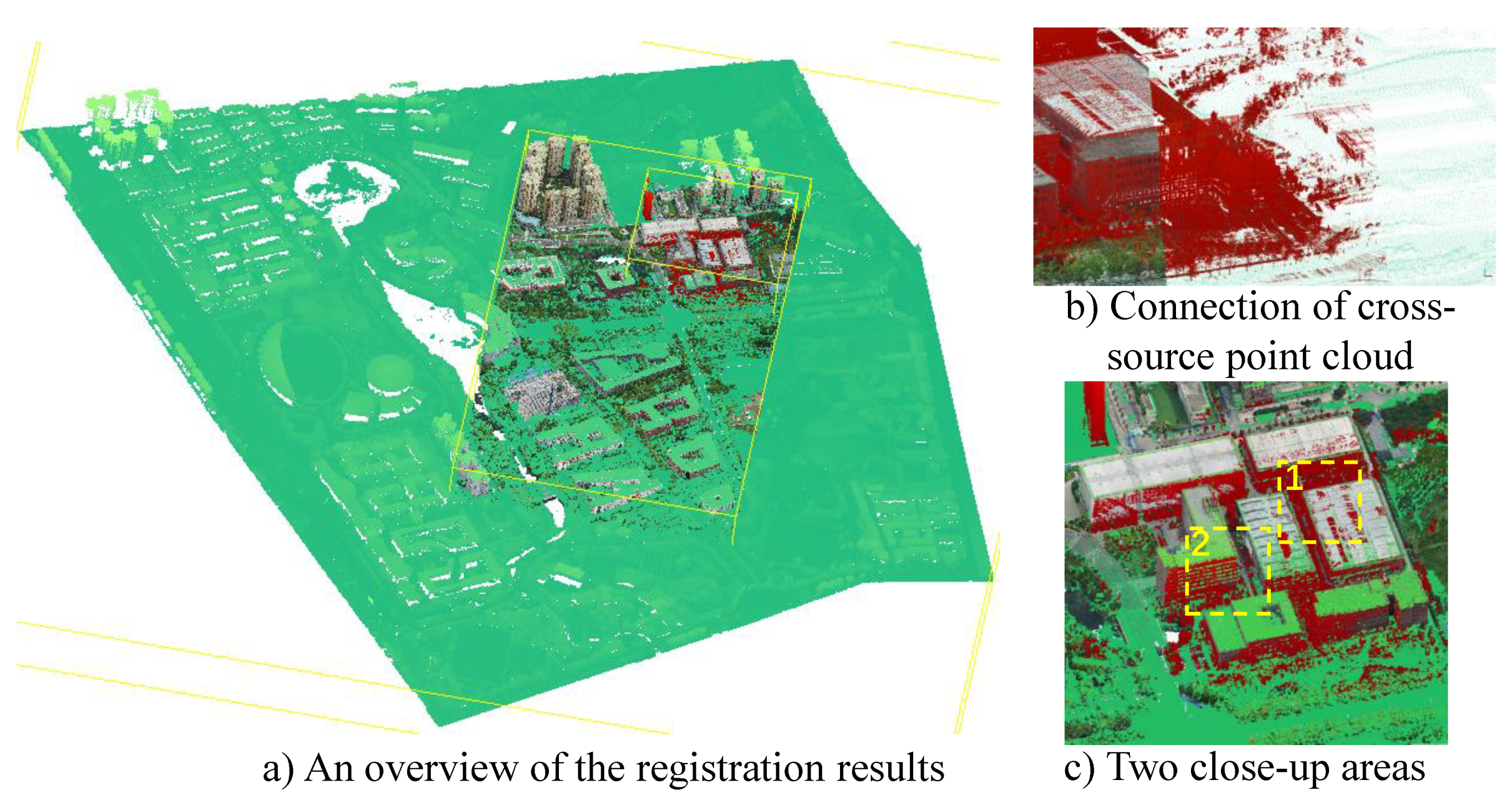
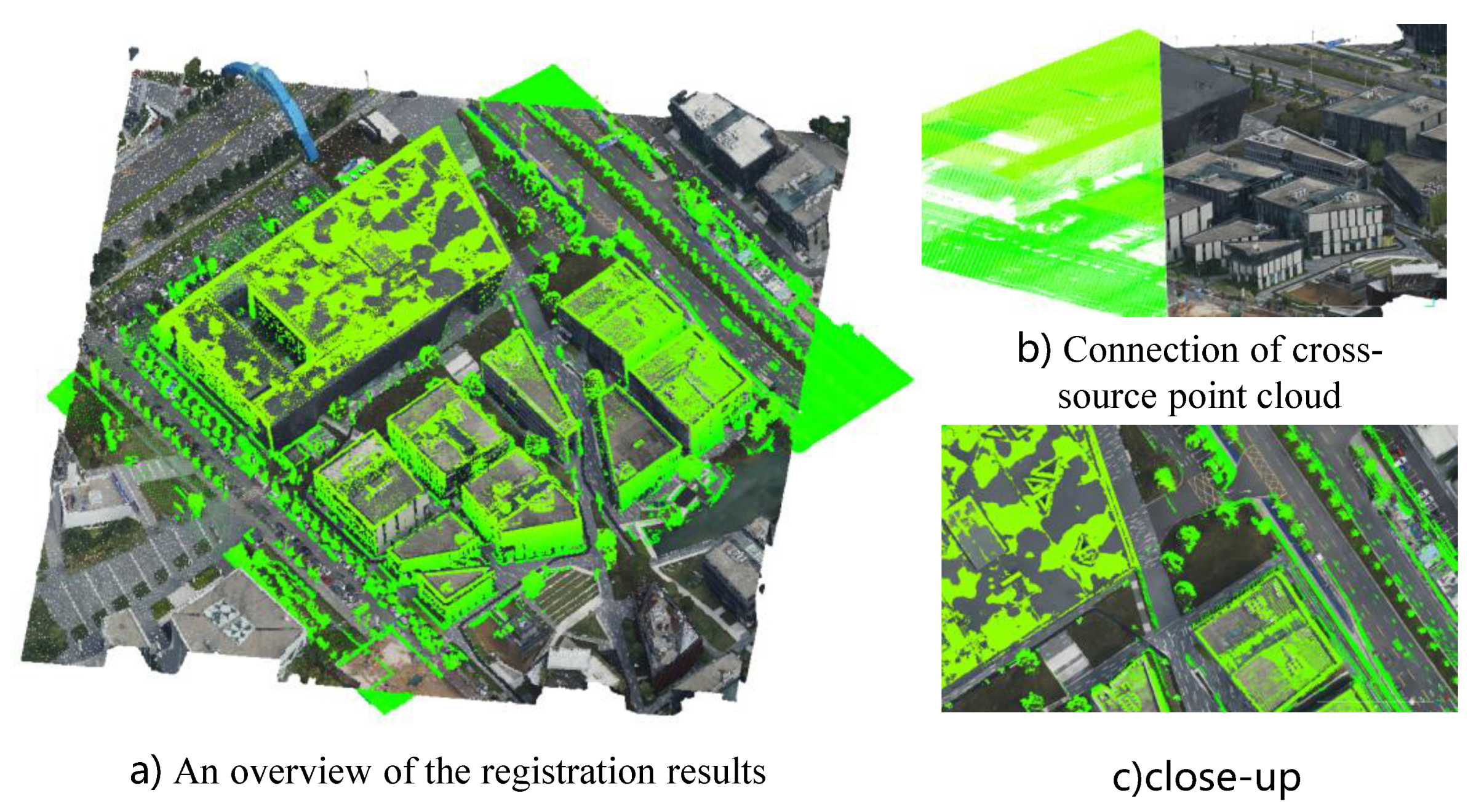
4.2.1. Qualitative Evaluations
4.2.2. Further Detailed Assessment
4.3. Quantitative Evaluations
4.4. Discussion and Limitations
- (1)
- Effective linear feature extraction and descriptions greatly reduce the influence of redundant information and errors in the registration process and overcome the important challenge of cross-source point-cloud registration, which involves a similar overall structure but significantly different details. In this method, similar linear features that lie on the building outline are highlighted to effectively improve the validity and robustness of the candidate features.
- (2)
- An automatic point-cloud scale-restoration method was developed. By using robust line feature extraction and similarity measurements of 2D line-segment groups, accurate corresponding feature mapping and 2D affine transformation were realized between the cross-source point clouds.
- (3)
- A cross-source point cloud automatic registration framework with strong applicability was designed and implemented. By extracting the principal structures and reducing the degrees of freedom, the complex registration process among the differentiated multi-source point clouds was decomposed into several independent and interrelated steps.
- (4)
- As a limitation, some mismatched feature pairs remained in the 2D line-segment group’s similarity measurement. Although no decisive interference was observed in our data set, there is no guarantee that the applicability of our algorithm will not be limited with a further increase in data diversity and differentiation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Wang, C.; Zai, D.; Huang, P.; Li, J. A Volumetric Fusing Method for TLS and SFM Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3349–3357. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Gennaro, S.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Wu, B.; Xie, L.; Hu, H.; Zhu, Q.; Yau, E. Integration of aerial oblique imagery and terrestrial imagery for optimized 3D modeling in urban areas. ISPRS J. Photogramm. Remote Sens. 2018, 139, 119–132. [Google Scholar] [CrossRef]
- Xiong, B.; Jancosek, M.; Elberink, S.O.; Vosselman, G. Flexible building primitives for 3D building modeling. ISPRS J. Photogramm. Remote Sens. 2015, 101, 275–290. [Google Scholar] [CrossRef]
- Berger, M.; Tagliasacchi, A.; Seversky, L.M.; Alliez, P.; Guennebaud, G.; Levine, J.A.; Sharf, A.; Silva, C.T. A Survey of Surface Reconstruction from Point Clouds. Comput. Graph. Forum 2016, 36, 301–329. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X. Advances in fusion of optical imagery and LiDAR point cloud applied to photogrammetry and remote sensing. Int. J. Image Data Fusion 2016, 8, 1–31. [Google Scholar] [CrossRef]
- Xie, L.; Zhu, Q.; Hu, H.; Wu, B.; Li, Y.; Zhang, Y.; Zhong, R. Hierarchical Regularization of Building Boundaries in Noisy Aerial Laser Scanning and Photogrammetric Point Clouds. Remote Sens. 2018, 10, 1996. [Google Scholar] [CrossRef]
- Ge, X. Automatic markerless registration of point clouds with semantic-keypoint-based 4-points congruent sets. ISPRS J. Photogramm. 2017, 130, 344–357. [Google Scholar] [CrossRef]
- Habib, A.; De Tchev, I.; Bang, K. A Comparative Analysis of Two Approaches for Multiple-Surface Registration of Irregular Point Clouds. In Proceedings of the 2010 Canadian Geomatics Conference and Symposium of Commission I, ISPRS Convergence in Geomatics—Shaping Canada’s Competitive Landscape, Calgary, AB, Canada, 15–18 June 2010. [Google Scholar]
- Zai, D.; Li, J.; Guo, Y.; Cheng, M.; Huang, P.; Cao, X.; Wang, C. Pairwise Registration of TLS Point Clouds using Covariance Descriptors and a Non-cooperative Game. ISPRS J. Photogramm. 2017, 134, 15–29. [Google Scholar] [CrossRef]
- Toschi, I.; Remondino, F.; Rothe, R.; Klimek, K. Combining Airborne Oblique Camera and Lidar Sensors: Investigation and New Perspectives. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-1, 437–444. [Google Scholar] [CrossRef]
- Huising, E.J.; Pereira, L.M.G. Errors and accuracy estimates of laser data acquired by various laser scanning systems for topographic applications. ISPRS J. Photogramm. Remote Sens. 1998, 53, 245–261. [Google Scholar] [CrossRef]
- Yan, L.; Tan, J.; Liu, H. Automatic Registration of TLS-TLS and TLS-MLS Point Clouds Using a Genetic Algorithm. Sensors 2017, 17, 1979. [Google Scholar] [CrossRef]
- Besl, P.J.; Mckay, N.D. A Method for Registration of 3-D Shapes. Proc. Spie Int. Soc. Opt. Eng. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Censi, A. An ICP variant using a point-to-line metric. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008. [Google Scholar]
- Koide, K.; Yokozuka, M.; Oishi, S.; Banno, A. Voxelized GICP for Fast and Accurate 3D Point Cloud Registration. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 5 2021. [Google Scholar]
- Cheng, L.; Chen, S.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of Laser Scanning Point Clouds: A Review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Hu, H.; Zhu, Q.; Wu, B.; Zhang, Y. Hierarchical Regularization of Polygons for Photogrammetric Point Clouds of Oblique Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-1/W1, 35–40. [Google Scholar] [CrossRef]
- Stamos, I.; Leordeanu, M. Automated Feature-Based Range Registration of Urban Scenes of Large Scale. In Proceedings of the IEEE Internal Conference of Computer Vision & Pattern Recognition, Madison, WI, USA, 18–20 June 2003. [Google Scholar]
- Yang, B.; Zang, Y.; Dong, Z.; Huang, R. An automated method to register airborne and terrestrial laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 109, 62–76. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Zhao, G.; Dai, W. Hierarchical extraction of urban objects from mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2015, 99, 45–57. [Google Scholar] [CrossRef]
- Wang, F.; Hu, H.; Ge, X.; Xu, B.; Zhong, R.; Ding, Y.; Xie, X. Multientity Registration of Point Clouds for Dynamic Objects on Complex Floating Platform Using Object Silhouettes. IEEE Trans. Geosci. Remote Sens. 2020, 59, 769–783. [Google Scholar] [CrossRef]
- Yang, B.; Zang, Y. Automated registration of dense terrestrial laser-scanning point clouds using curves. ISPRS J. Photogramm. 2014, 95, 109–121. [Google Scholar] [CrossRef]
- Cheng, L.; Wu, Y.; Chen, S.; Zong, W.; Yuan, Y.; Sun, Y.; Zhuang, Q.; Li, M. A Symmetry-Based Method for LiDAR Point Registration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 285–299. [Google Scholar] [CrossRef]
- Rabbani, T.; Dijkman, S.; Heuvel, F.; Vosselman, G. An integrated approach for modelling and global registration of point clouds —ScienceDirect. ISPRS J. Photogramm. 2007, 61, 355–370. [Google Scholar] [CrossRef]
- Zang, Y.; Yang, B.; Li, J.; Guan, H. An Accurate TLS and UAV Image Point Clouds Registration Method for Deformation Detection of Chaotic Hillside Areas. Remote Sens. 2019, 11, 647. [Google Scholar] [CrossRef]
- Cai, Z.; Chin, T.J.; Bustos, A.P.; Schindler, K. Practical optimal registration of terrestrial LiDAR scan pairs. ISPRS J. Photogramm. 2019, 147, 118–131. [Google Scholar] [CrossRef]
- Fan, B.; Wu, F.; Hu, Z. Line Matching Leveraged by Point Correspondences. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Vosselman, G.; Coenen, M.; Rottensteiner, F. Contextual segment-based classification of airborne laser scanner data. ISPRS J. Photogramm. 2017, 128, 354–371. [Google Scholar] [CrossRef]
- Nurunnabi, A.A.M.; Nasser, M.; Imon, A.H.M.R. Identification and classification of multiple outliers, high leverage points and influential observations in linear regression. J. Appl. Stats 2016, 43, 509–525. [Google Scholar] [CrossRef]
- Huang, Z. Extensions to the k-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Disc. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Gioi, R.G.V.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A Fast Line Segment Detector with a False Detection Control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar] [CrossRef]
- Lu, W.; Neumann, U.; You, S. Wide-Baseline Image Matching using Line Signatures. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009. [Google Scholar]
- Ferrari, V.; Fevrier, L.; Jurie, F.; Schmid, C. Groups of Adjacent Contour Segments for Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 36–51. [Google Scholar] [CrossRef]
- Ge, X.; Hu, H. Object-based incremental registration of terrestrial point clouds in an urban environment. ISPRS J. Photogramm. 2020, 161, 218–232. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Liang, F.; Huang, R.; Scherer, S. Hierarchical registration of unordered TLS point clouds based on binary shape context descriptor. ISPRS J. Photogramm. 2018, 144, 61–79. [Google Scholar] [CrossRef]






| Data Set | Abbreviation | Range (m) | Points | Average Point Distance (m) |
|---|---|---|---|---|
| SWJTU | SP | 1200 × 600 | 659,318,734 | 0.01 |
| SALS | 1800 × 1600 | 12,710,409 | 0.4 | |
| SMLS | 300 × 300 | 22,456,066 | 0.05 | |
| QEC | QP | 380 × 380 | 140,513,227 | 0.01 |
| QALS | 300 × 300 | 6,757,291 | 0.08 |
| Line1 | Line2 | Line3 | Line4 | |
|---|---|---|---|---|
| SMLS | 57.5366 | 38.4725 | 105.655 | 102.468 |
| SP | 44.7318 | 30.3245 | 81.548 | 78.8507 |
| SP * | 57.5932 | 39.0434 | 104.9948 | 101.522 |
| −0.0566 | −0.5709 | 0.6602 | 0.946 | |
| 99.9% | 98.5% | 99.4% | 99.0% |
| Data Set | Candidate Line Segment | The Number of Matches | Correct Match | Incorrect Match |
|---|---|---|---|---|
| Original SMLS | 373 | 12 | 2 | 10 |
| Original SP | 628 | |||
| Simplify SMLS | 121 | 35 | 32 | 3 |
| Simplify SP | 381 |
| SMLS + SP | SALS + SP | SMLS + SALS | QP + QALS | |
|---|---|---|---|---|
| 0.015 | 0.32 | 0.24 | 0.29 | |
| 0.03 | 0.09 | 0.12 | 0.08 |
| Average Nearest Point Distance | MSE | RMSE | ||
|---|---|---|---|---|
| SP-SMLS | GICP | 1.33954 | 6.3839 | 2.52664 |
| Purposed method | 1.47263 | 6.31827 | 2.51362 | |
| QP-QALS | Coarse registration | 3.25631 | 2.82787 | 1.68163 |
| GICP | 0.94886 | 1.71269 | 1.3087 | |
| Purposed method | 0.302516 | 0.613933 | 0.783539 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Ge, X.; Li, S.; Xu, B.; Wang, Z. Linear-Based Incremental Co-Registration of MLS and Photogrammetric Point Clouds. Remote Sens. 2021, 13, 2195. https://doi.org/10.3390/rs13112195
Li S, Ge X, Li S, Xu B, Wang Z. Linear-Based Incremental Co-Registration of MLS and Photogrammetric Point Clouds. Remote Sensing. 2021; 13(11):2195. https://doi.org/10.3390/rs13112195
Chicago/Turabian StyleLi, Shiming, Xuming Ge, Shengfu Li, Bo Xu, and Zhendong Wang. 2021. "Linear-Based Incremental Co-Registration of MLS and Photogrammetric Point Clouds" Remote Sensing 13, no. 11: 2195. https://doi.org/10.3390/rs13112195
APA StyleLi, S., Ge, X., Li, S., Xu, B., & Wang, Z. (2021). Linear-Based Incremental Co-Registration of MLS and Photogrammetric Point Clouds. Remote Sensing, 13(11), 2195. https://doi.org/10.3390/rs13112195







