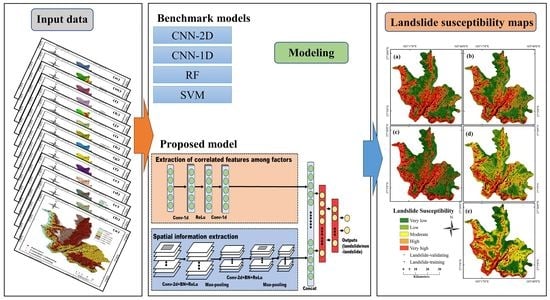
Incorporating Landslide Spatial Information and Correlated Features among Conditioning Factors for Landslide Susceptibility Mapping
Abstract
1. Introduction
2. Study Area and Materials
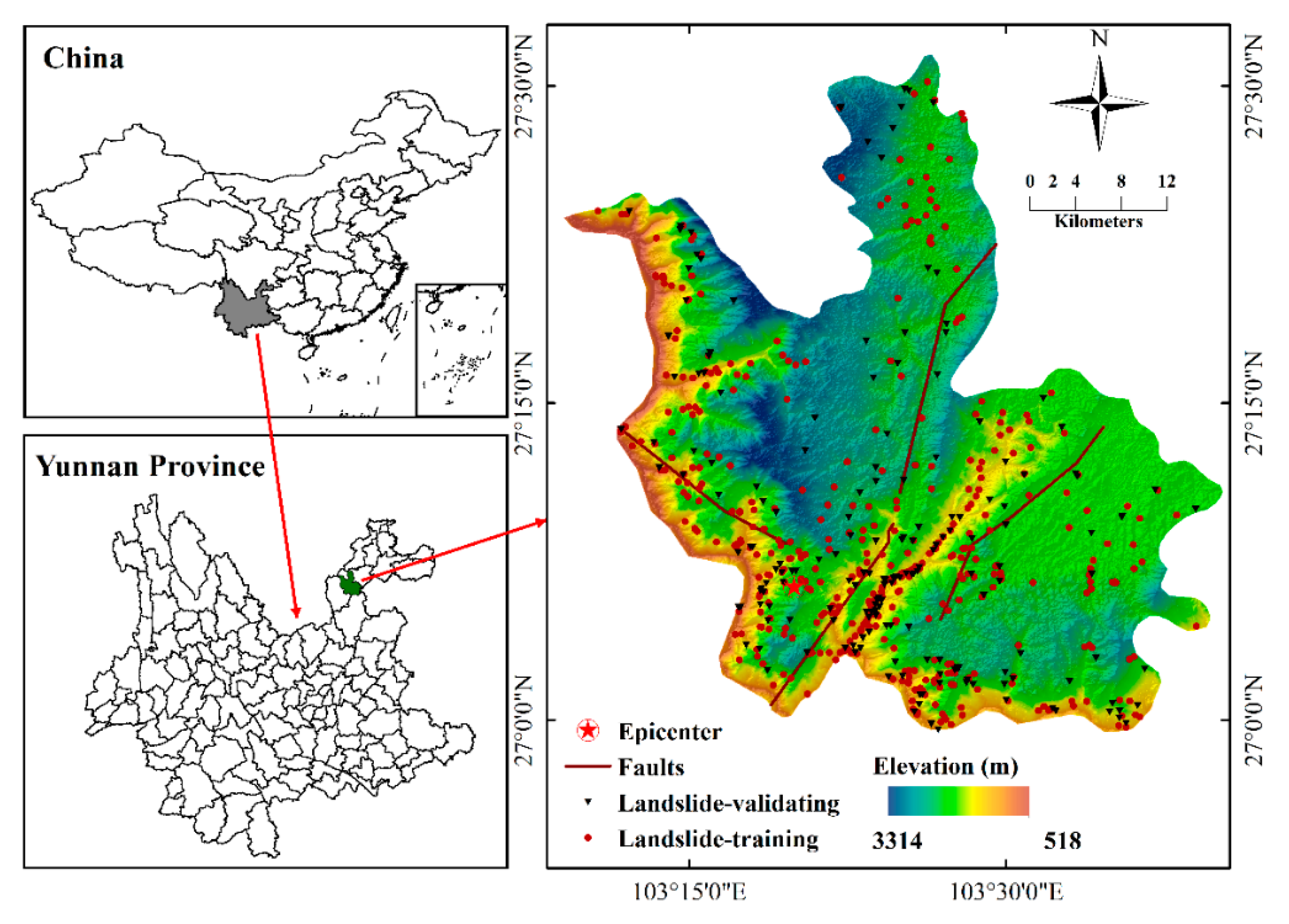
2.1. Description of the Study Area
2.2. Landslide Inventory Mapping
2.3. Landslide Conditioning Factors
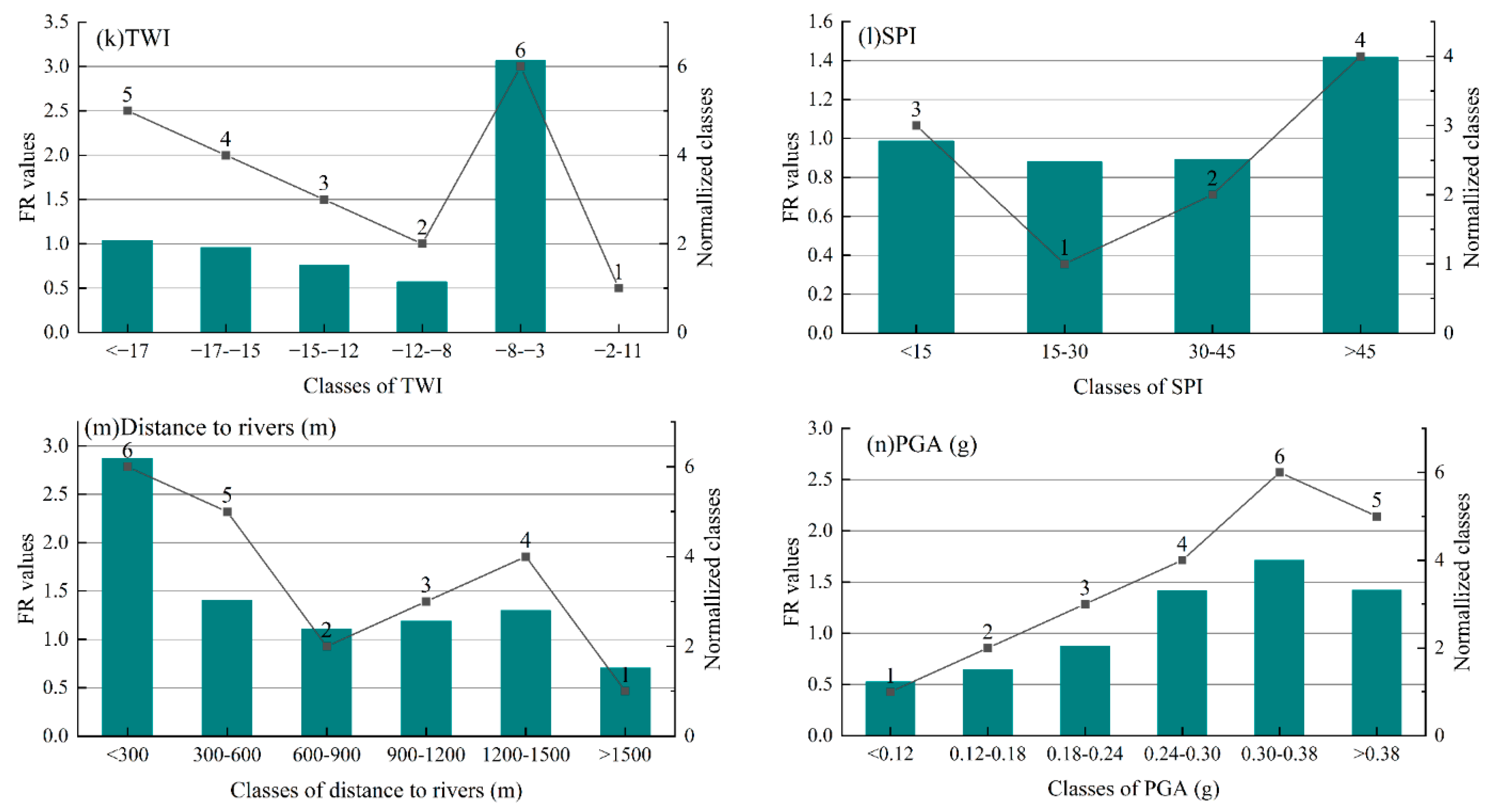
2.3.1. Topographic Factors
2.3.2. Geological Factors
2.3.3. Land Use and Land Cover Factors
2.3.4. Hydrological Factors
2.3.5. Geophysical Factor
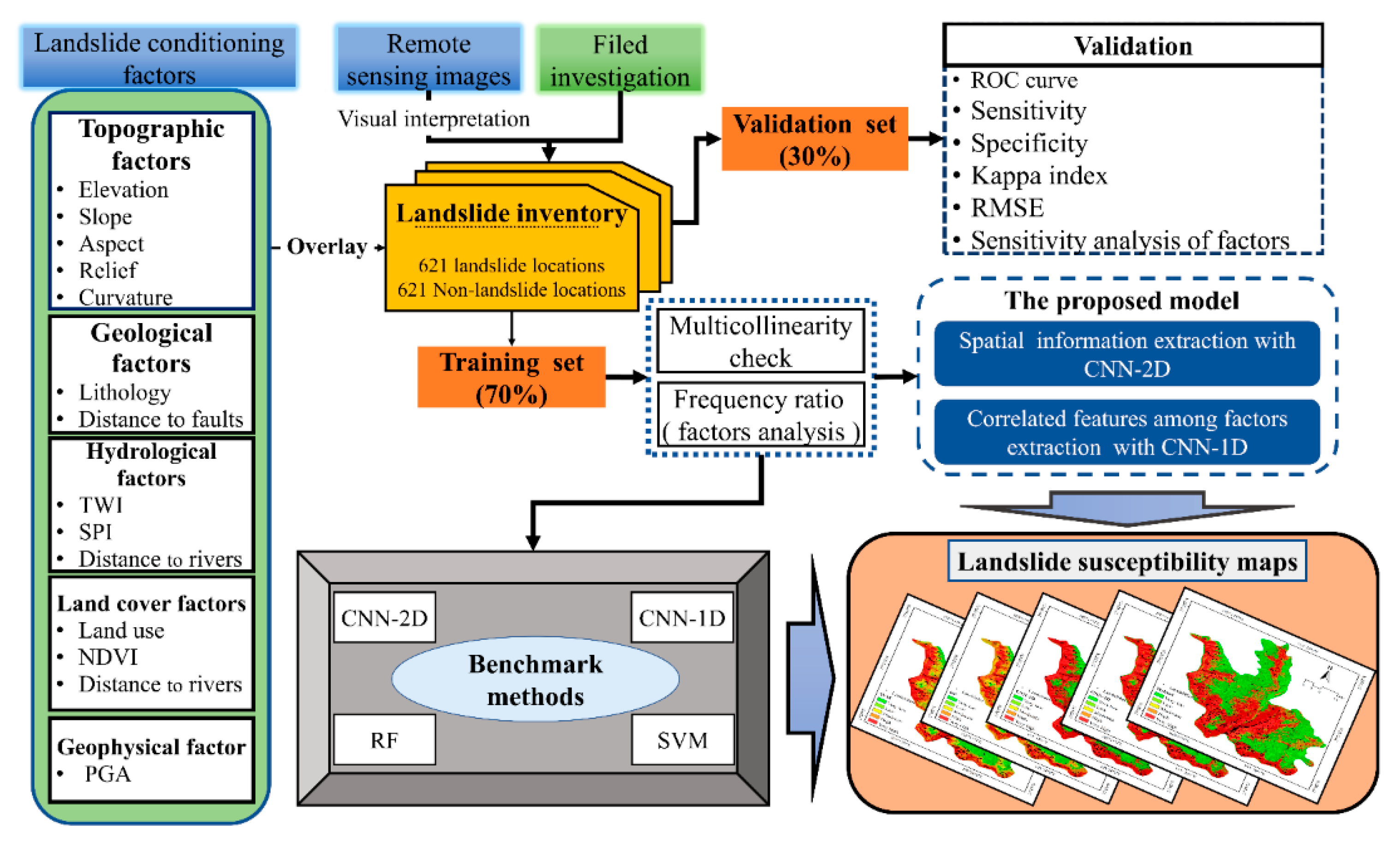
3. Methodology
3.1. Conditioning Factors Analysis
3.1.1. Multicollinearity Analysis
3.1.2. Frequency Ratio Method
3.2. Convolutional Neural Networks
3.3. Proposed Model
3.4. Evaluation and Comparison Methods
3.5. Sensitivity Analysis of Conditioning Factors
4. Results
4.1. Selection and Analysis of the Landslide Conditioning Factors
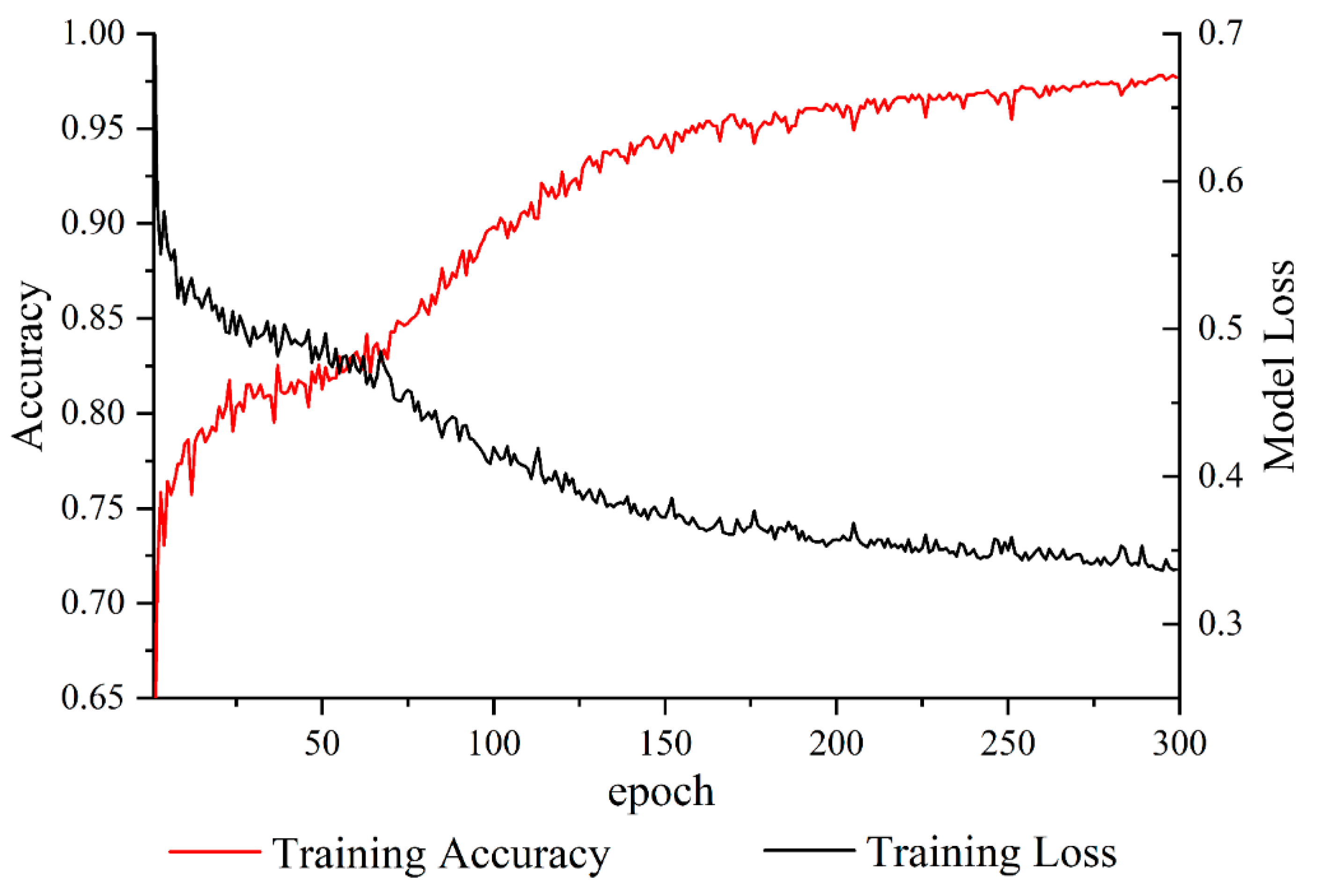
4.2. Construction of Proposed Model
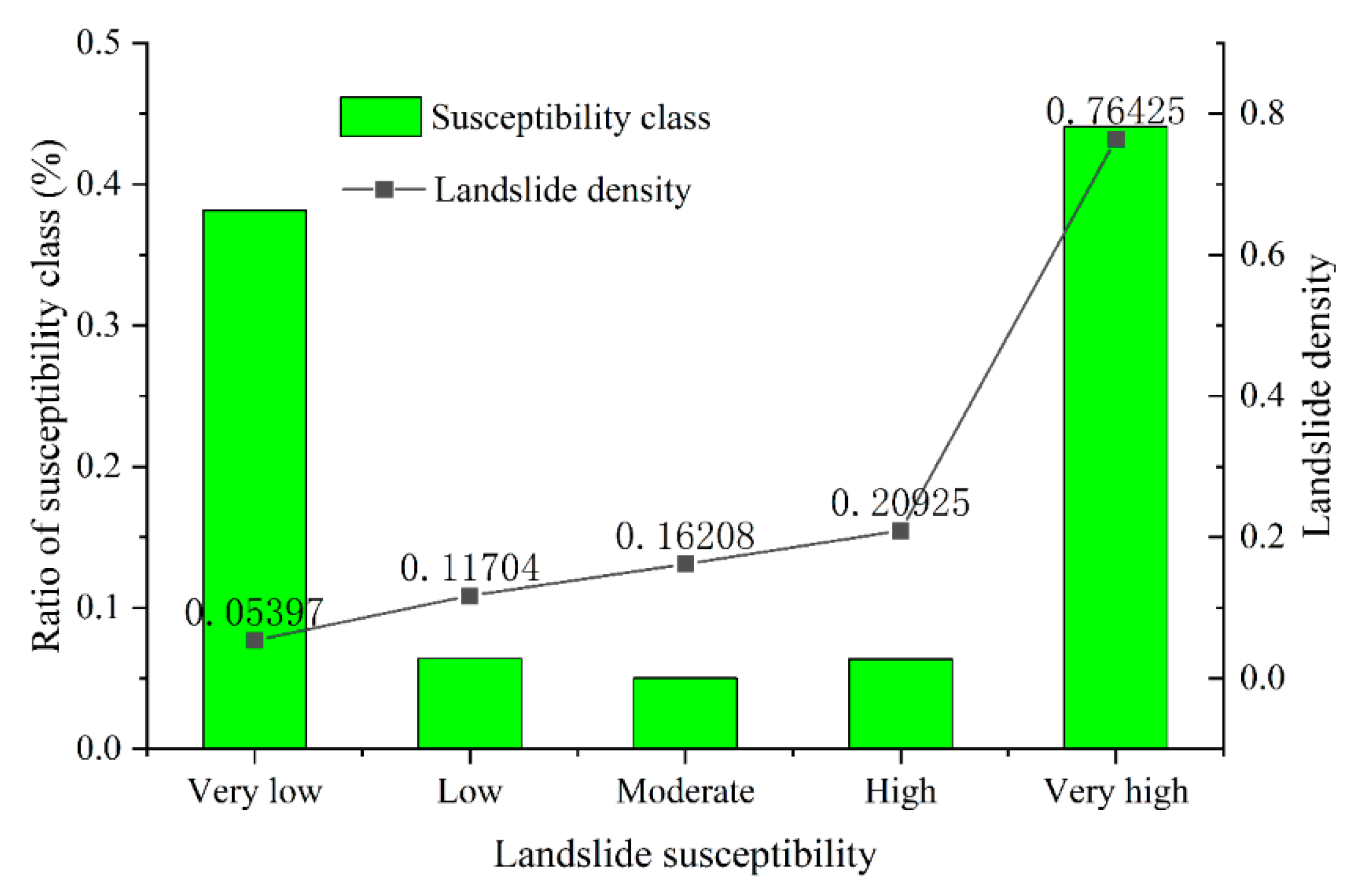
4.3. Generation of Landslide Susceptibility Maps
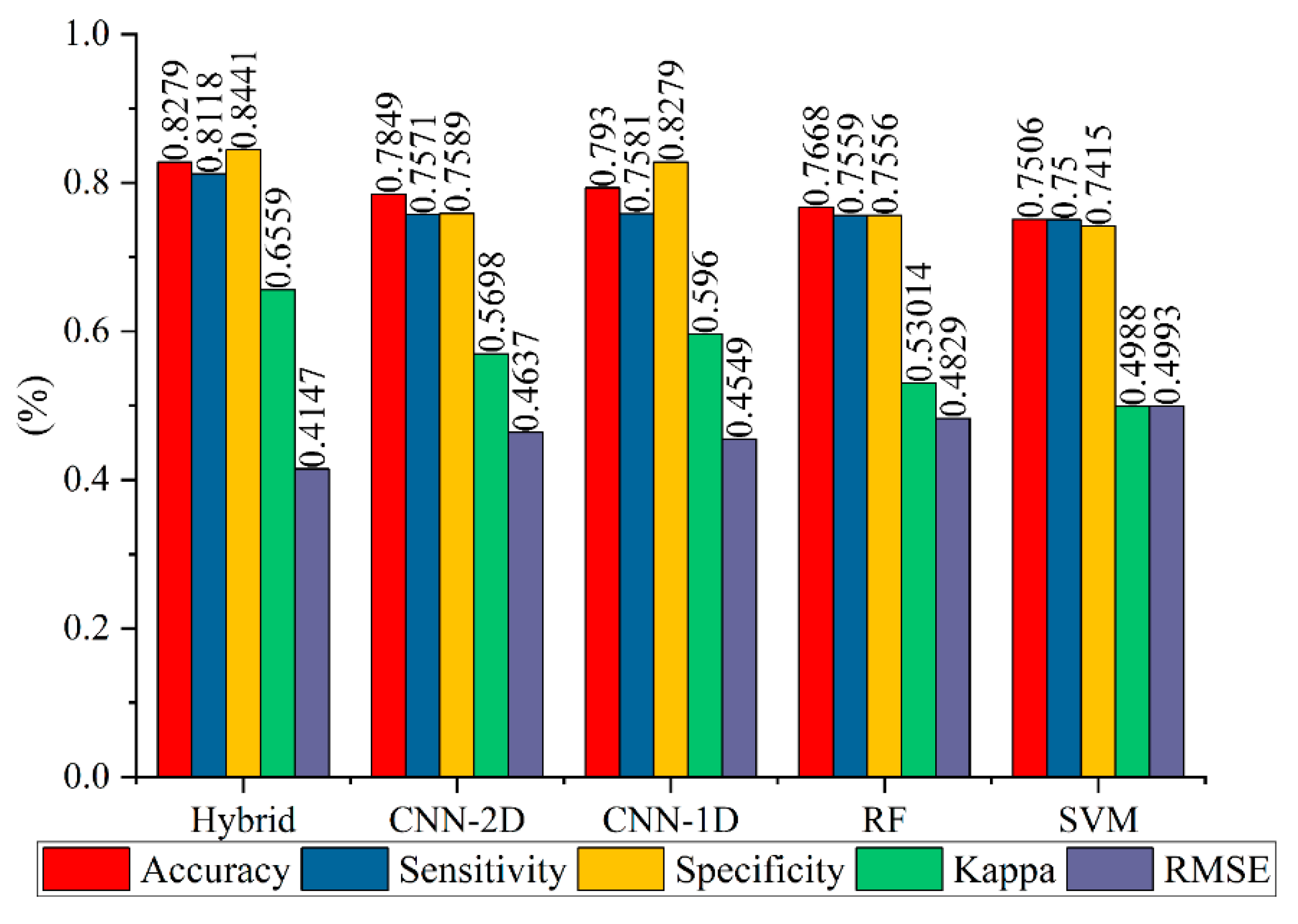
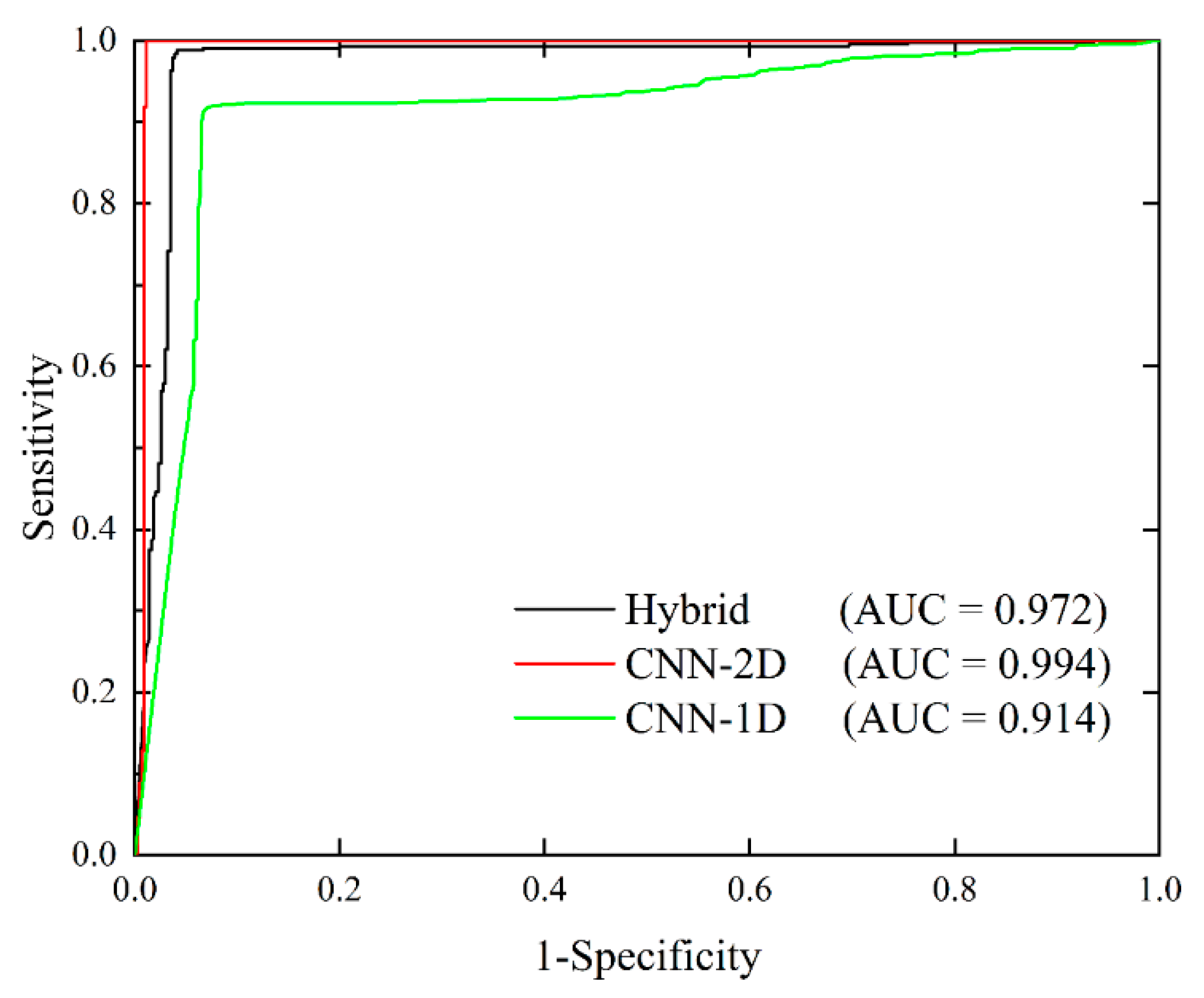
4.4. Evaluation and Comparison of Results
4.5. Sensitivity Analysis Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Hassangavyar, M.B.; Damaneh, H.E.; Pham, Q.B.; Linh, N.T.T.; Tiefenbacher, J.; Bach, Q.-V. Evaluation of re-sampling methods on performance of machine learning models to predict landslide susceptibility. Geocarto Int. 2020, 1–23. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Do landslides follow landslides? Insights in path dependency from a multi-temporal landslide inventory. Landslides 2016, 14, 547–558. [Google Scholar] [CrossRef]
- Hess, D.M.; Leshchinsky, B.A.; Bunn, M.; Benjamin Mason, H.; Olsen, M.J. A simplified three-dimensional shallow landslide susceptibility framework considering topography and seismicity. Landslides 2017, 14, 1677–1697. [Google Scholar] [CrossRef]
- Özdemir, A.; Delikanli, M. A geotechnical investigation of the retrogressive Yaka Landslide and the debris flow threatening the town of Yaka (Isparta, SW Turkey). Nat. Hazards 2008, 49, 113–136. [Google Scholar] [CrossRef]
- Chen, X.-L.; Liu, C.-G.; Wang, M.-M.; Zhou, Q. Causes of unusual distribution of coseismic landslides triggered by the Mw 6.1 2014 Ludian, Yunnan, China earthquake. J. Asian Earth Sci. 2018, 159, 17–23. [Google Scholar] [CrossRef]
- Li, W.-L.; Huang, R.-Q.; Tang, C.; Xu, Q.; van Westen, C. Co-seismic landslide inventory and susceptibility mapping in the 2008 Wenchuan earthquake disaster area, China. J. Mt. Sci. 2013, 10, 339–354. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, C.; Ma, S.; Xu, X.; Wang, S.; Zhang, H. Inventory and Spatial Distribution of Landslides Triggered by the 8th August 2017 MW 6.5 Jiuzhaigou Earthquake, China. J. Earth Sci. 2018, 30, 206–217. [Google Scholar] [CrossRef]
- Yang, Z.-H.; Lan, H.-X.; Gao, X.; Li, L.-P.; Meng, Y.-S.; Wu, Y.-M. Urgent landslide susceptibility assessment in the 2013 Lushan earthquake-impacted area, Sichuan Province, China. Nat. Hazards 2014, 75, 2467–2487. [Google Scholar] [CrossRef]
- Jaafari, A.; Panahi, M.; Pham, B.T.; Shahabi, H.; Bui, D.T.; Rezaie, F.; Lee, S. Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena 2019, 175, 430–445. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Constantin, M.; Bednarik, M.; Jurchescu, M.C.; Vlaicu, M. Landslide susceptibility assessment using the bivariate statistical analysis and the index of entropy in the Sibiciu Basin (Romania). Environ. Earth Sci. 2010, 63, 397–406. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. GIS-based landslide susceptibility assessment using optimized hybrid machine learning methods. Catena 2021, 196. [Google Scholar] [CrossRef]
- Panchal, S.; Shrivastava, A.K. Application of analytic hierarchy process in landslide susceptibility mapping at regional scale in GIS environment. J. Stat. Manag. Syst. 2020, 23, 199–206. [Google Scholar] [CrossRef]
- Moragues, S.; Lenzano, M.G.; Lanfri, M.; Moreiras, S.; Lannutti, E.; Lenzano, L. Analytic hierarchy process applied to landslide susceptibility mapping of the North Branch of Argentino Lake, Argentina. Nat. Hazards 2020, 105, 915–941. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. GIS-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping. Environ. Geol. 2007, 54, 311–324. [Google Scholar] [CrossRef]
- Li, L.; Lan, H.; Guo, C.; Zhang, Y.; Li, Q.; Wu, Y. A modified frequency ratio method for landslide susceptibility assessment. Landslides 2016, 14, 727–741. [Google Scholar] [CrossRef]
- Shafapour Tehrany, M.; Kumar, L.; Neamah Jebur, M.; Shabani, F. Evaluating the application of the statistical index method in flood susceptibility mapping and its comparison with frequency ratio and logistic regression methods. Geomat. Nat. Hazards Risk 2018, 10, 79–101. [Google Scholar] [CrossRef]
- Zhang, T.-Y.; Han, L.; Zhang, H.; Zhao, Y.-H.; Li, X.-A.; Zhao, L. GIS-based landslide susceptibility mapping using hybrid integration approaches of fractal dimension with index of entropy and support vector machine. J. Mt. Sci. 2019, 16, 1275–1288. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Kornejady, A.; Zhang, N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma 2017, 305, 314–327. [Google Scholar] [CrossRef]
- Liu, R.; Li, L.; Pirasteh, S.; Lai, Z.; Yang, X.; Shahabi, H. The performance quality of LR, SVM, and RF for earthquake-induced landslides susceptibility mapping incorporating remote sensing imagery. Arabian J. Geosci. 2021, 14. [Google Scholar] [CrossRef]
- Xu, C.; Xu, X.; Dai, F.; Saraf, A.K. Comparison of different models for susceptibility mapping of earthquake triggered landslides related with the 2008 Wenchuan earthquake in China. Comput. Geosci. 2012, 46, 317–329. [Google Scholar] [CrossRef]
- Kumar, D.; Thakur, M.; Dubey, C.S.; Shukla, D.P. Landslide susceptibility mapping & prediction using Support Vector Machine for Mandakini River Basin, Garhwal Himalaya, India. Geomorphology 2017, 295, 115–125. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at Hoa Binh province (Vietnam) using an adaptive neuro-fuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar] [CrossRef]
- Pham, V.D.; Nguyen, Q.-H.; Nguyen, H.-D.; Pham, V.-M.; Vu, V.M.; Bui, Q.-T. Convolutional Neural Network—Optimized Moth Flame Algorithm for Shallow Landslide Susceptible Analysis. IEEE Access 2020, 8, 32727–32736. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ming, D.; Ling, X.; Lv, X.; Zhou, C. Landslide Susceptibility Mapping Using Feature Fusion Based CPCNN-ML in Lantau Island, Hong Kong. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, Y.; Peng, G. Landslide Susceptibility Assessment Using Integrated Deep Learning Algorithm along the China-Nepal Highway. Sensors 2018, 18, 4436. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kornejady, A.; Kerle, N.; Shabani, F. Investigating the effects of different landslide positioning techniques, landslide partitioning approaches, and presence-absence balances on landslide susceptibility mapping. Catena 2020, 187. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Merghadi, A.; Shirzadi, A.; Nguyen, H.; Hussain, Y.; Avtar, R.; Chen, Y.; Pham, B.T.; Yamagishi, H. Different sampling strategies for predicting landslide susceptibilities are deemed less consequential with deep learning. Sci. Total Environ. 2020, 720, 137320. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Zhang, Z.; Zhang, W.; Jia, H.; Zhang, J. Landslide susceptibility mapping using multiscale sampling strategy and convolutional neural network: A case study in Jiuzhaigou region. Catena 2020, 195. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, L.; Hu, H.; Pirasteh, S.; Li, H.; Xie, X. Unsupervised Feature Learning to Improve Transferability of Landslide Susceptibility Representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3917–3930. [Google Scholar] [CrossRef]
- Jing-chun, X.; Rui, L.; Hui-wen, L.; Zi-li, L. Analysis of landslide hazard area in Ludian earthquake based on Random Forests. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2015. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Lu, P.-Y.; Hao, M.-H. Landslides triggered by the 3 August 2014 Ludian earthquake in China: Geological properties, geomorphologic characteristics and spatial distribution analysis. Geomat. Nat. Hazards Risk 2015, 7, 1219–1241. [Google Scholar] [CrossRef]
- Gnyawali, K.R.; Zhang, Y.; Wang, G.; Miao, L.; Pradhan, A.M.S.; Adhikari, B.R.; Xiao, L. Mapping the susceptibility of rainfall and earthquake triggered landslides along China–Nepal highways. Bull. Eng. Geol. Environ. 2019, 79, 587–601. [Google Scholar] [CrossRef]
- Douglas, J. Earthquake ground motion estimation using strong-motion records: A review of equations for the estimation of peak ground acceleration and response spectral ordinates. Earth Sci. Rev. 2003, 61, 43–104. [Google Scholar] [CrossRef]
- Huang, H.-P.; Yang, K.-C.; Lin, B.-W. Statistical evaluation of the effect of earthquake with other related factors on landslide susceptibility: Using the watershed area of Shihmen reservoir in Taiwan as a case study. Environ. Earth Sci. 2012, 69, 2151–2166. [Google Scholar] [CrossRef]
- Chen, K.; Yu, Y.X.; Gao, M.T.; Kang, C.C. ShakeMap of peak ground acceleration for 2014 Ludian, Yunnan, Ms6.5 earthquake. Acta Seismol. Sin. 2015, 429–436. [Google Scholar] [CrossRef]
- Hidalgo-Mompeán, F.; Gómez Fernández, J.F.; Cerruela-García, G.; Crespo Márquez, A. Dimensionality analysis in machine learning failure detection models. A case study with LNG compressors. Comput. Ind. 2021, 128. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2015, 13, 361–378. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Zhu, A.X. Landslide susceptibility evaluating using artificial intelligence method in the Youfang district (China). Environ. Earth Sci. 2019, 78. [Google Scholar] [CrossRef]
- Sfikas, K.; Pratikakis, I.; Theoharis, T. Ensemble of PANORAMA-based convolutional neural networks for 3D model classification and retrieval. Comput. Graph. 2018, 71, 208–218. [Google Scholar] [CrossRef]
- Ramakrishnan, S.; Muthanantha Murugavel, A.S.; Sathiyamurthi, P.; Ramprasath, J. Seizure Detection with Local Binary Pattern and CNN Classifier. J. Phys. Conf. Ser. 2021, 1767. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Guo, H.; Liu, J.; Xiao, Z.; Xiao, L. Deep CNN-based hyperspectral image classification using discriminative multiple spatial-spectral feature fusion. Remote Sens. Lett. 2020, 11, 827–836. [Google Scholar] [CrossRef]
- Shi, H.; Cao, G.; Ge, Z.; Zhang, Y.; Fu, P. Double-Branch Network with Pyramidal Convolution and Iterative Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 1403. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Lin, Z. Spatial-Spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Chen, T.; Zhu, L.; Niu, R.-Q.; Trinder, C.J.; Peng, L.; Lei, T. Mapping landslide susceptibility at the Three Gorges Reservoir, China, using gradient boosting decision tree, random forest and information value models. J. Mt. Sci. 2020, 17, 670–685. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Islam, A.; Talukdar, S.; Mahato, S.; Ziaul, S.; Eibek, K.U.; Akhter, S.; Pham, Q.B.; Mohammadi, B.; Karimi, F.; Linh, N.T.T. Machine learning algorithm-based risk assessment of riparian wetlands in Padma River Basin of Northwest Bangladesh. Environ. Sci. Pollut. Res. Int. 2021. [Google Scholar] [CrossRef] [PubMed]
- Shirvani, Z. A Holistic Analysis for Landslide Susceptibility Mapping Applying Geographic Object-Based Random Forest: A Comparison between Protected and Non-Protected Forests. Remote Sens. 2020, 12, 434. [Google Scholar] [CrossRef]
- Park, N.-W. Using maximum entropy modeling for landslide susceptibility mapping with multiple geoenvironmental data sets. Environ. Earth Sci. 2014, 73, 937–949. [Google Scholar] [CrossRef]
- Lujan-Moreno, G.A.; Howard, P.R.; Rojas, O.G.; Montgomery, D.C. Design of experiments and response surface methodology to tune machine learning hyperparameters, with a random forest case-study. Expert Syst. Appl. 2018, 109, 195–205. [Google Scholar] [CrossRef]
- Meunier, P.; Hovius, N.; Haines, A.J. Regional patterns of earthquake-triggered landslides and their relation to ground motion. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Chang, K.-T.; Chiang, S.-H.; Hsu, M.-L. Modeling typhoon- and earthquake-induced landslides in a mountainous watershed using logistic regression. Geomorphology 2007, 89, 335–347. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Duan, G.; Peng, L. Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sens. 2021, 13, 238. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Singh, S.K.; Shirzadi, A.; Shahabi, H.; Tran, T.-T.-T.; Bui, D.T. Landslide susceptibility modeling using Reduced Error Pruning Trees and different ensemble techniques: Hybrid machine learning approaches. Catena 2019, 175, 203–218. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186. [Google Scholar] [CrossRef]
- Sameen, M.I.; Sarkar, R.; Pradhan, B.; Drukpa, D.; Alamri, A.M.; Park, H.-J. Landslide spatial modelling using unsupervised factor optimisation and regularised greedy forests. Comput. Geosci. 2020, 134. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Zhang, Q.; Ye, S.; Ren, B. A novel hybrid approach for landslide susceptibility mapping integrating analytical hierarchy process and normalized frequency ratio methods with the cloud model. Geomorphology 2019, 327, 170–187. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2018, 112, 23–37. [Google Scholar] [CrossRef]







| Conditioning Factors | Collinearity Statistics | |
|---|---|---|
| Tolerance | VIF | |
| Aspect | 0.967 | 1.034 |
| Curvature | 0.892 | 1.121 |
| Elevation | 0.548 | 1.823 |
| Distance to faults | 0.92 | 1.087 |
| Land use | 0.787 | 1.271 |
| Lithology | 0.829 | 1.206 |
| NDVI | 0.741 | 1.35 |
| PGA | 0.806 | 1.241 |
| Relief | 0.32 | 3.124 |
| Distance to rivers | 0.566 | 1.766 |
| Distance to roads | 0.74 | 1.352 |
| Slope | 0.287 | 3.488 |
| SPI | 0.733 | 1.365 |
| TWI | 0.584 | 1.712 |
| No. | Parameters | Values |
|---|---|---|
| 1 | Conventional kernel size (1D) | (3, 3) |
| 2 | Conventional kernel size (2D) | (3, 3) |
| 3 | Pooling size (2D) | (2, 2) |
| 4 | Loss function | Cross entropy |
| 5 | Optimizer | Adagrad |
| 6 | Epoch | 300 |
| 7 | Batch size | 32 |
| 8 | Learning rate | 0.08 |
| 9 | Activation function | ReLU |
| Classes | Hybrid | CNN-2D | CNN-1D | RF | SVM |
|---|---|---|---|---|---|
| Very low | 611.7 (38.1%) | 552.81 (34.5%) | 741.69 (46.2%) | 294 (18.3%) | 377.93 (22.6%) |
| Low | 102.69 (6.4%) | 176.45 (11.0%) | 35.99 (2.2%) | 356.09 (22.2%) | 293.84 (18.3%) |
| Moderate | 80.43 (5.0%) | 145.57 (9.1%) | 23.37 (1.5%) | 338.2 (21.1%) | 340.86 (21.3%) |
| High | 101.91 (6.3%) | 172.21 (10.7%) | 78.34 (4.9%) | 320.72 (20.0%) | 313.56 (19.6%) |
| Very high | 706.95 (44.1%) | 556.62 (34.7%) | 724.29 (45.2%) | 294.66 (18.4%) | 227.49 (17.3%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Liu, R.; Yang, M.; Chen, J.; Liu, T.; Yang, Y.; Chen, W.; Wang, Y. Incorporating Landslide Spatial Information and Correlated Features among Conditioning Factors for Landslide Susceptibility Mapping. Remote Sens. 2021, 13, 2166. https://doi.org/10.3390/rs13112166
Yang X, Liu R, Yang M, Chen J, Liu T, Yang Y, Chen W, Wang Y. Incorporating Landslide Spatial Information and Correlated Features among Conditioning Factors for Landslide Susceptibility Mapping. Remote Sensing. 2021; 13(11):2166. https://doi.org/10.3390/rs13112166
Chicago/Turabian StyleYang, Xin, Rui Liu, Mei Yang, Jingjue Chen, Tianqiang Liu, Yuantao Yang, Wei Chen, and Yuting Wang. 2021. "Incorporating Landslide Spatial Information and Correlated Features among Conditioning Factors for Landslide Susceptibility Mapping" Remote Sensing 13, no. 11: 2166. https://doi.org/10.3390/rs13112166
APA StyleYang, X., Liu, R., Yang, M., Chen, J., Liu, T., Yang, Y., Chen, W., & Wang, Y. (2021). Incorporating Landslide Spatial Information and Correlated Features among Conditioning Factors for Landslide Susceptibility Mapping. Remote Sensing, 13(11), 2166. https://doi.org/10.3390/rs13112166