Simulating Imaging Spectroscopy in Tropical Forest with 3D Radiative Transfer Modeling
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Remotely Sensed Data
2.2.1. Imaging Spectroscopy
2.2.2. Airborne Laser Scanning (ALS)
2.2.3. Red, Green and Blue (RGB) Imagery
2.3. Ground Information
2.3.1. Field Plot Network and Selected Sites for Simulation
- A plot of 80 × 80 m, hereafter referred to as Site A was dedicated to the adjustment of statistical models for the estimation of vegetation biochemical properties;
- A plot of 300 × 300 m, hereafter referred to as Site B, was dedicated to the comparison of the simulations with experimental data.
2.3.2. Individual Tree Crown Delineation
3. Methods
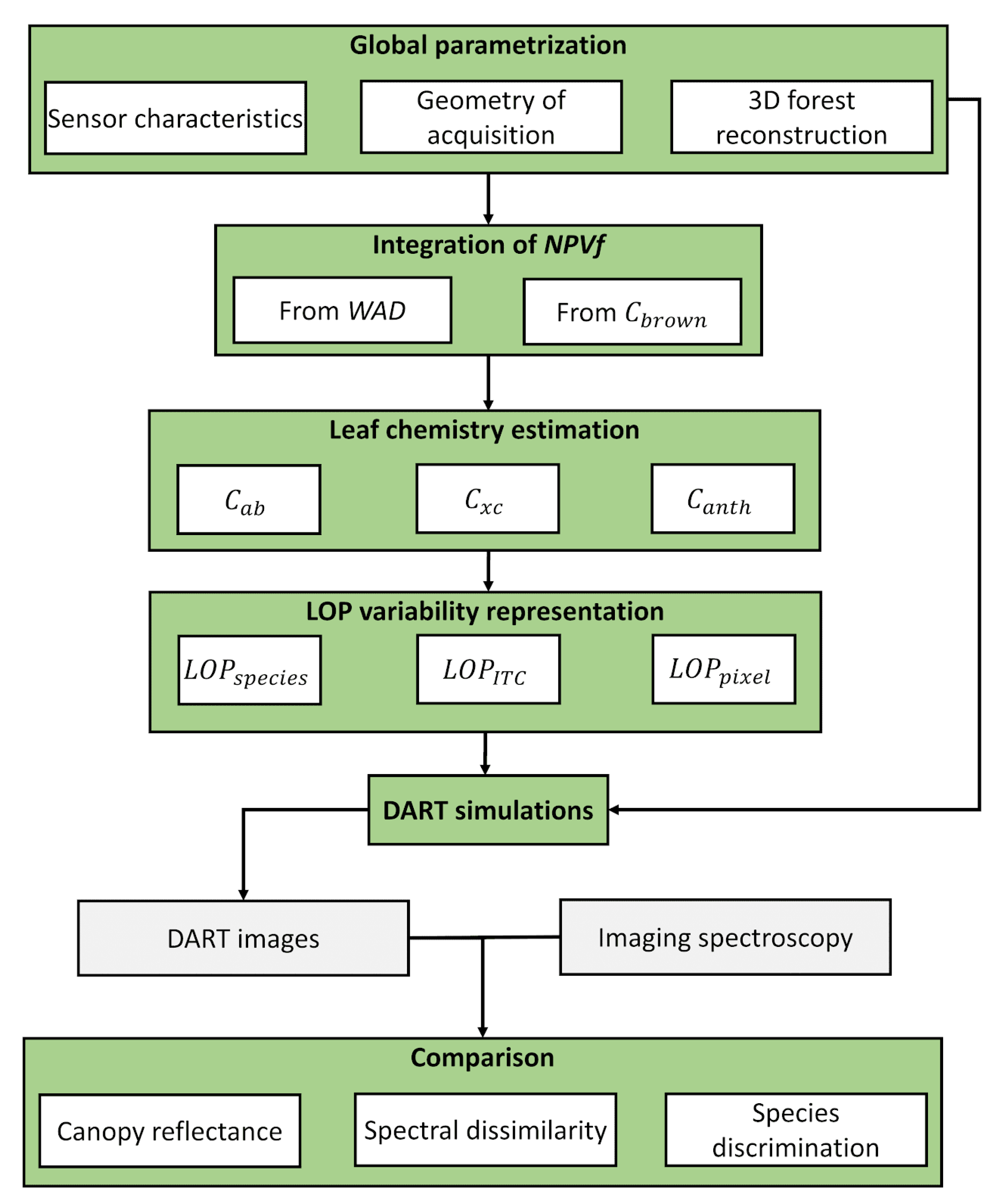
3.1. Overview of the Methodology
3.2. Presentation of Leaf and Canopy Models
3.2.1. Leaf Optical Properties Modeling with PROSPECT
3.2.2. Three-Dimensional (3D) Modeling of Canopy Reflectance with DART (Discrete Anisotropic Radiative Transfer)
3.3. Defining Scenarios for the Integration of Leaf Optical Properties (LOP) Heterogeneity in 3D Modeling
3.4. Definition of 3D Structure of the Canopy
- A hierarchical re-estimation of the transmittance based on a mixed linear model was performed in order to minimize the uncertainty associated with poor sampling of lower canopy voxels resulting from the gradual extinction of the laser beam (occlusion) [72].
- A reduction factor of 0.8 was applied to the re-estimated PAD in order to compensate for the limited penetration achieved by the LMSQ780 LiDAR when flying at 900 m. This factor was set to fit the extinction profile obtained over the same area while operating at lower altitude (450 m) (G. Vincent, in prep).
3.5. Integration of Non-Photosynthetic Vegetation Fraction (NPVf) into Simulations
3.5.1. Estimation of NPVfWAD
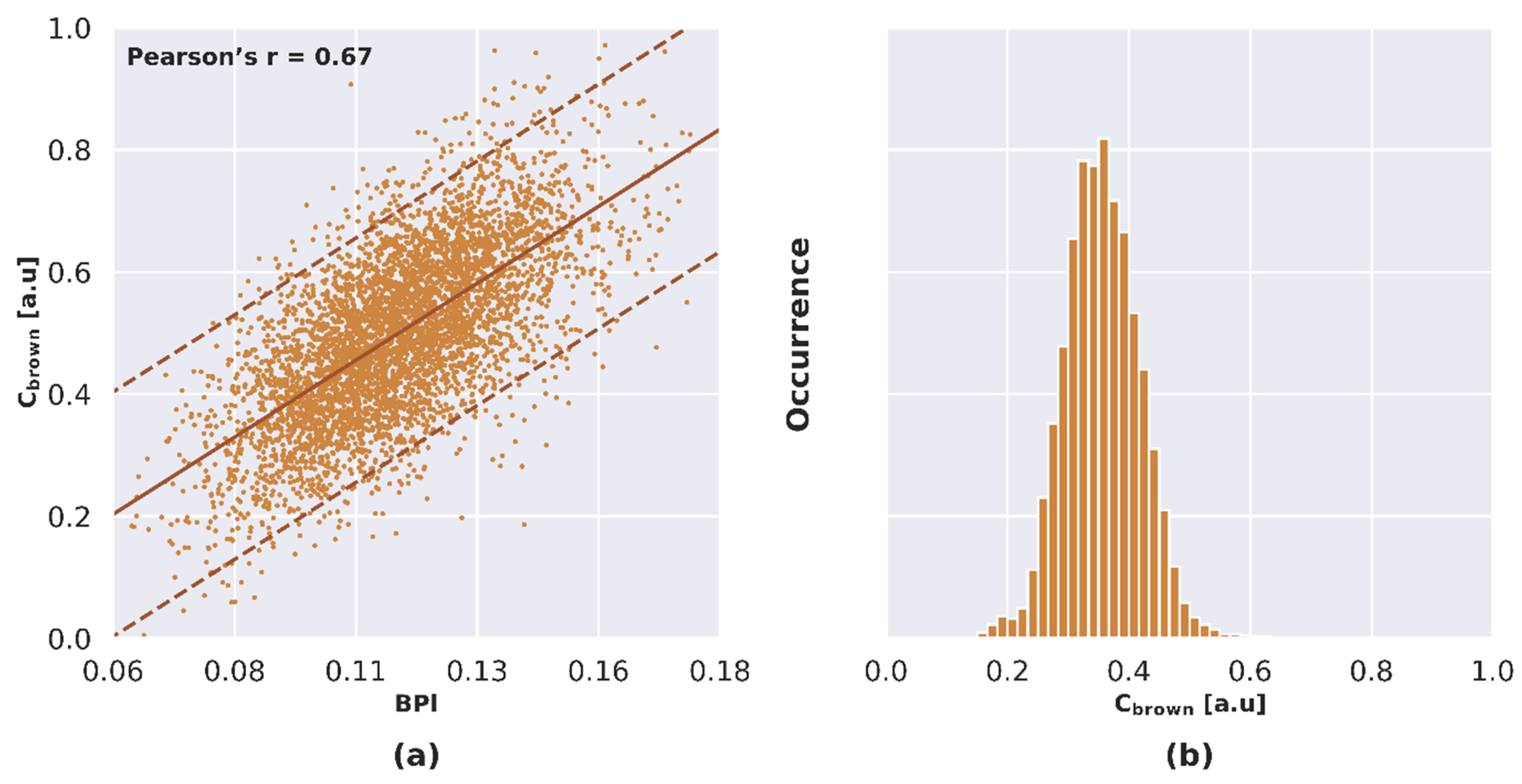
3.5.2. Estimation of Leaf Brown Pigment Content
3.6. Simulation of Leaf Optical Properties through the Estimation of Leaf Pigment Content
3.6.1. Adjustment of Models for the Estimation of Leaf Pigments (Site A)
3.6.2. Application of Models for the Estimation of Leaf Pigments (Site B)
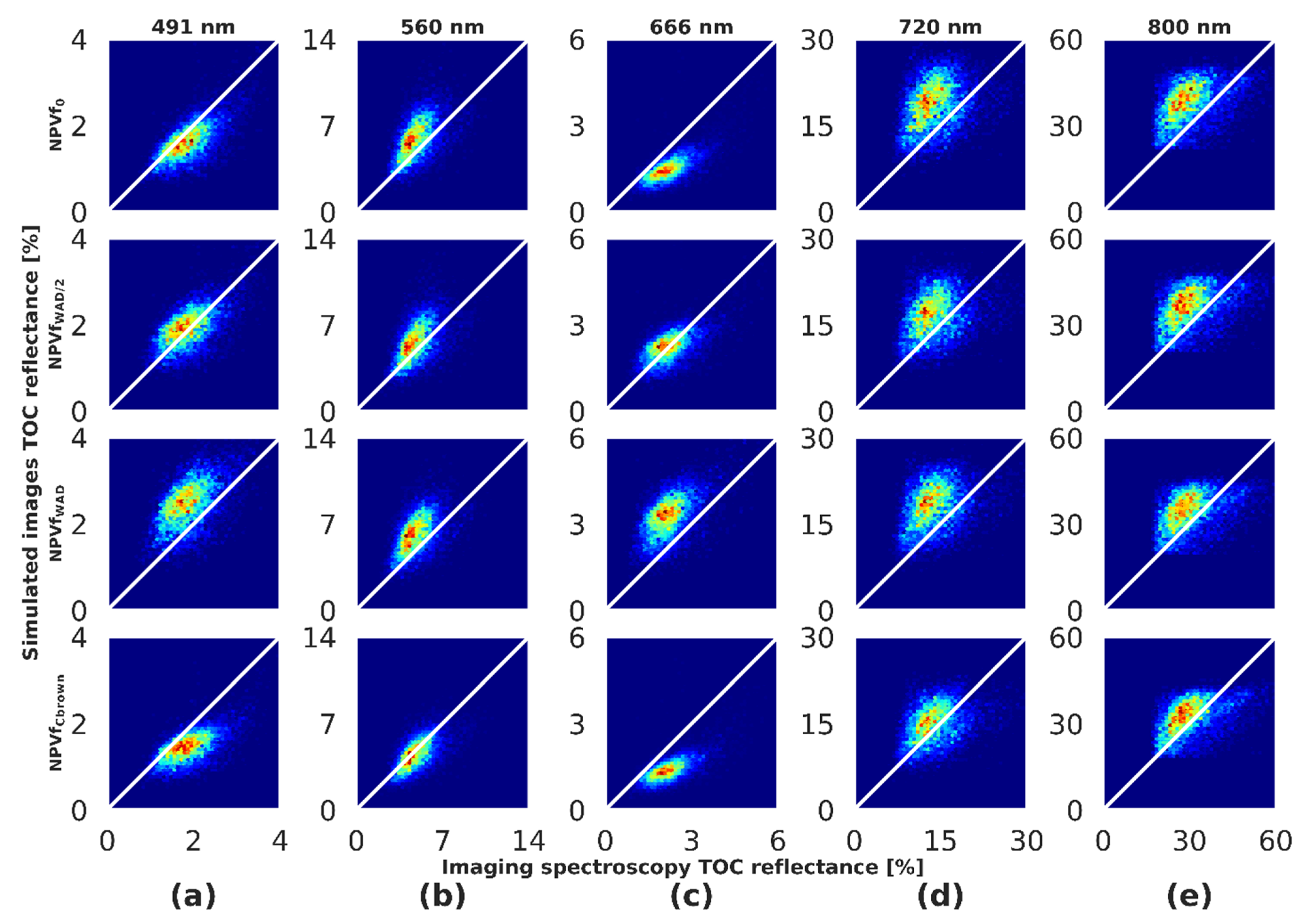
3.7. Comparing Simulations with Airborne Acquisitions
3.7.1. Radiometric Comparison
3.7.2. Analysis of Spectral Dissimilarity
3.7.3. Species Discrimination
4. Results
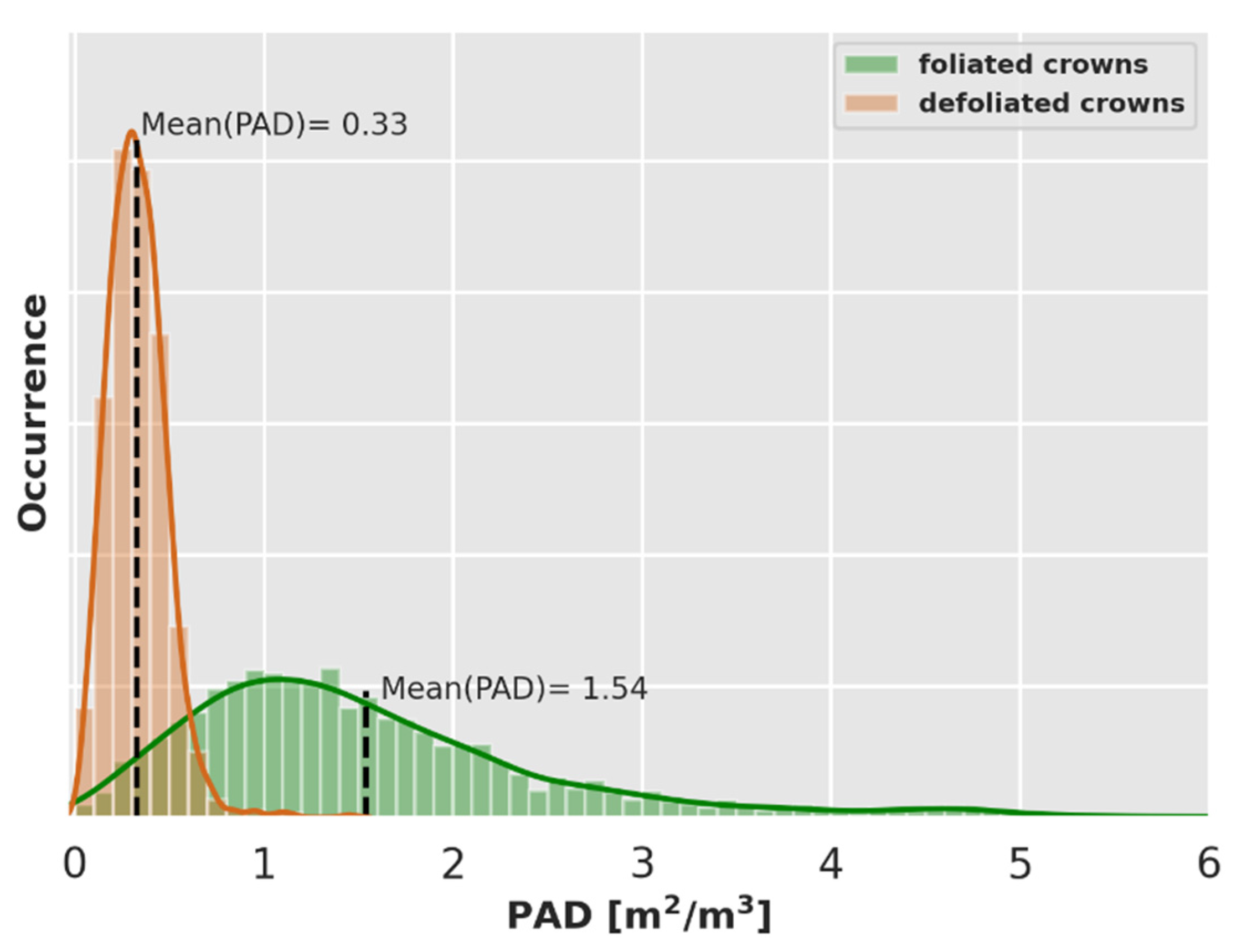
4.1. Definition of the 3D Structure of the Forest
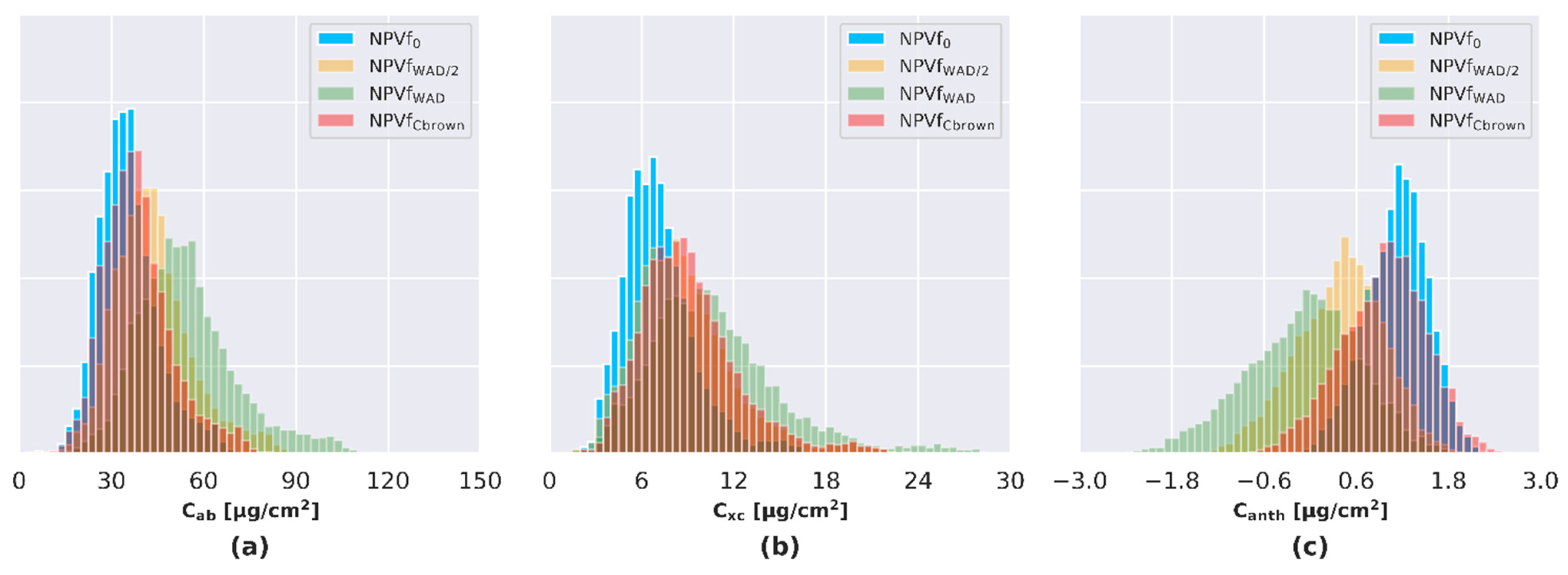
4.2. Estimation of NPVf
4.2.1. NPVf Derived from Wood Area Density (WAD)
4.2.2. NPVf Derived from Leaf Brown Pigment Content
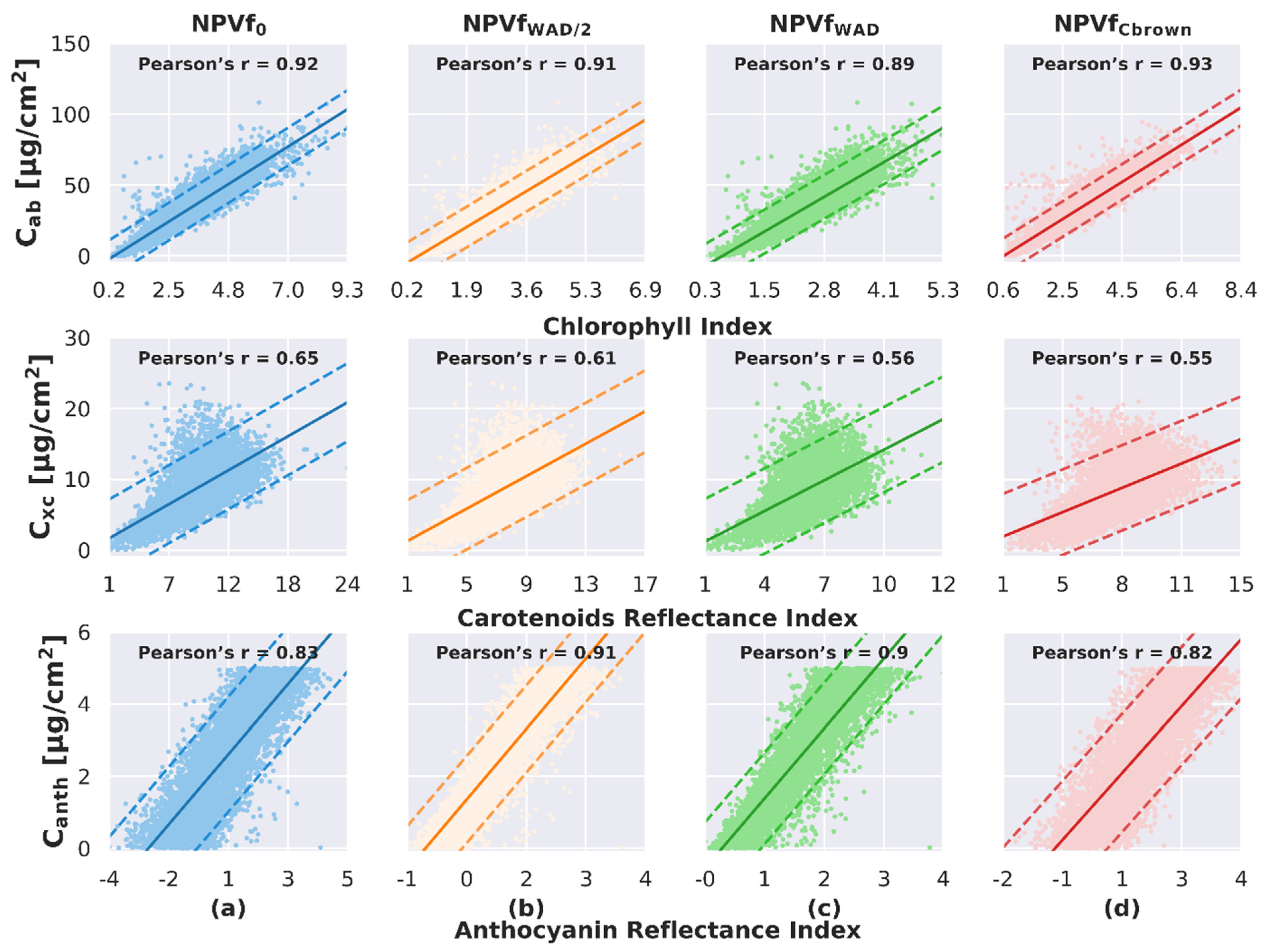
4.3. Influence of NPVf on the Pigment Content Estimate
4.3.1. Impact on the Adjustment of the Relationship between Spectral Indices and Pigment Content
4.3.2. Implication of the Application of the Models on Experimental Data
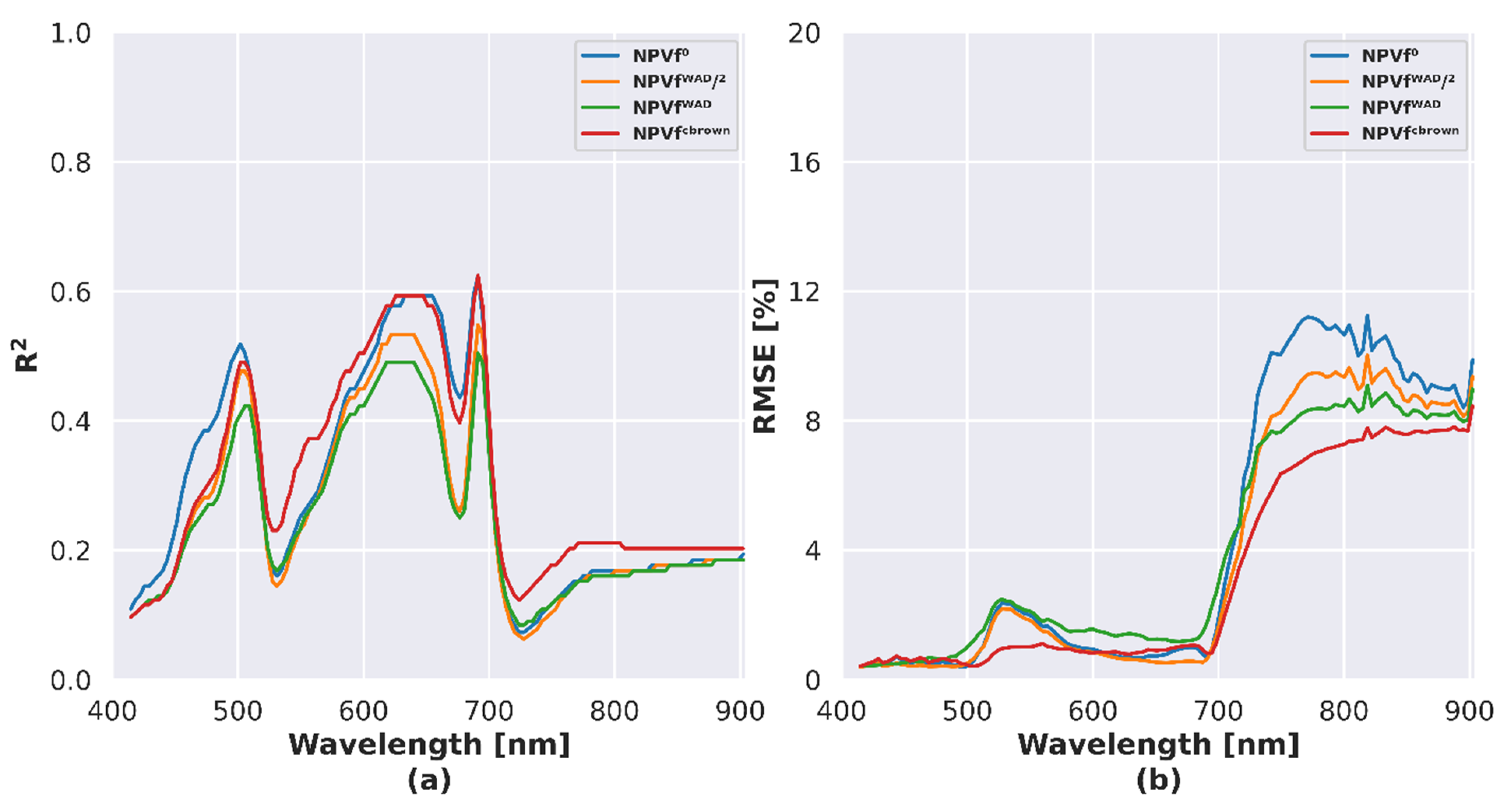
4.4. Influence of NPVf on Simulated Reflectance
4.5. Influence of LOP Variability on Simulated Reflectance
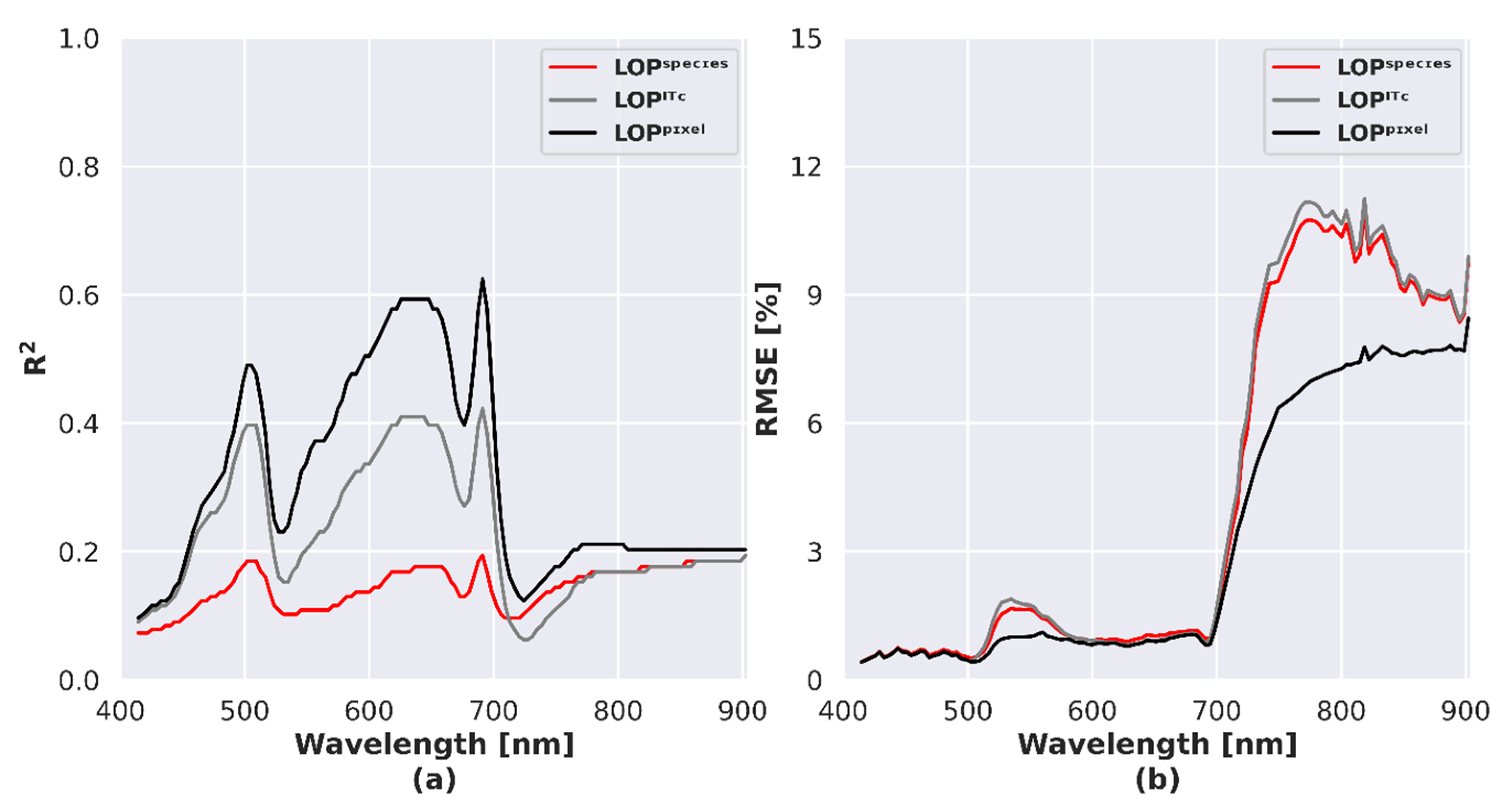
4.6. Analysis of Spectral Dissimilarity
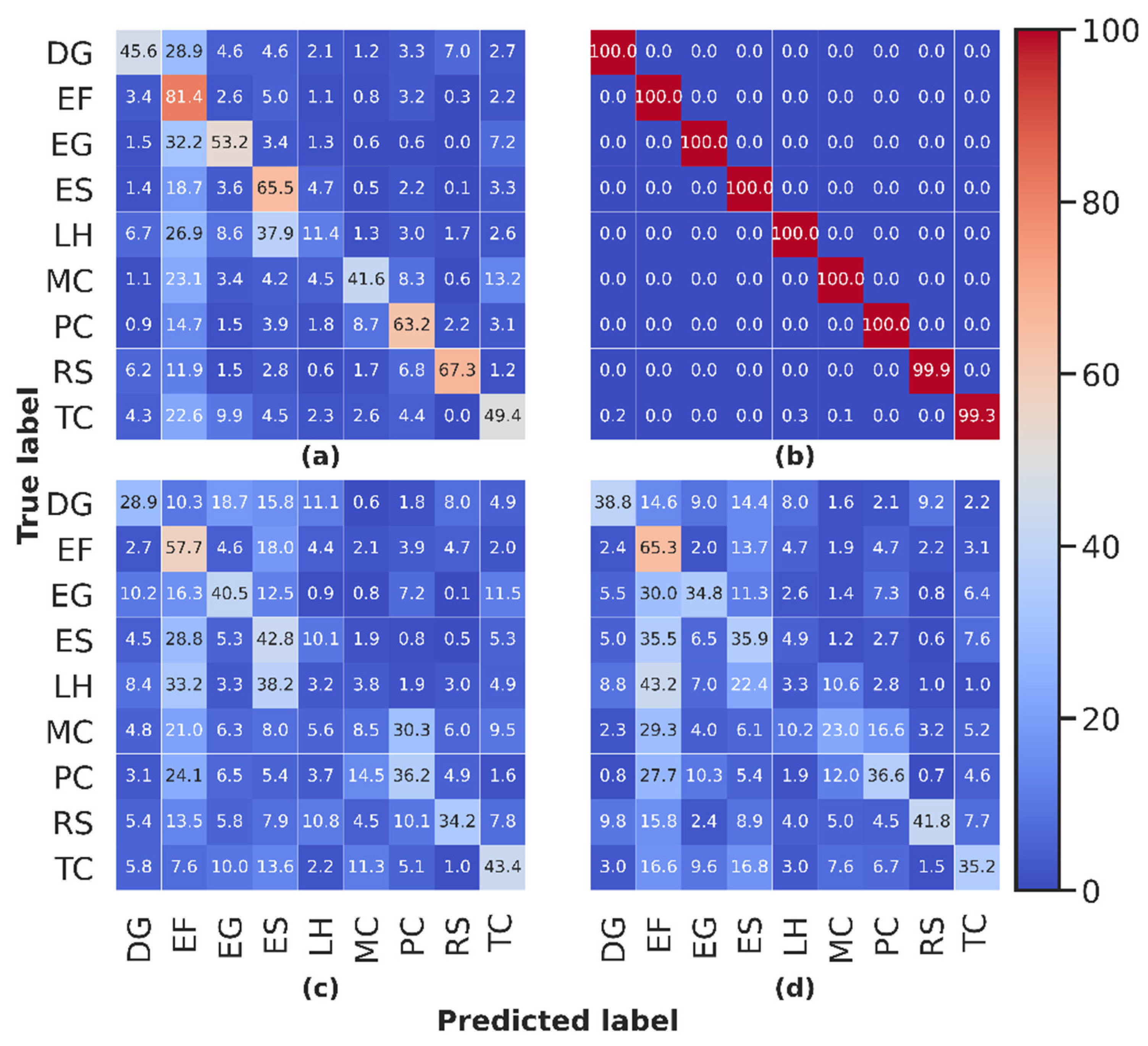
4.7. Assessing the Potential of Species Discrimination
4.8. Visual Comparison
5. Discussion
5.1. Three-Dimensional (3D) Forest Reconstruction
5.2. Influence of NPVf on Leaf Chemistry Estimate
5.3. Influence of NPVf on Simulation of Canopy Reflectance
5.4. Influence of LOP Variability on Species Separability and Discrimination
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Mulatu, K.A.; Mora, B.; Kooistra, L.; Herold, M. Biodiversity Monitoring in Changing Tropical Forests: A Review of Approaches and New Opportunities. Remote Sens. 2017, 9, 1059. [Google Scholar] [CrossRef]
- Hill, S.L.L.; Arnell, A.; Maney, C.; Butchart, S.H.M.; Hilton-Taylor, C.; Ciciarelli, C.; Davis, C.; Dinerstein, E.; Purvis, A.; Burgess, N.D. Measuring Forest Biodiversity Status and Changes Globally. Front. Glob. Chang. 2019, 2, 25. [Google Scholar] [CrossRef]
- Cusack, D.F.; Karpman, J.; Ashdown, D.; Cao, Q.; Ciochina, M.; Halterman, S.; Lydon, S.; Neupane, A. Global Change Effects on Humid Tropical Forests: Evidence for Biogeochemical and Biodiversity Shifts at an Ecosystem Scale. Rev. Geophys. 2016, 54, 523–610. [Google Scholar] [CrossRef]
- García-Montiel, D.C.; Scatena, F.N. The Effect of Human Activity on the Structure and Composition of a Tropical Forest in Puerto Rico. For. Ecol. Manag. 1994, 63, 57–78. [Google Scholar] [CrossRef]
- Miles, L.; Grainger, A.; Phillips, O. The Impact of Global Climate Change on Tropical Forest Biodiversity in Amazonia. Glob. Ecol. Biogeogr. 2004, 13, 553–565. [Google Scholar] [CrossRef]
- Wright, S.J.; Muller-Landau, H.C. The Future of Tropical Forest Species1. Biotropica 2006, 38, 287–301. [Google Scholar] [CrossRef]
- Lade, S.J.; Norberg, J.; Anderies, J.M.; Beer, C.; Cornell, S.E.; Donges, J.F.; Fetzer, I.; Gasser, T.; Richardson, K.; Rockström, J.; et al. Potential Feedbacks between Loss of Biosphere Integrity and Climate Change. Glob. Sustain. 2019, 2. [Google Scholar] [CrossRef]
- Bengtsson, J. Which Species? What Kind of Diversity? Which Ecosystem Function? Some Problems in Studies of Relations between Biodiversity and Ecosystem Function. Appl. Soil Ecol. 1998, 10, 191–199. [Google Scholar] [CrossRef]
- Clarke, D.A.; York, P.H.; Rasheed, M.A.; Northfield, T.D. Does Biodiversity–Ecosystem Function Literature Neglect Tropical Ecosystems? Trends Ecol. Evol. 2017, 32, 320–323. [Google Scholar] [CrossRef]
- Duffy, J.E. Biodiversity and Ecosystem Function: The Consumer Connection. Oikos 2002, 99, 201–219. [Google Scholar] [CrossRef]
- Hiddink, J.G.; Davies, T.W.; Perkins, M.; Machairopoulou, M.; Neill, S.P. Context Dependency of Relationships between Biodiversity and Ecosystem Functioning Is Different for Multiple Ecosystem Functions. Oikos 2009, 118, 1892–1900. [Google Scholar] [CrossRef]
- Brockerhoff, E.G.; Barbaro, L.; Castagneyrol, B.; Forrester, D.I.; Gardiner, B.; González-Olabarria, J.R.; Lyver, P.O.; Meurisse, N.; Oxbrough, A.; Taki, H.; et al. Forest Biodiversity, Ecosystem Functioning and the Provision of Ecosystem Services. Biodivers Conserv 2017, 26, 3005–3035. [Google Scholar] [CrossRef]
- Ferraz, S.F.B.; Ferraz, K.M.P.M.B.; Cassiano, C.C.; Brancalion, P.H.S.; da Luz, D.T.A.; Azevedo, T.N.; Tambosi, L.R.; Metzger, J.P. How Good Are Tropical Forest Patches for Ecosystem Services Provisioning? Landsc. Ecol 2014, 29, 187–200. [Google Scholar] [CrossRef]
- Pereira, H.M.; Ferrier, S.; Walters, M.; Geller, G.N.; Jongman, R.H.G.; Scholes, R.J.; Bruford, M.W.; Brummitt, N.; Butchart, S.H.M.; Cardoso, A.C.; et al. Essential Biodiversity Variables. Science 2013, 339, 277–278. [Google Scholar] [CrossRef] [PubMed]
- Proença, V.; Martin, L.J.; Pereira, H.M.; Fernandez, M.; McRae, L.; Belnap, J.; Böhm, M.; Brummitt, N.; García-Moreno, J.; Gregory, R.D.; et al. Global Biodiversity Monitoring: From Data Sources to Essential Biodiversity Variables. Biol. Conserv. 2017, 213, 256–263. [Google Scholar] [CrossRef]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote Sensing for Biodiversity Science and Conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Pettorelli, N.; Wegmann, M.; Skidmore, A.; Mücher, S.; Dawson, T.P.; Fernandez, M.; Lucas, R.; Schaepman, M.E.; Wang, T.; O’Connor, B.; et al. Framing the Concept of Satellite Remote Sensing Essential Biodiversity Variables: Challenges and Future Directions. Remote Sens. Ecol. Conserv. 2016, 2, 122–131. [Google Scholar] [CrossRef]
- Rocchini, D.; Hernández-Stefanoni, J.L.; He, K.S. Advancing Species Diversity Estimate by Remotely Sensed Proxies: A Conceptual Review. Ecol. Inform. 2015, 25, 22–28. [Google Scholar] [CrossRef]
- Seeley, M.; Asner, G.P. Imaging Spectroscopy for Conservation Applications. Remote Sens. 2021, 13, 292. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R.; Mücher, C.A.; O’Connor, B.; Paganini, M.; Pereira, H.M.; et al. Environmental Science: Agree on Biodiversity Metrics to Track from Space. Nat. News 2015, 523, 403. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A. Remote Sensing of Terrestrial Plant Biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
- Asner, G.P. Hyperspectral Remote Sensing of Canopy Chemistry, Physiology, and Biodiversity in Tropical Rainforests. Hyperspectral Remote Sens. Trop. Sub Trop. For. 2008, 261–296. [Google Scholar]
- Baldeck, C.A.; Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E.; Kellner, J.R.; Wright, S.J. Operational Tree Species Mapping in a Diverse Tropical Forest with Airborne Imaging Spectroscopy. PLoS ONE 2015, 10, e0118403. [Google Scholar] [CrossRef] [PubMed]
- Somers, B.; Asner, G.P. Multi-Temporal Hyperspectral Mixture Analysis and Feature Selection for Invasive Species Mapping in Rainforests. Remote Sens. Environ. 2013, 136, 14–27. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gamon, J.A. Remote Sensing of Plant Functional Types. New Phytol. 2010, 186, 795–816. [Google Scholar] [CrossRef] [PubMed]
- Durán, S.M.; Martin, R.E.; Díaz, S.; Maitner, B.S.; Malhi, Y.; Salinas, N.; Shenkin, A.; Silman, M.R.; Wieczynski, D.J.; Asner, G.P.; et al. Informing Trait-Based Ecology by Assessing Remotely Sensed Functional Diversity across a Broad Tropical Temperature Gradient. Sci. Adv. 2019, 5, eaaw8114. [Google Scholar] [CrossRef] [PubMed]
- Schneider, F.D.; Morsdorf, F.; Schmid, B.; Petchey, O.L.; Hueni, A.; Schimel, D.S.; Schaepman, M.E. Mapping Functional Diversity from Remotely Sensed Morphological and Physiological Forest Traits. Nat. Commun. 2017, 8, 1441. [Google Scholar] [CrossRef]
- Zheng, Z.; Zeng, Y.; Schneider, F.D.; Zhao, Y.; Zhao, D.; Schmid, B.; Schaepman, M.E.; Morsdorf, F. Mapping Functional Diversity Using Individual Tree-Based Morphological and Physiological Traits in a Subtropical Forest. Remote Sens. Environ. 2021, 252, 112170. [Google Scholar] [CrossRef]
- Palmer, M.W.; Earls, P.G.; Hoagland, B.W.; White, P.S.; Wohlgemuth, T. Quantitative Tools for Perfecting Species Lists. Environmetrics 2002, 13, 121–137. [Google Scholar] [CrossRef]
- Rocchini, D.; Chiarucci, A.; Loiselle, S.A. Testing the Spectral Variation Hypothesis by Using Satellite Multispectral Images. Acta Oecologica 2004, 26, 117–120. [Google Scholar] [CrossRef]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M.; et al. Remotely Sensed Spectral Heterogeneity as a Proxy of Species Diversity: Recent Advances and Open Challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Rocchini, D.; Luque, S.; Pettorelli, N.; Bastin, L.; Doktor, D.; Faedi, N.; Feilhauer, H.; Féret, J.-B.; Foody, G.M.; Gavish, Y.; et al. Measuring β-Diversity by Remote Sensing: A Challenge for Biodiversity Monitoring. Methods Ecol. Evol. 2018, 9, 1787–1798. [Google Scholar] [CrossRef]
- Féret, J.-B.; Asner, G.P. Mapping Tropical Forest Canopy Diversity Using High-Fidelity Imaging Spectroscopy. Ecol. Appl. 2014, 24, 1289–1296. [Google Scholar] [CrossRef]
- Laurin, G.V.; Chan, J.C.-W.; Chen, Q.; Lindsell, J.A.; Coomes, D.A.; Guerriero, L.; Frate, F.D.; Miglietta, F.; Valentini, R. Biodiversity Mapping in a Tropical West African Forest with Airborne Hyperspectral Data. PLoS ONE 2014, 9, e97910. [Google Scholar] [CrossRef]
- Asner, G.P. Biophysical and Biochemical Sources of Variability in Canopy Reflectance. Remote Sens. Environ. 1998, 64, 234–253. [Google Scholar] [CrossRef]
- Ollinger, S.V. Sources of Variability in Canopy Reflectance and the Convergent Properties of Plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance Quantities in Optical Remote Sensing—Definitions and Case Studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Suits, G.H. The Calculation of the Directional Reflectance of a Vegetative Canopy. Remote Sens. Environ. 1971, 2, 117–125. [Google Scholar] [CrossRef]
- Li, C.; Song, J.; Wang, J. Modifying Geometric-Optical Bidirectional Reflectance Model for Direct Inversion of Forest Canopy Leaf Area Index. Remote Sens. 2015, 7, 11083–11104. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-Optical Bidirectional Reflectance Modeling of the Discrete Crown Vegetation Canopy: Effect of Crown Shape and Mutual Shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Olpenda, A.S.; Stereńczak, K.; Będkowski, K. Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities. Remote Sens. 2018, 10, 694. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL Models: A Review of Use for Vegetation Characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Schlerf, M.; Maire, G.L. Suitability and Adaptation of PROSAIL Radiative Transfer Model for Hyperspectral Grassland Studies. Remote Sens. Lett. 2013, 4, 55–64. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL Model Capabilities for Future Hyperspectral Model Environments: A Review Study. Remote Sens. 2018, 10, 85. [Google Scholar] [CrossRef]
- Govaerts, Y.M.; Verstraete, M.M. Raytran: A Monte Carlo Ray-Tracing Model to Compute Light Scattering in Three-Dimensional Heterogeneous Media. IEEE Trans. Geosci. Remote Sens. 1998, 36, 493–505. [Google Scholar] [CrossRef]
- Chen, J.M.; Li, X.; Nilson, T.; Strahler, A. Recent Advances in Geometrical Optical Modelling and Its Applications. Remote Sens. Rev. 2000, 18, 227–262. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Tao, S.; Su, Y. VBRT: A Novel Voxel-Based Radiative Transfer Model for Heterogeneous Three-Dimensional Forest Scenes. Remote Sens. Environ. 2018, 206, 318–335. [Google Scholar] [CrossRef]
- Schneider, F.D.; Leiterer, R.; Morsdorf, F.; Gastellu-Etchegorry, J.-P.; Lauret, N.; Pfeifer, N.; Schaepman, M.E. Simulating Imaging Spectrometer Data: 3D Forest Modeling Based on LiDAR and in Situ Data. Remote Sens. Environ. 2014, 152, 235–250. [Google Scholar] [CrossRef]
- Yan, Y.; Tan, Z.; Su, N. A Data Augmentation Strategy Based on Simulated Samples for Ship Detection in RGB Remote Sensing Images. ISPRS Int. J. Geo Inf. 2019, 8, 276. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling Radiative Transfer in Heterogeneous 3-D Vegetation Canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.-B.; Lopes, M.; Guilleux, J.; Dedieu, G.; et al. Discrete Anisotropic Radiative Transfer (DART 5) for Modeling Airborne and Satellite Spectroradiometer and LIDAR Acquisitions of Natural and Urban Landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Mattar, C.; Gastellu-Etchegorry, J.P.; Jiménez-Muñoz, J.C.; Grau, E. Evaluation of the DART 3D Model in the Thermal Domain Using Satellite/Airborne Imagery and Ground-Based Measurements. Int. J. Remote Sens. 2011, 32, 7453–7477. [Google Scholar] [CrossRef]
- Malenovský, Z.; Martin, E.; Homolová, L.; Gastellu-Etchegorry, J.-P.; Zurita-Milla, R.; Schaepman, M.E.; Pokorný, R.; Clevers, J.G.P.W.; Cudlín, P. Influence of Woody Elements of a Norway Spruce Canopy on Nadir Reflectance Simulated by the DART Model at Very High Spatial Resolution. Remote Sens. Environ. 2008, 112, 1–18. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Féret, J.-B.; Grau, E.; Gastellu-Etchegorry, J.-P.; Shimabukuro, Y.E.; de Souza Filhod, S.F. Retrieving Structural and Chemical Properties of Individual Tree Crowns in a Highly Diverse Tropical Forest with 3D Radiative Transfer Modeling and Imaging Spectroscopy. Remote Sens. Environ. 2018, 211, 276–291. [Google Scholar] [CrossRef]
- Zhang, J.; Rivard, B.; Sánchez-Azofeifa, A.; Castro-Esau, K. Intra- and Inter-Class Spectral Variability of Tropical Tree Species at La Selva, Costa Rica: Implications for Species Identification Using HYDICE Imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Morton, D.C.; Rubio, J.; Cook, B.D.; Gastellu-Etchegorry, J.-P.; Longo, M.; Choi, H.; Hunter, M.; Keller, M. Amazon Forest Structure Generates Diurnal and Seasonal Variability in Light Utilization. Biogeosciences 2016, 13, 2195–2206. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R. Atmospheric Correction of Imaging Spectroscopy Data Using Shadow-Based Quantification of Aerosol Scattering Effects. Earsel Eproceedings 2017, 16, 21–28. [Google Scholar] [CrossRef]
- LASer (LAS) File Format Exchange Activities–ASPRS. Available online: https://www.asprs.org/divisions-committees/lidar-division/laser-las-file-format-exchange-activities (accessed on 20 May 2021).
- Gourlet-Fleury, S.; Guehl, J.-M.J.-M.; Laroussinie, O. Ecology and Management of a Neotropical Rainforest. Lessons Drawn from Paracou, a Long-Term Experimental Research Site in French Guiana; Elsevier: New York, NY, USA, 2004. [Google Scholar]
- Aubry-Kientz, M.; Dutrieux, R.; Ferraz, A.; Saatchi, S.; Hamraz, H.; Williams, J.; Coomes, D.; Piboule, A.; Vincent, G. A Comparative Assessment of the Performance of Individual Tree Crowns Delineation Algorithms from ALS Data in Tropical Forests. Remote Sens. 2019, 11, 1086. [Google Scholar] [CrossRef]
- Laybros, A.; Schläpfer, D.; Féret, J.-B.; Descroix, L.; Bedeau, C.; Lefevre, M.-J.; Vincent, G. Across Date Species Detection Using Airborne Imaging Spectroscopy. Remote Sens. 2019, 11, 789. [Google Scholar] [CrossRef]
- Laybros, A.; Aubry-Kientz, M.; Féret, J.-B.; Bedeau, C.; Brunaux, O.; Derroire, G.; Vincent, G. Quantitative Airborne Inventories in Dense Tropical Forest Using Imaging Spectroscopy. Remote Sens. 2020, 12, 1577. [Google Scholar] [CrossRef]
- Féret, J.-B.; Gitelson, A.A.; Noble, S.D.; Jacquemoud, S. PROSPECT-D: Towards Modeling Leaf Optical Properties through a Complete Lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A Model of Leaf Optical Properties Spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Allen, W.; Gausman, H.; Richardson, A.J.; Thomas, J. Interaction of Isotropic Light with a Compact Plant Leaf. Josa 1969. [Google Scholar] [CrossRef]
- Vincent, G.; Pimont, F.; Verley, P. A note on PAD/LAD estimators implemented in AMAPVox 1.7. 2021. Available online: https://amap-dev.cirad.fr/projects/amapvox (accessed on 26 May 2021).
- Liu, J.; Skidmore, A.K.; Wang, T.; Zhu, X.; Premier, J.; Heurich, M.; Beudert, B.; Jones, S. Variation of Leaf Angle Distribution Quantified by Terrestrial LiDAR in Natural European Beech Forest. ISPRS J. Photogramm. Remote Sens. 2019, 148, 208–220. [Google Scholar] [CrossRef]
- Pimmasarn, S.; Tripathi, N.K.; Ninsawat, S.; Sasaki, N. Applying LiDAR to Quantify the Plant Area Index Along a Successional Gradient in a Tropical Forest of Thailand. Forests 2020, 11, 520. [Google Scholar] [CrossRef]
- Schneider, F.D.; Kükenbrink, D.; Schaepman, M.E.; Schimel, D.S.; Morsdorf, F. Quantifying 3D Structure and Occlusion in Dense Tropical and Temperate Forests Using Close-Range LiDAR. Agric. For. Meteorol. 2019, 268, 249–257. [Google Scholar] [CrossRef]
- Tang, H.; Dubayah, R.; Swatantran, A.; Hofton, M.; Sheldon, S.; Clark, D.B.; Blair, B. Retrieval of Vertical LAI Profiles over Tropical Rain Forests Using Waveform Lidar at La Selva, Costa Rica. Remote Sens. Environ. 2012, 124, 242–250. [Google Scholar] [CrossRef]
- Vincent, G.; Antin, C.; Laurans, M.; Heurtebize, J.; Durrieu, S.; Lavalley, C.; Dauzat, J. Mapping Plant Area Index of Tropical Evergreen Forest by Airborne Laser Scanning. A Cross-Validation Study Using LAI2200 Optical Sensor. Remote Sens. Environ. 2017, 198, 254–266. [Google Scholar] [CrossRef]
- Grau, E.; Durrieu, S.; Fournier, R.; Gastellu-Etchegorry, J.-P.; Yin, T. Estimation of 3D Vegetation Density with Terrestrial Laser Scanning Data Using Voxels. A Sensitivity Analysis of Influencing Parameters. Remote Sens. Environ. 2017, 191, 373–388. [Google Scholar] [CrossRef]
- Bréda, N.J.J. Ground-based Measurements of Leaf Area Index: A Review of Methods, Instruments and Current Controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.M.; Black, T.A. Defining Leaf Area Index for Non-Flat Leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Siitonen, J. Forest Management, Coarse Woody Debris and Saproxylic Organisms: Fennoscandian Boreal Forests as an Example. Ecol. Bull. 2001, 49, 11–41. [Google Scholar]
- Zhu, X.; Skidmore, A.K.; Wang, T.; Liu, J.; Darvishzadeh, R.; Shi, Y.; Premier, J.; Heurich, M. Improving Leaf Area Index (LAI) Estimation by Correcting for Clumping and Woody Effects Using Terrestrial Laser Scanning. Agric. For. Meteorol. 2018, 263, 276–286. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and Bias in Active and Passive Ground-Based Measurements of Effective Plant, Wood and Leaf Area Index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Woodgate, W.; Armston, J.D.; Disney, M.; Jones, S.D.; Suarez, L.; Hill, M.J.; Wilkes, P.; Soto-Berelov, M. Quantifying the Impact of Woody Material on Leaf Area Index Estimation from Hemispherical Photography Using 3D Canopy Simulations. Agric. For. Meteorol. 2016, 226–227, 1–12. [Google Scholar] [CrossRef]
- Calders, K.; Origo, N.; Burt, A.; Disney, M.; Nightingale, J.; Raumonen, P.; Åkerblom, M.; Malhi, Y.; Lewis, P. Realistic Forest Stand Reconstruction from Terrestrial LiDAR for Radiative Transfer Modelling. Remote Sens. 2018, 10, 933. [Google Scholar] [CrossRef]
- Ustin, S.L.; Jacquemoud, S. How the Optical Properties of Leaves Modify the Absorption and Scattering of Energy and Enhance Leaf Functionality. In Remote Sensing of Plant Biodiversity; Cavender-Bares, J., Gamon, J.A., Townsend, P.A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 349–384. ISBN 978-3-030-33157-3. [Google Scholar]
- Verrelst, J.; Malenovský, Z.; Van der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2019, 40, 589–629. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral Indices for Estimating Photosynthetic Pigment Concentrations: A Test Using Senescent Tree Leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Gitelson, A.; Solovchenko, A. Non-Invasive Quantification of Foliar Pigments: Possibilities and Limitations of Reflectance- and Absorbance-Based Approaches. J. Photochem. Photobiol. B Biol. 2018, 178, 537–544. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Chivkunova, O.B.; Merzlyak, M.N. Nondestructive Estimation of Anthocyanins and Chlorophylls in Anthocyanic Leaves. Am. J. Bot. 2009, 96, 1861–1868. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-Band Model for Noninvasive Estimation of Chlorophyll, Carotenoids, and Anthocyanin Contents in Higher Plant Leaves. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Viña, A. Evaluating Vegetation Indices for Assessing Productivity along a Tropical Rain Forest Chronosequence in Western Amazonia. Isr. J. Plant Sci. 2012, 60, 123–133. [Google Scholar] [CrossRef]
- Féret, J.-B.; François, C.; Gitelson, A.; Asner, G.P.; Barry, K.M.; Panigada, C.; Richardson, A.D.; Jacquemoud, S. Optimizing Spectral Indices and Chemometric Analysis of Leaf Chemical Properties Using Radiative Transfer Modeling. Remote Sens. Environ. 2011, 115, 2742–2750. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Zortea, M.; Zanotta, D.C.; Shimabukuro, Y.E.; de Souza Filho, C.R. Mapping Tree Species in Tropical Seasonal Semi-Deciduous Forests with Hyperspectral and Multispectral Data. Remote Sens. Environ. 2016, 179, 66–78. [Google Scholar] [CrossRef]
- Price, J.C. How Unique Are Spectral Signatures? Remote Sens. Environ. 1994, 49, 181–186. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Dai, J.; Ruan, H.; She, G. Tree Species Classification in Subtropical Forests Using Small-Footprint Full-Waveform LiDAR Data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 39–51. [Google Scholar] [CrossRef]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral Discrimination of Tropical Rain Forest Tree Species at Leaf to Crown Scales. Remote Sens. Environ. 2005, 96, 375–398. [Google Scholar] [CrossRef]
- Féret, J.-B.; Asner, G.P. Spectroscopic Classification of Tropical Forest Species Using Radiative Transfer Modeling. Remote Sens. Environ. 2011, 115, 2415–2422. [Google Scholar] [CrossRef]
- Féret, J.-B.; Asner, G.P. Semi-Supervised Methods to Identify Individual Crowns of Lowland Tropical Canopy Species Using Imaging Spectroscopy and LiDAR. Remote Sens. 2012, 4, 2457–2476. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Malenovský, Z.; Clevers, J.G.P.W. Effects of Woody Elements on Simulated Canopy Reflectance: Implications for Forest Chlorophyll Content Retrieval. Remote Sens. Environ. 2010, 114, 647–656. [Google Scholar] [CrossRef]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and Indirect Estimation of Leaf Area Index, FAPAR, and Net Primary Production of Terrestrial Ecosystems. Remote Sens. Environ. 1999, 70, 29–51. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H. Estimation of LAI with the LiDAR Technology: A Review. Remote Sens. 2020, 12, 3457. [Google Scholar] [CrossRef]
- Qu, Y.; Shaker, A.; Silva, C.A.; Klauberg, C.; Pinagé, E.R. Remote Sensing of Leaf Area Index from LiDAR Height Percentile Metrics and Comparison with MODIS Product in a Selectively Logged Tropical Forest Area in Eastern Amazonia. Remote Sens. 2018, 10, 970. [Google Scholar] [CrossRef]
- Arellano, P.; Tansey, K.; Balzter, H.; Boyd, D.S. Field Spectroscopy and Radiative Transfer Modelling to Assess Impacts of Petroleum Pollution on Biophysical and Biochemical Parameters of the Amazon Rainforest. Env. Earth Sci 2017, 76, 217. [Google Scholar] [CrossRef]
- Blackburn, G.A. Hyperspectral Remote Sensing of Plant Pigments. J Exp Bot 2007, 58, 855–867. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying Forest Canopy Traits: Imaging Spectroscopy versus Field Survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
- Asner, G.P.; Martin, R.E. Spectral and Chemical Analysis of Tropical Forests: Scaling from Leaf to Canopy Levels. Remote Sens. Environ. 2008, 112, 3958–3970. [Google Scholar] [CrossRef]
- Smith, M.; Martin, M.E.; Plourde, L.; Ollinger, S.V. Analysis of Hyperspectral Data for Estimation of Temperate Forest Canopy Nitrogen Concentration: Comparison between an Airborne (AVIRIS) and a Spaceborne (Hyperion) Sensor. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1332–1337. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between Leaf Pigment Content and Spectral Reflectance across a Wide Range of Species, Leaf Structures and Developmental Stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sens. 2019, 11, 1150. [Google Scholar] [CrossRef]
- Hackenberg, J.; Morhart, C.; Sheppard, J.; Spiecker, H.; Disney, M. Highly Accurate Tree Models Derived from Terrestrial Laser Scan Data: A Method Description. Forests 2014, 5, 1069–1105. [Google Scholar] [CrossRef]
- Raumonen, P.; Kaasalainen, M.; Åkerblom, M.; Kaasalainen, S.; Kaartinen, H.; Vastaranta, M.; Holopainen, M.; Disney, M.; Lewis, P. Fast Automatic Precision Tree Models from Terrestrial Laser Scanner Data. Remote Sens. 2013, 5, 491–520. [Google Scholar] [CrossRef]
- Melendo-Vega, J.R.; Martín, M.P.; Pacheco-Labrador, J.; González-Cascón, R.; Moreno, G.; Pérez, F.; Migliavacca, M.; García, M.; North, P.; Riaño, D. Improving the Performance of 3-D Radiative Transfer Model FLIGHT to Simulate Optical Properties of a Tree-Grass Ecosystem. Remote Sens. 2018, 10, 2061. [Google Scholar] [CrossRef]
- Réjou-Méchain, M.; Barbier, N.; Couteron, P.; Ploton, P.; Vincent, G.; Herold, M.; Mermoz, S.; Saatchi, S.; Chave, J.; de Boissieu, F.; et al. Upscaling Forest Biomass from Field to Satellite Measurements: Sources of Errors and Ways to Reduce Them. Surv. Geophys. 2019, 40, 881–911. [Google Scholar] [CrossRef]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An Introduction to the NASA Hyperspectral InfraRed Imager (HyspIRI) Mission and Preparatory Activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Michel, S.; Gamet, P.; Lefevre-Fonollosa, M. HYPXIM—A Hyperspectral Satellite Defined for Science, Security and Defence Users. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Nieke, J.; Rast, M. Towards the Copernicus Hyperspectral Imaging Mission For The Environment (CHIME). In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 157–159. [Google Scholar]




| Species | Number of ITCs | Number of Pixels | Mean Number of Pixels Per ITC |
|---|---|---|---|
| Site A | |||
| Bocoa prouacensis | 1 | 72 | 72 |
| Dicorynia guianensis | 1 | 53 | 53 |
| Eschweilera sagotiana | 5 | 286 | 57 |
| Licania alba | 1 | 83 | 83 |
| Licania heteromorpha | 2 | 44 | 22 |
| Pradosia cochlearia | 2 | 433 | 216 |
| Sextonia rubra | 2 | 223 | 111 |
| Vouacapoua americana | 6 | 387 | 64 |
| Total | 20 | 1581 | 85 |
| Site B | |||
| Dicorynia guianensis (DG) | 11 | 1147 | 104 |
| Eperua falcata (EF) | 45 | 3102 | 68 |
| Eperua grandiflora (EG) | 8 | 694 | 86 |
| Eschweilera sagotiana (ES) | 30 | 1270 | 42 |
| Licania heteromorpha (LH) | 8 | 251 | 31 |
| Moronobea coccinea (MC) | 12 | 609 | 50 |
| Pradosia cochlearia (PC) | 14 | 1538 | 109 |
| Recordoxylon speciosum (RS) | 14 | 944 | 67 |
| Tapura capitulifera (TC) | 20 | 707 | 35 |
| Total | 162 | 10262 | 66 |
| Pearson’s r | RMSE [°] | ||||||
|---|---|---|---|---|---|---|---|
| LOP Scenario | LOPspecies | LOPITC | LOPpixel | LOPspecies | LOPITC | LOPpixel | |
| Spectral Dissimilarity | |||||||
| Within Crowns | 0.10 | 0.34 | 0.88 | 0.84 | 0.80 | 0.30 | |
| Within Species | 0.28 | 0.91 | 0.91 | 1.84 | 0.69 | 0.54 | |
| Among Species | 0.48 | 0.93 | 0.92 | 1.75 | 0.81 | 0.67 | |
| Confusion Matrix Elements | LOPspecies | LOPITC | LOPpixel |
|---|---|---|---|
| Correct classification | 0.05 | 0.86 | 0.92 |
| Misclassification | −0.04 | 0.71 | 0.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ebengo, D.M.; de Boissieu, F.; Vincent, G.; Weber, C.; Féret, J.-B. Simulating Imaging Spectroscopy in Tropical Forest with 3D Radiative Transfer Modeling. Remote Sens. 2021, 13, 2120. https://doi.org/10.3390/rs13112120
Ebengo DM, de Boissieu F, Vincent G, Weber C, Féret J-B. Simulating Imaging Spectroscopy in Tropical Forest with 3D Radiative Transfer Modeling. Remote Sensing. 2021; 13(11):2120. https://doi.org/10.3390/rs13112120
Chicago/Turabian StyleEbengo, Dav M., Florian de Boissieu, Grégoire Vincent, Christiane Weber, and Jean-Baptiste Féret. 2021. "Simulating Imaging Spectroscopy in Tropical Forest with 3D Radiative Transfer Modeling" Remote Sensing 13, no. 11: 2120. https://doi.org/10.3390/rs13112120
APA StyleEbengo, D. M., de Boissieu, F., Vincent, G., Weber, C., & Féret, J.-B. (2021). Simulating Imaging Spectroscopy in Tropical Forest with 3D Radiative Transfer Modeling. Remote Sensing, 13(11), 2120. https://doi.org/10.3390/rs13112120







